Dystrophin's central domain forms a complex filament that becomes disorganized by in-frame deletions

Abstract

Dystrophin, encoded by the DMD gene, is critical for maintaining plasma membrane integrity during muscle contraction events. Mutations in the DMD gene disrupting the reading frame prevent dystrophin production and result in severe Duchenne muscular dystrophy (DMD); in-frame internal deletions allow production of partly functional internally deleted dystrophin and result in less severe Becker muscular dystrophy (BMD). Many known BMD deletions occur in dystrophin's central domain, generally considered to be a monotonous rod-shaped domain based on the knowledge of spectrin family proteins. However, the effects caused by these deletions, ranging from asymptomatic to severe BMD, argue against the central domain serving only as a featureless scaffold. We undertook structural studies combining small-angle X-ray scattering and molecular modeling in an effort to uncover the structure of the central domain, as dystrophin has been refractory to characterization. We show that this domain appears to be a tortuous and complex filament that is profoundly disorganized by the most severe BMD deletion (loss of exons 45–47). Despite the preservation of large parts of the binding site for neuronal nitric oxide synthase (nNOS) in this deletion, computational approaches failed to recreate the association of dystrophin with nNOS. This observation is in agreement with a strong decrease of nNOS immunolocalization in muscle biopsies, a parameter related to the severity of BMD phenotypes. The structural description of the whole dystrophin central domain we present here is a first necessary step to improve the design of microdystrophin constructs toward the goal of a successful gene therapy for DMD.

Introduction

Mutations of the dystrophin DMD gene are the cause of two progressive muscle diseases of variable severity, Duchenne and Becker muscular dystrophy (DMD⁴ and BMD, respectively) (1). Dystrophin consists of an N-terminal actin-binding domain (ABD1), a central domain with 24 spectrin-like repeats interspaced by four hinge regions (2), and a cysteine-rich domain interacting with β-dystroglycan constituting the basis of the dystrophin–glycoprotein complex (3, 4) and a C-terminal domain. According to the Monaco rule (5), DMD is mostly a result of out-of-frame mutations in the DMD gene that result in a complete loss of the protein and a severe phenotype, whereas in-frame mutations of the DMD gene are mainly associated with BMD, where modified dystrophin is produced, resulting in less severe phenotypes. Most BMD mutations are in-frame genomic deletions that lead to proteins lacking part of the central domain repeats (6, 7) and constitute the pattern for therapeutic strategies aiming to transform DMD patients into BMD patients (8), either by exon skipping, by injection of microdystrophins (9–12) or by CRSIPR/cas9 gene editing (13, 14). Indeed, until now, the central domain has been considered a monotonous rod-shaped domain that could be internally truncated without dramatic functional effects (2, 15). However, the effects of in-frame mutations involving the central domain could be more severe than expected from the Monaco rule (16, 17). Therefore, it is crucial to understand the molecular causes of the severity of certain in-frame mutations to anticipate future therapies. This could be achieved by structural and functional studies of the dystrophin central domain and of its protein products related to in-frame mutations.

X-ray crystallization of dystrophin repeats has been largely unsuccessful, likely because of the monomeric state of dystrophin. Repeats of two other family members, spectrin and α-actinin, have been crystallized in their biologically relevant dimer form, and the only known crystal structure of a single R1 dystrophin repeat was obtained by chemically inducing dimerization (18), revealing a triple-helical coiled-coil structure typical of spectrin-like repeats. However, this structure does not allow for extrapolation of filament organization between successive repeats. Therefore, detailed structural data of larger domains are needed to acquire a precise understanding of dystrophin central domain organization and the effects of in-frame mutations on it. Because of its large size, the dystrophin central domain is not amenable to current solution structural methods. Therefore, we report three-dimensional structural models of eight fragments covering the native dystrophin central domain and of the in-frame deletion of exons 45 to 47, the most frequent and severe BMD deletion, obtained by an integrative approach using small-angle X-ray scattering (SAXS) and molecular modeling. The central domain of dystrophin is far from a rod-like monotonous protein but presents numerous kinks that confer to dystrophin a tortuous and complex topology. This feature may explain how dystrophin interacts specifically with numerous partners to form a large dystrophin-associated protein complex. The BMD in-frame mutation we studied profoundly modified the dystrophin filamentous structure. This BMD-induced structural disorganization of dystrophin is associated with an alteration of nNOS binding and with a strong decrease of nNOS labeling in patient muscle biopsies. These results show that the in-frame character of the deletion does not warrant a functional protein or a stable protein structure and that our structural characterization of the dystrophin central domain should lead to a better understanding of dystrophin-associated molecular assembly and help for the design of future DMD gene therapies.

Results

Native dystrophin fragments display SAXS profiles compatible with monomers in solution

We dissected dystrophin in eight native purified fragments of the central domain covering 23 of the 24 repeats (designated as R1 to R24) of the whole central domain (Fig. 1A and Table S1). Proteins were obtained as pure (Fig. 1B) and α-helix folded molecules, as observed previously (19, 20). The Guinier approximation analysis of the SAXS curves indicated that the fragments were nonaggregated (Fig. S1). However, because of the rod-shaped objects, the Guinier plots were obtained for narrow ranges of q values (qR_g < 0.8–1.0), especially for the longest dystrophin fragments such as R4–9, R11–15, R16–19 and R20–24, which cannot be considered globular, as shown previously (21). The radii of gyration R_g, obtained from the Guinier plots, range from 22.0 to 78.6 Å (Table S2). These R_g values as well as Porod volumes correlate linearly with the expected molecular weights (MWs) (Fig. S1). Moreover, the MWs obtained with the methods of Rambo and Tainer (22) and using Porod volumes are in good agreement with the MWs of monomers (Table S2). These data are supported by SEC-MALS experiments performed for the R1–3 and R11–15 fragments (Table S1). All of these data confirm that the proteins are monomeric in solution.

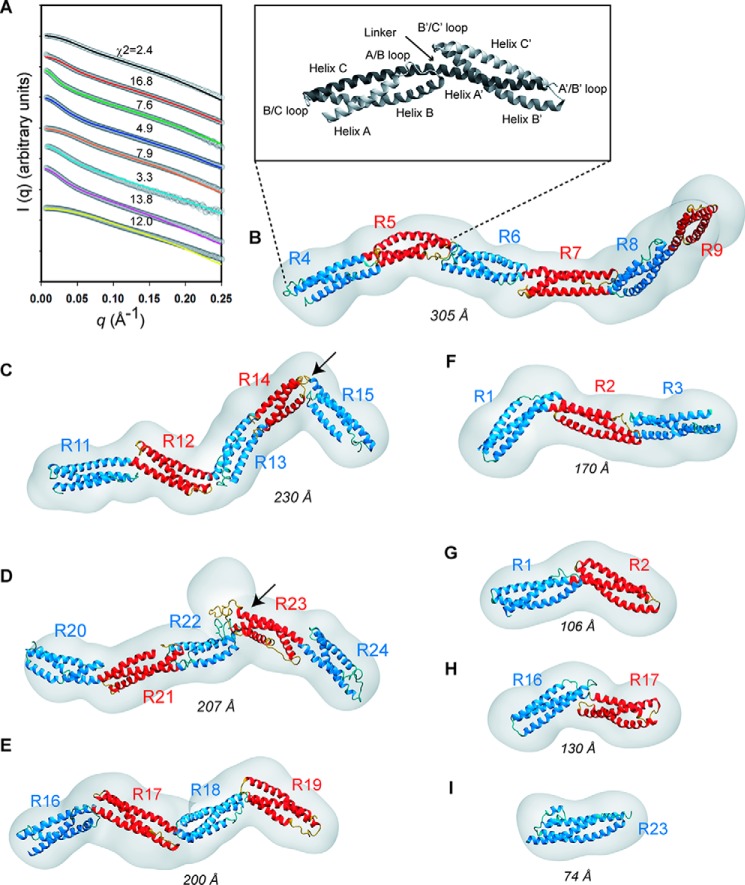
Figure 1.

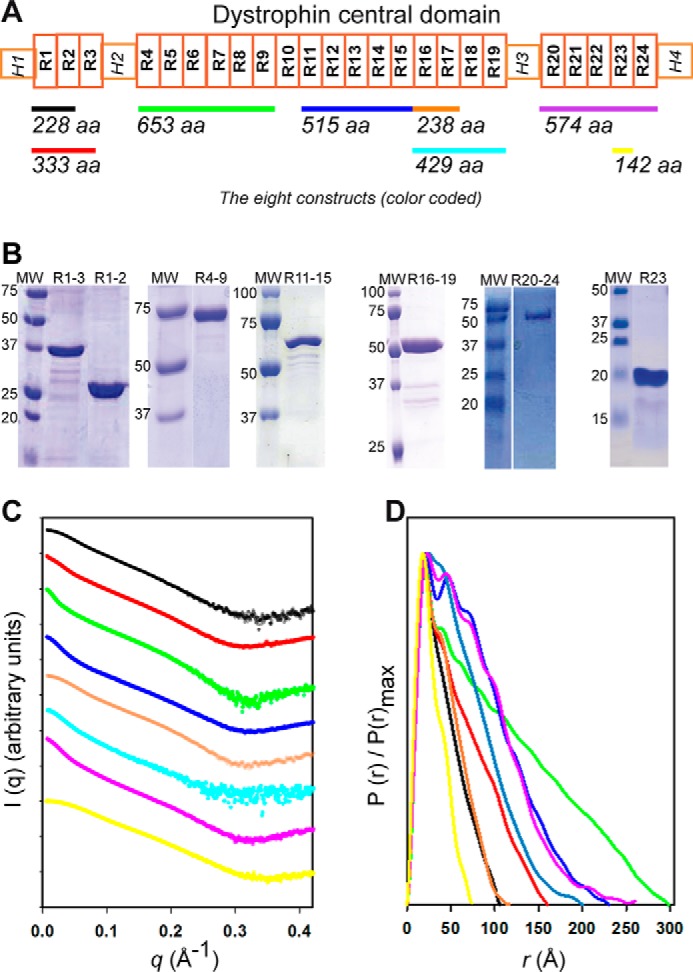
Experimental SAXS data obtained for the eight distinct native dystrophin fragments. A, schematic of the dystrophin central rod domain. It is comprised of 24 repeats (white boxes numbered R1 to R24) and four hinges (H1 to H4). The fragments studied here are highlighted by color-coded horizontal bars with indication of their length (number of amino acids). B, SDS-PAGE of the fragments (R16–17 is not shown) indicates that they are reasonably pure and that they migrate at the expected molecular weight. C, experimental SAXS scattering profiles. The intensity values of each curve are shifted by applying a simple scale factor along the logarithmic axis to achieve clearer visualization. From top to bottom: curves R1–2, R1–3, R4–9, R11–15, R16–17, R16–19, R20–24, and R23 are displayed in the colors used in A. D, the P(r) distribution functions obtained by GNOM analysis are shown for the eight fragments (color-coded as in A); the D_MAX of each fragment corresponds to its maximum dimension in the abscissa.

The eight native fragments showed smooth SAXS scattering profiles with few structural features typical of elongated molecules (Fig. 1C). The Kratky plots (Fig. S2A) present a bimodal shape with a well-defined maximum at a q value of ∼0.1 Å⁻¹ for all fragments and a linear increase at q > 0.3 Å⁻¹. However, the Porod–Debye plots show a large plateau assessing the compactness of the protein fragments, to the relative exception of the R16–19 fragment that could be slightly more dynamic given the calculated Porod–Debye exponent (Fig. S2B and Table S2). These features are consistent with dystrophin fragments being folded proteins and in agreement with CD observations (19). At the same time, these results are compatible with the putative inter-repeat region variability, as described previously (23). The maximum particle size (D_MAX) values obtained from the radial distribution function P(r) plots (Fig. 1D) increase with the molecular mass, confirming that the fragments are elongated in solution. All R_g values obtained from P(r) functions are in line with first Guinier approximations (Table S2). Finally, we should notice that the P(r) functions tail off smoothly, especially for the largest constructs. All P(r) functions present a common peak at a short distance of ∼20 Å, similar to the width of 21 Å reported for the crystallized dystrophin single repeat R1 (18), likely representing the width of the fragments. This feature is in agreement with the fact that all of the fragments were in a monomeric state in solution. In all cases, except for R23, the P(r) function plots presented additional peaks, notably one peak at around 40–50 Å that represents the distance correlation between adjacent domains (i.e. repeat length). In summary, the resulting data are characteristic of rather rigid but nonlinear macromolecules. These features could be attributed to specific kinks located at linker regions and delimiting the coiled-coil structured repeats, which would disrupt a purely rod-shaped filamentous molecule.

Three-dimensional analysis evidences a tortuous and complex structure of the dystrophin central domain

We used the SASFit program (24) to obtain values for radius, contour length, and Kuhn length according to three different models: long cylinder model, worm-like chain model, and Kholodenko worm model (Fig. S3). This analysis suggests that the Kholodenko model is the most appropriate to describe the physical characteristics of the dystrophin fragments in solution. The radius of about 10.8 Å obtained for all fragments is in accordance with the R1 monomer radius (18). A contour length higher than the D_MAX values calculated for the Kholodenko models indicates that the dystrophin fragments are shorter than a theoretical linear extended rod. This implies a dystrophin filament shape distinct from the rod-like structure assumed previously for the central domain of dystrophin (2, 15).

Twenty ab initio models, i.e. low-resolution molecular shapes, were simulated by the GASBOR method (25) for each protein fragment. All models were superimposed using DAMSUP and analyzed by DAMAVER programs (ATSAS suite (26). The molecular shapes converged remarkably for the R1–2, R1–3, R16–1,7 and R23 fragments, with normalized spatial discrepancy (NSD) values of 1.0 to 1.3 Å (Fig. S4). For the two fragments R11–15 and R20–24, higher NSD values were obtained. However, a look at the specific bulky volumes of the ab initio models indicates that DAMSUP placed some models head-to-tail regarding the rest of the collection, resulting in a less efficient superimposition. Remarkably, the longest fragment, R4–9, showed an NSD of less than 2.0 Å, evidencing a regular molecular shape. Consistent with the SASFit analysis, the GASBOR models presented sharp kinks, resulting in a highly tortuous topology.

Because most of the 20 calculated ab initio shapes converged to a globally homogeneous solution (Fig. S4), we considered the best χ² ab initio models, one for each fragment, as relevant guidelines to model dystrophin fragments at a higher resolution. These models were preferred to those generated by DAMAVER, which do not fit the scattering curves. However, the presence of kinks precludes the simple superimposition of straight homology models obtained from spectrin templates (supporting information) onto the kinked molecular shapes. Therefore, we applied the interactive flexible fitting procedure we developed previously (Ref. 27 and Movie S1) to explore the possible deformations of the spectrin-based homology models. A structure quality check (Table S3) of the final structural models indicates that the initial biological structure composed of a coiled-coil filament is properly modulated to match the SAXS-derived molecular shape (Fig. 2). In the final models, kinks placed at some inter-repeat linkers disrupt the straight rod-like structure of the dystrophin fragments. Finally, despite high χ² values, a problem already described and related to low-error detectors we used (28), experimental SAXS curves, and the CRYSOL theoretical curves produced from these structural models are in a range of less than 8% discrepancy for high q values that fall below 2% in low q values (Fig. 2A and Fig. S5). Consequently, these structural models suggest with confidence that the observed kinks are relevant features of the dystrophin central domain in solution (Fig. 2B). All models have been successfully deposited in the SASBDB database, an international curated repository for small-angle scattering data and models (Ref. 29, http://www.sasbdb.org/,⁵ supporting information).

Figure 2.

SAXS-derived three-dimensional structural models for the eight native dystrophin fragments. A, theoretical scattering curves obtained from the final structural models by a CRYSOL program calculation performed for each fragment. All theoretical curves are shown for q < 0.25 Å in a plain line superimposed onto its corresponding experimental gray dotted line (color code as in Fig. 1). Note that χ² values are quantitatively nonrelevant because of the detectors providing low-error data. B–I, the molecular shape obtained from GASBOR with the best χ² is shown for each fragment as a gray volume. The SAXS-derived structural models of each dystrophin fragment are overlaid onto its corresponding molecular shape in a schematic representation. The α-helices of a coiled-coil repeat are colored in red or blue for successive repeats. The longest to the shortest fragment are shown: R4–9 (B), R11–15 (C), R20–24 (D), R16–19 (E), R1–3 (F), R1–2 (G), R16–17 (H), and R23 (I). The D_MAX is indicated for each fragment. Arrows indicate the two more pronounced kinks observed at the linker regions on the R11–15 and R20–24 fragments. The inset shows the structural organization of a two-repeat coiled coil with the three helices A, B, and C of the first repeat and the helices A', B', and C' of the second repeat. The helices are connected by the A/B or A'/B' and B/C or B'/C' loops. The linker connecting the two repeats corresponds to an eight-amino acids common helix bridging C and A'.

Similar to the crystal structures of spectrin and α-actinin, the B helices are generally bent in their middle (30, 31). However, the largest bends of α-helices are located at the inter-repeat linkers (Fig. S6 and Movie S1). These kinks appear to be structured by several redundant features. Similar to successive spectrin repeats (30), the A/B loop of one repeat and the B'/C' loop of the following repeat interact strongly with each other and/or with the inter-repeat linker (Fig. S7). In addition, the diversity in helix length in dystrophin compared with spectrin repeats (32) enables the modulation of kink amplitude and/or of the relative orientation of two successive repeats, mainly through the bending or partial unfolding of the inter-repeat linker. Among remarkable exceptions, we noticed the opposite behavior in the case of two of the largest observed kinks. First, the repeats R22 and R23 have, respectively, two particularly long A/B and B'/C' loops that interact closely and induce a large kink at the linker (Fig. S7B). The loops' interaction results in a bulky extruded volume that can be clearly identified in the molecular shape (Fig. 2D). Second, helix A of R14 and helix B' of R15 are the two shortest helices found in dystrophin repeats. De facto, in R14-R15, an A/B and B'/C' loop contact is not possible in a linear organization but with a large inter-repeat kink stabilized by a contact between helices B and B' (Fig. S7C). Finally, kink angle values are modulated at the R1–2 and R16–17 inter-repeat linkers compared with the kinks observed in their longer overlapping fragments R1–3 and R16–19 (Table S4). This emphasizes the potential dynamic behavior of the kink angles located at the inter-repeat linkers influenced by the succession of repeats.

The in-frame deletion of exons 45–47 profoundly disorganizes the structure of dystrophin at the new junction site

Building on these results, we next investigated the structural impact of the in-frame deletion of exons 45–47 in a purified mutant fragment, R16–21Δ45–47 (Fig. 3, A and B). This mutation is the most frequently found in BMD and involves the loss of a part of the nNOS binding site (16). Guinier approximation gives an R_g value of 62.4 Å (Fig. S8A). The bimodal Kratky and Porod–Debye plots (Fig. S8, B and C) are consistent with an elongated and folded protein fragment, even if the fragment seems less compact than the native dystrophin fragments (Table S2). P(r) function from the SAXS curve of the mutant is leading to R_g and D_MAX values of 60.1 Å and 210 Å, respectively (Fig. 3C and Fig. S8D). Then, as done previously for the native fragments, the experimental SAXS data were used to constrain the molecular modeling calculations. Finally, even if the R16–21Δ45–47 protein fragment corresponds, with the R16–19 fragment, to the sample presenting the lowest signal-to-noise ratio, we could confirm a reasonable rigidity and compactness through advanced analysis, and we could conclude that ab initio models and the derived atomistic models are plausible structural representations of these protein fragments in solution. The final high-resolution model fitted into the best χ² ab initio model showed a highly disordered topology by comparison with the filamentous structure of the corresponding native fragments (Fig. 3D). A well-maintained coiled-coil structure is observed for the four repeats R16, R19, R20, and R21 conserved from the native dystrophin form (Fig. 3D). However, the R17//R18 nonnative repeat shows a loss of coiled-coil organization that is replaced by loosely folded loops (Fig. 3D, inset). All of this leads to a mutant model of less quality than those obtained for the native fragments (Table S3), probably because of the poorly structured regions, including hinge 3 (H3). This last H3 region is composed of 40 residues between the repeats R19 and R20 and could present a loose tendency to fold into β-hairpins (Fig. S9). In our final mutant model, the A/B loop of R16 seems to lose its interaction with the B'/C' loop of R17 as it does in the R16–17 native fragment. This feature induces a disorganization of both the R16-R17 and the R18–19 inter-repeat linkers on each side of the deletion, which drastically alters the filament organization. Interestingly, this disorganization is more dramatic than previously inferred from modeling not using any experimental data (16).

Figure 3.

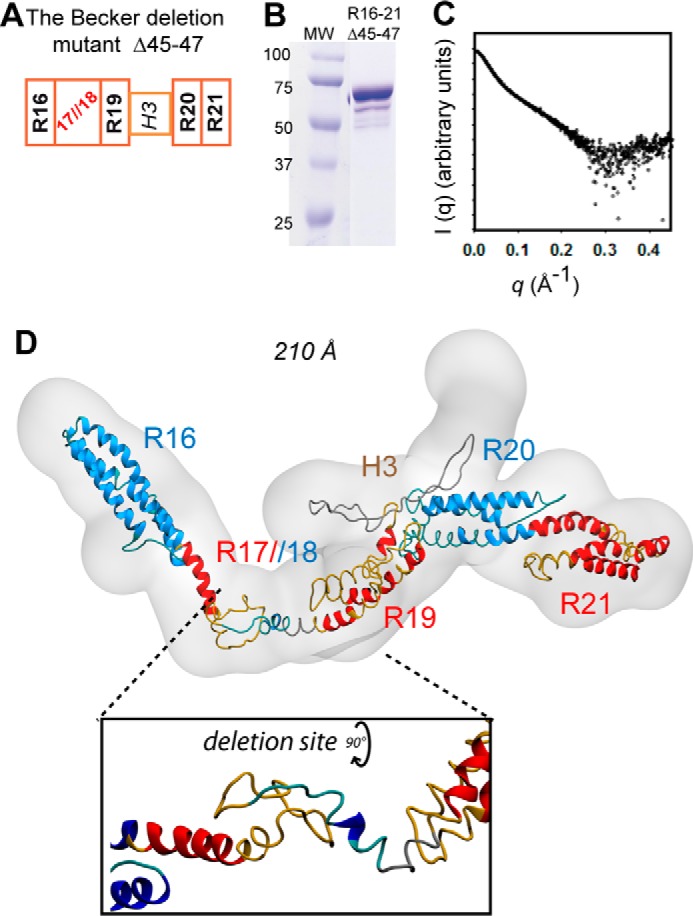
SAXS-based model of the R16–21Δ45–47 deletion mutant. A, schematic of the Becker Δ45–47deletion in the R16–21 fragment of dystrophin. This mutation results in deletion of the C-terminal part of R17 and the N-terminal part of R18, creating a nonnative repeat termed R17//18. B, SDS-PAGE of the fragment indicates that it is reasonably pure and migrates at the expected molecular weight. C, the experimental SAXS scattering curve shows a lower signal-to-noise ratio for large q (>0.2 Å⁻¹) than in native fragments because of a lower sample concentration. D, the structural model of the Becker Δ45–47 deletion mutant is shown overlaid on the SAXS-derived molecular shape in gray volume. The inset highlights filament disorganization at the newly created junction site caused by the deletion as obtained through flexible fitting simulation.

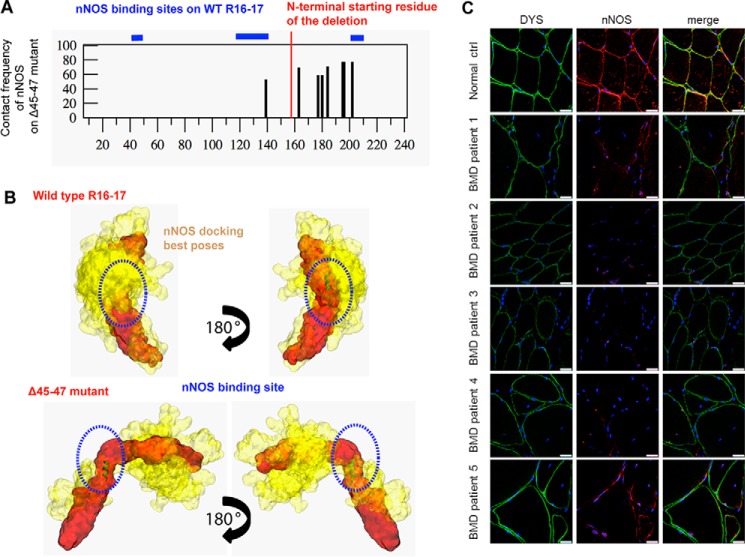
Despite the preservation of a large part of the nNOS binding site in the Δ45–47 mutant, exon deletion could impair the dystrophin–nNOS interaction. Two approaches were undertaken to investigate the nNOS binding by the Δ45–47 dystrophin mutant. First, a docking strategy identical to the one used in our previous work (33) showed that the contact frequencies of nNOS-PDZ onto the SAXS-derived Δ45–47 model were significantly decreased by comparison with the WT R16–17 fragment (Fig. 4A). In particular, the two binding sites situated in the A/B helix of R16 and the linker R16–17 conserved in the Δ45–47 mutant did not show any contacts with nNOS-PDZ. Low frequency contacts on the deleted dystrophin C-terminal domain could be insufficient for its interaction with nNOS-PDZ (Fig. 4B). Secondly, immunostaining experiments of dystrophin and nNOS localization were carried out on muscle sections of five Δ45–47 BMD patients and compared with normal muscle (Fig. 4C). Dystrophin from normal muscle appears as an intense labeling surrounding the fibers. The nNOSμ positioning was validated by its sarcolemmal co-localization with dystrophin in normal muscle. In the muscles of BMD patients, dystrophin was detected at a level comparable with that of control muscle and was properly localized at the inner face of the membrane fibers. Despite the presence of dystrophin, in none of the patients could labeling of nNOS be detected at a sufficient level (Fig. S10). These results suggest that the nNOS binding would be altered in the in-frame deletion mutant despite the preservation of two sequences of the WT protein involved in the binding (33, 34). This observation could be mainly related to the disordered structure induced by the Δ45–47 deletion, as shown from SAXS results.

Figure 4.

nNOS and dystrophin R16–17 binding in the BMD Δ45–47 deletion mutant. A, contact frequency of nNOS on the deletion mutant Δ45–47 compared with the three binding sites of the WT dystrophin repeats R16–17 (blue lines above the graph). The abscissa represents the primary sequence of the dystrophin fragment, where the amino acids 1 to 158 are similar for the two proteins, and the amino acids from 159 to 240 are specific for each of the proteins (the deletion starts at residue 159). B, interaction sites with a high contact frequency (>60%) projected onto dystrophin WT R16–17 (top panel) and Δ45–47 mutant (bottom panel). The dystrophin proteins are shown in red, and the ensemble of best nNOS poses are shown in yellow. C, nNOS localization in Becker Δ45–47 muscles. Fixed frozen muscle sections (8 μm) from normal control (Normal ctrl) and 5 Becker patients (BMD patients 1 to 5) were immunolabeled with anti-C-terminal dystrophin (green) and anti-nNOSμ (red) antibodies and nuclei with DAPI (blue) and imaged by confocal microscopy. Scale bars = 25 μm.

Discussion

The results presented here indicate that the classical concept of the central domain of dystrophin as a rod-shaped succession of 24 monotonous repeats (2, 15) should be revisited. Evidence that the structure of this domain is complex and tortuous was obtained using an experimental SAXS methodology associated with molecular modeling. We suggest that the linker regions connecting rigid repeats confer kinked and nonrod-shaped features to the central domain. Such large deviations from filament linearity have not yet been observed in crystal structures of the three-repeat spectrin fragments or of the four-repeat α-actinin, but angle values in the range of 10–15° were reported for inter-repeat linkers in spectrin dimers by molecular simulation (35). The large kink angles observed here in dystrophin might be due to its monomeric nature, whereas spectrin and α-actinin filaments are tetramers or dimers. Notably, they could also be “coded” by specific inter-region linker sequences. Indeed, the dimeric–tetrameric filaments of α-actinin and spectrin are structurally maintained by inter-repeat interactions enabled by similar lengths of all repeats, whereas, in the monomeric dystrophin filament, the repeats display highly heterogeneous lengths, thereby precluding dimerization (32). The presence of specific kinks within the dystrophin filament raises the question of their biological relevance and whether they represent hinge regions with adaptable angles. Indeed, the final structural models were obtained by interactively exploring the possible angles between successive repeats without unfolding of the repeats themselves, indicating that modifications of these kink angles could occur at low energy cost. It is interesting to note that the kink angle values between successive repeats are slightly modified when appearing in two different fragments, such as the R1–2 kink angle in R1–2 and R1–3 and the R16–17 kink angle in R16–17 and R16–19. However, these modifications are restricted to specific spatial directions as imposed by the structural biology restraints established for coiled coils. Incidentally, the looseness of the linkers could preclude the crystallization of the central domain of dystrophin.

The tortuous filamentous organization of the central dystrophin domain raises important questions about the biological construction of the entire dystrophin scaffold. Large inter-repeat kink angles break the spatial alignment of the central domain by changing the direction of neighboring repeats. This feature suggests that dystrophin should no longer be considered a succession of independent building blocks (repeats) but rather a succession of highly interdependent multirepeat blocks constituting structural and/or interaction modules. This view is in line with the cooperative behavior of dystrophin repeats observed under unfolding conditions when stretched by optical tweezers (36). This compartmentalization may allow dystrophin to recruit protein partners simultaneously while bound to the plasma membrane (37). In particular, the bulkiest molecules, intermediate filaments and F-actin, are recruited by the large R11–17 domain, whereas microtubules are recruited by R20–23 (38), and because of steric hindrance, these interactions could not occur simultaneously with a straight central domain. Remarkably, these regions overlap with DMD gene mutational hot spots (exons 44 to 55) (6, 7). Other modules for binding smaller protein partners emerge from the kinked filament topology of dystrophin, including PAR-1b by repeats 8 and 9 (39, 40) and nNOS by repeats 16 and 17 (33, 34).

The emergence of multirepeat blocks as functional interaction modules is particularly evidenced here by the consequences of the BMD in-frame 45–47 deletion. Even though quite a large part of the nNOS-binding sequence of dystrophin is conserved at the N-terminal side of the nonnative junction in the Δ45–47 mutant, docking simulations suggest the difficulty for nNOS to associate with the deleted dystrophin. Our main hypothesis is that the structural disorganization of the nNOS binding module on WT R16–17 induced by the Δ45–47 deletion could explain why we observed a strong decrease of nNOS protein expression in skeletal muscle and a loss of its localization to the sarcolemma in BMD patients. Nevertheless, it is still unclear whether nNOS mislocalization to the sarcolemma is the source or the consequence of the low protein levels we observed. Absence of nNOS binding to the deleted dystrophin could be related to the severity of this Δ45–47 in-frame deletion (16) and could account at least partly for the heterogeneity of BMD phenotypes encountered with different deletions starting from exon 45 that may impair nNOS binding to various degrees (41). Among these deletions, we are currently studying the deletion of exons 45 to 55, which could rescue 65% of DMD patients (13, 42).

Therefore, the maintenance of the best native-like dystrophin functional modules appears to be crucial in the design of therapeutic micro-dystrophins or exon-skipping/gene-editing products. Shortened micro-dystrophins have been designed based on BMD phenotypes by deleting some repeats that were assumed to be more dispensable than others (10, 12). Most of them were designed according to the less severe BMD deletion of exons 17 to 48 (8) and to the repeat phasing proposed by Harper et al. (43). However, these micro-dystrophins were designed by considering repeats as elemental building blocks, without a true knowledge about the structural impact of disruption of the interdependent multirepeat blocks, and this remains to be investigated. Exon-skipping is a transcriptional therapeutic strategy expected to change DMD patients into BMD patients by subtracting additional exon(s) to restore the reading frame (9, 11). BMD deletions thus serve as patterns for a DMD cure, and until now they were all considered to be equivalent based on the hypothesis that parts of the central domain could be subtracted without severely affecting dystrophin structure and function. Our results clearly indicate that this is not the case and that the longest in-frame transcript produced by exon-skipping is not necessarily optimal. Therefore, BMD deletions should be studied in more detail from a protein structure to function point of view to anticipate the results of therapy for DMD patients before inducing their therapeutic production.

Experimental procedures

Cloning, protein expression, purification, and biochemical characterization

The cloning, expression, and purification procedures for five of the eight fragments (R1–2, R1–3, R11–15, R23, and R20–24) have been described extensively in our previous papers (19) (details about sequences of fragments are shown in Table S1). R16–17 was obtained from Nick Menhart's team (20). The fragments R4–9 and R16–19 were newly overexpressed in Escherichia coli and purified by similar procedures. The deletion mutant R16–21Δ45–47 was cloned, expressed, and purified as described previously in detail (16). Proteins were characterized by CD (for details, see the supporting information). The hinge 3 region of human dystrophin was produced by Proteogenix (http://www.proteogenix.fr/)⁵ as a peptide of 47 residues with a molecular mass of 4.9 kDa and a purity of > 95%, analyzed by CD and NMR.

SAXS experiments

SAXS measurements were conducted either at the European Synchrotron Radiation Facility (Grenoble, France) on the ID14-eh3 beamline (sample R11–15) or at the French Synchrotron SOLEIL (St. Aubin, France) on the SWING beamline (all other samples). All experiments were performed at 15 °C. For both setups, the scattering vector is defined as q = 4 π/λ sinθ, where 2θ is the scattering angle. Data were collected in a q range of 0.005–0.5 Å⁻¹.

ID14-eh3 setup

The data were collected on a 2D Pilatus 1 M detector at a distance of 2.43 m (λ = 0.933 Å). For R11–15, a series of 5 concentrations (1.1, 2.1, 4.6, 6.4, and 10.8 mg/ml) was prepared prior to injection into the SAXS capillary. Ten frames of 1.5 s each were collected with alternating TNE buffer (20 mm Tris (pH 7.5), 150 mm NaCl, and 0.1 mm EDTA) and R11–15 protein samples at increasing concentrations. All frames were then averaged for each dataset after visual inspection. SAXS data were directly evaluated using the Primus software, as implemented in the ATSAS 2.3 Suite (26). The experimental SAXS data for all samples were linear in a Guinier plot of the low q region. These observations indicated that the sample did not aggregate. The radius of gyration R_g for R11–15 was derived from the Guinier approximation I(q) = I(0) exp (−q²R_g²/3) for qR_g < 0.8. Data collected at high q using high protein concentrations and at low q using low protein concentrations were then merged with the aim to minimize the particle interference occurring at low q and to maximize the signal/noise ratio at high q.

SWING setup

All other sample data were recorded using an AVIEX170170 CCD detector at a distance of 1.807 to 1.845 m (λ = 1.033 Å). For constructs R1–2, R1–3, R4–9, R16–17, R16–19, R16–21Δ45–47, R23, and R20–24 a stock solution of each fragment was prepared at a final concentration between 8 and 15 mg/ml. A volume between 60 to 120 μl of protein samples was injected into a size exclusion column (Bio SEC-3 300 Å, Agilent) and eluted directly into the SAXS flow-through capillary cell at a flow rate of 0.2 ml/min. The overall SEC-SAXS setup has already been described in previous work (44). The elution buffer consisted of TNE supplemented with 2% glycerol and 10% acetonitrile for R16–19 and the BMD mutant. Two hundred fifty SAXS frames were collected continuously during the elution at a frame duration of 1.5 s and a dead time between frames of 0.5 s. One hundred frames accounting for buffer scattering were collected before the void volume. The averaged buffer scattering was then subtracted from the protein signal. SAXS curves displaying a constant R_g in an R_g versus frame number plot were averaged (Fig. S1A) and were used for further characterization. Data reduction to absolute units and frame averaging and subtraction were performed in FOXTROT (7).

SAXS data analysis

All subsequent data processing and analysis were conducted with the Scatter (http://www.bioisis.net/,⁵ 22), SASFit (45), or PRIMUS software and other programs of the ATSAS Suite. The SAXS data have been successfully deposited in the SASBDB database (29) and were validated following an expert quality control procedure (http://www.sasbdb.org/,⁵ see supporting information).

Guinier plots assess that all samples were not aggregated (Figs. S1B and S7A). The distance-distribution function P(r) and the maximum particle diameter (D_MAX) were calculated using the GNOM program (46). This approach offers an alternative calculation of R_g that is based on the entire scattering spectrum (Table S2). Within a margin of error, these R_g values match those deduced from the first Guinier approximation. Scattering patterns I(q) are also shown as Kratky plots (q²I(q) versus q, Fig. S2A), indicating that all proteins are properly folded in solution. Typically, a globular, structured protein exhibits a pronounced maximum (bell-shaped curve), whereas a random chain (for example, an unfolded protein) will plateau (47, 48). Then, Porod–Debye plots (q⁴I(q) versus q⁴) were generated and confirmed the compactness of all proteins (Fig. S2B and Table S2).

MWs are generally derived from the SAXS data using the I₀ or using a standard protein, generally BSA. Both methods need an accurate determination of the protein concentration. In the SEC-SAXS experiments, the UV detector saturated and the protein concentration could not be accurately determined. Therefore, we relied on alternative methods to control the MWs of dystrophin fragments in solution: size exclusion chromatography multiangle light scattering (SEC-MALS) for two of our constructs (R1–3 and R11–15), the Porod volume-based method, and that proposed by Rambo and Tainer (22). SEC-MALS experiments were performed with an HPLC system (Agilent) equipped with an UV detector coupled with light scattering (miniDAWN Treos, Wyatt) and refractive index (Viscotek, Malvern) detectors. The refractive index increment value (dn/dc) of the proteins used to determine their molecular weight was 0.185 ml/g. Data were collected using a customized Bio SEC3 column (Agilent) equilibrated with TN buffer (20 mm Tris (pH 7.4) and 150 mm NaCl) with a flow rate of 0.3 ml min⁻¹. Data were processed with ASTRA software v6.1. For the Porod volume-based method, we assumed that the Porod volume in square nanometers is about 1.6 times the molecular mass in kilodaltons (46). The method developed by Rambo and Tainer (22) was used to assess the monomeric state of all protein fragments employing the volume of correlation (Vc).

Structural models derived from the SAXS data

The overall ab initio models of the protein fragments were obtained from the SAXS experimental data using the GASBOR program (26). Following the standard procedure and using 50 harmonics, the scattering profiles were fitted to a q_max = 0.45 Å⁻¹ for all samples, except for R16–19 and R16–21Δ45–47, q_max = 0.3 Å⁻¹ (Fig. S4A). Twenty independent GASBOR computations were performed for each scattering profile (each protein sample) and were superimposed using the SUPCOMB and DAMAVER programs (Fig. S4, B and C). This allowed to identify general structural features over the models of a given fragment, and thus, the result of the GASBOR computation with the smallest χ² was finally conserved as the unique ab initio model of each dystrophin fragment. This unique ab initio model was converted to volume grid constraints (molecular shape) to guide the interactive flexible fitting simulations, as described in previous work (27). Dystrophin fragment homology models (with spectrin as a structural pattern) were adjusted to the molecular shape by multiple interactive simulations exploring head-to-tail initial positions of the protein fragment (see Movie S1 and supporting information for details). All final models were refined by standard energy minimization (27). Evaluation of the final structural models was performed using standard quality controls (Table S3; data provided by http://services.mbi.ucla.edu/SAVES⁵). α Helix curvature in the structural models (Fig. S5) was measured using the measure of kink amplitude between two consecutive dystrophin repeats by defining a main axis for each coiled coil (Table S4). Validation of these models was done by calculating their theoretical SAXS curves with the CRYSOL program (26).

Analysis of dystrophin and nNOS interaction

First, a docking strategy already described (33) was used to search for contact frequencies between the SAXS-derived structural model of Δ45–47 dystrophin mutant and the nNOS PDZ subdomain. Second, nNOS immunolocalization was performed on muscle biopsies obtained from five BMD patients presenting deletion of exons 45–47 from the French population (7). All details are described in the supporting Materials and methods.

Author contributions

O. D., J.-F. H., M. C., and E. L. R. conceived and coordinated the study and wrote the paper. O. D., A.-E. M., E. P., E. G., and A. N. designed, performed, and analyzed the molecular simulations. O. D., N. F., and M. B. designed the interactive simulation tools. A. C., C. R.-N., C. T., J.-F. H., and E. L. R. designed, performed, and analyzed the protein fragment samples for SAXS experiments. O. D., R. D. S. M., J. P., P. R., J.-F. H., M. C., and E. L. R. designed, performed, and analyzed the SAXS experiments. A. B. designed, performed, and analyzed the NMR experiments. M. G., F. L., and F. P.-R. designed, performed, and analyzed the BMD patient cell experiments. All authors reviewed the results and approved the final version of the manuscript.