Abstract
The extent to which current force fields faithfully reproduce conformational properties of lipids in bilayer membranes, and whether these reflect the structural principles established for phospholipids in bilayer crystals, are central to biomembrane simulations. We determine the distribution of dihedral angles in palmitoyl-oleoyl phosphatidylcholine from molecular dynamics simulations of hydrated fluid bilayer membranes. We compare results from the widely used lipid force field of Berger et al. with those from the most recent C36 release of the CHARMM force field for lipids. Only the CHARMM force field produces the chain inequivalence with sn-1 as leading chain that is characteristic of glycerolipid packing in fluid bilayers. The exposure and high partial charge of the backbone carbonyls in Berger lipids leads to artifactual binding of Na+ ions reported in the literature. Both force fields predict coupled, near-symmetrical distributions of headgroup dihedral angles, which is compatible with models of interconverting mirror-image conformations used originally to interpret NMR order parameters. The Berger force field produces rotamer populations that correspond to the headgroup conformation found in a phosphatidylcholine lipid bilayer crystal, whereas CHARMM36 rotamer populations are closer to the more relaxed crystal conformations of phosphatidylethanolamine and glycerophosphocholine. CHARMM36 alone predicts the correct relative signs of the time-average headgroup order parameters, and reasonably reproduces the full range of NMR data from the phosphate diester to the choline methyls. There is strong motivation to seek further experimental criteria for verifying predicted conformational distributions in the choline headgroup, including the 31P chemical shift anisotropy and 14N and CD3 NMR quadrupole splittings.
Introduction
General principles governing lipid conformations in bilayer membranes have been established from x-ray crystal structures for a range of different phospholipids, glycolipids, diglycerides, and ceramides (1, 2, 3, 4). The bilayer crystal structure of glycerolipids is characterized by the backbone dihedrals, and by which of the sn-1 and sn-2 chains is the leading one, i.e., the one which proceeds directly into the bilayer from attachment to the glycerol. To achieve parallel chain packing, the other chain is then bent by 90°. The polar headgroup structure is bent down, parallel to the bilayer plane, and is characterized by a limited number of conformations in the case of phosphatidylcholine, or, for phosphatidylethanolamine, by just two mirror-image conformers.
In contrast, some of the crystal structures of lipids associated with both soluble and membrane proteins that are deposited in the Protein Data Bank (PDB) violate several of the conformational principles derived from small-molecule x-ray methods (5, 6, 7). This includes incorrect stereochemistry. Much of the chain configurational disorder arises from energetically disallowed skew conformations. Eclipsed conformations occur in some glycerol backbone torsion angles and in C−C torsion angles of the lipid headgroups. A high proportion of the carboxyl ester groups are in nonplanar configurations, and certain of the carboxyls are in the disallowed cis configuration. Some structures have the incorrect enantiomeric configuration of the glycerol backbone, and many branched methyl groups in the phytanyl chains of archaeal lipids are in the incorrect S-configuration. Whatever the dynamic state of the lipids, these incorrect structures cannot describe lipid-protein interactions in biological membranes.
Experimental data on the dynamic lipid structures that occur in fluid bilayer membranes come mostly from magnetic resonance studies. Universally, the sn-1 and sn-2 acyl chains are inequivalent in fluid bilayers, with sn-1 as the leading chain (8, 9, 10). In particular, 2H-NMR studies suggest that the headgroup structures can be explained minimally by exchange between two mirror conformations (11, 12). Correspondingly, liquid-state NMR of phospholipid micelles is interpreted in terms of exchange between stable conformers of the glycerol backbone (1). A single consensus structure was proposed that is consistent with a considerable range of different solid-state NMR couplings for phosphatidylcholine bilayers (13). However, this incorporates a conformationally forbidden nonplanar ester carboxyl and a relatively high-energy glycerol backbone configuration. This, therefore, also suggests the presence of a limited number of interconverting conformers.
Molecular dynamics (MD) simulations, in principle, are capable of yielding the dynamic configurations of lipid molecules assembled in bilayer membranes, and at a level of atomic detail that is not available directly from spectroscopic studies. However, we can expect these time-averaged configurations to depend more or less sensitively on the force fields chosen for the simulations (14, 15, 16). In general, force fields are optimized to reproduce a range of experimental parameters that characterize the ensemble bilayer structure (17, 18). It is therefore of direct relevance to inquire how this impacts the molecular configurations of the constituent lipids. Specifically, correct conformational structures are needed for a realistic and effective description of intermolecular interactions, for example, in lipid-protein interactions, and in lipid-cholesterol interactions that give rise to formation of liquid-ordered membrane domains (i.e., rafts).
Here, we determine dihedral-angle distributions for a representative membrane phospholipid, 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC), in fully hydrated bilayers. These are equilibrated in MD simulations under the action of two different widely used phospholipid force fields. We compare the earlier united-atom model of Berger et al. (19, 20) with the most recent version of the CHARMM 36 all-atom force field for lipids (21). The natural equilibrium state of a flat bilayer membrane is one that is essentially free of tension, even when undulations are taken into account (22, 23). Although the force field of Berger et al., with Lennard-Jones potential adjusted to experimental results for pentadecane and headgroup partial charges of Chiu et al. (24), produces fluid-phase packing for tension-free bilayers above the chain-melting temperature, this was not the case until the C36 release of the CHARMM force field, for NPT ensembles (17). A significant feature of the nonbonded interactions is the partial charge on the carboxyl ester groups (18), which, besides affecting lipid packing, can exaggerate the degree of monovalent cation binding (25, 26, 27). Thus, we might expect this also to affect the configuration of the glycerolipid backbone and attached chains.
The motivation behind this study is twofold: to assess the extent to which the MD structures from the different force fields conform to the configurational principles established from crystal structures and time-average NMR order parameters, and to identify structural features that might be used for future validation. Force field development is a continual process (17), and there is a constant need for further targets with which to test them (28). A previous survey of lipid force fields concludes the need for improved agreement with NMR data on the glycerol backbone and choline headgroup (29). We strengthen this here with consideration of 31P-NMR chemical shift anisotropy and 14N-NMR quadrupole splittings. Furthermore, we find that headgroup orientations (i.e., order parameters) may be interpreted realistically in terms of rapid exchange between the principal crystalline conformers. This analytic strategy has been challenged as oversimplifying but never specifically tested. The possibility to describe the dynamic structure of fluid lipid bilayers in terms of a limited number of molecular configurations then gives us a conceptual framework for understanding and interpreting the properties of biological membranes, which are at the same time both highly dynamic and highly ordered.
These results should be of wide interest to workers in the field of lipid membranes (i.e., all biological membranes), as well as to all those wishing to appreciate both the implications and limitations of MD simulations in biological systems. Ever since the first crystal structure of a phospholipid was determined, conformational principles have inspired our thinking about the molecular role of the lipid bilayer in biological membranes. At the same time, NMR spectroscopy, and also spin-label electron paramagnetic resonance spectroscopy, has led our ideas about the dynamic features of the ordered membrane environment, as characterized by molecular order parameters. The representation of these features by MD calculations therefore extends our conceptual frame to wholescale membrane simulations.
To appreciate the power and potential problems of this latter approach, we should look back to the historical development as well as forward to future improvements (17). Early all-atom lipid force fields produced gel-like membranes above the chain-melting temperature, but this could be discovered only after sufficiently long simulations were possible (30). Up to that point, the area per lipid was severely underestimated in tension-free ensembles, and simulations were made at constant area instead of at constant pressure, thus limiting predictive ability and interpretative value in combination with diffraction techniques (31). Similarly, there have been continuous developments in nucleic-acid force fields, and good agreement (rmsd < 0.1 nm) with high-resolution DNA structure is obtained only with the most recent modifications (32). For folded proteins, different force fields reproduce similar structural ensembles (33, 34, 35), but further development was needed to treat intrinsically disordered proteins successfully (36).
It is clear that, although possibly subtle, adjustments in force fields are necessary to reproduce correct structural ensembles and conformer distributions for all biomolecular types. Modern experimental biophysics often relies on accurate and sufficiently long simulations to aid in the interpretation of a variety of biophysical data, such as that from spin-label electron paramagnetic resonance (37, 38, 39), NMR (40, 41, 42), and Förster resonance energy transfer (43, 44, 45). It is therefore important to address the impact of force fields on the configurations of biomolecules, including lipid assemblies.
Methods
Definition of dihedral angles and conformations
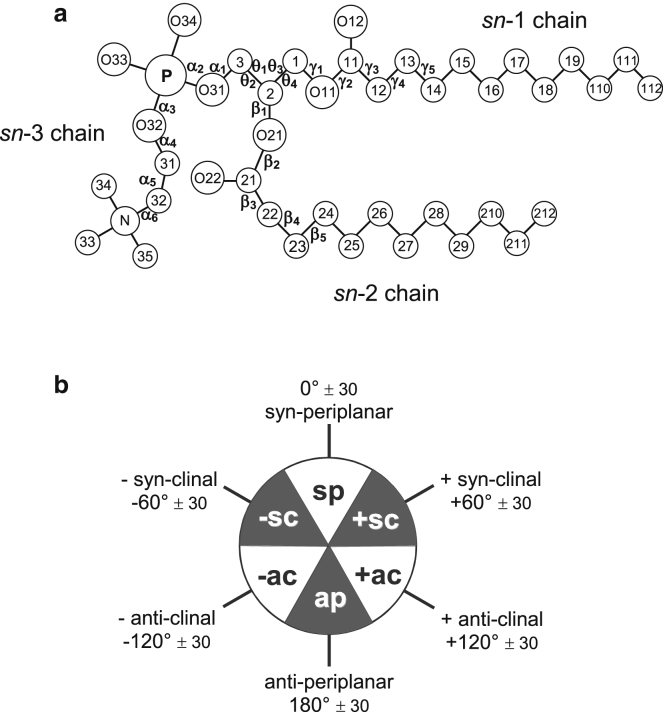
Fig. 1 a shows the notation used for the dihedral angles in sn-3 phosphatidylcholine, with explicit angles as listed in Table 1 (46). Dihedral angles are defined as in (47), which also is the current convention for protein structures (48). Fig. 1 b gives the classification of the staggered and eclipsed rotamers used for conformational description of lipids according to the range of dihedral angle (49). Equivalent conformational designations frequently used are as follows: trans, t (ap); gauche, g (sc); skew, s (ac); and cis, c (sp).
Figure 1.
(a) Notation for dihedral angles in sn-3 diacyl phosphatidylcholine (46). (b) Designation of dihedral-angle ranges for staggered and eclipsed rotamers (49).
Table 1.
Definition of Dihedral Angles
| θ1 | O31−C3−C2−C1 | β1 | C3−C2−O21−C21 |
| θ2 | O31−C3−C2−O21 | β2 | C2−O21−C21−C22 |
| θ3 | C3−C2−C1−O11 | β3 | O21−C21−C22−C23 |
| θ4 | O21−C2−C1−O11 | β4 | C21−C22−C23−C24 |
| α1 | C2−C3−O31−P | γ1 | C2−C1−O11−C11 |
| α2 | C3−O31−P−O32 | γ2 | C1−O11−C11−C12 |
| α3 | O31−P−O32−C31 | γ3 | O11−C11−C12−C13 |
| α4 | P−O32−C31−C32 | γ4 | C11−C12−C13−C14 |
| α5 | O32−C31−C32−N | – | – |
Atom numbering is taken from Fig. 1.
In the Pascher notation (2), the chain-backbone configuration is specified as θ4/leadingchain/θ2, where the leading chain is the one which proceeds directly into the bilayer from the attachment at the glycerol backbone.
MD simulations
We performed all-atom MD simulations of POPC bilayers using GROMACS v 5.1 (50, 51, 52) with the CHARMM36 (charmm36-jul2017.ff.tgz) (21) or BERGER (20) force field. The duration of the simulation trajectories used was 500 ns. The CHARMM bilayer contained 96 lipids. Trial simulations with 120 lipids did not result in any change in order parameters and dihedral distributions (data not shown). The Berger bilayer contained 120 lipids. The water models used were the CHARMM version of TIP3P (53) and SPC (54), for CHARMM and Berger force fields, respectively. The LINCS algorithm (55) was used to constrain all bonds in the Berger simulations, and bonds containing hydrogen in the CHARMM simulations. The leapfrog integrator was used with a time step of 2 fs.
For the Berger force field, simulations were carried out with standard parameters as described in (56). A neighbor list with a 1.0 nm cutoff was used for nonbonded interactions and was updated every 10 steps. van der Waals interactions were truncated with a cutoff of 1.0 nm. The particle mesh Ewald method with a 0.12-nm Fourier spacing and 1.0-nm short-range cutoff was used for electrostatic interactions (57, 58). Temperature and semiisotropic pressure coupling was performed using the Berendsen thermostat and barostat (59). Trajectories were sampled every 10 ps.
For CHARMM simulations, particle mesh Ewald had a short-range cutoff of 1.2 nm, and van der Waals interactions were switched off over the range from 1.0 to 1.2 nm. The Nose-Hoover thermostat was used (60). Parrinello-Rahman (61) pressure coupling was used for production runs after equilibrating the systems with Berendsen pressure coupling.
Order parameters
The 2H-quadrupole splitting of the perpendicular peaks in a Pake doublet is as follows:
| (1) |
where for an aliphatic C−D bond (62) and is the order parameter of the C−D bond referred to the membrane normal. Because rotation is rapid about the N−C bond of choline methyls, their C−D or (C−H) order parameter is where is the order parameter of the three equivalent N−C33, N−C34, and N−C35 bonds. The effective quadrupole coupling for rapidly rotating CD3 methyls is (62); both this and the CD2 value are from the crystalline lamellar phase (Lc) of a phospholipid with perdeuterated chains (10).
The order parameter of the C32−N bond measured by 14N-NMR is related directly to the choline methyl CD3 order parameter (63):
| (2) |
where (4, 64) is the mean C32-N-C33, -C34, and -C35 choline bond angle. Using the value of for dipalmitoyl phosphatidylcholine (PC) at 317 K from Ref. (63) with the corresponding value of from 14N-NMR (65), we deduce a 14N-quadrupole coupling of from Eqs. 1 and 2.
The 31P chemical shift anisotropy (csa) with axial averaging is (66):
| (3) |
where and for hydrated dimyristoyl PC at 248 K (67); and are the order parameters of the csa-principal axes, which lie close to the O31−O32 and O33−O34 vectors, respectively, of the phosphate diester. An approximate model relates the chemical shift anisotropy to the value obtained simply by uniaxial rotation about the principal molecular axis (68):
| (4) |
where is the order parameter of this principal axis relative to the membrane normal. A reasonable estimate for rotational averaging is , which we get by using the value of from the gel phase (62, and see also 69). Typical errors in are ±1 ppm or better (70).
Motionally averaged 1H-13C dipolar couplings are determined by
| (5) |
where the rigid-limit dipolar coupling is kHz (71) and is the order parameter of the C−H bond. Typical errors in recoupled dipolar frequencies are ±0.4 kHz (71) or larger (72), whereas those from direct measurement of 31P-csa or quadrupole splittings are typically ±(0.1−0.2) kHz, including those for 14N (65, 70).
Results
Headgroup conformation
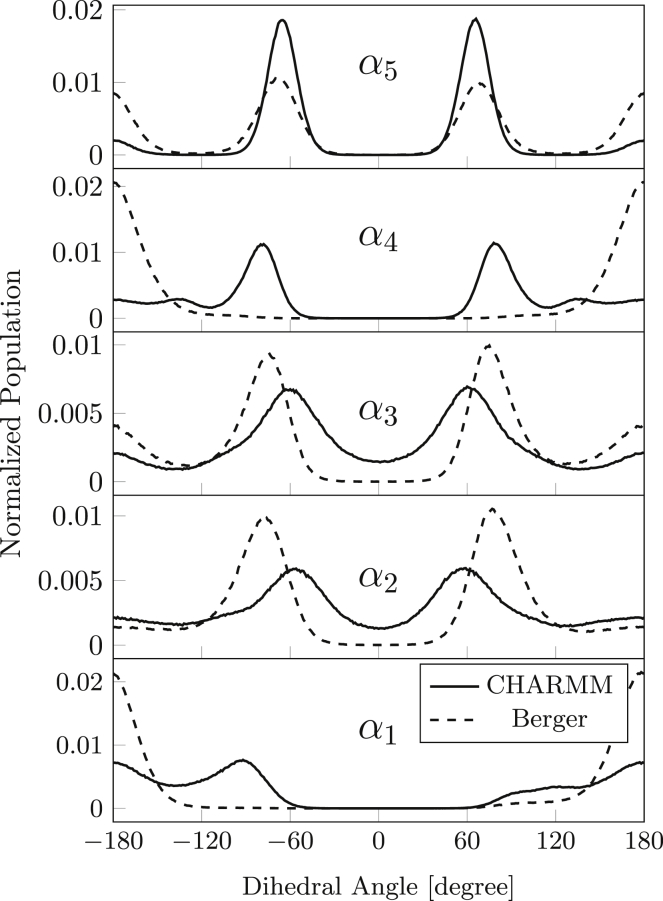
Fig. 2 shows the distributions of dihedral angles in the polar headgroups for the Berger et al. (dotted line) and CHARMM36 (solid line) force fields. Results for α5 are similar to those reported previously by Botan et al. (29). There are clear differences between simulation results from the two force fields, particularly as regards the α1 and α4 dihedrals. Significantly, the distributions for both are identical for the Berger force field, whereas they differ considerably from one another for the CHARMM36 force field. On the other hand, the distributions of α2 and α3 dihedrals are more similar both to each other and between the two force fields. Differences within the α1/α4 and α2/α3 pairs must reflect differences in nonbonded interactions beyond those between immediate pendant groups.
Figure 2.
Distribution of dihedral angles in the polar headgroup of POPC. From bottom to top: α1 about the C3−O31 bond, α2 about the O31−P bond, α3 about the P−O32 bond, α4 about the O32−C31 bond, and α5 about the C31−C32 bond. CHARMM force field (solid line) and that of Berger et al. (dotted line).
Table 2 lists the distribution of headgroup dihedrals binned into ±30° ranges about the staggered and eclipsed positions for sp3-bonds, as in Fig. 1 b. These are compared with distributions found from crystal structures available for glycerophospholipids, namely phosphatidylcholine, phosphatidylethanolamine, mono- and dimethylphosphatidylethanolamine, phosphatidic acid, and phosphatidylglycerol.
Table 2.
Conformation of Polar Headgroup in MD Simulations of POPC
| Dihedral | ap | sc | −sc | ac | −ac | sp | |
|---|---|---|---|---|---|---|---|
| α1 | Berger | 0.865 | 0.010 | 0.001 | 0.103 | 0.041 | 0 |
| CHARMM | 0.359 | 0.028 | 0.130 | 0.190 | 0.294 | 0 | |
| crystal | 0.79 | 0 | 0 | 0.10 | 0.10 | 0 | |
| α2 | Berger | 0.079 | 0.307 | 0.300 | 0.159 | 0.151 | 0.002 |
| CHARMM | 0.120 | 0.274 | 0.270 | 0.110 | 0.118 | 0.107 | |
| crystal | 0 | 0.60 | 0.40 | 0 | 0 | 0 | |
| α3 | Berger | 0.188 | 0.285 | 0.272 | 0.132 | 0.122 | 0.001 |
| CHARMM | 0.099 | 0.303 | 0.302 | 0.093 | 0.091 | 0.112 | |
| crystal | 0 | 0.64 | 0.36 | 0 | 0 | 0 | |
| α4 | Berger | 0.833 | 0.003 | 0.004 | 0.078 | 0.082 | 0 |
| CHARMM | 0.152 | 0.252 | 0.257 | 0.172 | 0.166 | 0.000 | |
| crystal | 0.21 | 0 | 0 | 0.57 | 0.21 | 0 | |
| α5 | Berger | 0.286 | 0.306 | 0.330 | 0.036 | 0.037 | 0.003 |
| CHARMM | 0.062 | 0.461 | 0.462 | 0.007 | 0.006 | 0.001 | |
| crystal | 0.14 | 0.50 | 0.29 | 0 | 0.07 | 0 |
We see that the headgroup conformation for the Berger force field is predominantly α1 = ap, α2 = ±sc, α3 = ±sc, α4 = ap, and α5 = sc but with a comparable contribution from ap. This is close to that found in bilayer crystals, except for the ap component of α5, which occurs in crystals only for phosphatidylglycerol. Berger et al. retain the original GROMOS force field for the headgroup bonded interactions, and use OPLS for nonbonded Lennard-Jones interactions. In earlier simulations of fluid dipalmitoyl PC bilayers using the GROMOS force field, but with reduced atomic charges, Egberts et al. (19) also find choline headgroup rotamers similar to those in lipid crystals. For CHARMM36, the headgroup conformation is less like that of phosphatidylcholine bilayer crystals, predominantly α1 = ap and −ac, α2 = ±sc, α3 = ±sc, α4 = ±sc, and α5 = ±sc. These conformational deviations exhibited by the MD simulations may diminish the internal electrostatic attraction that directs the positively charged nitrogen to the phosphate oxygens in the crystal structures. Also, we must remember that the phosphocholine headgroup occupies a larger cross-sectional area than the crystalline chains. This is accommodated by tilting the chains in the crystal, as in phosphatidylcholine gel phases. Note that a correlated α2/α3 = ±sc/±sc conformation is expected on energetic grounds for a phosphate diester (73). As seen in Fig. 2 and Table 2, the relative populations of α2 and α3 are consistent with this pairing, for both force fields. Raman spectroscopy shows that torsion angle α5 is predominantly sc in hydrated phosphatidylcholine bilayers (74), as predicted with both force fields.
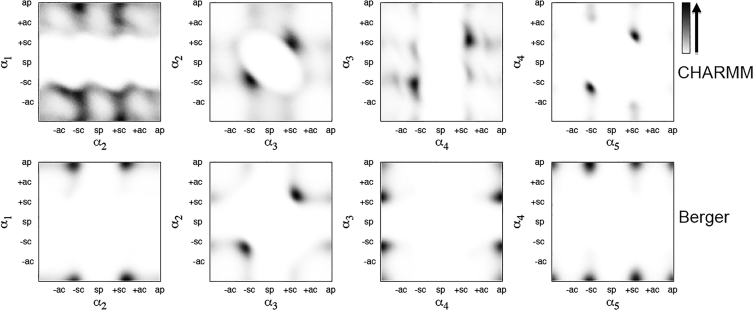
Correlations between adjacent dihedral angles αi/αi+1 in the headgroup are shown by the doublet distributions that are given in Fig. 3. In the second column, we see very clearly that α2/α3 = ±sc/±sc as expected, for both force fields. For the CHARMM36 force field, we get the correlated sequence α2/α3/α4/α5 = ±sc/±sc/±sc/±sc, without sign reversal for α5. For the force field of Berger et al., the correlated sequence is predominantly α2/α3/α4/α5 = ±sc/±sc/ap/sc, with sign reversal for α5, where we use the doublet distribution α3/α5 (data not shown) to bridge the ap conformation of α4.
Figure 3.
Doublet distributions for pairs of adjacent headgroup dihedrals αi/αi+1, from simulations with the CHARMM force field (upper row) and that of Berger et al. (lower row).
Glycerol backbone
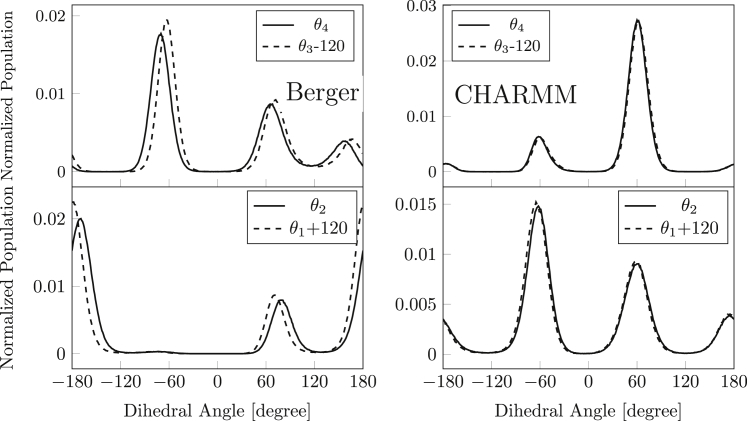
The θ4 dihedral angle, about the glycerol C1−C2 bond, specifies the relative orientation of the sn-1 and sn-2 chains. Correspondingly, the θ2-dihedral, about C2−C3, defines the orientation of the headgroup relative to the sn-2 chain. The θ3/θ1 combination of complementary dihedral angles specifies the glycerol configuration. For tetrahedral bond angles, the complementary dihedral angles of sn-3 glycerol are related by and .
Fig. 4 compares distributions of the and dihedrals (solid lines) with their complements and (dotted lines). Results for θ3 are similar to those reported previously by Botan et al. (29). Displacements of the solid and dotted lines by ≈±8°, respectively, with the Berger force field indicate departures from strictly tetrahedral geometry, or an insufficient constraint on the improper dihedrals that maintain the enantiomeric configuration of the backbone. For the CHARMM force field, however, the complementary pairs of dihedrals coincide as expected. The major peaks in population differ considerably between the two force fields. For the Berger force field they occur close to (trans, ap), (gauche+, sc), and to (gauche±, ±sc), but with significant deviations (∼5–10°) from the canonical staggered positions for sp3-bond dihedrals of glycerol. In addition, the -distribution has a further peak at 158°. On the other hand, the CHARMM force field produces two major peaks in population at and , with only a minor contribution in the trans region.
Figure 4.
Distribution of dihedral angles in the glycerol backbone of POPC. Top: the C2−C3 bond θ2 (solid line) and θ1+120° (dotted line). Bottom: the C1−C2 bond θ4 (solid line) and θ3−120° (dotted line). CHARMM force field (right) and that of Berger et al. (left).
Table 3 lists the distribution of backbone dihedrals grouped in ±30° ranges about the staggered and eclipsed positions for C−C bonds (see Fig. 1 b). Again, comparison is made with distributions from the available range of crystal structures (4). The -dihedral is 50% −sc, 29% sc, and 9% ap (12% eclipsed) for the Berger force field, and 16% −sc, 78% sc, and 4% ap (2% eclipsed) for CHARMM36. Only backbones with θ4 = +sc or −sc allow parallel chain stacking characteristic of a membrane bilayer arrangement. The -dihedral is 66% ap, 19% sc, and 1% −sc (14% eclipsed) for the Berger force field, and 14% ap, 32% sc, and 48% −sc (6% eclipsed) for CHARMM36. Backbones with ±sc conformations for θ4 and θ2 are favored by the “gauche effect” found in polyoxyethylene (75). However, combinations of θ4/θ2 dihedral angles −sc/sc, and sc/−sc with sn-2 as the leading chain, are excluded because each would rotate the headgroup back into the bilayer, and the former also exhibits a sterically forbidden θ3/θ1 = g+g− glycerol configuration (2). For a similar reason, the θ4/θ2 = ap/ap configuration (with θ3/θ1 = g−g+) is also strongly disfavored on intramolecular grounds. The values in Table 3 allow the favorable combinations θ4/θ2 = −sc/ap, sc/sc, and sc/ap with diminishing frequency for the Berger force field, and predominantly sc/−sc and sc/sc for CHARMM36. Of these, the sc/−sc and sc/sc combinations are strongly represented in the available crystal structures, and those involving ap conformers considerably less so. Correspondingly, the potential energy wells in CHARMM36 are deepest for θ4/θ2 = sc/−sc and sc/sc, and are less deep for sc/ap, ap/−sc, −sc/−sc, and −sc/ap (21).
Table 3.
Conformations of Glycerol Backbone and Chain Carboxyl Links in MD Simulations of POPC
| Dihedral | ap | sc | −sc | ac | −ac | sp | |
|---|---|---|---|---|---|---|---|
| Backbone | |||||||
| θ1 | Berger | 0.009 | 0.695 | 0.233 | 0.025 | 0.000 | 0.037 |
| CHARMM | 0.484 | 0.133 | 0.319 | 0.025 | 0.019 | 0.018 | |
| crystal | 0.45 | 0.14 | 0.36 | 0 | 0 | 0.05 | |
| θ2 | Berger | 0.657 | 0.194 | 0.010 | 0.068 | 0.071 | 0 |
| CHARMM | 0.138 | 0.323 | 0.476 | 0.020 | 0.023 | 0.019 | |
| crystal | 0.15 | 0.45 | 0.40 | 0 | 0 | 0 | |
| θ3 | Berger | 0.285 | 0.514 | 0.116 | 0.003 | 0.078 | 0.004 |
| CHARMM | 0.783 | 0.158 | 0.038 | 0.008 | 0.013 | 0.000 | |
| crystal | 0.76 | 0.24 | 0 | 0 | 0 | 0 | |
| θ4 | Berger | 0.091 | 0.293 | 0.498 | 0.089 | 0.025 | 0.004 |
| CHARMM | 0.040 | 0.778 | 0.163 | 0.009 | 0.000 | 0.008 | |
| crystal | 0 | 0.74 | 0.26 | 0 | 0 | 0 | |
| Chains | |||||||
| β1 | Berger | 0.192 | 0.472 | 0.022 | 0.312 | 0.001 | 0.000 |
| CHARMM | 0.271 | 0.362 | 0.005 | 0.362 | 0 | 0.000 | |
| crystal | 0.33 | 0.25 | 0 | 0.42 | 0 | 0 | |
| β2 | Berger | 0.970 | 0 | 0 | 0.022 | 0.003 | 0.004 |
| CHARMM | 0.992 | 0 | 0 | 0.005 | 0.003 | 0 | |
| crystal | 1.0 | 0 | 0 | 0 | 0 | 0 | |
| β3 | Berger | 0.100 | 0.105 | 0.308 | 0.110 | 0.303 | 0.077 |
| CHARMM | 0.374 | 0.015 | 0.214 | 0.037 | 0.334 | 0.024 | |
| crystal | 0.46 | 0 | 0.36 | 0 | 0.18 | 0 | |
| β4 | Berger | 0.760 | 0.089 | 0.083 | 0.034 | 0.032 | 0.000 |
| CHARMM | 0.422 | 0.314 | 0.173 | 0.059 | 0.031 | 0.000 | |
| crystal | 0.73 | 0.27 | 0 | 0 | 0 | 0 | |
| γ1 | Berger | 0.749 | 0.046 | 0.014 | 0.091 | 0.099 | 0.000 |
| CHARMM | 0.171 | 0.313 | 0.065 | 0.219 | 0.232 | 0 | |
| crystal | 0.54 | 0.05 | 0 | 0.32 | 0.09 | 0 | |
| γ2 | Berger | 0.979 | 0 | 0 | 0.006 | 0.014 | 0 |
| CHARMM | 0.995 | 0 | 0 | 0.002 | 0.003 | 0 | |
| crystal | 1.0 | 0 | 0 | 0 | 0 | 0 | |
| γ3 | Berger | 0.119 | 0.209 | 0.167 | 0.260 | 0.184 | 0.061 |
| CHARMM | 0.417 | 0.103 | 0.113 | 0.153 | 0.166 | 0.048 | |
| crystal | 0.73 | 0.09 | 0.04 | 0.09 | 0.04 | 0 | |
| γ4 | Berger | 0.755 | 0.087 | 0.091 | 0.032 | 0.034 | 0.000 |
| CHARMM | 0.646 | 0.141 | 0.133 | 0.041 | 0.038 | 0 | |
| crystal | 0.86 | 0.09 | 0.04 | 0 | 0 | 0 | |
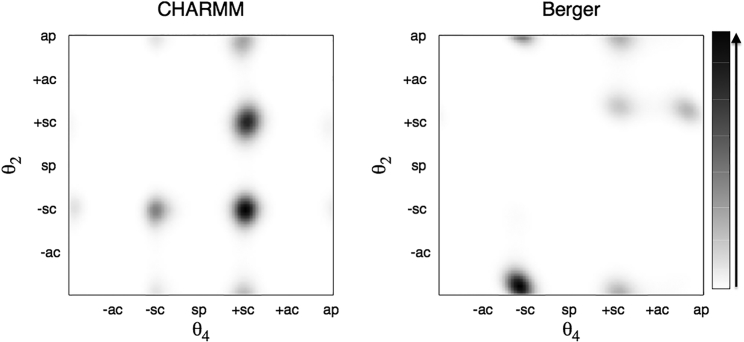
Fig. 5 shows the doublet distribution θ2/θ4 that confirms the above correlations, which were based on relative populations. For CHARMM36, we get θ4/θ2 = +sc/±sc with small contributions from sc/ap and −sc/−sc. For the Berger force field, we find predominantly θ4/θ2 = −sc/ap, with smaller contributions from sc/sc, sc/ap, and ap/sc.
Figure 5.
Doublet distributions for the pair of backbone dihedrals θ2/θ4 from simulations with the CHARMM force field (left) and that of Berger et al. (right).
Chain attachment
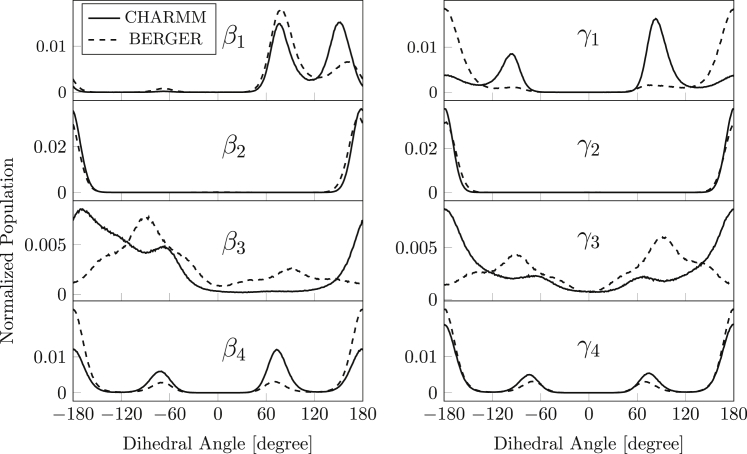
Fig. 6 shows the distributions of dihedral angles about the first four bonds in the attachment of the sn-1 and sn-2 acyl chains. For β1, γ1 and β3, γ3, there are considerable differences between the dihedral distributions produced by the two force fields. Steric interactions arising from torsion about the C−O bond restricts β1 and γ1 less than for C−C bonds (76). This makes differences between the two force fields difficult to interpret unambiguously for the first dihedral. The unique ap conformation for β2 and γ2 that is found with both force fields reflects the planar nature of the carboxyl ester, and is a feature common to all known bilayer phospholipid crystal structures (see Table 3). The subsequent β3 and γ3 C−C dihedrals specify which of the acyl chains, if any, is the leading chain. For γ3 = ap, sn-1 is the leading chain, and correspondingly for β3 = ap, sn-2 is the leading chain. Although either γ3 or β3 is in the ap conformation in phospholipid crystals, this is certainly not the case for simulations with the Berger force field (see Fig. 6; Table 3). Compared with bilayer crystal structures, the wide dihedral distribution for γ3 and β3 with maxima at approximately ±90° for the Berger force field is highly unusual. Moreover, the reflection symmetry of the two distributions indicates equivalence of the two chains. For the CHARMM36 force field, on the other hand, γ3 is mostly ap, which indicates that sn-1 is the leading chain, and β3 has a considerable –sc population, which favors a bent sn-2 chain.
Figure 6.
Distribution of dihedral angles at the carboxyl end of the POPC chains. Left sn-2 chain: β1 about the C2−O21 bond, β2 about the O21−C21 bond, β3 about the C21−C22 bond, and β4 about the C22−C23 bond. Right sn-1 chain: γ1 about the C1−O11 bond, γ2 about the O11−C11 bond, γ3 about the C11−C12 bond, and γ4 about the C12−C13 bond. CHARMM force field (solid line) and that of Berger et al. (dotted line).
The ap (trans) and mostly less populated ±sc (gauche) conformations for β4 and γ4 are characteristic of fluid lipid hydrocarbon chains, and persist throughout the remainder of the two chains except in the region of the 9,10-cis double bond of the sn-2 chain. This applies for both force fields.
Acyl chains
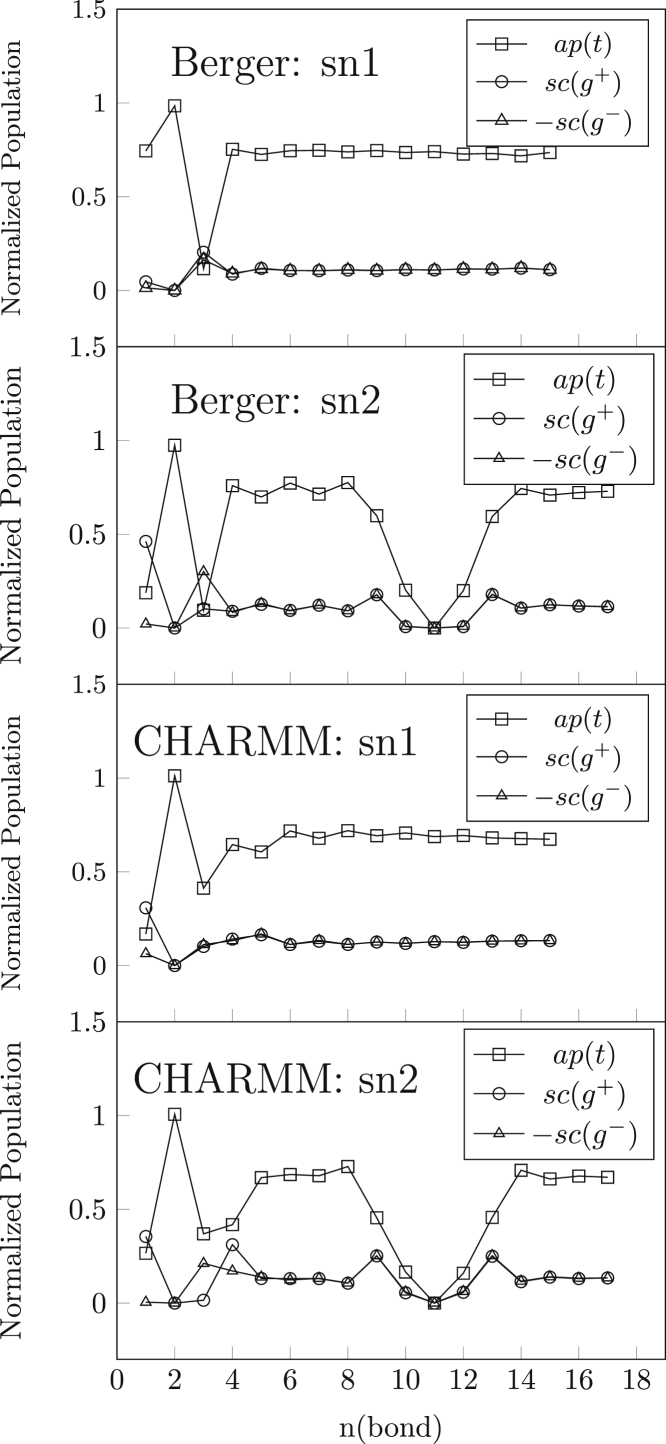
Fig. 7 shows the profile of rotamer populations in the sn-1 and sn-2 acyl chains. After the bonds that characterize the chain attachment, the populations of trans and gauche rotamers remain approximately constant throughout the length of the sn-1 chain. We see a similar pattern in the sn-2 chain except for bonds that immediately surround the 9,10-cis double bond, which are in skew (s) conformations. Quasi straight-chain packing about the double bond (Δ) arises with rotamer sequences such as g+s+Δs+ (77). Beyond the fourth bond, the chain profiles are similar for both force fields, with only slight quantitative differences in conformational populations. The dips in population profiles where gauche or trans conformations are replaced by skew conformations are directly reflected in the order profiles for the sn-2 chain that are presented in Fig. S1.
Figure 7.
Chain profiles of trans (ap, squares) and gauche± (+sc, circles; −sc, triangles) conformational populations of POPC. CHARMM force field (right) and that of Berger et al. (left). Top: sn-1 chain (γn-dihedrals); bottom: sn-2 chain (βn-dihedrals).
Discussion
The conformational populations given here represent the combined effects of both nonbonded interactions and torsional potentials in the corresponding force field. In addition, harmonic constraints maintain the cis configuration of the oleoyl chain and planarity of the carboxyl groups. The glycerol backbone is similarly restrained in the Berger force field to give the correct enantiomer. Correct stereochemistry is thereby achieved with both force fields, but considerable differences are found in the conformational distributions. The results raise two important general issues. Can the two force fields describe the universal sn-1/sn-2 chain inequivalence that characterizes molecular packing in tension-free fluid bilayers of sn-3 glycerophospholipids? Furthermore, to what extent do the MD conformations agree with the combined data from crystal structures of glycerophospholipids and spectroscopic (NMR and infrared) studies of their fluid-bilayer phases?
Headgroup conformation
Comparison of the headgroup conformation from MD simulations with those found in bilayer crystals is significant. This is because deuterium and phosphorus NMR anisotropies (or order parameters) can be explained by rapid interconversion between two mirror-image configurations that are related to those observed in glycerophosphocholine crystals (11, 12, 78). The two-enantiomer interpretation has been questioned as being oversimplified (79), but until now this has not been tested. Therefore, a detailed examination of headgroup configurations is warranted here. The polar-group structure produced by simulations with the Berger force field is that of the crystal conformation DMPC B (dimyristoyl phosphatidylcholine B) of the complete phosphatidylcholine molecule, whereas that from the CHARMM36 force field is closer to glycerophosphocholine alone.
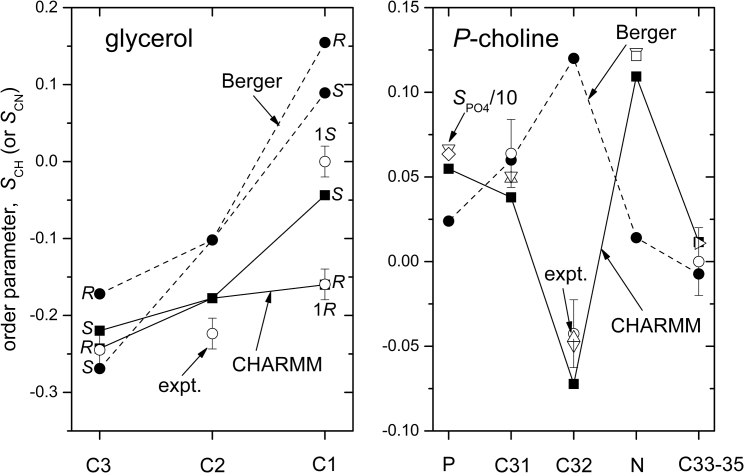
A direct experimental check on whether conformations predicted by simulation are appropriate to fluid hydrated bilayers comes from calculating explicitly the order parameters that we measure from NMR. The right panel of Fig. 8 gives the C−H (or C−D) order parameters for the C31 and C32 atoms, and the three equivalent C33−C35 methyl atoms. Experimental data for POPC are given by open symbols, with that from egg PC by the right-pointing triangle. The diastereotopic H-atoms of prochiral C31 and C32 methylenes (47) are dynamically near equivalent. Acceptable dynamic structures should therefore predict these experimentally observed equivalences. The order parameters predicted by CHARMM36 simulations (solid lines) describe the experimental measurements quite well. In contrast to the Berger force field (dashed lines), they predict the correct sign for the C32−H order parameter and for that of C33−H to C35−H. Otherwise, the Berger force field reproduces the measured C31−H order parameter reasonably well. Because the Berger force field uses united atoms, we introduced C−H vectors for these calculations at the tetrahedral angles specified by the positions of the united (i.e., heavy) atoms.
Figure 8.
Order parameter of the C−H (or C−D) bond in the headgroup (right panel) and glycerol backbone (left panel). Values for the C32−N bond and the phosphate group (×0.1) are also included. The C3 and C1 methylenes are prochiral with dynamically distinguishable pro-R and pro-S H-atoms (47); experimental assignments (1R, 1S) are from Ref. (97). The two H-atoms on C31 and C32 are dynamically equivalent. Open symbols are experimental values for POPC (circles: Ref. (85), at 300 K; triangles: Ref. (98), at 296 K; inverted triangles: Ref. (82), at 288 K; square: Ref. (70) at 308 K; diamond: Refs. (80, 81), at 299, 303 K), except the right triangle is for egg PC (Ref. (99), at 303 K). Signs are taken from (71, 72) for PC. Error bars are no greater than the size of the symbols, except for open circles. Solid lines connect values simulated with CHARMM36 (solid squares), and dashed lines those with the force field of Berger et al. (solid circles), but have no other significance. All samples are in water without ions, except for where 50 mM Tris, 1 mM EDTA pH 7.4 (82), or 20 mM NaCl, 30 mM HEPES, 5 mM EDTA pH 7.0 (80, 81) buffers are used.
The order parameter of the C32−N bond that is measured by 14N-NMR is related directly to the choline methyl CD3 order parameter (as explained in Methods) but is much larger in size. The right panel of Fig. 8 compares MD predictions with the experimental values for POPC. CHARMM36 produces much better agreement than does the Berger force field, as in the case of the C32−H and CD3 order parameters. Uncertainties in order parameters from these measurements are no larger than the open symbols. The prediction from CHARMM36 is close to the experimental values, but still lies outside the estimated error range.
The order parameters for the principal axes of the 31P-phosphate diester chemical shift anisotropy are , 0.058 (O31−O32) and , −0.105 (O33−O34) from CHARMM36 and the Berger force field, respectively. From Eq. 3 we then predict measured chemical shift anisotropies: , and −18 ppm for CHARMM36 and Berger, respectively. These are smaller (in absolute terms) than the experimental values for POPC of −47 ± 0.5 ppm at 298 and 303 K (80, 81) and −49.4 ppm at 288 K (82). However, the prediction from CHARMM36 is much closer than that from the force field of Berger et al. These calculations depend somewhat on the principal values chosen for the csa tensor. Values of the order parameter derived from Eq. 4 are included in the comparison of simulation with experiment that we show in Fig. 8; the uncertainty is less than the size of the symbols, and the CHARMM prediction lies well outside this.
An extensive survey of different force fields shows that CHARMM36 is best at predicting C31−H and C32−H order parameters of the choline headgroup and the only one to give the correct sign for C32−H (29). In this work and a later review (83), it was concluded that one must improve existing force fields for the choline headgroup and also the glycerol backbone. However, the two choline order parameters considered by no means sample all dihedral angles of the phosphocholine headgroup, e.g., the relative sign of α5. Comparison with the phosphatidylcholine crystal conformation (see above) shows that CHARMM36 predictions for fluid membranes differ in the α4 dihedral and in the sense of α5. Interpretation of C−D order parameters from fluid-phase dipalmitoyl PC bilayers suggests that α4 is in a ± ac conformation and that α5 might assume either relative sign (78). On the other hand, C−D order parameters from POPC bicelles at 35°C are well fitted by a single α3/α4/α5 = −sc/ap/+sc conformation, coupled to rapid axial rotation (84). Further force field development clearly should include the entire phosphocholine headgroup, making use of 31P-csa and quadrupole splittings of 14N and choline CD3 groups, as is done here.
Glycerol backbone and chain attachment
The conformations of the glycerol backbone produced by the CHARMM36 force field are closer to those of the majority species in crystal structures than are those produced by the force field of Berger et al. This consensus configuration also corresponds to one of the conformers sc/sn-1/−sc found in bilayer crystals of dimyristoyl sn-3 phosphatidylcholine (viz., DMPC B) (64). The other is sc/sn-1/ap (viz., DMPC A), which appears weakly with the Berger force field.
The sn-1 and sn-2 chains are equivalent with the Berger force field, which therefore produces no leading chain. In contrast, CHARMM36 simulations produce chain inequivalence with sn-1 as the leading chain, as established experimentally from measurement of deuterium-NMR order parameters SCD (8, 9). This is not entirely surprising, because the β1, θ4, and θ2 potential surfaces in CHARMM36 are optimized empirically to fit the anomalous SCD for C-2 of the sn-2 chain (i.e., C22), which is the hallmark of fluid-phase chain inequivalence (21). Indeed, CHARMM36 is the only force field so far to produce inequivalent order parameters for the two C-2 deuterons. Chain order-parameter profiles from both force fields are shown in Fig. S1. These confirm the above remarks. In particular, sn-1 is the leading chain in the CHARMM36 simulation, and −SCD for the C-2 methylene of the sn-2 chain is much smaller than for sn-1, although the inequivalence between the two C−D bonds is less than that found experimentally. It is no larger than predicted by CHARMM36 for C-2 at sn-1; after adding H-atoms, the Berger et al. force field predicts negligible inequivalence. Also, order profiles down the chain differ in detail between the CHARMM36 and Berger force fields. Comparison of MD-simulated profiles with experimental chain order parameters of POPC are shown already in (21, 85).
The unusual symmetrical chain packing configuration of the Berger lipids may be responsible for overbinding of Na+ ions. Fluid-bilayer simulations with the Berger et al. force field predict Na+ binding to the carboxyl ester groups of phosphatidylcholine (see 25, 27, 86; and references therein). Experimental studies, however, exclude the possibility that Na+ binds significantly to phosphatidylcholine bilayers (4). The electrophoretic mobility of pure phosphatidylcholine vesicles is very low, independent of NaCl concentration (87, 88). Experimental estimates for the Na+ association constant are 0.15 M−1 (89, 90), which puts the dissociation constant at a concentration above the maximal solubility of NaCl in water. Comparing the partial atomic charges of the Berger et al. force field with those of CHARMM36 (see Table S1) reveals a considerably higher negative charge on the ester oxygens for the Berger force field, in addition to the difference in chain accessibility. Note, however, that a small increase in radius for the Lennard-Jones O−Na+ interaction in CHARMM36 is still needed to reduce residual binding to POPC (26; see also Ref. 27 in the Supporting Material).
The left panel of Fig. 8 gives the C−H order parameters for the C1−C3 atoms of the glycerol backbone. Experimental values are shown as open symbols. The pro-R and pro-S H-atoms attached at C1, and to a lesser extent those at C3, are inequivalent (47). Predictions from CHARMM36 simulations (solid line) agree rather well with the experimental order parameters, particularly the difference between the diastereomers for C1−H. We expect this from the good agreement with the backbone conformation in bilayer crystals and the fact that CHARMM36 is specifically tailored to reproduce the sn-1/sn-2 chain inequivalence (see above). There is little agreement between experiment and predictions for the glycerol backbone from the Berger force field (dashed line), as we anticipate from the very different conformation produced by using this approach (see above). These differences between predictions for the glycerol-backbone order parameters are indeed found for a much wider range of lipid force fields (29, 83). As already mentioned, the latter authors conclude that further improvements in force fields could help to match the backbone order parameters better.
Chain conformation
Both force fields agree in predicting a relatively constant rotamer population throughout the length of the hydrocarbon chain, except close to the cis double bond of the sn-2 oleoyl chain. The well-known chain-order-parameter profile (see Fig. S1) is the cumulative effect of these gauche rotamers down the chain. In total, the sn-1 chain (γ4−γ15) contains approximately 3.1 gauche rotamers using CHARMM36 (2.6 from Berger), with a roughly equal distribution between g+ and g−: (0.11 for Berger). Outside the region of the double bond, the gauche probability in the sn-2 chain (β4−β8, β14−β17) is similar to that in the sn-1 chain: (0.11 for Berger). These values are in the region of earlier statistical mechanical estimates using the isomeric state model (91, 92) and more recent spectroscopic measurements (reviewed in 93; see also 94, 95, 96). The differences in gauche probability between CHARMM36 and Berger are reflected in the different chain-order profiles for these two force fields that are shown in Fig. S1. Although the probability of an individual gauche conformation does not vary greatly along the chain, the cumulative effect at a given chain segment depends on the absolute value of pg. Also, the probability of higher-order combinations of neighboring gauche conformations increases on proceeding down the chain.
Unlike the lipid structures in the PDB to which we referred in the Introduction, none of the chains from MD simulations are in high-energy eclipsed conformations, even for the united-atom force field.
Conclusion
The ultimate aim of atomistic MD is to describe the properties of membranes by the behavior of real lipid molecules. Only then can we access all properties down to the shortest scales. To do this, the constituent lipids must have realistic molecular structures that conform to the configurational and packing principles established in lipid crystals. This a fundamental question of wide and general interest that lies at the heart of molecular approaches to biophysics.
The dynamic lipid structures produced by MD simulations display none of the conformational irregularities that are a frequent feature of lipid structures deposited in the PDB (5, 6, 7). Nevertheless, the two popular force fields used here differ in the structures predicted, particularly for the phosphatidylcholine polar headgroup and the glycerol backbone. Not surprisingly, CHARMM36 performs extremely well for the backbone, for which it specifically is optimized. The situation for the polar group is more interesting. The order parameters and the order parameter, and the 31P-csa, are all reproduced quite well by CHARMM36; most importantly, this includes the signs (see Fig. 8). The predicted α4 dihedral is not that found in the favored phosphatidylcholine crystal structure (DMPC B), nor that used in one case to describe order parameters of the POPC headgroup (84). However, α4 = ±ac is the dihedral used originally for interpreting the order parameters, which were based on the crystal structure of glycerophosphocholine, not that of phosphatidylcholine (11, 78). Note that the set of α-dihedral values used originally (11) predicted the negative sign of for C32 correctly, before this was established experimentally. The relative sign predicted for α5 by CHARMM36 is that found in the phosphatidylethanolamine headgroup, not that in the crystal structure of phosphatidylcholine (see, e.g., 4, 6), nor that used originally for the phosphatidylcholine order parameters (11). This is probably related to difficulties in packing choline headgroups in bilayer crystals, which are alleviated in fluid bilayers.
The success of CHARMM36 in accounting for the whole range of experimentally available headgroup order parameters in Fig. 8 suggests that the original interpretation of the 2H-NMR results in terms of exchange between two mirror-image headgroup conformations could be substantially correct. This is because the dihedral distributions in Figs. 2 and 3 are predominantly symmetrical, and hence approximately consistent with interconverting enantiomers. The detailed conformational populations differ, and more work would be useful to test the predictions of headgroup conformation from MD simulations with different force fields. It would help to concentrate further on the extended range of headgroup order parameters, i.e., including 31P-csa and (or ) as experimental targets for validation in force field development. The phosphate group, in particular, is central to the dynamic behavior of the entire lipid molecule because it is located directly at the interface between polar and hydrophobic regions, and reflects the angular fluctuations of the whole molecule (68). Because of the close link between molecular conformation and bilayer dimensions, improvements in agreement with NMR order parameters are unlikely to compromise agreement with area/molecule and molecular thicknesses. But whether this extends from dimensional properties to the elastic and thermodynamic properties of lipid bilayers is less certain.
Author Contributions
D.M. and H.K. designed research. W.P. performed research. D.M. wrote paper together with the other authors.
Acknowledgments
D.M. thanks the Hans Christian Andersen Foundation (University of Southern Denmark) and Christian Griesinger and the Department of NMR-Based Structural Biology (Max-Planck-Institut) for financial assistance.
Editor: Markus Deserno.
Footnotes
One figure and one table are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(18)30246-7.
Supporting Material
References
- 1.Hauser H., Pascher I., Sundell S. Preferred conformation and molecular packing of phosphatidylethanolamine and phosphatidylcholine. Biochim. Biophys. Acta. 1981;650:21–51. doi: 10.1016/0304-4157(81)90007-1. [DOI] [PubMed] [Google Scholar]
- 2.Pascher I., Lundmark M., Sundell S. Crystal structures of membrane lipids. Biochim. Biophys. Acta. 1992;1113:339–373. doi: 10.1016/0304-4157(92)90006-v. [DOI] [PubMed] [Google Scholar]
- 3.Pascher I. The different conformations of the glycerol region of crystalline acylglycerols. Curr. Opin. Struct. Biol. 1996;6:439–448. doi: 10.1016/s0959-440x(96)80107-2. [DOI] [PubMed] [Google Scholar]
- 4.Marsh D. CRC Press; Boca Raton, FL: 2013. Handbook of Lipid Bilayers. [Google Scholar]
- 5.Marsh D. Lipid-binding proteins: structure of the phospholipid ligands. Protein Sci. 2003;12:2109–2117. doi: 10.1110/ps.0396803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Marsh D., Páli T. Lipid conformation in crystalline bilayers and in crystals of transmembrane proteins. Chem. Phys. Lipids. 2006;141:48–65. doi: 10.1016/j.chemphyslip.2006.02.005. [DOI] [PubMed] [Google Scholar]
- 7.Marsh D., Páli T. Orientation and conformation of lipids in crystals of transmembrane proteins. Eur. Biophys. J. 2013;42:119–146. doi: 10.1007/s00249-012-0816-6. [DOI] [PubMed] [Google Scholar]
- 8.Seelig A., Seelig J. Bilayers of dipalmitoyl-3-sn-phosphatidylcholine. Conformational differences between the fatty acyl chains. Biochim. Biophys. Acta. 1975;406:1–5. doi: 10.1016/0005-2736(75)90037-1. [DOI] [PubMed] [Google Scholar]
- 9.Seelig J., Browning J.L. General features of phospholipid conformation in membranes. FEBS Lett. 1978;92:41–44. [Google Scholar]
- 10.Marsh D., Watts A., Smith I.C.P. Dynamic structure and phase behavior of dimyristoylphosphatidylethanolamine bilayers studied by deuterium nuclear magnetic resonance. Biochemistry. 1983;22:3023–3026. doi: 10.1021/bi00281a036. [DOI] [PubMed] [Google Scholar]
- 11.Seelig J., Gally H.U., Wohlgemuth R. Orientation and flexibility of the choline head group in phosphatidylcholine bilayers. Biochim. Biophys. Acta. 1977;467:109–119. doi: 10.1016/0005-2736(77)90188-2. [DOI] [PubMed] [Google Scholar]
- 12.Seelig J., Gally H.U. Investigation of phosphatidylethanolamine bilayers by deuterium and phosphorus-31 nuclear magnetic resonance. Biochemistry. 1976;15:5199–5204. doi: 10.1021/bi00669a001. [DOI] [PubMed] [Google Scholar]
- 13.Hong M., Schmidt-Rohr K., Zimmermann H. Conformational constraints on the headgroup and sn-2 chain of bilayer DMPC from NMR dipolar couplings. Biochemistry. 1996;35:8335–8341. doi: 10.1021/bi953083i. [DOI] [PubMed] [Google Scholar]
- 14.Schlenkrich M., Brickmann J., Karplus M. An empirical potential energy function for phospholipids: criteria for parameter optimization and applications. In: Merz K.M. Jr., Roux B., editors. Biological Membranes: A Molecular Perspective from Computation and Experiment. Birkhäuser; 1996. pp. 31–81. [Google Scholar]
- 15.Klauda J.B., Venable R.M., Pastor R.W. Considerations for lipid force field development. In: Feller S.E., editor. Current Topics in Membranes: Computational Modeling of Membrane Bilayers. Elsevier; 2008. pp. 1–48. [Google Scholar]
- 16.Sapay N., Tielemann D.P. Molecular dynamics simulation of lipid-protein interactions. In: Feller S.E., editor. Current Topics in Membranes: Computational Modeling of Membrane Bilayers. Elsevier; 2008. pp. 111–130. [Google Scholar]
- 17.Pastor R.W., Mackerell A.D., Jr. Development of the CHARMM force field for lipids. J. Phys. Chem. Lett. 2011;2:1526–1532. doi: 10.1021/jz200167q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Venable R.M., Brown F.L.H., Pastor R.W. Mechanical properties of lipid bilayers from molecular dynamics simulation. Chem. Phys. Lipids. 2015;192:60–74. doi: 10.1016/j.chemphyslip.2015.07.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Egberts E., Marrink S.-J., Berendsen H.J.C. Molecular dynamics simulation of a phospholipid membrane. Eur. Biophys. J. 1994;22:423–436. doi: 10.1007/BF00180163. [DOI] [PubMed] [Google Scholar]
- 20.Berger O., Edholm O., Jähnig F. Molecular dynamics simulations of a fluid bilayer of dipalmitoylphosphatidylcholine at full hydration, constant pressure, and constant temperature. Biophys. J. 1997;72:2002–2013. doi: 10.1016/S0006-3495(97)78845-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Klauda J.B., Venable R.M., Pastor R.W. Update of the CHARMM all-atom additive force field for lipids: validation on six lipid types. J. Phys. Chem. B. 2010;114:7830–7843. doi: 10.1021/jp101759q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Marsh D. Lateral pressure in membranes. Biochim. Biophys. Acta. 1996;1286:183–223. doi: 10.1016/s0304-4157(96)00009-3. [DOI] [PubMed] [Google Scholar]
- 23.Marsh D. Renormalization of the tension and area expansion modulus in fluid membranes. Biophys. J. 1997;73:865–869. doi: 10.1016/S0006-3495(97)78119-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Chiu S.W., Clark M., Jakobsson E. Incorporation of surface tension into molecular dynamics simulation of an interface: a fluid phase lipid bilayer membrane. Biophys. J. 1995;69:1230–1245. doi: 10.1016/S0006-3495(95)80005-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Khandelia H., Witzke S., Mouritsen O.G. Interaction of salicylate and a terpenoid plant extract with model membranes: reconciling experiments and simulations. Biophys. J. 2010;99:3887–3894. doi: 10.1016/j.bpj.2010.11.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Venable R.M., Luo Y., Pastor R.W. Simulations of anionic lipid membranes: development of interaction-specific ion parameters and validation using NMR data. J. Phys. Chem. B. 2013;117:10183–10192. doi: 10.1021/jp401512z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Catte A., Girych M., Vilov S. Molecular electrometer and binding of cations to phospholipid bilayers. Phys. Chem. Chem. Phys. 2016;18:32560–32569. doi: 10.1039/c6cp04883h. [DOI] [PubMed] [Google Scholar]
- 28.Poger D., Caron B., Mark A.E. Validating lipid force fields against experimental data: progress, challenges and perspectives. Biochim. Biophys. Acta. 2016;1858:1556–1565. doi: 10.1016/j.bbamem.2016.01.029. [DOI] [PubMed] [Google Scholar]
- 29.Botan A., Favela-Rosales F., Tynkkynen J. Toward atomistic resolution structure of phosphatidylcholine headgroup and glycerol backbone at different ambient conditions. J. Phys. Chem. B. 2015;119:15075–15088. doi: 10.1021/acs.jpcb.5b04878. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Sonne J., Jensen M.O., Peters G.H. Reparameterization of all-atom dipalmitoylphosphatidylcholine lipid parameters enables simulation of fluid bilayers at zero tension. Biophys. J. 2007;92:4157–4167. doi: 10.1529/biophysj.106.087130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Klauda J.B., Kucerka N., Nagle J.F. Simulation-based methods for interpreting x-ray data from lipid bilayers. Biophys. J. 2006;90:2796–2807. doi: 10.1529/biophysj.105.075697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Galindo-Murillo R., Robertson J.C., Cheatham T.E., III Assessing the current state of AMBER force field modifications for DNA. J. Chem. Theory Comput. 2016;12:4114–4127. doi: 10.1021/acs.jctc.6b00186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Lindorff-Larsen K., Maragakis P., Shaw D.E. Systematic validation of protein force fields against experimental data. PLoS One. 2012;7:e32131. doi: 10.1371/journal.pone.0032131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Piana S., Lindorff-Larsen K., Shaw D.E. How robust are protein folding simulations with respect to force field parameterization? Biophys. J. 2011;100:L47–L49. doi: 10.1016/j.bpj.2011.03.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Lange O.F., van der Spoel D., de Groot B.L. Scrutinizing molecular mechanics force fields on the submicrosecond timescale with NMR data. Biophys. J. 2010;99:647–655. doi: 10.1016/j.bpj.2010.04.062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Huang J., Rauscher S., MacKerell A.D., Jr. CHARMM36m: an improved force field for folded and intrinsically disordered proteins. Nat. Methods. 2017;14:71–73. doi: 10.1038/nmeth.4067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Sezer D., Freed J.H., Roux B. Multifrequency electron spin resonance spectra of a spin-labeled protein calculated from molecular dynamics simulations. J. Am. Chem. Soc. 2009;131:2597–2605. doi: 10.1021/ja8073819. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Kuprusevicius E., White G., Oganesyan V.S. Prediction of nitroxide spin label EPR spectra from MD trajectories: application to myoglobin. Faraday Discuss. 2011;148:283–298. doi: 10.1039/c004855k. [DOI] [PubMed] [Google Scholar]
- 39.Budil D.E., Sale K.L., Fajer P.G. Calculating slow-motional electron paramagnetic resonance spectra from molecular dynamics using a diffusion operator approach. J. Phys. Chem. A. 2006;110:3703–3713. doi: 10.1021/jp054738k. [DOI] [PubMed] [Google Scholar]
- 40.Kassem M.M., Wang Y., Lindorff-Larsen K. Structure of the bacterial cytoskeleton protein bactofilin by NMR chemical shifts and sequence variation. Biophys. J. 2016;110:2342–2348. doi: 10.1016/j.bpj.2016.04.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Rauscher S., Gapsys V., Grubmüller H. Structural ensembles of intrinsically disordered proteins depend strongly on force field: a comparison to experiment. J. Chem. Theory Comput. 2015;11:5513–5524. doi: 10.1021/acs.jctc.5b00736. [DOI] [PubMed] [Google Scholar]
- 42.Beauchamp K.A., Lin Y.-S., Pande V.S. Are protein force fields getting better? A systematic benchmark on 524 diverse NMR measurements. J. Chem. Theory Comput. 2012;8:1409–1414. doi: 10.1021/ct2007814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Best R.B., Hofmann H., Schuler B. Quantitative interpretation of FRET experiments via molecular simulation: force field and validation. Biophys. J. 2015;108:2721–2731. doi: 10.1016/j.bpj.2015.04.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Reif M.M., Oostenbrink C. Molecular dynamics simulation of configurational ensembles compatible with experimental FRET efficiency data through a restraint on instantaneous FRET efficiencies. J. Comput. Chem. 2014;35:2319–2332. doi: 10.1002/jcc.23756. [DOI] [PubMed] [Google Scholar]
- 45.Hoefling M., Lima N., Grubmüller H. Structural heterogeneity and quantitative FRET efficiency distributions of polyprolines through a hybrid atomistic simulation and Monte Carlo approach. PLoS One. 2011;6:e19791. doi: 10.1371/journal.pone.0019791. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Sundaralingam M. Discussion paper: molecular structures and conformations of the phospholipids and sphingomyelins. Ann. N. Y. Acad. Sci. 1972;195:324–355. [PubMed] [Google Scholar]
- 47.IUPAC Commission on Nomenclature of Organic Chemistry Rules for the nomenclature of organic chemistry. Section E: stereochemistry. Pure Appl. Chem. 1976;45:11–30. [Google Scholar]
- 48.IUPAC-IUB Commission on Biochemical Nomenclature (CBN) Nomenclature of lipids. Amendments 1968. Eur. J. Biochem. 1970;12:1–2. doi: 10.1111/j.1432-1033.1967.tb00116.x. [DOI] [PubMed] [Google Scholar]
- 49.Klyne W., Prelog V. Description of steric relationships across single bonds. Experientia. 1960;16:521–523. [Google Scholar]
- 50.Berendsen H.J.C., van der Spoel D., van Drunen R. GROMACS: a message-passing parallel molecular dynamics implementation. Comput. Phys. Commun. 1995;91:43–56. [Google Scholar]
- 51.Van Der Spoel D., Lindahl E., Berendsen H.J.C. GROMACS: fast, flexible, and free. J. Comput. Chem. 2005;26:1701–1718. doi: 10.1002/jcc.20291. [DOI] [PubMed] [Google Scholar]
- 52.Hess B., Kutzner C., Lindahl E. GROMACS 4: algorithms for highly efficient, load-balanced and scalable molecular simulation. J. Chem. Theory Comput. 2008;4:435–447. doi: 10.1021/ct700301q. [DOI] [PubMed] [Google Scholar]
- 53.MacKerell A.D., Bashford D., Karplus M. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. B. 1998;102:3586–3616. doi: 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
- 54.Berendsen H.J.C., Postma J.P.M., Hermans J. Interaction models for water in relation to protein hydration. In: Pullman B., editor. Intermolecular Forces (Jerusalem Symposia) Springer; 1981. pp. 331–342. [Google Scholar]
- 55.Hess B., Bekker H., Fraaije J.G.E.M. LINCS: a linear constraint solver for molecular simulations. J. Comput. Chem. 1997;18:1463–1472. [Google Scholar]
- 56.Kopec W., Khandelia H. Reinforcing the membrane-mediated mechanism of action of the anti-tuberculosis candidate drug thioridazine with molecular simulations. J. Comput. Aided Mol. Des. 2014;28:123–134. doi: 10.1007/s10822-014-9737-z. [DOI] [PubMed] [Google Scholar]
- 57.Darden T., York D., Pedersen N.C. Particle mesh Ewald: an N-log(N) method for Ewald sums in large systems. J. Chem. Phys. 1993;98:10089–10092. [Google Scholar]
- 58.Essmann U., Perera L., Pedersen L.G. A smooth particle mesh Ewald method. J. Chem. Phys. 1995;103:8577–8593. [Google Scholar]
- 59.Berendsen H.J.C., Postma J.P.M., Haak J.R. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984;81:3684–3690. [Google Scholar]
- 60.Hoover W.G. Canonical dynamics: equilibrium phase-space distributions. Phys. Rev. A Gen. Phys. 1985;31:1695–1697. doi: 10.1103/physreva.31.1695. [DOI] [PubMed] [Google Scholar]
- 61.Parrinello M., Rahman A. Polymorphic transitions in single-crystals - a new molecular-dynamics method. J. Appl. Phys. 1981;52:7182–7190. [Google Scholar]
- 62.Schorn K., Marsh D. Dynamic chain conformations in dimyristoyl glycerol-dimyristoyl phosphatidylcholine mixtures. 2H-NMR studies. Biophys. J. 1996;71:3320–3329. doi: 10.1016/S0006-3495(96)79524-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Gally H.U., Niederberger W., Seelig J. Conformation and motion of the choline head group in bilayers of dipalmitoyl-3-sn-phosphatidylcholine. Biochemistry. 1975;14:3647–3652. doi: 10.1021/bi00687a021. [DOI] [PubMed] [Google Scholar]
- 64.Pearson R.H., Pascher I. The molecular structure of lecithin dihydrate. Nature. 1979;281:499–501. doi: 10.1038/281499a0. [DOI] [PubMed] [Google Scholar]
- 65.Siminovitch D.J., Rance M., Jeffrey K.R. The use of wide-line 14N nitrogen NMR as a probe in model membranes. FEBS Lett. 1980;112:79–82. doi: 10.1016/0014-5793(80)80132-3. [DOI] [PubMed] [Google Scholar]
- 66.Seelig J. 31P nuclear magnetic resonance and the head group structure of phospholipids in membranes. Biochim. Biophys. Acta. 1978;515:105–140. doi: 10.1016/0304-4157(78)90001-1. [DOI] [PubMed] [Google Scholar]
- 67.Dufourc E.J., Mayer C., Kothe G. Dynamics of phosphate head groups in biomembranes. Comprehensive analysis using phosphorus-31 nuclear magnetic resonance lineshape and relaxation time measurements. Biophys. J. 1992;61:42–57. doi: 10.1016/S0006-3495(92)81814-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Griffin R.G., Powers L., Pershan P.S. Head-group conformation in phospholipids: a phosphorus-31 nuclear magnetic resonance study of oriented monodomain dipalmitoylphosphatidylcholine bilayers. Biochemistry. 1978;17:2718–2722. doi: 10.1021/bi00607a004. [DOI] [PubMed] [Google Scholar]
- 69.Marsh D., Swamy M.J. Derivatised lipids in membranes. Physico-chemical aspects of N-biotinyl phosphatidylethanolamines, N-acyl phosphatidylethanolamines and N-acyl ethanolamines. Chem. Phys. Lipids. 2000;105:43–69. doi: 10.1016/s0009-3084(99)00132-2. [DOI] [PubMed] [Google Scholar]
- 70.Santos J.S., Lee D.-K., Ramamoorthy A. Effects of antidepressants on the conformation of phospholipid headgroups studied by solid-state NMR. Magn. Reson. Chem. 2004;42:105–114. doi: 10.1002/mrc.1327. [DOI] [PubMed] [Google Scholar]
- 71.Gross J.D., Warschawski D.E., Griffin R.G. Dipolar recoupling in MAS NMR: a probe for segmental order in lipid bilayers. J. Am. Chem. Soc. 1997;119:796–802. [Google Scholar]
- 72.Hong M., Schmidt-Rohr K., Nanz D. Study of phospholipid structure by 1H, 13C, and 31P dipolar couplings from two-dimensional NMR. Biophys. J. 1995;69:1939–1950. doi: 10.1016/S0006-3495(95)80064-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Gorenstein D.G., Kar D. Effect of bond angle distortion on torsional potentials. Ab initio and CNDO/2 calculations on dimethoxymethane and dimethyl phosphate. J. Am. Chem. Soc. 1977;99:672–677. [Google Scholar]
- 74.Akutsu H. Direct determination by Raman scattering of the conformation of the choline group in phospholipid bilayers. Biochemistry. 1981;20:7359–7366. doi: 10.1021/bi00529a006. [DOI] [PubMed] [Google Scholar]
- 75.Abe A., Mark J.E. Conformational energies and the random-coil dimensions and dipole-moments of the polyoxides CH3O[(CH2)yO]xCH3. J. Am. Chem. Soc. 1976;98:6468–6476. [Google Scholar]
- 76.Flory P.J. Wiley; London or New York: 1969. Statistical Mechanics of Chain Molecules. [Google Scholar]
- 77.Li S., Lin H.N., Huang C. Identification and characterization of kink motifs in 1-palmitoyl-2-oleoyl-phosphatidylcholines: a molecular mechanics study. Biophys. J. 1994;66:2005–2018. doi: 10.1016/S0006-3495(94)80993-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Akutsu H., Nagamori T. Conformational analysis of the polar head group in phosphatidylcholine bilayers: a structural change induced by cations. Biochemistry. 1991;30:4510–4516. doi: 10.1021/bi00232a020. [DOI] [PubMed] [Google Scholar]
- 79.Skarjune R., Oldfield E. Physical studies of cell surface and cell membrane structure. Determination of phospholipid head group organization by deuterium and phosphorus nuclear magnetic resonance spectroscopy. Biochemistry. 1979;18:5903–5909. doi: 10.1021/bi00593a022. [DOI] [PubMed] [Google Scholar]
- 80.Zhang L., Liu L., Dabney-Smith C. Investigating the interaction between peptides of the amphipathic helix of Hcf106 and the phospholipid bilayer by solid-state NMR spectroscopy. Biochim. Biophys. Acta. 2014;1838:413–418. doi: 10.1016/j.bbamem.2013.10.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Lu J.X., Blazyk J., Lorigan G.A. Exploring membrane selectivity of the antimicrobial peptide KIGAKI using solid-state NMR spectroscopy. Biochim. Biophys. Acta. 2006;1758:1303–1313. doi: 10.1016/j.bbamem.2006.02.002. [DOI] [PubMed] [Google Scholar]
- 82.Tamm L., Seelig J. Lipid solvation of cytochrome c oxidase. Deuterium, nitrogen-14, and phosphorus-31 nuclear magnetic resonance studies on the phosphocholine head group and on cis-unsaturated fatty acyl chains. Biochemistry. 1983;22:1474–1483. doi: 10.1021/bi00275a023. [DOI] [PubMed] [Google Scholar]
- 83.Ollila O.H.S., Pabst G. Atomistic resolution structure and dynamics of lipid bilayers in simulations and experiments. Biochim. Biophys. Acta. 2016;1858:2512–2528. doi: 10.1016/j.bbamem.2016.01.019. [DOI] [PubMed] [Google Scholar]
- 84.Semchyschyn D.J., Macdonald P.M. Conformational response of the phosphatidylcholine headgroup to bilayer surface charge: torsion angle constraints from dipolar and quadrupolar couplings in bicelles. Magn. Reson. Chem. 2004;42:89–104. doi: 10.1002/mrc.1333. [DOI] [PubMed] [Google Scholar]
- 85.Ferreira T.M., Coreta-Gomes F., Topgaard D. Cholesterol and POPC segmental order parameters in lipid membranes: solid state 1H-13C NMR and MD simulation studies. Phys. Chem. Chem. Phys. 2013;15:1976–1989. doi: 10.1039/c2cp42738a. [DOI] [PubMed] [Google Scholar]
- 86.Khandelia H., Mouritsen O.G. Lipid gymnastics: evidence of complete acyl chain reversal in oxidized phospholipids from molecular simulations. Biophys. J. 2009;96:2734–2743. doi: 10.1016/j.bpj.2009.01.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.McDaniel R.V., McLaughlin A., McLaughlin S. Bilayer membranes containing the ganglioside GM1: models for electrostatic potentials adjacent to biological membranes. Biochemistry. 1984;23:4618–4624. doi: 10.1021/bi00315a016. [DOI] [PubMed] [Google Scholar]
- 88.Winiski A.P., McLaughlin A.C., McLaughlin S. An experimental test of the discreteness-of-charge effect in positive and negative lipid bilayers. Biochemistry. 1986;25:8206–8214. doi: 10.1021/bi00373a013. [DOI] [PubMed] [Google Scholar]
- 89.Tatulian S.A. Binding of alkaline-earth metal cations and some anions to phosphatidylcholine liposomes. Eur. J. Biochem. 1987;170:413–420. doi: 10.1111/j.1432-1033.1987.tb13715.x. [DOI] [PubMed] [Google Scholar]
- 90.Macdonald P.M., Seelig J. Calcium binding to mixed phosphatidylglycerol-phosphatidylcholine bilayers as studied by deuterium nuclear magnetic resonance. Biochemistry. 1987;26:1231–1240. doi: 10.1021/bi00379a005. [DOI] [PubMed] [Google Scholar]
- 91.Cevc G., Marsh D. Wiley-Interscience; New York: 1987. Phospholipid Bilayers. Physical Principles and Models. [Google Scholar]
- 92.Marsh D. Statistical mechanics of the fluidity of phospholipid bilayers and membranes. J. Membr. Biol. 1974;18:145–162. [Google Scholar]
- 93.Feller S.E., MacKerell A.D., Jr. An improved empirical potential energy function for molecular simulations of phospholipids. J. Phys. Chem. B. 2000;104:7510–7515. [Google Scholar]
- 94.Moser M., Marsh D., Kothe G. Chain configuration and flexibility gradient in phospholipid membranes. Comparison between spin-label electron spin resonance and deuteron nuclear magnetic resonance, and identification of new conformations. Biophys. J. 1989;55:111–123. doi: 10.1016/S0006-3495(89)82784-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Mendelsohn R., Davies M.A., Dluhy R.A. Quantitative determination of conformational disorder in the acyl chains of phospholipid bilayers by infrared spectroscopy. Biochemistry. 1989;28:8934–8939. doi: 10.1021/bi00448a037. [DOI] [PubMed] [Google Scholar]
- 96.Casal H.L., McElhaney R.N. Quantitative determination of hydrocarbon chain conformational order in bilayers of saturated phosphatidylcholines of various chain lengths by Fourier transform infrared spectroscopy. Biochemistry. 1990;29:5423–5427. doi: 10.1021/bi00475a002. [DOI] [PubMed] [Google Scholar]
- 97.Gally H.U., Pluschke G., Seelig J. Structure of Escherichia coli membranes. Glycerol auxotrophs as a tool for the analysis of the phospholipid head-group region by deuterium magentic resonance. Biochemistry. 1981;20:1826–1831. doi: 10.1021/bi00510a017. [DOI] [PubMed] [Google Scholar]
- 98.Bechinger B., Seelig J. Conformational changes of the phosphatidylcholine headgroup due to membrane dehydration. A 2H-NMR study. Chem. Phys. Lipids. 1991;58:1–5. doi: 10.1016/0009-3084(91)90105-k. [DOI] [PubMed] [Google Scholar]
- 99.Stockton G.W., Polnaszek C.F., Smith I.C.P. Molecular motion and order in single-bilayer vesicles and multilamellar dispersions of egg lecithin and lecithin-cholesterol mixtures. A deuterium nuclear magnetic resonance study of specifically labeled lipids. Biochemistry. 1976;15:954–966. doi: 10.1021/bi00650a003. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.