Topological Distances Between Brain Networks

Abstract

Many existing brain network distances are based on matrix norms. The element-wise differences may fail to capture underlying topological differences. Further, matrix norms are sensitive to outliers. A few extreme edge weights may severely affect the distance. Thus it is necessary to develop network distances that recognize topology. In this paper, we introduce Gromov-Hausdorff (GH) and Kolmogorov-Smirnov (KS) distances. GH-distance is often used in persistent homology based brain network models. The superior performance of KS-distance is contrasted against matrix norms and GH-distance in random network simulations with the ground truths. The KS-distance is then applied in characterizing the multimodal MRI and DTI study of maltreated children.

1 Introduction

There are many similarity measures and distances between networks in literature [2,7,14]. Many of these approaches simply ignore the topology of the networks and mainly use the sum of differences between either node or edge measurements. These network distances are sensitive to the topology of networks. They may lose sensitivity over topological structures such as the connected components, modules and holes in networks.

In standard graph theoretic approaches, the similarity and distance of networks are measured by determining the difference in graph theory features such as assortativity betweenness centrality, small-worldness and network homogeneity [4,17]. Comparison of graph theory features appears to reveal changes of structural or functional connectivity associated with different clinical populations [17]. Since weighted brain networks are difficult to interpret and visualize, they are often turned into binary networks by thresholding edge weights [11,20]. However, the choice of thresholding the edge weights may alter the network topology. To obtain the proper optimal threshold, the multiple comparison correction over every possible edge has been proposed [16,18,20]. However, depending on what p-value to threshold, the resulting binary graph also changes. Others tried to control the sparsity of edges in the network in obtaining the binary network [11,20]. However, one encounters the problem of thresholding sparse parameters. Thus existing methods for binarizing weighted networks cannot escape the inherent problem of arbitrary thresholding.

Until now, there is no widely accepted criteria for thresholding networks. Instead of trying to come up with an optimal threshold for network construction that may not work for different clinical populations or cognitive conditions [20], why not use all networks for every possible threshold? Motivated by this question, new multiscale hierarchical network modeling framework based on persistent homology has been developed recently [7,14]. In persistent homology based brain network analysis as first formulated in [14], we build the collection of nested networks over every possible threshold using the graph filtration, a persistent homological construct [14]. The graph filtration is a threshold-free framework for analyzing a family of graphs but requires hierarchically building specific nested subgraph structures. The graph filtration shares similarities to the existing multi-thresholding or multi-resolution network models that use many different arbitrary thresholds or scales [11,14]. Such approaches are mainly used to visually display the dynamic pattern of how graph theoretic features change over different thresholds and the pattern of change is rarely quantified. Persistent homology can be used to quantify such dynamic pattern in a more coherent mathematical framework.

In persistent homology, there are various metrics that have been proposed to measure network distance. Among them, Gromov-Hausdorff (GH) distance is possibly the most popular distance that is originally used to measure distance between two metric spaces [19]. It was later adapted to measure distances in persistent homology, dendrograms [5] and brain networks [14]. The probability distributions of GH-distance is unknown. Thus, the statistical inference on GH-distance has been done through resampling techniques such as jack-knife, bootstraps or permutations [7,14,15], which often cause computational bottlenecks for large-scale networks. To bypass the computational bottleneck associated with resampling large-scale networks, the Kolmogorov-Smirnov (KS) distance was introduced in [6,8,15]. The advantage of using KS-distance is its easiness to interpret compared to other less intuitive distances from persistent homology. Due to its simplicity, it is possible to determine its probability distribution exactly [8].

Many distance or similarity measures are not metrics but having metric distances makes the interpretation of brain networks easier due to the triangle inequality. Further, existing network distance concepts are often borrowed from the metric space theory. Let us start with formulating networks as metric spaces.

2 Matrix Norms

Consider a weighted graph or network with the node set V = {1, …, p} and the edge weights w = (w_ij), where w_ij is the weight between nodes i and j. We may assume that the edge weights satisfy the metric properties: nonnegativity identity, symmetry and the triangle inequality such that

$$\begin{array}{cccc}{w}_{i,j}\ge 0,& w_{ii}=0,& w_{ij}=w_{ji},& w_{ij}\le w_{ik}+w_{kj}\end{array}.$$

With theses conditions, χ = (V, w) forms a metric space. Although the metric property is not necessary for building a network, it offers many nice mathematical properties and easier interpretation on network connectivity.

Example 1

Given measurement vector x_i = (x_1i, …, x_ni)^T ∈ ℝⁿ on the node i. The weight w = (w_ij) between nodes is often given by some bivariate function f: w_ij = f(x_i, x_j). The correlation between x_i and x_j, denoted as corr(x_i, x_j), is a bivariate function. If the weights w = (w_ij) are given by $w_{ij}=\sqrt{1-\text{corr}({\mathbf{x}}_i,{\mathbf{x}}_j)},$, it can be shown that χ = (V, w) forms a metric space.

Matrix norm of the difference between networks is often used as a measure of similarity between networks [2,21]. Given two networks χ¹ = (V, w¹) and χ² = (V, w²), the L_l-norm of network difference is given by

$$D_l({\chi }^1,{\chi }^2)={\Vert w^1-w^2\Vert }_l={\left({\sum _{i,j}|w_{ij}^1-w_{ij}^2|}^l\right)}^{1/l}.$$

Note L_l is the element-wise Euclidean distance in l-dimension. When l = ∞, L_∞-distance is written as

$$D_{\infty }({\chi }^1,{\chi }^2)={\Vert w^1-w^2\Vert }_{\infty }=\underset{\forall i,j}{max}|w_{ij}^1-w_{ij}^2|.$$

The element-wise differences may not capture additional higher order similarity. For instance, there might be relations between a pair of columns or rows [21]. Also L₁ and L₂-distances usually surfer the problem of outliers. Few outlying extreme edge weights may severely affect the distance. Further, these distances ignore the underlying topological structures. Thus, there is a need to define distances that are more topological.

3 Gromov-Hausdorff Distance

GH-distance for brain networks is first introduced in [14]. GH-distance measures the difference between networks by embedding the network into the ultrametric space that represents hierarchical clustering structure of network [5]. The distance s_ij between the closest nodes in the two disjoint connected components R₁ and R₂ is called the single linkage distance (SLD), which is defined as

$$s_{ij}=\underset{l\in {\mathbf{R}}_1,k\in {\mathbf{R}}_2}{min}{w}_{lk}.$$

Every edge connecting a node in R₁ to a node in R₂ has the same SLD. SLD is then used to construct the single linkage matrix (SLM) S = (s_ij) (Fig. 1). SLM shows how connected components are merged locally and can be used in constructing a dendrogram. SLM is a ultrametric which is a metric space satisfying the stronger triangle inequality s_ij ≤ max(s_ik, s_kj) [5]. Thus the dendrogram can be represented as a ultrametric space = (V, S), which is again a metric space. GH-distance between networks is then defined through GH-distance between corresponding dendrograms. Given two dendrograms ¹ = (V, S¹) and ² = (V, S²) with SLM $S^1=(s_{ij}^1)$ and $S^2=(s_{ij}^2)$,

Fig. 1.

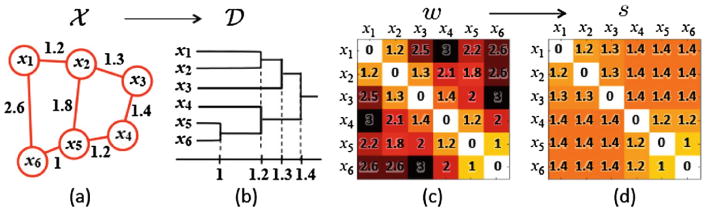
(a) Toy network, (b) its dendrogram, (c) the distance matrix w based on Euclidean distance, (d) the single linkage matrix (SLM) S.

$$D_{GH}(D^1,D^2)=\frac{1}{2}\underset{\forall i,j}{max}|s_{ij}^1-s_{ij}^2|.$$ (1)

For the statistical inference on GH-distance, resampling techniques such as jack-knife or permutation tests are often used [14,15].

4 Kolmogorov-Smirnov Distance

Recently a new network distance based on the concept of graph filtration has been proposed in [8]. Given weighted network χ = (V, w), the binary network ℬ_∊(χ) = (V, ℬ_∊(w)) is a graph consisting of the node set V and the edge weight ℬ_∊(w) = (ℬ_∊(w_ij)) given by

$${ℬ}_{\in }(w_{ij})=\{\begin{array}{cc}1& \text{if}{w}_{ij}\le \in ;\\ 0& \text{otherwise}.\end{array}$$ (2)

Note ℬ_∊(w) is the adjacency matrix of ℬ_∊(χ). Then it can be shown that

$${ℬ}_{{\in }_0}(\chi )\subset {ℬ}_{{\in }_1}(\chi )\subset {ℬ}_{{\in }_2}(\chi )\subset \cdots$$

for 0 = ∊₀ ≤ ∊₁ ≤ ∊₂ …. The sequence of such nested multiscale graph structure is called the graph filtration [7,14]. The sequence of thresholded values ∊₀, ∊₁, ∊₂ … are called the filtration values.

The graph filtration can be quantified using monotonic function f satisfying

$$f\circ {ℬ}_{{\in }_j}(\chi )\ge f\circ {ℬ}_{{\in }_{j+1}}(\chi )$$

for ∊_j ≤ ∊_j+1. The number of connected components, the zeroth Betti number β₀, satisfies the monotonicity property (3). The size of the largest cluster, denoted as γ, satisfies a similar but opposite relation of monotonic increase [7].

Given two networks χ¹ = (V, w¹) and χ² = (V, w²), Kolmogorov-Smirnov (KS) distance between X¹ and X² is defined as [7,15]

$$D_{KS}({\chi }^1,{\chi }^2)=\underset{\in \ge 0}{sup}|f\circ {ℬ}_{\in }{(\chi )}^1-f\circ {ℬ}_{\in }({\chi }^2)|.$$

The distance D_KS is motivated by Kolmogorov-Smirnov (KS) test for determining the equivalence of two cumulative distribution functions [8,10].

Example 2

Consider network with edge weights r_ij = 1 – corr(x_i, x_j). Such network is not a metric space. To make it a metric space, we need to scale the edge weight to $w_{ij}=\sqrt{r_{ij}}$ (Example 1). However, KS-distance is invariant under such monotonic scaling since the distance is taken over every possible filtration value.

The distance D_KS can be discretely approximated using the finite number of filtrations:

$$D_q=\underset{1\le j\le q}{sup}|f\circ {ℬ}_{{\in }_j}({\chi }^1)-f\circ {ℬ}_{{\in }_j}({\chi }^2)|.$$

If we choose enough number of q such that ∊_j are all the sorted edge weights, then D_KS(χ¹, χ²) = D_q [8]. This is possible since there are only up to p(p – 1)/2 number of unique edges in a graph with p nodes and f ○ ℬ_∊ increases discretely. In practice, ∊_j may be chosen uniformly.

The probability distribution of D_q under the null is asymptotically given by

$$\underset{q\to \infty }{lim}(D_q/\sqrt{2q}\ge d)=2\sum _{i=1}^{\infty }{(-1)}^{i-1}{e}^{-2i^2{d}^2}.$$ (3)

The result is first given in [8]. p-value under the null is then computed as

$$p-\text{value}=2e^{-d_o^2}-2e^{-8d_o^2}+2e^{-18d_o^2}\cdots ,$$

where the observed value d_o is the least integer greater than $D_q/\sqrt{2q}$ in the data. For any large value d₀ > 2, the second term is in the order of 10⁻¹⁴ and insignificant. Even for small observed d₀, the expansion converges quickly and 5 terms are sufficient. KS-distance method does not assume any statistical distribution on graph features other than that they has to be monotonic. The technique is very general and applicable to other monotonic graph features such as node degrees.

5 Comparisons

Five different network distances (L₁, L₂, L_∞, GH and KS) were compared in simulation studies with modular structures. The simulations below were independently performed 100 times and the average results were reported.

There were four groups and the sample size was n = 5 in each group and the number of nodes was p = 100 (Fig. 2). We follow notations in Example 1. In Group I, the measurement vector x_i at node i was simulated as multivariate normal, i.e., x_i ∼ N(0, I_n) with n by n identity matrix I_n as the covariance matrix. The edge weights for group I was $w_{ij}^1=\sqrt{1-\text{corr}({\mathbf{x}}_i,{\mathbf{x}}_j)}$. In Group II, the measurement vector y_i at node i was simulated as y_i = x_i + N(0, σ²I_n) with noise level σ = 0.01. The edge weight for group II was $w_{ij}^2=\sqrt{1-\text{corr}({\mathbf{y}}_i,{\mathbf{y}}_j)}$.

Fig. 2.

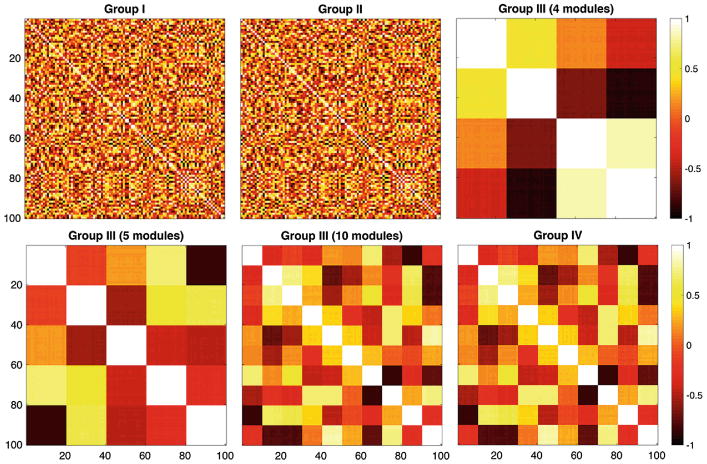
Randomly simulated correlation matrices. Group I and Group II were generated independently and identically. Group III was generated from Group I but additional dependency was added to introduce modular structures. Group IV was generated from Group III (10 modules) by adding small noise.

Group III was generated by adding additional dependency to Group I:

$${\mathbf{y}}_i=0.5{\mathbf{x}}_{ci+1}+N(0,\sigma I_n).$$

This introduce modules in the network. We assumed there were total k = 4, 5, 10 modules and each module consists of c = p/k number of points. Group IV was generated by adding noise to Group III: z_i = y_i + N(0, σ²I_n).

No network difference

It was expected there was no network difference between Groups I and II. We applied the 5 different distances. For the first four distances, permutation test was used. Since there were 5 samples in each group, the total number of permutations was $\left(\begin{array}{c}10\\ 5\end{array}\right)=272$ making the permutation test exact and the comparisons fair. All the distances performed well and did not detect network differences (1st row in Table 1). It was also expected there is no network difference between Groups III and IV. We compared 4 module network to 4 module network. All the distances performed equally well and did not detect differences (2nd row in Table 1).

Table 1.

Simulation results given in terms of p-values. In the case of no network differences (0 vs. 0 and 4 vs. 4), higher p-values are better. In the case of network differences (4 vs. 5 and 5 vs. 10), smaller p-values are better.

	L1	L2	L∞	GH	KS (β0)	KS (γ)
0 vs. 0	0.93 ± 0.04	0.93 ± 0.04	0.93 ± 0.04	0.87 ± 0.14	1.00 ± 0.00	1.00 ± 0.00
4 vs. 4	0.89 ± 0.02	0.89 ± 0.02	0.90 ± 0.03	0.86 ± 0.17	0.87 ± 0.29	0.88 ± 0.28
4 vs. 5	0.14 ± 0.16	0.06 ± 0.10	0.03 ± 0.06	0.29 ± 0.30	(0.07 ± 0.67)**	(0.07 ± 0.67)**
5 vs. 10	0.47 ± 0.25	0.19 ± 0.18	0.10 ± 0.10	0.33 ± 0.30	0.01 ± 0.08	(0.06 ± 0.53)*

^*and ** indicates multiplying 10⁻³ and 10⁻⁴.

Network difference

Networks with 4, 5 and 10 modules were generated using Group III models. Since the number of modules were different, they were considered as different networks. We compared 4 and 5 module networks (3rd row in Table 1), and 5 and 10 module networks (4th row in Table 1). L₁, L₂, L_∞ distances did not performed well for 5 vs. 10 module comparisons. Surprisingly, GH-distance performed worse than L_∞ in all cases. On the other hand, KS-distance performed extremely well.

The results of the above simulations did not change much even if we increased the noise level to σ = 0.1. In terms of computation, distance methods based on the permutation test took about 950 s (16 min) while the KS-like test procedure only took about 20 s in a computer. The MATLAB code for performing these simulations is given in http://www.cs.wisc.edu/∼mchung/twins. The results given in Table 1 may slightly change if different random networks are generated.

6 Application

The methods were applied to multimodal MRI and DTI of 31 normal controls and 23 age-matched children who experienced maltreatment while living in post-institutional settings before being adopted by families in US. The detailed deception of the subject and image acquisition parameters are given in [7]. Ages range from 9 to 14 years. The average amount of time spend in institutional care was 2.5 ± 1.4 years. Children were on average 3.2 years when they were adapted.

For MRI, a study specific template was constructed using the diffeomorphic shape and intensity averaging technique through Advanced Normalization Tools (ANTS) [1]. White matter was also segmented into tissue probability maps using template-based priors, and registered to the template [3]. The Jacobian determinants of the inverse deformations from the template to individual subjects were obtained. DTI were corrected for eddy current related distortion and head motion via FSL (http://www.fmrib.ox.ac.uk/fsl) and distortions from field inhomogeneities were corrected [12] before performing a non-linear tensor estimation using CAMINO [9]. Subsequently, iterative tensor image registration strategy was used for spatial normalization [13]. Then fractional anisotropy (FA) were calculated for diffusion tensor volumes diffeomorphically registered to the study specific template. Jacobian determinants and FA-values are uniformly sampled at 1856 nodes along the white mater template boundary.

Correlation within modality

The correlations of the Jacobian determinant and FA-values were computed between nodes within each modality. This results in 1856 × 1856 correlation matrix for each group and modality. Using KS-distance, we determined the statistical significance of the correlation matrix differences between the groups for each modality separately. The statistical results in terms of p-values are all below 0.0001 indicating the very strong overall structural network differences in both MRI and DTI.

Cross-correlation across modality

Following the hyper-network framework in [8], we also computed the cross-correlation between the Jacobian determinants and FA-values on 1856 nodes. This results in 1856 × 1856 cross-correlation matrix for each group. The statistical significance of the cross-correlation matrix differences is then determined using KS-distance (p-value < 0.0001). The KS-distance method is robust under the change of node size and we also obtained the similar result when the node size changed to 548.

7 Discussion

The limitation of GH- and KS-distances

The limitation of the SLM is the inability to discriminate a cycle in a graph. Consider two topologically different graphs with three nodes (Fig. 4). However, the corresponding SLM are identically given by

Fig. 4.

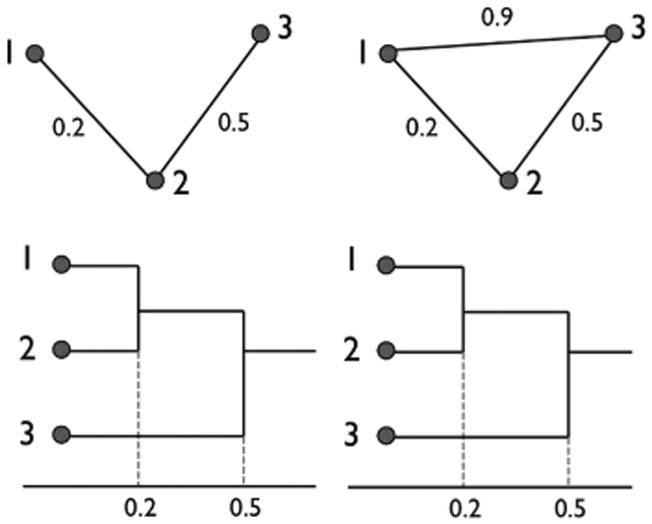
Two topologically distinct graphs may have identical dendrograms, which results in zero GH-distance.

$$\begin{array}{ccc}\left(\begin{array}{ccc}0& 0.2& 0.5\\ 0.2& 0& 0.5\\ 0.5& 0.5& 0\end{array}\right)& \text{and}& \left(\begin{array}{ccc}0& 0.2& 0.5\\ 0.2& 0& 0.5\\ 0.5& 0.5& 0\end{array}\right)\end{array}.$$

The lack of uniqueness of SLMs makes GH-distance incapable of discriminating networks with cycles [6]. KS-distance also treat the two networks in Fig. 4 as identical if Betti number β₀ is used as the monotonic feature function. Thus, KS-distance also fail to discriminate cycles.

Computation

The total number of permutations in permuting two groups of size q each is [8] $\left(\begin{array}{c}2q\\ q\end{array}\right)~\frac{4^q}{\sqrt{2\pi q}}$. Even for small q = 10, more than tens of thousands permutations are needed for the accurate estimation the p-value. On the other hand, only up to 10 terms are needed in the KS-distance method. The KS-distance method avoids the computational burden of permutation tests.

Fig. 3.

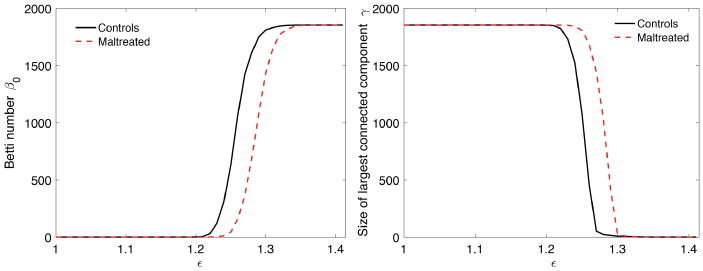
The plots of β₀ (left) and γ (right) over $\sqrt{1-\text{corr}.}$ showing structural network differences between maltreated children (dotted red) and normal controls (solid black) on 1856 nodes. (Color figure online)