Abstract
Biomembranes with as few as three lipid components can form coexisting liquid-disordered (Ld) and liquid-ordered (Lo) phases. In the coexistence region of Ld and Lo phases, the lipid mixtures 1,2-distearoyl-sn-glycero-3-phosphocholine (DSPC)/1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC)/chol or brain sphingomyelin (bSM)/DOPC/chol form micron-scale domains that are easily visualized with light microscopy. Although large domains are not observed in the mixtures DSPC/1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC)/chol and bSM/POPC/chol, lateral heterogeneity is nevertheless detected using techniques with nanometer-scale spatial resolution. We propose a simple and accessible method to measure domain sizes below optical resolution (∼200 nm). We measured nanodomain size for the latter two mixtures by combining experimental Förster resonance energy transfer data with a Monte-Carlo-based analysis. We found a domain radius of 7.5−10 nm for DSPC/POPC/chol, similar to values obtained previously by neutron scattering, and ∼5 nm for bSM/POPC/chol, slightly smaller than measurable by neutron scattering. These analyses also detect the domain-size transition that is observed by fluorescence microscopy in the four-component lipid mixture bSM/DOPC/POPC/chol. Accurate measurements of fluorescent-probe partition coefficients are especially important for the analysis; therefore, we exploit three different methods to measure the partition coefficient of fluorescent molecules between Ld and Lo phases.
Introduction
The plasma membrane (PM) plays important roles in cell function (1, 2, 3). Cell membranes have numerous lipid species (4) with mixing properties that can promote lateral organization (5, 6, 7, 8). When the nonideality of lipid mixing is strong enough, phase separation occurs. Liquid-liquid phase separation is related to the existence of membrane rafts in the cell PM and should be taken into account to understand protein sorting and trafficking, membrane signal transduction, and viral assembly (1, 2, 3, 9, 10). The size scale of any phase heterogeneities is relevant to how many proteins could be accommodated in or bound to a small domain. Moreover, the size scale of domains could influence the transmission of information across the bilayer (7).
Lipidomics studies have identified thousands of different lipids in the PM (11, 12, 13, 14, 15), making the study of the plasma membrane challenging. On the other hand, the most abundant lipids in the PM can be grouped into a few categories, such as high- or low-melting, or small headgroup (16) and cholesterol. Simplified model membranes can be produced in vitro, enabling accurate control of lipid composition (5, 6, 17, 18, 19, 20, 21, 22, 23). The phase diagrams of lipid mixtures with as few as three components—a high-melting lipid, a low-melting lipid, and cholesterol (chol)—exhibit multiple phase regions (6, 19, 22).
The coexistence of liquid-ordered (Ld) and liquid-disordered (Lo) phases falls within the composition range that describes the exoplasmic surface of living cells (4). In chemically simple lipid mixtures with coexisting Ld and Lo phases, domains with micrometer sizes have been explored by observation of giant unilamellar vesicles (GUVs) using fluorescence microscopy (6, 18, 23, 24, 25, 26, 27). GUVs of lipid mixtures such as 1,2-distearoyl-sn-glycero-3-phosphocholine (DSPC)/1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC)/chol or brain sphingomyelin (bSM)/DOPC/chol exhibit macroscopic phase separation, i.e., micron-scale domains, whereas GUVs of DSPC/1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC)/chol or bSM/POPC/chol appear uniform under the light microscope (6, 24). Although domains for these latter mixtures cannot be directly visualized by optical microscopy, several experimental methods have detected the existence of domains below the optical resolution limit, including electron spin resonance (21), Förster resonance energy transfer (FRET) (6, 19, 22, 28), atomic recombination in dynamic secondary ion mass spectroscopy (29), and small-angle neutron scattering (SANS) (19, 20, 30). In addition, using an interferometric scattering microscope, nanodomains were observed even in the absence of any extrinsic labels (31).
High-resolution optical techniques have provided evidence of nanodomains in vivo (32, 33). Besides the nanoscopic size, the short lifetime of the domains (31) makes the direct visualization of nanodomains beyond the detection of many current techniques. Thus, fluorescence spectroscopic techniques, with a time response of nanoseconds, are useful to detect and study nanodomains. We model the PM by use of controlled lipid compositions with lipid bilayers of three or four components. Mixtures studied here are DSPC/DOPC/chol and DSPC/POPC/chol, as well as bSM/DOPC/POPC/chol with different relative amounts of DOPC and POPC. We use a simple method to measure the size of nanodomains using FRET in an ordinary fluorimeter. FRET experiments rely on the partitioning of donor and acceptor probes; the average separation distance between probes is influenced by nanodomain size, leading to differences in FRET efficiency.
The simplicity of these principles facilitates application to diverse systems because FRET is able to detect phase separation for scales of nanometers to micrometers (6, 19). However, quantitative analysis of the FRET from nanodomains is not simple: the FRET signal from the domain interface is not negligible, as could be safely assumed in an analytical treatment of FRET from macrodomains (28). To solve this interface problem, we use a Monte Carlo method to explicitly account for changes in the distribution of distances between donors and acceptors that lead to changes in the FRET efficiency, from which we then calculate the fluorescence of the acceptor stimulated by the donor. As we demonstrate, changes in the acceptor signal along phase-coexistence tielines can be used to obtain nanodomain size only if sufficiently accurate dye partition coefficients can be obtained independently.
In this work, we provide a brief overview of the versatility of FRET analyses. This overview includes the detection of phase boundaries (6, 19, 22, 34), the quantification of the partition coefficient of fluorescent probes in macroscopically phase-separated lipid mixtures (28, 34), and the investigation of nanodomain sizes. Because both nanodomain size and partition coefficient, Kp, influence the FRET signal similarly, we measure the Kp of the fluorescent probes independently of the FRET measurements.
In addition to the importance of accurate partition coefficients for our FRET analysis, the partition coefficients provide useful information. As an example, when Ld and Lo phases coexist in the PM, then membrane proteins will tend to sort between these phases by physical-chemical partitioning. The methods discussed here can be extended to fluorescently labeled proteins, thereby providing a more complete picture of protein behavior in the presence of nanodomains.
Materials and Methods
Chemicals
DOPC (1,2-dioleoyl-sn-glycero-3-phosphocholine), POPC (1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine), bSM (Sphingomyelin - brain), and DSPC (1,2-distearoyl-sn-glycero-3-phosphocholine) were from Avanti Polar Lipids (Alabaster, AL), and chol from Nu Chek Prep (Elysian, MN). PIPES (piperazine-N,N′-bis(2-ethanesulfonic acid)), KCl (potassium chloride), and EDTA (ethylenediaminetetraacetic acid) from Sigma-Aldrich (St Louis, MO). Phospholipid concentration was determined to <1% error using inorganic phosphate assay (35). Thin-layer chromatography (TLC) of ∼20 μg lipid samples confirmed the purity of lipids as >99%. Briefly, lipids were spotted onto prewashed, activated silica gel GHLF plates (Analtech, Newark, DE). Plates were developed with chloroform/methanol/water (65/25/4). Chol stock purity was checked with TLC in petroleum ether/diethyl ether/chloroform (7/3/3). Fluorescent dyes dehydroergosterol (DHE; Sigma-Aldrich), naphthopyrene (Tokyo Chemical Industry, Tokyo, Japan), tryptophan oleoyl ester (TOE, synthetized in the laboratory of Erwin London), and Bodipy-PC (16:0, Bodipy-PC; Invitrogen, Carlsbad, CA) were prepared as stock solutions in chloroform. Dye concentrations were measured in methanol by absorbance spectroscopy. Extinction coefficients were 12,900 (M cm)−1 at 324 nm for DHE; 23,749 (M cm)−1 at 454 nm for naphthopyrene; 91,800 (M cm)−1 at 504 nm for Bodipy-PC, according to the lot certificate of each dye; and 5500 (M cm)−1 at 280 nm for TOE. TLC confirmed >99% purity of the dye stocks. The solvents for TLC analysis were as follows: Bodipy-PC in chloroform/methanol/water (65/25/4), TOE in hexane/ethyl acetate (3/1), and DHE in petroleum ether/diethyl ether/chloroform (7/3/3).
Lipid dispersion preparation: sample trajectories
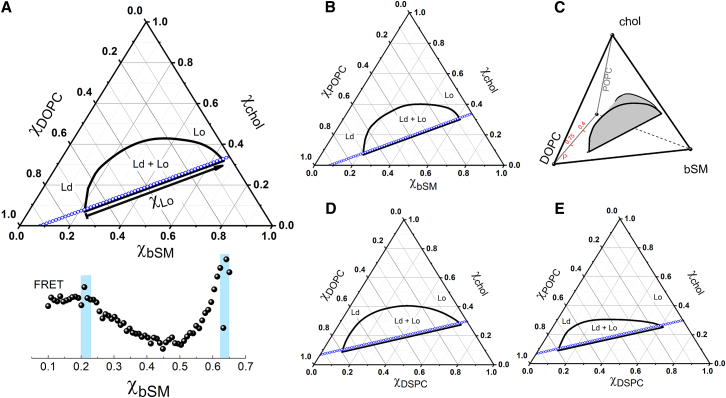
Samples were prepared along a thermodynamic tieline taken from the phase diagrams for DSPC/DOPC/chol and DSPC/POPC/chol (6), bSM/DOPC/chol, and bSM/POPC/chol (19). Examples of trajectories and their respective tielines are shown in Fig. 1 for each lipid mixture. An inserted axis in the phase coexistence region (Fig. 1 A) indicates the mole fraction of Lo phase, , which starts at zero at the left-hand side phase boundary and ends at the right-hand side phase boundary, = 1. In 13 × 100 mm glass tubes with fluorinated ethylene propylene-lined screw caps, samples of defined compositions were prepared with 1 mol% increments of the high-melting lipid (DSPC or bSM). Phospholipid, chol, and dyes were added from stock solutions using a 25 μL syringe attached to a repeating dispenser from Hamilton (Reno, NV). Aliquots of 0.5 mL of aqueous buffer (5 mM PIPES, 200 mM KCl, EDTA 1 mM, pH = 7.0) were added to each sample. Bilayers were formed by rapid solvent exchange (RSE) (36). Briefly, samples at room temperature were vortexed under vacuum for 1 min. The RSE procedure was used to avoid the chol demixing that can occur when a dry lipid film is prepared (37) and yields fully hydrated bilayers containing one to a few lamellae (36). Samples were sealed under argon and placed in a water bath at 55°C. Water bath temperature was lowered to room temperature of 23°C at a rate of 2°C/h. For each sample, we monitored the fluorescence or FRET signal. Fig. 1 A shows an example of FRET measurements. Control samples with only donor or acceptor probes and blank samples without fluorescent probes were also prepared along the same tieline and were used to correct for non-FRET contributions to the signal as described elsewhere (34).
Figure 1.
Phase diagrams and sample trajectories prepared along thermodynamic tielines. (A) The phase diagram of bSM/DOPC/chol displays a region of coexisting Ld + Lo phases. In the two-phase region, the lipid composition of each sample can be expressed as a function of the phase fraction. The second axis indicates the fraction of Lo phase (χLo) that varies from χLo = 0 to χLo = 1. The FRET signal of each sample is plotted as a function of the fraction of high-melting lipid, bSM. (B) shows a phase diagram of bSM/POPC/chol, (C) a four-component phase diagram of bSM/DOPC/POPC/chol, (D) a phase diagram of DSPC/DOPC/chol, and (E) a phase diagram of DSPC/POPC/chol. Dots in each phase diagram display each lipid composition that was examined (61 samples in total). To see this figure in color, go online.
Fluorescence probes and data collection
Fluorescence measurements were carried out at T = 23°C in a spectrofluorimeter model F7000 equipped with a high-sensitivity cell holder (Hitachi High Technologies America, Schaumburg, IL). Excitation- and emission-slit widths were set to 5 nm, and signal integration time was 10 s. Light scattering was monitored at λ = 400 nm without dye excitation. Fluorescence measurement of samples containing a single dye was performed for both Bodipy-PC and TOE. For Bodipy-PC, the dye/lipid ratio was 1/2500 with excitation/emission wavelengths, λex/λem = 500/520 nm. For TOE, the dye/lipid ratio was 1/100, with λex/λem = 284/335 nm. The fluorescence emission of the acceptor stimulated by the donor (referred to here as FRET) was measured for three different donor/acceptor pairs, with probe/lipid ratios given in parentheses: TOE donor (1/100) and DHE acceptor (1/100); DHE donor and Bodipy-PC acceptor (1/2500); and TOE donor and Bodipy-PC acceptor. Samples and controls that contained 1 mol% of DHE (a chol analog) had the chol concentrations reduced by 1 mol%. The DHE fluorescence was measured at λex/λem = (327/393). The sensitized acceptor emission for each pair was monitored at the donor excitation wavelength and the acceptor emission wavelength. The signal from single-dye fluorescence or FRET experiments exceeds that of the light scattering by 10- to 100-fold. For comparison, see Fig. S8.
Steady-state fluorescence for single-dye data analysis
Fluorescence properties (emission wavelength, quantum yield, lifetime, and emission anisotropy) can be used to determine the partition coefficient Kp of a molecule equilibrated between different environments (38). We used probes exhibiting different fluorescence quantum yield in Ld and Lo phases. Thus, the dye fluorescence intensity in a two-phase coexistence region can be expressed as a function of the fluorescence intensity in Ld and Lo phases:
| (1) |
where and are fractions of probe partitioning into Ld or Lo, and and are fluorescence intensities of individual dyes in the corresponding phase. The probe partition coefficient is given by the following:
| (2) |
where > 1 indicates preferential partitioning into Ld phase. Combining Eqs. 1 and 2 and writing the fraction of Ld phase in terms of gives an expression for dye intensity in terms of and :
| (3) |
We describe the composition change along the tieline as a function of the fraction of phases following the lever rule (34). For details, see Supporting Material.
For the dye concentrations used, self-quenching was negligible (data not shown). We have investigated fluorescence self-quenching as a function of dye concentration and corrected the fluorescence signal with only small quenching corrections needed (see Supporting Material).
FRET data analysis
FRET is a powerful tool for characterizing phase coexistence of lipid mixtures (19, 28). FRET is sensitive to phase domains with sizes below optical resolution (5, 6, 19, 20, 39, 40). Fluorescence of an acceptor probe stimulated by energy transfer from an excited-state donor (sensitized acceptor emission, here termed FRET) changes markedly at the phase boundaries and exhibits characteristic profiles in the phase coexistence region. For freely diffusing probes, FRET efficiency depends strongly on the instantaneous distribution of donor-acceptor separation distances. Partitioning of dyes acts to decrease or increase the average separation distance of the donor-acceptor pair: relative to uniformly distributed probes, FRET efficiency is enhanced when both dyes partition into the same phase, resulting in a hill-shaped profile within the two-phase region. When dyes prefer different phases, FRET efficiency is reduced, and the FRET signal exhibits a valley-shaped profile (28) (see Fig. S7). The FRET profile along a tieline is given by the following:
| (4) |
where and are the FRET signals observed in Ld (= 0) and Lo (= 1) phases obtained directly from the experimental data, and and are the donor and acceptor partition coefficients, respectively. Eq. 4 is valid for the case of macrodomains.
Phase boundary determination
To determine precisely the single-dye fluorescence ( and ) and the FRET ( and ) signals at = 0 and = 1, phase boundaries were found by analyzing FRET trajectories that cross the phase coexistence region and extend on either side into the single-phase composition space (see Figs. S3 and S4). Fig. 1 A shows an example of FRET signals monitored along this sample trajectory. The phase boundaries and their uncertainty are marked by a shaded interval displayed in the plot of FRET as a function of the mole fraction of high-melting lipid (χbSM, for this example). We summarize the lipid composition at the phase boundaries used in this work in Table S1. These phase boundaries agree with previously reported phase diagrams (6, 19).
Giant unilamellar vesicle preparation
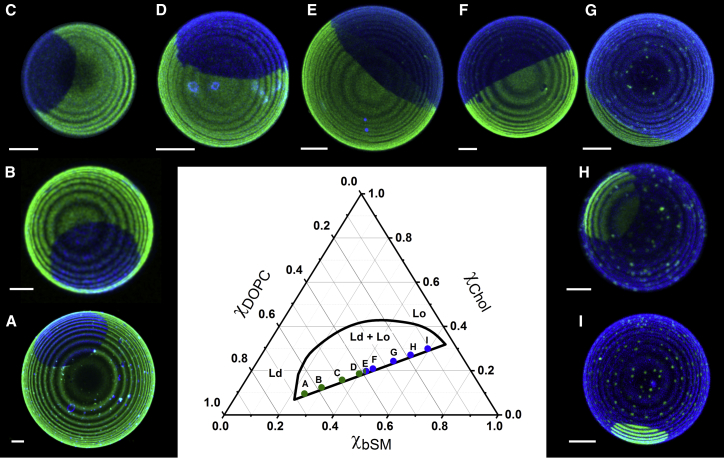
GUVs were prepared using the electroformation method (41). Briefly, lipids and dyes dissolved in chloroform were spread on glass slides coated with indium tin oxide. Slides with lipid films were placed in a glass desiccator under vacuum for 2−3 h at room temperature to remove traces of organic solvent. Lipid films were hydrated and swelled in a 100 mM sucrose solution at 55°C. A 5 Hz potential of 1.0 V peak-to-peak was applied for 2 h. GUVs were cooled to room temperature at a rate of 2°C/h, then removed from the preparation chamber using large-orifice pipette tips and diluted into 100 mM glucose. Osmotic pressure of sugar solutions was measured using an osmometer (model 5004; Precision Systems, Natick, MA). For partition coefficient studies, GUVs were prepared with Bodipy-PC (dye/lipid = 1/2500) at lipid compositions DSPC/DOPC/chol = 0.4/0.4/0.2 and bSM/DOPC/chol = 0.4/0.4/0.2.
For macroscopic domain size observation along tielines, GUVs were prepared with an increasing fraction of Lo phase (see Fig. 6). GUVs were cooled to room temperature at a rate of 0.8°C/h. Naphthopyrene (dye/lipid = 1/200) was used to label the Lo phase.
Figure 6.
Macroscopic phase separation is observed in GUVs of bSM/DOPC/chol. The fraction of Lo phase gradually increases for the GUVs as shown from (A)–(I). The size of Lo domains increases until the lipid composition reaches the percolation threshold, at which point the Lo phase becomes the continuous phase surrounding the Ld domain. To see this figure in color, go online.
Fluorescence microscopy
GUVs were visualized at 23°C using a confocal microscope, Nikon Eclipse C2+ (Nikon Instruments, Melville, NY). Sample chambers for observation with volume ∼2−5 μL were prepared using a no. 1.5 coverslip and a traditional microscope slide separated by a silicone spacer (Sigma-Aldrich) of 0.25 mm thickness. Bodipy-PC and naphthopyrene were excited by 488 and 405-nm laser lines, respectively.
Probe partition coefficient determination for GUVs
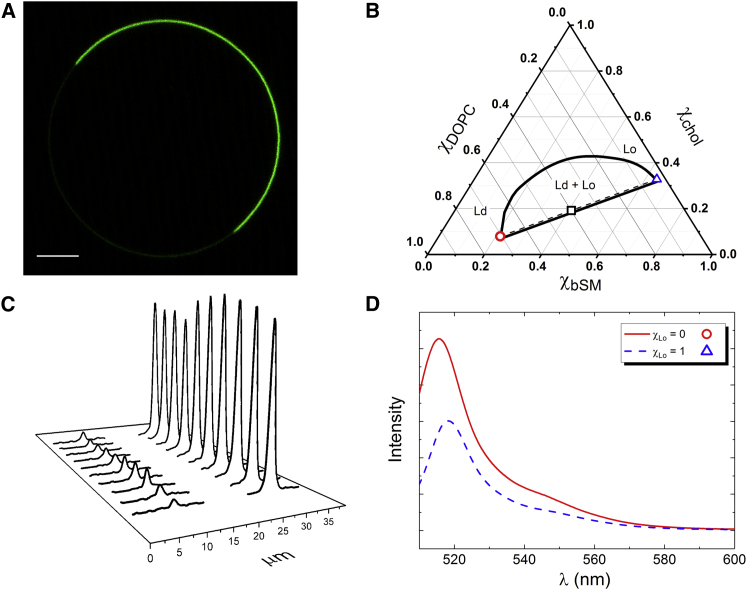
Partition coefficients of Bodipy-PC were measured in GUVs (Fig. 2 A). GUVs were prepared with the same mole fraction of Ld and Lo phases. Fig. 2 shows an example for a GUV with lipid composition bSM/DOPC/chol = 0.4/0.4/0.2 (square near the middle of the tieline in Fig. 2 B). To determine the Ld/Lo intensity ratio, we performed 10 line scans in the Ld and Lo phases (Fig. 2 C), averaging the scans for each phase. The background was subtracted, and the peak areas were integrated. The area of the intensity peak for Ld and Lo phases was corrected for the fluorescence quantum yield of the probe in each phase according to the following equation:
| (5) |
where is the phase-specific fluorescence quantum yield calculated from integrated fluorescence emission spectra. As shown in Fig. 2 D, and were calculated from the emission spectra at the endpoints of the tieline for Bodipy-PC in bSM/DOPC/chol. To compare KpGUV to the Kp obtained using single-dye fluorescence, Eqs. 2 and 3, we calculated the total intensities from Ld and Lo phases for each GUV: intensities from Ld and Lo phases were integrated over the Ld and Lo surfaces. As displayed in Fig. 2 C, similar intensity values in each phase were found for 10 random line scans. Thus, we can assume the dye to be homogeneously distributed in each phase. Hence, ILd and ILo are assumed to be constant, and these integrations can be written as ILd × SLd and ILo × SLo, where S represents the surface area of each phase. If the area occupied by Ld and Lo phases were identical to the mole fraction, then the term SLd/SLo would cancel because these GUVs were prepared with the same mole fraction of Ld and Lo phases. However, the average molecular area of the Ld phase is ∼30% greater than that of the Lo phase (18, 42, 43) so that SLd/SLo can be approximated by the factor 1.3 (see Supporting Material).
Figure 2.
Partition coefficient of fluorescent probes between Ld and Lo phases measured in GUVs. (A) A snapshot of a GUV equatorial plane is shown. Bodipy-PC favors the Ld phase (brighter). Scale bars, 5 μm. (B) The GUV (square) has equal mole fractions of Ld and Lo phases, χLo = 0.5. The tieline connects the GUV lipid composition to the lipid composition of pure Ld phase (circle) and pure Lo phase (triangle). (C) Intensity profiles from 10 different line scans across Ld and Lo phases are shown. (D) Fluorescence emission spectra of Bodipy-PC in Ld and Lo phases show the intensity of Bodipy-PC to be intrinsically brighter in the Ld phase (Intensity, arbitrary units (arb. u.)). Symbols are coded with the lipid composition at the endpoints of the tieline Ld phase (circle) and Lo phase (triangle). To see this figure in color, go online.
Monte Carlo simulations of FRET
Experimental tieline FRET trajectories were analyzed using off-lattice Monte Carlo simulations of phase-separated vesicles. When the instantaneous concentration of excited-state donors is low, energy transfer efficiency depends only on the Förster distance and the local acceptor surface density in the bilayer (44). Given a static spatial configuration of acceptors in a phase-separated spherical vesicle, we calculated the probability of different decay outcomes for excited-state donors (45). The possible decay outcomes considered here are 1) direct fluorescence emission, 2) energy transfer to an acceptor located in the Ld phase, or 3) energy transfer to an acceptor located in the Lo phase. The relative, unnormalized probability of energy transfer from an excited-state donor to a ground-state acceptor i is given by the following equation:
| (6) |
where is the separation distance between the donor and acceptor i, and is assumed to be identical for all donor/acceptor pairs and independent of separation distance. The probability of donor fluorescence decay,
| (7) |
is then combined with Eq. 6 to give the normalized probability of energy transfer to acceptor i,
| (8) |
The underlying principle of the Monte Carlo method for calculating FRET is the placement of donors and acceptors in three dimensions, subject to physical constraints that restrict the probe locations to subspaces within the 3D space; within a given subspace, the locations are chosen randomly. For the case of lipid-like probes in a uniform vesicle, the probe locations are confined to a spherical shell defined by a typical vesicle radius and bilayer thickness. In a phase-separated vesicle, additional constraints include the relative amounts and locations of coexisting phase domains, the partitioning of donors and acceptors between the two phases, and the transverse location of probes within a given phase. Although only the probe positions (and not the individual lipid positions) are specified in an off-lattice simulation, information about the average lipid size is required to properly capture the distribution of donor-acceptor distances (and hence the FRET efficiency) (see Tables S4 and S5). This information is not found in the tieline, which only gives the mole fraction of each phase that coexists at a particular composition. We calculated the phase area fractions by estimating the average molecular area of each phase as a mole-fraction-weighted sum of individual lipid areas. Fixed global parameters included these phase molecular areas, as well as a percolation threshold (given in terms of Lo phase mole fraction) at which the continuous phase changes from Ld to Lo.
Ensemble-averaged FRET for a given tieline composition was calculated by performing the following computational steps:
-
1)
Four donor-decay outcome counters (see item 3) were initialized to zero: direct fluorescence of a donor located in a domain, ; direct fluorescence of a donor located in the surround, ; energy transfer to an acceptor located in a domain, ; and energy transfer to an acceptor located in the surround, .
-
2)
The mole fraction of Lo phase was calculated from the lever rule, and the area fractions of the Ld and Lo phases were calculated from phase molecular areas. Domain centers were then generated randomly on the vesicle surface. Domains were assumed to be round, monodisperse, nonoverlapping, and randomly arranged, i.e., there is no domain-domain interaction other than hard-core repulsion.
-
3)
Acceptor and donor coordinates were randomly generated within the bilayer. The average, generally nonintegral number of donor or acceptor probes in each phase was calculated from the bulk probe concentration, phase fraction, probe partition coefficient, and vesicle size; for a particular simulated vesicle, the actual number of probes was a random integer drawn from a corresponding Poisson distribution.
-
4)
For each donor, the absolute probability of direct donor fluorescence or energy transfer to each acceptor within a fixed cutoff distance equal to four was calculated using Eqs. 6, 7, and 8. A random, probability-weighted outcome was then chosen, and the corresponding outcome counter was incremented.
-
5)
Steps 2–4 were repeated a large number of times, typically 100–300, to generate an ensemble average of donor decay outcomes.
-
6)
Outcome counters were normalized to the total number of events to yield outcome probabilities. Experimental observables of donor fluorescence, FRET efficiency (44), and sensitized acceptor emission adjusted for phase-specific acceptor quantum yield were calculated from this set of probabilities as described in the Supporting Material.
Custom simulation code (available upon request) was written in Mathematica v. 10.0 (Wolfram Research, Champaign, IL) and validated by comparison to the analytical solution, Eq. 4, as shown in Fig. S7. Fixed simulation parameters included the average molecular areas and bilayer thicknesses of Ld and Lo phases, concentration and transverse bilayer location of donor and acceptor probes, and . Adjustable parameters included the domain radius, probe partition coefficients, and vesicle size, as described below. A complete list of simulation parameters is given in Tables S4 and S5, and additional simulation details are found in the Supporting Material.
Determination of domain size
Domain size was found by comparing experimentally determined FRET profiles to simulated FRET profiles. After constraining most of the model parameters with values obtained from the literature or with independent experiments, as shown in Tables S3 and S4, we performed simulations of different domain radii = 4, 5, 7.5, 10, 20, and 40 nm. The limiting factor for the range of domain size choices is due solely to computational time demands. The best fit between the theoretical and the experimental FRET was then found by minimizing the sum of the square residuals normalized by the number of degrees of freedom. The reported uncertainty in domain size corresponds to the standard error of the fits with coefficient of determination greater than 0.94 (R2 > 0.94). Most of the best fits exhibit R2 = 0.95–0.97.
We report the analysis of three FRET pairs: TOE donor to DHE acceptor, DHE donor to Bodipy-PC acceptor, and TOE donor to Bodipy-PC acceptor. The availability of three independent measurements enabled an estimation of uncertainties related to probe-specific factors, including differences in .
Terminology
We studied mixtures of low-melting lipids POPC or DOPC, high-melting lipids bSM or DSPC, and chol. Such mixtures are well-established models for the compositional control of domain size, which we accomplished by varying the ratio of the two low-melting lipids (6, 18, 23). We describe this ratio by defining a compositional parameter that quantifies the ratio of DOPC to total low-melting lipid:
| (9) |
Experimental tieline trajectories were measured at constant values of ρ, corresponding to a triangular plane within a tetrahedral (four-component) phase diagram, Fig. 1 C, as described in (6).
Important to this study, the mixtures DSPC/DOPC/chol (ρ = 1), bSM/DOPC/chol (ρ = 1), and bSM/DOPC/POPC/chol (ρ = 0.75) show macroscopic phase separation. We use the term “macrodomains” and “macroscopic phase separation” interchangeably to describe the micron-sized phase domains observed in GUVs of these mixtures. For the mixtures DSPC/POPC/chol (ρ = 0), bSM/POPC/chol (ρ = 0), and bSM/DOPC/POPC/chol (ρ = 0.4), GUVs appear uniform. However, studies using techniques such as electron spin resonance (21), FRET (6, 19, 22, 28), atomic recombination in dynamic secondary ion mass spectroscopy (29), and SANS (19, 20, 30) detect phase separation in these mixtures. Together, these observations imply the existence of domains with sizes well below optical resolution. Of these techniques, only SANS yields a measured domain size, obtained with a model-based analysis that assumed circular domains of uniform size (20, 30). For the four-component lipid mixtures bSM/DOPC/POPC/chol, a domain size transition was observed at ρ = 0.55 ± 0.1. Thus, the ρ values studied here (ρ = 0.4, 0.75) correspond to regions of the phase diagram where the nanoscopic regime ends and the macroscopic regime begins, respectively.
Vesicles used in our FRET experiments are hundreds of nanometers in diameter, a size that is comparable to the wavelength of visible light; therefore, no phase domains can be micrometers in size. Although the sizes of macrodomains observed in GUVs are different from the sizes discussed here, our results with these small vesicles show an abrupt transition in domain size between the lipid mixtures that form nano- or macrodomains in GUVs. Thus, we adopted the terminology commonly used in microscopy to describe the regime of small and large domains.
Results and Discussion
Reliable measurement of probe Kp is crucial for use of FRET for domain size analysis. To find Kp values, we either monitored the fluorescence emission of a single dye or measured FRET between two different probes, in both cases for sets of lipid compositions along a thermodynamic tieline. We also measured fluorescence from GUVs observed with a confocal microscope. We first show measurements of the partition coefficient between Ld or Lo phases of different fluorescent dyes in six different lipid mixtures. We then describe FRET measurements made in lipid mixtures that form macro- and nanodomains. These measurements enable not only finding domain size, but also detection of phase regions and values of partition coefficients.
Measuring the partition coefficient of fluorescent probes between Ld and Lo phases
Single-dye fluorescence is an efficient method to measure the partition coefficient of fluorescent molecules between Ld and Lo phases. One advantage of this method is its simplicity: along a thermodynamic tieline, the observed fluorescence intensity is a simple hyperbolic function of a single unknown parameter, the probe Kp. Of special importance is that, unlike FRET intensity, single-dye intensity is independent of domain size. Indeed, observation of hyperbolic single-dye fluorescence along a tieline within a composition space is clear evidence of phase separation.
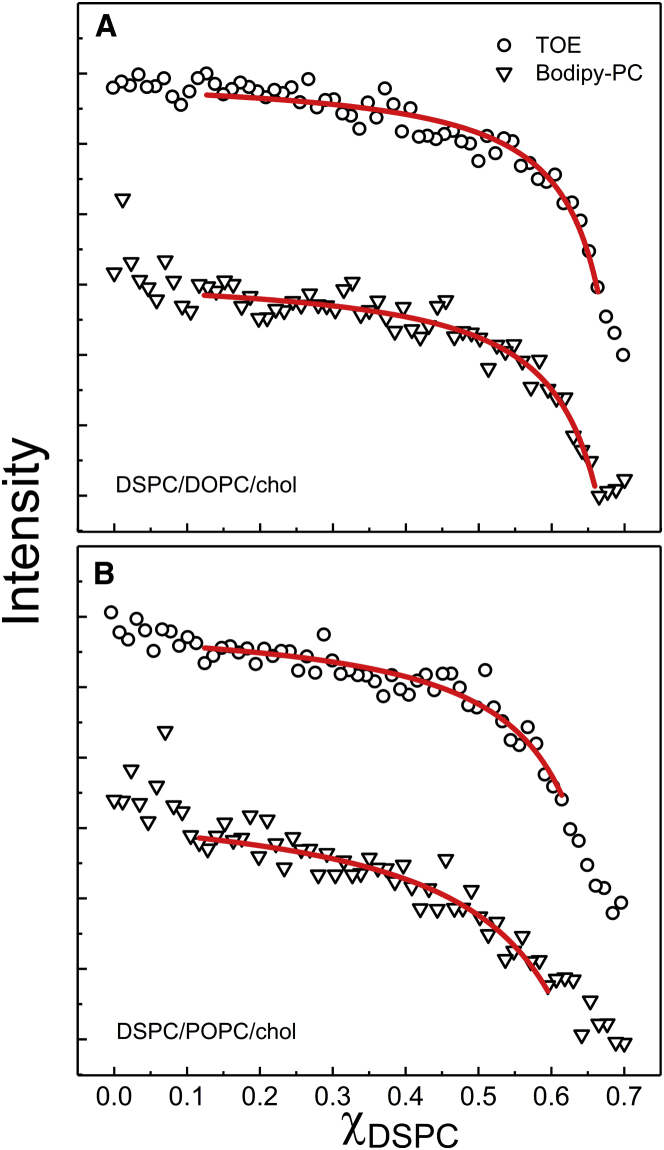
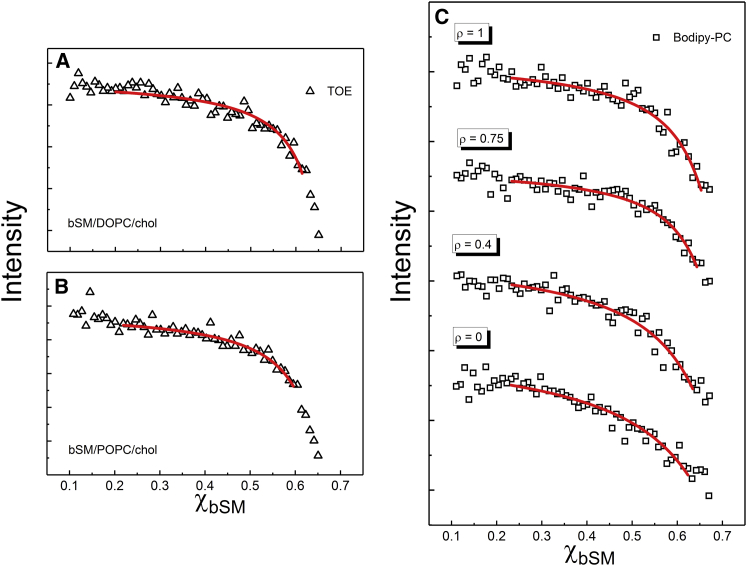
Fig. 3 shows the single-dye fluorescence of Bodipy-PC and of TOE in the macroscopic mixture DSPC/DOPC/chol and in the nanoscopic mixture DSPC/POPC/chol . For bSM mixtures, we measured single-dye fluorescence of Bodipy-PC and TOE in bSM/DOPC/chol and bSM/POPC/chol , as shown in Fig. 4. Also shown in Fig. 4 is Bodipy-PC fluorescence measured in four-component mixtures of bSM/DOPC/POPC/chol at ρ = 0.4 and 0.75. Sample trajectories were prepared along a thermodynamic tieline within the Ld + Lo region at low chol concentration, Fig. 1 (for details see Supporting Material).
Figure 3.
Single-dye fluorescence measures the partition coefficient between Ld and Lo phases of probes in DSPC-containing mixtures. The fluorescence emission (arb. u.) of TOE (circles) and Bodipy-PC (inverted triangles) is measured for a trajectory along a thermodynamic tieline of (A) macrodomain DSPC/DOPC/chol and (B) nanodomain DSPC/POPC/chol. The profiles are vertically shifted for clarity. Fitting of the experimental data (line) was performed using Eq. 3 to determinate the partition coefficient Kp of the fluorescent probes. Kp values are given in Table 1. To see this figure in color, go online.
Figure 4.
Single-dye fluorescence measures the partition coefficient between Ld and Lo phases in bSM mixtures. The fluorescence emission (arb. u.) of TOE is measured along a thermodynamic tieline of (A) macrodomain bSM/DOPC/chol (ρ = 1) and (B) nanodomain bSM/POPC/chol (ρ = 0). (C) The fluorescence emission (arb. u.) of Bodipy-PC monitored along tielines in the lipid mixture bSM/DOPC/POPC/chol is shown at different ρ values as described in the text. The profiles are vertically shifted for clarity. Mixtures at ρ = 0.75 and ρ = 0.4 form macro- and nanodomains, respectively. Fits of the experimental data (lines) to Eq. 3 were used to obtain probe Kp in each system, shown in Table 1. To see this figure in color, go online.
The fluorescence intensity of Bodipy-PC and TOE are each intrinsically different in Ld and Lo phases. In all mixtures studied here, fluorescence emission of both dyes is brighter in the Ld phase than in the Lo phase. Moreover, for all sample trajectories, including the nanodomain-forming mixtures DSPC/POPC/chol and bSM/POPC/chol, the fluorescence intensity profile is hyperbolic, showing that probe partitioning follows the lever rule (46). In this respect, nanoscopic Ld and Lo domains behave as if they were true thermodynamic phases. By visual inspection, both Bodipy-PC and TOE favor the Ld phase (i.e., Kp > 1 as defined by Eq. 2).
Kp was quantified by fitting the intensities within the two-phase region using Eq. 3, which uses the lever rule to determine the phase fractions along a thermodynamic tieline (28, 47). Table 1 summarizes the partition coefficients of Bodipy-PC (KpBod) and TOE (KpTOE) for these mixtures. The fittings were performed by use of OriginPro 2017 (OriginLab, Northampton, MA), and the uncertainties correspond to standard error obtained from a nonlinear regression analysis (48, 49), numerically calculated by the software.
Table 1.
Partition Coefficients of Bodipy-PC and TOE
| Lipid Mixture | Dye | Single-Dye Fluorescence | FRET (with DHE) | FRET (with Bodipy-PC) | Microscopy (GUVs) |
|---|---|---|---|---|---|
| DSPC/DOPC/chol | Bodipy-PC | 10 ± 2 | 11 ± 2 | NA | 15 ± 4 |
| DSPC/POPC/chol | Bodipy-PC | 4 ± 1 | ∗ | NA | NA |
| DSPC/DOPC/chol | TOE | 9 ± 1 | 9 ± 2 | 7 ± 1 | NA |
| DSPC/POPC/chol | TOE | 5 ± 1 | ∗ | ∗ | NA |
| bSM/DOPC/chol | Bodipy-PC | 9 ± 2 | 8 ± 1 | NA | 10 ± 2 |
| bSM/DOPC/POPC/chol | Bodipy-PC | 8 ± 2 | 6 ± 1 | NA | 9 ± 2 |
| bSM/DOPC/POPC/chol | Bodipy-PC | 5 ± 1 | ∗ | NA | NA |
| bSM/ POPC/chol | Bodipy-PC | 3 ± 1 | ∗ | NA | NA |
| bSM/DOPC/chol | TOE | 8 ± 1 | 10 ± 2 | 8 ± 1 | NA |
| bSM/POPC/chol | TOE | 5 ± 1 | ∗ | ∗ | NA |
Kps of Bodipy-PC and TOE measured for different lipid mixtures, using single-dye fluorescence, FRET and fluorescence microscopy. Errors in Kp by single-dye fluorescence and FRET measurements are standard error of the free parameter calculated from nonlinear regression analysis of Eqs 3 and 4, respectively. Errors in Kp using fluorescence microscopy correspond to the standard error of 7–10 GUV measurements. NA (not available) represents the noninvestigation of Bodipy-PC homo-FRET or the limitation in measuring Kp using a microscope. The symbol (∗) marks the FRET profiles used in the domain size investigation.
For both DSPC- and bSM-containing mixtures, replacement of DOPC by POPC resulted in smaller Kp. For DSPC/DOPC/chol, KpTOE = 9 ± 1; for DSPC/POPC/chol, KpTOE = 5 ± 1. A similar result is observed for bSM-containing mixtures. This difference in the partition coefficient arises from the different probe environments created by DOPC versus POPC. As POPC replaces DOPC, differences in the physical properties of Ld and Lo phases become less pronounced. For example, the hydrophobic mismatch between these phases decreases (30), as do bending moduli difference between Ld and Lo phases (23). Similarly, the difference in the energetic cost that makes a probe prefer one phase over the other also decreases, reducing the partition coefficient.
We have previously reported studies in GUVs in which an abrupt domain size transition was observed upon replacement of DOPC by POPC. We identified the composition range within which this size transition occurs for 12 different lipid mixtures (23). For bSM/DOPC/POPC/chol, the domain size transition was observed at around ρ = 0.55. Here, we measure the partition coefficient for this lipid mixture at ρ = 0.4 for nanodomains and at ρ = 0.75 for macrodomains. Although these different ρ values correspond to different fractions of DOPC and POPC, the difference in the lipid composition is much less than with the extremes of bSM/DOPC/chol (ρ = 1) and bSM/POPC/chol (ρ = 0). For compositions at ρ = 0.4 and 0.75, a small difference in the partition coefficient was observed, at which KpBod increases by a factor of 1.6 (Table 1) for compositions that form nano- (ρ = 0.4) and macrodomains (ρ = 0.75), respectively. Thus, a 1.6-fold change in the partition coefficient is observed in the range within which a 100-fold domain size transition is observed.
Monitoring FRET in lipid composition space
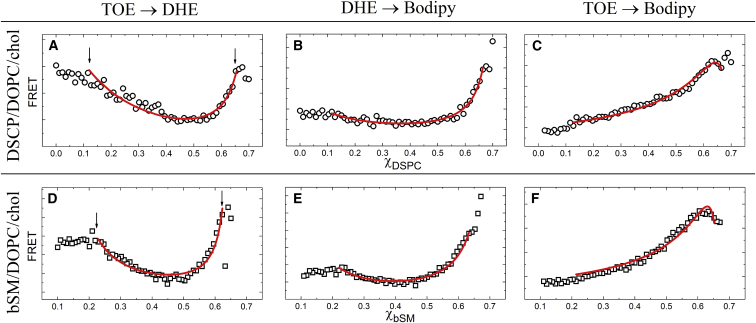
For freely diffusing fluorophores in a fluid membrane, FRET efficiency depends on the distribution of separation distances between donor and acceptor molecules, which, in a phase-separated bilayer, in turn depends on the probe partition coefficients. Probes that partition strongly between coexisting phases are especially useful for determining phase boundaries of lipid mixtures (6, 19, 22), and measurements of steady-state FRET efficiency (or any suitable FRET metric) within a composition space provide a direct means to detect phase coexistence regions. Figs. 5 A and 7 A are examples in which FRET change marks the phase boundaries of the coexistence region Ld + Lo in the composition space. Analysis of FRET along a thermodynamic tieline also enables the measurement of the probe partition coefficient and can be used to investigate the partition coefficient of any fluorescent molecule of interest that partitions between Ld and Lo phases.
Figure 5.
FRET measures the partition coefficient between Ld and Lo phases of fluorescent probes for lipid mixtures that exhibit macroscopic phase separation. Experimental FRET profiles (arb. u.) were performed along a tieline of (A–C) DSPC/POPC/chol and (D–F) bSM/DOPC/chol. Arrows mark the phase boundaries. DHE was assumed to partition identically to chol (favoring the Lo phase) as described in the text. Best-fit values for Kp are shown in Table 1. To see this figure in color, go online.
Figure 7.
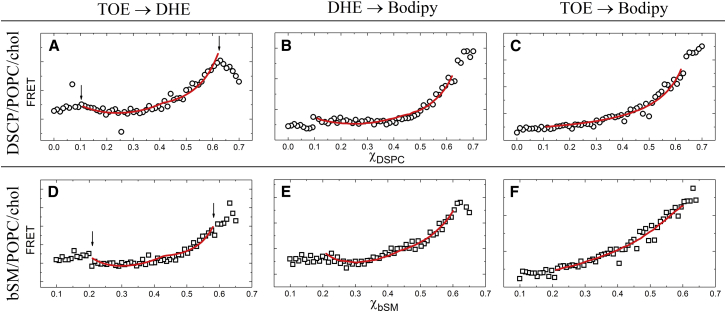
FRET reveals nanodomain sizes. FRET (arb. u.) between different pairs described as donor → acceptor. Experimental FRET profiles were performed along a tieline of (A–C) DSPC/POPC/chol and (D–F) bSM/POPC/chol. Arrows mark the phase boundaries. Theoretical FRET profiles (lines) from MC simulations, with separation distance between donor and acceptor calculated from a random distribution of probes in simulated round domains of radius Rd, are shown. Simulations use the Kp of the probes measured using single-dye fluorescence. The domain sizes are described in Table 2. To see this figure in color, go online.
FRET analysis is straightforward in lipid mixtures that form macrodomains because the analytical solution shown by Eq. 4 describes the FRET behavior along a tieline, assuming negligible domain interface as a distinct probe location. However, nanodomain-forming mixtures require attention to FRET between probes located in different phases. A simple visualization of how the small domain size affects the FRET measurements can be pictured by domains with sizes of the same order of magnitude of R0. In this scenario, probes in different phases that are just across a domain boundary from each other transfer energy with about the same efficiency as a pair that is colocalized in the same phase. Although a few analytical solutions have been proposed for this case (48, 49), none are suitable for the analysis of sensitized acceptor emission. Instead, we used a modified Monte Carlo approach that explicitly accounts for individual donor decay events (45). Such simulations are well-suited for calculating both the FRET efficiency and the sensitized acceptor emission for arbitrary domain geometries.
In the following section, we first describe FRET results for macrodomain-forming mixtures obtained from the application of Eq. 4. We compare the probe partition coefficients obtained from this analysis with those obtained from a separate analysis of single-dye fluorescence data.
FRET measures partition coefficients between macroscopic Ld and Lo phases
Fig. 5 shows FRET for DSPC and bSM mixtures that form macrodomains using the following FRET pairs (donor → acceptor): TOE → DHE, DHE → Bodipy-PC, and TOE → Bodipy-PC. The fluorescent probe DHE is a chol analog that partitions similarly to chol (50). We therefore constrained DHE to partition identically to chol per the phase diagram tielines (21). For DSPC mixtures, KpDHE = 0.39, and for bSM mixtures, KpDHE = 0.27 at the tieline used in this study (see Table S2). The experimental data points were fitted using Eq. 4, where the best fit minimized the sum of squared residuals. Because KpDHE was fixed, FRET from TOE → DHE (Fig. 5, A and D) or DHE → Bodipy-PC (Fig. 5, B and E) were fit using a single free parameter, KpBod or KpTOE. For FRET from TOE → Bodipy-PC, we constrained KpBod to the value obtained from single-dye fluorescence experiments to determine the single unknown parameter, KpTOE. Table 1 summarizes the partition coefficients measured from FRET analyses.
For macrodomains, the fraction of the overall FRET that occurs near the domain boundary is minimal for the following reason: the typical domain size for macroscopic phase separation (1−10 μm) is several orders of magnitude larger than typical R0 (1−10 nm). Lateral diffusion of probes in the membrane is negligible on the timescale of energy transfer, comparable to the fluorescence lifetime ≤10−8 s (28, 51). Thus, the FRET signal can be approximated as a weighted sum of the contributions from the Ld and Lo phases considered separately (28), resulting in Eq. 4 (see Supporting Material). The dependence of the FRET signal on probe partitioning therefore allows Kp values to be determined from the fits. However, for nanoscopic phase separation, the domain sizes are comparable to R0, and therefore Eq. 4 is not appropriate for determining Kp. The lack of Kp data for mixtures that form nanodomains is represented by an asterisk in Table 1. These FRET curves were instead used in the investigation of nanodomain sizes, as discussed below.
Fluorescence microscopy
The study of macrodomains can provide a reasonable estimate of probe partitioning in the nanodomain systems. Nanodomains rather than micron-scale domains are found in the cell plasma membrane (32, 33). Therefore, in terms of size at least, lipid mixtures that form nanodomains represent better models. However, the partition coefficient depends on the lipid composition, as in Table 1 for mixtures with a single low-melting lipid DOPC or POPC. To diminish the difference of lipid compositions in the comparison between macro- and nanodomains mixtures, partition coefficient measurements can be performed in four-component mixtures as described above. For mixtures that form macrodomains, we also measured Kp using GUVs. We next compare Kp measured using different methods.
Comparison of partition coefficients measured in GUVs
The partition coefficient of Bodipy-PC was measured using fluorescence microscopy in lipid mixtures with macroscopic phase separation. We measured the fluorescence intensity in the Ld and Lo phases observed in GUVs and, using Eq. 5, we calculated the dye partition coefficient.
For Bodipy-PC, we measured dye partition coefficient using three independent methods: single-dye fluorescence, FRET, and fluorescence intensities from microscopy, with results shown in Table 1. For lipid mixtures that form macrodomains, the agreement among the Kp values suggests that these methods are equally appropriate for Kp studies.
However, fluorescence microscopy is limited to the subset of fluorescent probes that can be excited and observed using a microscope. Of course, because of the optical resolution limit (∼200 nm), this method to study Kp cannot be performed on mixtures that form nanodomains, such as DSPC/POPC/chol and bSM/POPC/chol. The absence of fluorescence microscopy measurements, due to the limitation of this technique, is represented in Table 1 as NA.
Macrodomains and domain area fractions
Study of visible domains in GUVs is a straightforward way to identify the phase behavior along a tieline and to observe the relation between macrodomain size and phase fraction. Fig. 6 shows a selection of GUVs along a tieline, with domain sizes varying from a few % to ∼40% of GUV area for bSM/DOPC/chol. The Lo phase is labeled by the blue dye naphthopyrene and the Ld phase by the green dye Bodipy-PC. These GUVs were equilibrated to room temperature with a slow cooling rate of 0.8°C/h to avoid multiple small domains that are kinetically trapped during faster cooling (18). Along the tieline, the fraction of Lo phase increases from χLo = 0 to χLo = 1; the size of Lo domains increases until approximately the middle of the tieline, at which point the mole fractions of Ld and Lo phases are similar. From χLo ≈ 0.5 to χLo = 1, we observe Ld domain size decreases. We define domain as the minor phase within the other, percolating phase.
It is interesting that this phase behavior establishes a constraint between phase fraction and domain area fraction, revealing for macroscopic phase separation that the domain size must depend on the vesicle size. For GUVs with the same lipid composition, as, for example, χLo = 0.5, domains have similar area fraction. However, if GUVs have different sizes, the sizes of their domains would also be different (see example, Fig. S11). Lipid mixtures that form macrodomains exhibit high line tension (23) and higher hydrophobic mismatch between Ld and Lo phases compared to lipid mixtures that form nanodomains (30). To avoid the energetic costs of the hydrophobic mismatch, domains coalesce, minimizing the total perimeter of the domains (30).
We analyzed a FRET curve for a mixture that forms macrodomains using Monte Carlo simulations. We investigated the sizes of macrodomains by simulating vesicles of different sizes and found dependence of domain size on vesicle size. For these studies along a tieline, we found either one or a few large domains. From observations of GUVs with a few domains, we identified a percolation threshold at χLo ≈ 0.5, at which the continuous phase switches between Ld and Lo (18).
In contrast, in nanoscopic phase separation at equilibrium, domains do not coalesce into one or a few large domains. In this case, what interactions could possibly control the domain sizes?
FRET detects nanodomain sizes
We previously reported that line tension controls the size transition between nanoscopic and macroscopic domains (23). The line tension in four-component lipid mixtures such as DSPC/DOPC/POPC/chol and bSM/DOPC/POPC/chol decreases as DOPC is replaced by POPC (23). A competition between line tension and a repulsive interaction, such as dipole-dipole repulsion, might explain both the stability of nanodomains as well as the observed abrupt transition in domain size. At low line tension, the repulsion could dominate the domain boundary energy that favors decreasing interface, and the total energy of the system would be minimized with several small domains, rather than one or a few large domains (23).
Fig. 7 shows FRET profiles along thermodynamic tielines of DSPC- and bSM-containing mixtures that form nanodomains. We performed three independent experiments using different FRET pairs to analyze the domain size in each lipid mixture. Table 2 summarizes the domain size obtained from each experiment.
Table 2.
Domain Size of DSPC/POPC/chol and bSM/POPC/chol
| Mixture | FRET Pair |
Kp |
Kp |
Domain Size |
|---|---|---|---|---|
| Donor/Acceptor | Donor | Acceptor | Radius (Rd, nm) | |
| DSPC/POPC/chol | TOE/DHE | 5 ± 1 | 0.39 ± 0.01 | 10 ± 1 |
| DSPC/POPC/chol | DHE/Bodipy-PC | 0.39 ± 0.01 | 4 ± 1 | 7.5 ± 1.3 |
| DSPC/POPC/chol | TOE/Bodipy-PC | 5 ± 1 | 4 ± 1 | 7.5 ± 1.3 |
| bSM/POPC/chol | TOE/DHE | 5 ± 1 | 0.27 ± 0.01 | 5 ± 1 |
| bSM/POPC/chol | DHE/Bodipy-PC | 0.27 ± 0.01 | 3 ± 1 | 5 ± 1 |
| bSM/POPC/chol | TOE/Bodipy-PC | 5 ± 1 | 3 ± 1 | 5 ± 3 |
Experimental FRET curves were analyzed with theoretical FRET profiles obtained from MC simulations. Different FRET pairs were analyzed for each lipid mixture. The partition coefficient used in the simulations was obtained from single-dye experiments or according to the chol partition coefficient. The error in the domain size was calculated from the theoretical curves that best fit the experimental data.
DSPC-containing mixtures
Our Monte Carlo (MC) analysis uses these FRET data together with Kp values for the probes to find that DSPC/POPC/chol forms domains with radius of 7.5−10 nm. Previously, using SANS, Heberle et. al. measured the domain radius to be 6.8 nm for the same lipid mixture, DSPC/POPC/chol = 0.39/0.39/0.22 (30). This agreement with the previous domain size determination suggests that our FRET method can measure domain size with a precision of a few nanometers.
We do not know whether the size of nanodomains changes along a tieline, but clearly the line tension and dipole repulsion (23) that control domain size do not coalesce nanodomains into macrodomains. In contrast to SANS measurements made at a single lipid composition, FRET experiments were performed at many compositions along a thermodynamic tieline, at which the fraction of Ld and Lo phases varies from zero to one. However, in contrast to the macroscopic phase separation, in which higher line tensions favor larger domains and the domain sizes are intrinsically correlated with the fractions of phases, nanodomains are stable at their small sizes, and changes in the phase fractions along the tieline more likely reflect changes in the number of domains dispersed in the continuous phase. If a balance of competing interactions between line tension and dipole repulsion controls the sizes of nanodomains, a narrower distribution of the sizes for nanodomains is possible, or even expected, in comparison with macrodomains.
An advantage of the FRET experiment is its accessibility: 1) these experiments enable the study of lipids that are not easily deuterated, and hence cannot be studied by neutron scattering; and 2) a specialized neutron scattering facility is not required.
bSM-containing mixtures
bSM/POPC/chol forms domains that are smaller than domains in the DSPC mixtures. Petruzielo et al. reported phase boundaries for bSM/POPC/chol obtained with FRET, implying the coexistence of Ld and Lo phases, but SANS data could not be interpreted to measure the size of these small domains. The authors suggested that the SANS apparatus used had a limitation to measuring domain sizes larger than ∼7 nm radius. This limitation is primarily related to the contrast between the domain and its surroundings, which is strongly affected by the partitioning of deuterated lipids (19). Other factors that degrade signal-to-noise, such as source brightness and incoherent background from hydrogen, also affect the sensitivity of SANS measurements. The observation without a size measurement of smaller domains in the bSM/POPC/chol mixtures has been termed “ultrananodomains” (52). Especially significant, we previously measured that bSM/DOPC/POPC/chol has lower line tension than does DSPC/DOPC/POPC/chol, which is consistent with bSM mixtures forming the smaller domains as we report here, because line tension controls domain size (23).
Domain size transition
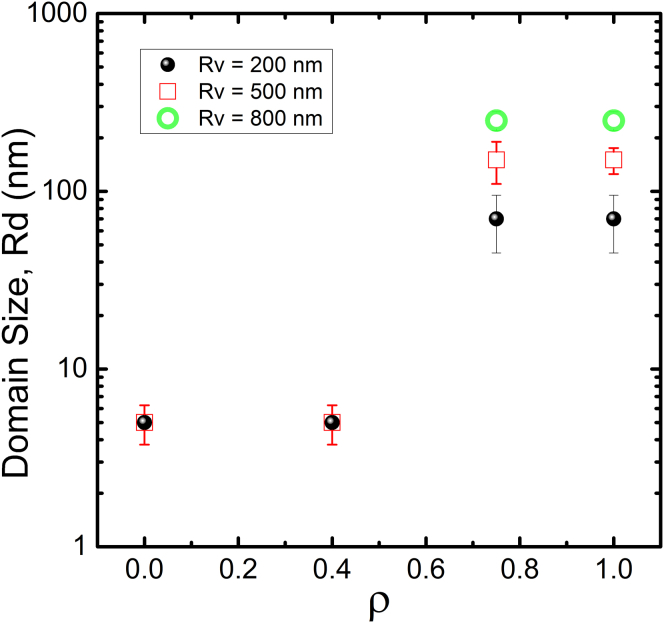
For bSM mixtures, we measured domain sizes for the lipid mixture bSM/DOPC/POPC/chol (Fig. 1 C) along different values of ρ (Eq. 9). An abrupt domain size transition was observed with GUVs at ρ = 0.55 (23), at which the domain size changes from nanometers (for ρ < 0.45) to micrometers (for ρ > 0.55) in a narrow compositional range (23). In this section, we investigate this domain size transition and the dependence of domain size on vesicle size.
Nanodomains
Fig. 8 shows the results obtained from FRET trajectories along thermodynamic tielines for different values of ρ. A least-squares comparison of experimental (in vitro) and simulation (in silico) data enables us to determine an average domain size. In the simulations, we examined the effect of vesicle size, represented by the vesicle radius Rv, on FRET by performing simulations with Rv = 200, 500, and 800 nm. For ρ = 0 and 0.4, the best agreement between simulation and experiment occurs for a domain radius of 5 nm, independent of the simulated vesicle size. It should be noted that, in principle, the FRET analysis is insensitive to vesicle sizes for small domains. Indeed, we previously measured the sizes of nanodomains using extruded vesicles of different size, using SANS for DSPC/POPC/chol (ρ = 0) mixtures, and found the domain size to be independent of vesicle size (23) (see Fig. S12).
Figure 8.
FRET analysis reveals a domain size transition in bSM/DOPC/POPC/chol as POPC is replaced by DOPC. FRET experiments and simulations show a domain size of Rd = 5 ± 1 nm for ρ = 0 and 0.4 independent of vesicle size. For ρ = 0.75 and 1, FRET analyses show an abrupt transition in domain size, with Rd increasing more than 10-fold compared to the values for ρ = 0 and 0.4. The domain-size dependence on vesicle size disappears for true nanodomains. To see this figure in color, go online.
Macrodomains
In contrast, for domains that would be macroscopic on a GUV, comparison of experimental and simulated data at ρ = 0.75 and 1 shows a different domain size and vesicle size dependence. First, when the experimental data are fitted with simulated FRET calculated for Rv = 200 nm, best agreement occurs with a domain radius of 70 nm. This analysis yields domain sizes that are more than 10× larger for mixtures at ρ = 0.75 and 1 that reveal macrodomains on GUVs, compared to mixtures at ρ = 0 and 0.4 that reveal uniform GUVs. Although Rd = 70 nm is at the nanometer-scale, the vesicle size is limiting the phase domain size. FRET experiments use RSE vesicles with a range of sizes from hundreds of nanometers (36, 53) up to a few microns for a small population (54). Therefore, even the largest domains are limited to the nanometer-scale for most of the vesicles.
Second, for ρ = 0.75 and 1, as simulated vesicle size increases, the domain size that best fits experimental data also increases. For vesicle sizes Rv = 200, 500, and 800 nm, domain sizes show Rd = 70, 150, and 250 nm, respectively. As mentioned above, in the macroscopic regime, domain sizes change along the tieline because the fraction of phases changes along the tieline and the high line tension favors larger domains (23). Our computational FRET analysis relies on an average domain size value, and we also observed a dependence of domain size on vesicle size, as expected in the macroscopic phase separation regime.
Thus, when macroscopic phase separation occurs, domain size can depend on phase fraction and vesicle size. Our computational analysis does not account for a distribution of domain sizes, size change along a tieline, or a distribution of vesicles sizes; our domain size values for the macroscopic regime (Rd = 70, 150 and 250 nm) are approximations from a simplified model. However, considering this domain-size dependence on vesicle size, it is straightforward to predict micron-size domains on GUVs. Thus, our FRET analyses are consistent with the abrupt domain size transition previously observed on GUVs for 12 different lipid mixtures as reported (23).
Assumptions and limitations of the MC analysis
The off-lattice MC simulations used to analyze FRET trajectories are conceptually similar to simulations described by Towles et al. (48), with modifications to the calculation of FRET efficiency based on the work of Corry et al. (45). Lipid-lipid interaction energies are not explicitly included in these simulations as they are in a lattice-based approach, in which the equilibrium spatial distribution of probes is found through Metropolis sampling (55). Instead, differences in interaction energies are implicitly accounted for by the partition coefficient of the probes between the coexisting phases, which results in a nonrandom probe distribution that is governed by the strength of partitioning as well as the size and spatial arrangement of phase domains.
The simulations assume Ld and Lo phase compositions that are given by the fixed tieline endpoints. As domains decrease in size, the total number of lipids per domain is small enough (a few hundred, in the case of a 5-nm-radius domain) that purely statistical fluctuations will result in some variation in the composition of individual domains. The simulations are designed to capture these compositional fluctuations in the following way: 1) the actual number of probe molecules in each simulated vesicle is not fixed, but rather is drawn from a Poisson distribution centered at the number of probes expected to be found in the vesicle, given the probe concentration; and 2) the probes are randomly assigned to the available domains. In this way, the “probe concentration” within individual domains is also not fixed, but instead follows a distribution that reflects the statistical variation in domain composition because of small size. For computational convenience, the simulations also assume round domains, which, though a reasonable approximation for the average shape of a nanodomain found in a fluid-fluid coexistence region, is not likely to be strictly true for individual domains (23). Although it is possible to construct a model for more complicated domain geometries, the increased complexity would not be justified, given the excellent agreement with the experimental data provided by the simpler approximation of circular domains.
Conclusions
We propose a simple and accessible method to measure domain size with nanometer resolution using an ordinary fluorimeter. Because of the importance of the dye partition coefficient in our analysis, we used three different methods to measure the Kp of fluorescent probes between Ld and Lo phases. We measured the size of nanodomains for the lipid mixtures DSPC/POPC/chol and bSM/POPC/chol. We found that DSPC/POPC/chol forms domains with a radius size of 7.5−10 nm. Our results agree with a previous domain-size determination by SANS for this mixture of domain radius 6.8 nm (30). Our results indicate that bSM mixtures form nanodomains with smaller sizes than the nanodomains observed in DSPC mixtures. This is consistent with our previous report that bSM mixtures exhibit lower line tension compared to DSPC mixtures (23).
We examined two different regimes of domain size. For macroscopic phase-separated mixtures, the Ld/Lo line tension is sufficiently high that phase domains coalesce into one or a few large domains. These domains are easily observed using fluorescence microscopy, and the domain sizes are related to vesicle size and area fraction of each phase. In contrast, for nanoscopic phase-separated mixtures, domain size is independent of the vesicle size, with the lower line tension for these mixtures (23) favoring small domains. Our analysis reproduces the domain size transition from nanometers to micrometers that is experimentally observed in GUVs (6, 17, 22).
Author Contributions
T.A.E. performed the experiments. F.A.H. developed the Monte Carlo simulation code. T.A.E., F.A.H., and G.W.F. designed and performed the research, analyzed data, and cowrote the manuscript.
Acknowledgments
We thank Rebecca D. Usery for helpful comments.
This work was supported by U.S. National Science Foundation grant MCB-1410926, National Institutes of Health grant no. GM105684 to G.W.F., a Brazilian Fellowship from Sao Paulo Research Foundation (grant number 2013/00473-6), and National Council for Scientific and Technological Development grant no. 201124/2015-7 to T.A.E.
Editor: David Cafiso.
Footnotes
Supporting Materials and Methods, twelve figures, and five tables are available at http://www.biophysj.org/biophysj/supplemental/S0006-3495(18)30380-1.
Supporting Material
References
- 1.Rietveld A., Simons K. The differential miscibility of lipids as the basis for the formation of functional membrane rafts. Biochim. Biophys. Acta. 1998;1376:467–479. doi: 10.1016/s0304-4157(98)00019-7. [DOI] [PubMed] [Google Scholar]
- 2.Simons K. Cell membranes: a subjective perspective. Biochim. Biophys. Acta. 2016;1858:2569–2572. doi: 10.1016/j.bbamem.2016.01.023. [DOI] [PubMed] [Google Scholar]
- 3.Simons K., Ehehalt R. Cholesterol, lipid rafts, and disease. J. Clin. Invest. 2002;110:597–603. doi: 10.1172/JCI16390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.van Meer G., Voelker D.R., Feigenson G.W. Membrane lipids: where they are and how they behave. Nat. Rev. Mol. Cell Biol. 2008;9:112–124. doi: 10.1038/nrm2330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Feigenson G.W., Buboltz J.T. Ternary phase diagram of dipalmitoyl-PC/dilauroyl-PC/cholesterol: nanoscopic domain formation driven by cholesterol. Biophys. J. 2001;80:2775–2788. doi: 10.1016/S0006-3495(01)76245-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Konyakhina T.M., Wu J., Feigenson G.W. Phase diagram of a 4-component lipid mixture: DSPC/DOPC/POPC/chol. Biochim. Biophys. Acta. 2013;1828:2204–2214. doi: 10.1016/j.bbamem.2013.05.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Ackerman D.G., Feigenson G.W. Multiscale modeling of four-component lipid mixtures: domain composition, size, alignment, and properties of the phase interface. J. Phys. Chem. B. 2015;119:4240–4250. doi: 10.1021/jp511083z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Ingólfsson H.I., Melo M.N., Marrink S.J. Lipid organization of the plasma membrane. J. Am. Chem. Soc. 2014;136:14554–14559. doi: 10.1021/ja507832e. [DOI] [PubMed] [Google Scholar]
- 9.Wen Y., Dick R.A., Vogt V.M. Effects of membrane charge and order on membrane binding of the retroviral structural protein Gag. J. Virol. 2016;90:9518–9532. doi: 10.1128/JVI.01102-16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Dick R.A., Goh S.L., Vogt V.M. HIV-1 Gag protein can sense the cholesterol and acyl chain environment in model membranes. Proc. Natl. Acad. Sci. USA. 2012;109:18761–18766. doi: 10.1073/pnas.1209408109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Wenk M.R. The emerging field of lipidomics. Nat. Rev. Drug Discov. 2005;4:594–610. doi: 10.1038/nrd1776. [DOI] [PubMed] [Google Scholar]
- 12.Klose C., Surma M.A., Simons K. Flexibility of a eukaryotic lipidome--insights from yeast lipidomics. PLoS One. 2012;7:e35063. doi: 10.1371/journal.pone.0035063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.McDonald J.G., Thompson B.M., Russell D.W. Extraction and analysis of sterols in biological matrices by high performance liquid chromatography electrospray ionization mass spectrometry. Methods Enzymol. 2007;432:145–170. doi: 10.1016/S0076-6879(07)32006-5. [DOI] [PubMed] [Google Scholar]
- 14.Ivanova P.T., Milne S.B., Brown H.A. Glycerophospholipid identification and quantitation by electrospray ionization mass spectrometry. Methods Enzymol. 2007;432:21–57. doi: 10.1016/S0076-6879(07)32002-8. [DOI] [PubMed] [Google Scholar]
- 15.Tulodziecka K., Diaz-Rohrer B.B., Levental I. Remodeling of the postsynaptic plasma membrane during neural development. Mol. Biol. Cell. 2016;27:3480–3489. doi: 10.1091/mbc.E16-06-0420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Feigenson G.W. Phase diagrams and lipid domains in multicomponent lipid bilayer mixtures. Biochim. Biophys. Acta. 2009;1788:47–52. doi: 10.1016/j.bbamem.2008.08.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Zhao J., Wu J., Feigenson G.W. Phase studies of model biomembranes: complex behavior of DSPC/DOPC/Cholesterol. Biochim. Biophys. Acta. 2007;1768:2764–2776. doi: 10.1016/j.bbamem.2007.07.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Goh S.L., Amazon J.J., Feigenson G.W. Toward a better raft model: modulated phases in the four-component bilayer, DSPC/DOPC/POPC/CHOL. Biophys. J. 2013;104:853–862. doi: 10.1016/j.bpj.2013.01.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Petruzielo R.S., Heberle F.A., Feigenson G.W. Phase behavior and domain size in sphingomyelin-containing lipid bilayers. Biochim. Biophys. Acta. 2013;1828:1302–1313. doi: 10.1016/j.bbamem.2013.01.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Heberle F.A., Doktorova M., Feigenson G.W. Hybrid and nonhybrid lipids exert common effects on membrane raft size and morphology. J. Am. Chem. Soc. 2013;135:14932–14935. doi: 10.1021/ja407624c. [DOI] [PubMed] [Google Scholar]
- 21.Heberle F.A., Wu J., Feigenson G.W. Comparison of three ternary lipid bilayer mixtures: FRET and ESR reveal nanodomains. Biophys. J. 2010;99:3309–3318. doi: 10.1016/j.bpj.2010.09.064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Konyakhina T.M., Feigenson G.W. Phase diagram of a polyunsaturated lipid mixture: brain sphingomyelin/1-stearoyl-2-docosahexaenoyl-sn-glycero-3-phosphocholine/cholesterol. Biochim. Biophys. Acta. 2015;1858:153–161. doi: 10.1016/j.bbamem.2015.10.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Usery R.D., Enoki T.A., Feigenson G.W. Line tension controls liquid-disordered + liquid-ordered domain size transition in lipid bilayers. Biophys. J. 2017;112:1431–1443. doi: 10.1016/j.bpj.2017.02.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Konyakhina T.M., Goh S.L., Feigenson G.W. Control of a nanoscopic-to-macroscopic transition: modulated phases in four-component DSPC/DOPC/POPC/Chol giant unilamellar vesicles. Biophys. J. 2011;101:L8–L10. doi: 10.1016/j.bpj.2011.06.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Fricke N., Dimova R. GM1 softens POPC membranes and induces the formation of micron-sized domains. Biophys. J. 2016;111:1935–1945. doi: 10.1016/j.bpj.2016.09.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Baumgart T., Hunt G., Feigenson G.W. Fluorescence probe partitioning between Lo/Ld phases in lipid membranes. Biochim. Biophys. Acta. 2007;1768:2182–2194. doi: 10.1016/j.bbamem.2007.05.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Puff N., Watanabe C., Staneva G. Lo/Ld phase coexistence modulation induced by GM1. Biochim. Biophys. Acta. 2014;1838:2105–2114. doi: 10.1016/j.bbamem.2014.05.002. [DOI] [PubMed] [Google Scholar]
- 28.Buboltz J.T. Steady-state probe-partitioning fluorescence resonance energy transfer: a simple and robust tool for the study of membrane phase behavior. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2007;76:021903. doi: 10.1103/PhysRevE.76.021903. [DOI] [PubMed] [Google Scholar]
- 29.Moss F.R., III, Boxer S.G. Atomic recombination in dynamic secondary ion mass spectrometry probes distance in lipid assemblies: a nanometer chemical ruler. J. Am. Chem. Soc. 2016;138:16737–16744. doi: 10.1021/jacs.6b10655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Heberle F.A., Petruzielo R.S., Katsaras J. Bilayer thickness mismatch controls domain size in model membranes. J. Am. Chem. Soc. 2013;135:6853–6859. doi: 10.1021/ja3113615. [DOI] [PubMed] [Google Scholar]
- 31.de Wit G., Danial J.S., Wallace M.I. Dynamic label-free imaging of lipid nanodomains. Proc. Natl. Acad. Sci. USA. 2015;112:12299–12303. doi: 10.1073/pnas.1508483112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Lagerholm B.C., Andrade D.M., Eggeling C. Convergence of lateral dynamic measurements in the plasma membrane of live cells from single particle tracking and STED-FCS. J. Phys. D Appl. Phys. 2017;50:063001. doi: 10.1088/1361-6463/aa519e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Eggeling C., Ringemann C., Hell S.W. Direct observation of the nanoscale dynamics of membrane lipids in a living cell. Nature. 2009;457:1159–1162. doi: 10.1038/nature07596. [DOI] [PubMed] [Google Scholar]
- 34.Heberle F.A., Buboltz J.T., Feigenson G.W. Fluorescence methods to detect phase boundaries in lipid bilayer mixtures. Biochim. Biophys. Acta. 2005;1746:186–192. doi: 10.1016/j.bbamcr.2005.05.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Kingsley P.B., Feigenson G.W. The synthesis of a perdeuterated phospholipid: 1,2-dimyristoyl-sn-glycero-3-phosphocholine-d72. Chem. Phys. Lipids. 1979;24:135–147. [Google Scholar]
- 36.Buboltz J.T., Feigenson G.W. A novel strategy for the preparation of liposomes: rapid solvent exchange. Biochim. Biophys. Acta. 1999;1417:232–245. doi: 10.1016/s0005-2736(99)00006-1. [DOI] [PubMed] [Google Scholar]
- 37.Huang J., Buboltz J.T., Feigenson G.W. Maximum solubility of cholesterol in phosphatidylcholine and phosphatidylethanolamine bilayers. Biochim. Biophys. Acta. 1999;1417:89–100. doi: 10.1016/s0005-2736(98)00260-0. [DOI] [PubMed] [Google Scholar]
- 38.Vaz W.L.C., Melo E. Fluorescence spectroscopic studies on phase heterogeneity in lipid bilayer membranes. J. Fluoresc. 2001;11:255–271. [Google Scholar]
- 39.Silvius J.R., Nabi I.R. Fluorescence-quenching and resonance energy transfer studies of lipid microdomains in model and biological membranes. Mol. Membr. Biol. 2006;23:5–16. doi: 10.1080/09687860500473002. [DOI] [PubMed] [Google Scholar]
- 40.de Almeida R.F., Loura L.M., Prieto M. Lipid rafts have different sizes depending on membrane composition: a time-resolved fluorescence resonance energy transfer study. J. Mol. Biol. 2005;346:1109–1120. doi: 10.1016/j.jmb.2004.12.026. [DOI] [PubMed] [Google Scholar]
- 41.Angelova M.I., Dimitrov D.S. Liposome electroformation. Faraday Discuss. Chem. Soc. 1986;81:303. [Google Scholar]
- 42.Alwarawrah M., Dai J., Huang J. A molecular view of the cholesterol condensing effect in DOPC lipid bilayers. J. Phys. Chem. B. 2010;114:7516–7523. doi: 10.1021/jp101415g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Mills T.T., Toombes G.E., Nagle J.F. Order parameters and areas in fluid-phase oriented lipid membranes using wide angle X-ray scattering. Biophys. J. 2008;95:669–681. doi: 10.1529/biophysj.107.127845. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Fung B.K., Stryer L. Surface density determination in membranes by fluorescence energy transfer. Biochemistry. 1978;17:5241–5248. doi: 10.1021/bi00617a025. [DOI] [PubMed] [Google Scholar]
- 45.Corry B., Jayatilaka D., Rigby P. A flexible approach to the calculation of resonance energy transfer efficiency between multiple donors and acceptors in complex geometries. Biophys. J. 2005;89:3822–3836. doi: 10.1529/biophysj.105.069351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Moore W.J. Third Edition. Prentice-Hall, Inc.; London: 1957. Physical Chemistry. [Google Scholar]
- 47.Chiang Y.W., Zhao J., Feigenson G.W. New method for determining tie-lines in coexisting membrane phases using spin-label ESR. Biochim. Biophys. Acta. 2005;1668:99–105. doi: 10.1016/j.bbamem.2004.11.010. [DOI] [PubMed] [Google Scholar]
- 48.Towles K.B., Brown A.C., Dan N. Effect of membrane microheterogeneity and domain size on fluorescence resonance energy transfer. Biophys. J. 2007;93:655–667. doi: 10.1529/biophysj.106.090274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Brown A.C., Towles K.B., Wrenn S.P. Measuring raft size as a function of membrane composition in PC-based systems: part II--ternary systems. Langmuir. 2007;23:11188–11196. doi: 10.1021/la7006342. [DOI] [PubMed] [Google Scholar]
- 50.Mukherjee S., Zha X., Maxfield F.R. Cholesterol distribution in living cells: fluorescence imaging using dehydroergosterol as a fluorescent cholesterol analog. Biophys. J. 1998;75:1915–1925. doi: 10.1016/S0006-3495(98)77632-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Kuśba J., Li L., Lakowicz J.R. Lateral diffusion coefficients in membranes measured by resonance energy transfer and a new algorithm for diffusion in two dimensions. Biophys. J. 2002;82:1358–1372. doi: 10.1016/S0006-3495(02)75491-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Pathak P., London E. The effect of membrane lipid composition on the formation of lipid ultrananodomains. Biophys. J. 2015;109:1630–1638. doi: 10.1016/j.bpj.2015.08.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Caffrey M., Feigenson G.W. Fluorescence quenching in model membranes. 3. Relationship between calcium adenosinetriphosphatase enzyme activity and the affinity of the protein for phosphatidylcholines with different acyl chain characteristics. Biochemistry. 1981;20:1949–1961. doi: 10.1021/bi00510a034. [DOI] [PubMed] [Google Scholar]
- 54.Rieder A.A., Koller D., Pabst G. Optimizing rapid solvent exchange preparation of multilamellar vesicles. Chem. Phys. Lipids. 2015;186:39–44. doi: 10.1016/j.chemphyslip.2014.12.001. [DOI] [PubMed] [Google Scholar]
- 55.Frazier M.L., Wright J.R., Almeida P.F. Investigation of domain formation in sphingomyelin/cholesterol/POPC mixtures by fluorescence resonance energy transfer and Monte Carlo simulations. Biophys. J. 2007;92:2422–2433. doi: 10.1529/biophysj.106.100107. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.