A Simple Test Identifies Selection on Complex Traits

Important traits are often controlled by a large number of genes that each impact a small proportion of total variation; however, the majority of tools in population genomics are designed to identify single genes...

Abstract

Important traits in agricultural, natural, and human populations are increasingly being shown to be under the control of many genes that individually contribute only a small proportion of genetic variation. However, the majority of modern tools in quantitative and population genetics, including genome-wide association studies and selection-mapping protocols, are designed to identify individual genes with large effects. We have developed an approach to identify traits that have been under selection and are controlled by large numbers of loci. In contrast to existing methods, our technique uses additive-effects estimates from all available markers, and relates these estimates to allele-frequency change over time. Using this information, we generate a composite statistic, denoted $\widehat{G},$ which can be used to test for significant evidence of selection on a trait. Our test requires pre- and postselection genotypic data but only a single time point with phenotypic information. Simulations demonstrate that $\widehat{G}$ is powerful for identifying selection, particularly in situations where the trait being tested is controlled by many genes, which is precisely the scenario where classical approaches for selection mapping are least powerful. We apply this test to breeding populations of maize and chickens, where we demonstrate the successful identification of selection on traits that are documented to have been under selection.

QUANTITATIVE traits encompass an inexhaustible number of phenotypes that vary in populations, from characters such as height (Yang et al. 2010), to weight (Barsh et al. 2000), to disease resistance (Poland et al. 2009). These types of traits are so essential for agriculture and human health that the entire field of quantitative genetics revolves around their study (Plomin et al. 2009; Wallace et al. 2014). However, the nature of quantitative traits makes it difficult to study their genetic basis; for nearly a century, scientists have modeled quantitative traits by assuming that their underlying control involves many loci each contributing a very small proportion to genetic variance (Fisher 1918), the so-called “infinitesimal model.” Therefore, conducting studies with enough power to identify a substantial proportion of the loci that contribute to a quantitative trait requires a massive sample size, imposing financial and logistical barriers. However, this model of quantitative trait variation does an excellent job when predicting important characteristics such as response to selection (Visscher et al. 2008). For instance, genomic prediction methodologies (Meuwissen et al. 2001) allow the breeding value and/or phenotype of individuals to be predicted with remarkable precision from genomic information alone.

The models of quantitative genetics have had a less dramatic impact on studies of evolutionary adaptation, where genomes are often scanned to identify adaptive loci with large effects (Akey 2009). Positive selection on such loci leaves behind pronounced signatures, deemed “selective sweeps.” There is an abundance of evidence for such sweeps in humans (Sabeti et al. 2007), natural populations (Schweizer et al. 2016), livestock (Qanbari and Simianer 2014), and crops (Hufford et al. 2012). However, alternative forms of selection, including purifying selection against new mutations (Lawrie et al. 2013), selection on standing variation (Garud et al. 2015), or selection on many loci of small effect (Turchin et al. 2012) rarely leave these discernible signatures at individual loci. Evidence of these forms of selection can be difficult to identify. When they are found, it is often through the pooling of weak evidence at individual loci into a stronger signal across a class of loci. For example, Beissinger et al. (2016) demonstrated the importance of purifying selection during maize evolution by combining evidence from all maize genes. An approach implemented by Berg and Coop (2014) tests for evidence of selection on a quantitative trait by evaluating allele frequencies at all loci that have previously been implicated by genome-wide association studies (GWAS) as putatively associated with that trait. This approach has since been used to test for selection on multiple human traits, including height (Mathieson et al. 2015) and telomere length (Hansen et al. 2016).

In studies of model organisms or agricultural species, large collections of previously identified “GWAS hits” are not as abundant as in humans, on which the Berg and Coop (2014) method depends. This is partly due to the more modest sample sizes that tend to be used in experimental settings compared to clinical studies, which are often combined in large-scale meta-analyses (Evangelou and Ioannidis 2013). Conversely, genotypic data across at least two time points are often readily available for model and agricultural species. Due to improving technologies for sequencing ancient DNA (Berg et al. 2017; Mathieson et al. 2018), and/or by leveraging populations that have benefited from excellent historical record keeping (Kong et al. 2017), genetic data with a temporal component is increasingly available in humans. We have developed a test for selection on complex traits that leverages such genotype-over-time data. Our test depends on the relationship between the change in allele frequency between two generations and the estimated additive effect of the same allele, computed for every genotyped locus. We use these values to compute an estimate of the direction of genetic gain, which can be shown to be additive across all loci considered. Our estimate lends itself to a simple permutation-based test for significance that avoids many of the demographic history- and population structure-related caveats that complicate determining significance when testing for selection (de Villemereuil et al. 2014). The method uses additive-effects estimates for each locus calculated simultaneously by using shrinkage-based methods that have been honed over the past 15 years for the purpose of genomic selection and prediction (de Los Campos et al. 2013). Therefore, this test can be considered analogous to reverse genomic selection; rather than using predictions of breeding value to drive selection and hence future changes in allele frequency, we use the same data coupled with knowledge of past changes in allele frequency to make inferences regarding which traits were effectively under selection in the past. Interestingly, we find by simulation that this approach is most powerful for identifying selection on traits controlled by many loci of small effect, which is exactly the situation where other tests for selection and/or association are least powerful.

Herein, we first motivate and describe our test for selection on complex traits, which we call $\widehat{G}G.$ We then perform simulations demonstrating the validity of the method and explore the situations where it is most and least powerful. Finally, we apply the method to breeding populations of maize and chicken. In both of these experimental situations, we successfully identify the traits that are known to have been selected. Collectively, our results demonstrate that this approach may be leveraged to identify novel traits or component traits that may be used to inform future breeding decisions and/or for enhanced historical, ecological, and basic scientific understanding. Software for implementing this test is provided in the accompanying Github repository: http://github.com/timbeissinger/ComplexSelection.

Materials and Methods

Theoretical motivation

Assume that a trait is fully controlled by additive di-allelic loci $j=1,\dots m.$ The genotypic value, a_j, of an allele at locus j, is then equal to its gene substitution effect, α_j. Based on this equivalency, the mean phenotypic effect (M_j) attributable to the locus is given by M_j = α_j(2p_j − 1), where p_j is the frequency of the reference allele at this locus. It follows that the change in the population mean resulting from selection on this locus, what we may consider the locus-specific response to selection, is given by

$${\mathit{R}}_{\mathit{j}}={\mathit{M}}_{\mathit{j}1}\mathrm{-}{\mathit{M}}_{\mathit{j}0}={\mathit{\alpha }}_{\mathit{j}}\left(2{\mathit{p}}_{\mathit{j}1}\mathrm{-}1\right)-{\mathit{\alpha }}_{\mathit{j}}\left(2{\mathit{p}}_{\mathit{j}0}-1\right)=2{\mathit{\alpha }}_{\mathit{j}}\left({\mathit{p}}_{\mathit{j}1}-{\mathit{p}}_{\mathit{j}0}\right),$$

where p_j0 is the allele frequency before selection and p_j1 is the allele frequency after selection. Define Δ_j = (p_j1 − p_j0), leading to R_j = 2Δ_jα_j. Based on our earlier assumption of complete additivity, summing over all m loci provides a genome-wide estimate of the response to selection (Falconer and Mackay 1996):

$$\widehat{R}R=2{\displaystyle \sum }_{j=1}^m{\Delta }_j{\alpha }_j.$$ (1)

Strictly speaking, since relative effect sizes may change each generation with changing allele frequencies throughout the genome, (1) is applicable for a single generation. However, under the assumption of many loci affecting a trait, (1) may approximately apply for many generations of selection. This estimate of selection response also naturally arises from the logic of random regression best linear unbiased prediction (RRBLUP) (Meuwissen et al. 2001). Here, a model is used:

$$\mathit{y}=\mathit{Xb}+\mathit{Zs}+\mathit{e}\mathit{,}$$ (2)

where $\mathit{y}$ is a vector of length $n$ containing phenotypes for a specific trait, $\mathit{b}$ are fixed effects, $\mathit{s}\sim N(0,\mathit{I}{\sigma }_s^2)$ is the vector of length $m$ containing additive SNP effects at $m$ loci; $\mathit{e}\sim N(0,\mathit{I}{\sigma }_e^2)$ is the vector of random residual terms and ${\sigma }_s^2$ and ${\sigma }_e^2$ are the corresponding variance components. $\mathit{X}$ and $\mathit{Z}$ are incidence matrices linking observations in $y$ to the respective levels of fixed effects in $\mathit{b}$ and random SNP effects in $\mathit{s}.$ In more detail, $\mathit{Z}$ is an $n\times m$ matrix where element $z_{ij}$ contains the genotype of individual $i$ at SNP locus $j.$ Since such models are invariant with respect to linear transformations of the allele coding (Strandén and Christensen 2011), we may use the notation $z_{ij}=0,1/2, \text{or} 1;$ standing for zero, one, or two copies of the reference allele. Note that with this coding, $s_j$ is equivalent to $2{\alpha }_j$ in the coding above since it reflects the contrast between the two homozygous genotypes at locus $j.$ Due to the equivalence of genomic BLUP (GBLUP) (VanRaden 2008) and RRBLUP (Endelman 2011), it is possible to calculate genomic breeding values of the genotyped individual as $\widehat{\mathit{u}}=\mathit{Z}\widehat{\mathit{s}},$ where $\widehat{\mathit{s}}$ are the solutions for the SNP effects obtained using RRBLUP with model (2).

Now assume that individuals in the vector $\mathit{y}$ can be assigned to $g$ discrete generations and that the individuals of the oldest generation come first and the individuals of the last generation come last. We then can define a $g\times n$ matrix

$$\mathit{L}=\left[\begin{array}{ccc}{l}_1& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & l_g\end{array}\right],$$

where $l_p$ is a row vector of length $n_p,$ which is the number of individuals in generation p, of which all elements are $1/n_p.$ With this, a vector $\overline{\mathit{u}}$ of length $g$ reflecting average breeding values per generation can be calculated as $\overline{\mathit{u}}=\mathit{L}\widehat{\mathit{u}},$ and estimated selection response results as $\widehat{R}={\overline{u}}_g-{\overline{u}}_1.$ Now, $\overline{\mathit{u}}\mathit{u}=\mathit{L}\widehat{\mathit{u}}=\mathit{LZ}\widehat{\mathit{s}},$ where $\mathit{LZ}$ is a $g\times m$ matrix in which element $p,j$reflects the average allele frequency of the reference allele at SNP $j$ in generation $p.$ The allele-frequency change between generation 1 and generation g can be obtained as a linear contrast between the first and the last row of this matrix as $\mathit{\Delta } =\mathit{k}\prime \mathit{LZ}\mathit{,}$ where $k$ is a vector of length g with $k_1=-1, k_g=1,$ and all other elements are 0. Finally, the selection response can be written as $\widehat{R}=\Delta \widehat{\mathit{s}},$ which is identical to Equation 1, given that $s$ is equivalent to $2\alpha .$

Furthermore, theory suggests that under the assumption that selection intensity is equal for all loci across the genome, the change of allele frequency ${\Delta }_j$ should be approximately proportional to the allele effect ${\alpha }_j$ such that, for a trait under selection, a nonzero correlation between allele-frequency change and the additive effect of alleles on that trait is expected (Wright 1937). Alternatively stated, (1) emphasizes the temporal component of the Breeder’s equation, R = h²S, where h² is the narrow-sense heritability of a trait and S is the selection differential. Given a population of individuals with two time points of genotypic data, it is simple to compute ${\Delta }_j$ for every genotyped locus. Furthermore, the shrinkage methods of genomic prediction (de Los Campos et al. 2013), including ridge regression (Endelman 2011) and GBLUP (VanRaden 2008), allow additive effects (α_j) to be approximated for every genotyped position. For this, a set of individuals genotyped and phenotyped in at least one generation is needed.

A notable benefit of the estimator in (1) is that by leveraging pre- and postselection data from genotypes rather than from phenotypes, it only requires one generation of phenotyping. Additionally, this suggests that if we consider $R$ a random variable, then given the distribution of R in a scenario without selection, a test of whether or not $\widehat{R}$ is different from zero may be performed. Since $\widehat{R}$ is the genomic response to selection, this is equivalent to testing whether or not a trait has been under selection during the time frame under study.

Test statistic and significance testing

We implemented a permutation-based strategy to test whether or not $\widehat{R}$ is significantly different from zero. Genetic drift and selection jointly determine changes in allele frequency, ${\Delta }_j,$ but without selection these changes in frequency should not be related to effect size or direction. The reverse is also true; effect sizes, ${\alpha }_j,$ are estimated based on a genomic prediction model applied to phenotypes measured in a single panel of individuals. Therefore they are not correlated with changes in allele frequency. While a correlation between minor allele frequency (MAF) and the magnitude of SNP effects is possible due to estimation error during genomic prediction; without ongoing selection, allele frequency should not correlate with the direction of SNP effects. This suggests that a null distribution for $\widehat{R}$ in a no-selection scenario may be generated via a permutation approach. Assuming no linkage disequilibrium (LD) between markers, a simple shuffling of ${\Delta }_j$ and ${\alpha }_j$ can be implemented to generate the desired null distribution. However, LD between markers compromises the applicability of this simplified technique for most populations: such an approach overestimates the sample size of the permutation test by treating each marker as an independent observation, while in reality any level of LD between markers leads to fewer independent observations than markers. Therefore, we have employed a semiparametric method that scales the variance of the permutation test statistic according to the realized extent of LD to alleviate this discrepancy.

Let $\widehat{G}={\displaystyle {\sum }_{j=1}^m{\Delta }_j{\alpha }_j},$ which is proportional to $\widehat{R}$ as defined in (1). This value, colloquially “G-hat,” serves as our test statistic. The summation is over all m genotyped markers, and effect sizes are estimated based on genomic prediction using available phenotypes with corresponding genotypes from any generation. Often, phenotypes from the most recent generation will be the most readily available, but individuals with phenotypes scored in any generation may suffice. To test whether or not the observed value of $\widehat{G}$ can be significantly attributed to selection, define p to be a vector of length m that is a permutation of the vector J = [1,..,m]. A permuted value of $\widehat{G}$ may be obtained via ${\widehat{G}}_{\mathrm{perm}}={\displaystyle {\sum }_{j=1}^m{\Delta }_j{\alpha }_{p_j}}.$ Because ${\Delta }_j$ and ${\alpha }_{p_j}$ are no longer indexed to the same locus, ${\widehat{G}}_{\mathrm{perm}}$ does not reflect selection but instead captures genetic drift over time (${\Delta }_j$ terms) as well as the genetic architecture of the underlying trait (${\alpha }_{p_j}$ terms). Generating repeated values of ${\widehat{G}}_{\mathrm{perm}}$ through repeated permutations of J therefore generates a null distribution for $\widehat{G}$ which assumes no selection and complete linkage equilibrium.

The central limit theorem dictates that realizations of ${\widehat{G}}_{\mathrm{perm}}$ are normally distributed with approximate mean $\overline{{\widehat{G}}_{\mathrm{perm}}}$ and SD $SE({\widehat{G}}_{\mathrm{perm}}).$ Therefore, σ, the underlying SE of a single-locus estimate for ${\widehat{G}}_{\mathrm{perm}},$ is given by $\sigma =SE({\widehat{G}}_{\mathrm{perm}})\sqrt{m},$ where $SE({\widehat{G}}_{\mathrm{perm}})$ is the observed SE of ${\widehat{G}}_{\mathrm{perm}}.$ Consider the quantity m_ind, representing the effective number of independent loci. If the SD of ${\widehat{G}}_{\mathrm{perm}}$ was calculated using m_ind independent markers, its expectation would be $S{E}_{ind}\left({\widehat{G}}_{\mathrm{perm}}\right)= \sigma /\sqrt{m_{ind}}.$ Plugging in the estimate for $\sigma$ obtained above, $S{E}_{ind}\left({\widehat{G}}_{\mathrm{perm}}\right)$ becomes $S{E}_{ind}\left({\widehat{G}}_{\mathrm{perm}}\right)= SE\left({\widehat{G}}_{\mathrm{perm}}\right)\sqrt{m/m_{ind}}.$

In practice, the above implies that to test for selection, $\widehat{G}={\displaystyle {\sum }_{j=1}^m{\Delta }_j{\alpha }_j}$ may be calculated from data, and then a permuted null distribution for $\widehat{G}$ that assumes linkage equilibrium can be generated. This permutation distribution may then be approximated with a normal distribution, whose variance can be scaled according to the effective number of independent markers, $m_{ind},$ which can be efficiently estimated based on LD decay. Ultimately, significance may be evaluated by comparing $\widehat{G}$ to a normal distribution with mean $\overline{{\widehat{G}}_{\mathrm{perm}}}$ and SD $SE\left({\widehat{G}}_{\mathrm{perm}}\right)\sqrt{m/m_{ind}}.$

Simulations

We conducted a series of simulations to evaluate the power of the $\widehat{G}$ statistic for identifying selection on complex traits. Genotypic data were simulated with the software program QMSim (Sargolzaei and Schenkel 2009). An overview of our simulation strategy at the most general level is that we simulated selection in a generic species with 1000 QTL dispersed along 10 100-cM chromosomes, with a total of 100,000 equally spaced markers (10,000 per chromosome). In the first step of each simulation, the total population was established based on 10,000 individuals randomly mating for 5000 generations. Selection then began and simulations proceeded for 20 generations with more control over each generation. Truncation selection was performed based on high phenotype. Except where otherwise noted, 1000 individuals (500 males and 500 females) were permitted to mate each generation out of a population of 5000, providing a selection proportion of 0.2. For each simulation, heritability was set to 0.5. Drift simulations were identical to selection simulations in terms of genome layout and genetic basis of the trait, but individuals were selected randomly.

This general scheme encapsulates characteristics of most plant and animal breeding populations, including the large number of progeny typical of plants and the truncation selection protocol often associated with animal breeding and/or selection in the wild. Additional details regarding the simulated population are included in Supplemental Material, Table S1. All simulation scripts can be found at http://github.com/timbeissinger/ComplexSelection. We varied the specific simulation parameters shown below:

• Number of QTL: Genetic architectures with 10, 50, 100, 1000, or 10,000 QTL were simulated.

• Number of individuals phenotyped: After selection was simulated, the phenotypes from a subset including 1000, 500, 250, 100, or 50 individuals were sampled and used for estimating SNP effects.

• Selected proportion: The respective number of males and females reproducing each generation was always simulated to be 500. To vary the selected proportion, we simulated litter sizes of 4, 20, 40, and 200.

• Number of generations of selection: Selection simulations were conducted for 1, 10, 20, 50, and 100 generations.

• Phenotyping generation: For 20-generation simulations, phenotypes were analyzed from preselection individuals (generation 0), midselection individuals (generation 10), and postselection individuals (generation 20).

• Number of generations after selection: After 20 generations of selection, we evaluated whether $\widehat{G}$ was still significant after 5, 20, 50, or 100 generations without selection.

Selection mapping in simulations

For the set of simulations where the number of QTL were varied, pre- and postselection simulated allele frequencies were output from QMSim. These were used to calculate marker-specific F_ST values, as was performed by Lorenz et al. (2015). F_ST was computed according to $F_{ST}= s^2/\left[\overline{p}\left(1-\overline{p}\right)+s^2/2\right],$ where s² is the sample variance of allele frequency between pre- and postselection populations and $\overline{p}$ is the mean allele frequency (Weir and Cockerham 1984). Experiment-wide 5% significance thresholds were identified based on the 95% F_ST quantile observed from drift simulations. These thresholds were applied to F_ST values obtained from selection simulations to determine detection and false-positive rates. Simulated QTL were declared detected if a significant marker was identified within a 0.1-cM window surrounding the QTL. False positives were defined as markers that were not within a 0.1-cM window surrounding any simulated QTL.

Maize data

All maize data were previously published and described by Lorenz et al. (2015). In brief, a selection index comprising silage-quality traits was used to perform reciprocal recurrent selection. Traits comprising the index were yield, dry matter (DM) content, neutral detergent fiber (NDF), protein content, starch content, and in vitro digestibility (http://www.cornbreeding.wisc.edu). Phenotypic data included five cycles of selection, encompassing ∼20 generations in total. Tens to hundreds of individuals were sampled from each cycle of selection to be genotyped. Genotyping was performed with the MaizeSNP50 BeadChip, which includes 56,110 markers in total (Ganal et al. 2011). After removing monomorphic SNPs, redundant SNPs, quality filtering, and imputing as described in Lorenz et al. (2015), 10,023 informative SNPs remained.

Allele frequencies were computed for each cycle of selection. Because only 5 and 11 individuals from cycles 0 and 1, respectively, were genotyped; allele-frequency change from cycle 2 (n = 163) to cycle 5 (n = 211) was computed for each SNP. Since all SNPs were di-allelic, the frequency of only one allele was tracked and the frequency change for that allele perfectly mirrored the change for the other allele. For the tracked allele only, allelic effects were estimated using the R package RR-BLUP (Endelman 2011). Phenotypic information was available from individuals representing selection cycles 1 through 4 and, since population size was small, we used all phenotyped individuals to estimate SNP effects. To accomplish this without biasing effect estimates due to drift, a fixed effect for cycle was included in our model. Our exact analysis scripts are available at http://github.com/timbeissinger/ComplexSelection.

Chicken data

Data were available for one white-layer (WL) and one brown-layer (BL) line from a commercial breeding program. Both closed lines have been selected over decades with a similar composite breeding goal which consists of, among others, laying rate, body weight and feed efficiency of the hens, as well as egg weight and egg quality; where the respective weights of the different traits varied between lines and over time. In total, 673 (743) WL (BL) individuals were genotyped, of which >80% were from the last generation and the remaining animals were parents, grandparents, and great-grandparents of the actual birds. Complete pedigree data were available for all genotyped individuals and consisted of 2109 (1879) individuals going back 13 (9) generations in WL (BL). The oldest generation was defined as the base population and it comprised 111 (64) ungenotyped individuals and was separated from the majority of genotyped individuals by 12 (8) generations.

Current individuals were genotyped with the Affymetrix Axiom Chicken Genotyping Array which initially carries 580K SNPs. These data were pruned by discarding sex chromosomes, unmapped linkage groups, and SNPs with MAF <0.5% or genotyping call rate <97%. Individuals with call rates <95% were also discarded. Subsequently, missing genotypes at the remaining loci were imputed with Beagle version 3.3.2 (Browning and Browning 2009), resulting in sets of 277,522 (334,143) SNPs for the WL (BL) individuals.

To calculate the allele-frequency change in the chicken populations, the allele frequency in the base population individuals had to be reconstructed by statistical means. This was done using the approach of Gengler et al. (2007), which, in short, considers the allele frequency in an individual as a quantitative and heritable trait and uses a mixed-model approach to obtain a BLUP for the allele frequency of all ungenotyped individuals. This is done by linking the genotyped offspring to the ungenotyped ancestors via the pedigree information (for details, see Gengler et al. 2007). This required solving 277,522 (334,143) linear equation systems of dimension 2109 (1879) for the WL (BL) data set. Next, ${\Delta }_i$ for locus $i$ was calculated as the difference of the observed allele frequency of the genotyped individuals in the current and the three ancestral generations and the average estimated allele frequency of the 111 (64) base population individuals 12 (8) generations back.

For each genotyped individual, conventional (nongenomic) BLUP breeding values and the respective reliabilities for a wide set of traits were available. SNP effects were estimated in a two-step procedure: first, for each trait in each line, genomic breeding values were estimated via GBLUP, followed by a back-solution of estimated SNP effects. In the GBLUP step, the model $\mathit{y}=1\mu +\mathit{Zg}+\mathit{e}$ was solved, where $\mathit{y}$ is the vector of deregressed proofs (DRPs) of genotyped individuals for a specific trait, $\mu$ is the overall mean, $\mathit{g}$ is the vector of additive genetic values (i.e., genomic breeding values) for all genotyped chickens, $\mathit{e}$ is the vector of residual terms, $1$ is a vector of ones, and$\mathit{Z}$ is a squared design matrix assigning DRPs to additive genetic values with dimension number of all genotyped individuals. Residual terms were assumed to be distributed $\mathit{e} \sim N(0, \mathit{R}{\sigma }_e^2),$ where $\mathit{R}$ is a diagonal matrix with diagonal elements $R_{ii}=\left[c+(1-r_{\mathrm{DRP}i}^2)/r_{\mathrm{DRP}i}^2\right]h^2/\left(1-h^2\right)$ (Garrick et al. 2009) for an individual i in the training set. $r_{\mathrm{DRP}i}^2$ is the reliability of DRP for individual i and ${\sigma }_e^2$ is the residual variance using $c$ set to 0.1. The distribution of additive genetic values is assumed to be $\mathit{g} \sim N(0, \mathit{G}{\sigma }_g^2),$ where ${\sigma }_g^2$ is the additive genetic variance and $\mathit{G}$ is a realized genomic relationship matrix which was constructed according to method 1 in VanRaden (2008). Estimation of variance components and genomic breeding values was done with ASReml 3.0 (Gilmour et al. 2009).

Next, estimated SNP effects $\widehat{s}$were obtained following Strandén and Garrick (2009) as

$$\widehat{\mathit{s}}=\frac{1}{2{{\displaystyle \sum }}_{1=1}^m{p}_i(1-p_i)}{\mathit{M}}^T{\mathit{G}}^{-1}\widehat{\mathit{g}},$$

where $\mathit{M}$ is a matrix of dimension number of genotyped individuals × number of genotyped SNPs with entry $m_{ij}=x_{ij}-2p_j$. $x_{ij}$ is the genotype of individual$i$ at locus $j$ (coded as 0, 1, or 2, which are counts of the reference allele) and $p_j$ is the population frequency of the reference allele at SNP $j.$

Computational resources

Computation was performed using the University of Missouri Informatics Core Research Facility BioCluster (https://bioinfo.ircf.missouri.edu/). Computational nodes where simulations were performed had 64 cores and 512 GB of RAM. Analysis of maize and chicken data were performed on a mediocre laptop with 8 GB of RAM.

Data availability

Maize data are available from Lorenz et al. (2015). All scripts used for simulations and analysis are available at http://github.com/timbeissinger/ComplexSelection. Supplemental material containing chicken data, including allele-frequency change and estimated SNP effects, are available at Figshare: https://doi.org/10.6084/m9.figshare.5899267.

Results

Simulations

Simulations identified a wide assortment of scenarios for which $\widehat{G}$ is powerful for identifying traits that have been under selection, as well as several potential limitations of the method. Our generalized simulation scenario involved 20 generations of truncation selection in a population of 1000 individuals, with a genetic architecture of 1000 QTL controlling the trait and a heritability of 0.5. Phenotyping was performed on 1000 individuals from the final generation of selection. Below, we describe how $\widehat{G}$ is affected when specific parameters deviate from this scenario.

Number of QTL:

We simulated variable numbers of additive QTL-controlling traits, from 10, representing a simple trait controlled by large-effect QTL; to 10,000, representing a highly quantitative trait controlled nearly infinitesimally. QTL were evenly spaced along each chromosome and QTL themselves were not included in the marker set for analysis. A total of 100 simulations were performed for each level of trait complexity. First, we used these simulations to establish the appropriate number of independent markers, m_ind as described previously, for this test. We calculated how distant two markers must be to have an expected LD level of $R^2\le \mathrm{0.03.}$ We then counted the total number of blocks of this size genome wide. The 0.03 level was established by performing a grid search of potential values and tuning the false-positive rate (Figure S1). An LD cutoff that is too high leads to a high false-positive rate, while one that is too low weakens the power of the test. For populations similar to those discussed here, we observe that requiring $R^2\le 0.03$ is appropriate.

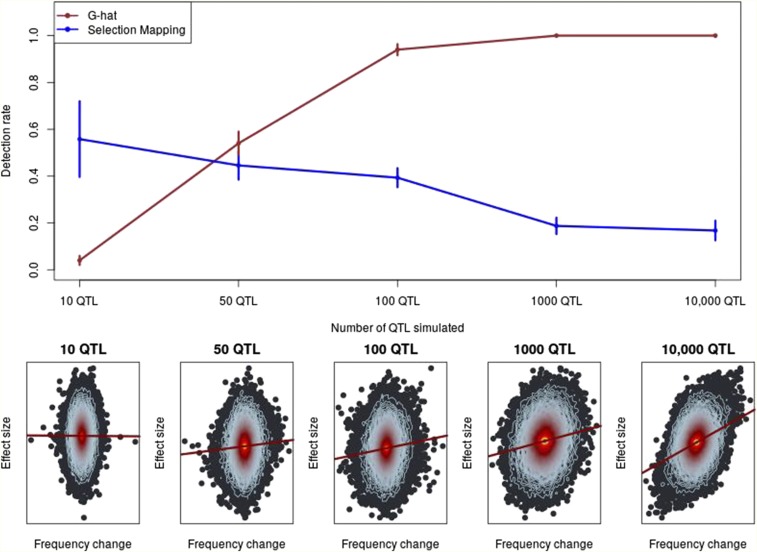
When we tested for selection in our simulated data, we observed a direct relationship between the number of QTL controlling a trait and the power of $\widehat{G}$ to identify selection on that trait. $\widehat{G}$ powerfully identifies selection on highly polygenic traits, but is not powerful for identifying selection on traits controlled by a small number of QTL. Analyses of the same simulations using F_ST-based selection mapping, which involves mapping loci that have been previously subjected to selection (Wisser et al. 2008; Lorenz 2015), showed that traits controlled by a small number of QTL can be mapped using traditional selection-mapping approaches. However, as traits become increasingly polygenic, our simulations demonstrate that the ability to map individual, selected genes diminishes (Figure 1). These findings demonstrate how $\widehat{G}$ and traditional selection mapping can be complementary, depending on the underlying genetic architecture of a trait. Table 1 depicts detection and false-positive rates for $\widehat{G}$ and F_ST-based mapping under different genetic architectures.

Figure 1.

The power of $\widehat{G}$ to identify selection. Top: The detection rate, or proportion of true positives, of $\widehat{G}$ compared to F_ST-based selection mapping. Vertical lines indicate 1 SD. SD for selection mapping were estimated empirically. SD for $\widehat{G}$ were estimated based on the binomial distribution. Bottom: Exemplary heat plots depicting individual SNP allelic effect estimates linearly regressed on allele-frequency change over time. Each point represents a SNP and the contour lines indicate the density of SNPs, with red contours indicating a greater density of points than blue. From the regression line, observe that a stronger relationship between frequency change and effect size corresponds to increasing polygenicity. G-hat, $\widehat{G}.$

Table 1. True-positive and false-positive rates for $\widehat{\mathit{G}}$ and selection mapping.

Genetic architecture	10 QTL	50 QTL	100 QTL	1000 QTL	10,000 QTL
$\widehat{G}$
True-positive rate	0.04	0.54	0.94	1.0	1.0
False-positive rate	0.03	0.03	0.02	0.03	0.04
FST-based selection mapping
Mean no. true positives (rate)	5.6 (56%)	22 (44%)	39 (39%)	187 (18.7%)	1676 (16.8%)
Mean no. false positives	52	280	715	1745	—

One $\widehat{G}$ test is conducted per simulation, so the true- and false-positive rates shown are simply the proportion of positives in selection simulations and no-selection simulations, respectively. For selection mapping, one test is conducted per marker in each simulation, so the mean number of markers that were declared true and false positives is shown. A marker was declared a false positive in selection mapping if it exceeded a 5% simulation-based, experiment-wide significance threshold but was not within a 0.1-cM region around a simulated QTL. Note that there are no selection mapping false positives in the 10,000 QTL simulation because every marker was within 0.1 cM of a simulated QTL.

Number of generations:

Simulations showed an interesting relationship between the number of generations of selection and the power of $\widehat{G}.$ We observed a definite sweet spot from ∼10 to just under 50 generations for which $\widehat{G}$ was most powerful. Conversely, if selection took place for 100 generations or only for a single generation, $\widehat{G}$ became dramatically less powerful (Table 2). We suspect that two forces interact to reduce the power of $\widehat{G}$ in the case of a large number of generations of selection. First, over the course of many generations, our simulated populations became highly inbred, which notably increased LD and therefore reduced m_ind. Since $\widehat{G}$ is summed over markers and then scaled by m_ind, this substantially reduces power. Second, our simulations involved a predetermined number of QTL with fixed effects at the onset of selection but, as selection persisted, these QTL could be lost to fixation; or as allele frequencies change, their effects could decrease (Sargolzaei and Schenkel 2009). Since we estimated SNP effects based on phenotypes in the final generation (but see the following section on Phenotyping generation), power could be reduced by the fixation of a lost QTL that previously had an effect. Although these issues weakened $\widehat{G}$ in our simulations, it is unclear whether or not they would have the same impact in a real application, and it is unlikely that the powerful sweet spot would be the same. Regarding the weak power of $\widehat{G}$ to identify selection after only one generation: this is not unexpected since, for quantitative traits, a single generation is rarely long enough to appreciably shift allele frequencies.

Table 2. Detection rate of $\widehat{\mathit{G}}$ as simulation parameters vary.

Parameter varied	Tested values
No. individuals phenotyped	1000	500	250	100	50
Detection rate	1	0.99	0.83	0.4	0.21
Proportion of individuals selected	0.01	0.05	0.2	0.5	—
Detection rate	0.95	0.99	1.0	1.0	—
No. of generations of selection	100	50	20	10	1
Detection rate	0	0.81	1.0	1.0	0.18
Phenotyping generation	20	10	0	—	—
Detection rate	1	1	0.86	—	—
No. of generations postselection	5	20	50	100	—
Detection rate	1	1	0.26	0	—

Aside from whichever parameter was being explored, simulations assumed 20 generations of selection with a selected proportion of 0.2, a genetic architecture of 1000 QTL, a selection population consisting of 500 males and 500 females, and the additional parameters of our “generalized” selection scenario are given in Table S1.

We also investigated how the power of $\widehat{G}$ is affected by temporary selection. Specifically, we simulated 20 generations of selection followed by different numbers of generations without selection. We observe that $\widehat{G}$ remains powerful for at least 20 generations postselection; but after 100 generations without selection, the ability of $\widehat{G}$ to identify selection is lost. Like above, this loss of power can likely be attributed to inbreeding and the fixation of QTL.

Phenotyping generation:

In practical applications, we predict that phenotypes will typically be more readily available from later generations of selection than early generations. However, since this generalization will not always apply, we explored how the power of $\widehat{G}$ is affected by the generation in which individuals are phenotyped. We observed the highest power when phenotypes were scored in recent time points or midway through selection, but power was still high (0.86) when phenotypes were scored in generation 0, at the onset of selection (Table 2). As discussed above in Number of generations, changing QTL effects as allele frequencies change during evolution are likely to explain this drop in power. We explored whether or not the generation of phenotyping can lead to bias by evaluating the false-positive rate for simulations where phenotypes were scored at different time points, out of 20 generations of selection. False-positive rates were 0.02, 0.08, and 0.0 when phenotyping occurred in generation 20, 10, and 0, respectively.

Proportion of individuals selected:

The proportion of individuals that reproduce each generation directly affects the efficacy of a selection regime. Therefore, we explored the ability of $\widehat{G}$ to identify selection across several realistic values observed in experimental and agricultural selection programs (Table 2). To achieve this, in our simulations we varied the total number of progeny in each generation rather than altering the total number of individuals reproducing, because a reduced number of individuals would rapidly lead to high levels of inbreeding. When the proportion of individuals selected was intermediate to low, from 50 to 5% of individuals reproducing (selected proportion 0.5–0.05), we observed that $\widehat{G}$ was highly effective for identifying selection, with power at or near 1.0. Only in the case of very strong selection, when the proportion selected was 0.01 (1% of individuals reproduced each generation), did we observe a minor reduction in the power of $\widehat{G}.$ Despite our attempts to minimize inbreeding in these simulations, in the case of a selection proportion of 0.01, inbreeding was likely still generated via a large number of progeny originating from the same combination of superior parents. We suspect this is what resulted in the reduction in power.

Sample size:

Since the accuracy of estimated marker effects depends on sample size, we explored the impact that the number of phenotyped individuals has on the power of $\widehat{G}.$ Unsurprisingly, as sample size decreases so does the power of $\widehat{G}$ to identify selection (Table 2). However, it is notable that even with sample sizes as small as 250 individuals the power remains >0.8. Even with only 50 phenotyped individuals, selection can be identified in one out of five scenarios. Together, these observations emphasize that the power of $\widehat{G}$ comes from its accumulation of information across markers rather than from a small number of highly informative markers.

Selection on maize silage traits

We reanalyzed data from a previous study that tested for selection in a decades-long breeding program for maize silage quality (Lorenz et al. 2015). Very briefly, a selection index comprising experimentally measured traits related to silage quality was used to perform reciprocal recurrent selection for breeding improved maize. Traits composing the index included acid detergent fiber, protein content, starch content, in vitro digestibility, and yield (http://www.cornbreeding.wisc.edu). In total, 648 individuals from various stages of selection were genotyped. Between 240 and 300 of these individuals were also phenotyped, depending on the trait. Selection mapping was previously performed using simulations of drift to scan for selection, but the analysis did not identify any loci that showed significant evidence of selection. This is despite quantifiable improvement of the population and demonstrated heritability of the index-composing traits (Lorenz et al. 2015). We reanalyzed the same data to evaluate evidence for polygenic selection on the measured traits, which included NDF, in vitro digestibility, crude protein content, starch content, yield, and DM. After filtering for quality, but not MAF, these data consisted of 10,023 polymorphic markers. Genomic prediction for these traits was generally effective (Figure S2). Due to the relatively small population size and recurrent selection breeding scheme, we expect slow LD decay and therefore for most of the genome to be represented with this marker set. Further analysis of LD to determine the value of m_ind to use in our test for selection confirms this (Figure S3).

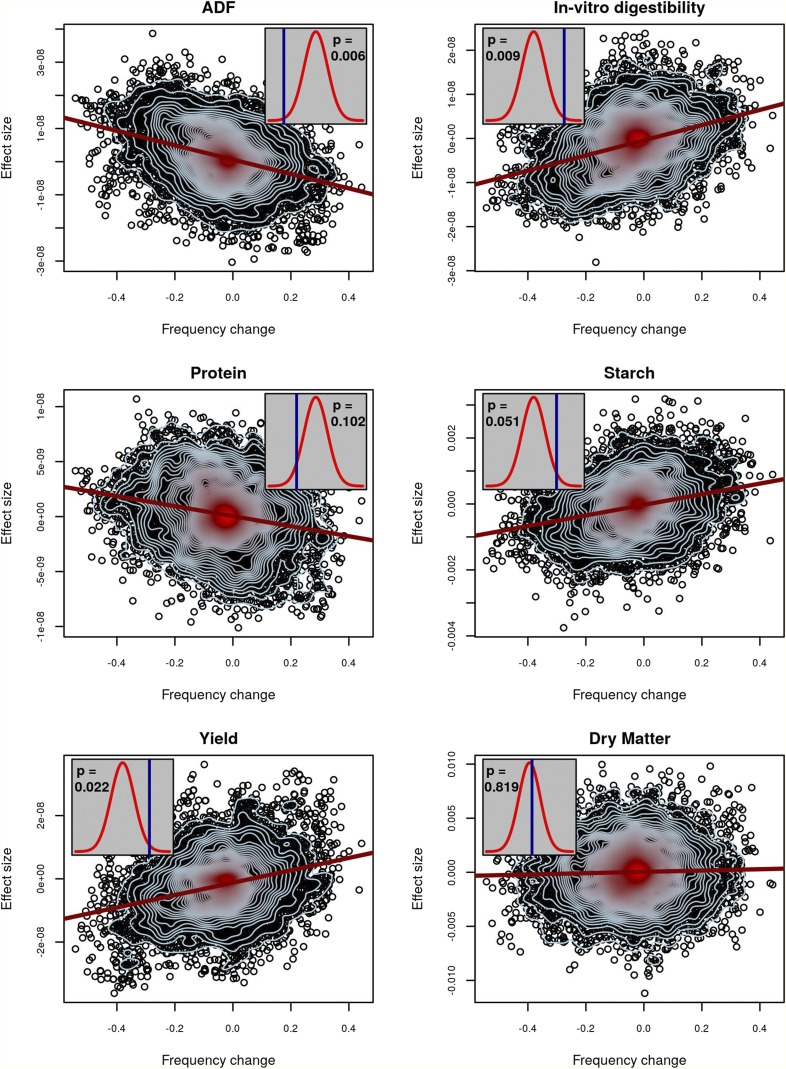
Figure 2 depicts the maize patterns of selection that were observed in our analysis. In these plots, the histogram shows the null distribution of $\widehat{G}$ that was observed from a permutation test, while the vertical line depicts the observed value of $\widehat{G}$ when applied to the experimental data. We observed that, with the exception of protein, for the traits where we had an a priori expectation of selection, we not only identified that selection did occur, but we correctly estimated the direction of selection (positive or negative) from the data. One of the traits measured was silage DM, which was not a part of the selection index. We did not identify evidence of selection on DM, as was expected. To ensure that the existence of a single individual with a high breeding value does not lead to spurious false positives, we reanalyzed the maize data after removing all SNPs with MAF <0.05. This did not lead to any appreciable change in the results (Figure S6).

Figure 2.

Evidence of selection for maize silage traits. For six traits, the relationship between estimated allelic effects at individual SNPs and the change in allele frequency over generations is plotted. The red line is a regression of effect size on allele-frequency change. Contour lines indicate the density of points, with blue contours indicating fewer points than red. Inset plots depict observed values of $\widehat{G}$ (blue lines) and their statistical significance based on a comparison to permuted null distributions (red densities) for no-selection scenarios. An exact two-sided P-value is given within each inset. Significant values of $\widehat{G}$ above the permuted mean indicate selection operated in the positive direction, while significant values below the permutation mean indicated selection operated in the negative direction.

Selection on chicken traits

We tested for evidence of selection in two panels of commercial lines of laying hens: one WL and one BL. Both closed lines have been selected over decades with a similar composite breeding goal which consisted of laying rate, body weight and feed efficiency, egg weight, and egg quality, among other objectives. The respective weights applied to the different traits varied between lines and over time. Traits analyzed included laying rate, egg weight, and breaking strength of eggs. Genotypes were available only for the postselection population, so initial allele frequencies were inferred based on pedigree data (Gengler et al. 2007). m_ind was determined based on separate evaluations of LD in the WL (Figure S4) and BL (Figure S5) populations.

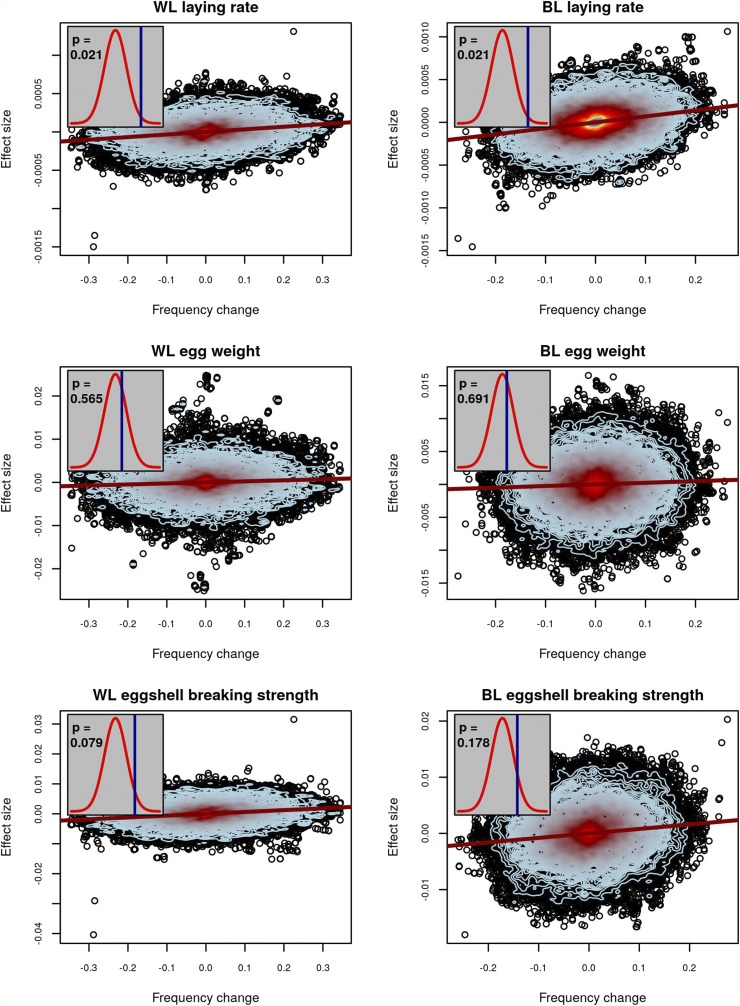
Among the traits evaluated, we observed significant evidence of selection for increased laying rate in both WLs (P = 0.021) and BLs (P = 0.021). Tests were also suggestive of selection for increased eggshell-breaking strength in WLs (P < 0.1; one-sided P < 0.05), while there was no evidence of directed selection for egg weight (Figure 3). To verify that these results were not driven by a small number of SNPs with high estimated effect sizes, we repeated the analysis with the 10 largest effect-size SNPs removed and saw virtually identical results (Figure S7). The result for egg weight can be seen as a “negative control” since for this trait an optimum value is already achieved and maintained by stabilizing selection. The fact that we were not able to detect significant evidence of selection in a trait such as eggshell-breaking strength in both lines (although a tendency can be observed) may be due to the fact that improving those traits is part of a complex multi-objective breeding program, or simply that our test was underpowered for these traits. The unavailability of experimentally estimated initial frequencies and our alternative use of pedigree-inferred initial allele frequencies likely weakened the power of the test as compared to the more complete data available for maize and in the simulations.

Figure 3.

Evidence of selection for chicken traits. For three traits in WL (left column) and BL (right column) hens, the relationship between estimated allelic effects at individual SNPs and the change in allele frequency over generations is plotted. The red line is a regression of effect size on allele-frequency change. Contour lines indicate the density of points, with blue contours indicating fewer points than red. Inset plots depict observed values of $\widehat{G}$ (blue lines) and their statistical significance based on a comparison to permuted null distributions (red densities) for no-selection scenarios. An exact two-sided P-value is given within each inset. Significant values of $\widehat{G}$ above the permuted mean indicate selection operated in the positive direction, while significant values below the permutation mean indicated selection operated in the negative direction.

Discussion

We have defined a test statistic, $\widehat{G},$ that combines phenotypic and genotypic information to test for selection on traits controlled by many loci of small effect. The approach uses estimated effect sizes for individual loci and allele-frequency changes across two time points reflecting possible selection on those loci. Therefore, $\widehat{G}$ is most applicable in experimental or breeding populations, where both pieces of information are readily available via genotyping individuals from multiple generations. However, phenotypic information for estimating allelic effects is only required from a single time point, so this approach can be applied post hoc using DNA samples from previous generations even if phenotyping is no longer possible. As the practice of sequencing ancient DNA from archeological sites, museum samples, or other sources becomes progressively commonplace (Orlando et al. 2015), it will be interesting to explore whether or not this approach may prove applicable for ecological questions, evolutionary studies, and for human research. However, simulations showed a decrease in power as the number of postselection generations increased, so there is a limit to how far back our test statistic can be fruitfully applied.

Powerful for highly quantitative traits

Methods for mapping genes associated with important traits or for identifying loci that are under selection are most powerful for large-effect genes. A simple explanation for the disappointing number of associations that have been uncovered to date through GWAS is that complex traits are often controlled by many genes of small effect (Yang et al. 2011). If this is the case, enormous sample sizes are required to map loci regardless of the methodological enhancements that can be applied. Human geneticists have had success studying complex traits by using extremely large sample sizes (Rietveld et al. 2013; Wood et al. 2014). But, sample sizes of this magnitude are not yet achievable within resource limitations for most species and, arguably, will never be. Conversely, population-genetic studies aiming to scan for selection have been most successful at identifying hard sweeps, where a new mutation of large effect rapidly rises to fixation as a result of selection (Pritchard et al. 2010). Only few methodologies with limited power exist for mapping soft sweeps, where the beneficial allele is already at an intermediate frequency at the start of selection (Garud et al. 2015; Ma et al. 2015). A likely explanation for the presence of soft sweeps is that they often result from loci of small effect increasing in frequency slowly in a population and therefore existing on multiple distinct haplotypes or mutating multiple times before fixation. In an agricultural context, many soft sweeps may be due to newly defined breeding goals which put selection pressure on genes that were previously segregating in the populations, but were selectively neutral. The $\widehat{G}$ statistic does not attempt to map specific genes—instead it pools information from all SNPs to test for selection on specific traits. This approach completely avoids the question of which loci are associated with a trait. Instead of testing each SNP, we perform one test based on information from all SNPs. Therefore, a strong statistical signal arises when a large proportion of SNPs behave similarly, but not when a few SNPs portray strong signals on their own. That said, researchers are often interested in identifying selected traits whether they correspond to selection on many genes at once or simply a few large-effect genes. In this case, the implementation of our $\widehat{G}$ test in conjunction with a traditional selection-mapping approach aimed at identifying selected loci will likely be powerful for identifying selection, regardless of the underlying genetic architecture (Figure 1).

It was recently argued that most complex disease traits in humans are controlled by small-effect genes dispersed throughout the genome (Boyle et al. 2017). Likewise, many important traits in agricultural animal and plant species tend to be quantitative in nature and are presumably controlled by small-effect genes (Goddard and Hayes 2009; Wallace et al. 2014). For these agricultural organisms, geneticists and breeders have long recognized the benefits that can be achieved by predicting breeding values and/or phenotypes based on models that use all SNPs simultaneously (Meuwissen et al. 2001; Goddard and Hayes 2009; Heffner et al. 2009). In fact, the development of these models has led to dramatic redesigns of modern breeding protocols (Schaeffer 2006; Cabrera-Bosquet et al. 2012). The $\widehat{G}$ statistic represents one avenue to leverage information from all measured SNPs to gain an understanding of the evolutionary history of a population. This approach is analogous to genomic selection/prediction, as used by animal and plant breeders, with an important distinction: instead of predicting breeding values to determine which individuals should be selected for the future, it uses genotypic frequencies over time coupled with phenotypic information to unravel the history of selection in the past.

Genotypes from the base population provide high power

Compared to other methods that test for selection on quantitative traits (Berg and Coop 2014; Zeng et al. 2017), $\widehat{G}$ leverages genotypic information from multiple time points and it incorporates information from all SNPs instead of restricting to a previously identified set of SNPs from one or multiple independent GWAS. With the exception of a few traits in heavily studied species, such as human height (Wood et al. 2014); few species, if any, provide the enormous sample sizes required to implicate a large number of loci for any quantitative traits. This includes situations where scientists are reasonably certain that a genetic architecture consisting of small-effect loci persists. Importantly, $\widehat{G}$ is powerful because of the independence of the estimation of allele-frequency changes across generations and effect sizes, respectively. Even when allelic effects and/or allele-frequency changes are small, they cumulatively generate a powerful test since they can be compared across all genotyped loci. However, our analysis of the chicken data suggested that the power of the test can be reduced through noisy estimation of allele-frequency change. Our reliance on pedigree data to derive initial allele frequencies was not as precise as the direct measurement of initial allele frequencies that was conducted for maize. Although we were still able to find evidence of selection on traits including laying rate, which was almost certainly under the strongest selection; there were selected traits we did not detect, potentially because of this noise.

Future directions and conclusions

The use of $\widehat{G}$ to test for selected traits avoids the requirement of preliminarily identifying candidate genes or regions. Therefore, the approach is particularly applicable in experimental, agricultural, and natural populations for which available resources dictate limited sample sizes for conducting massive mapping studies for such preliminary identification. In contrast to purely population-genetic analyses, which rely solely on genotypic information, the method requires that phenotypic data be collected from at least one time point of genotyped individuals. Additionally, two time points of genotypic information are needed, either directly or through pedigree-based imputation.

While the $\widehat{G}$ statistic is most directly applicable for the discovery of traits that have been previously under selection during recent evolution, it may have additional applications. Recent studies have demonstrated that distinct physical regions of the genome, such as individual chromosomes, often contribute a disproportionate amount to trait variance (Bernardo and Thompson 2016). Rather than applying the $\widehat{G}$ statistic genome wide, future research should be done to determine whether it can be applied across any collections of loci—such as individual chromosomes, pathways, gene families, functional classes, or other categories—to test if these show evidence of selection on a quantitative trait. This would represent a process allowing researchers to map significant features as opposed to individual genes. Likewise, thus far we have estimated the direction of selection (positive or negative) from $\widehat{G},$ but not the magnitude. Further research should be performed to determine whether or not this or a similar statistic can be used to recapitulate the selection gradient.

As it stands, using $\widehat{G}$ simply to identify traits that have been under selection in the past may prove enormously useful. Whether agricultural, experimental, or natural; it is often difficult to determine all of the traits that are advantageous in a population or that respond to natural or anthropogenic selection, including undesired selection responses. The application of the $\widehat{G}$ statistic genome wide allows this determination, which may help scientists select the right traits for maximum agricultural production, determine inadvertently selected laboratory traits affecting experimental outcomes, and establish ecologically important traits for survival in the wild.