Abstract
Evolutionary rescue describes a situation where adaptive evolution prevents the extinction of a population facing a stressing environment. Models of evolutionary rescue could in principle be used to predict the level of stress beyond which extinction becomes likely for species of conservation concern, or, conversely, the treatment levels most likely to limit the emergence of resistant pests or pathogens. Stress levels are known to affect both the rate of population decline (demographic effect) and the speed of adaptation (evolutionary effect), but the latter aspect has received less attention. Here, we address this issue using Fisher’s geometric model of adaptation. In this model, the fitness effects of mutations depend both on the genotype and the environment in which they arise. In particular, the model introduces a dependence between the level of stress, the proportion of rescue mutants, and their costs before the onset of stress. We obtain analytic results under a strong-selection–weak-mutation regime, which we compare to simulations. We show that the effect of the environment on evolutionary rescue can be summarized into a single composite parameter quantifying the effective stress level, which is amenable to empirical measurement. We describe a narrow characteristic stress window over which the rescue probability drops from very likely to very unlikely as the level of stress increases. This drop is sharper than in previous models, as a result of the decreasing proportion of stress-resistant mutations as stress increases. We discuss how to test these predictions with rescue experiments across gradients of stress.
Keywords: antibiotic resistance, evolutionary rescue, Fisher’s geometric model, fitness landscape, mutation
UNDERSTANDING the persistence or decline to extinction of populations facing environmental stress is a crucial challenge both for the conservation of biodiversity and the eradication of pests or pathogens (Gonzalez et al. 2013; Alexander et al. 2014; Carlson et al. 2014; Bell 2017). In evolutionary biology, environmental stress describes any conditions in the environment that induces a reduction in individual fitness (Koehn and Bayne 1989; Bijlsma and Loeschcke 2005). Here, we will focus on the case where environmental stress causes a reduction of population mean fitness that is harsh enough to trigger a decline in abundance (Hoffmann and Parsons 1997). In such a stressful environment, if heritable variation in fitness is available or arises by mutation, adaptive evolution may allow the population to escape extinction. This phenomenon has been called evolutionary rescue (ER) (Gomulkiewicz and Holt 1995). ER is of particular importance for understanding the emergence of genetic resistance to drugs or treatments in medicine and agronomy (Davies and Davies 2010).
Empirical evidence supports the idea that stress levels critically determine ER probabilities (Samani and Bell 2010; Moser and Bell 2011; Lindsey et al. 2013). For example, the probability that bacteria evolve antibiotic resistance (that is, the probability of avoiding antibiotic-induced extinction through ER) typically declines sharply, in a strongly nonlinear way, with increasing drug concentration (Drlica 2003). Evolutionary rescue thus shifts from being highly likely to highly unlikely over a narrow window of stress levels. This critical range of stress depends on the strain, especially on its evolutionary history with respect to exposure to the stress (Gonzalez and Bell 2013). Stress level, as controlled by drug concentration, has also been shown to affect the genetic basis of resistance (e.g., Harmand et al. 2017), with a wider diversity of genes and alleles conferring resistance at low than at high doses. However, the underlying causes for the relationship between stress level and ER are still poorly understood. Our aim here is to derive new analytical predictions for this relationship. In particular, we want to predict the critical window of stress levels above which ER is very unlikely, allowing direct comparison with experimental data.
In the theoretical literature (reviewed in Alexander et al. 2014), most ER models predict that ER probability decreases with increasing stress level, measured by the decay rate of the stressed population. Indeed, a faster decay of the population leaves less time for adaptation to occur before extinction (e.g., Gomulkiewicz and Holt 1995). But beyond this direct demographic effect, stress level may also have indirect effects on ER. Indeed, a stressful environment may not only affect the demographic properties of the population, but also its rate of adaptation, by modifying the determinants of genetic variance in fitness (Hoffmann and Parsons 1997; De Visser and Rozen 2005; Agrawal and Whitlock 2010). First, the rate of mutations and the distribution of their effects on fitness change across environments (Martin and Lenormand 2006b; Wang et al. 2009, 2014; Agrawal and Whitlock 2010). In particular, the fraction of beneficial mutations was found to increase in stressful environments (Remold and Lenski 2001, 2004). Standing genetic variation for quantitative traits (notably fitness components), also frequently depends on the environment (Hoffmann and Merilä 1999; Sgrò and Hoffmann 2004; Charmantier and Garant 2005). Finally, the initial frequency of preexisting variants able to rescue the population from extinction in a stressful environment may depend on their selective cost in the past environment. In light of this empirical evidence, it seems clear that progress toward understanding and predicting ER across stress levels requires addressing, in a quantitative way, the joint effect of stress on the demography and genetic variation in fitness of a population exposed to stressful conditions. This is our goal in the present article.
To do so, we develop a model that is a hybrid between two modeling traditions in ER theory, summarized by Alexander et al. (2014): discrete genetic models, and quantitative genetic models. Discrete genetic models assume a narrow genetic basis for adaptation (and ER), whereby a single beneficial mutation can rescue an otherwise monomorphic population (Orr and Unckless 2008, 2014; Martin et al. 2013; Uecker et al. 2014; Uecker and Hermisson 2016). This approach was initially proposed for ER by Gomulkiewicz and Holt (1995), and later extended to account for (i) evolutionary and demographic stochasticity (e.g., Orr and Unckless 2008), and (ii) variation in the selection coefficients of mutations that may cause rescue, with an arbitrary distribution of fitness effects (Martin et al. 2013). However, such models do not predict how the distribution of fitness effects of mutations vary along gradients of stress level. For this reason, they make it difficult to jointly address the two fundamental components of stress mentioned above. On the contrary, quantitative genetics models of ER inherently address the influence of stress on the rate of adaptation by assuming that adaptation (and ER) is caused by evolution of a quantitative trait whose optimum changes with the environment (Lynch et al. 1991; Burger and Lynch 1995; Gomulkiewicz and Holt 1995). In these models, both the rate of population decline and the rate of adaptation under stress depend on the distance between the phenotypic optima in the past and present environments. However, analytical predictions are derived assuming a broad, polygenic basis for adaptation with a stable genetic variance of the quantitative trait. The population genetic processes underlying adaptation are not explicitly modeled, and the stochasticity involved in fixation and establishment of mutations neglected. These complications are only explored by simulations (e.g., Gomulkiewicz et al. 2010).
In order to take the best of both approaches, we rely on Fisher’s (1930) geometrical model (hereafter “FGM”). Fitness variation in the FGM is assumed to emerge from variation in multiple putative phenotypic traits undergoing stabilizing selection that depends on the environment. This model is analytically tractable, while retaining various aspects of realism (reviewed in Tenaillon 2014). In particular, it accurately predicts how fitness effects of mutations change across environments (Martin and Lenormand 2006b; Hietpas et al. 2013; Harmand et al. 2017) or genetic backgrounds (Martin et al. 2007; MacLean et al. 2010; Trindade et al. 2012). The FGM naturally relates environmental stress to (i) the rate of population decline, (ii) the rate and effect of rescue mutants, and (iii) their potential costs in the past environment. Here, we combine this FGM with population dynamic approaches that account for demographic and evolutionary stochasticity (Martin et al. 2013), in a regime where selection is strong relative to the rate of mutation. We consider rescue in asexual populations, stemming either from de novo mutations or standing genetic variance. Interestingly, we show that all effects of stress on demography and on the distribution of the fitness effects of mutations can be summarized into a single composite measure of effective stress level. Evolutionary rescue shifts abruptly from very likely to very unlikely over a narrow window of effective stress level, which can be predicted from empirically measurable quantities.
Methods
We here detail the ecological (environmental), genetic, and demographic assumptions of the model, and the approximations used for its mathematical analysis.
Abrupt environmental shift
We define two environments: (1) a nonstressful one, denoted as “previous environment,” in which the population has a positive mean growth rate, and a large enough population size that demographic stochasticity can be ignored; and (2) a stressful one, denoted “new environment,” in which the population initially has a negative mean growth rate, and the population size is subject to demographic stochasticity. Conditions shift abruptly from the previous to the new environment at at which time the population size is
Eco-evolutionary dynamics
Extinction or rescue ultimately depends on details of the stochastic population dynamics of each genotype. These are assumed to be mutually independent (no density or frequency-dependence, see Chevin 2011), and sufficiently “smooth” (moderate growth or decay) that they can be approximated by a Feller diffusion (Feller 1951), following Martin et al. (2013). This approximation reduces all the complexity of the life cycle into two key parameters for each genotype its expected growth rate (our fitness here), and its variance in reproductive output Our simulations below are performed for discrete generations with Poisson offspring distributions. In this case, for any genotype, as long as their growth rate is not too large ( per-generation, see Appendix section I, subsections 1 and 2 and Martin et al. 2013). Note that the approximation extends to various other forms of reproduction (see Martin et al. 2013).
To cause a rescue, a resistant mutant () must establish, by avoiding extinction when rare. The probability that this happens, for a lineage with growth rate starting from a single copy is (still assuming with in the example used in simulations). The number of individuals from which such mutations can arise declines in time, and we ignore stochasticity in these decay dynamics. This is accurate as long as the population has large initial size, of order (Martin et al. 2013).
Finally, we assume that mutation rates per capita per unit time are constant over time. This is exact in models with discrete generations. In continuous-time models, where mutations occur during birth events, mutation rates vary between genotypes with different birth rates, and over time as these genotypes change in frequency. However, the constant mutation rate model can still be approximately valid (see Martin et al. 2013).
ER from standing variance vs. de novo mutation
At the onset of stress (), the population either consists of a single ancestral clone, or is polymorphic at mutation-selection balance in the previous environment. In the first case, we must derive the distribution of fitness effects, in the new environment, of mutants arising from the ancestral clone. In the second case, we must also describe the potential rescue variants already present in the previous environment.
Mutations under FGM
We assume that the expected growth rate of a given genotypic class (its Malthusian fitness, or log-multiplicative fitness in discrete-time models), is a quadratic function of its phenotype for quantitative (continuous) traits. Denoting as the vector of breeding values (heritable components) for all traits, and as the single optimum phenotype with maximal growth the expected growth rate is
| (1) |
while the stochastic variance in reproductive success is assumed constant across genotypes.
The key assumption of our model is that the optimum depends on the environment. Without loss of generality, we set the phenotypic origin at the optimum in the new environment, in which In the previous environment, the optimum coincides with the mean phenotype of the ancestral population (“A”): which implies that the ancestral population was well-adapted in its original environment. The fitness of the mean ancestral phenotype in the new environment is thus where is its rate of decay, and the phenotypic magnitude of the stress-induced shift of the optimum phenotype (from to ) is
Mutations occur as a Poisson process with rate per unit time per capita, constant over time and across genotypes, but potentially variable across environments. Each mutation adds a random perturbation to the phenotype, drawn from an unbiased and isotropic multivariate Gaussian distribution where is the identity matrix in dimensions and is a scale parameter. Note that, since traits are not our main interest here, we choose to measure mutation effects on them in units that directly relate to their fitness effects. Therefore, can be understood as the variance of mutational effects on traits, standardized by the strength of selection (see Appendix section II, subsection 1 for more details). Note that mutation effects are additive on phenotypes (no epistasis), but not on fitness, because is nonlinear (Martin et al. 2007).
Figure 1 illustrates the rescue process in the FGM. At the onset of stress (), the optimum shifts abruptly to a new position, such that the mean growth rate becomes negative with (Figure 1C). Meanwhile, the population size starts to drop from an initial value (Figure 1C), facing extinction in the absence of evolution. However, one or several mutants or pre-existing variants may be close enough to the new optimum to have a positive growth rate (“resistant genotypes,” Figure 1, A and B). These may then establish, and ultimately rescue the population (“rescue genotypes” Figure 1, A and B).
Figure 1.
Evolutionary rescue in Fisher’s geometric model (FGM). In all panels, black refers to deleterious and neutral mutations (), blue to beneficial but not resistant mutations (), and orange to resistant mutations (), around the dominant genotype of the ancestral population with phenotype (A) Fitness landscape (FGM) with growth rate (z-axis) determined by two phenotypic traits and Dots represent the distribution of random mutant phenotypes around the dominant genotype of the ancestral population. The growth rate of this dominant genotype, in the stressful environment, is − and is the maximal fitness at the phenotypic optimum. (B) Distribution of growth rates among random mutants arising from the dominant genotype (distribution of mutation effects on fitness) for two decay rates (left) and (right). (C) Dynamics of the population size and mean fitness of a population starting from a clone at at size The black line represents the case without fixation of a beneficial mutation, the blue line the case with extinction in spite of the fixation of a beneficial, but nonresistant, mutation, and the orange line the case of a rescue. Parameters for the simulations are and
Within the context of the FGM, increasing stress level may have different effects, also discussed in Harmand et al. (2017). First, stronger stress may cause a larger shift in the position of the optimum phenotype, resulting in a larger initial drop in fitness (higher ), as assumed in most models of adaptation to a changing environment (Kopp and Matuszewski 2014). In addition, the maximal possible fitness may also be lower in the new than in the previous environment (reduced environmental quality). Moreover, the mutational parameters ( and ) may change with stress, causing shifts in evolvability. Note that a change in may reflect a change in the phenotypic effects of mutations, of the strength of stabilizing selection, or both. For instance, higher stress may release cryptic genetic variance on underlying phenotypic traits (Scharloo 1991; Hermisson and Wagner 2004), or cause increased mutation rates via SOS responses in bacteria (Foster 2007). Finally, although less easy to conceptualize, some environments may change the effective dimensionality of the landscape. However, in the present paper, we only consider such changes in dimensionality in the context of rescue from de novo mutations (where it can readily be handled by studying the effect of the parameter ).
As we will see, all our results can be expressed in terms of five parameters (). Table 1 summarizes all notations in the article.
Table 1. Notations.
| Notation | Description | Formula |
|---|---|---|
| : population size at time after the onset of the stress. | ||
| : initial population size at the onset of the stress. | ||
| Mutation rate per individual per unit time. | ||
| Number of traits under stabilizing selection, or phenotypic dimensionality. | ||
| Variance of mutational effects: variance of the phenotypic effects of mutations, per trait, in a trait space scaled by the strength of stabilizing selection | ||
| Critical mutation rate below which the SSWM regime is valid. | ||
| -dimensional vector of (breeding values for) phenotype | ||
| optimal phenotype in a given environment | new environment | |
| average phenotype of the ancestral population (before the onset of stress) | previous environment | |
| Growth rate () and reproductive variance () of a given genotype, in the new environment. | Equation (1) | |
| Maximum possible growth rate in the new environment. | ||
| Rate of decay of the ancestral phenotype in the new environment. | ||
| Cost of a mutation: selective disadvantage of the mutant, relative to the optimal phenotype, in the previous environment. | ||
| Harmonic mean of the cost among de novo mutations with scaled growth rate in the new environment | Equation (3) | |
| Growth rate of a genotype, in the new environment, scaled by . | ||
| Probability density function of among random single step mutations | Equation (2) | |
| Rate of decay scaled by | ||
| Alternative measure of | (Equation (6)) | |
| Effective stress level | Equation (6) | |
| Characteristic stress level () or decay rate () beyond which ER probability drops below | Equation (8) | |
| Function driving the dependence of rescue probabilities on stress levels. | Equations (7a) and (7b) | |
| rate of rescue from de novo mutations scaled by | Equations (5), (7a) and (7b) | |
| corresponding approximation when | ||
| rate of rescue from standing variance scaled by | Equations (5) and (10) | |
| corresponding approximation when | ||
| Probability of rescue. | ||
| Proportion of rescue events caused by standing variants | Equation (10) |
Strong selection and weak mutation regime
The FGM described in the previous section, produces epistasis for fitness between different mutations, which makes the problem highly intractable in general. To make analytical progress, we assume a regime of strong selection and weak mutation (SSWM; Gillespie 1983), which allows neglecting multiple mutants and epistasis. This regime arises when mutation rates are small relative to their typical fitness effect (as detailed below). In our context, this assumption implies that most rescue variants (pre-existing or de novo) are only one mutational step away from the ancestral genotype, allowing for two key simplifications. First, with a purely clonal ancestral populations, we can ignore ER by genotypes that have accumulated multiple de novo mutations. Second, in populations initially at mutation-selection balance, we can consider that all mutations arise from a single dominant genotype, optimal in the previous environment. Indeed, in the SSWM regime at mutation-selection balance, most segregating phenotypes remain within a narrow neighborhood of the optimum (relative to the magnitude of mutation effects on traits), so the mutation-selection balance is well-approximated by assuming that all mutations originate from the optimum phenotype. This is essentially the House-of-Cards approximation (Turelli 1984) extended to the FGM of arbitrary dimensionality (Martin and Roques 2016).
Overall, the SSWM assumption implies that the evolutionary aspects of ER are entirely determined by a single joint distribution of fitness, in the previous and new environment. This distribution corresponds to that of mutants arising from the optimal genotype of the previous environment. We thus apply the results of Martin et al. (2013), to this particular distribution.
Note that the SSWM approximations used in this article should apply even when multiple single-step mutants cosegregate (generating “soft selective sweeps,” as detailed in Wilson et al. 2017). Indeed, the probability of ER as computed for example in Orr and Unckless (2008) or Martin et al. (2013) and used here, is one minus the probability that no single mutant arises that ultimately causes ER. This means that we ignore ER requiring multiple mutational steps, but allow several single-step rescue mutations to cosegregate. Consistently, our simulations did not show any particular deviation from the theory at very mild stress, where such cosegregation of several single-step mutants is expected.
Maximal mutation rate for the SSWM regime
We conjecture that the SSWM approximation should be accurate below some threshold mutation rate i.e., whenever Indeed, Martin and Roques (2016) found that, as long as the fitness distribution at mutation-selection balance corresponds exactly to that expected under the House-of-Cards approximation (with a dominant optimal genotype plus its deleterious mutants). Whether this same condition is sufficient for most rescue events to stem from single-step mutations is not justified theoretically, and was simply tested by extensive stochastic simulations. Supplemental Material, Figure S1 in File S1 further explores the range of validity of this approximation. It shows, in a rescued population, the proportion of wild type, single mutant, double mutant, and so on, as a function of the mutation rate.
Distribution of single-step mutation fitness effects in the new environment
Let be the selection coefficient (difference in growth rate), in the new environment, of a random mutant (with phenotype ) relative to its ancestor (with phenotype ). The distribution of among random mutants has a known exact form in the isotropic FGM (Martin 2014; Martin and Lenormand 2015), from which the distribution of growth rates () in the new environment is readily obtained. It proves simpler and sufficient (see Appendix section II, subsection 2) to consider the scaled (and unitless) growth rate such that is the decay rate of the ancestor scaled to the maximum possible growth rate. The scaled growth rates have the following probability density function:
| (2) |
where is the confluent hypergeometric function and is the gamma function. In the SSWM regime, this probability density function approximately describes de novo mutations produced after the onset of stress by the whole population, be it initially clonal or at mutation-selection balance.
Fitness cost of single-step pre-existing mutants in the previous environment
Consider the subset of random mutations, among those that arise from the dominant genotype of the ancestral population, that have a scaled growth rate within the infinitesimal class in the new environment. We introduce the conditional random variable which is the cost, in the previous environment, of a random mutant within this subset (thus, conditional on ). This cost is equal to the negative of the selection coefficient of the mutation relative to the dominant genotype with phenotype More precisely, the cost of a mutant with phenotype is [using Equation (1), with for the previous environment]. Note that, because the mutation-selection balance in the previous environment is fully characterized by relative fitnesses, which do not depend on the maximal growth rate in this environment, the latter may differ from without impacting the distribution of the costs and our results. Importing results from Martin et al. (2013) for the SSWM regime, the total number of pre-existing variants within the class is Poisson distributed with mean where is the harmonic mean of the cost among mutations with effect in the new environment. This conditional harmonic mean depends on the joint distribution of mutation effects on fitness across two environments in the FGM (given in Martin and Lenormand 2015). In our context, the dominant genotype of the ancestral population is optimal in the previous environment and far from the optimum in the new environment. In this case, using Equation (9) in Martin and Lenormand (2015), the resulting conditional harmonic mean takes a tractable form [see Equation (A6) for and (A8) for in Appendix section II, subsection 4 and 5]:
| (3) |
where is the exponential integral function. In most of the article we focus on the case when considering ER from standing variance. The distributions of mutation effects on fitness in both the previous [Equation (3)] and the new environment [Equation (2)] can then be integrated to yield the probability of ER, as we show next.
General expression and assumptions for the rescue probability
Extinction occurs when no resistant mutation manages to establish (i.e., to avoid stochastic loss). For compactness, we define a rate of rescue per individual present at the onset of stress (i.e., scaled by ), such that, following Martin et al. (2013), ER probabilities take the general form (similar to that in e.g., Orr and Unckless 2008):
| (4) |
The rate of rescue from de novo mutations alone is (“” for de novo), while that from pre-existing variance alone is (“” for standing variants). For a purely clonal population, the rate of rescue is while for a population initially at mutation-selection balance, it is in the SSWM regime assumed here (Martin et al. 2013). Applied to the context of the FGM using Equations (2) and (3), the rates and are given by [see Appendix Equations (A5) and (A7)]:
| (5) |
where and are defined in Equation (3) and is the probability of establishment of a resistant genotype with scaled growth rate in the new environment. in Equation (5) is simply the average establishment probability of de novo resistant mutants times the genomic mutation rate, divided by the rate of decay. In previous ER models (e.g., Orr and Unckless 2008; Martin et al. 2013), which we denote “context-independent,” the probability of rescue takes the exact same form as Equation (4). The expressions for the rates of rescue per capita also take a form similar to Equation (5): for de novo mutations, and for standing variance, where is the proportion of rescuers among random mutations [ in Equation (5)] and is again the harmonic mean of the cost of rescue mutations. The important difference is that in previous models, and do not depend on while the corresponding quantities in Equation (5) do depend on the rate of decay, through its effect on and
The linearity of ER rates with the mutation rate () arises here because of the SSWM regime, where multiple mutations are ignored: it might not hold at higher mutation rates (when ). As such, Equation (5) makes no further assumption than the SSWM regime (); it can easily be evaluated numerically to provide a general testable theory for rescue probabilities across stress levels, in the FGM. Yet, in order to gain more quantitative/intuitive insight into the effects of stress, we study approximate closed forms for the rates in Equation (5).
Small mutational effects approximation
Although selection is assumed to be strong relative to mutation ( SSWM regime), it is still fairly realistic to assume that mutation effects on traits (and thus fitness) are weak relative to the maximal growth rate in the new environment, namely that Taking a limit where simpler expressions for Equation (5) are derived in the Appendix section III.
With this approximation, single-step resistance mutations are still rare and of large phenotypic effect, in that they pertain to the tail of the mutant phenotype distribution. However, even resistance mutations typically remain far from the optimum in the new environment, so that their scaled growth rate is small: Overall, mutation effects must fall within the range: for both the SSWM and the small mutational effects (SME) approximation to apply (see Appendix section III). In the Appendix, we study the convergence, as decreases, of the results from Equation (5) to their asymptotic limit (Figure S3 and Figure S4 in File S1).
Stochastic simulations of a discrete-time model
We checked the robustness of our assumptions and approximations using stochastic simulations, where we tracked the population size and genetic composition of a population across discrete, nonoverlapping generations. The size of population at generation was drawn as a Poisson number with the mean multiplicative fitness () and the population size, in the previous generation. The genotypes forming this new generation were then sampled with replacement from the previous one with weight This is faster and exactly equivalent to drawing independent Poisson reproductive outputs for each individual, or genotype. Because of the underlying assumptions of the simulations, the corresponding analytical approximation for the stochastic reproductive variance is (assuming small growth rates ). Mutations occurred according to a Poisson process, with a constant rate per capita per generation. Mutation phenotypic effects were drawn from a multivariate normal distribution with multiple mutants having additive effects on phenotype, and their fitness computed according to the FGM [Equation (1)].
Rescue probability was estimated by running replicate simulations until either extinction or rescue occurred. A population was considered rescued when it reached a population size and mean growth rate such that its ultimate extinction probability, if it were monomorphic, would lie below []. This is a conservative criterion: once has become positive, we expect it to remain so, yielding further increases in population size and thus further decreasing the probability of future extinction. We checked on a subset of simulations that the above procedure gave the same rescue probabilities as obtained in simulations performed until the population rebounded back to its (large) initial size .
For rescue from populations at mutation-selection balance, eight replicate initial equilibrium populations were generated, each by starting from an optimal clone and running the same algorithm with fixed population size () until the mean growth rate had visually stabilized to a fixed value (close to its theoretical equilibrium value , for) for more than 1000 generations. Then the optimum was shifted by phenotypic units, and replicate ER simulations were performed (same algorithm as for de novo rescue), from each of the eight replicate equilibrium populations.
All simulations and mathematical derivations were performed in MATHEMATICA v. 9.0 (Wolfram Research 2012).
Data availability
File S1 contains appendices describing all analytical derivations and supplemental figures. File S2 provides the details of the analytical derivations as a Mathematica© source code (MATHEMATICA v. 9.0 Wolfram Research 2012). File S3 provides the simulation code also as a Mathematica© source code (MATHEMATICA v. 9.0 Wolfram Research 2012). Supplemental material available at Figshare: https://doi.org/10.25386/genetics.5975008.
Results
The ER rates in Equation (5) are analytical but only implicit functions of the model parameters. In a SME limit, they take simpler closed forms (indicated by a “*”). As we will see below, these simpler forms mostly depend on the following two compound variables, which summarize the various effects of stress on the fitness landscape:
| (6) |
Both and increase with the decay rate decrease with increasing peak height and are independent of The parameter further increases with decreasing variance of mutational effects We can already see how qualitatively reflects an “effective stress level”: stress is harder to cope with if decay rate is larger, the maximum growth rate is lower, and mutation effects are smaller.
Rescue from de novo mutations
Under the SME approximation and in the SSWM regime () the rate of de novo rescue [Equation (5)], converges to [Equation (A12) in the Appendix]:
| (7a) |
| (7b) |
with
where is the complementary error function. Equation (7b) gives the approximate closed form of Equation (7a) for mild stress Note that this approximation converges faster (with decreasing ) with fewer dimensions, due to the faster vanishing of the factor (in the limit it vanishes for all ). We now discuss the biological implications of these expressions.
Effect of FGM parameters on rescue
The partial derivatives of in Equations (7a) and (7b) with respect to the FGM parameters () quantify the sensitivities of ER probability to each of them (Appendix section III, subsection 4). First, note that is a strictly decreasing function of When and with mild stress (), Equation (7b) applies and ER then becomes less likely with a higher decay rate a lower peak and a smaller variance of mutational effects and is independent of dimensionality For stronger stress levels, Equation (7a) applies: these qualitative dependencies to the parameters still hold, except that ER probability now decreases with increasing dimensionality.
Sharp drop of ER probability with stress levels
Figure 2 shows the agreement between simulations (stochastic discrete-time demographic model, see Methods) and the analytical expressions in Equations (5), (7a), and (7b), over a wide range of stress levels (quantified by ), and for two values of and (Figure S3 in File S1 further explores the range of validity of the approximation). Interestingly, ER probability drops sharply with stress levels (with decay rate here), which is well captured by the term alone [Equation (7b), dashed red lines in Figure 2]. This drop is much more pronounced than in a context-independent model (gray lines in Figure 2), where stress does not affect the distribution of mutation effects. The difference between context-independent models and the FGM is that, in the latter, increased stress implies both faster decay (as in the former), and fewer and weaker resistance mutations. In the FGM, these effects on the properties of rescue mutations are the main drivers of ER probabilities across stress levels.
Figure 2.
Rescue probability from de novo mutations. The ER probability as a function of stress levels, expressed as the initial mean decay rate of the population, is given for various values of the mutation rate (blue) or (orange) and the maximal fitness reachable in new the environment (A) or (B). Dots give the results from simulations and solid lines (blue and orange) show the corresponding theory computed numerically [Equation (5)]. The black dot-dashed and red dashed lines give the corresponding analytical approximations Equations (7a) and (7b), respectively. The gray lines correspond to an equivalent theory without the FGM (named context-independent model as described in the Methods section, “CI”) modified from Orr and Unckless (2008). This last model was computed using a fixed proportion of resistant mutations equal to the one in Equation (5) for a rescue probability of (which explains why the two curves cross exactly at ). Other parameters are
Composite parameter describing an effective stress level
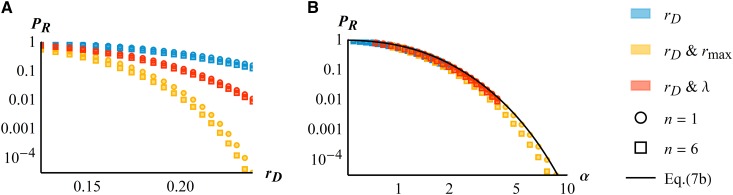
The results in Equations (6), (7a), and (7b) suggest that a single composite parameter [ in Equation (6)] can capture the various ways in which stress may alter the parameters of the fitness landscape, that is, fitness peak height variance of mutational effects or distance to the optimum We denote this parameter the “effective stress level.” In Figure 2, considering the effect of stress only via [Equation (7b)] is equally accurate as using the more complex Equation (7a), or the numerical computation from Equation (5).
This simplification is further illustrated in Figure 3, where we use exact numerical computations from Equation (5) to explore different possible effects of stress. Regardless of whether stress affects only the maladaptation of the ancestral clone ( blue symbols), or also the quality of the environment (joint change in and orange symbols) or the variance of mutational effects (joint change in and red symbols), its effect on the rescue probability is accurately predicted by (Figure 3B, black line). As predicted by Equation (7b), the relationship between rescue probability and is approximately independent of dimensionality (compare circles and squares in Figure 3B). We also note that Equation (7b) slightly overestimates the “exact” numerical computations of the ER probability from Equation (5), so it provides a conservative bound when considering the control of resistant pathogens.
Figure 3.
The effective stress level. Rescue probability for clonal populations vs. initial decay rate (A) or the effective stress level (B). In both panels the axes are in logarithmic scale, symbols show Equation (5) and colors refer to different effects of increased stress level: blue symbols show only increasing (with and orange symbols increasing and decreasing linearly with (according to with ) and red symbols increasing and decreasing linearly with (according to with ). In each case, the results for both (circles) and (squares) are shown. The black plain line on the right panel gives the result from Equation (7b): a single composite measure of stress approximately captures the impact of stress-induced variations in the various parameters Other parameters are and
Characteristic stress level
Figure 2 shows that ER drops from highly likely to highly unlikely around a “characteristic stress level,” which can be characterized analytically (as detailed in the Appendix section IV, subsection 1). Consider the set of values of parameters for which the rescue probability is of given value From Equation (7b), this corresponds to the set for which . Using the approximation [from Equations (7a) and (7b) with ], the corresponding can be derived explicitly [Equation (A17)]. In particular, for the characteristic stress level at which the ER probability is is [Equation (A19) in the Appendix]:
| (8) |
Under the conditions of the SME approximation (detailed in Methods), Equation (8) applies for large (approximately when ), a necessary condition for this equation to be self-consistent (detailed in Appendix section IV, subsection 2).
The characteristic stress level that a population can typically withstand increases only log-linearly with population size and mutation rate. Consider the characteristic decay rate for which the rescue probability is i.e., the decay rate that populations can overcome half of the times. From Equation (8) with [Equation (6)], this decay rate is for large For comparison, we would have which is linear in in a context-independent model where the proportion of random mutations causing a rescue is independent of The difference in the effect of on rescue probability thus stems from the strong nonlinearity (i.e., sharp drop) of rescue probability with stress level (decay rate) under the FGM. In the FGM, overcoming a given environmental harshness requires much more mutational input than in a context-independent model.
Characteristic stress window
It is also important to predict how sharply the ER probability drops around the characteristic stress level. This drop can be characterized by a “characteristic stress window” of over which the ER probability drops from 75 to 25%. The width of this window can be scaled by the value of the characteristic stress level to get a scale-free measure of its steepness (i.e., how sharp the drop in ER probability is, relative to the stress level around which it occurs). This gives [from Equation (A20) in the Appendix]:
| (9) |
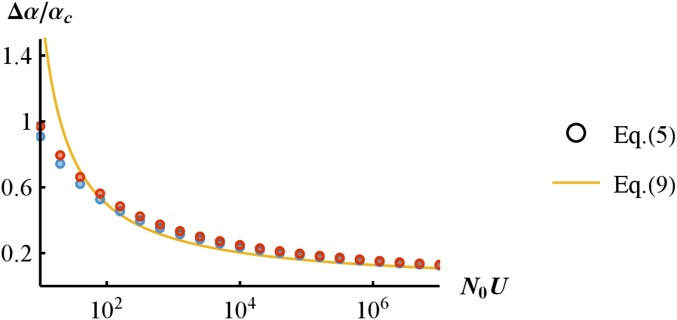
The width increases with increasing until it saturates (at ) (see Appendix section IV, subsection 3 for further details). However, when scaled by the center of the window (), the width of this scaled characteristic stress window drops below as increases [and hence with increasing from Equation (8)]. This result shows formally that the drop in ER probability with increasing stress gets proportionally sharper (relative to the position where it occurs) as increases, but this is entirely driven at large by shifts of a window with constant absolute width. This is illustrated in Figure 4, which also shows the accuracy of Equation (9) compared to “exact” numerical computations from Equation (5) [as expected, the exact result deviates from Equation (9) for smaller ].
Figure 4.
Scaled width of the characteristic stress window vs. the population-scale mutation rate The dots are obtained by numerical inversion of the “exact” Equation (5) with two values of (blue) and (red). The orange line shows the approximate scaled width of the characteristic stress window derived in Equation (9). Other parameters are
Interestingly, Equation (9) provides a scale-free measure that may be compared across experiments, as it only depends on the genomic mutational input (via ). However, like all results so far, Equation (9) only considers ER from de novo mutation. We now turn to ER from standing genetic variation.
Rate of rescue from a population at mutation-selection balance
In the SSWM regime, and for a population at mutation-selection balance in the previous environment, each rescue event can be tracked back to either a pre-existing variant, or a de novo mutation (Orr and Unckless 2008, 2014; Martin et al. 2013). The proportion of rescue events caused by standing variance is then simply given by A simple expression can be obtained again under the SME for [see Equation (A21) in the Appendix], but the approximation () now further requires that decay rates are not vanishingly small ().
| (10) |
where is defined in Equation (6).
Equation (10) captures the main features of how standing variance contributes to ER across (nonvanishing) stress levels (here, decay rate). Contrary to context-independent models, this contribution changes nonmonotonically with increasing stress level (Figure 5). At very mild decay rate rescue relies on mild-effect mutations. The cost of such mutations—and hence their frequency before stress—is roughly independent of (Martin and Lenormand 2015), while their rate of production by de novo mutation decreases as (demographic effect), so the contribution of standing variance to ER increases with at small In contrast at large stress levels, rescue stems from strong effect mutations. These mutations pay a substantial “incompressible cost” before stress that increases faster than (Martin and Lenormand 2015), while their rate of de novo production still decreases as so the contribution of standing variance to ER decreases with at large In the limit of very large the distance between the two optima is very large and makes the most of both the cost and decay rate, so that for all mutations. Hence, de novo mutations and standing variants contribute equally to ER in this limit ().
Figure 5.
Relative contribution of standing genetic variation to ER. The proportion of ER from standing variance is shown across scaled decay rates The numerical computation for [using Equations (5) and (10)], for two values of (blue) and (orange), is compared to the approximate [Equation (10), black dashed line]. Other parameters as in Figure 2.
These different behaviors are illustrated in Figure 5, showing the variation of over a very wide range of scaled decay rates . The limit in Equation (10) provides a fairly accurate approximation across the full range of stress levels. The limits when and are in fact of limited biological interest, as they correspond to stress levels where ER becomes de facto certain or impossible, respectively. When focusing on the more biologically relevant range corresponding to the characteristic stress window, which occurs near the peak in in Figure 5 (see Appendix section IV, subsection 4), the variation of across stress levels becomes negligible. As illustrated in Figure 6B, remains close to [see Appendix Equation (A22)] as varies over a range where ER probabilities span several orders of magnitude (see Appendix Section IV subsection 5). Note that this behavior arises when stress only shifts the optimum (effect on ), but does not affect peak height () or the variance of mutational effects ().
Figure 6.
ER probability in the presence of standing genetic variation. In each panel, stress only affects the decay rate (shifting optimum). In both panels, blue solid lines show the theory for de novo and standing variance (“DN”+“SV”) computed numerically [Equation (5)] and the gray lines correspond to an equivalent theory without the FGM (named context-independent model as described in the Methods section, “CI”) modified from Orr and Unckless (2008). This last model was computed using a fixed proportion of resistant mutations equal to the one in Equation (5) for a rescue probability of (which explains why the two curves cross exactly at ). The dashed red line gives the simpler expression for the overall rescue rate: [Equation (11)] with given in Equation (10) and by Equations (7a) and (7b). (A) ER probability in the presence of standing genetic variation as a function of The dots give the results from simulations. (B) Proportion of rescue from standing variance as a function of The black dashed-line give the approximate theory from Equation (10) and the dashed red line from Equation (11). The shaded area shows the range of for which the ER probability drops from to Other parameters as in Figure 2.
Therefore the rate of rescue in the presence of standing variance is approximately proportional to that with only de novo mutation, with proportionality constant largely independent of the decay rate:
| (11) |
where is defined in Equation (10). The rough constancy of also means that all the results obtained previously for ER from de novo mutations apply in the presence of standing variance, when stress only shifts the optima (as long as .
The ER probability profile across stress levels (shown in Figure 6A) is the same as that from de novo mutations alone (Figure 2), but with a higher characteristic stress [ from Equation (8) with]. Moreover, when considering the contribution from standing variance, the difference between the FGM and context-independent models (gray line on Figure 6A) is striking. Indeed in the latter, the ER rate from standing variance () is independent of the decay rate, hence saturates with stress to a constant value where all ER events stem from standing variance.
Finally, note that when considering rescue from preexisting variance, may change across environments, from (for previous) to (for new). For example, a stress-induced increase in DNA copy error would yield Accounting for such shifts in mutation rate at the onset of stress, the total ER rate simply becomes [from Equation (11)].
Discussion
Main results
We investigated the persistence of a population of asexual organisms under an abrupt environmental alteration. We assumed that this stress causes a shift in a multidimensional fitness landscape with a single peak (FGM), which the population must “climb” to avoid extinction. In such a landscape, faster population decline (due to stress-induced increase in the decay rate ) necessarily means that resistance mutations are fewer, have lower growth rates in the presence of stress, and higher costs in its absence. We believe that this constraint, not included in previous studies, adds a key element of realism to ER models. In our model, variation in stress levels may affect the landscape in various ways: shifting the optimum, changing the peak height, or altering the phenotypic scale of mutations (or the strength of stabilizing selection). Under a SSWM regime and assuming SME, all these effects of stress on the distribution of mutation fitness effects are approximately captured by the variation, across stress levels, of a single composite parameter which is approximately independent of the dimensionality of the organism (number of orthogonal traits under selection). The probability of ER drops sharply with this effective stress level, more so than in previous ER models where the rate of population decline is decoupled from the input of resistant mutations. The characteristic stress window over which this drop occurs only depends on the initial population size and genomic rate of mutation As gets large, the characteristic stress window reaches an asymptotic width [ in Equation (9)] while its center [the characteristic stress level in Equation (8)] shifts toward higher values, approximately as
When standing variance is available (population at mutation-selection balance before stress), its contribution to ER is dominant, and approximately constant across a wide range of stress levels that encompasses the characteristic stress window.
In Table 2, we summarize how these features compare to properties of previous ER models. We consider only the situation where stress shifts the position of the optimum, affecting (as in previous models), because other effects of stress we investigate here ( and ) are not treated in previous models.
Table 2. Main results of “context-independent” modelsa and the present model (FGM) when stress only affects (only shifts the optimum position in our model).
| Context-Independent Model | FGM Rescue Model | |
|---|---|---|
| Impact of decay rate | (1) | |
| Impact of mutational input | ||
| “Characteristic decay rate” () for DN rescue vs. | ||
| Relative contribution of standing variance to ER | Increases with | ∼ Stable with |
When the dependence to the parameters is given for the overall rate of rescue it applies to both the rate of rescue from de novo mutations and from pre-existing variance (1) derived from the approximate expression
Genetic basis of ER patterns across environments
Our model allows identification of three ranges of stress levels that yield different eco-evolutionary patterns, despite all leading to extinction in the absence of evolution. First, at low stress levels (), although evolutionary change is required for persistence and demographic dynamics typical of ER may be observed (decay/rebounce), extinctions are de facto undetectable (ER is pervasive, ). In this regime, we expect several resistance mutations to establish and cosegregate (frequent “soft sweeps” as in Wilson et al. 2017). Their number is predictable (), but the ultimate composition of the population in asexuals will depend on more complex clonal interference dynamics. Second, at intermediate stress levels [], small variation in stress conditions has large impact on the probability of population survival. Over this range, so the expected overall number of rescue mutations in the population is less than one []. Therefore, “hard sweeps” (including from standing variation) should be the most frequent: a single mutation typically establishes and rescues the population. Finally, at higher stress levels (), very few populations overcome the imposed stress, and when they do it is typically through a hard sweep ().
Estimating parameters and testing the model
Studies on the emergence of resistance to controlled stress (e.g., antibiotics, fungicides, and chemotherapy in cancer), especially in microbes, can generate a set of estimates of (the probability of resistance emergence), across stress levels. In general, to test (or use) predictions from ER models, it is critical to empirically relate physical measures of stress level (e.g., concentrations, temperatures, salinities, etc.) with demographic measures (e.g., decay rates). If we assume that the main effect of stress is to shift optimum positions, given a set of measurements of (“dose-kill curves;” Regoes et al. 2004), the change in ER probability with stress can be predicted via Equations (7a) and (7b). This simple scenario of optimum shifting is the one that is considered by most of the literature on evolutionary ecology across environmental gradients, so it would seem natural to test it first. Furthermore, this scenario has received empirical support from an analysis of a few experimental studies of distribution of mutation effects on fitness across stress levels (Martin and Lenormand 2006b). However, these studies used mild stresses, which reduce growth without causing population decay. A more recent study on bacteria facing lethal doses of antibiotics, i.e., in the presence of decay (Harmand et al. 2017), suggests that factors other than the position of the optimum may also change with stress (). Estimating these extra parameters across environments can be challenging. The variance of mutational effects and the dimensionality can be estimated by fitting the distributions of single random mutation effects on fitness (Martin and Lenormand 2006b; Perfeito et al. 2014), in a single environment if it is to be assumed constant, or in each environment otherwise. The maximal growth rate in the stress could be measured on lines well-adapted to the environment considered.
The effective stress level is also amenable to empirical measurement and circumvents the issue of measuring joint changes in with stress. Consider a set of estimates across a range of empirically controlled stress levels, and some knowledge of the genomic (non-neutral) mutation rate (e.g., as estimated by mutation accumulation experiments) of the species and environment under study (). The initial population size is easily controlled by the experimenter. Then Equation (7b) suggests a simple estimator of in each environment:
Finally, it is also possible to circumvent the problem of stress-induced variation in the parameters of the fitness landscape by considering multiple genetic backgrounds, in a single environment. Each background would have a given measurable decay rate and other parameters () would be held fixed; while and may change with the genetic background, this seems less likely than with the environment. The isotropic FGM assumes a strict equivalence between shifts in optima (multiple environments) from a given ancestor phenotype (single genetic background), and shifts in ancestor phenotypes (multiple genetic backgrounds) with a fixed optimum (single environment). The model could thus be applied and tested in this context. This could yield useful insights into the effect of epistasis (background dependence) on resistance emergence, an issue of notable importance when considering the fate of horizontally transferred resistance or multidrug resistance (as discussed in Wong 2017)
Potential implications for resistance management
Our results suggest that stress levels have a strongly nonlinear impact on ER probabilities (Figure 2), at least in the context of abrupt environmental changes, in asexuals. This context may be particularly relevant to the chemical treatment of pathogens (cancer therapy, antivirals, antibiotics, fungicides, herbicides, etc.). In particular, the nonlinear impact of stress on ER, if empirically confirmed, can provide insights regarding the optimization of treatment regimens or the quantification of the effect of poor treatment adherence on resistance emergence (e.g., in HIV, Harrigan et al. 2005). Our results point to the risk that even a slight lowering of drug doses (below prescribed treatment levels) could radically change the outcome of the treatment (making it de facto inefficient). On the contrary, a slight increase in prescribed doses could sometimes prove sufficient to allow efficient eradication.
Limits and possible extensions
Density-dependence and competitive release:
Our model ignores density dependence, but some form may be easily introduced by considering a single density dependence coefficient (common to all genotypes) and using logistic diffusion approximations (Lambert 2005). This would potentially allow for “competitive release” (Read et al. 2011), whereby higher stresses may favor the emergence of resistance by rapidly depleting the sensitive wild-type population, thus releasing limiting resources for resistant genotypes. Previous models on competitive release assumed that the number of standing resistant mutants is independent of stress level (Read et al. 2011; Day and Read 2016). In this case, stress mostly limits de novo rescue mutation, with limited impact on the contribution from standing variance. On the contrary, the FGM imposes a similar drop, with stress, in the rate of rescue from de novo and preexisting mutants. The positive effects of competitive release on ER probability may thus be less important, in the FGM, than predicted from these previous models. Note however that more generally, the effect of density dependence on ER is more safely investigated by accounting explicitly for the effect of stress on the density-independent intrinsic rate of increase on the one hand (as done here in a density-independent model), vs. on the competition component on growth (e.g., carrying capacity) on the other hand, than by compounding their effects into an overall density-dependent decay rate (e.g., Chevin and Lande 2010). This would require modeling the effect of stress on both the intrinsic rate of increase and the competition component, possibly through a landscape with two fitness functions, describing each component.
Anisotropy and parallel evolution in drug resistance:
The present model is isotropic: all directions in phenotype space are equivalent (in terms of mutation and selection). In contrast, module-dependent anisotropy (where particular genes mutate along favored directions) can lead to substantial parallel evolution in the FGM (Chevin et al. 2010). Parallel evolution of resistance, whereby some (portions or sets of) genes contribute most of the resistance mutations, is often observed among drug-resistance alleles, and can increase with stress (Harmand et al. 2017), contrary to parallel evolution in a growing population, which is expected to decrease with increasing maladaptation (Chevin et al. 2010). Although not explored here, we conjecture that our model may accommodate mild anisotropy. Indeed, mild anisotropy (even environment-dependent) might have limited impact. If mutational covariances between traits merely “turn,” “shrink” or “expand” the phenotypic mutant cloud, this would approximately amount to a mere change in in an equivalent isotropic landscape (Martin and Lenormand 2006a; Martin 2014). However, a particular form of strong anisotropy may also arise where mutant phenotypes (in a given module) spread along a single favored direction (Martin 2014). Only this level of anisotropy would generate clear parallel evolution, and it will likely require implementing a fully anisotropic model.
High mutation rates:
Our results relied on a SSWM approximation. When the mutation rate is higher (e.g., viruses or mutator bacterial strains), multiple mutants must be accounted for as a source of ER. These can in principle be introduced in the framework used here (Martin et al. 2013), but, especially when applied to the FGM, the results quickly become intractable. Alternative population genetics assumptions would then have to be used, but this is beyond the scope of the present work.
Conclusion
Recently, the FGM has received renewed interest for its ability to provide testable, quantitative, and often accurate predictions regarding patterns of mutation effects on fitness, across various species and contexts (Tenaillon 2014). The present model is an attempt to extend its scope to model the evolution of resistance to stress. We hope that future experimental tests will evaluate its accuracy and potential to tackle various pressing applied issues.
Acknowledgments
We thank the editor Joachim Hermisson and the reviewers for their help in improving this manuscript. In particular we thank Michael Kopp for extensive and very useful comments on our manuscript. This work benefited from discussions with S. Gandon, R. Gomulkiewicz, O. Tenaillon, F. Débarre, and L. Roques. This work was supported by the French Ministry of Higher Education, Research and Innovation (MESRI allocation doctorale to Y.A.), Agence Nationale de la Recherche (ANR-13-ADAP-0016 “Silentadapt” to G.M. and ANR-13-ADAP-0006 “MeCC” to O.R.) and European Research Council (ERC-2015-STG-678140-FluctEvol to L.-M.C.). This is ISEM publication ISEM 2018-032.
Footnotes
Supplemental material available at Figshare: https://doi.org/10.25386/genetics.5975008.
Communicating editor: J. Hermisson
Literature Cited
- Agrawal A. F., Whitlock M. C., 2010. Environmental duress and epistasis: how does stress affect the strength of selection on new mutations? Trends Ecol. Evol. 25: 450–458. [DOI] [PubMed] [Google Scholar]
- Alexander H. K., Martin G., Martin O. Y., Bonhoeffer S., 2014. Evolutionary rescue: linking theory for conservation and medicine. Evol. Appl. 7: 1161–1179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bell G., 2017. Evolutionary rescue. Annu. Rev. Ecol. Evol. Syst. 48: 605–627. [Google Scholar]
- Bijlsma R., Loeschcke V., 2005. Environmental stress, adaptation and evolution: an overview. J. Evol. Biol. 18: 744–749. [DOI] [PubMed] [Google Scholar]
- Burger R., Lynch M., 1995. Evolution and extinction in a changing environment: a quantitative-genetic analysis. Evolution 49: 151. [DOI] [PubMed] [Google Scholar]
- Carlson S. M., Cunningham C. J., Westley P. A. H., 2014. Evolutionary rescue in a changing world. Trends Ecol. Evol. 29: 521–530. [DOI] [PubMed] [Google Scholar]
- Charmantier A., Garant D., 2005. Environmental quality and evolutionary potential: lessons from wild populations. Proc. Biol. Sci. 272: 1415–1425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chevin L.-M., 2011. On measuring selection in experimental evolution. Biol. Lett. 7: 210–213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chevin L.-M., Lande R., 2010. When do adaptive plasticity and genetic evolution prevent extinction of a density-regulated population? Evolution 64: 1143–1150. [DOI] [PubMed] [Google Scholar]
- Chevin L.-M., Martin G., Lenormand T., 2010. Fisher’s model and the genomics of adaptation: restricted pleiotropy, heterogenous mutation, and parallel evolution. Evolution 64: 3213–3231. [DOI] [PubMed] [Google Scholar]
- Davies J., Davies D., 2010. Origins and evolution of antibiotic resistance. Microbiol. Mol. Biol. Rev. 74: 417–433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Day T., Read A. F., 2016. Does high-dose antimicrobial chemotherapy prevent the evolution of resistance? PLoS Comput. Biol. 12: e1004689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Visser J. G. M., Rozen D. E., 2005. Limits to adaptation in asexual populations. J. Evol. Biol. 18: 779–788. [DOI] [PubMed] [Google Scholar]
- Drlica K., 2003. The mutant selection window and antimicrobial resistance. J. Antimicrob. Chemother. 52: 11–17. [DOI] [PubMed] [Google Scholar]
- Feller W., 1951. Diffusion processes in genetics, pp. 227–246 in Proceedings of the Second Berkeley Symposium on Mathematical Statistics and Probability University of California Press, Berkeley, CA. [Google Scholar]
- Foster P. L., 2007. Stress-induced mutagenesis in bacteria. Crit. Rev. Biochem. Mol. Biol. 42: 373–397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gillespie J. H., 1983. Some properties of finite populations experiencing strong selection and weak mutation. Am. Nat. 121: 691–708. [Google Scholar]
- Gomulkiewicz R., Holt R. D., 1995. When does evolution by natural selection prevent extinction? Evolution 49: 201. [DOI] [PubMed] [Google Scholar]
- Gomulkiewicz R., Holt R. D., Barfield M., Nuismer S. L., 2010. Genetics, adaptation, and invasion in harsh environments. Evol. Appl. 3: 97–108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gonzalez A., Bell G., 2013. Evolutionary rescue and adaptation to abrupt environmental change depends upon the history of stress. Philos. Trans. R. Soc. Lond. B Biol. Sci. 368: 20120079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gonzalez A., Ronce O., Ferriere R., Hochberg M. E., 2013. Evolutionary rescue: an emerging focus at the intersection between ecology and evolution. Philos. Trans. R. Soc. B Biol. Sci. 368: 20120404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harmand N., Gallet R., Jabbour-Zahab R., Martin G., Lenormand T., 2017. Fisher’s geometrical model and the mutational patterns of antibiotic resistance across dose gradients. Evolution 71: 23–37. [DOI] [PubMed] [Google Scholar]
- Harrigan P. R., Hogg R. S., Dong W. W. Y., Yip B., Wynhoven B., et al. , 2005. Predictors of HIV drug-resistance mutations in a large antiretroviral-naive cohort initiating triple antiretroviral therapy. J. Infect. Dis. 191: 339–347. [DOI] [PubMed] [Google Scholar]
- Hermisson J., Wagner G. P., 2004. The population genetic theory of hidden variation and genetic robustness. Genetics 168: 2271–2284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hietpas R. T., Bank C., Jensen J. D., Bolon D. N. A., 2013. Shifting fitness landscapes in response to altered environments. Evolution 67: 3512–3522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoffmann A. A., Merilä J., 1999. Heritable variation and evolution under favourable and unfavourable conditions. Trends Ecol. Evol. 14: 96–101. [DOI] [PubMed] [Google Scholar]
- Hoffmann A. A., Parsons P. A., 1997. Extreme Environmental Change and Evolution. Cambridge University Press, Cambridge, New York. [Google Scholar]
- Koehn R. K., Bayne B. L., 1989. Towards a physiological and genetical understanding of the energetics of the stress response. Biol. J. Linn. Soc. Lond. 37: 157–171. [Google Scholar]
- Kopp M., Matuszewski S., 2014. Rapid evolution of quantitative traits: theoretical perspectives. Evol. Appl. 7: 169–191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lambert A., 2005. The branching process with logistic growth. Ann. Appl. Probab. 15: 1506–1535. [Google Scholar]
- Lindsey H. A., Gallie J., Taylor S., Kerr B., 2013. Evolutionary rescue from extinction is contingent on a lower rate of environmental change. Nature 494: 463–467. [DOI] [PubMed] [Google Scholar]
- Lynch M., Gabriel W., Wood A. M., 1991. Adaptive and demographic responses of plankton populations to environmental change. Limnol. Oceanogr. 36: 1301–1312. [Google Scholar]
- MacLean R. C., Perron G. G., Gardner A., 2010. Diminishing returns from beneficial mutations and pervasive epistasis shape the fitness landscape for rifampicin resistance in Pseudomonas aeruginosa. Genetics 186: 1345–1354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin G., 2014. Fisher’s geometrical model emerges as a property of complex integrated phenotypic networks. Genetics 197: 237–255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin G., Lenormand T., 2006a A general multivariate extension of Fisher’s geometrical model and the distribution of mutation fitness effects across species. Evolution 60: 893–907. [PubMed] [Google Scholar]
- Martin G., Lenormand T., 2006b The fitness effect of mutations across environments: a survey in light of fitness landscape models. Evolution 60: 2413–2427. [PubMed] [Google Scholar]
- Martin G., Lenormand T., 2015. The fitness effect of mutations across environments: Fisher’s geometrical model with multiple optima. Evolution 69: 1433–1447. [DOI] [PubMed] [Google Scholar]
- Martin G., Roques L., 2016. The nonstationary dynamics of fitness distributions: asexual model with epistasis and standing variation. Genetics 204: 1541–1558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin G., Elena S. F., Lenormand T., 2007. Distributions of epistasis in microbes fit predictions from a fitness landscape model. Nat. Genet. 39: 555–560. [DOI] [PubMed] [Google Scholar]
- Martin G., Aguilée R., Ramsayer J., Kaltz O., Ronce O., 2013. The probability of evolutionary rescue: towards a quantitative comparison between theory and evolution experiments. Philos. Trans. R. Soc. Lond. B Biol. Sci. 368: 20120088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moser C., Bell G., 2011. Genetic correlation in relation to differences in dosage of a stressor. J. Evol. Biol. 24: 219–223. [DOI] [PubMed] [Google Scholar]
- Orr H. A., Unckless R. L., 2008. Population extinction and the genetics of adaptation. Am. Nat. 172: 160–169. [DOI] [PubMed] [Google Scholar]
- Orr H. A., Unckless R. L., 2014. The population genetics of evolutionary rescue. PLoS Genet. 10: e1004551. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perfeito L., Sousa A., Bataillon T., Gordo I., 2014. Rates of fitness decline and rebound suggest pervasive epistasis. Evolution 68: 150–162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Read A. F., Day T., Huijben S., 2011. The evolution of drug resistance and the curious orthodoxy of aggressive chemotherapy. Proc. Natl. Acad. Sci. USA 108: 10871–10877. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Regoes R. R., Wiuff C., Zappala R. M., Garner K. N., Baquero F., et al. , 2004. Pharmacodynamic functions: a multiparameter approach to the design of antibiotic treatment regimens. Antimicrob. Agents Chemother. 48: 3670–3676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Remold S. K., Lenski R. E., 2001. Contribution of individual random mutations to genotype-by-environment interactions in Escherichia coli. Proc. Natl. Acad. Sci. USA 98: 11388–11393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Remold S. K., Lenski R. E., 2004. Pervasive joint influence of epistasis and plasticity on mutational effects in Escherichia coli. Nat. Genet. 36: 423–426. [DOI] [PubMed] [Google Scholar]
- Samani P., Bell G., 2010. Adaptation of experimental yeast populations to stressful conditions in relation to population size. J. Evol. Biol. 23: 791–796. [DOI] [PubMed] [Google Scholar]
- Scharloo W., 1991. Canalization: genetic and developmental aspects. Annu. Rev. Ecol. Syst. 22: 65–93. [Google Scholar]
- Sgrò C. M., Hoffmann A. A., 2004. Genetic correlations, tradeoffs and environmental variation. Heredity 93: 241–248. [DOI] [PubMed] [Google Scholar]
- Tenaillon O., 2014. The utility of Fisher’s geometric model in evolutionary genetics. Annu. Rev. Ecol. Evol. Syst. 45: 179–201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trindade S., Sousa A., Gordo I., 2012. Antibiotic resistance and stress in the light of Fisher’s model. Evolution 66: 3815–3824. [DOI] [PubMed] [Google Scholar]
- Turelli M., 1984. Heritable genetic variation via mutation-selection balance: Lerch’s zeta meets the abdominal bristle. Theor. Popul. Biol. 25: 138–193. [DOI] [PubMed] [Google Scholar]
- Uecker H., Hermisson J., 2016. The role of recombination in evolutionary rescue. Genetics 202: 721–732. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uecker H., Otto S. P., Hermisson J., 2014. Evolutionary rescue in structured populations. Am. Nat. 183: E17–E35. [DOI] [PubMed] [Google Scholar]
- Wang A. D., Sharp N. P., Spencer C. C., Tedman‐Aucoin K., Agrawal A. F., 2009. Selection, epistasis, and parent‐of‐origin effects on deleterious mutations across environments in Drosophila melanogaster. Am. Nat. 174: 863–874. [DOI] [PubMed] [Google Scholar]
- Wang A. D., Sharp N. P., Agrawal A. F., 2014. Sensitivity of the distribution of mutational fitness effects to environment, genetic background, and adaptedness: a case study with Drosophila. Evolution 68: 840–853. [DOI] [PubMed] [Google Scholar]
- Wilson B. A., Pennings P. S., Petrov D. A., 2017. Soft selective sweeps in evolutionary rescue. Genetics 205: 1573–1586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolfram Research , 2012. Mathematica. Wolfram Research, Inc, Champaign, IL. [Google Scholar]
- Wong A., 2017. Epistasis and the evolution of antimicrobial resistance. Front. Microbiol. 8: 246. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
File S1 contains appendices describing all analytical derivations and supplemental figures. File S2 provides the details of the analytical derivations as a Mathematica© source code (MATHEMATICA v. 9.0 Wolfram Research 2012). File S3 provides the simulation code also as a Mathematica© source code (MATHEMATICA v. 9.0 Wolfram Research 2012). Supplemental material available at Figshare: https://doi.org/10.25386/genetics.5975008.