Peptide Retention in Hydrophilic Strong Anion Exchange Chromatography Is Driven by Charged and Aromatic Residues

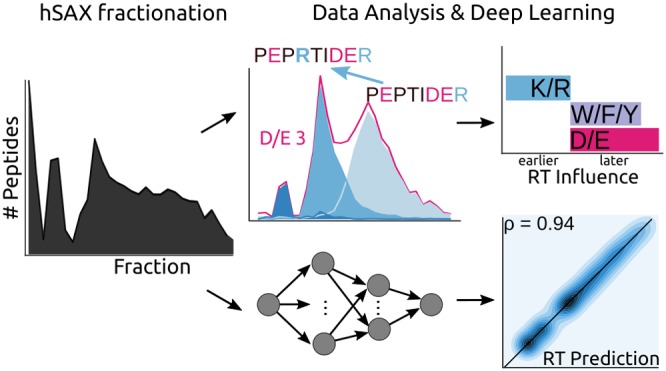
Abstract

Hydrophilic strong anion exchange chromatography (hSAX) is becoming a popular method for the prefractionation of proteomic samples. However, the use and further development of this approach is affected by the limited understanding of its retention mechanism and the absence of elution time prediction. Using a set of 59 297 confidentially identified peptides, we performed an explorative analysis and built a predictive deep learning model. As expected, charged residues are the major contributors to the retention time through electrostatic interactions. Aspartic acid and glutamic acid have a strong retaining effect and lysine and arginine have a strong repulsion effect. In addition, we also find the involvement of aromatic amino acids. This suggests a substantial contribution of cation−π interactions to the retention mechanism. The deep learning approach was validated using 5-fold cross-validation (CV) yielding a mean prediction accuracy of 70% during CV and 68% on a hold-out validation set. The results of this study emphasize that not only electrostatic interactions but rather diverse types of interactions must be integrated to build a reliable hSAX retention time predictor.

Mass spectrometry (MS)-based proteomics is the driving technology for the characterization and quantification of complex protein samples.¹⁻³ With the current advancements in instrumentation and software solutions, the number of peptides and proteins that can be identified in a minimal amount of time have increased dramatically.⁴ However, deep proteome coverage of higher eukaryotes, mammalian cell lines, or tissue is currently only feasible with extensive fractionation.^5,6 The wide dynamic range of all the expressed proteins in a cell remains a major challenge, leaving the least abundant proteins (and peptides) undiscovered. In these cases, online (1D) reverse phase liquid chromatography (RP-LC) does not yield the necessary separation of the proteome. Instead, prefractionation is commonly applied to further reduce the complexity. Ideally, the combined separation methods are as orthogonal as possible^5,7,8 to ensure the separation of similar analytes. Interestingly, high-pH RP is often used as prior fractionation method even though it is not truly orthogonal to standard RP (low pH). Importantly, there is no universal best prefractionation method. Rather, the optimal separation method needs to be chosen based on the analytes.^9,10

While fractionation methods offer great possibilities to reduce the sample complexity, they usually require larger sample amounts and preparation time. Usually, most fractions are injected separately without pooling. Therefore, the peptide identification is fraction aware. This extra piece of information can be incorporated into the database search.¹¹⁻¹³ To fully utilize this information, a computational model needs to be developed that can confidently predict the retention time of a peptide based on its amino acid sequence. The proteomics community has successfully developed accurate models for the prediction of the retention time in low pH RP-LC, which typically is coupled directly to a mass spectrometer and therefore widely applied in proteomics.^14,15 Retention times have also been predicted for other chromatographic methods including high-pH RP-LC,^16,17 hydrophilic interaction liquid chromatography (HILIC),¹⁸ and strong cation exchange chromatography (SCX).¹⁹ Various algorithms have been applied for the described prediction task: simple linear regression models,²⁰ nonlinear models,²¹ support vector regression models,^11,16 artificial neural networks,²² or a physical model describing the chromatographic process.²³ For a comprehensive review, the reader is referred to Tarasova et al.¹⁴ and Moruz and Käll.¹⁵

For standard shotgun proteomics, hydrophilic strong anion exchange chromatography (hSAX) is largely orthogonal to RP-LC.⁵ Currently, there is no model to predict the retention time for hSAX. Moreover, the sequence specific features that influence the retention behavior of peptides during hSAX are still unknown. A common approach is to incorporate (limited) sequence information into the prediction model by creating position specific retention coefficients¹⁸ or neighboring amino acid effects.²⁴ It would be desirable to (1) better understand the mechanisms governing the retention behavior of peptides during hSAX and (2) build a predictive machine learning model that confidently predicts the retention time of a peptide based on its sequence information.

In this study, we analyzed the chromatographic behavior of 59 297 peptides based on 29 hSAX fractions. We aim to contribute new insights into the interaction of peptides during hSAX and quantify how sequence features affect the retention behavior. To accomplish this, a machine learning workflow is applied and validated using 5-fold cross-validation. We developed a neural network model that predicts the retention time for peptides from an hSAX fractionation. The predictive model and the preprocessing are available in the Python package DePART (https://github.com/Rappsilber-Laboratory/DePART).

Methods

Experimental Details

The experimental data taken for this study were published by Ritorto et al.⁵ In brief, the authors performed hydrophilic strong anion exchange (hSAX) chromatography on macrophage cells from Mus musculus to test the peptide separation capabilities of hSAX followed by mass spectrometry. The tryptic digest of the cell lysate was analyzed with a LTQ Orbitrap Velos Pro (Thermo Fisher Scientific, West Palm Beach, FL). The fractionation was performed using an Ion Pac AS24²⁵ column (2 × 250 mm, 2000 Å pore size, Thermo Fisher Scientific, Part No.: 064153) with a 35 min gradient (0 to 1 M NaCl; solvent A, 20 mM Tris-HCl at pH 8.0; solvent B, 20 mM Tris-HCl at pH 8.0, 1 M NaCl). The functional group of the AS24 is an alkanol quaternary ammonium ion on a solid support that aims at minimal hydrophobicity. Details of the sample preparation protocols can be found in the original manuscript.⁵

Data Processing

For our study, Ritorto et al. made the results of their previous experiments available as MaxQuant result files. We postprocessed the MaxQuant evidence file. In total, 466 495 peptides were identified in 34 fractions. We applied stringent filtering to avoid ambiguity in the training data. This initial set of peptides was reduced by removing contaminants, decoys, “only by site” identifications, and modified peptides (other than carbamidomethylated cysteine). In addition, for peptides identified in two adjacent fractions, the identification with the lowest intensity was removed from the data set. Peptides identified in more than two fractions or in fractions that were not adjacent were also removed from the data. Finally, fractions with less than 300 unique peptide identifications were removed—leaving 59 297 unique peptide sequences distributed over 29 fractions for the data analysis. As an independent data set, we used PXD006188,²⁶ which was analyzed using MaxQuant²⁷ (v. 1.6.1.0) and filtered as described above, resulting in 93 372 peptides being identified in 32 fractions.

All processing was performed using Python 3.5 using the packages numpy, scipy, matplotlib, scikit-learn, pandas, and seaborn.

Machine Learning

For the computational modeling of the retention time we followed two separate strategies, a regression and a classification approach. In the regression case, a simple linear model (LM) with a length correction parameter (LCP) was used. The Python package pyteomics²⁰ with LCP optimization was used for the LM implementation. In the classification case, a logistic regression (LR) and a feedforward neural network (FNN) were used. In both cases, we evaluated (and trained) the model using the accuracy metric, defined as the proportion of correctly predicted fractions from all predictions. With the LM, such a metric is ill-defined since no discrete fraction is predicted. Therefore, we defined a forced accuracy metric by first rounding the predictions to the nearest integer and then computing the accuracy.

The FNN was implemented using Keras²⁸ with the Theano²⁹ backend. The network architecture consisted of four fully connected layers with 50, 40, 35, and 29 neurons. As final activation, the softmax function was used (Table S4). One strength of the simple additive model is the intuitive interpretation of the learned coefficients: a peptide’s elution time increases (or decreases) by a certain factor based on the amino acid count. For neural networks, with nonlinear activation functions, the interpretation is not as straightforward. Therefore, we added peptide features (e.g., pI or aromaticity) based on the literature^11,30 and our initial exploratory data analysis to increase the predictive power in the classification task. The complete definition of features is available in Table S2.

The evaluation of the prediction performance was based on a 5-fold cross-validation (CV) strategy (including 75% of the data, 44 471 peptides). In addition, a hold-out validation set was used for the final model assessment (25% of the data, 14 825 peptides). In the CV setup, the training splits had 35 578 observations, and the validation splits had 8894 observations. We describe the machine learning workflow in more detail in the Supporting Information, including a performance comparison with other classifiers.

Results

In the following section, we present our results and propose a model for the driving interactions in hydrophilic strong anion exchange chromatography (hSAX) for peptides. The result section is divided into four parts: (1) A general overview is given of the data and how the retention time during prefractionation is influenced by charged amino acids. (2) The influence of the charged amino acids is compared. (3) The influence of usually noncharged amino acids is compared, and finally, (4) a machine learning model is built to model peptide retention during hSAX.

Peptide Retention in hSAX Is Driven by the Charged Amino Acids

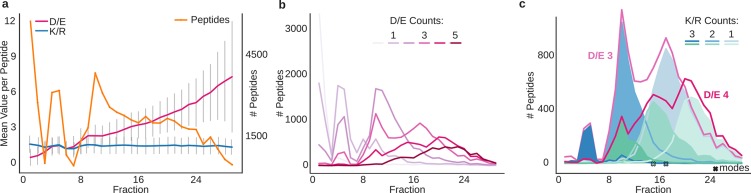
We first investigated the influence of acidic (E, D) and basic (K, R) amino acids on the retention behavior of peptides in an hSAX fractionation experiment. Note that histidine residues will be uncharged under the pH conditions used during fractionation. We used elution data of 59 297 tryptic peptides from murine macrophage cells separated into 29 fractions. Positively charged peptides elute early (fractions 1 and 2) and are separated from uncharged peptides (fractions 4 and 5) which in turn are separated from negatively charged peptides (fractions 7–29), where charge was calculated from the residues E, D, K, and R (Figure 1a).

Figure 1.

Effect of the charged residues on peptide retention in hSAX. (a) Mean residue count per peptide for D/E (red) and K/R (blue) over fraction. Error bars denote the standard deviation. Peptide count per fraction is shown in orange (total 59 297 unique peptides). (b) Effect of D/E count (range 0–5) on peptide retention. (c) Extracted chromatogram of peptides with three and four D/E (red). Subpopulations were defined according to the number of K/R residues (one to three, blue tones for peptides with three D/E residues and green tones for peptides with four D/E residues). Crosses mark the mode of the respective distributions.

While the mean count of D or E (D/E) residues in a peptide increases with the fraction number, the mean count of K/R residues stays constant (Figure 1a). In agreement with this, missed cleavages are not enriched in any of the fractions (Figure S1). The average retention behavior of tryptic peptides appears to be mainly influenced by the occurrences of D/E residues in the peptide sequence. These observations are also supported numerically by their Pearson correlation coefficients (PCC) of the summed residue charge per peptide and the observed fraction number: for D/E residues, the PCC is −0.75; for K/R, −0.03; and for D/E/K/R residues, the PCC is −0.83. The peptide length on the other hand has a much smaller overall influence across all fractions (PCC 0.33). Peptides with 0, 1, 2, 3, 4, and 5 D/E residues correspond on average to the fractions 3, 6, 10, 14, 18, and 20, respectively (Table S1), thus, leading to a mean increase per D/E residue of three fractions in retention time.

Even though the mean increase of fraction numbers highly correlates with the number of acidic residues, so does the D/E peak width (Figure 1b). In addition, the higher the number of D/E residues in the peptide, the more complex the distributions appear. Peptides with two D/E residues distribute on two peak fractions, while peptides with four D/E residues distribute on four to six peak fractions.

Therefore, we investigated the influence of basic residues on the retention time. Positively charged residues, lysine and arginine, should weaken peptide retention during hSAX. Indeed, K and R residues explain the multiple peak fractions of peptides with one D/E (Figure 1c). With an increasing number of K/R residues, the retaining effect of D/E diminishes, and thus peptides elute earlier. Since the effect is quite strong, in terms of retention shift by a single K/R residue, there is most likely a repulsion mechanism involved. Interestingly, the elution strength of K/R residues seems slightly stronger than the retaining effect of D/E residues: The mean fraction value of peptides with four D/E residues and two K/R residues (summed residue charges equal to 2) is 16.5, while for peptides with three D/E residues and one K/R (summed residue charge also equal to 2), the mean fraction is 18.1. However, this additional information on the K/R distribution does not fully explain the observed substructures; there are clearly peak tails visible, especially on the right side of the distributions (e.g., D/E, 4; K/R, 3 in Figure 1c).

Lysine Exhibits Stronger Electrostatic Repulsion than Arginine

We next evaluated if R and K differed in their effect on peptide retention (Figure 2a). Peptides with four D/E residues were found in the factions 22, 17, and 11 (median fraction values) if they had one, two, or three arginines while they were found in the fractions 21, 15, and 10 if they had one, two, or three lysines. This means that lysines are more strongly repelled than arginines in hSAX (on average, 1.3 fractions). Statistical analysis using a Mann–Whitney–U (MWU) test supports this observation. However, since the observed effect size is rather small, the statistical significance should be interpreted with caution (Figure S2a).

Figure 2.

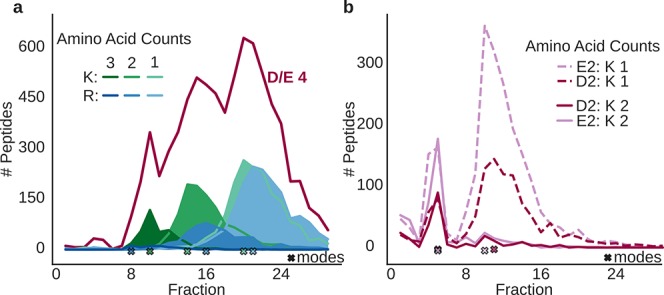
Detailed comparison of relative contributions of positively (K/R) and negatively (D/E) charged residues on peptide retention in hSAX. (a) Effect size of K/R residues. Peptides with four D/E residues were divided according to their K and R count (K, green tones; R, blue tones). (b) Effect size of E/D residues. Peptides with either two E or two D residues are shown, split according to their number of K residues (1 or 2).

Similarly, we investigated possible differences between aspartate and glutamate, peptides with either two D or two E residues and either one, two, or three lysines (Figure 2b shows data for up to two lysines). For this subset, the rounded median fraction number for peptides with two D or two E residues is 12, 11, and 5 and 12, 11, and 5, respectively. This leads to an average increase of 0.33 per fraction if there is an aspartate instead of a glutamate in the peptide sequence. For the negatively charged amino acids, we also conducted an MWU-test: although the observable effect was even smaller, the test still resulted in a significant difference between the retention behavior of D and E (Figure S2b).

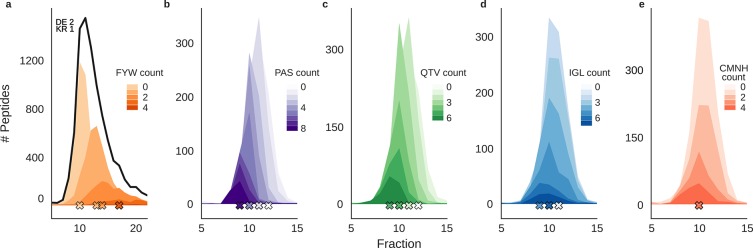
Aromatic Amino Acids Play a Key Role in Peptide Retention during hSAX

As expected, peptide retention during hSAX is dominated by charged residues. However, peptides with one set of charged residues elute over many fractions. Therefore, charged amino acids do not suffice to explain peptide retention alone.

As a first step to search for additional contributions, a subset of peptides was selected (two D/E residues, one R/K residue). Then, the effect size of an amino acid on the retention time was estimated using the slope from a linear regression model. The response variable was set to the mean composition contribution of an amino acid, while the explanatory variable was set to the fraction number. On the basis of the regression slope and the derived p-value (under the null hypothesis that the slope is equal to zero), the remaining amino acids can be divided into three categories: (1) retaining—if the slope is positive and the p-value is smaller than 0.05, (2) eluting—if the slope is negative and the p-value is smaller than 0.05, and (3) no (significant) effect—if the p-value is larger than 0.05. Accordingly, the (aromatic) amino acids F, Y, and W show the strongest retaining effect based on the regression slope (Figure 3, Figure S4). Interestingly, peptides with 0 aromatic residues are found in a sharp symmetrical distribution. With increasing aromatic amino acids in the peptide sequence, the distributions shift to later retention, become broader, and develop a right tail (Figure S6). In contrast, the amino acid contributions of A, P, and S and Q, T, and V show an eluting effect. For these amino acids, the subpopulation peaks look very sharp, even with increasing residues of the same group. The remaining amino acids C, I, N, G, L, V, H, and M do not show a clear trend and thus could be classified neither as eluting nor as retaining. Subtracting the weighted counts of the aromatic residues (0.8W + 0.6Y + 0.3F) to the residue charge increases the initial PCC from −0.83 to −0.86. Adding the weighted counts of the residues A, P, Q, S, T, and V (factor 0.1) further increases the retention PCC to −0.88.

Figure 3.

The effect of neutral amino acids on peptide retention in hSAX. Amino acids were grouped according to their influence on peptide retention in hSAX by linear regression (Supporting Information). (a) Elution behavior of peptides with different numbers of F/Y/W and two D/E, one K/R residues. (b–e) Elution behavior of peptides with different numbers of the indicated amino acids (b, P/A/S; c, Q/T/V; d, I/G/L; e, C/M/N/H) and two D/E, one K/R, zero F/Y/W. Crosses mark the mode of the subpopulations.

A Neural Network Achieves the Highest Prediction Accuracy

As the final step in our analysis, we built a machine learning model to predict the retention time of a peptide based on its sequence features. After initial hyperparameter optimization for a set of classifiers and regressors (Supporting Information S3), we chose a linear regression model (LM), a logistic regression model (LR), and a feedforward neural network (FNN) for further analysis. The coefficients of the LM are shown in Figure 4a. As expected, the sign and magnitude of the coefficients largely match our manual analysis: First, the basic residues have a strong eluting effect on the retention time (large negative coefficient). Second, the acidic residues and the aromatic residues have a strong retaining effect on the retention time (large positive coefficient). In addition, the nuances regarding the effect size of the basic residues also fit our previous description that R is marginally stronger repelled than K. This is most likely due to the lower basicity of K. Similar to the coefficient representation from LM, FNNs can be used to estimate approximately the influence of the input features by analyzing the input weights of the first layer. Since we also used position specific features in the machine learning workflow, the average of the input weights can be used to roughly measure these position dependent contributions to the retention in hSAX. Most importantly, it appears that the influence of D/E residues decreases with distance from the termini (Figure S7). Further, S/T/V/A/P/Q residues roughly follow a similar trend. In contrast, W/Y/F/H do not show decreasing weights for internal residues—the influence is rather stable across the positions. For the remaining amino acids (I/G/L/C/M/N), the weights are noisy and do not follow a clear pattern. This observation fits the estimation of their influence from the regression model. Therefore, the influence of these amino acids cannot be clearly defined.

Figure 4.

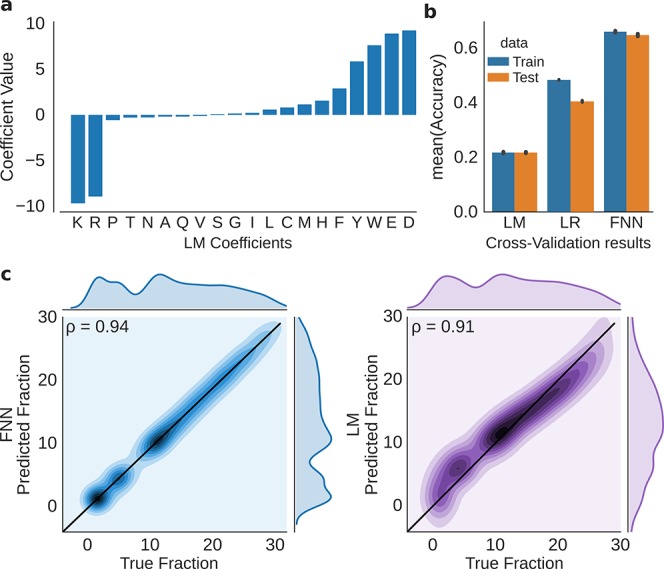
Peptide retention time prediction for hSAX using machine learning. (a) Residue retention coefficients from a linear model with length correction parameter. (b) Fraction of correct predictions (accuracy) of different prediction methods, estimated by 5-fold cross-validation based on 35 578 (train) and 8894 (test) peptides in each split. (c) Elution time prediction for the hold-out validation set, FNN classifier (left) and LM (right); ρ indicates the Pearson correlation. Linear Model (LM), Logistic Regression (LR), Feedforward Neural Network (FNN).

A neural network was most successful in predicting the correct peptide fraction, as assessed by 5-fold cross-validation (Figure 4b). With an accuracy of 70 ± 0.81% (mean ± standard error of the mean), the classification algorithm outperformed the linear regression model (22 ± 0.13% accuracy) and the logistic regression model (48 ± 0.07% accuracy). With a lower prediction resolution, e.g., evaluating the accuracy in a window of ±1 fraction (1-off-accuracy), 92 ± 0.19% were correctly classified. Although optimization aimed for accuracy, the best performing FNN classifier also achieves a higher correlation coefficient on a hold-out validation set (never used for training) than the LM. The FNN achieves here a PCC of 0.94 where the LM achieves a PCC of 0.9 (Figure 4c). The accuracy on this validation set was comparable to the CV error with 68% accuracy and 92% one-off accuracy. As the accuracy metric already indicates, the LM performs much worse as seen in the marginal distributions (Figure 4c). The distribution of the predicted fractions does not appear similar to the observed fraction distribution. The FNN can better capture the nonlinear relationship and thus predicts the true fraction with a higher accuracy—which is supported by the similarity of the marginal distributions of the predicted and true fractions of the peptides in the validation set.

Finally, we wondered if the results obtained for data by Ritorto et al. would also be obtained with a different data set by independent investigators. We downloaded an hSAX data set from ProteomeXchange (PXD00618826) and repeated our analysis. For these data, the training set comprised 70 029 unique peptides and the validation set, 23 343 unique peptides. The accuracy during CV increased on the test data to 69 ± 0.21% and on the validation data to 72%. The one-off accuracy even increased to 96%, most likely due to higher number of training instances.

Discussion

Fractionation methods such as ion exchange chromatography (IEX) are popular tools for enrichment of certain analytes and separation of complex samples. To perfect the separation process, a basic understanding of the underlying principles must be developed. For the principles behind the retention time of peptides in hSAX chromatography, a linear model is a useful starting point.

Our exploratory analysis as well as the modeling approach showed that electrostatic forces, as expected, are the most important interactions in hSAX. A previous study that compared several fractionation methods for phosphopeptides also reported a strong correlation of the acidic amino acids with the elution time of peptides.⁹ The resolution based on simply counting the D/E/R/K residues is enough to roughly map the elution time of a peptide to ±5 fractions (on average). This simple approach is supported by a good PCC (−0.83) of the summed residue charge and the elution time. However, differentiating the repelling (K/R) and retaining (D/E) effect sizes should further improve the resolution. Additional improvements can be achieved by including the influence of the aromatic amino acids (W, Y, F; PCC −0.86).

The retaining effect of the aromatic amino acids could be explained through cation−π interactions: a well-known interaction from organic chemistry. Since aromatic amino acids have a delocalized π electron system, the flat face of the aromatic ring has a partial negative charge which attracts cations and thus enables strong electrostatic interactions.^31,32 Cation−π interactions are also essential for many biological processes and protein folding, in which K/R residues can also function as cations and thus reinforce bonds within a protein structure. Possibly, cation−π interactions also happen within a single peptide and therefore lead to a competition between the stationary phase and the side chains of K/R. Multiple aromatic amino acids in a peptide sequence lead to nonlinearity in the retention behavior, i.e., multiple aromatic amino acids support the interactions with the stationary phase more than expected from adding individual contributions, possibly by forming sandwich complexes of two aromatic amino acids and a cation.

For tryptic phosphopeptides, it has been shown that the peptide C-terminus is likely oriented toward the stationary phase³³ during the separation in anion exchange chromatography. Presumably, this also holds true for peptides in hSAX. However, comparing the neural network weights revealed that the influence of, e.g., D or E residue is not per se decreasing from the N-terminus to the C-terminus as has been observed for the SCX model.³³ Thus, it is possible that the peptide orientation in hSAX is bidirectional—or that D/E residues show a different elution behavior when near the termini. If the orientation of the peptide is indeed with the N-terminus toward the stationary phase, the decrease of the neural network weights is explainable with the limited accessibility of the acidic side chains when the residue is buried in the sequence. The same argumentation holds true for the orientation of the N-terminus toward the stationary phase. However, since we only analyzed tryptic peptides with basic side chains on the C-terminus, it seems unlikely that they would prefer this orientation. Another hypothesis is that the influence of C-terminal D/E residues is not directly through the interaction of the residues with the column but through intrapeptide interactions. For example, acidic side chains of D/E and basic side chains of K/R could form salt bridges. Thus, the closer the D/E residues are to the C-terminus, the larger is the contribution or effect in the determination of the retention time.

The retention time prediction field is fairly mature, and a selection of published tools achieved an R² ≥ 0.90, according to a recent literature review.¹⁴ While most solutions achieve a very high correlation (and R²), the true accuracy (defined as true predictions/(true + false predictions)) is seldom evaluated. The models used to predict the fraction either do not provide an easily accessible probability or prefer to model the prediction task as a regression problem¹⁹ allowing R² to be calculated. We modeled the prediction in a classification setup, using a feed-forward neural network (FNN). Here, accuracy is an appropriate evaluation metric. Accuracy is used to evaluate classification problems, and the algorithm was trained to optimize the accuracy and not R². With the current implementation, the FNN achieved an accuracy of 70 ± 0.81% during CV and 68% on the hold-out validation set. The accuracy is a stricter metric than the correlation coefficient or R²; the one-off accuracy increases on the CV data set to 92 ± 0.19% and on the hold-out validation data set to 92%. One additional advantage of the FNN is that each prediction is associated with a probability. This is a useful feature since it allows selection of more confident predictions or incorporation of the uncertainty in postprocessing.

Conclusion

We presented a first description of the parameters that influence the retention of peptides during hSAX chromatography. As expected, the charged amino acids largely define the retention behavior of tryptic peptides. However, the aromatic amino acids also have a large impact on the retention behavior presumably through cation−π interactions, which makes the retention mechanism of hydrophilic anion exchange chromatography more challenging to describe. Nevertheless, the proposed neural network model achieves a high accuracy of 68% on the hold-out validation set paired with a high correlation value of 0.94—which enables the usage of our model for statistical modeling of the confidence of peptide identifications based on prefractionation. In the future, we want to further improve our model with more training data, support for post-translational modifications, and incorporation into a robust scoring metric for peptide identification.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.analchem.7b05157.

• Missed cleavage data, statistical comparison of the effect size of K/R and D/E residues, amino acid classification and details on the machine learning workflow (PDF)

The authors declare no competing financial interest.