Hierarchical Region-Network Sparsity for High-Dimensional Inference in Brain Imaging

Abstract

Structured sparsity penalization has recently improved statistical models applied to high-dimensional data in various domains. As an extension to medical imaging, the present work incorporates priors on network hierarchies of brain regions into logistic-regression to distinguish neural activity effects. These priors bridge two separately studied levels of brain architecture: functional segregation into regions and functional integration by networks. Hierarchical region-network priors are shown to better classify and recover 18 psychological tasks than other sparse estimators. Varying the relative importance of region and network structure within the hierarchical tree penalty captured complementary aspects of the neural activity patterns. Local and global priors of neurobiological knowledge are thus demonstrated to offer advantages in generalization performance, sample complexity, and domain interpretability.

1 Introduction

Many quantitative scientific domains underwent a recent shift from the classical “long data” regime to the high-dimensional “wide data” regime. In the brain imaging domain, many contemporary technologies for acquiring brain signals yield many more variables per observation than total observations per data sample. This n ≪ p scenario challenges various statistical methods from classical statistics. For instance, estimating generalized linear models without additional assumptions yields an underdetermined system of equations. Many such ill-posed estimation problems have benefited from sparsity assumptions [3]. Those act as regularizer by encouraging zero coefficients in model selection. Sparse supervised and unsupervised learning algorithms have proven to yield statistical relationships that can be readily estimated, reproduced, and interpreted. Moreover, structured sparsity can impose domain knowledge on the statistical estimation, thus shrinking and selecting variables guided by expected data distributions [3]. These restrictions to model complexity are an attractive plan of attack for the >100,000 variables per brain map. Yet, what neurobiological structure best lends itself to exploitation using structured sparsity priors?

Neuroscientific concepts on brain organization were long torn between the two extremes functional specialization and functional integration. Functional specialization emphasizes that microscopically distinguishable brain regions are solving distinct computational problems [14]. Conversely, functional integration emphasizes that neural computation is enabled by a complex interplay between these distinct brain regions [19]. However, local neuronal populations and global connectivity profiles are thought to go hand-in-hand to realize neural processes. Yet, probably no existing brain analysis method acknowledges that both functional design principles are inextricably involved in realizing mental operations.

Functional specialization has long been explored and interpreted. Single-cell recordings and microscopic tissue examination revealed the segregation of the occipital visual cortex into V1, V2, V3, V3A/B, and V4 regions [22]. Tissue lesion of the mid-fusiform gyrus of the visual system was frequently reported to impair recognition of others’ identity from faces [11]. As a crucial common point, these and other methods yield neuroscientific findings naturally interpreted according to non-overlapping, discrete region compartments as the basic architecture of brain organization. More recently, the interpretational focus has shifted from circumscribed regions to network stratifications in neuroscience. Besides analyses of electrophysiological oscillations and graph-theoretical properties, studies of functional connectivity correlation and independent component analysis (ICA) became the workhorses of network discovery in neuroimaging [6]. As a common point of these other methods, neuroscientific findings are naturally interpreted as cross-regional integration by overlapping network compartments as the basic architecture of brain organization, in contrast to methods examining regional specialization.

Building on these two interpretational traditions in neuroscience, the present study incorporates neurobiological structure underlying functional segregation and integration into supervised estimators by hierarchical structured sparsity. Every variable carrying brain signals will be a-priori assigned to both region and network compartments to improve high-dimensional model fitting based on existing neurobiological knowledge. Learning algorithms exploiting structured sparsity have recently made much progress in various domains from processing auditory signals, natural images and videos to astrophysics, genetics, and conformational dynamics of protein complexes. The hierarchical tree penalties recently suggested for imaging neuroscience [12] will be extended to introduce neurobiologically plausible region and network priors to design neuroscience-specific classifiers. Based on the currently largest public neuroimaging repository (Human Connectome Project [HCP]) and widely used region [8] and network [18] atlases, we demonstrate that domain-informed supervised models gracefully tackle the curse of dimensionality, yield more human-interpretable results, and generalize better to new samples than domain-naive black-box estimators.

2 Methods

This paper contributes a neuroscience adaptation of hierarchical structured tree penalties to jointly incorporate region specialization and network integration priors into high-dimensional prediction. We capitalize on hierarchical group lasso to create a new class of convex sparse penalty terms. These conjointly acknowledge local specialization and global integration when discriminating defined psychological tasks from neural activity maps. Rather than inferring brain activity from psychological tasks by independent comparisons of task pairs, this approach simultaneously infers a set of psychological tasks from brain activity maps in a multivariate setting and allows for prediction in unseen neuroimaging data.

2.1 Rationale

3D brain maps acquired by neuroimaging scanners are high-dimensional but, luckily, the measured signal is also highly structured. Its explicit dimensionality, the number of brain voxels, typically exceeds 100,000 variables, while the number of samples rarely exceeds few hundreds. This n ≪ p scenario directly implies underdetermination of any linear model based on dot products with the voxel values. However, the effective dimensionality of functional brain scans has been shown to be much lower [7]. Two types of low-dimensional neighborhoods will be exploited by injecting accepted knowledge of regional specialization (i.e., region priors) and spatiotemporal interactions (i.e., network priors) into statistical estimation.

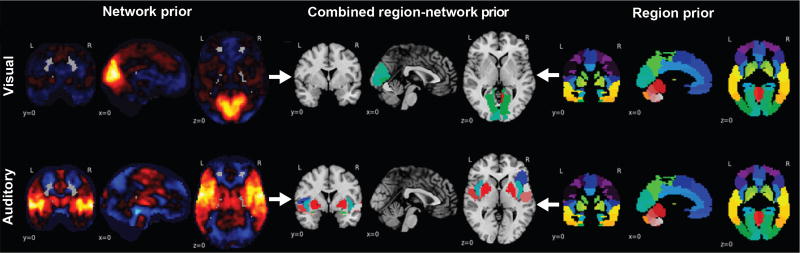
Major brain networks emerge in human individuals before birth [9]. Their nodes have more similar functional profiles than nodes from different networks [2]. As a popular method for network extraction, ICA [6] yields continuous brain maps with voxel-level resolution. The region nodes of ICA network are spatially disjoint sets of voxel groups that agree with boundaries of brain atlases. Hence, each region from a brain atlas can be uniquely associated with one of the extracted ICA networks. Here, previously published network definitions obtained using ICA [18] and region definitions obtained from spatially constrained clustering [8] allowed constructing a hierarchy of global ICA networks with their assigned local cluster regions (Figure 1). The ensuing network-region tree was used as a frequentist prior of expected weight distributions to advantageously bias supervised model fitting.

Fig. 1. Building blocks of the hierarchical region-network tree.

Displays the a-priori neurobiological knowledge introduced into the classification problem by hierarchical structured sparsity. Left: Continuous, partially overlapping brain network priors (hot-colored, network atlas taken from [18]) accommodate the functional integration perspective of brain organization. Right: Discrete, non-overlapping brain region priors (single-colored, region atlas taken from [8]) accommodate the functional segregation perspective. Middle: These two types of predefined voxel groups are incorporated into a joint hierarchical prior of parent networks with their descending region child nodes. Top to bottom: Two exemplary region-network priors are shown, including the early cortices that process visual and sound information from the environment.

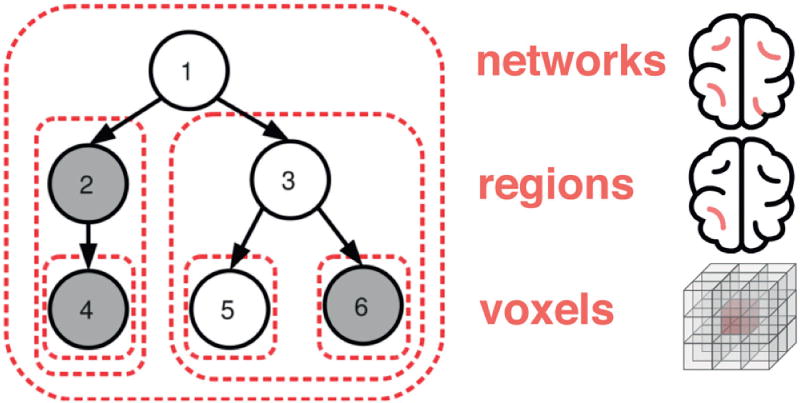
Specifically, this tree structure was plugged into hierarchical sparsity penalty terms [12]. It extends the group lasso [21] by permitting variable groups that contain each other in a nested tree structure. The first hierarchical level are the network groups with all the voxels of the brain regions associated with them. Each network node in turn descends into a second hierarchical level with brain regions of neighboring voxels (Figure 2). Induced by the region-network sparsity tree, a child node enters the set of relevant voxel variables only if its parent node has been selected [3]. Conversely, if a parent node is deselected, also the voxel variables of all child nodes are deselected. Moreover, the coefficients of all region or all network groups can be weighed individually. Trading off the voxel penalties of the network level against the voxel penalties of the region level we can design distinct estimation regimes.

Fig. 2. Hierarchical Tree Prior.

2.2 Problem formulation

We formulate our estimation problem in the framework of regularized empirical risk minimization applied to linear models. The goal is to estimate a good predictor of psychological tasks given a single brain image. Let the set X ∈ ℝ^n×p represent brain images of p > 0 voxels. We then minimize the risk ℒ(ŷ, y) with ŷ = f(Xŵ + b̂), where f is a link function (e.g., sigmoid for logistic regression, identity for linear regression), and ℒ usually represents an appropriate negative loglikelihood. We incorporate an informative prior through regularization:

$$\hat{\mathbf{w}},\hat{\mathbf{b}}={\text{argmin}}_{w,b}ℒ(f(\mathbf{\text{Xw}}+\mathbf{b}),y)+\lambda \Omega (\mathbf{w}),$$

where λ > 0 and Ω is the regularizer. Brain regions are defined as disjoint groups of voxels. Let 𝒢 be a partition of {1, …, p}, i.e.

$$\underset{i}{\cup }{g}_i=\{1,\dots ,p\}\text{ and }{g}_i\cap g_i=\varnothing \forall i\ne j$$

Brain networks consist of one or several brain regions. The set of brain networks ℋ also forms a partition of {1, …, p} that is consistent with 𝒢 in the sense that

$$\forall g\in 𝒢,h\in \mathscr{H},\text{either }g\subset h\text{ or }g\cap h=\varnothing .$$

This allows for an unambiguous assignment of each region g ∈ 𝒢 to one network h ∈ ℋ and thus generates a tree structure. A root node is added to contain all voxels. For a brain image w ∈ ℝ^p and a group g, the vector w_g ∈ ℝ^|g| is defined as the restriction of w to the coordinates in g. The penalty structured by network and region information can then be written as

$$\Omega (\mathbf{w})=\alpha \sum _{h\in \mathscr{H}}{\eta }_h{\Vert {\mathbf{w}}_h\Vert }_2+\beta \sum _{g\in 𝒢}{\eta }_g{\Vert {\mathbf{w}}_g\Vert }_2.$$

As originally recommended [21], we set ${\eta }_g=1/\sqrt{|g|}$ to account for discrepancy in group sizes. The hierarchy-level-specific factors α > 0 and β > 0 can tradeoff region-weighted and network-weighted models against each other. Decreasing α leads to less penalization of brain networks and thus the tendency for fully active groups and dense brain maps. If at the same time β is increased to induce group sparsity, then only the structure of brain regions encoded by 𝒢 is acknowledged. Conversely, if β is chosen sufficiently small and α increased, the detected structure will derive from ℋ, leading to the selection of brain networks rather than regions.

Please note that the above tradeoff enables predominance attributed to either brain regions or networks, although the penalty structure remains hierarchical. If the network penalty layer sets a network group to zero, then all the contained region groups are forced to have activity zero. Conversely, if a brain region has non-zero coefficients, then necessarily the network containing it must be active. This relation is asymmetric, the roles of 𝒢 and ℋ cannot be swapped: A brain region can set all its coefficients to zero without forcing the corresponding network to zero. A brain network can be active without its subregions being active. When evaluating the tradeoff in (α, β), this needs to be taken into account.

The prediction problem at hand is a multiclass classification. We choose to attack this using one-versus-rest scheme on a binary logistic regression. The one-versus-rest classification strategy is chosen to obtain one weight map per class for display and model diagnostics. Its loss can be written as

$$\sum _{i=1}^n\text{log}(1+\text{exp}(-y_i\langle x_i,\mathbf{w}\rangle ))+\lambda \Omega (\mathbf{w}),$$

if y ∈ {−1, 1} and with x_i ∈ ℝ^p the training sample brain images. We optimize parameters w using an iterative forward-backward scheme analogous to the FISTA solver for the lasso [5].

2.3 Hyperparameter optimization

Stratified and shuffled training sets were repeatedly and randomly drawn from the whole dataset with preserved class balance and submitted to a nested cross-validation (CV) scheme for model selection and model assessment. In the inner CV layer, the logistic regression estimators have been trained in a one-versus-rest design that distinguishes each class from the respective 17 other classes (number of maximal iterations=100, tolerance=0.001). In the outer CV layer, grid search selected among candidates for the respective λ parameter by searching between 10⁻² and 10¹ in 9 steps on a logarithmic scale. Importantly, the thus selected sparse logistic regression classifier was evaluated on an identical test set in all analysis settings.

2.4 Implementation

All experiments were performed in Python. We used nilearn to process and resphape the extensive neuroimaging data [1], scikit-learn to design machine-learning data processing pipelines [16], and SPAMs for numerically optimized implementations of the sparse learners (http://spams-devel.gforge.inria.fr/). All Python scripts that generated the results are accessible online for reproducibility and reuse (http://github.com/banilo/ipmi2017).

2.5 Data

As the currently biggest open-access dataset in brain imaging, we chose brain data from the HCP [4]. Neuroimaging data with labels of ongoing psychological processes were drawn from 500 healthy HCP participants. 18 HCP tasks were selected that are known to elicit reliable neural activity across participants. The HCP data incorporated n = 8650 first-level activity maps from 18 diverse paradigms in a common 60 × 72 × 60 space of 3mm isotropic gray-matter voxels. Hence, the present analyses were based on task-labeled HCP maps of neural activity with p = 79,941 z-scored voxels.

3 Experimental Results

3.1 Benchmarking hierarchical tree sparsity against common sparse estimators

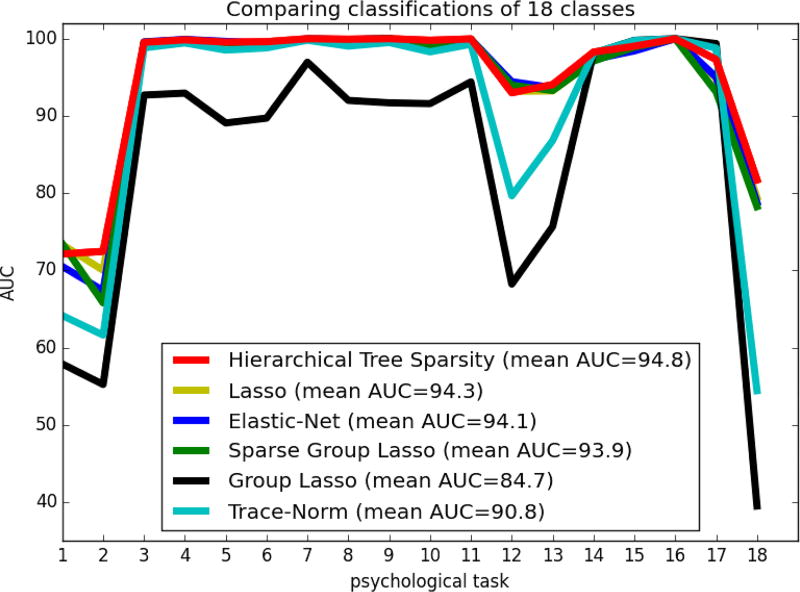
Hierarchical region-network priors have been systematically evaluated against other popular choices of sparse classification algorithms in an 18-class scenario (Figure 2.3). Logistic regression with ℓ₁/ℓ₂-block-norm penalization incorporated a hierarchy of previously known region and network neighborhoods for a neurobiological bias of the statistical estimation (α = 1, β = 1). Vanilla logistic regression with ℓ₁-penalization and ℓ₁–ℓ₂-elastic-net penalization do not assume any previously known special structure. These classification estimators embrace a vision of neural activity structure that expects a minimum of topographically and functionally independent brain voxels to be relevant. Logistic regression with (sparse) group sparsity imposes a structured ℓ₁/ℓ₂-block norm (with additional ℓ₁ term) with a known region atlas of voxel groups onto the statistical estimation process. These supervised estimators shrink and select the coefficients of topographically compact voxel groups expected to be relevant in unison. Logistic regression with trace-norm penalization imposed low-rank structure [10]. This supervised classification algorithm expected a minimum of unknown “network” patterns to be relevant.

Fig. 3. Prediction performance across sparsity priors.

Comparing the performance of logistic regression estimators with 6 different structured and unstructered sparse regularization penalties (colors) in classifying neural activity from 18 psychological tasks. The area under the curve (AUC) is provided on an identical test set as class-wise measure (y-axis) and across-class mean (legend). Simultaneous knowledge of both region and network neighborhoods was hence most beneficial for predicting tasks from neural activity.

Across experiments with Stratified and shuffled cross-validation (90%/10% train/test set) across pooled participant data, hierarchial tree sparsity was most successful in distinguishing unseen neural activity maps from 18 psychological tasks (89.7% multi-class accuracy, mean AUC 0.948 [+/− 0.091 standard deviation] mean precision 0.87, mean recall 0.92). It was closely followed by logistic regression structured by trace-norm regularization (89.4%, mean AUC 0.908 [+/− 0.148], precision 0.86, recall 0.91). Lasso featured an average performance comparing to the other sparse estimators (88.6%, mean AUC 0.943 [+/− 0.093], precision 0.86, recall 0.90). Elastic-Net, in turn, featured an average performance comparing to the other sparse estimators (88.1%, mean AUC 0.941 [+/− 0.102], precision 0.85, recall 0.84). Introducing a-priori knowledge of brain region compartments by sparse group sparsity (87.9%, mean AUC 0.939 [+/− 0.101], precision 0.85, recall 0.90) and by group sparsity (87.9%, mean AUC 0.847 [+/− 0.173], precision 0.85, recall 0.90) performed worst.

In an important subanalysis, the advantage of the combined region-network prior was confirmed by selectively zeroing either the η_g coefficients of all region groups or the η_h coefficients of all network groups in the hierarchical prior. Removing region structure from the sparsity penalty achieved 88.8% accuracy, while removing network structure from the sparsity penalty achieved 87.1% accuracy. These results from priors with impoverished a-priori structure were indeed outperformed by the full region-network tree prior at 89.7% out-of-sample accuracy.

In sum, driving sparse model selection by domain knowledge of region-network hierarchies outcompeted all other frequently used sparse penalization techniques for high-dimensional data.

3.2 Sample complexity of naive versus informed sparse model selection

Subsequently, the sample complexity of ℓ₁-penalized and hierarchical-tree-penalized logistic regression (α = 1, β = 1) was empirically evaluated and quantitatively compared (Figure 4). Region-network priors should constrain model selection towards more neurobiologically plausible classification estimators. This should yield better out-of-sample generalization and support recovery than neurobiologynaive ℓ₁-constrained logistic regression in the data-scarce and data-rich scenarios. The HCP data with examples from 18 psychological tasks were first divided into 90% of training set (i.e., 7584 neural activity maps) and 10% of test set (i.e., 842 maps). Both learning algorithms were fitted based on the training set at different subsampling fractions: 20% (1516 neural activity maps), 40% (3033 maps), 60% (4550 maps), 80% (6067 maps), and 100% (7584 maps).

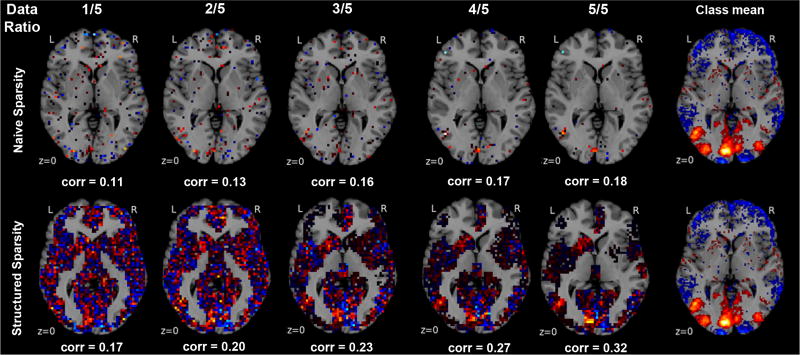
Fig. 4. Sample complexity in naive versus informed sparse model selection.

Ordinary ℓ₁-penalized logistic regression (upper row) is compared to hierarchical-tree-penalized logistic regression (α = 1, β = 1, lower row) with increasing fraction of the available training data to be fitted (left to right columns). For one example (i.e., “View tools”) from 18 psychological tasks, unthresholded axial maps of recovered model weights are are quanitatively compared against the sample average of that class (right-most column, thresholded at the 75^th percentile). This notion of weight recovery was computed by Pearson correlation (corr). In the data-scarce scenario, ubiquitous in brain imaging field, hierarchical tree sparsity achieves much better support recovery. In the data-rich scenario, neurobiologically informed logistic regression profits more from the available information quantities than neurobiologically naive logistic regression.

Regarding classification performance on the identical test set, ℓ₁-penalized versus hierarchical-tree-penalized logistic regression achieved 83.6% versus 88.7% (20% of training data), 85.0% versus 89.2% (40%), 86.8% versus 89.8% (60%), 88.9% versus 90.3% (80%), 88.6% versus 89.7% (100%) accuracy. Regarding model sparsity, the measure $s=\frac{{\Vert w\Vert }_1}{{\Vert w\Vert }_F}$ was computed from the model weights w of both penalized estimators for each of the 18 classes. The ℓ₁-penalized logistic regression yielded the mean sparsities 50.0, 45.4, 40.0, 30.9, and 24.0 after model fitting with 20% to 100% training data. The hierarchical-tree-penalized logistic regression yield the sparsities 163.2, 160.2, 132.1, 116.2, and 88.4 after fitting 20% to 100% of the training data. To quantitative a measure of support recovery, we computed Pearson correlation r between vectors of the z-scored model coefficients and the z-scored across-participant average maps for each class. ℓ₁-penalized versus hierarchical-tree-penalized logistic regression achieved a mean correlation r of 0.10 versus 0.13, 0.11 versus 0.13, 0.13 versus 0.17, 0.16 versus 0.22, and 0.19 versus 0.29 across classes based on 20% to 100% training data. Finally, regarding model variance, we quantified the agreement between ℓ₁-penalized versus hierarchical-tree-penalized model weights after fitting on 5 different 20%-subsamples of the training data. For each classifier, the absolute model weights were concatenated for all 18 classes, thresholded at 0.0001 to binarize variable selection, and mutual information was computed on all pairs of the 5 trained models. This agreement metric of model selection across fold pairs yielded the means 0.001 (ℓ₁) versus 0.506 (hierarchical tree).

Three observations have been made. First, in the data-scarce scenario (i.e., 1/5 of available training data), hierarchical tree sparsity achieved the biggest advantage in out-of-sample performance by 5.1% as well as better support recovery with weight maps already much closer to the respective class averages [20]. In the case of scarce training data, which is typical for the brain imaging domain, regularization by region-network priors thus allowed for more effective extraction of classification-relevant structure from the neural activity maps. Second, across training data fractions, the weight maps from ordinary logistic regression exhibited higher variance and more zero coefficients than hierarchical tree logistic regression. Given the usually high multicollinearity in neuroimaging data, this observation is likely to reflect instable selection of representative voxels among class-responsive groups due to the ℓ₁-norm penalization. Third, in the data-rich scenario (i.e., entire training data used for model fitting), neurobiologically informed logistic regression profited much more from the increased information quantities than neurobiologically naive logistic regression. That is, the region-network priors actually further enhanced the support recovery in abundant input data. This was the case although the maximal classification performance of ≈90% has already been reached with small training data fractions by the structured estimator. In contrast, the unstructured estimator approached this generalization performance only with bigger input data quantities.

3.3 Support recovery as a function of region-network emphasis

Finally, the relative importance of the region and network group penalties within the hierarchical tree prior was quantified (Figure 5). The group weight η_g of region priors was multiplied with a region-network ratio, while the group weight η_h of network priors was divided by that region-network ratio. For instance, a region-network ratio of 3 increased the relative importance of known region structure by multiplying $\beta =\frac{3}{1}$ to η_g of all region group penalties and multiplying $\alpha =\frac{1}{3}$ to η_h of all network group penalties (Table 1).

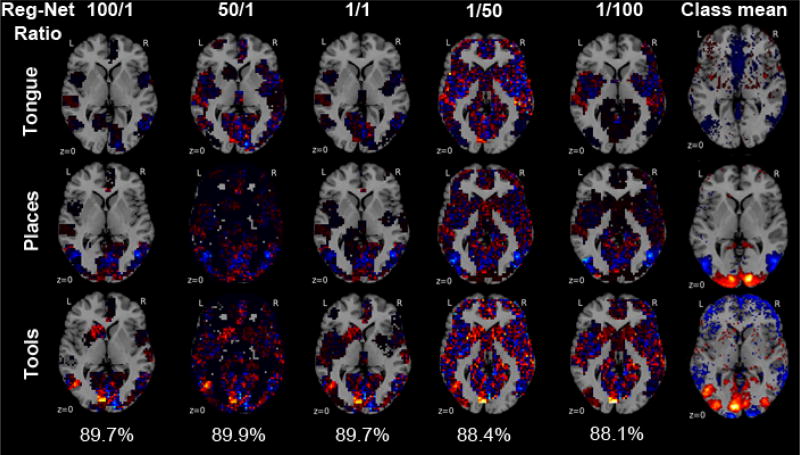
Fig. 5. Support recovery as a function of region and network emphasis.

The relative strength of the region and network priors on the regularization is systematically varied against each other (i.e., α and β are changed reciprocally). Horizontal brain slices are shown with the voxel-wise weights for each class from the fitted predictive model. The region-network ratio (columns) weighted voxel groups to priviledge sparse models in function space that acknowledge known brain region neighborhoods (left columns) or known brain networks neighborhoods (right columns). Among the 18 classes, the model weights are shown for 3 exemplary psychological tasks followed by participants lying in a brain imaging scanner (from top to bottom): tongue movement, viewing locations and tools. The 18-class out-of-sample accuracy bottom and the class-wise mean neural activity (rightmost column, thresholded at the 75^th percentile) are indicated. Different emphasis on regions versus networks in hierarchical structured sparsity can yield very similar out-of-sample generalization. Favoring region versus network structure during model selection recovers complementary, non-identical aspects of the neural activity pattern underlying the psychological tasks.

Table 1.

Out-of-sample performance by region-network emphasis

Reg-Net Ratio	100	50	10	5	2	1	$\frac{1}{2}$	$\frac{1}{5}$	$\frac{1}{10}$	$\frac{1}{50}$	$\frac{1}{100}$
Accuracy [%]	89.7	89.9	90.1	90.5	88.0	89.7	87.8	88.0	87.7	88.4	88.1

As the most important observation, a range between region-dominant and network-dominant structured penalties yielded quantitatively similar generalization to new data but qualitatively different decision functions manifested in the weight maps (Figure 5, second and forth column). Classification models with many zero coefficients but high absolute coefficients in either region compartments or network compartments can similarly extrapolate to unseen neural activity maps. Second, these achieve classification performance comparable to equilibrated region-network priors that set less voxel coefficients to zero and spread the probability mass across the whole brain with lower absolute coefficients (Figure 5, third column in the middle). Third, overly strong emphasis on either level of the hierarchical prior provides the neurobiologically informative results with maps of the most necessary region or network structure for statistically significant generalization (Figure 5, leftmost and rightmost columns). In sum, stratifying the hierarchical tree penalty between region and network emphasis suggests that class-specific region-network tradeoffs enable more performant and more interpretable classification models for neuroimaging analyses [17].

4 Conclusion

Relevant structure in brain recordings has long been investigated according to two separate organizational principles: functional segregation into discrete brain regions [15] and functional integration by interregional brain networks [19]. Both organizational principles are however inextricable because a specialized brain region communicates input and output with other regions and a brain network subserves complex function by orchestrating its region nodes. Hierarchical statistical models hence suggest themselves as an underexploited opportunity for neuroimaging analysis. The present proof-of-concept study demonstrates the simultaneous exploitation of both neurobiological compartments for sparse variable selection and high-dimensional prediction in an extensive reference dataset. Introducing existing domain knowledge into model selection allowed privileging members of the function space that are most neurobiologically plausible. This statistically and neurobiologically desirable simplification is shown to enhance model interpretability and generalization performance.

Our approach has important advantages over previous analysis strategies that rely on dimensionality reduction of the neuroimaging data to tackle the curse of dimensionality. They often resort to preliminary pooling functions based on region atlases or regression against network templates for subsequent supervised learning on the ensuing aggregated features. Such lossy approaches of feature engineering and subsequent inference i) can only satisfy either the specialization or the integration account of brain organization, ii) depend on the ground truth being either a region or network effect, and iii) cannot issue individual coefficients for every voxel of the brain. Hierarchical region-network sparsity addresses these shortcomings by estimating individual voxel contributions while benefitting from their biological multi-level stratification to restrict statistical complexity. Viewed from the bias-variance tradeoff, our modification to logistic regression entailed a large decrease in model variance but only a modest increase in model bias.

In the future, region-network sparsity priors could be incorporated into various pattern-learning methods applied in systems neuroscience. This includes supervised methods for whole-brain classification and regression in single- and multi-task learning settings. The principled regularization scheme could also inform unsupervised structure-discovery by matrix factorization and clustering algorithms [13]. Additionally, hierarchical regularization could be extended from the spatial activity domain to priors of coherent spatiotemporal activity structure. The deterministic choice of a region and network atlas could further be avoided by sparse selection of overcomplete region-network dictionaries. Ultimately, successful high-dimensional inference on brain scans is a prerequisite for predicting diagnosis, disease trajectories, and treatment response in personalized psychiatry and neurology.