A Uniaxial Testing Approach for Consistent Failure in Vascular Tissues

Abstract

Although uniaxial tensile testing is commonly used to evaluate failure properties of vascular tissue, there is no established protocol for specimen shape or gripping method. Large percentages of specimens are reported to fail near the clamp and can potentially confound the studies, or, if discarded will result in sample waste. The objective of this study is to identify sample geometry and clamping conditions that can achieve consistent failure in the midregion of small arterial specimens, even for vessels from older individuals. Failure location was assessed in 17 dogbone specimens from human cerebral and sheep carotid arteries using soft inserts. For comparison with commonly used protocols, an additional 22 rectangular samples were tested using either sandpaper or foam tape inserts. Midsample failure was achieved in 94% of the dogbone specimens, while only 14% of the rectangular samples failed in the midregion, the other 86% failing close to the clamps. Additionally, we found midregion failure was more likely to be abrupt, caused by cracking or necking. In contrast, clamp failure was more likely to be gradual and included a delamination mode not seen in midregion failure. Hence, this work provides an approach that can be used to obtain consistent midspecimen failure, avoiding confounding clamp-related artifacts. Furthermore, with consistent midregion failure, studies can be designed to image the failure process in small vascular samples providing valuable quantitative information about changes to collagen and elastin structure during the failure process.

Introduction

Mechanical failure of vascular tissues, such as rupture of abdominal aortic aneurysms and cerebral aneurysms, arterial dissections, and cerebral vessel damage due to head injury, can cause severe health issues or even death [1–6]. Accurate measurements of mechanical properties and an understanding of the failure process itself are vital for improving diagnostic tests and treatment of these diseases. Uniaxial tensile testing is a common approach to evaluate failure properties of vascular tissue as well as other soft tissues. In such tests, both rectangular and dogbone specimens (also known as I-shaped and dumbbell-shaped specimens) are widely used, as an array of clamping methods, Table 1. Even though sample geometry and clamping methods are known to influence the stress and strain distribution within the sample, there are currently no clear guidelines for selecting sample geometry or clamping methods for vascular tissues during uniaxial testing.

Table 1.

Uniaxial failure testing methods and clamp failure data for arterial tissue from representative published work

Study	Species	Tissue	Sample shape	Unclamped sample size (mm)	Clamping method	Quantity failed at clamp
Claes et al. [7]	Human	Coronary artery	Rectangle	7 × 1	Grip with cyanoacrylate glue	NF
Holzapfel et al. [8]	Human	Coronary artery	Rectangle	(7.21±1.21) ×(2.81±0.38)	Sandpaper with super-adhesive gel	Majority
Pichamuthu et al. [9]	Human	Ascending thoracic aortic aneurysm	Rectangle	NF	Sandpaper with cyanoacrylate glue	8.4% (15 out of 178)a
Raghavan et al. [10]	Human	Abdominal aortic aneurysm	Rectangle	40 × 10	Uneven clamp with glue	11.4% (10 out of 88)a
Raghavan et al. [11]	Human	Abdominal aortic aneurysm	Rectangle	Width: 4	NF	22% (32 out of 145)
Robertson et al. [12]	Human	Aneurysm, basilar and carotid artery	Rectangle	Minimum: 5 × 4	Clamp with fine-grade sandpaper	NF
Teng et al. [13]	Human	Atherosclerotic carotid artery	Rectangle	(9∼15) × 2	Rubber coated grips with sandpaper using super glue	37% (27 out of 73)
Vorp et al. [14]	Human	Aortic tissue	Rectangle	30 × 8	Clamp with cyanoacrylate glue	NF
Ferrara et al. [15]	Human	Dilated ascending aorta	Dogbone	NF	Fine grit sandpaper with super-adhesive gel	39% (160 out of 407)b
Forsell et al. [16]	Human	Abdominal aortic aneurysm	Bone	Length: 10∼27 (neck: 4)	Sandpaper with super-adhesive glue	20% (3 out of 15)
García-Herrera et al. [17]	Human	Ascending aortic tissue	Dogbone	18 × 5 (neck: 2)	Grip with cyanoacrylate glue	NF
Mohan and Melvin [18]	Human	Midthoracic descending aorta	Dumbbell	57.15 × 19.05 (neck: 6.35) 31.23 × 12.7 (neck:4.57)	Low-mass air-piston grips	5.3% (2 out of 38)a
Okamoto et al. [19]	Human	Dilated ascending aorta	Dumbbell	35 × 10 (neck: 4)	Sandpaper	NF
Korenczuk et al [20]	Porcine	Abdominal aorta	Dogbone	10 × 5 (neck: 3)	NF	NF
Stemper et al. [21]	Porcine	Aorta	I-shaped	NF	NF	NF
Shah et al. [22]	Swine	Ascending thoracic aorta	Dogbone	20 × 5	NF	28%

Failure location was frequently not found (NF) in the publication. In some cases, clamp failure was reported in a group with other testing artifacts.

These cases are denoted by

^aFailed at clamp or slipped from grips.

^bFailed near clamp, slipped from grips, or, as reported by authors, data not included because of low quality of the stress--strain curve.

For uniaxial failure testing of rubber-like materials, the ASTM standard recommends dogbone-shaped samples with long central regions where the stress field is relatively homogeneous and higher in magnitude, enabling consistent failure away from the grips [23]. Such long midregions are often impossible to achieve in vascular tissues due to insufficient sample length, or because the tissue is highly heterogeneous and so the region of interest is relatively short. The grips of tensile testing machines create stress concentrations and can even damage the specimen in the neighborhood of the clamped region [24–26] causing failure at the clamps even for samples where the midregion is long, Table 1. To date, a protocol for uniaxial testing of vascular tissues with consistent failure away from the clamping region has yet to be established.

Currently, some studies exclude data from specimens that failed at the clamps to avoid confounding the data with grip-related artifacts while others pool data regardless of failure location, Table 1. Often, no information is given about inclusion/exclusion of such samples. While the more cautious approach would seem to be preferable, this can result in substantial waste of tissue samples, Table 1. Furthermore, failure at the grips precludes imaging of the tissue at the failure location during mechanical testing. If failure in the middle of the sample could be achieved consistently, the structural basis of failure could be analyzed using imaging modalities such as multiphoton microscopy [27].

The objective of the current study is to identify clamping conditions and sample geometry that can achieve consistent failure in the middle of small specimens, even for arteries from older individuals. We conjecture that dogbone-shaped specimens with a short midsection, combined with soft grips, can achieve this objective. To test this hypothesis, we assessed failure location during uniaxial testing of dogbone specimens from human cerebral and sheep carotid arteries using soft inserts between the grip face and tissue sample. For comparison with commonly used protocols for uniaxial testing, we also tested two groups of rectangular-shaped samples—those with sandpaper inserts and others with soft inserts. In addition to assessing rupture location, failure modes were evaluated (e.g., delamination, necking, cracking) and the mechanical response curves were also analyzed and classified.

In this work, extremely small samples of only 6 mm in length were chosen, motivated by the need to develop effective failure testing protocols for cerebral arteries, cerebral aneurysms, and other small tissue samples. Successful testing protocols for small samples are not only valuable in situations where larger specimens are unavailable, but will also enable multiple specimens to be tested from a single larger specimen as needed for measurements of anisotropic material properties and also for studies of highly heterogeneous tissues.

Methods

Sample Acquisition.

Human basilar arteries from five circles of Willis without severe visible calcification or atheroma were included in this study (Alzheimer's Disease Research Center Brain Bank, University of Pittsburgh) that were obtained post-mortem using protocols approved by the Committee for Oversight of Research and Clinical Training Involving Decedents (CORID). The average subject age was 73.6 ± 4.3 years. Following harvest, the circles of Willis were snap frozen to −80 °C and then stored at −20 °C. Prior to testing, the circles were thawed at 4 °C for 24 h, after which the basilar arteries were harvested. The average post-mortem interval was 9.5 h.

Three carotid arteries were harvested from 7 month old (juvenile) female sheep (Suffolk and Dorset sheep), stored in phosphate buffered saline at 4 °C after harvest, and tested within 72 h of sacrifice. Sheep arteries were provided for this study in compliance with protocols approved by the Institutional Animal Care and Use Committee (IACUC) of the University of Pittsburgh following NIH guidelines for the care and use of laboratory animals.

Study Population.

Three test groups were considered for both the human basilar arteries and sheep carotid arteries, (i) DB-FT: Dogbone-shaped specimens with a foam tape insert (n = 17); (ii) Rect-FT: Rectangular-shaped specimens with a foam tape insert (n = 11); and (iii) Rect-SP: Rectangular specimens with a sandpaper insert (n = 11). To facilitate discussion of the results, within a single tissue type (sheep carotid, human basilar), each specimen was given a numeric identifier (sample number).

Specimen Preparation.

In preparation for uniaxial testing, arteries were cut open along the long axis of the vessel, Fig. 1(a). Then, rectangular strips approximately 6 mm long and 2.4 mm wide were cut from the flayed vessel, with long axis aligned in the circumferential direction, Figs. 1(b) and 1(c). Arterial regions with branch arteries and other visible nonhomogenous factors such as plaque were avoided. For dogbone-shaped samples, an additional step was added whereby a circular die (4.5 mm in diameter) was used to mark an arc on each side of the rectangular strip such that the width of the middle region was approximately 1.2 mm. This arc was then excised using a #15 scalpel under a dissecting scope, Fig. 1(d). Prior to mechanical testing, wall thickness and width were measured at three positions in the midregion of the unloaded sample using a 0–150 mm digital caliper (Marathon watch company Ltd) and then averaged.

Fig. 1.

Sample preparation and experimental setup for failure testing: (a) Arterial segment, (b) Sample opened longitudinally with schematic of dogbone- and rectangular-shaped specimens, (c) Rectangular specimen, (d) Dogbone specimen, and (e) Custom mechanical testing system with: A—linear actuator, B—the load cell, C—metal clamping system, and D—CMOS camera. In (f) foam tape attached to underside of both grips on all four surfaces and (g) enlarged image of clamps showing grip region.

Mechanical Testing.

All rectangular and dogbone specimens were mechanically tested to failure using a custom-built uniaxial tensile testing system with displacement control [27], Figs. 1(e)–1(g). Briefly, tissue specimens were held between metal grips located within a bath filled with 0.9% (w/v) saline at room temperature, Fig. 1(g). Prior to loading, insert materials (sandpaper or foam tape) were attached to the face of the metal clamps to prevent slippage of the specimen during loading, Fig. 1(f). Sandpaper inserts were glued to the grip face (Loctite 414, Henkel) prior to clamping the specimen. The adhesive on the foam tape (7626A213, multipurpose foam tape, McMaster-Carr) was fixed to the face of the clamp and a few droplets of the same glue were applied between the sample and insert materials.

After mounting, samples were preconditioned with three cycles to 20% extension and then tested to failure. The zero strain configuration was defined as the sample configuration under 0.005 N load. To approximate quasi-static deformation, displacement of the left grip was set at 20 μm/s using a high performance linear actuator (ANT-25 LA, Aerotech Inc., Pittsburgh, PA) with simultaneous force measurements obtained using a 5 lb load cell (MDB-5, Transducer Techniques, Rio Nedo Temecula, CA), Fig. 1(e). Images of the tissue were recorded using a high-resolution CMOS camera mounted above the uniaxial system (EO-5012C, Edmund Optics, Barrington, NJ) at a frame rate of 1 fps with a pixel size of 2.2 μm, Fig. 1(e).

The applied stretch (λ) was calculated as the ratio of the current to unloaded grip to grip distance. The non-zero component of the Cauchy stress (σ) was calculated as the external load (F) measured by the load cell, divided by the current cross-sectional area in the test region, (A). The current cross-sectional area A was defined as the unloaded cross-sectional area (A₀) in the middle of the sample (unloaded width times thickness) divided by the stretch, where in doing so, the deformation was approximated as isochoric (material idealized as incompressible).

Classification of Failure Location and Failure Mode.

Based on the videos obtained during mechanical testing, the failure locations were classified into three groups, “clamp,” “middle,” and “transition.” In particular, specimens that failed within 0.5 mm of the edge of the grips were defined as “clamp” failure. Those that failed in the middle 50% of the sample were defined as “middle” failure. Failure in between these two regions was considered a “transition” region failure. Locations were defined in the deformed configuration.

Three failure modes, namely, (i) cracking, (ii) necking, and (iii) delamination, were defined for each specimen based on the following definitions:

Cracking mode: Visible crack is seen to initiate and then propagate across the width of the sample as a through-thickness crack, ending in sample failure.

Delamination mode: A visible tear starts in a single layer and then propagates across the width of the sample. Often, a retraction of this layer follows. As the applied stretch increases, the crack ultimately proceeds in both layers across the sample width, until complete sample failure is seen.

Necking mode: The width of the middle region of the sample narrows without cracking until complete failure of the sample is seen.

Classification of Failure Process as Abrupt or Gradual.

The failure process was categorized as abrupt or gradual based on the nature of the mechanical loading curves. In particular, an R factor [28] was defined as

$$R=\frac{\mathrm{a}\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{u}\mathrm{n}\mathrm{d}\mathrm{e}\mathrm{r}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{C}\mathrm{a}\mathrm{u}\mathrm{c}\mathrm{h}\mathrm{y}\mathrm{s}\mathrm{t}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{s}\mathrm{s}\mathrm{t}\mathrm{r}\mathrm{e}\mathrm{t}\mathrm{c}\mathrm{h}\mathrm{c}\mathrm{u}\mathrm{r}\mathrm{v}\mathrm{e}\mathrm{a}\mathrm{f}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{u}\mathrm{l}\mathrm{t}\mathrm{i}\mathrm{m}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{s}\mathrm{t}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{s}}{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}\mathrm{a}\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{u}\mathrm{n}\mathrm{d}\mathrm{e}\mathrm{r}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{C}\mathrm{a}\mathrm{u}\mathrm{c}\mathrm{h}\mathrm{y}\mathrm{s}\mathrm{t}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{s}\mathrm{s}\mathrm{t}\mathrm{r}\mathrm{e}\mathrm{t}\mathrm{c}\mathrm{h}\mathrm{c}\mathrm{u}\mathrm{r}\mathrm{v}\mathrm{e}}$$

and used to distinguish between abrupt and gradual failure, Fig. 2:

Fig. 2.

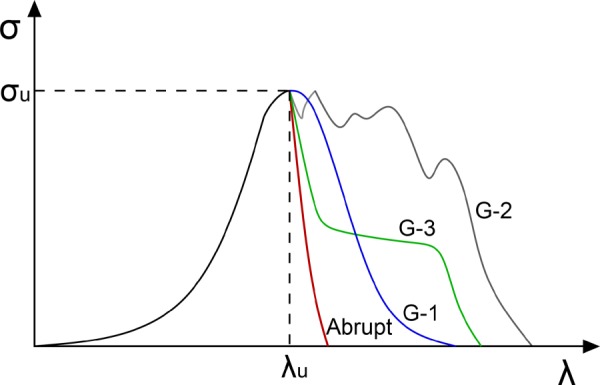
Illustration of abrupt and gradual failure in mechanical loading curves. Shown are idealized loading curves to illustrate nature of abrupt failure and the three types of gradual failure (G-1, G-2, G-3).

Abrupt failure: Once the ultimate Cauchy stress (σ_U) is reached, stress rapidly drops down in a “brittle” manner. Specifically, loading curves with an R factor less than 1/3 (0.33) are categorized as having abrupt failure.

Gradual failure: The stress diminishes over a relatively long stretch. This was defined quantitatively by an R factor greater than 1/3.

Gradual failure was further classified in three different groups, Fig. 2,

G-1. The stress displays a single maximum σ_U and drops down gradually to zero after this single peak.

G-2. There are multiple peaks before complete sample failure.

G-3. The stress drops down abruptly after σ_U followed by a plateau before stress falls to zero gradually.

Statistical Analysis.

Statistical analysis was conducted with SAS Analytics (SAS Institute Inc.). The association between testing methods and the failure location of the sample was evaluated using Fisher's exact test. This test was also used to compare the failure process in three failure modes. Analysis of variance (ANOVA) was utilized to test whether the ultimate stress and stretch between test categories were statistically different. Differences were considered significant if the p value was less than 0.05.

Results

The mechanical curves along with sample images for representative cases from each of the three test categories (DB-FT, Rect-FT, Rect-SP) are shown in Fig. 3 (sheep carotid) and Fig. 4 (human basilar). Images were chosen to show the specimen at stretches of interest including low stretch, ultimate stretch, and post-ultimate stress prior to complete failure. The associated data for all cases are provided in Tables 2 (sheep carotid) and Table 3 (human basilar).

Fig. 3.

Failure process in sheep carotid artery specimens. Four levels of deformation during loading to failure are shown: Row 1: DB-FT for (a) #S2 and (b) #S7; Row 2: Rect-FT for samples (c) #S13 and (d) #S15; as well as Row 3: Rect-SP for (e) #S19 and (f) #S21. Location of crack that led to catastrophic failure is marked by a white arrowhead, where identifiable. Adventitial side of specimen is facing camera.

Fig. 4.

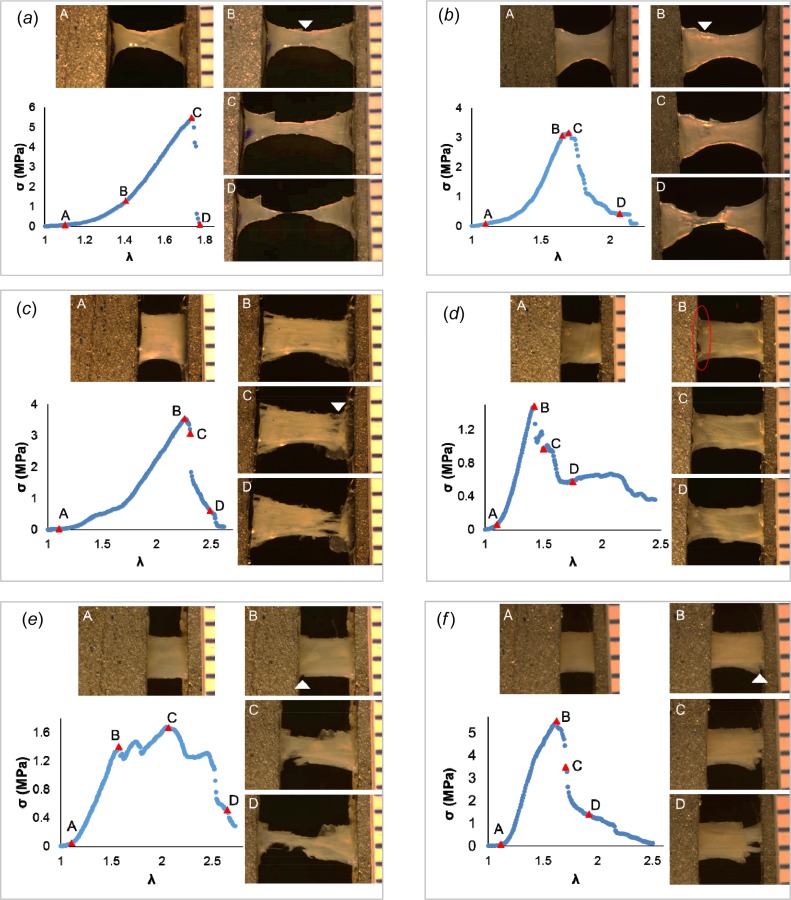
Failure process in human basilar artery specimens. Four levels of deformation during loading to failure are shown. Row 1: DB-FT for (a) #H2 and (b) #H5; Row 2: Rect-FT for (c) #H8 and (d) #H11; as well as Row 3: Rect-SP for (e) #H14 and (f) #H17. Location of tear that led to catastrophic failure is marked by a white arrowhead or circled, where identifiable. Adventitial side of sample is facing camera.

Table 2.

Results of failure testing for sheep carotid artery specimens. The notation N/A is used for cases where there was no visible initial crack before total failure.

		Failure initiation location		Ultimate failure location						Failure Process
	#	Clamp	Middle	Clamp	Middle	Ultimate stress (MPa)	Ultimate stretch	Stress drop caused by	Failure Mode	Gradual	Abrupt
DB-FT	S1		✓		✓	N/A	N/A	Total breakage	Cracking		A
	S2		✓		✓	3.83	2.65	Total breakage	Cracking		A
	S3		✓		✓	4.81	3.2	Media tear partially	Delamination	G-1
	S4		✓		✓	4.35	2.85	Total breakage	Cracking		A
	S5		✓		✓	3.85	2.62	Total breakage	Cracking		A
	S6	N/A			✓	1.15	2	Total breakage	Necking		A
	S7	N/A			✓	2.03	2.94	Total breakage	Necking		A
	S8	N/A			✓	1.89	2.66	Total breakage	Necking		A
	S9	N/A			✓	2.34	2.53	Total breakage	Necking		A
S10		✓		✓	3.11	2.51	Media tear initiated	Cracking		A
Rect-FT	S11	✓		✓		2.63	2.49	Media tear initiated	Delamination	G-2
	S12	✓		✓		2.49	2.48	Outside FOV	N/A	G-1
	S13	✓		✓		2.51	2.75	Media tear partially	Delamination	G-1
	S14	✓		✓		3.91	3.08	Media tear partially	Delamination	G-1
	S15		✓		✓	3.49	3.33	Necking	Necking	G-1
S16		✓		✓	2.9	2.92	Partial tear	Necking	G-1
Rect-SP	S17	✓		✓		4.5	2.43	Media tear partially	Delamination	G-1
	S18	✓		✓		2.55	2.59	Media tear partially	Delamination	G-1
	S19	✓		✓		3.48	2.41	Media tear partially	Delamination	G-3
	S20	✓		✓		2.96	2.44	Media tear initiated	Delamination	G-3
	S21	✓		✓		3.35	3.4	Partial tear	Necking	G-1
S22	✓		✓		3.07	2.45	Media tear initiated	Delamination	G-1

Table 3.

Results of failure testing for human basilar artery specimens

		Failure initiation location		Ultimate failure location						Failure process
	#	Clamp	Middle	Clamp	Middle	Ultimate stress (MPa)	Ultimate stretch	Stress drop caused by	Failure mode	Gradual	Abrupt
DB-FT	H1		✓		✓	4.72	1.7	Total breakage	Cracking		A
	H2		✓		✓	5.48	1.74	Total breakage	Cracking		A
	H3		✓		✓	6.21	2.09	Total breakage	Cracking	G-1
	H4	✓		✓		6.26	1.98	Total breakage	Cracking		A
	H5		✓		✓	3.16	1.7	Total breakage	Cracking	G-1
	H6		✓		✓	3.79	1.67	Total breakage	Cracking		A
H7		✓		✓	3.43	1.77	Total breakage	Cracking		A
Rect-FT	H8	✓		✓		3.54	2.27	Partial breakage	Cracking		A
	H9	✓		✓		7.77	2.86	Media tear	Cracking		A
	H10	✓		✓		3.88	1.77	Partial tear	Necking	G-3
	H11	✓		✓		1.48	1.42	Media tear	Delamination	G-3
H12	✓		✓		1.54	2.13	Partial tear	Necking	G-2
Rect-SP	H13	✓		✓		2.62	2.1	Media breakage	Delamination	G-1
	H14	✓		✓		1.68	2.04	Media breakage	Delamination	G-2
	H15	✓		✓		2.85	1.9	Media breakage	Delamination	G-3
	H16	✓	✓		✓	5.72	1.89	Total breakage	Cracking		A
H17	✓		✓		5.51	1.63	Partial breakage	Cracking	G-1

Good control of the desired specimen dimensions was achieved during sample preparation yielding unloaded rectangular specimen dimensions of 6.0 ± 0.2 mm × 2.4 ± 0.3 mm and width of the midregion of the dogbone samples of 1.2 ± 0.15 mm, Figs. 1(c) and 1(d). The average thickness of human basilar artery samples was 322 ± 28 μm and the average thickness of the sheep carotid arteries samples was 548 ± 19 μm.

There were no “transition” failure cases as all samples fell into either the “middle” or “clamp” failure categories. While “middle” failure was defined as the middle 50% of the sample, in fact, for the sheep carotid arteries, all “middle” failure cases failed within 10% of the center of the sample. For the human basilar arteries, the “middle” failure cases always occurred within 45% of the center.

Dogbone Specimen Failure Testing.

Tests on the dogbone specimens showed great consistency. Sixteen out of 17 dogbone samples failed in the midregion of the sample, supporting the hypothesis underlying this work. Loading beyond the maximum Cauchy stress was associated with immediate tissue failure (total breakage) in 15 out of 17 cases.

The DB-FT sheep carotid artery specimens showed substantial uniformity in failure location and process. All dogbone sheep samples failed in the middle (n = 10) and all but one of the specimens failed abruptly (n = 9). The cause of failure was due to cracking (n = 5, e.g., Fig. 3(a)) or by necking (n = 4, e.g., Fig. 3(f)).

Six of the seven human basilar arteries failed in the middle. All seven of these specimens failed due to cracking, e.g., Figs. 4(a) and 4(b). Two of the seven samples displayed gradual failure, though with relatively low R factor values of 0.36 and 0.42, e.g., Fig. 4(b).

Rectangular Specimen Failure Testing.

In contrast to the dogbone samples, most (19/22) of the rectangle strips failed in the clamp region, suggesting the artifacts at the grip often dominated the failure process in rectangular samples, even in the presence of a soft insert. More precisely, the failure location was not significantly affected by insert material (Rect-SP versus Rect-FT, p = 1 for human and p = 0.4545 for sheep), Fig. 5. In all 19 cases, the failure process initiated at the clamp.

Fig. 5.

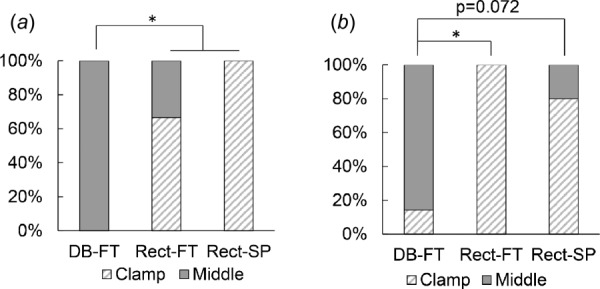
Middle failure consistently achieved in dogbone specimens with foam tape. Distribution of clamp versus middle failure for three test groups for (a) sheep carotid artery and (b) human basilar artery. No samples failed in the “transition” region.

In rectangular-shaped samples, all three failure modes were seen: cracking (Figs. 4(c) and 4(f)), delamination (Figs. 3(c) and 3(e), Figs. 4(d) and 4(e)) and necking (Figs. 3(d) and 3(f)). In contrast to the dogbone specimens, most rectangular samples displayed gradual failure (19/22), e.g., Figs. 3(c)–3(f), Figs. 4(d)–4(f).

For the sheep carotid artery, 10 out of 12 of the rectangular samples failed at the clamp. When the sandpaper insert was used, the most common failure mode was delamination (5/6 cases), while with the soft foam tape insert, failure was mixed between delamination and necking. Delamination always initiated with a tear on the lumenal side (intima/media), regardless of the insert material. The drop from ultimate stress was never associated with complete failure; rather, the drop most frequently occurred when only minor tears to the medial layer were visible, Figs. 3(c) and 3(e).

For the human basilar arteries, only one rectangular sample failed in the middle (1/11).

Comparison of Dogbone and Rectangular Specimens.

Middle failure was achieved in 94% of the dogbone specimens and only 14% of the rectangular samples. Furthermore, the failure location differed significantly between DB-FT and Rect-FT specimens (human basilar p = 0.0152; sheep carotid artery p = 0.0082), Fig. 5.

The choice of specimen shape and insert material did not significantly impact the ultimate stress or ultimate stretch in either human or sheep samples, despite the significant differences in failure location, Fig. 6, with average ultimate stress of 4.1 ± 1.84 MPa for human basilar arteries across all protocols. These are consistent with values of ultimate stress reported in the literature for cerebral arteries with reported average Cauchy stress from 3.0 MPa to 4.75 MPa [12,29]. The ultimate stress across protocols for the sheep carotid arteries was 3.01 ± 0.92 MPa. No prior results were found in the literature for failure of sheep carotid arteries.

Fig. 6.

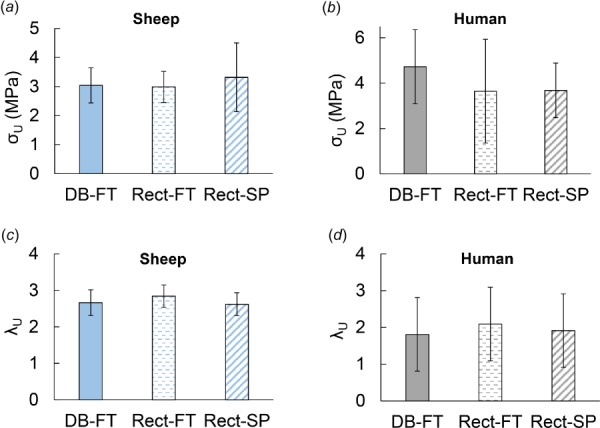
No significant difference in ultimate stress or strain for different testing methods. Row 1: Ultimate stress in (a) sheep carotid and (b) human basilar arteries: Row 2: Ultimate strain in (c) sheep carotid and (d) human basilar arteries. The bars show average ultimate failure stress and stretch with standard deviation.

Relationship Between Failure Mode and Mechanical Response.

The failure process (abrupt versus gradual) differed with failure mode (p < 0.0001), Fig. 7(a). In cracking mode, the stress decreased abruptly after the ultimate stress was reached for most cases, Tables 2 and 3. In contrast, materials failing in a delamination mode always showed gradual failure. Those showing necking displayed a mix of abrupt and gradual failure process.

Fig. 7.

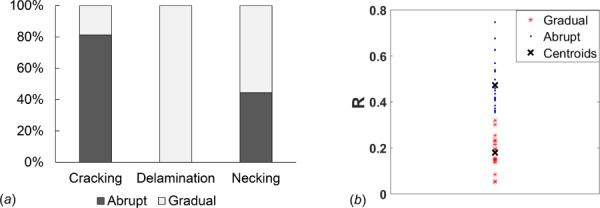
Failure process differs significantly between failure modes. (a) Distribution of abrupt and gradual failure are significantly different for three failure modes in ensemble of 39 samples of vascular tissue (p < 0.0001) and (b) cluster diagram showing distribution of samples into abrupt and gradual failure groups based on area under mechanical loading curve using the R factor.

Discussion

This work has shown that failure in the central region of even small vascular samples can be achieved consistently using dogbone-shaped specimens with soft grip inserts, avoiding grip-associated artifacts and, in the future, will enable imaging of the changes to the collagen fibers during the failure process. In contrast, less than 14% of rectangular specimens failed in the middle region, with no significant improvement from soft insert material. These conclusions are based on uniaxial testing in 39 specimens of only 6 mm in length from the carotid arteries of young sheep as well as from cerebral vessels of older adults (mean age 73.6 ± 4.3 years).

Despite an increasing focus on failure for a wide range of vascular tissues [12,20,30–33], prior to the current study, very little quantitative information was available on failure location or mode for uniaxial testing of vascular tissue, Table 1. Furthermore, there were no established best practices for selecting sample shape or gripping method. An underlying assumption in much of the literature is that both rectangular- and dogbone-shaped samples are appropriate. While frequently unreported, clamp failure rates as high as 37% have been reported in rectangular specimens, even when rubber coated grips were used [13]. In a very relevant study on small rectangular specimens (7.2 mm × 2.81 mm) of coronary arteries using sandpaper inserts, it was found that only “… a small number of samples fractured within the gauge section” and the authors conjectured that, “Dumbbell-shaped samples might increase the success rate of fracture tests”[8]. Consistent with this work, we found that few rectangular samples with sandpaper inserts failed in the midregion (only 1/11). We found even less information on failure location for dogbone specimens, Table 1. Shah [22] performed failure testing on the medial layer of healthy ascending thoracic aorta and reported a 28% failure rate at the grips; details were not found on use of inserts.

A recent study on meniscus tissue1 provides an extensive analysis of the impact of sample shape on uniaxial failure results, using cloth sandpaper inserts for all samples [34]. Failure in the midregion was rare for their circumferentially aligned samples, found in only 1 out of 11 of the dogbone and none of the 23 rectangular specimens. The radial samples showed higher, but still low, midregion failure. Using an elegant assessment of the strain fields, the authors demonstrated artifacts from the grips extend to the midsample region for both dogbone and rectangular samples when sandpaper inserts were used. This low midregion failure is consistent with the current study, where a combination of dogbone shape and soft inserts was needed to obtain regular failure away from the clamps. Our own preliminary studies on dogbone samples with sandpaper inserts gave unacceptable levels of grip failure (more than 75%), prompting us to shift to soft insert materials and leading to the current investigation.

As previously noted, in a desire to avoid possible artifacts associated with clamping, some researchers explicitly discard samples that fail at the clamps. Such artifacts include stress concentration and shearing damage associated with deformations adjacent to the clamps. Hence, the methodology developed here for consistent midregion failure in small samples will enable meaningful data to be obtained from a larger percentage of specimens. This is an important consideration for biological samples, which are often difficult to obtain and heterogeneous across specimens.

This study found important differences in the failure process at the clamp region compared with midregion failure, which we conjecture arise due to the stress concentrations and shearing near the clamp/tissue interface. We anticipate that the stress concentration will vary across the clamp/tissue interface in contrast to the more uniform stress distribution at the midregion of the tissue sample. We found that in the human basilar arteries from aged adults, the midregion failure was always due to cracking, regardless of the sample shape or grip insert (7/7 cases), Table 3. In contrast, all three failure modes were seen for clamp failure. For sheep carotid arteries, midregion failure was associated with necking as well as cracking, almost equally split between these groups, while clamp failure was nearly always associated with delamination, Table 2. These substantial differences suggest artifacts associated with clamping may introduce an alternate failure process—an important consideration when designing studies to understand causes of tissue failure or strength in vascular samples [35].

We did not find any published guidelines for small dogbone samples of soft biological tissues. In fact, this lack of guidelines was a motivation for the current work, where we focused on introducing and using a methodology for testing the minimum sample size we could test to failure in a reproducible manner. After iterative preliminary testing, we found this to be about 6 mm in length. This 6 mm length then served as a constraint for the length of the narrow test region of the dogbone sample given the need to firmly grip the ends of the sample for failure testing. The choice of the width of the dogbone sample was made after iterative mechanical testing with the objective to create reproducible geometries and consistent results. The methodology developed here for consistent uniaxial failure testing of dogbone samples of only 6 mm in length and 1.2 mm width at the midregion opens the possibility for efficiently testing multiple specimens of different orientations obtained from a single vascular sample. Given the focus on small samples, we did not investigate whether larger samples would display similar results with respect to failure location and process.

Another method used to analyze the failure process in arteries is inflation testing (burst tests) of either intact vessel segments or circular clamped membranes, enabling biaxial loading of the tissue (e.g., [36–41]). The tubular inflation tests generate loading that is similar to the in vivo kinematics and inherently reproduce the in vivo residual stress, neither of which is possible in uniaxial testing. For example, Bellini et al. considered inflation failure in mice with impaired collagen fiber formation, finding these mice largely displayed a delamination failure compared with failure due to a transmural crack in control mice [41]. Burst tests on clamped circular membranes also involve biaxial loading, though with one degree less control than for the tubular geometry. Burst tests on clamped circular segments of human aortic aneurysms have yielded important results on failure direction [40] and localized wall thinning prior to failure [42]. An advantage for both the uniaxial testing protocol used here and clamped membrane testing is that failure occurs in a prescribed location, so the failure process is readily imaged. Uniaxial testing enables smaller samples to be used than currently possible in clamped membrane testing and with the potential to concurrently image both sides of the tissue to assess subfailure changes (e.g., [43]).

In this work, when the delamination mode was seen, it always initiated with subfailure on the lumenal side of the artery that propagated across the width of the tissue without penetrating through the wall (e.g., only in the intima/medial layers of the wall). Delamination was evidenced by the retraction of these layers and separation from the deeper layers. These aspects of delamination failure are consistent with previous reports of delamination in uniaxial, tubular inflation, and clamped membrane testing of arterial tissue with initial failure on the lumenal side [13,40,41,43,44]. In Bellini et al. [41], histological analysis was used to confirm delamination occurred between the media and adventitia for an inflation study of the descending thoracic aorta of mice (lacking thrombospondin-2).

An interesting finding in the current work was the drop from ultimate stress most frequently occurred when only minor tears to the medial layer were visible. Hence, the area used to determine peak stress and strain could be consistently estimated. These results suggest that the post peak failure process considered here is of importance in understanding tissue failure in clinical applications and is worthy of further investigation.

Limitations and Future Directions.

There are several limitations to the current study that suggest directions for future work. While the present study included tissues from two different species, two age groups and a large range in ultimate stress (1.15–6.26 MPa, for DB-FT), this work was not a comprehensive study of all soft tissue types. For example, we did not consider tissues heavily laden with atherosclerotic plaque, nor did we consider stiffer and stronger tissues such as ligaments and tendons. While we avoided samples with gross variations in thickness, it is possible that modest variations in wall thickness would not be captured using digital calipers. For tissue with more heterogeneous thickness, methods such as micro-CT could be used to characterize these variations over the sample in the unloaded state (e.g., see Ref. [45]). Residual stress is not considered in this study as it cannot be imposed in uniaxial testing. The opened segment of tissue is presumed to be stress free. Additional artifacts could arise from tissue storage including time between tissue harvest and testing as well as from freezing-related artifacts. To avoid bias in the study from the artifacts, samples within each species were handled and stored in a consistent manner.

We also note that the definition of abrupt and gradual is not unique. Here, we chose a method that is user independent based on the relative areas under the loading curves pre and post ultimate stress. A cluster analysis, Fig. 7(b), supported the choice of an R factor cut off value of 1/3, though there are two cases that could be viewed as close to this demarcation value.

Another limitation of this work is that stretch levels were estimated using grip to grip distance rather than using methods such as digital image correlation (DIC). Our preliminary studies for this work demonstrated that DIC could not be used to estimate strain during the failure process in cases where the specimen failed in delamination mode or in other cases where the strain across the thickness of the sample was not heterogeneous and/or the deformation was far from affine. For consistency, we therefore chose to use grip to grip distance. Errors associated with this approach would not change the central conclusions in this work including failure location.

While DIC has inherent challenges and complexities, the use of DIC is of particular value in failure analysis to understand the local nature of the failure process, (e.g., see Ref. [40]). Even so, challenges arise when the failure process cannot be well tracked by the markers used in DIC, such as during retraction due to delamination. The present work does suggest some opportunities for DIC going forward. The delamination mode was nearly always associated with clamp failure. Therefore, it is expected that measurement problems associated with DIC during delamination failure could be avoided using the DB-FT protocol. For example, a system could be used to obtain DIC data from both the adventitial and medial sides, providing a more localized and layer-dependent assessment of the strain field past failure initiation. Such an approach would not be possible with inflation studies of failure.

While it was not the objective of this study to characterize the failure properties of sheep carotid and human basilar arteries, we did find it striking that the ultimate stress and strains were not significantly different across the test groups in this study (DB-FT, Rect-FT, and Rect-SP), Fig. 6. Similarly, there were no significant differences in these values between middle and clamp failure groups, which is consistent with earlier reports on tendon and ligament [46]. While this could suggest that the clamp artifacts may have only small to moderate influence on the failure stress, it could also suggest that more samples are needed to reach statistical significance due to the large degree of heterogeneity in arterial tissues. For example, even in the carotid arteries of young sheep where all DB-FT specimens failed in the middle region, the ultimate stress ranged from 1.15 MPa to 4.81 MPa with an average value of 3.0 MPa ± 1.3 MPa. This large range in values is consistent with recent reports on ultimate stress in sheep cerebral arteries where values of ultimate stress (though under biaxial loading) in juvenile sheep (3–7 months) ranged from 1.5 to 6.0 MPa [47]. Hence, a comprehensive study of possible artifacts in strength measurements caused by clamp failure might require a larger sample size for arterial tissues. Alternatively, in silico experiments could be run to assess how failure stress and stretch are altered under the different test conditions for fixed material properties [24], ideally including multi-scale modeling of the extracellular matrix [22]. Given the large range in material properties in even young animals, it is perhaps even more striking that midregion failure was consistently attained in these dogbone specimens using the DB-FT protocol.

The findings in this study introduce new questions related to the failure process in arterial tissue that can be addressed in the future using combined optical/mechanical testing—made possible with consistent midregion failure as well as complimentary histology work. For example, what structural differences within the young sheep population lead to the different failure modes (cracking and necking). Are there age-related changes in the extracellular matrix that promote brittle type failure (abrupt, cracking) in the older human arteries? Or, is this failure also typical of basilar arteries in younger adults. More generally, with consistent midregion failure, new questions on failure in arterial tissue can be answered using modalities such as multiphoton or confocal microscopy, simultaneous with mechanical testing so that, for example, the delamination process can be observed in situ. Such studies have the potential to provide new insights and valuable quantitative information about changes to collagen and elastin structure during the failure process [35,48].

Funding Data

• National Institute of Neurological Disorders and Stroke of the National Institutes of Health (Award Nos. 1R01NS097457-01 for AMR, SM, RF and 1R21NS088256-01A1 (for AMR, CS)).

• Human basilar arteries were provided from the Alzheimer Disease Research Center (ADRC) (Grant No. NIA P50 AG005133).

Nomenclature

A =

current cross-sectional area

A₀ =

unloaded cross-sectional area

DB-FT =

dogbone shape specimen with foam tape

F =

force applied in uniaxial testing

Rect-FT =

rectangular shape specimen with foam tape

Rect-SP =

rectangular shape specimen with foam tape

λ =

applied stretch

λ_U =

ultimate stretch

σ =

applied force divided by current cross-sectional area

σ_U =

ultimate stress