Some methods for heterogeneous treatment effect estimation in high dimensions

Abstract

When devising a course of treatment for a patient, doctors often have little quantitative evidence on which to base their decisions, beyond their medical education and published clinical trials. Stanford Health Care alone has millions of electronic medical records that are only just recently being leveraged to inform better treatment recommendations. These data present a unique challenge because they are high dimensional and observational. Our goal is to make personalized treatment recommendations based on the outcomes for past patients similar to a new patient. We propose and analyze 3 methods for estimating heterogeneous treatment effects using observational data. Our methods perform well in simulations using a wide variety of treatment effect functions, and we present results of applying the 2 most promising methods to data from The SPRINT Data Analysis Challenge, from a large randomized trial of a treatment for high blood pressure.

1 INTRODUCTION

In February 2017, at the Grand Rounds of Stanford Medicine, one of us (N.S.) unveiled a new initiative—the “Informatics Consult.” Through this service, clinicians can submit a consultation request online and receive a report based on insights drawn from hundreds of millions of electronic medical records (EMRs) from Stanford Health Care. While the system is in its early stages, a future version will include treatment recommendations: helping a doctor to choose between treatment options for a patient, in cases where there is no randomized controlled trial that compares the options. This announcement was met with excitement from the doctors in attendance, considering that they generally need to make decisions without any support from quantitative evidence (about 95% of the time).¹ Building such a system is a priority in many medical centers in the United States and around the world.

In the problem setting here, a doctor is presented with a patient who has some medical ailment, and the doctor is considering one or more treatment options. A relevant question from the patient’s perspective is, “what is the effect of these treatments on patients like me?” Devising a meaningful definition for “patients like me” is especially difficult given the high-dimensional nature of the problem: We may observe thousands of features describing each patients, any of which could be used to describe patient similarity. The other significant complication is that our goal is to infer causal effects from observational data. The task of mining EMRs to support physician decision making is what motivates this paper. We propose and study methods for estimation and inference of heterogeneous treatment effects, for both randomized experiments and observational studies. We focus on the case of a choice between 2 treatments, which for the purposes of this manuscript we label as treatment and control.

In detail, we have an n × p matrix of features X, a treatment indicator vector T ∈ {0, 1}ⁿ, and a vector of quantitative responses Y ∈ ℝⁿ. Let X_i denote the ith row of X, likewise T_i and Y_i. We assume the n observations (X_i, T_i, and Y_i) are sampled independent and identically distributed from some unknown distribution. The number of treated patients is N₁ = |{i ∶ T_i = 1}|, and the number of control patients is N₀ = |{i ∶ T_i = 0}|. We adopt the Neyman-Rubin potential outcomes model^2,3: Each patient i has potential outcome $Y_i^{\left(1\right)}$ and $Y_i^{\left(0\right)}$, only one of which is observed. $Y_i^{\left(1\right)}$ is the response that the patient would have under treatment, and $Y_i^{\left(0\right)}$ is the response the patient would have under control. Hence, the outcome that we actually observe is $Y_i=Y_i^{\left(T_i\right)}$. We consider both randomized controlled trials, where T_i is independent of all pretreatment characteristics,

$$\left(X_i,Y_i^{\left(0\right)},Y_i^{\left(1\right)}\right)╨T_i,$$ (1)

and observational studies, where the distribution of T_i is dependent on the covariates. This latter scenario is discussed in further detail in Section 2.1.

We describe 4 important functions for modeling data of this type. The first is the propensity function, which gives the probability of treatment assignment, conditional on covariates

$$\pi \left(x\right)\equiv \mathrm{\mathbb{P}}\left(T=1|X=x\right).$$ (2)

The next 2 functions are the conditional mean functions, the expected response given treatment and the expected response given control:

$${\mu }_1\left(x\right)\equiv \mathbb{E}\left[Y|X=x,T=1\right]\text{and}{\mu }_0\left(x\right)\equiv \mathbb{E}\left[Y|X=x,T=0\right],\text{respectively}.$$

The fourth function, and the one of greatest interest, is the treatment effect function, which is the difference between the 2 conditional means:

$$\tau \left(x\right)\equiv {\mu }_1\left(x\right)-{\mu }_0\left(x\right).$$

We seek regions in predictor space where the treatment effect is relatively large or relatively small. This is particularly important for the area of personalized medicine, where a treatment might have a negligible effect when averaged over all patients but could be beneficial for certain patient subgroups.

An outline of this paper is as follows. Section 2 reviews related work. In Section 3, we describe the 2 high-level approaches to the estimation of heterogeneous treatment effects: transformed outcome regression and conditional mean regression. Sections 4, 5, and 6 introduce pollinated transformed outcome (PTO) forests, causal boosting, and causal multivariate adaptive regression splines (MARS), respectively. In Section 7, we report the results of a simulation study comparing all of these methods, and 2 real-data applications are illustrated in Section 8. We end with a discussion.

2 RELATED WORK

Early work on heterogeneous treatment effect estimation⁴ was based on comparing predefined subpopulations of patients in randomized experiments. To characterize interactions between a treatment and continuous covariates, Bonetti and Gelber⁵ formalized the subpopulation treatment effect patter plot. Sauerbrei et al⁶ proposed an efficient algorithm for flexible model building with multivariable fractional polynomial interaction and compared the empirical performance of multivariable fractional polynomial interaction with the subpopulation treatment effect patter plot.

Identifying subgroups within the patient population is becoming especially challenging in high-dimensional data, as in EMRs. In recent years, a great amount of work has been done to apply methods from machine learning to enable the data to inform what are the important subgroups in terms of treatment effect. Su et al⁷ proposed interaction trees for adaptively defining subgroups based on treatment effect. Athey and Imbens⁸ proposed causal trees, which are similar, and constructed valid confidence intervals.

A causal tree is the building block of our causal boosting algorithm in Section 5, so we will briefly describe it here. A causal tree is like a decision tree except that instead of estimating a mean outcome in each leaf, we are interested in estimating an average treatment effect. So the estimate in each leaf is not the sample mean $\overline{y}$ but rather ${\overline{y}}_1-{\overline{y}}_0$, the sample mean in the treatment group minus the sample mean in the control group. Regression trees model a mean function μ by finding the splits that maximize the heterogeneity of μ, so the causal tree, which models τ, chooses the splits that result in the greatest heterogeneity in τ. Athey and Imbens⁸ propose a few different criteria, and we will use the T-statistic criterion:

$$\frac{\left|{\widehat{\tau }}_{\mathcal{l}}-{\widehat{\tau }}_r\right|}{\sqrt{\widehat{\text{Var}}\left({\widehat{\tau }}_{\mathcal{l}}\right)+\widehat{\text{Var}}\left({\widehat{\tau }}_r\right)}}.$$

When a parent node is split into 2 child nodes ℓ and r, ${\widehat{\tau }}_{\mathcal{l}}$ and ${\widehat{\tau }}_r$ are the estimated treatment effects in each child node, with estimated variances $\widehat{\text{Var}}\left({\widehat{\tau }}_{\mathcal{l}}\right)$ and $\widehat{\text{Var}}\left({\widehat{\tau }}_r\right)$, respectively. For the purposes of this manuscript, we treat the causal tree as estimating not just a treatment effect function $\widehat{f}\left(x\right)$ but 2 separate conditional mean functions $\widehat{g}\left(x,1\right)$ and $\widehat{g}\left(x,0\right)$, corresponding to treatment and control groups, respectively, so that $\widehat{f}\left(x\right)=\widehat{g}\left(x,1\right)-\widehat{g}\left(x,0\right)$.

Wager and Athey⁹ improved on this line of work by growing random forests¹⁰ from causal trees. These tree-based methods all use shared-basis conditional mean regression in the framework of Section 3.1. An example of a transformed outcome estimator is the FindIt method of Imai and Ratkovic,¹¹ which trains an adapted support vector machine on a transformed binary outcome. Tian et al¹² introduced a simple linear model based on transformed covariates and showed that it is equivalent to transformed outcome regression in the Gaussian case. In a novel approach, Zhao et al¹³ used outcome-weighted learning to directly determine individualized treatment rules, skipping the step of estimating individualized treatment effects. The problem of estimating heterogeneous treatment effects has also received significant attention in Bayesian literature. Hill¹⁴ and Green and Kern¹⁵ approached the problem using Bayesian additive regression trees,¹⁶ and Taddy et al¹⁷ proposed a method based on Bayesian forests. Chen et al.¹⁸ developed a Bayesian method for finding qualitative interactions between treatment and covariates, and there are other Bayesian methods for flexible nonlinear modeling of interactive/nonadditive relationships between covariates and response.^19,20

What all of the above work (except Hill¹⁴) have in common is that they assume randomized treatment assignment. Athey and Imbens⁸ discussed the possibility of adapting their method to observational data but go no further. Wager and Athey⁹ proposed the propensity forest when treatment is not randomized, but this method does not target heterogeneity in the treatment effect. Similarly, Xie et al²¹ model treatment effect as a function of propensity score, missing out on how it depends on the covariates except through treatment propensity. Crump et al²² devised a nonparametric test for the null hypothesis that the treatment effect is constant across patients, but that is not suited to high-dimensional data. One promising approach that flexibly handles high-dimensional and observational data is the generalization of the causal forest by Athey et al²³ Their gradient forest addresses more generally the problem of parameter estimation using random forests, and in particular, they developed a very fast implementation of the causal forest against which we compare the performance of our methods in Section 7.

2.1 Propensity score methods

Much of causal inference is based on the propensity score,²⁴ which is the estimated probability that a patient would receive treatment, conditioned on the patient’s covariates. If the estimate of the propensity function (2) is $\widehat{\pi }(\cdot )$, then the propensity score for a patient with covariate vector x is $\widehat{\pi }\left(x\right)$. Throughout the present work, we estimate the propensity function using the probability forests of Malley et al.²⁵ We are able to do so quickly using the fast implementation in the R package ranger.²⁶

For the estimation of a population average treatment effect (ATE), propensity score methods for reducing bias in observational studies have been established.²⁷ Propensity score matching emulates a randomized control trial by choosing pairs of patients with similar propensity scores, one each in the treatment and control arms, and discarding the unmatched patients. Stratification on the propensity score groups patients into bins of similar propensity scores to compute the ATE within each bin. The overall ATE is the average of these treatment effects, weighted by the overall frequency of each bin. Inverse probability weighting assigns a weight to each patient equal to the inverse of the propensity score if the patient is treated, or else the inverse of 1 minus the propensity score if the patient is not treated. Hence, patients who tend to be underrepresented in their arm are given more weight. Propensity score stratification and inverse probability weighting are discussed in more detail in the Appendix, along with an additional method: transformed outcome averaging.

The assumption that enables these methods to generate causal conclusions from observational data is known alternatingly across the literature as unconfoundedness, exogeneity, or strong ignorability:

$$\left(Y_i^{\left(1\right)},Y_i^{\left(0\right)}\right)╨T_i|X_i.$$

This is the assumption made in the present work. It means that the relationship between each of the potential outcomes and treatment must be fully explained by X. There can be no additional unmeasured confounding variable that effects a dependence between potential outcomes and treatment. Note, however, that the outcome itself is not independent of treatment because the treatment determines which potential outcome is observed.

3 TO REGRESSION AND CONDITIONAL MEAN REGRESSION

Methods for estimating heterogeneous treatment effects generally fall into one of 2 categories: transformed outcome regression and conditional mean regression. In this section, we describe the 2 approaches and explain why we prefer conditional mean regression. The propensity transformed outcome method (Section 4) uses a combination of the 2 approaches, while causal forests (Section 2), causal boosting (Section 5), and causal MARS (Section 6) are all conditional mean regression methods.

Transformed outcome regression is based on the same idea as transformed outcome averaging, which is laid out in detail in the appendix. Given the data described in Section 1, we define the transformed outcome (TO) as

$$Z\equiv T\frac{Y}{\pi \left(X\right)}+\left(1-T\right)\frac{-Y}{1-\pi \left(X\right)}.$$

This quantity is interesting because, as shown in the Appendix, for any covariate vector x, $\mathbb{E}\left[Z|Z=x\right]=\tau \left(x\right)$. So the TO gives us for each patient an unbiased estimate of the personalized treatment effect for that patient. Using this, we can simply use the tools of supervised learning to estimate a regression function for the mean of Z given X. The weakness of this approach is that while Z is unbiased for the treatment effect, its variance can be large owing to the presence of the propensity score, which can be close to 0 or 1, in the denominator.

An alternative approach—conditional mean regression—is based on the idea that because τ(x) is defined as the difference between μ₁(x) and μ₀(x), if we can get good estimates of these conditional mean functions, then we have a good estimate of the treatment effect function. Estimating the functions μ₁(x) and μ₀(x) are supervised learning problems. If they are both estimated perfectly, then there is no need to estimate propensity scores. The problem is that in practice we never estimate either function perfectly, and differences between the covariate distributions in the 2 treatment groups can lead to bias in treatment effect estimation if propensity scores are ignored.

We compare these 2 approaches with a simple example: Consider the task of estimating an ATE using data from a randomized trial. This may seem far removed from heterogeneous treatment effect estimation, but we will describe how 2 of our methods are based on estimating local ATEs for subpopulations in our data. In this case, the TO is

$$Z=T\frac{Y}{1/2}+\left(1-T\right)\frac{-Y}{1/2}=2TY-2\left(1-T\right)Y,$$

and the corresponding estimate of the ATE is

$${\widehat{\tau }}_{\text{TO}}=\frac{1}{n}{\displaystyle \sum _{i=1}^n{Z}_i=\frac{2N_1{\overline{Y}}_1-2N_0{\overline{Y}}_0}{N_1+N_0}=\frac{N_1}{n/2}{\overline{Y}}_1-\frac{N_0}{n/2}}{\overline{Y}}_0,$$

where ${\overline{Y}}_1$ is the average response of patients who received treatment and ${\overline{Y}}_0$ is the average response of control patients. Meanwhile, the conditional mean estimator of the ATE would be

$${\widehat{\tau }}_{\text{CM}}={\overline{Y}}_1-{\overline{Y}}_0$$

Here, we are implicitly assuming that neither N₁ nor N₀ is 0. It is worth noting that

$${\widehat{\tau }}_{\text{TO}}={\widehat{\tau }}_{\text{CM}}+\frac{N_1-N_0}{n}\left({\overline{Y}}_1+{\overline{Y}}_0\right),$$

so if N₁ = N₀ or ${\overline{Y}}_1+{\overline{Y}}_0=0$, then ${\widehat{\tau }}_{\text{TO}}={\widehat{\tau }}_{\text{CM}}$. However N₁, N₀, ${\overline{Y}}_1$, and ${\overline{Y}}_0$ are all random. Given a fixed sample size n, N₁ follows a Binomial(n, 1∕2) distribution (truncated to exclude 0 and n), and N₀ is the difference between n and N₁. Suppose ${\overline{Y}}_1$ and ${\overline{Y}}_0$ have normal distributions with variances inversely proportional to sample size:

$${\overline{Y}}_1\sim \text{Normal}\left({\mu }_1,{\sigma }^2/N_1\right)\text{and}{\overline{Y}}_0\sim \text{Normal}\left({\mu }_0,{\sigma }^2/N_0\right).$$

Note that both ${\widehat{\tau }}_{\text{CM}}$ and ${\widehat{\tau }}_{\text{TO}}$ are unbiased for τ ≡ μ₁ − μ₀, but the 2 estimators have different variances. Conditioning on N₁, the variance of ${\widehat{\tau }}_{\text{CM}}$ is

$$\mathbb{E}\left[{\left({\widehat{\tau }}_{\text{CM}}-\tau \right)}^2|N_1\right]=\mathbb{V}\left({\overline{Y}}_1-{\overline{Y}}_0|N_1\right)={\sigma }^2/N_1+{\sigma }^2/N_0,$$

while the variance of ${\widehat{\tau }}_{\text{TO}}$ given N₁ is

$$\mathbb{E}\left[{\left({\widehat{\tau }}_{\text{TO}}-\tau \right)}^2|N_1\right]=\mathbb{V}\left({\widehat{\tau }}_{\text{TO}}|N_1\right)+{\left(\mathbb{E}\left[{\widehat{\tau }}_{\text{TO}}-\tau |N_1\right]\right)}^2=\frac{4}{n}{\sigma }^2+{\left(\frac{N_1-N_0}{n}\right)}^2{\left({\mu }_1+{\mu }_0\right)}^2.$$

So the key is the ratio of the main effect (μ₁ + μ₀)/2 to the noise level σ. if

$$\left|\frac{{\mu }_1+{\mu }_0}{2\sigma }\right|<\sqrt{\frac{N_1^{-1}+N_0^{-1}-4n^{-1}}{{\left(N_1-N_0\right)}^2}},$$

then ${\widehat{\tau }}_{\text{TO}}$ has less variance. If the inequality is reversed, then ${\widehat{\tau }}_{\text{CM}}$ has less variance. Marginalizing over the truncated binomial distribution of N₁ is difficult to do analytically, but we can numerically estimate the marginal variance of each estimator for any n > 1. Figure 1 illustrates the results for a few different choices of n.

FIGURE 1.

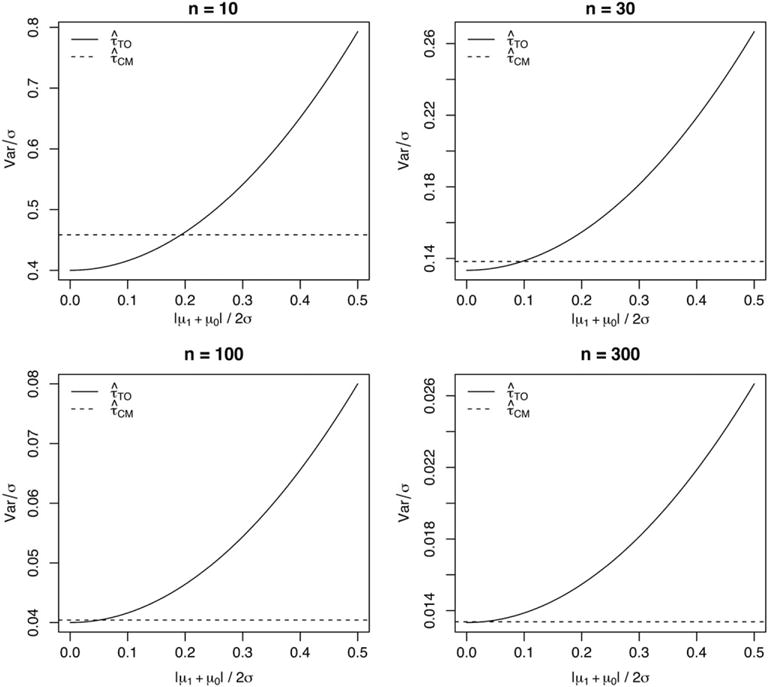
The variance of 2 average treatment effect estimators for n = 10, 30, 100, and 300, as the ratio of the absolute main effect |μ₁ + μ₀|/2 to the noise level σ increases from 0 to 0.5

We observe that for small n, ${\widehat{\tau }}_{\text{TO}}$ can have slightly smaller variance than ${\widehat{\tau }}_{\text{CM}}$ if the absolute value of the main effect is close to 0. But this advantage tends to 0 as n increases, and ${\widehat{\tau }}_{\text{TO}}$ has much greater variance if the main effect is large. In conclusion, we prefer the conditional mean estimator because of the potentially high variance of the TO estimator. This is reflected in the following sections as all of our methods use some version of conditional mean regression.

3.1 Shared-basis conditional mean regression

In high-dimensional data, it is often necessary to choose a subset of variables to include in a model. Beyond that, nonparametric methods adaptively choose transformations of variables. Collectively, we refer to the variables and transformations selected as the basis of the regression. In conditional mean regression, it is to be expected that the selected basis be different between the 2 regression functions. This can cause differences between the conditional means attributable not to a heterogeneous treatment effect but rather to randomness in the basis selection.

The 3 methods that we propose are based on 2 principles. First, we prefer to use conditional mean regression rather than TO regression, with a shared basis for the treatment and control arms. Second, when adaptively constructing this basis, we want to do so in a way that reflects the heterogeneity in the treatment effect, not the response itself. For example, we want to include variables on which the treatment effect depends. How exactly this shared basis is determined is different for each method.

4 PTO FORESTS

Our first method for estimating heterogeneous treatment effects is based on the TO described in Section 3. The algorithm can be implemented using preexisting software packages for building random forests. We first present the idea of a PTO forest in detail and then explain its components.

Algorithm 1.

PTO forest.

Require: Data (Xi, Ti, Yi). estimated propensity function $\widehat{\pi }(·)$

$Z_i\leftarrow T_i\frac{Y_i}{\widehat{\pi }\left(X_i\right)}+\left(1-T_i\right)\frac{-Y_i}{1-\widehat{\pi }\left(X_i\right)}$

1. (TO forest) Build a depth-controlled random forest F on X to predict Z.

2. (Pollination) For each tree in the forest F, replace the node estimates $\overline{Z}$ with ${\overline{Y}}_1-{\overline{Y}}_0$. This entails sending each observation down each tree to get the mean response in treatment and control groups for each leaf, replacing the mean TO. This yields treatment effect estimates ${\widehat{\tau }}_i$.

3. (Optional) Build an additional random forest G on X to predict $\widehat{\tau }$. This adds a layer of regularization and interpretability (through variable importance) of the results.

We start with the TO, an unbiased point estimate of the treatment effect for each individual; in step 1, we fit a random forest using this effect as the outcome. In principle, this should estimate our personalized treatment effect. Per Section 3, we do not trust these estimates too much, because the outcome can be highly variable. But we will put faith in the trees they produce.

Thus in step 2, we “pollinate” the trees separately with the treated and untreated populations. That is, we send data down each tree and compute new predictions for each terminal node. The resulting estimates ${\widehat{\tau }}_i$ of the treatment effect have lower variance, as explained in Section 3, because we are replacing a TO estimator with a conditional mean estimator. Finally, in step 3, we can postprocess these predictions by fitting one more forest, primarily for interpretation.

Figure 2 illustrates the benefits of pollination. In this example, n = 100, p = 50, and the response is simulated in each arm according to $Y_i\sim \mathcal{N}\left(1-X_{i1}+X_{i2},1\right)$ for treated patients and $Y_i\sim \mathcal{N}\left(X_{i1}+X_{i2},1\right)$ for untreated patients. Hence, the true personalized treatment effect for patient i is 1 + 2X_i1. In the top row, the treatment is randomly assigned, while in the bottom row, the probability of treatment assignment is ${\left(1+e^{X_{i1}+X_{i2}}\right)}^{-1}$. The raw estimates correspond to a random forest (as in step 2) grown to predict the TO. The pollinated estimates correspond to reestimating (as in step 3) the means of the leaves within each arm. We observe that in each case, the pollination improves the estimates.

FIGURE 2.

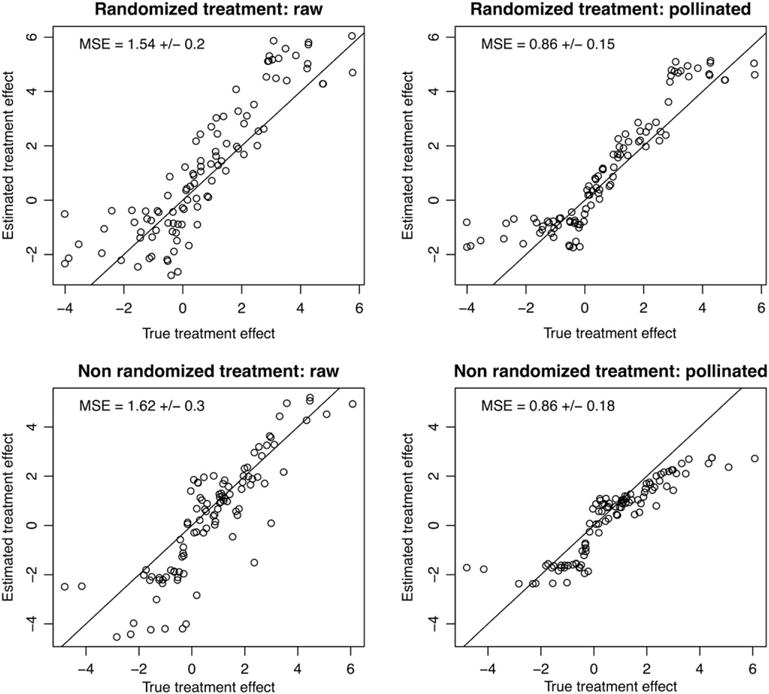
A comparison of raw and pollinated transformed outcome forests. Each method is applied to a randomized simulation and a nonrandomized simulation, and we visually compare the estimated treatment effect with the true treatment effect. We see that in each case, the pollination improves the estimates. For each method, we report the mean square error (MSE) for the treatment effect estimates, along with standard errors

5 CAUSAL BOOSTING

The PTO forest has the advantage of being implementable through preexisting software, but we would prefer to build our regression basis using conditional means rather than the TO. The causal tree and causal forest described in Section 2 accomplish this using specialized software. An alternative to a random forest for least squares regression is boosted trees. Boosting builds up a function approximation by successively fitting weak learners to the residuals of the model at each step. In this section, we adapt least squares boosting for regression²⁸ to the problem of heterogeneous treatment effect estimation.

Given data of the form (X_i, Y_i), i = 1, …, n, least squares boosting starts with a regression function $\widehat{F}\left(x\right)=0$ and residuals $R_i=Y_i-\widehat{F}\left(x_i\right)$. We fit a regression tree to R_i, yielding predictions ${\widehat{f}}_1\left(x\right)$. Then we update $\widehat{F}\left(x\right)\leftarrow \widehat{F}\left(x\right)+\epsilon \cdot {\widehat{f}}_1\left(x\right)$ and $R_i\leftarrow R_i-\epsilon \cdot {\widehat{f}}_1\left(x_i\right)$ and repeat this (say) a few hundred times. The final prediction is simply $\widehat{F}\left(x\right)$, a sumof trees shrunk by ε.

For our current problem, our data have the form (X_i, T_i, Y_i), i = 1, …, n, with T_i ∈ {0, 1}. For now, assume randomized treatment assignment: In the next subsection, we show to handle the nonrandomized case. Here is how we propose to adapt least squares boosting. As with causal forests,⁹ our building block is a causal tree, which returns a function $\widehat{g}\left(x,t\right)$ as described in Section 2. The estimated causal effect for an observation X = x is $\widehat{\tau }\left(x\right)=\widehat{g}\left(x,1\right)-\widehat{g}\left(x,0\right)$. This is a standard causal tree, except that for each terminal node, we return the pair of treatment-specific means rather than the treatment effect. In other words, if observation X_i = x gets you into terminal node k, where the pair of estimated means are ${\widehat{\mu }}_{1k}$ (treated) and ${\widehat{\mu }}_{0k}$ (untreated), then these are the values returned, respectively, for $\widehat{g}\left(x,1\right)$ and $\widehat{g}\left(x,0\right)$. The algorithm is summarized in Algorithm 2. The estimated treatment effect for any observation x is ${\widehat{G}}_K\left(x,1\right)-{\widehat{G}}_K\left(x,0\right)$.

Algorithm 2.

Causal boosting.

Require: Data (Xi, Ti, Yi), parameters K,ε > 0

Initialize Ri = Yi and Ĝ0(x, t) = 0.

for k in 1,…,K do

Fit a causal tree ĝk to data (Xi, Ti, Ri)

Ri ← Ri − ε · ĝk(Xi, Ti)

Gk ← Ĝk−1 + ε · ĝk

end for

Return ĜK(x, t).

Note that this generalizes to loss functions other than squared error. For example, if the causal tree was trained for a binary outcome, then each terminal node would return a pair of logits ${\widehat{\eta }}_{1k}=\text{logit}\left[\mathrm{Pr}\left(Y=1|X=x,T=1\right)\right]$ and ${\widehat{\eta }}_{0k}=\text{logit}\left[\mathrm{Pr}\left(Y=1|X=x,T=0\right)\right]$. Thus, Ĝ_K(x, t) would be a function that returned a pair of logits at x, and hence treatment success probabilities. The treatment effect would be the appropriate function of these differences of log-odds. Other enhancements to boosting, such as stochastic boosting, are also applicable in the setting.

Note that causal boosting is not strictly a gradient boosting algorithm, because there is no loss function for which we are evaluating the gradient at each step, in order to minimize this loss. Rather, causal boosting is an adaptation of gradient boosting on the observed response, with a different function in each arm of the data. The adaptation is that we use causal trees as our weak learners instead of a standard regression technique. This tweak encourages the learned function to find treatment effect heterogeneities.

5.1 Cross-validation for causal boosting

Unlike random forests, gradient boosting algorithms can overfit the training data as the number of trees increases.²⁹ This is because each successive tree is not built independently of the previous ones but rather with the goal of fitting to the residuals of the previous trees. Whereas a random forest will only benefit from using more trees, the number of trees in gradient boosting is itself an important parameter that needs to be tuned.

Complicating matters, the usual cross-validation framework does not apply to the setting of estimating a heterogeneous treatment effect because in this setting each observation does not come with a response corresponding directly to the function we are interested in estimating. We do not observe a response τ_i for the ith patient. What we observe is either $Y_i^{\left(0\right)}$ or $Y_i^{\left(1\right)}$, depending on whether or not the patient received the treatment.

We describe our approach in the context of a held-out validation set, but this fully specifies our cross-validation procedure. Cross-validation is simply validation done by partitioning the training set into several folds and averaging the results obtained by holding out each fold as a validation set and training on all other folds. The data in this context are a training set (X^tr, T^tr, Y^tr) and a validation set (X^v, T^v, Y^v). After training causal boosting on (X^tr, T^tr, Y^tr), we are left with a sequence of models G₁(x, t), …, G_K(x, t), and we would like to determine which of these models gives us the best estimates of treatment effect.

Our validation procedure uses a pollination of the causal boosting model much like Step 2 of the PTO forest (Algorithm 1). We construct a new sequence of models H₁(x, t), …, H_K(x, t) using the same tree structures (split variables and split points) as G₁(x, t), …, G_K(x, t), but we send the validation points X^v down each tree to get new estimates in the terminal nodes based on T^v and Y^v. The first causal tree ${\widehat{g}}_1\left(x,t\right)$ is pollinated with the data (X^v, T^v, Y^v), yielding a new tree ${\widehat{h}}_1\left(x,t\right)$. The validation set residuals of this first tree are given by $Y_i-{\widehat{h}}_k\left(X_i,T_i\right)$, and these validation set residuals are used to reestimate the terminal nodes of the next causal tree and so on. The sequential sum of these trees (times the learning rate ε) is H₁(x, t), …, H_K(x, t).

We are ready to define our validation error for each of the original models G₁(x, t), …, G_K(x, t). The validation error for a causal boosting model with k trees is given by

$${\displaystyle \sum _{x\in v}(\{G_k\left(x,1\right)-G_k\left(x,0\right)\}}-{\{H_K\left(x,1\right)-H_K\left(x,0\right)\})}^2.$$

We have several remarks to make about this form. G_k(x, 1) − G_k(x, 0) is the estimated treatment effect at x, for causal boosting with k trees. H_K(x, 1) − H_K(x, 0) is the estimated treatment effect corresponding to the maximum number of trees, using the responses from the validation set. For a large number of trees, we can be sure that this is overfitting to the response, and this is the analog of traditional cross-validation, which compares predictions on the validation set with observed response in the validation set. This observed response, corresponding to the saturated model, is as overfitted as possible. Intuitively, we are comparing our estimated treatment effect for each validation point against another estimate, which uses the same structure as the model fit to find similar patients and estimate the treatment effect based on those similar patients, some of whom will have received treatment and some of who will have received control. The better the structure is that causal boosting has learned for the heterogeneous treatment effect, the more the local ATE in the training set will mirror the local ATE in the validation set. For the results in Section 7, we use this procedure to do cross-validation for causal boosting.

5.2 Within-leaf propensity adjustment

When the goal is to estimate not an ATE but rather an individualized treatment effect, the propensity score methods described in Section 2.1 and in the Appendix do not immediately extend. Consider for example propensity score stratification. Because each patient belongs to only 1 stratum of propensity score, we cannot average treatment effect estimates for a patient across strata. Technically, if we were to fit a causal boosting model within each stratum, each of these models would be able to make a prediction for the query patient. But then all but one of these models would be unwisely extrapolating outside of its training set to make this prediction. An alternative to propensity score stratification, inverse probability weighting is still viable, but the volatility of this method is exacerbated by the attempt to estimate a varying treatment effect, rather than a constant one.

Within each leaf of a causal tree, however, we estimate an ATE. This is where causal boosting adjusts for nonrandom treatment assignment, using propensity score stratification to reduce the bias in the estimate of the within-leaf ATE. Before initiating the causal boosting algorithm, we begin by evaluating the propensity score for each patient, which is an estimate of probability of being assigned the treatment, conditioned on the observed covariates. Any binomial regression technique could be used here. We fit a probability forest,²⁵ which is similar to a random forest for classification,¹⁰ except that each tree returns a probability estimate rather than a classification. The trees are combined by averaging the probability estimates and not by majority vote. We denote the treatment assignment probability function by $\pi \left(x\right)\equiv \mathrm{\mathbb{P}}\left(T=1|X=x\right)$ and the corresponding propensity scores by ${\widehat{\pi }}_i\equiv \widehat{\pi }\left(x_i\right)$.

We group the patients into S strata of similar propensity scores denoted 1, …, S. For example, there could be S = 10 strata, with the first comprising $\widehat{\pi }\in \left[0,0.1\right)$ and the last comprising $\widehat{\pi }\in \left[0.9,1\right]$, with equal-length intervals in between. We use s_i ∈ {1, …, S} to denote the stratum to which patient i belongs. Hence, the data that we observe within each leaf of a causal tree are of the form (X_i, s_i, T_i, Y_i) ∈ ℝ^p × {1, …, S} × {0, 1} × ℝ. We use n_ℓ to denote the number of patients in leaf ℓ and index these patients by i = 1, …, n_ℓ. The propensity-adjusted ATE estimate in leaf ℓ is given by

$${\widehat{\tau }}_{\mathcal{l}}=\frac{{\displaystyle {\sum }_{s=1}^S{n}_{s\mathcal{l}}\left({\overline{Y}}_{1s\mathcal{l}}-{\overline{Y}}_{0s\mathcal{l}}\right)}}{{\displaystyle {\sum }_{s=1}^S{n}_{s\mathcal{l}}}},\text{where}{\overline{Y}}_{ts\mathcal{l}}=\frac{{\displaystyle {\sum }_{i=1}^{n_{\mathcal{l}}}{\mathbb{I}}_{\left\{T_i=t\wedge s_i=s\right\}}}{Y}_i}{n_{ts\mathcal{l}}}$$ (3)

is the mean response among the treatment (t = 1) or control (t = 0) group in stratum s and $n_{ts\mathcal{l}}={\displaystyle {\sum }_{i=1}^{n_{\mathcal{l}}}{\mathbb{I}}_{\left\{s_i=s\right\}}}$ is the corresponding number of patients in leaf ℓ for t ∈ {0, 1}, s ∈ {1, …, S}. Finally, n_sℓ = n_1sℓ + n_0sℓ.

The estimated variance of ${\widehat{\pi }}_{\mathcal{l}}$ is

$$\widehat{\text{Var}}\left({\widehat{\tau }}_{\mathcal{l}}\right)=\frac{{\displaystyle {\sum }_{s=1}^S{n}_{2\mathcal{l}}^2{\widehat{\sigma }}_{2\mathcal{l}}^2}}{{\left({\displaystyle {\sum }_{s=1}^S{n}_{s\mathcal{l}}}\right)}^2},\text{where}{\widehat{\sigma }}_{s\mathcal{l}}^2=\frac{s_{1s\mathcal{l}}^2}{n_{1s\mathcal{l}}}+\frac{s_{0s\mathcal{l}}^2}{n_{0s\mathcal{l}}}$$

and $s_{ts\mathcal{l}}^2$ is the sample variance of the response for arm t of stratum s in leaf ℓ.

Hence, for 2 candidate daughter leaves ℓ and r of the same parent, the natural extension of the squared T-statistic splitting criterion from Athey and Imbens⁸ is

$$\frac{\left|{\widehat{\tau }}_{\mathcal{l}}-{\widehat{\tau }}_r\right|}{\sqrt{\widehat{\text{Var}}\left({\widehat{\tau }}_{\mathcal{l}}\right)\text{+}\widehat{\text{Var}}\left({\widehat{\tau }}_r\right)}}.$$

This is the propensity-stratified splitting criterion used by causal boosting. This criterion could also be used by a causal forest as it applies directly to its constituent causal trees.

We use this propensity adjustment not only for determining the split in a causal tree but also for estimating the treatment effect in the node. Specifically, the causal tree returns 2 values in each leaf: the propensity-adjusted mean response in the treatment and control groups.

$$\frac{{\displaystyle {\sum }_{s=1}^S{n}_{s\mathcal{l}}{\overline{Y}}_{1sl}}}{{\displaystyle {\sum }_{s=1}^S{n}_{s\mathcal{l}}}}\text{and}\frac{{\displaystyle {\sum }_{s=1}^S{n}_{s\mathcal{l}}{\overline{Y}}_{0sl}}}{{\displaystyle {\sum }_{s=1}^S{n}_{s\mathcal{l}}}}$$

6 CAUSAL MARS

One drawback of tree-based methods is that there could be high bias in this estimate because they use the average treatment effect within each leaf as the prediction for that leaf. This is especially problematic when it comes to confidence interval construction for personalized treatment effects. The variance of the estimated treatment effect is relatively straightforward to estimate, but the bias presents more of a challenge. We do not develop confidence intervals in this manuscript, but we want to develop a more promising method for this endeavor in future work.

Multivariate adaptive regression splines³⁰ can be thought of as a modification to classification and regression tree (CART), which alleviates this bias problem. Multivariate adaptive regression splines starts with the constant function f(x) = β₀ and considers adding pairs of functions of the form {(x_j − c)₊, (c − x_j)₊} and also the products of variables in the model with these pairs, choosing the pair that leads to the greatest drop in training error when it is added to their model, with regression coefficients estimated via ordinary least squares. The difference between this and CART is that in CART the pairs of functions considered are of the form $\left\{{\mathbb{I}}_{\left\{x_j-c\ge 0\right\}},{\mathbb{I}}_{\left\{c-x_j>0\right\}}\right\}$, and when a product with one of the included terms is chosen, it replaces the included term in the model.²⁹ Because MARS does not replace but adds terms, it can do a better job of capturing lower-order regression functions.

We propose causal MARS as the adaptation of MARS to the task of treatment effect estimation. We fit 2 MARS models in parallel in the 2 arms (treatment and control) of the data, at each step choosing the same basis functions to add to each model. The criterion that we use identifies the best basis in terms of explaining treatment effect: We compare the drop in training error from including the basis in both models with different coefficients to the drop in training error from including the basis in both models with the same coefficient in each model. The steps of causal MARS are as follows. The parameter D controls the maximum dimension of the regression basis, and in practice, we use 11 in our examples. Algorithm 3 has the details. In Section 7, we illustrate the lower bias of causal MARS (relative to the causal forest) in a simulation.

Algorithm 3.

Causal MARS.

Require: Data (Xi, Yi, Yi), parameter D

Define ℱ ≡ {{(xj − c)+, (c −xj)+} : c ∈ {Xij}, j ∈ {1,…,p}}

Initialize ℬ = {1}

$\widehat{\beta }\leftarrow \arg {min}_{\beta }{{\displaystyle {\sum }_{i=1}^n\left(Y_i-{\beta }_h^1{\mathbb{I}}_{T_i=1}-{\beta }_h^0{\mathbb{I}}_{T_i=0}\right)}}^2$

$R_i\leftarrow Y_i-{\widehat{\beta }}_h^1{\mathbb{I}}_{T_i=1}-{\widehat{\beta }}_h^0{\mathbb{I}}_{T_i=0}$

for d in 1,…,D do

for {f, g} in {{b(x)f*(x), b(x)g*(x)} : b ∈ ℬ, {f*,g*} ∈ ℱ} do

$RS{S}_{\mu }\leftarrow {min}_{\beta }{\displaystyle {\sum }_{i=1}^n{\left(R_i-{\displaystyle {\sum }_{h\in \left\{f,g\right\}}{\beta }_{h}h\left(X_i\right)}\right)}^2}$

$RS{S}_{\tau }\leftarrow {min}_{\beta }{\displaystyle {\sum }_{i=1}^n{\left(R_i-{\displaystyle {\sum }_{h\in \left\{f,g\right\}}{\beta }_h^{1}h\left(X_i\right){\mathbb{I}}_{T_i=1}}-{\displaystyle {\sum }_{h\in \left\{f,g\right\}}{\beta }_h^{0}h\left(X_i\right){\mathbb{I}}_{T_i=0}}\right)}^2}$

dRSS = RSSτ − RSSμ

end for

Choose {f,g} which maximize dRSS

$\widehat{\beta }\leftarrow \arg {min}_{\beta }{\displaystyle {\sum }_{i=1}^n{\left(Y_i-{\displaystyle {\sum }_{h\in \left\{f,g\right\}}{\beta }_h^{1}h\left(X_i\right){\mathbb{I}}_{T_i=1}}-{\displaystyle {\sum }_{h\in \left\{f,g\right\}}{\beta }_h^{0}h\left(X_i\right){\mathbb{I}}_{T_i=0}}\right)}^2}$

$R_i\leftarrow Y_i-{\displaystyle {\sum }_{h\in \left\{f,g\right\}}{\widehat{\beta }}_h^{1}h\left(X_i\right){\mathbb{I}}_{T_i=1}}-{\displaystyle {\sum }_{h\in \left\{f,g\right\}}{\widehat{\beta }}_h^{0}h\left(X_i\right){\mathbb{I}}_{T_i=0}}$

$\mathcal{B}\leftarrow \mathcal{B}\cup \left\{f,g\right\}$

end for

Backward deletion: delete terms one at a time, using the same criterion dRSS = RSSτ − RSSμ

Use out-of-hag dRSS to estimate the optimal model size.

To reduce the variance of causal MARS, we perform bagging by taking B bootstrap samples of the original dataset and fitting the causal MARS model to each one. The estimated treatment effect for an individual is the average of the estimates for this individual by the B models. When bagging, we can save on computation time by skipping the backward deletion and model selection steps in Algorithm 3. We found in simulation that this gives similar results to including these steps.

Note that the algorithm described above applies to the randomized case, not observational data. Given S propensity strata and membership s ∈ 1, …, S, for each patient, we use the same basis functions within each stratum but different regression coefficients. Within each stratum, the coefficients are estimated separately from the coefficients in other strata. Given the entry criterion dRSS_s in each stratum, we simply combine these into a single criterion Σ_s dRSS_s. This is the propensity-adjusted causal MARS.

7 SIMULATION STUDY

In the design of our simulations to evaluate performance of methods for heterogeneous treatment effect estimation, there are 4 elements to the generation of synthetic data:

1. The number n of patients in the training set and the number p of features observed for each patient.

2. The distribution ${\mathcal{D}}_X$ of the feature vectors X_i. Across all scenarios, we draw odd-numbered features independently from a standard Gaussian distribution. We draw even-numbered features independently from a Bernoulli distribution with probability 1/2.

3. The propensity function π(·), the mean effect function μ(·), and the treatment effect function τ(·). We take the conditional mean effect functions to be μ₁(x) = μ(x) + τ(x)/2 and μ₀(x) = μ(x) − τ(x)/2.

4. The conditional variance ${\sigma }_Y^2$ of Y_i given X_i and T_i. This corresponds to the noise level, and for most of the scenarios ${\sigma }_Y^2=1$. In scenarios 2 and 4, the variance is lower to make the problem easier; in scenarios 7 and 8, the variance is higher.

Given the elements above, our data generation model is, for i = 1, …, n,

$$\begin{gathered} X_i\stackrel{\text{iid}}{\sim }{\mathcal{D}}_X, \\ {T}_i\stackrel{\text{iid}}{\sim }\text{Bernoulli}\left(\pi \left(X_i\right)\right), \\ {Y}_i\stackrel{\text{iid}}{\sim }\text{Normal}\left(\mu \left(X_i\right)+\left(T_i-1/2\right)\tau \left(X_i\right),{\sigma }_Y^2\right). \end{gathered}$$

The third element above, encompassing π(·), μ(·), and τ(·), is most interesting. Note that π(·) and μ(·) are nuisance functions and τ(·) is the function we are interested in estimating. In this section, we present 2 batches of simulations, the first of which represent randomized experiments. The second batch of simulations represent observational studies. Within each set of simulations, we make 8 different choices of mean effect function and treatment effect function, meant to represent a wide variety of functional forms: both univariate and multivariate, both additive and interactive, and both linear and piecewise constant. The 8 functions that we chose are as follows:

$$\begin{gathered} f_1\left(x\right)=0,f_2\left(x\right)=5{\mathbb{I}}_{\left\{x_1>1\right\}}-5,f_3\left(x\right)=2x_1-4, \\ {f}_4\left(x\right)=x_2{x}_4{x}_6+2x_2{x}_4\left(1-x_6\right)+3x_2\left(1-x_4\right)x_6+4x_2\left(1-x_4\right)\left(1-x_4\right)+5\left(1-x_2\right)x_4{x}_6 \\ +6\left(1-x_2\right)x_4\left(1-x_6\right)+7\left(1-x_2\right)\left(1-x_4\right)x_6+8\left(1-x_2\right)\left(1-x_4\right)\left(1-x_6\right), \\ {f}_5\left(x\right)=x_1+x_3+x_5+x_7+x_8+x_9-2, \\ {f}_6\left(x\right)=4{\mathbb{I}}_{\left\{x_1>1\right\}}{\mathbb{I}}_{\left\{x_3>0\right\}}+4{\mathbb{I}}_{\left\{x_5>1\right\}}{\mathbb{I}}_{\left\{x_7>0\right\}}+2x_8{x}_9, \\ {f}_7\left(x\right)=\frac{1}{2}\left(x_1^2+x_2+x_3^2+x_4+x_5^2+x_6+x_7^2+x_8+x_9^2-11\right), \\ {f}_8\left(x\right)=\frac{1}{\sqrt{2}}\left(f_4\left(x\right)+f_5\left(x\right)\right). \end{gathered}$$

Each of the 8 functions above is centered and scaled so that with respect to the distribution ${\mathcal{D}}_X$, each has a mean close to 0 and all have roughly the same variance. Table 1 gives the mean and treatment effect functions for the 8 randomized simulations, in terms of the 8 functions above. In these simulations, π(x) = 1/2 for all x ∈ ℝ^p. In addition to the methods described in Sections 4, 5, and 6, we include results for 4 additional estimators for comparison. First, the null estimator is simply the difference ${\overline{Y}}_1-{\overline{Y}}_0$ in mean response between treated and untreated patients. This provides a naive baseline. Second, the TO forest is a random forest built on the TO, as in step 1 of Algorithm 1. Hence, it is a straightforward TO regression as in Section 3. Third, the different-basis (DB) forests are 2 separate forests constructed, one predicting the response in the control group and the other predicting the response in the treatment group. The difference between these 2 predictions is the estimated treatment effect. This method reflects conditional mean regression from Section 3 without using a shared basis. The other competitor is the causal forest of Athey et al,²³ using the gradient. forest R package made available online by the authors. The results of the first batch of simulations are shown in Figure 3.

TABLE 1.

Specifications for the 16 simulation scenarios

	Scenarios
	1, 9	2, 10	3, 11	4, 12	5, 13	6, 14	7, 15	8, 16
n	200	200	300	300	400	400	1000	1000
p	400	400	300	300	200	200	100	100
μ(x)	f8(x)	f5(x)	f4(x)	f7(x)	f3(x)	f1(x)	f2(x)	f6(x)
τ(x)	f1(x)	f2(x)	f3(x)	f4(x)	f5(x)	f6(x)	f7(x)	f8(x)
${\sigma }_Y^2$	1	1/4	1	1/4	1	1	4	4

Note. The 5 rows of the table correspond, respectively, to the sample size, dimensionality, mean effect function, treatment effect function, and noise level. Simulations 1 through 8 use randomized treatment assignment, meaning π(x) = 1∕2. Simulations 9 through 16 have a bias in treatment assignment, specified by 4.

FIGURE 3.

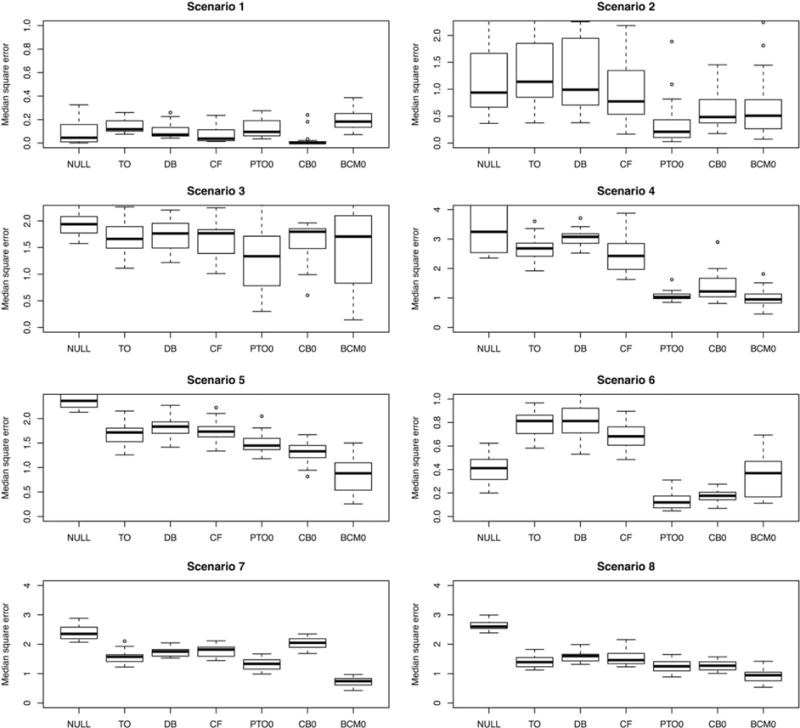
Results across 8 simulated randomized experiments. For details of the generating distributions, see Table 1. The 7 estimators being evaluated are as follows: NULL = the null prediction, TO = transformed outcome forest, DB = different-basis forest, CF = causal forest, PTO0 = pollinated transformed outcome forest (using propensity = 1/2), CB0 = causal boosting, and BCM0 = causal MARS. The ranges of the y axis are chosen to start from 0 and be at least as great as the response standard deviation in each scenario while showing at least 95% of the data

If we pick “winners” in each of the simulation scenarios based on which method has the lowest distribution of errors, causal MARS would win in scenarios 5, 7 and 8, tying with the PTO forest in scenario 4. The PTO forest would win in scenarios 2 and 3, tying with causal boosting in scenario 6. In general, all of the methods outperform the null estimator except in scenario 1, when the treatment effect is constant, and in scenario 6, when the causal forest performed worst. We also observe that the TO regression and conditional mean regression without shared-basis (DB) estimators are not competitive with the ones that we propose, illustrating the value of shared-basis conditional mean regression.

The second batch of simulations matches the parameters listed in Table 1: Scenario 9 is like scenario 1, scenario 10 is like scenario 2, and so on. The difference is in the propensity function. For this second batch of simulations, we use

$$\pi \left(x\right)=\frac{e^{\mu \left(x\right)-\tau \left(x\right)/2}}{1+e^{\mu \left(x\right)-\tau \left(x\right)/2}}.$$ (4)

The interpretation of this propensity function is that patients with greater mean effect are more likely to receive the treatment. This resembles a situation in which greater values of the outcome are worse for the patient, and only patients who have need for treatment will receive it. There are many possible forms for the propensity function, but we focus on this one because it is particularly troublesome, and a good estimator of the treatment effect needs to avoid the pitfall of overestimating the effect because the treated patients have greater mean effect. This is exactly the kind of bias we are most concerned about in observational studies. The results of this second batch of simulations are shown in Figure 4.

FIGURE 4.

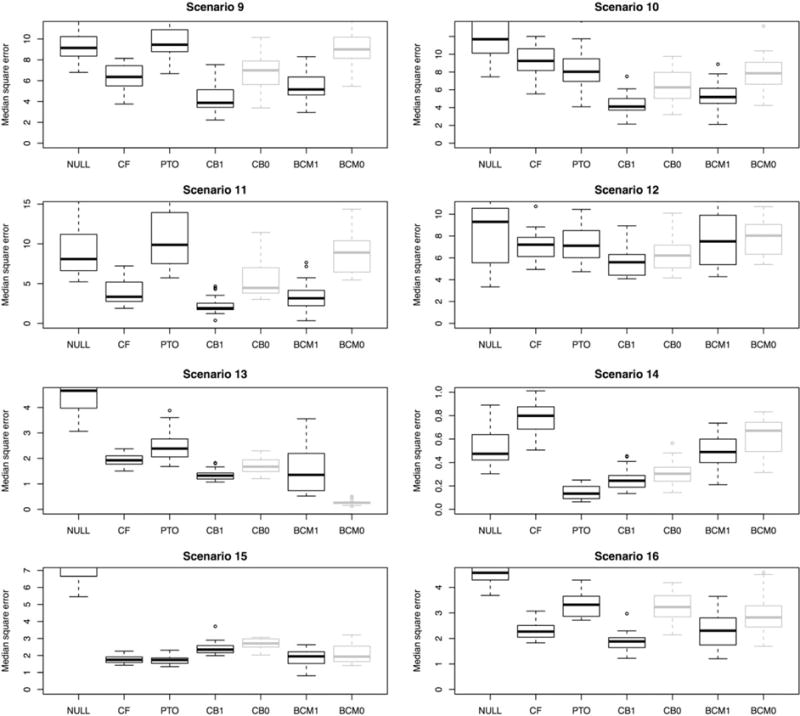
Results across 8 simulated observational studies, in which treatment is more likely to be assigned to those with a greater mean effect. The 7 estimators being evaluated are as follows: NULL = the null prediction, CF = causal forest, PTO = pollinated transformed outcome forest, CB1 = causal boosting (propensity adjusted), CB0 = causal boosting, BCM1 = causal MARS (propensity adjusted), BCM0 = causal MARS. CB0 and CM0 are in gray because they would not be used in this setting. They are provided for reference to assess the effect of the propensity adjustment. The ranges of the y axis are chosen to start from 0 and be at least as great as the response standard deviation in each scenario while showing at least 95% of the data

In the batch of simulations with biased treatment assignments, propensity-adjusted causal boosting shines. In 6 of the 8 simulations, causal boosting as either the lowest error distribution or is one of the 2 methods with the lowest error distribution. Curiously, in scenario 13, unadjusted causal MARS performs very well, but the propensity adjustment ruins this performance. In scenario 15, PTO forest and causal forest produce the best results although all of the methods perform well. Overall, across the 16 simulation scenarios, causal boosting and causal MARS stand out as having the best performance.

Figure 5 illustrates the promised reduction in bias achieved by causal MARS relative to the causal forest, in scenario 8. In this scenario, we have the most complex treatment effect function, with quadratic terms and stepwise interactions between variables. With a large number of observations (n = 1000) relative to the number of variables (p = 100), it pays to use the more flexible causal MARS algorithm, which has much lower bias than the causal forest. The greater flexibility comes at the cost of greater variance, but reducing the bias makes for a more promising candidate for confidence interval construction in future work.

FIGURE 5.

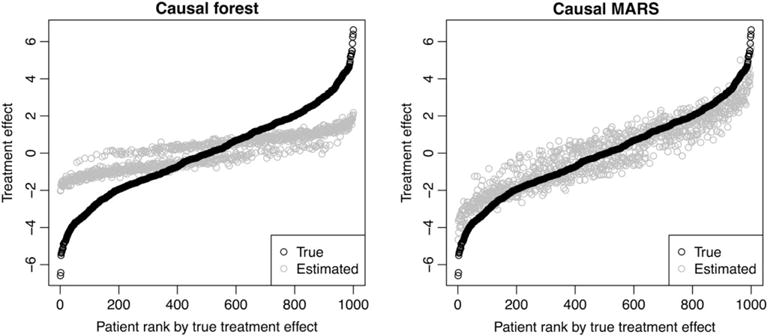
Illustration of the bias of causal forest and causal multivariate adaptive regression splines (MARS). Patient features were simulated once, and then treatment assignment and response were simulated 50 times. Causal forest and causal MARS were applied to each of the 50 simulations, and the average estimate for each patient is plotted

8 REAL-DATA APPLICATIONS

8.1 Randomized trial

In September 2016, the New England Journal of Medicine opened The SPRINT Data Analysis Challenge, based on the complete dataset from a randomized trial of a novel intervention for the treatment of hypertension (high blood pressure).³¹ The goal was open-ended: to draw novel or clinically useful insights from the SPRINT dataset, possibly in tandem with other publicly available data.

The intervention in the randomized trial³¹ was a more intensive control of systolic blood pressure (target 120 mm Hg) than is standard (target 140 mm Hg). The primary outcome of interest was whether the patient experienced any of the following events: myocardial infarction (heart attack), other acute coronary syndrome, stroke, heart failure, or death from cardiovascular causes. The trial, which enrolled 9361 patients, ended after a median follow-up period of 3.26 years, when researchers determined at a preplanned checkpoint that the population average outcome for the intensive treatment group (1.65% incidence per year) was significantly better than that of the standard treatment group (2.19% incidence per year).

In addition to the primary event, for each patient, researchers tracked several other adverse events, as well as 20 baseline covariates recorded at the moment of treatment assignment randomization: 3 demographic variables, 6 medical history variables, and 11 laboratory measurements. The question that we seek to answer in this section is whether we can use these variables to give personalized estimates of treatment effect, which are more informative than the population-level average treatment effect. To answer this question, we apply causal boosting (with 500 trees) and bagged causal MARS to these data.

Of the 9361 patients who underwent randomization, 1172 (12.5%) died, discontinued intervention, withdrew consent, or were lost to follow-up before the conclusion of the trial. There is little evidence (χ² P value = 31%) that this censorship was more common in either arm of the trial. To extract a binary outcome from these survival data, we use as our response the indicator that a patient experiences the primary outcome within 1000 days of beginning treatment, ignoring patients who were censored before 1000 days. Additionally, we dropped the 1.8% of patients who have at least 1 laboratory measure missing. This leaves us with a sample of 7344 patients, which we split into equally sized training and validation sets. In the training set, 223 patients (6.1%) experienced the primary outcome within 1000 days, compared with 244 patients (6.6%) in the validation set.

The results of fitting causal boosting and bagged causal MARS on the training sample of 3672 patients are shown in Figure 6. We proceeded with these 2 methods based on their strength in the simulation study. We observe that the 2 methods yield very different distributions of estimated personalized treatment effects in the aggregate. Causal boosting produces estimates resembling a normal distribution with a standard deviation of about 3.5% risk. In contrast, bagged causal MARS estimates almost all patients to have a treatment effect between −5% risk and +0% risk, but for a small percentage of patients, the treatment effect is much greater or much lesser. The tails of this distribution are much heavier than those of a normal distribution. In fact, a very small number of patients (0.4% of the training sample) are not included in this figure because their treatment effect estimate from bagged causal MARS falls outside of the plotted region.

FIGURE 6.

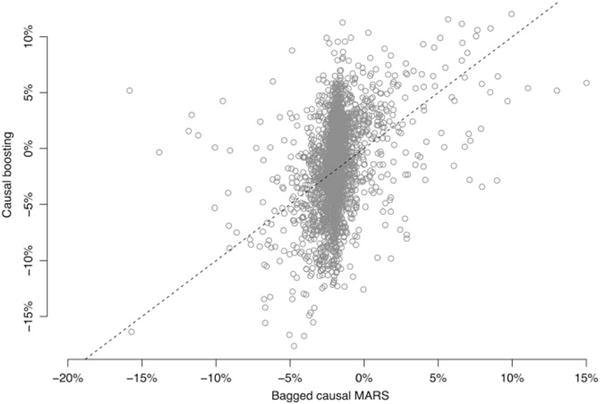
Personalized treatment effect estimates from causal boosting and (bagged) causal multivariate adaptive regression splines (MARS). Each circle represents a patient, who gets a personalized estimate from each method. The dashed line represents the diagonal, along which the 2 estimates are the same

Figure 7 depicts decision trees that summarize the key inferences made by causal boosting and bagged causal MARS. Each leaf gives the average estimated treatment effect for patients who belong to that leaf. Such a decision could be reported to a physician to explain the basis for these personalized treatment effect estimates. According to causal boosting, for example, older patients with high triglycerides stand to gain more from the intensive blood pressure treatment than younger patients with high triglycerides. Among patients with low triglycerides and high glucose, those with low creatinine stand to benefit more from the intensive treatment than those with high creatinine. The decision tree for bagged causal MARS makes the extreme claim that for patients with urine albumin/creatinine ratio above 1874, the average treatment effect is a 21% increase in risk. Discussions with practitioners suggest that the distribution of personalized treatment effects estimated by causal boosting is more plausible than that of bagged causal MARS. As such, we focus our interpretation on the results of causal boosting for the remainder of this section.

FIGURE 7.

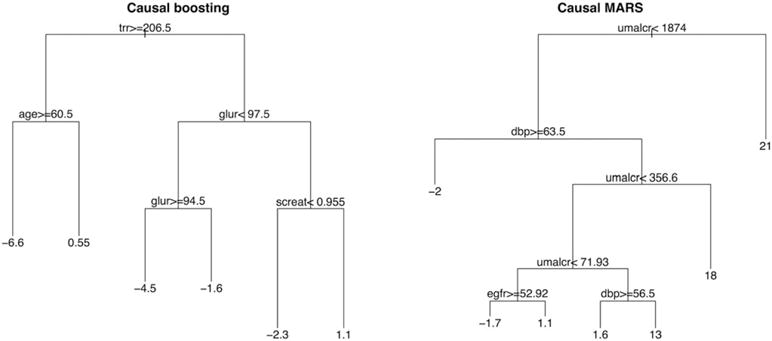
Decision trees summarizing with broad strokes the inferences of causal boosting and (bagged) causal multivariate adaptive regression splines (MARS). The variables are as follows: trr = triglycerides (mg/dL) from blood draw; age = age (y) at beginning of trial; glur = glucose (mg/dL) from blood draw; screat = creatinine (mg/dL) from blood draw; umalcr = albumin/creatinine ratio from urine sample; dbp = diastolic blood pressure (mm Hg); egfr = estimated glomerular filtration rate (mL/min/1.73m²). If the inequality at a split is true for a patient, then that patient is on the left side of the split. The number in each terminal node is the estimated increase in risk due to treatment for a patient in that terminal node

To simplify the results even more than the decision tree does, we note that for both causal boosting and bagged causal MARS, the 2 features that correlate most to the personalized treatment effect estimates are estimated glomerular filtration rate (eGFR) and creatinine. These two variables are highly correlated with each other, as creatinine is one of the variables used to estimate the glomerular filtration rate. Both are used to assess kidney health, and patients with eGFR below 60 are considered to have chronic kidney disease (CKD). Figure 8 shows the relationship between eGFR and the estimated personalized treatment effects from both methods. Despite there being no manual notation in the data that there is something special about an eGFR of 60, we have learned from causal boosting that patients below this cutoff have less to gain from the intensive blood pressure treatment than patients above this cutoff.

FIGURE 8.

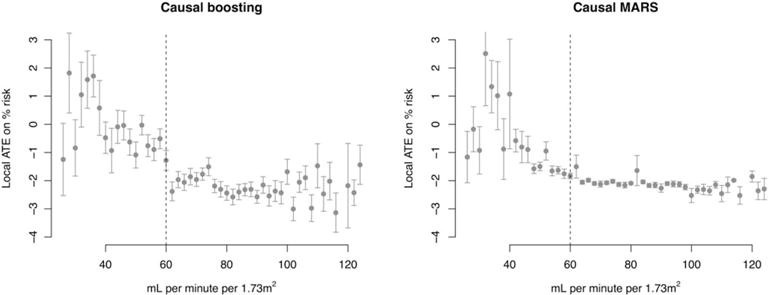
Training set personalized treatment effects, estimated via causal boosting and (bagged) causal multivariate adaptive regression splines (MARS), versus the estimated glomerular filtration rate. Patients are stratified according to the estimated glomerular filtration rate on the x axis, and each point gives the average personalized treatment effect among patients in that stratum. Error bars correspond to 1 standard error for the mean personalized treatment effect. The vertical dashed line represents a medical cutoff, below which patients are considered to suffer from chronic kidney disease. ATE, average treatment effect

Note that we are not only interested in whether a patient’s personalized treatment effect is positive or negative. Intensive control of blood pressure comes with side effects and should only be assigned to patients for whom the benefit of reducing the risk of an adverse coronary event is substantial. The results of causal boosting on the training set suggest that patients with CKD have less to gain from this treatment than do other patients.

8.1.1 Validation

The results above tell an interesting story: If you are a patient with CKD (eGFR < 60), you are expected to benefit less from intensive blood pressure control. As discussed in Section 5.1, validating treatment effect estimates is challenging because we do not observe the treatment effect for any individual patient. In this section, we make an attempt to validate the more general conclusion from the previous section: that the treatment has less benefit for patients with CKD.

Figure 9 shows the results of fitting causal boosting and bagged causal MARS on the held-out validation set of 3672 patients. Bagged causal MARS again picks up on a similar negative relationship between eGFR and the treatment effect. Meanwhile, causal boosting does not tell the same story as in the training set. For these estimates, there is no clear relationship with eGFR in the validation set.

FIGURE 9.

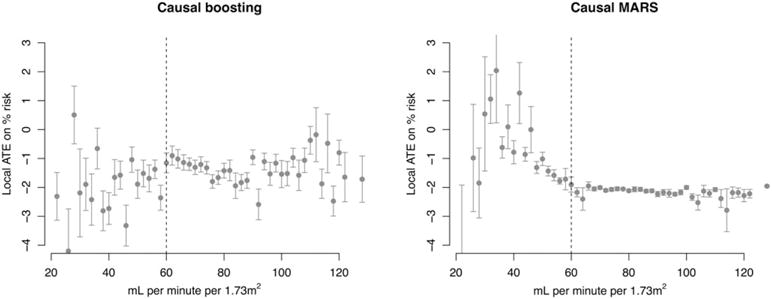
Validation set personalized treatment effects, estimated via causal boosting and (bagged) causal multivariate adaptive regression splines (MARS), versus the estimated glomerular filtration rate. Patients are stratified according to the estimated glomerular filtration rate on the x axis, and each point gives the average personalized treatment effect among patients in that stratum. Error bars correspond to 1 standard error for the mean personalized treatment effect. The vertical dashed line represents a medical cutoff, below which patients are considered to suffer from chronic kidney disease. ATE, average treatment effect

It is promising that at least bagged causal MARS leads us to the same finding as both methods do in the training set. The team from Boston University, which placed second in the SPRINT Data Analysis Challenge, made the same finding as shown in the causal boosting results. They found that intensive blood pressure management does not improve primary outcomes for patients with CKD.³² Something that the authors do not address is why they chose to analyze patients with CKD. Presumably, they used some combination of prior medical knowledge and manual hypothesis selection. In our training set, we came to the same conclusion using both methods without the benefit of either of these steps. The lack of agreement by causal boosting on the validation set could be explained by insufficient power. The ratio of primary outcome-positive patients (223) to covariates (20) in the training set may not be enough, considering that we cannot know the true signal-to-noise ratio in this application.

In addition to the qualitative validation above, we considered and ultimately rejected more quantitative validation techniques. As described in Section 5.1, validation for causal inference is more complicated than for supervised learning, which relies on measures like mean square error and misclassification error. Because we do not observe point estimates of the treatment effect for individual patients, treated and untreated patients need to be grouped together in some way to yield a treatment effect point estimate. One idea is to pair each treated patient with the nearest untreated neighbor and vice versa. In simulations (where the truth is known), this did not work well because even in moderately small dimensions, like 20 covariates, nearest neighbors tend not to be very similar to each other. One solution is to use an adaptive nearest-neighbor technique that learns variable importance, and this is the approach used in Section 5.1. But this is not well suited for comparing between methods because it requires substantial modeling assumptions beyond summarizing the data. We settled on a qualitative validation addressing the question, “Are the actionable conclusions from the training set borne out in the validation set?”

8.2 Observational study

In this section, we continue to investigate heterogeneous treatment effects for treatments of high blood pressure. Four common classes of treatment are angiotensin-converting enzyme (ACE) inhibitors, beta blockers, calcium channel blockers, and diuretics. Literature suggests that ACE inhibitors tend to work well for patients who do well on beta blockers and that calcium channel blockers tend to work well for patients who do well on diuretics.³³ For a patient newly diagnosed with hypertension, it would be useful to know whether they would respond better to a drug in the ACE inhibitors/beta blockers (A/B) groups or a drug in the calcium channel blockers/diuretics (C/D) groups.

We used anonymized EMRs from Stanford Health Care to construct a cohort of 5242 patients who were diagnosed with high blood pressure and then were prescribed one of the antihypertensives above within 1 year of the diagnosis and were not prescribed an antihypertensive drug from a different group within 90 days of the initial prescription. We required that the medical record include blood pressure measurements at one point before antihypertensive prescription and another point at least 30 days after prescription. In addition to blood pressure data, we have 644 additional variables describing the patients: 9 demographic variables, 25 laboratory measurements, 250 recent prescriptions, and 360 recent diagnoses. Laboratory values present in over 85% patients in the time prior to initial treatment were included as features. If a patient had more than one value recorded, the most recent value was used. Patients without recorded values had those values imputed as column means. The recent prescription and recent diagnosis variables indicate whether the patient has been prescribed each drug or diagnosed with each ailment within the past 6 months.

We randomly split the data into equally sized training and validation sets of 2621 patients each. In the training set, 1837 patients received an antihypertensive in the A/B group, which we label as treatment. Patients who were prescribed a drug in the C/D group are considered control group patients. In the validation set, 1834 patients are in the treatment group. As described in Section 2.1, we trained a random forest on the training and validation sets together to estimate the probability of each patient being in the treatment group, based on covariates. We used cross-validation to determine the number of variables to try at each split (25) and the minimum node size (5) for each tree. Figure 10 shows the distribution of propensity scores across both training and validation sets, along with the cutoffs for 5 propensity strata into which the patients were binned.

FIGURE 10.

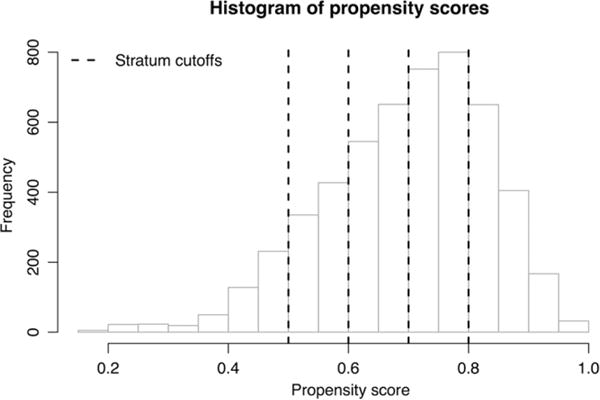
Histogram of propensity scores for real observational data application. The propensity score is the estimated probability that the patient would receive an A/B treatment (instead of a C/D treatment) based on the patient's covariates. Patients were binned into propensity score strata with cutoffs at 0.5, 0.6, 0.7, and 0.8

The response of interest is change in systolic pressure from pretreatment measurement to posttreatment measurement. We applied causal boosting (with cross-validation) and causal MARS to these data to estimate personalized treatment effects for the patients, fitting each method on both training and validation sets. Here, the agreement between models and between data subsets was much greater than in Section 8.1, but the conclusion is less interesting. The number of trees selected for causal boosting was 1 in the training set and 2 in the validation set—effectively a null result. In the training set, 96.4% of patients are estimated to have a treatment effect of +0.01 mm Hg, meaning that there is no practical difference between the treatments. The standard deviation in response (change in systolic blood pressure) is 20 mm Hg. In the validation set, 96.0% of patients are estimated to have a treatment effect of −0.01 mm Hg. The training set and validation set distributions of personalized treatment effects from causal MARS are shown in Figure 11. Almost all estimates are between −0.1 and +0.1 mm Hg.

FIGURE 11.

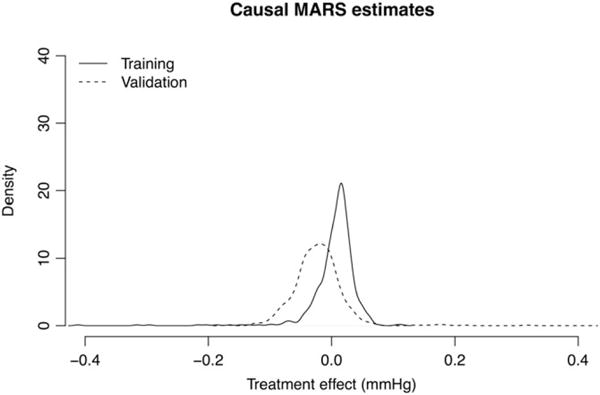
Densities of causal multivariate adaptive regression splines (MARS) treatment effect estimates in training and validation sets. The results on both data subsets agree that almost all personalized treatment effects are practically 0

The results of both models suggest that there is no evidence in these data for a practical difference between the A/B drug group and the C/D drug group and there is no evidence for heterogeneity between patients in this null treatment effect. This is likely a limitation of the particular dataset. Noisy blood pressure measurements and unreliable follow-up could cover up a true treatment effect heterogeneity. Despite prior evidence of the A/B and C/D groupings, there is likely heterogeneity being hidden by grouping those classes together—each drug class (ie, A, B, C, or D) is already an amalgamation of 10 to 50 unique drugs. Nonetheless, this dataset is useful for illustrating the application of our methods to observational data, and the null finding is consistent between both methods.

9 DISCUSSION

We have proposed and compared a number of different methods for estimating heterogeneous treatment effects from high-dimensional covariates. The causal boosting and bagged causal MARS approaches seem particularly promising in simulations. Both of these methods found in the SPRINT data a relationship between kidney health and the treatment effect that has also been identified by other researchers.³² An important next step is confidence interval construction. We have developed causal MARS so that it would be conducive to confidence interval construction, but we leave this task to future work.

Another area of future work is to generalize these methods to handle other data types. In Sections 7 and 8.2, the outcome variables are continuous. In Section 8.1, the SPRINT dataset has survival (time-to-event) outcome that we dichotomize into a binary variable, sacrificing some power. It would be preferable to adapt the techniques to make full use of survival data with censorship. This would mean developing data type–specific methods for choosing the regression basis (see Section 3.1) and estimating the treatment effect given the basis.

APPENDIX A

In this appendix, we outline the already-established techniques for using propensity score to adjust for bias in treatment assignment for observational studies in which the goal is to estimate a population ATE. Define f(x) as themarginal feature density and f₁(x) as the conditional density of X given T = 1 (and likewise f₀(x)), where T is the binary treatment indicator, and let ${\pi }_1=\mathrm{\mathbb{P}}\left(T=1\right)$ be the marginal proportion of treated. Let ${\mu }_1\left(X\right)=\mathbb{E}\left[Y|T=1,X\right]$, and likewise μ₀(X), and τ(X) = μ₁(X) − μ₀(X). Finally, let $\pi \left(X\right)=\mathrm{\mathbb{P}}\left[T=1|X\right]$ be the treatment propensity.

A.1 | TO averaging

Note that the TO

$$Z\equiv T\frac{Y}{\pi \left(X\right)}+\left(1-T\right)\frac{-Y}{1-\pi \left(X\right)}$$

satisfies

$$\begin{gathered} \mathbb{E}\left[Z|X\right]=\mathrm{\mathbb{P}}\left(T=1|X\right)\frac{1}{\pi \left(x\right)}\mathbb{E}\left[Y|T=1,X\right]-\mathrm{\mathbb{P}}\left(T=0|X\right)\frac{1}{1-\pi \left(x\right)}\mathbb{E}\left[Y|T=1,X\right] \\ =\mathbb{E}\left[Y|T=1,X\right]-\mathbb{E}\left[Y|T=0,X\right]={\mu }_1\left(X\right)-{\mu }_0\left(X\right)=\tau \left(X\right). \end{gathered}$$

Hence, if the expectation of Z is evaluated with respect to the distribution of X,

$${\mathbb{E}}_X\left[Z\right]={\mathbb{E}}_X\left[\mathbb{E}\left[Z|X\right]\right]={\mathbb{E}}_X\left[\tau \left(X\right)\right].$$

In other words, the TO is unbiased for the ATE. So a natural estimator for the ATE in a sample of patients would be the sample mean of the TO. This justifies for example using Z as a response to grow a random forest in our PTO forest.

A.2 | Propensity score stratification

Note that it is not necessarily the case that E[Y|T = 1] = E[μ₁(X)|T = 1] and E_X[μ₁(X)] are the same; it is possible that conditioning on T changes the distribution of X and consequently the distribution of μ₁(X). This is the essence of why we cannot ignore nonrandomized treatment assignment in observational studies. However, it is the case that

$$\mathbb{E}\left[Y|T=1,\pi \left(X\right)\right]=\mathbb{E}\left[{\mu }_1\left(X\right)|\pi \left(X\right)\right].$$

To see this, note that X ⫫ T|π(X) because by assumption T ∼ Binomial(1, π(X)). Hence, the conditional distribution of X given π(X) and T is the same as the conditional distribution of X given π(X). This implies that

$$\mathbb{E}\left[Y|T=1,\pi \left(X\right)\right]=\mathbb{E}\left\{\mathbb{E}\left[Y|T=1,X\right]|T=1,\pi \left(X\right)\right\}=\mathbb{E}\left[{\mu }_1\left(X\right)|\pi \left(X\right)\right].$$

What this says is that for fixed π(X), the mean response under treatment is unbiased for the conditional expectation of μ₁(X). This equality holds for any value of X, so the expectations of these 2 quantities are the same with respect to the distribution of π(X):

$${\mathbb{E}}_{\pi \left(X\right)}\left[\mathbb{E}\left[Y|T=1,\pi \left(X\right)\right]\right]={\mathbb{E}}_{\pi \left(X\right)}\left[\mathbb{E}\left[{\mu }_1\left(X\right)|\pi \left(X\right)\right]\right]={\mathbb{E}}_X\left[{\mu }_1\left(X\right)\right].$$

This leads to the following estimator for ${\mathbb{E}}_X\left[{\mu }_1\left(X\right)\right]$: Compute the average response for all treated patients for each value of the propensity, and integrate with respect to the distribution of the propensity. In practice, we approximate this by using a rough approximation to the distribution of π(X): Define strata (or bins) of the propensity score, for example (0, 0.1], …, (0.9, 1). Within each stratum, find the average response among treated patients. Then combine these values in a weighted average, weighting according to the frequency of each stratum. This is our estimate of ${\mathbb{E}}_X\left[{\mu }_1\left(X\right)\right]$. We follow the same procedure in the control arm to estimate ${\mathbb{E}}_X\left[{\tau }_1\left(X\right)\right]$, and the difference is our estimate of ${\mathbb{E}}_X\left[{\tau }_1\left(X\right)\right]$.

A.3 | Inverse probability weighting

From Bayes’ theorem, f₁(x) = f(x)π(x)/π₁. Consider weighting this density with weights proportional to 1/π(x). The density of this weighted distribution is given by

$${\stackrel{\sim }{f}}_1\left(x\right)=\frac{\frac{1}{\pi \left(x\right)}f\left(x\right)\pi \left(x\right)/{\pi }_1}{{\displaystyle {\int }_{\mathrm{ℝ}}\frac{1}{\pi \left(x\right)}f}\left(x\right)\pi \left(x\right)/{\pi }_1}dx=\frac{f\left(x\right)/{\pi }_1}{{\displaystyle {\int }_{\mathrm{ℝ}}f\left(x\right)/{\pi }_{1}dx}}=\frac{f\left(x\right)/{\pi }_1}{1/{\pi }_1}=f\left(x\right).$$

Hence, the weighted conditional distribution of X given T = 1 is the same as the marginal distribution of X. So the expectation of any function of X with respect to this distribution is the same as with respect to the marginal distribution of X. Specifically, using $\stackrel{\sim }{X}$ to denote the random variable following the weighted density ${\stackrel{\sim }{f}}_1\left(x\right)$,

$${\mathbb{E}}_{\stackrel{\sim }{X}}\left[{\mu }_1\left(\stackrel{\sim }{X}\right)\right]={\mathbb{E}}_X\left[{\mu }_1\left(X\right)\right].$$

On the basis of this result, we use the sample mean of the response in the treatment arm, with weights proportional to the inverse of the propensity, as an unbiased estimator for ${\mathbb{E}}_X\left[{\mu }_1\left(X\right)\right]$. Similarly, in the control arm, we use weights proportional to 1/(1 − π(x)) to get an unbiased estimate for ${\mathbb{E}}_X\left[{\mu }_0\left(x\right)\right]$. The difference between these 2 is our estimate for ${\mathbb{E}}_X\left[\tau \left(X\right)\right]$.