Quantitative image analysis for evaluation of tumor response in clinical oncology

Abstract

The objective, accurate, and standardized evaluation of tumor response to treatment is an indispensable procedure in clinical oncology. Compared to manual measurement, computer-assisted linear measurement can significantly improve the accuracy and reproducibility of tumor burden quantification. For irregular-shaped and infiltrating or diffuse tumors, which are difficult to quantify by linear measurement, computer-assisted volumetric measurement may provide a more objective and sensitive quantification to evaluate tumor response to treatment than linear measurement does. In the evaluation of tumor response to novel oncologic treatments such as targeted therapy, changes in overall tumor size do not necessarily reflect tumor response to therapy due to the presence of internal necrosis or hemorrhages. This leads to a new generation of imaging biomarkers to evaluate tumor response by using texture analysis methods, also called radiomics. Computer-assisted texture analysis technology offers a more comprehensive and in-depth imaging biomarker to evaluate tumor response. The application of computer-assisted quantitative imaging analysis techniques not only reduces the inaccuracy and improves the reliability in tumor burden quantification, but facilitates the development of more comprehensive and intelligent approaches to evaluate treatment response, and hence promotes precision imaging in the evaluation of tumor response in clinical oncology. This article summarizes the state-of-the-art technical developments and clinical applications of quantitative imaging analysis in evaluation of tumor response in clinical oncology.

Quantitative image analysis for evaluation of tumor response is the extraction of quantifiable tumor characteristics (such as tumor size and viability) in medical images (such as computed tomography, CT; or magnetic resonance imaging, MRI), termed tumor imaging biomarkers, for monitoring of tumor progression or assessment of tumor response to treatment.¹ Quantitative imaging analysis provides a wide range of techniques for extracting objective and quantifiable tumor imaging biomarkers for the application of precision imaging in clinical oncology.²

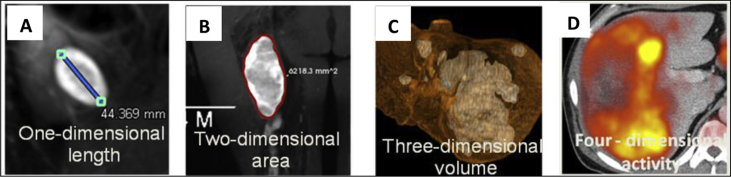
Tumor imaging biomarker quantifies the tumor burden describing the macroscopic and/or microscopic structures of a tumor³ (Fig. 1). Macroscopic structures refer to the overall characteristics of a tumor such as tumor size and shape. The quantification of tumor size tends to be represented as unidimensional (measurement of the longest diameter), bidimensional (measurement of the product of the longest diameter and its longest perpendicular diameter, i.e., the area), and volumetric (measurement of tumor volume) measurements. Whereas, microscopic structures refer to the biological or pathological characteristics within a tumor such as the local image textural patterns (e.g., signal intensity and heterogeneity), the hemodynamics parameters (e.g., dynamic perfusion parameters). Tumor imaging biomarkers are deemed to be accurate and reproducible.

Fig. 1.

Tumor imaging biomarker. Tumor imaging biomarker quantifies the tumor burden describing the macroscopic and/or microscopic structures of a tumor such as the unidimensional (A), bidimensional (B), volumetric (C), and viability (D) measurements of a tumor.

The imaging evaluation of tumor response to treatment measures the changes of tumor imaging biomarkers before and after treatment, and classifies tumor responses into four categories: complete response (CR), partial response (PR), stable disease (SD), and progressive disease (PD).⁴

The criteria for tumor response evaluation vary in terms of tumor types and treatment methods. In 1981, the World Health Organization (WHO) published the first criteria for solid tumor response evaluation.⁵ The WHO criteria adopted bidimensional measurement for quantifying tumor burden and have been widely implemented around the world since the end of the last century until early this century.4, 5 The Response Evaluation Criteria in Solid Tumors (RECIST) published in 2000 and its revised version (RECIST 1.1) in 2009 adopted the unidimensional instead of bidimensional measurement to quantify tumor burden.⁶ Nowadays, RECIST represents the internationally recognized evaluation criteria for solid tumors.4, 6 The modified RECIST (mRECIST) published in 2005 exploits changes observed in arterial-phase dynamically enhanced CT or MRI to evaluate changes of viable tumors.⁷ The mRECIST criteria are the consensus criteria for evaluating the response of primary hepatocellular carcinoma (HCC) to targeted therapy.4, 7 The immune related response criteria (irRC) published in 2009 are a set of criteria for the assessment of immunotherapy.⁸ With the advent of oncologic therapies (targeted therapy, immunotherapy, etc.), imaging modalities [positron emission tomography (PET), nuclear imaging, etc.], and understanding of tumor biology, the response assessment criteria are also evolving.⁴ Various disease specific and therapy specific criteria were proposed (Table 1).

Table 1.

Comparison of response assessment criteria.

Criteria	Expanded abbreviation	Versions	Image index	Disease group
WHO	World Health Organization	1981	SPD	Solid tumors
RECIST	Response Evaluation Criteria in Solid Tumors	2000, 2009	Longest diameter	Solid tumors
Cheson	Cheson	1999, 2007, 2014	SPD	Lymphoma
Choi	Choi criteria	2007	Longest diameter and CT attenuation	Sarcoma
irRC	Immune Related Response Criteria	2009	SPD	Melanoma, lung cancer, etc
irRECIST	Immune Related RECIST	2013	Longest diameter	Melanoma, lung cancer
mRECIST	Modified RECIST	2005	Longest diameter	Hepatocellular cancer
PCWG	Prostate Cancer Working Group	1999, 2007	Number of tumors	Bone lesions in prostate cancer
MDA	MD Anderson criteria	2004	Longest diameter	Bone lesions in breast cancer

SPD: Sum of the product of the perpendicular diameters; CT: computed tomography.

Reliable evaluation of tumor response depends on two aspects: the accurate and reproducible measurement of tumor burden, and the implementation of standardized assessment criteria of tumor response. For the purpose of a reliable and efficient evaluation of tumor response in clinical practice and clinical trials, we are still confronted with a number of challenges: (1) How to perform accurate and reproducible linear measurements of tumor burden? (2) How to perform advanced volumetric measurements of tumor burdens that are difficult to quantify by conventional linear measurement? (3) How to develop novel texture-based imaging biomarkers that provide more comprehensive and effective quantification of tumor burden when size-based measurements do not necessarily reflect tumor response to therapy? (4) How to implement the standardized response evaluation criteria in clinical environments?

Computer-assisted quantitative image analysis techniques may provide a solution to the aforementioned challenges, and play important roles in the implementation of standardized tumor assessment criteria in clinical practice. This article summarizes the state-of-the-art of technical developments and clinical applications of quantitative image analysis in tumor quantification in evaluation of tumor response in clinical oncology.

How to perform accurate and reproducible linear measurements of tumor burden?

Linear measurement is the conventional tumor imaging measurement, which quantifies tumor burden by using the longest diameter (RECIST criteria) or the product of perpendicular longest diameters (WHO criteria) of a tumor on transversal images. Tumor responses are evaluated in terms of the changes in tumor size represented by the sum of linear measurements of all targeted lesions. The current internationally recognized tumor response evaluation criteria (e.g., RECIST and WHO) are established based on linear measurements. These criteria are intently designed for evaluation of tumors treated by conventional cytotoxic radiotherapy or chemotherapy, which aims to annihilate tumor cells or trigger tumor regression (shrink down).

The advantages of linear measurement are the simplicity of the method, clearness to interpret, generalizability to practice, and the sufficient experiences accumulated from its long-term use in clinical applications and clinical trials. However, several important factors may affect the reliability of measurement and assessment including the quality of imaging examination, the choice of the targeted lesions, and the accuracy and reproducibility of the measurement. The subjective linear measurement has been criticized for its low reproducibility and high inter- and intra-observer variabilities of the assessment. Several studies observed that the intra-observer variability was among 6%–14%, and the inter-observer variability was approximately 10%–25%.⁹ These measurement variabilities may lead to a misinterpretation of tumor response. Some studies observed that the misclassification of tumor responses caused by inter-observer measurement variabilities was as high as 43% (WHO) and 30% (RECIST).¹⁰

A precise linear measurement depends on two technical aspects: (1) whether the user-defined endpoints of diameters are located on the boundary of a tumor; and (2) whether the user-measured diameter or the perpendicular diameters are the largest.

Computer-assisted linear measurement may provide a technical solution for the more accurate and reproducible measurements of tumor diameters.11, 12

Edge detection is a fundamental technique in image processing and computer vision. Edge is defined as the discontinuities in intensity or color. Edge position is defined mathematically by using the maximum gradient (first-order derivative) or zero-crossing of second-order derivatives of signal intensity. Although the edge model is clearly defined, the boundary detection is a non-trivial task considering the noise in the images and the variance of signal intensities. There is a large body of different edge detection methods developed in literature,13, 14, 15, 16, 17, 18 which mainly differ in the types of smoothing filters that are applied and the way the measures of edge strength are computed.

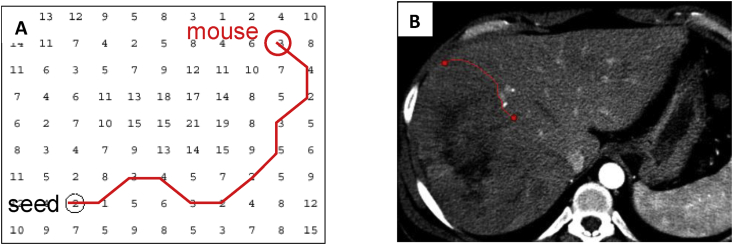
A transversal image can be represented by a 2D weighted bi-directed graph, in which one node corresponds to a pixel in the image. Each node (pixel) has 8 connecting links (edges) to its neighboring nodes (pixels), and each node and link has an associated cost. Edge features such as Laplacian zero-crossing, gradient magnitude and gradient direction are incorporated into the computation of local cost.¹⁹ The cost between two nodes (pixels) is a weighted sum of each corresponding local costs on both nodes and the link between these nodes. The local boundary of a region-of-interest (ROI) on a 2D transversal image is defined as the optimal path with the minimum cost between two corresponding nodes in the graph, as illustrated in Fig. 2. This path is considered to be the global optimal solution and thus a stable solution, which ensures the stability and reproducibility to detect the boundary of a tumor.

Fig. 2.

(A) A contour on a 2D transversal image is defined as the optimal path with the minimum cost between two corresponding nodes in the graph, which can be searched by dynamic-programming methods such as Dijkstra's algorithm.20, 21 (B) A contour in the image corresponds to the optimal path in (A).

The user-defined seed points in boundary tracking may cause some variability. A possible solution is the re-selection of seed points with minimum cost on adjacent segments of traced boundaries.¹⁹ Active contour models,22, 23 which use an energy minimizing spline curve guided by external constraint forces and image forces toward image boundaries, are more general models for boundary extraction and may be less sensitive than interactive seed-pointing by extraction of the entire contour. However, the accuracy of active contour models are sensitive to local minimum values and depends on the convergence policy.²⁴

Boundary separates an ROI such as a tumor from its background. The diameter of an ROI equals to the diameter of the vertices of its convex hull in computational geometry. Consequently, to compute the diameter of a set of points (or pixels) on the plane, we only need to consider the vertices on its convex hull. The rotating calipers algorithm calculates the diameter in a point set or a mask by evaluating the antipodal distance between any pair of vertices in a convex hull.²⁵ This algorithm is very computationally efficient thus “real-time” calculating of the diameter.

Therefore, computer-assisted linear measurements may substantially reduce subjective errors by using automated tumor boundary detection and longest diameter calculation techniques.

How to perform advanced volumetric measurements of tumor burdens?

Linear measurement for response evaluation is based on the assumption that tumors grow or shrink in a symmetrical and spherical manner.²⁶ This assumption rarely holds in practice due to the facts that tumors are inhomogeneous and their growth patterns are constrained by neighboring anatomies. Thus, linear measurements tend to result in misinterpretation of tumor response. First, linear measurement only quantifies the 1-dimensional (1D) size of a 3-dimensional (3D) object, which may not reflect the changes related to the actual tumor size in a precise manner. Second, the defined range of tumor size for the stable disease (SD) category is too wide based on linear measurement, which reduces the sensitivity of evaluation. For example, a tumor with a baseline diameter of 4 cm is considered SD within diameters of 2.8–4.8 cm in the follow-up according to RECIST. Third, tumors may be difficult or even impossible to be quantified or represented by linear measurements such as in the case of irregularly-shaped lesions, or lesions attached to hollow organs that vary in size depending on the filling status of the organ, and thereby prevent them from being quantified by an accurate and reproducible linear measurement.

Computer-assisted volumetric measurement becomes clinically available with the advent of recent improvements in CT and MRI scanning technology and the developments in image-segmentation software. Unlike linear measurements, volumetric measurements directly quantify the volume of a tumor, which reflects the actual size of a tumor.²⁶ Various studies have indicated that response evaluation based on volumetric quantization is better correlated to disease progression than those based on linear measurement.27, 28

Image segmentation is the core technology to computer-assisted volumetric tumor measurement. Image segmentation separates images into a group of volumetric ROIs or clinically meaningful regions such as organs or tumors. A 3D ROI can be represented by a group of contours or a set of voxels. In terms of the ROI identification, region-based segmentation methods classify images into regions that have common cohesive properties such as using region-growing,²⁹ clustering30, 31, 32 methods; whereas contour-based segmentation methods detect boundaries (contours) separating different structures such as using edge tracking,33, 34 live-wire19, 35 methods. Based on user interaction, image segmentation may be performed interactively (e.g., the active contour method,22, 36 intelligent scissors,¹⁹ or interactive contouring³⁷), semi-automatically (e.g., region growing,³⁸ graph cut,39, 40 or the deformation model22, 23), or automatically (e.g., iso-surface,⁴¹ level set,42, 43 probability atlas,⁴⁴ or feature classification⁴⁵). Interactive methods outperform semi-automated methods in accuracy and reliability, which in turn outperform fully automated approaches.⁴⁶ However, interactive methods tend to be more time-consuming and require additional user efforts compared to semi- and fully-automated methods, which result in lower repeatability caused by the intra- and inter-observer variability. There is no universal algorithm for segmentation of ROIs in every medical image. Different types of tumors and different image modalities may require different image-segmentation techniques.⁴⁷ For example, requirements of brain tumor segmentation are different from those of lung cancers. The partial volume effect is the major artifact in brain imaging whereas motion artifact is more prominent in thoracic imaging. MRI images are affected by the bias field noise [intensity inhomogeneities in the radiofrequency (RF) field]; whereas CT images encounter mental artifacts, beam hardening, ring artifacts, etc. Thus, a proper segmentation algorithm is deemed to consider all these aspects.⁴⁸

Currently, volumetric measurements based on automated segmentation methods are mainly restricted to the research environment, and have not gained wide acceptance in daily clinical practice.⁴⁹ A highly accurate and robust automated tumor segmentation method remains a challenging problem due to the unpredictability of the tumor appearance, the imaging noise/artifacts, and the specialized anatomical knowledge such as size, shape, location, bilateral symmetry. Noise reduction filters have been developed decades for lowering image noise as a pre-processing step to improve image segmentation.50, 51 There are a large body of automated or semi-automated tumor segmentation techniques developed to directly extract tumor regions using raw intensities. Thresholding-based segmentation technique was widely applied to distinguish tumor from its background.⁵² However, determining optimal threshold in a histogram53, 54, 55 is a difficult task because tumor inhomogeneity and image noises may cause under- and/or over-segmentation. Many researchers combined the threshold-based approach with other methods such as snakes,²² physics-based deformation model,⁵⁶ watershed,⁵⁷ fuzzy clustering,⁵⁸ active contour⁵⁹ and level set⁶⁰ to improve tumor segmentation by combining desirable features such as connectivity and smoothness to counteract noise and boundary irregularities. Recently, machine-learning based segmentation methods have been introduced into this field that gained significant attention including statistical methods and fuzzy logic approaches,⁶¹ support vector machines (SVM),62, 63 neural networks and deep learning.64, 65, 66

The response evaluation using volumetric tumor measurement may overcome many of the defects and insufficiencies of evaluation criteria based on linear measurement.67, 68 First, even for a regular-shaped lesion with simple morphology (e.g., a spherical lesion), volumetric measurements are more sensitive than linear measurements in reflecting changes in the growth or regression of the tumor. When the diameter of a spherical lesion increases by 20% (the threshold of PD defined by RECIST), the volume increases by 72.8%. When the diameter of a spherical lesion decreases by 30% (the threshold of PR defined by RECIST), the volume decreases by 65.7%. For morphologically complex lesions that are more commonly seen in practice, the differences (i.e., in the changes observed by the different methods) can be greater.⁶⁷ Volumetric measurements had showed better sensitivity for detecting PR and disease progression than linear measurement in advanced lung cancer patients.⁶⁹ For example, the NELSON trial demonstrated that the sensitivity of the volume-based protocol (90.9%) was comparable to the linear protocol (90.9%) with a higher specificity (94.9% vs. 87.2%), suggesting that lung nodule management based on nodule size and volume-doubling time performs better in lung cancer screening.⁷⁰ Therefore, volumetric measurements are more sensitive to quantify changes in tumor burden than the linear measurements for both doubling time as well as percentage annual growth. Second, volumetric measurements quantify the total tumor burden of all lesions, and thus overcome the limitation in linear measurements of tumor burden caused by the limited number and the subjective selection of target lesions. Because of its higher sensitivity and overall quantification, response evaluations using volumetric tumor burden may be performed sooner with relatively smaller number of time points and shorter periods for clinical research, and statistical analyses may be more effective.

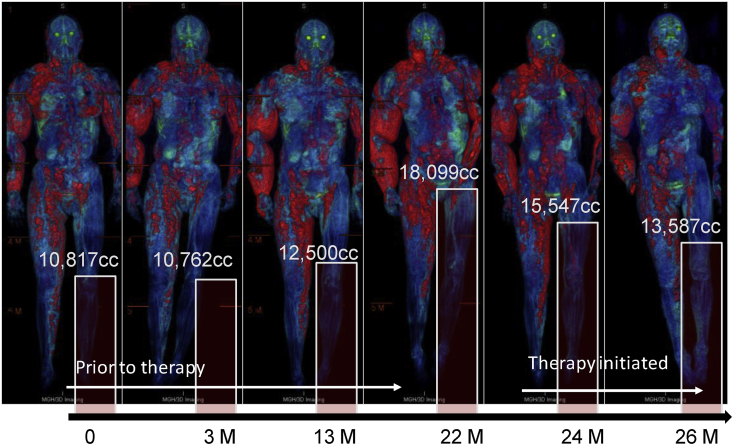
Volumetric tumor measurements have been applied to various types of tumors. In a study observing type II neurofibromatosis patients via volumetric measurements, researchers found that when the tumor diameter (long diameter) increased by (8 ± 6)%, the cubed linear diameter increased by (31 ± 26) %, and the volume measured increased by (61 ± 34) %.⁷¹ Compared to the currently implemented criteria based on linear measurements [e.g., RECIST, mRECIST, and European Association for Study of the Liver (EASL)], the study found that volumetric measurements could more quickly evaluate the prognosis of HCC treated by transcatheter arterial chemoembolization (also called transarterial chemoembolization or TACE).²⁶ Volumetric measurement is becoming a new imaging biomarker for response evaluation and tumor prognosis in clinical routine (Fig. 3).

Fig. 3.

Volumetric quantification of tumor burden of a neurofibromatosis patient illustrates the power of volumetric tumor quantification in delineating the total tumor burden – presence, location, extent and severity, for monitoring of tumors progression and treatment response.

How to develop novel texture-based imaging biomarkers for evaluation of tumor response?

Conventional size-based tumor quantification methods using either linear or volumetric measurements have demonstrated significant limitations in the evaluation of tumor response when being treated with novel oncology therapies such as targeted antiangiogenic therapies or locoregional therapies.⁷² Instead of simply killing all rapidly dividing cells in conventional cytotoxic radiotherapy or chemotherapy, targeted therapy “targets” the molecular difference between cancer cell and normal cell by preventing or blocking tumor development and progression (including cell proliferation, regulation of apoptotic cell death, angiogenesis and metastatic spread) via interfering with specific targeted molecules needed for carcinogenesis and tumor growth.⁴ Because tumors treated in targeted therapy may show formation of internal necrosis with or without a decrease in lesion size (presenting in conventional cytotoxic therapy), size-based tumor measurements do not necessarily reflect tumor response to therapy. Additionally, due to the heterogeneity of the internal structure of a tumor, size-based measurements alone may be insufficient to describe the changes within a tumor before and after treatment.

Texture-based imaging biomarkers quantify the tumor heterogeneity from imaging data using a variety of texture analysis methods to characterize the changes of biological or pathological micro-structures within a tumor for evaluations of treatment responses and tumor prognosis.73, 74, 75 Texture analysis methods provide additional and independent information by quantifying the regional variations in the images, which were divided into four categories: non-spatial methods, local spatial distribution methods, fractal analysis, and a category consisting of filters and transforms.⁷⁶ These methods suggest that specific heterogeneity features, computed from both spatial and temporal images, show potentials as a biomarker for monitoring tumor response.74, 77

Texture is a regular repetition of an element or pattern in an image with the characteristics of intensity, shape, size, etc.⁷⁸ Texture analysis calculates the characteristic imaging features such as histogram statistics features describing signal intensity distribution,⁷⁹ run-length (RL) texture features⁸⁰ encoding the tumor image coarseness, gray level co-occurrence matrix (GLCM) texture features⁸¹ characterizing the gray-level spatial dependence of tumor image, shape-based features depicting the spatial shape of a tumor, for classification, segmentation, and identification of different ROIs.82, 83

Skeletonization, which represents complex 3D shapes as a set of 1D connected lines, is an alternative approach to lower dimensionality while preserving key topological and geometrical features of the object,⁸⁴ which has been widely used in vessel segmentation⁸⁵ and determination of their branching patterns to assess the structural properties of the vessels and their relationship with tumors.⁸⁶ The accurate characterization and description of the vascular network of a lesion provides a new topological texture biomarker to assess the effectiveness of anti-angiogenesis treatments using such as the density of vascular trees, and the 3D curvature of the vessels.87, 88

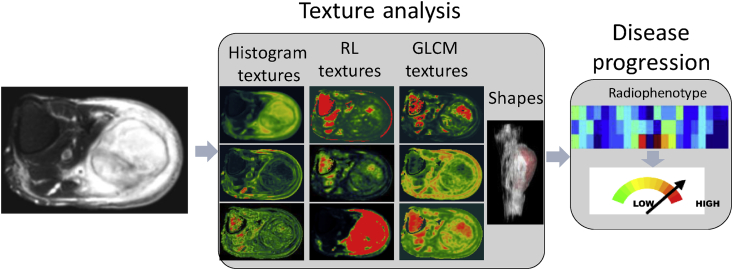
Texture analysis is a new quantitative image analysis technique that has been developing in recent years for evaluating the heterogeneity of a tumor (Fig. 4).

Fig. 4.

Texture analysis for evaluating tumor malignance. RL: run-length; GLCM: gray level co-occurrence matrix.

The Choi criteria were the first to incorporate changes in CT values (or image intensity) within a tumor for evaluating targeted therapy in the treatment of gastrointestinal stromal tumors.⁴ Tumor response is defined as a reduction in lesion size by ≥10% as shown in CT or a reduction in the tumor CT value of ≥15% without the appearance of new lesions. This criteria to some extent improved the less-accurate size-only evaluation of response by RECIST and gained a consensus in community studies and among care providers for gastrointestinal stromal tumor patients.⁴ With additional research, the modified Choi criteria in 2010 determine tumor response as reductions both in maximum diameter by 10% and in CT value by 15% (i.e., both size and functional changes are required to meet the criteria).

Computer-aided texture analysis, by quantifying the distribution pattern of pixels in lesions, provides comprehensive information relating to tumor hypoxia, angiogenesis, and other features.73, 74, 75, 89, 90, 91 Some of these features are related to image properties that are visually perceived by the radiologist, whereas others are more abstract.⁹² For example, heterogeneity is one of the important characteristics of malignant tumors. Quantitative analysis of tumor heterogeneity has potential to become a non-invasive tumor imaging biomarker for tumor prognosis and response evaluation.

This has been demonstrated by prior studies in non-small cell lung cancer, esophageal carcinoma, and colorectal cancer.73, 74 Early studies suggested that imaging-based biomarkers quantifying intra-tumor vascular heterogeneity were related to tumor angiogenesis and the growth factor expression of lesions in breast and liver.73, 74, 75 CT texture analysis reflecting heterogeneity has potential as an early imaging marker for evaluating treatment responses in metastatic renal cell carcinoma.⁹³ Andersen et al⁷⁵ employed CT texture analysis in a study for differentiation of benign and malignant mediastinal lymph nodes in suspected lung cancer patients. The study found that the unfiltered mean CT values of malignant lymph nodes were higher than those of benign lymph nodes. Regression analysis indicated that the sensitivity was 53%, the specificity 97%, and the area under the receiver operating characteristic (ROC) curve 83.4%.⁷⁵

Radiomics is an emerging advanced texture analysis technique for identification of the linkage between tumor imaging biomarkers and the underlying genetic heterogeneity of the tumors.94, 95 The underlying hypothesis of radiomics is that genomic and proteomic microscopic changes or patterns can be expressed in terms of macroscopic image-based features. This hypothesis has been sustained by prior studies in glioblastoma, hepatocarcinoma, lung and head-and-neck cancer.94, 95 By employing machine learning and statistical analysis, tumor image biomarkers (also known as radio-phenotypes) that describe the characteristics of tumor intensity (e.g., high or low signal), tumor heterogeneity (e.g., homogeneous or heterogeneous), as well as tumor shapes (e.g., round or spiculated), are correlated to the clinical manifestations or genotypes of tumors.

Radiogenomics can predict prognosis or therapeutic response.94, 95 Diehn et al⁹⁶ identified that the overexpression of epidermal growth factor receptor (EGFR) was associated with the ratio of the contrast-enhancing volume to the necrotic tumor volume. Aerts et al⁹⁷ revealed that a prognostic radiomic signature was associated with underlying gene-expression patterns in patients with lung or head-and-neck cancer in a clinical study that collected 440 image features (e.g., intensity histogram of tumor images, shape-based features, and texture structure-based features) from 1019 patients with lung cancer and head and neck tumors. In a recent study by Jamshidi et al,⁹⁸ a combination of 28 image features was used as a surrogate of molecular assay to predict disease-specific survival in patients with clear-cell renal cell carcinoma.

Thus, for tumor burdens that present challenges to volumetric measurements, computer-assisted texture analysis and radiomics techniques provide a new dimension to comprehensive and in-depth evaluation of tumor response by decoding the underlying microscopic information within tumors.

How to implement the standardized response evaluation criteria?

The implementation of standardized response evaluation criteria is an indispensable procedure in clinical oncology. Overall survival (OS) is considered to be the gold standard for the endpoint of a clinical trial, which is the best and most reliable index for evaluation of the treatment. However, it takes quite a long time and requires a recorded time of death. In addition, due to the mixing influences of subsequent anti-tumor therapies, the actual impact of a particular tested drug on OS is hard to determine. Therefore, imaging-based response criteria are widely applied as a surrogate for OS as the endpoint of clinical trials.

In the implementation of response evaluation criteria, the main issues are measurement inaccuracy and unregulated evaluation. A retrospective study after re-examination of 876 cases found that 52% (459 cases) of inconsistencies between two observers when employing RECIST to evaluate best overall response, response date, and date of progression.⁹⁹ The main identified sources of these inconsistencies are the selection of the target tumor, the diagnosis of non-target tumors, the determination of non-target tumor development, and tumor measurement errors.

Computer-assisted tumor measurement and response evaluation tools may provide a solution to standardization of the tumors measurement and evaluation, and further reduce subjective errors. Specifically, computer-assisted standardization can be achieved via the following measures in a clinical setting: (1) Selection of appropriate evaluation criteria [e.g., RECIST, mRECIST, immune related RECIST (irRECIST), etc.] based on the type of tumor and the applied treatment for a given patient. (2) Conduction of the standardized evaluation process guided by the built-in evaluation logic in the computer-assisted tool. (3) Management of longitudinal tumor measurement data and image registration of tumors at different time points such as using statistical shape matching100, 101, 102, 103 to ensure the evaluation of the same target lesions. (4) Generation of a separated tumor measurement and evaluation report in addition to the radiologist reading report for cancer patient management.

There are several commercialized software tools available for the aforementioned response evaluation, including Multi-Modality Tracking Tool (MMTT) from Phillips (Koninklijke Philips Electronics N.V., Eindhoven, Netherlands), Vue picture archiving and communication system (PACS) Lesion Management from Carestream Health (Rochester, NY, USA), Mint Lesion from Mint Medical (San Francisco, CA, USA), which allow quantitative tumor measurements and evaluation by RECIST, Cheson, Choi and other criteria. Both MMTT and Vue PACS Lesion Management are PACS dependent, which are only accessible via vender's PACS application; whereas Mint Lesion is a third-party solution.

Hence, the implementation of computer-assisted tools for quantitative image analysis in clinical practice provides a more accurate and standardized manner in tumor response evaluation, which will significantly benefit accurate tumor-node-metastasis (TNM) classification and staging and survival predictions.

Summary

Quantitative tumor imaging biomarker is critical for diagnosis, staging, and treatment evaluation in oncology. Computer-assisted linear measurement is more accurate and reproducible for the quantification of tumor burden than manual measurement. For irregular-shaped and infiltrating or diffuse tumors, which are difficult to quantify by linear measurement, computer-assisted volumetric measurement is a more objective and sensitive method to evaluate tumor response than linear measurement. In the evaluation of tumor response to novel oncologic treatments such as targeted therapy, computer-assisted texture analysis technology may offer a more comprehensive and in-depth imaging biomarker than size-based measurements. The application of computer-assisted quantitative imaging analysis techniques will not only reduce the inaccuracy and improve the objectiveness in quantification of tumor burden, but also facilitate the development of more comprehensive and intelligent approaches to evaluate treatment response, and hence promote precision imaging in the evaluation of tumor response in clinical oncology.

Conflicts of interest

The authors declare that they have no conflicts of interest.

Edited by Pei-Fang Wei