DRUG-NEM: Optimizing drug combinations using single-cell perturbation response to account for intratumoral heterogeneity

Significance

Single-cell high-throughput technologies enable the ability to identify combination cancer therapies that account for intratumoral heterogeneity, a phenomenon that has been shown to influence the effectiveness of cancer treatment. We developed and applied an approach that identifies top-ranking drug combinations based on the single-cell perturbation response when an individual tumor sample is screened against a panel of single drugs. This approach optimizes drug combinations by choosing the minimum number of drugs that produce the maximal intracellular desired effects for an individual sample.

Abstract

An individual malignant tumor is composed of a heterogeneous collection of single cells with distinct molecular and phenotypic features, a phenomenon termed intratumoral heterogeneity. Intratumoral heterogeneity poses challenges for cancer treatment, motivating the need for combination therapies. Single-cell technologies are now available to guide effective drug combinations by accounting for intratumoral heterogeneity through the analysis of the signaling perturbations of an individual tumor sample screened by a drug panel. In particular, Mass Cytometry Time-of-Flight (CyTOF) is a high-throughput single-cell technology that enables the simultaneous measurements of multiple ($>$40) intracellular and surface markers at the level of single cells for hundreds of thousands of cells in a sample. We developed a computational framework, entitled Drug Nested Effects Models (DRUG-NEM), to analyze CyTOF single-drug perturbation data for the purpose of individualizing drug combinations. DRUG-NEM optimizes drug combinations by choosing the minimum number of drugs that produce the maximal desired intracellular effects based on nested effects modeling. We demonstrate the performance of DRUG-NEM using single-cell drug perturbation data from tumor cell lines and primary leukemia samples.

Combination drug therapy promises to improve cancer treatment by targeting multiple signaling and regulatory pathways maintaining tumor progression. As the number of potential FDA-approved cancer drugs increases, the likelihood of identifying effective combination strategies tailored to an individual patient’s tumor increases. Several computational methods have been proposed to identify the optimal combinatorial drug strategies that rely on methods to reconstruct the tumor’s biological network based on high-throughput genomic and proteomic assays (1–4). These approaches and others are often predicated on the idea that an individual tumor’s biology is dominated by a single molecular network under the control of a limited number of master regulators. While this formulation may be a feasible approach for addressing tumor complexity, it can oversimplify the characterization of an individual tumor, which is composed of many different cell types, including different malignant cell types, where each cell type is likely to be under the influence of different networks and/or regulators. This more complex viewpoint challenges the field of combination therapy by suggesting that optimal drug combinations need to account for intratumoral heterogeneity (ITH) at the single-cell level.

ITH is increasingly being recognized as a critical barrier to overcome drug resistance. The most commonly recognized form of ITH is the polyclonal nature of tumors whereby combination therapy largely aims to target divergent clones. A computational algorithm to address this type of heterogeneity by Zhao et al. (5) demonstrates that targeting the predominant clonal subpopulations is not necessarily the best overall strategy. A different type of ITH often described as nongenetic may render even a sensitive monoclonal subpopulation of malignant cells resistant to a given treatment. In this work, we focus on identifying optimal combination strategies based on the single-cell signaling heterogeneity, without necessarily addressing the source of the heterogeneity as genetic or nongenetic. We view this work as a step toward a broader strategy that will ultimately account for ITH at the single-cell level to optimize combination treatments for the individual patient.

Assessing and measuring signaling heterogeneity at the single-cell level has become possible for nonsolid tumors and increasingly for solid tumors. Using mass cytometry (MCM) time-of-flight (CyTOF), one can measure roughly 40 intracellular and surface markers at the level of single cells for hundreds of thousands of cells in an individual sample. Such single-cell data are being generated to study the effects of intracellular signaling changes before and shortly after treatment, thereby providing a high-dimensional drug-induced perturbation response for a single tumor (6, 7). Here, we assume desired changes associated with intracellular signaling markers, before and after treatment, serve as a surrogate for drug effectiveness. Several studies demonstrate that intracellular signaling perturbations to short-term drug exposure can be predictive of long-term drug response (8–10). Assuming this association, we provide a formal optimization method denoted as Drug Nested Effects Models (DRUG-NEM) to analyze single-cell single-drug screening perturbation data for the purpose of identifying optimal drug combinations that account for ITH. In the current context, DRUG-NEM is optimized to select the minimum number of drugs that produces the maximal desired intracellular effect, but the optimization criterion can be easily modified.

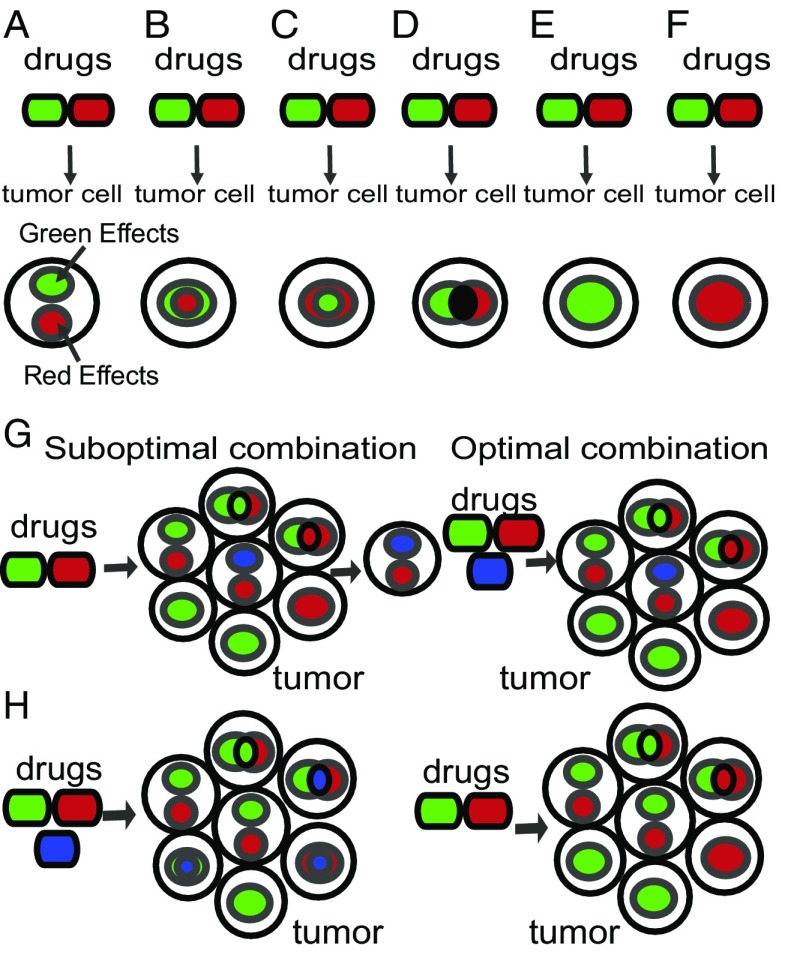
A conceptual illustration of DRUG-NEM is given in Fig. 1, where drugs are color coded by their intracellular effects: red vs. green drug causes red vs. green intracellular effects, respectively. The combination of the green and red drugs may result in a variety of possible desired effects in a single cell (Fig. 1 A–F). For example, use of the two drugs might result in intracellular effects that are (i) disjoint (Fig. 1A), (ii) superset (Fig. 1 B and C), (iii) intersecting (Fig. 1D), or (iv) dominant (Fig. 1 E and F). Depending on the subsetting of the effects, eradication of the single cell would require a single drug (Fig. 1 B, C, E, and F) or both drugs (Fig. 1 A and D). Because a tumor is a collection of cell types, aggregating the drug responses across all of the cell types would be necessary to identify the optimal drug combination. For example, targeting the entire population of cancer cells with red, green, and blue targets using only drug green + drug red may miss cells with uniquely blue targets (Fig. 1G, Left), making it necessary to use the red + green + blue drugs (Fig. 1G, Right). However, if the blue effects are shared with the green and red effects, then using three drugs is suboptimal (Fig. 1H, Left) compared with using only the red + green drugs (Fig. 1H, Right). DRUG-NEM essentially identifies the optimal combination by subsetting drug effects from individual drug responses to identify the minimal number of drugs with the maximal desired intracellular effects.

Fig. 1.

Complexity of drug effectiveness for single-cell intratumor heterogeneity. Phenotypes from targeting a single cell within a tumor with two drugs green + red may result in either (A) disjoint target effects, (B) green targets effects being superset of red targets, (C) red target effects superset of green targets, (D) disjoint and shared effects, (E and F) dominant effects, (G) tumor requiring an additional drug to target all cells with blue effects for maximum effect, or (H) tumor requiring only two drugs instead of three drugs to target all cells.

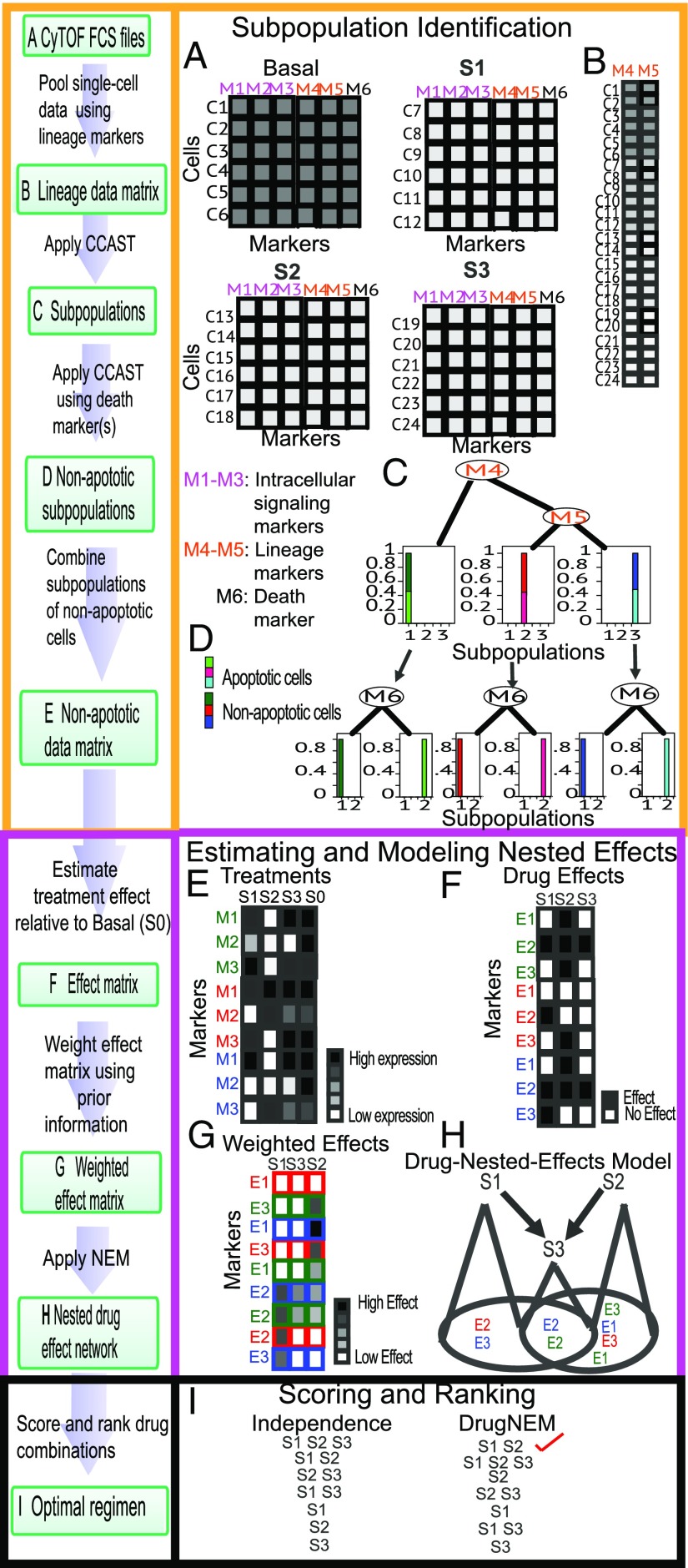
Before applying DRUG-NEM, it is necessary to identify the desired intracellular effects associated with drugs of interest and identify surface markers that capture the heterogeneity of the sample. Single-cell data, before and after drug treatment, are collected and used to quantify changes in the expression of intracellular markers across a panel of drugs. To process these data, DRUG-NEM uses four main steps. The first step identifies the subpopulations within the tumor that are likely to respond differently to drug perturbations (Fig. 2 A–C), thereby accounting for ITH. For the second step, DRUG-NEM computes the drug effect in terms of the probability that a drug $S_j$ has altered intracellular marker $M_i$ in each subpopulation $k$ and this effect is associated with a desired response. These effects are weighted to produce the probability of a desired effect for each marker in each subpopulation. In the third step, DRUG-NEM creates a drug nested effects model (NEM) that accounts for the effects for each marker across all of the subpopulations across all drugs using a graphical model where nodes are drugs and edges define shared or nested effects. The details for computing the DRUG NEM are given below. Using this model, the fourth step of DRUG-NEM is to rank all drug combinations based on a defined scoring function. We have optimized DRUG-NEM to identify the minimal combination of drugs that maximizes the desired intracellular effects for an individual tumor.

Fig. 2.

Framework of DRUG-NEM algorithm. (A) MCM FCS files for each treatment with measured expressions for lineage, intracellular, and death markers. (B) Pooled data matrix from A with rows corresponding to cells and columns representing lineage markers. (C) Output of CCAST applied to pooled data using markers M4 and M5. (D) Decision tree from second run of CCAST based on a significant death marker (M6) showing apoptotic and nonapoptotic cells for each subpopulation. (E) Expression of cells from each subpopulation showing the average intracellular signaling expression measurements for each labeled marker $M_i$ in each nonapoptotic subgroup labeled here as green, red, and blue, respectively, under treatment conditions including no drug (S0). The rows correspond to intracellular signaling markers and the columns to treatments. The legend box corresponds to the gradient from high (black) to low expression (white). (F) Matrix of probability of intracellular signaling effect ($E_i$) associated with each marker across all drugs. A dark box corresponds to an effect and a white box to no effect. An effect is simply the change of state in terms of probability from the baseline condition (S0) due the drugs S1–S3 in E. (G) Subpopulation-level sorted desired effect matrix derived by weighting the intracellular signaling effects in F using data-driven priors. (H) Drug nested effects network optimized using the desired effects from G. (I) Rank of all drug combinations with the best drug combination at the top using scoring distribution estimated from the network in H (DrugNEM) compared with rankings from independent drug effects (Independence).

We first analyze the performance of DRUG-NEM on simulated data to demonstrate key aspects of the algorithm. Next, we demonstrate DRUG-NEM’s performance on HeLa cells, a cervical cancer cell line, analyzed under a CyTOF-based perturbation study with four different treatments: TNF-related apoptosis ligand (TRAIL), MEK inhibitor, pP38MAPK inhibitor, and phosphoinositide 3-kinase (PI3K) inhibitor. DRUG-NEM identified TRAIL and MEK inhibitor as the optimal drug combination. This finding was experimentally validated by measuring fractional cell kill under the different drug combinations. Finally, we demonstrate the application of DRUG-NEM on 30 acute lymphoblastic leukemia (ALL) primary patient samples that were analyzed with a CyTOF-based perturbation study with three separate small molecules: Dasatinib (Das) [ABL-Src tyrosine kinase inhibitor (TKI)], Tofacitinib (Tof) (JAK inhibitor), and BEZ-235 (Bez) (PI3K/mTOR kinase inhibitor). For the majority of the ALL samples, DRUG-NEM selects Das and Bez as the optimal two-drug combination. This finding was confirmed by analyzing the intracellular effects of the two-drug combinations under CyTOF. This two-drug combination was also shown to be effective on 3 ALL-derived cell lines. Together, the HeLa analysis and ALL analyses provide initial results to demonstrate how DRUG-NEM leverages the richness of single-cell perturbation data to account for ITH with the goal of prioritizing drug combinations.

Results

The DRUG-NEM Framework.

DRUG-NEM is an optimization framework designed to identify the minimal combination of drugs that maximizes the desired intracellular perturbation effects for an individual tumor based on single-cell analysis before and after exposure to a panel of single drugs. Key features of DRUG-NEM are illustrated in Fig. 2 for an individual sample analyzed under no treatment (basal state) and following treatment by one of three hypothetical drugs—S1, S2, and S3. Under each condition, single-cell data are collected for six hypothetical markers, M1–M6, measured per cell, where M1–M3 represent the desired intracellular markers, M4 and M5 represent lineage markers that are assumed to be unchanged following short-term treatment response, and M6 is a death marker. For all drug combinations (namely, S1, S2, S3, S1 + S2, S1 + S3, S2 + S3, S1 + S2 + S3), DRUG-NEM ranks the drug combinations in terms of maximum desired effects with the minimum number of drugs based on desired intracellular effects to the individual drugs. DRUG-NEM is comprised of four key steps: (i) subpopulation identification, (ii) estimation of desired effects, (iii) estimation of drug NEM, and (iv) drug combination scoring and ranking based on the drug NEM parameters.

Step 1: Subpopulation identification.

DRUG-NEM accounts for the possibility that the tumor is composed of subpopulations that respond differently to drugs, making it necessary to first identify the subpopulations. To facilitate this step, the selected markers are ideally divided into two types: (i) lineage and (ii) intracellular signaling markers. The lineage markers are used to identify the subpopulations, because they are assumed to remain constant before and shortly after treatment. Changes in the intracellular signaling markers are used to identify the perturbation effects before and shortly after treatment within each distinct subpopulation. We illustrate the subpopulation identification step in Fig. 2 on MCM data produced by CyTOF, even though DRUG-NEM can be extended to other high-dimensional single-cell datasets. MCM data are typically stored in a flow cytometry standard (FCS) file as a data frame with rows representing the cells or events and the columns corresponding to the lineage and intracellular signaling markers of interest as shown in Fig. 2A. Each FCS file or data matrix would correspond to a perturbation. The lineage markers (M4, M5) are preselected for identifying the subpopulations. While the subpopulations can be identified through manual gating using these markers, we recommend a more automated process that starts by pooling all of the single-cell data across all of the conditions including the control (Basal) (Fig. 2B). Several unsupervised subpopulation identification algorithms have been developed for such single-cell data analysis (11–15). We apply Clustering, Classification and Sorting Tree (CCAST) (15) to identify subpopulations of relatively homogeneous cells represented here as three subpopulations, color-coded as green, red, and blue in Fig. 2C. In the case where lineage markers are not available to define the subpopulations, intracellular markers may serve as surrogates, as we will demonstrate later. In each subpopulation, using a single or set of death markers, we apply an additional data filtering step to remove the cells that are fully committed to apoptosis. We illustrate this step with a single death marker (M6), used by CCAST to identify nonapoptotic versus apoptotic cells from each subpopulation (Fig. 2D). We gate out the apoptotic cells and then summarize the signaling expression measurements for each intracellular marker in each nonapoptotic subgroup shown here as a 2D matrix, with rows corresponding to the intracellular markers (M1–M3) and the columns to the treatments including no treatment (S0) (Fig. 2E).

Step 2: Estimation of desired effects.

Once we identify the tumor subpopulations, the next step is to quantify the desired signaling changes for the intracellular markers M1–M3 for each drug $S_j$ in each subpopulation. For each subpopulation, we estimate the probability that a marker is differentially expressed with respect to its baseline (no treatment) expression, under each drug (Fig. 2F) using Bayesian linear models (16) in the limma R package (Materials and Methods). For simplicity, we create a probability-of-effects matrix for each subpopulation, where white versus black color-coding represents no effect versus effect, respectively. The probability of an effect on marker $M_i$ by drug $S_j$ conditioned on subpopulation $k$ is represented by $E_{ij|k}$. In practice, prior knowledge that a desired phenotype such as cell death is associated with up-regulation of death markers can be used to weight intracellular effects. (Fig. 2G) (Materials and Methods). The desired effects is best informed by prior knowledge depending on the drug mechanism of cancer. For example, one could consider down-regulation of survival markers in targeted signaling pathways, up-regulation of death markers, or a combination of both. In SI Text, we describe how to estimate the desired effects in the absence of prior knowledge.

Step 3: Estimation of drug NEM.

We use this weighted probability-of-effects matrix for each subpopulation to build a drug nested effects network (Fig. 2H) across all of the subpopulations. Fig. 2H shows the drug effect profiles in Fig. 2G integrated across all three subpopulations using a network representation where the nodes are the drugs and a directed edge between two drugs captures a subsetting of effects associated with each drug. For example, the mapping is represented here as a directed graph between S1, S2, and S3, with S3 downstream of both S1 and S2. These relationships are represented with a directed edge from S1 to S3 and S2 to S3, respectively. In brief, drugs S1 and S2 effects are a superset of S3 effects (E2, blue; E2, green). The network captures not only the subsetting relationships of the drugs but also the possible assignment of the effects to the drug network, referred to later as a “position” or parameters of the network. In practice, obtaining such a mapping with many more drugs and intracellular signaling markers can be challenging. We adapt the use of NEMs (17–21), a class of probabilistic models suitable for reconstructing these kinds of hierarchical graphical models, from high dimensional perturbation data.

Step 4: Drug combination scoring and ranking based on drug-effects network.

The objective of DRUG-NEM is to identify the minimum number of drugs that will produce the most desired intracellular effects across all subpopulations within a single tumor. We score and rank all drug combinations under the nested effects assumption, using the hierarchy and posterior weights from the optimized drug NEM (Fig. 2H) to determine the combination with the minimum number of drugs that maximizes the sum of the nested desired effects (Fig. 2I) (Materials and Methods). For comparison purposes, motivated by the traditional Bliss independence (4, 22) assumption for quantifying the effects of drug combinations, we also score each drug combination under additivity of independent drug effects using the probability-of-effect matrix without knowledge of the structure of drug interactions from the drug NEM. The independent effects scoring metric results in a closed form expression for scoring each combination [Eq. S1 1. Optimizing Drug Combinations Using Expected Additive Independent Effects (Independence Scoring Metric)]. Fig. 2I provides a hypothetical exhaustive ranking for all drug combinations assuming noisy effect data across subpopulations under both approaches: independent and nested effects. Note that although S1 + S2 and S1 + S2 + S3 affect all markers in all subpopulations, S1 + S2 does so with only two drugs and therefore is ranked higher under the nested effects scoring metric (DrugNEM). Compared with scoring under the nested effects metric, scoring under the independence metric produces a less optimal solution, particularly on noisy data, as demonstrated by the detailed sensitivity analysis on six network models in 2. Robustness Analysis of DRUG-NEM on Simulated Data and Figs. S1 and S2.

It is important to also recognize that optimizing the objective function under independent effects assumptions would generally produce a continuous monotonic function with an expected maximum (Fig. S3), which may not yield the optimal solution under certain drug network structures. In contrast, optimizing the objective function under the nested effects assumptions would generally produce a monotonic step-wise function (Fig. S4), whereby equivalent-scoring strategies (ties) can be further assessed based upon other considerations. In the current implementation of DRUG-NEM, the optimal nested solution is the highest scoring combination with the minimum number of drugs.

DRUG-NEM Selects TRAIL and MEK Inhibitor as an Optimal Combination on HeLa Cells.

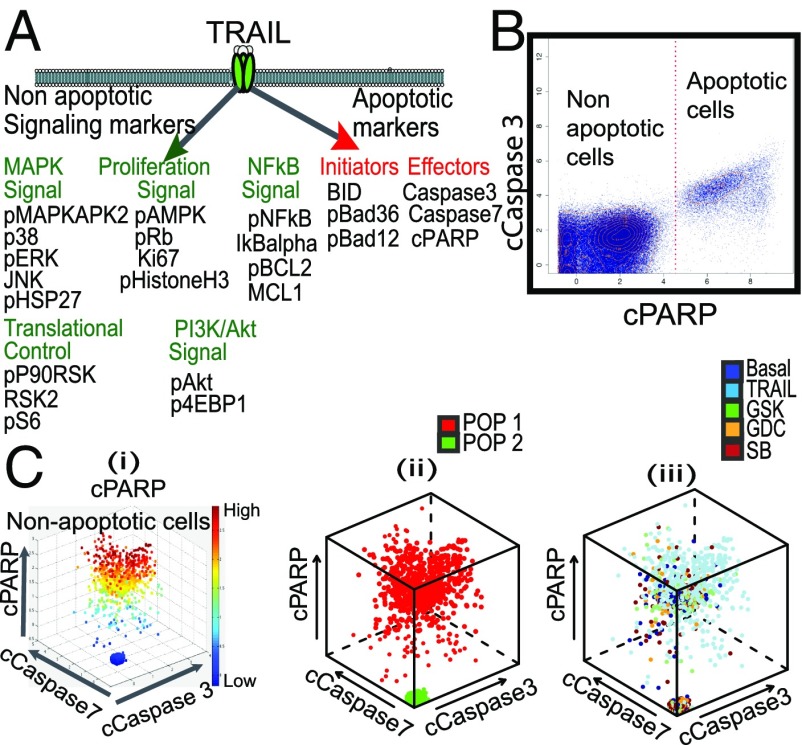
TRAIL, a death ligand member of the TNF ligand superfamily (23), is a potent stimulator of apoptosis and has been considered as a cancer therapy (24). However, poor results from TRAIL alone are likely due to pathway-specific resistance mechanisms to TRAIL (24, 25) and possibly ITH. Ongoing interest in TRAIL is now more focused on its effect within a drug combination strategy. To assess potential companion drugs to TRIAL, we consider critical intracellular signaling markers associated with TRAIL in Fig. 3A and consider potential inhibitors to these pathways. Using a CyTOF panel against the 24 TRAIL-specific intracellular markers in Fig. 3A, single-cell data on HeLa cells were collected pretreatment and in response to one of four treatments: TRIAL alone and one of the three small molecular inhibitors—(i) MEK inhibitor (GSK), GSK1120212, which is a potent and highly specific MEK1/2 inhibitor (26); (ii) pP38MAPK inhibitor (SB), SB203580, which directly binds competitively to the ATP site of the enzyme of p38 MAPK (27); and (iii) PI3K inhibitor (GDC), GDC0941, which inhibits one or more of the PI3K enzymes, part of the PI3K/AKT/mTOR pathway.

Fig. 3.

Critical single-cell signaling markers associated with TRAIL pathway in HeLa cells. (A) Potential nonapoptotic and apoptotic signaling markers affected by activation of TRAIL. (B) Apoptotic and nonapoptotic subpopulation identification of basal and treated cells using cleaved PARP (cPARP) selected by CCAST from three death markers: cPARP, cCaspase3, and cCaspase7. (C) 3D scatter plot of random nonapoptotic cells (i) representing cPARP high- and low-cell condition on above three death effectors, (ii) showing the subpopulation of cells color-coded as cell state 1 (POP1, red) and cell state 2 (POP2, green), (iii) across all treatment conditions color-coded here as blue (Basal), light blue (TRAIL), green MEK inhibitor (GSK), orange PI3K inhibitor (GDC), and red pP38MAPK inhibitor (SB).

DRUG-NEM shows intracellular signaling response heterogeneity in HeLa subpopulations.

The DRUG-NEM analysis on single-cell perturbation data of the HeLa cell line is summarized in Figs. 3 B and C and 4. CCAST (15) selects cPARP to identify and gate out the cells already committed to apoptosis, namely those with high cPARP (Fig. 3B). Given the lack of lineage markers in this particular experiment, cPARP was manually selected to identify high versus low cPARP-expressing subpopulations among the nonapoptotic cells illustrated in Fig. 3 C, i. Fig. 3 C, ii depicts the two subpopulations as POP1 (red: high cPARP) and POP2 (green: low cPARP). These two subpopulations were manually selected because they were readily observed in the basal cells (pretreatment) and posttreatment under all four treatment conditions. Fig. 3 C, iii shows the distribution of the cells across all conditions color-coded here as blue (Basal), light blue (TRAIL), green (GSK), orange (GDC), and red (SB). We can regard these two subpopulations as “cell states” because it is possible that some cells in the low-cPARP subpopulation may move to the high-cPARP subpopulation posttreatment. Regardless, our analysis relies on the change in signaling of the remaining intracellular markers, pre- and posttreatment, in these two subpopulations.

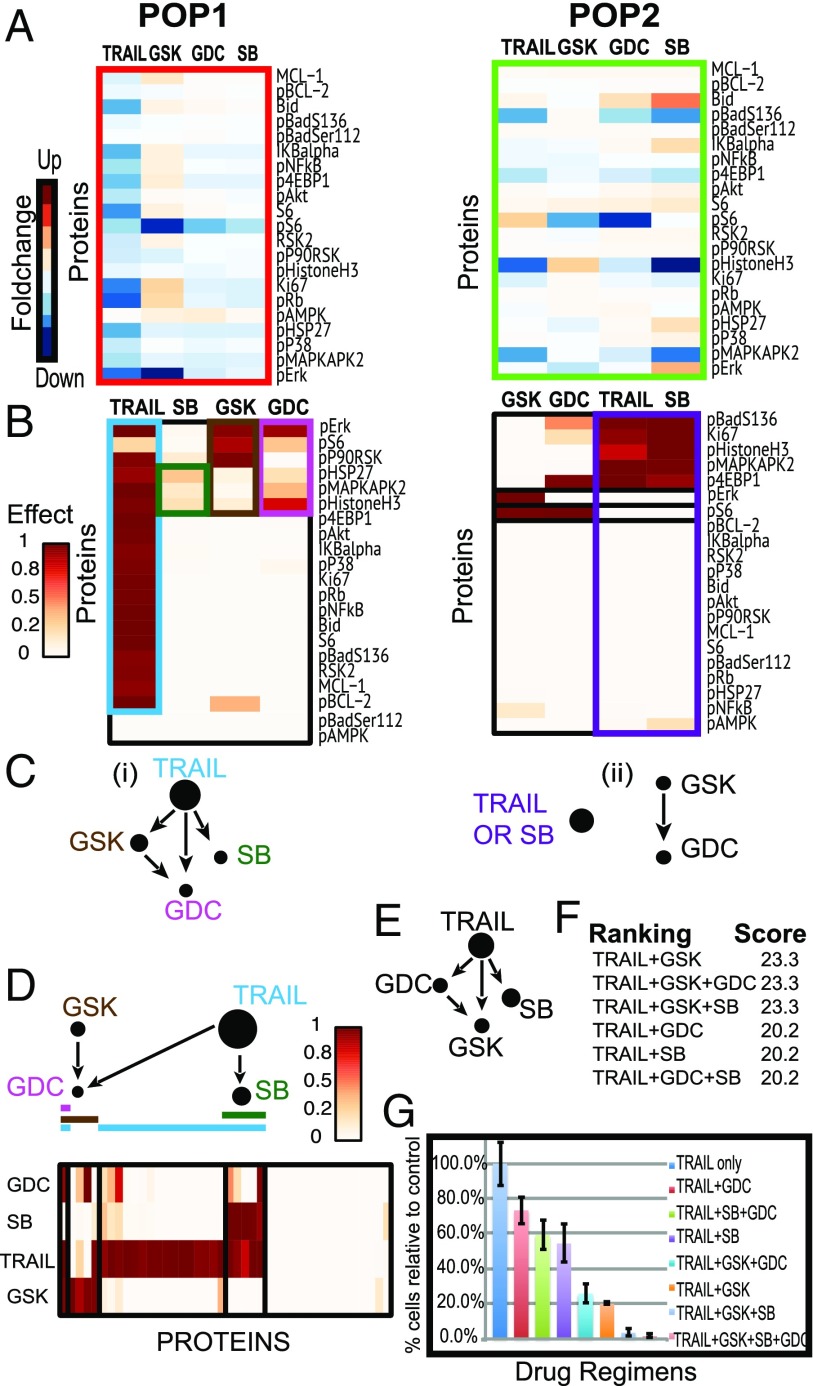
Fig. 4.

DRUG-NEM analysis on HeLa cells. (A) Heatmaps of normalized fold change (FC) of intracellular markers with respect to the baseline across all treatments for two survival subpopulations (POP1–POP2). (B) Heatmaps of probability of effects associated with down-regulation of all intracellular signaling markers. Rows and columns of the effect matrix for each subpopulation have been sorted to show the nested effects across drugs. (C) Drug NEM for each subpopulation. (D) Integrated drug nested effects network (Top) with heatmap (Bottom) of integrated desired effect data across all subpopulations of cells portraying the effects of GDC (pink line) and SB (green line) are a subset of the effects of TRAIL (blue line) and GSK (brown line). Node sizes depict the conditional number of desired effects connected to the associated node. (E) Drug nested effects network with TRAIL on top under a nonheterogeneous model using average desired effects derived from pooling all of the cells in Fig. 3 C, iii. The GSK effects from D not associated with TRAIL have been lost. (F) DRUG-NEM ranking for top-scoring drug combinations with TRAIL. (G) Survival in vitro analysis for several drug combinations involving TRAIL plus GSK, GDC, and SB using clonogenic assays showing that any drug combination including TRAIL and the GSK results in higher cell death levels compared with combinations without these two treatments.

Fig. 4A shows the heatmap of FCs of intracellular markers, normalized with respect to the basal (no treatment) condition in each subpopulation. In POP1, TRAIL and GSK each down-regulate most of the intracellular signaling proteins, particularly pERK and pS6 in the case of GSK. POP2, which corresponds to the most surviving cells (low cPARP), shows more up-regulation than down-regulation across all of the treatment conditions, especially by SB on Bid and pERK.

DRUG-NEM ranks drug combinations by integrating nested drug effects across subpopulations.

We consider effects associated with intracellular signaling markers that are down-regulated following treatment as desired intracellular effects. We choose the down-regulated effects as opposed to weighting the effects by the death marker cPARP, because cPARP was used to identify the subpopulations. Fig. 4B shows the heatmaps of these down-regulated effects. The rows and columns of the probability-of-effects matrix have been sorted to show the nested relationships among drugs. This sorting is achieved using NEMs (17, 19, 28) (Materials and Methods). In POP1, TRAIL down-regulated effects form a superset of GSK, GDC, and SB effects while GSK effects form a superset of the GDC effects. Within the NEM framework, this directed transitively closed network in Fig. 4 C, i infers that within POP1, TRAIL will likely have the greatest response because it down-regulates the greatest number of intracellular markers. In POP2, TRIAL has disjoint effects between GSK and GDC, with GSK effects forming a superset of GDC effects. Although we infer different nested drug effects networks for the two subpopulations, we want to optimize drug combinations across all cells since all of the cells will be treated simultaneously. Integrating the effects across the two subpopulations results in the sorted probability-of-effects matrix shown in Fig. 4D with the drug NEM shown on the top. Note the size of the nodes reflects the underlying number of effects attached to the node. Interestingly, this integrated network differs from networks derived from the individual subpopulations shown in Fig. 4C; it also differs from the predicted network that ignores ITH (Fig. 4E), where the effects are derived from averaging across all of the cells. The integrated nested drug effects network in Fig. 4D and associated drug combination ranking for the top regimens shown in Fig. 4F identifies TRAIL and GSK as the highest scoring two-drug combination.

Validation of DRUG-NEM drug combination ranking on HeLa cells based on viability analysis.

To validate the DRUG-NEM finding, an independent in vitro survival analysis was performed on HeLa cells under several drug combinations involving combinations of TRAIL plus either GSK, GDC, and SB using clonogenic assays in triplicate (Materials and Methods and Dataset S1). The percentage of surviving cells in Fig. 4G was calibrated relative to TRAIL to depict the additional fractional killing of cells due to the drugs in combination with TRAIL versus TRAIL alone. The top three most effective regimes (TRAIL + GSK, TRAIL + GSK + GDC, TRAIL + GSK + SB) were consistent with the top three DRUG-NEM rankings (Fig. 4F). These results provide empirical evidence that any strategy that combines TRAIL with the GSK (MEK inhibitor) is most effective compared with those without. DRUG-NEM chooses TRAIL + GSK among these tied strategies because it consists of the least number of drugs. TRAIL + GSK killed 60% more cells compared with TRIAL alone. Interestingly, adding GDC to TRAIL + GSK produced similar results to TRAIL + GSK.

DRUG-NEM Identifies PI3k/mTOR and ABL/Src Inhibitors as a Predominant Optimal Combination in ALL Patient Samples.

ALL is the most common cancer diagnosed in children and represents ∼25% of cancer diagnoses among children younger than 15 y (29). Despite dramatic improvements in clinical outcome for pediatric ALL over the last 40 y, relapse remains the most significant cause of mortality in 20% of patients (30, 31). Combination of targeted drugs and chemotherapy are being suggested as potential therapeutic solutions to improve these outcomes (32). Using DRUG-NEM, we demonstrate a potential role for single-cell drug screening analysis to help guide rational choice of combination therapy for the individual ALL patient.

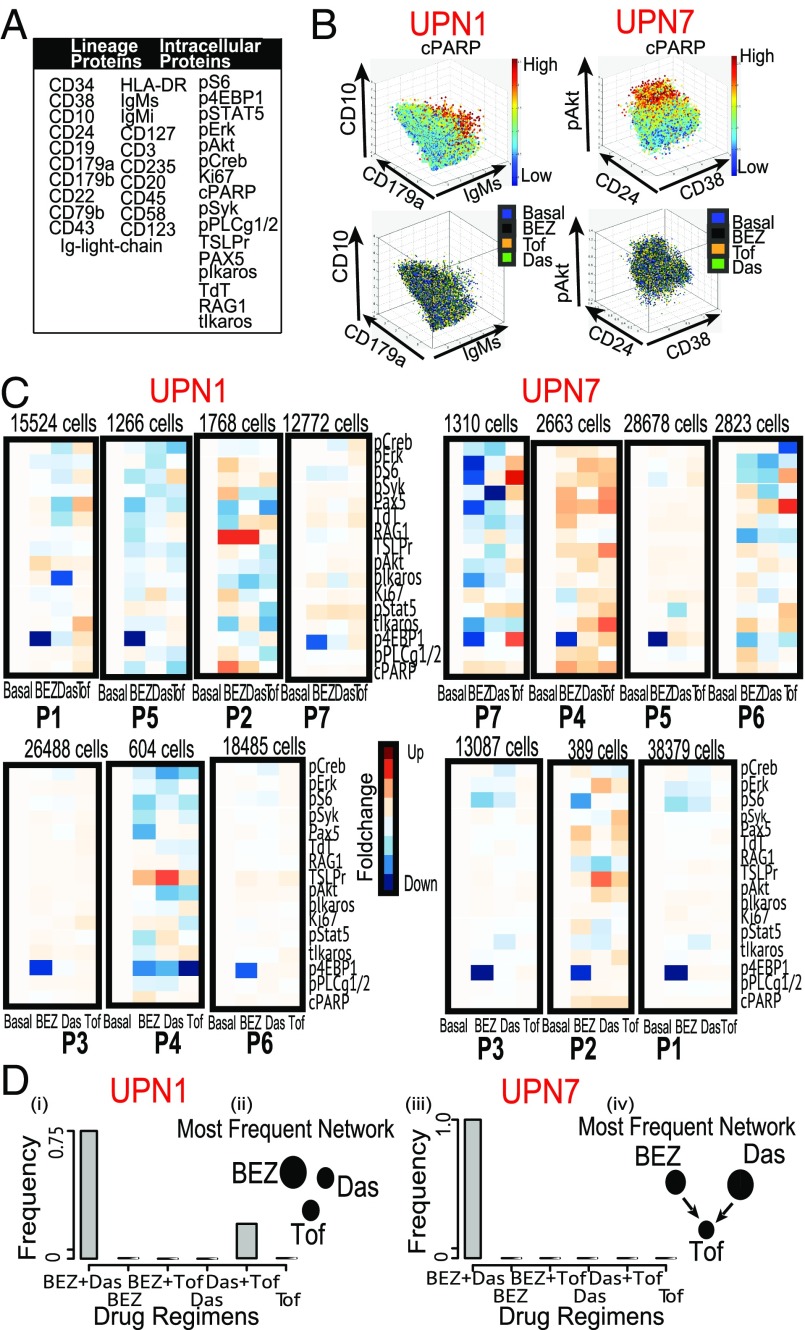
We apply DRUG-NEM on a CyTOF-based drug screening dataset generated from 30 B-cell progenitor ALL pediatric patient samples denoted here as UPN1–UPN30. Each sample was analyzed using a CyTOF panel of 21 B-cell lineage markers and 16 intracellular protein expression responses, summarized in Fig. 5A. CyTOF analysis was performed before and after 30 min of single drug treatment at optimal doses for three drugs: Das (BCR-ABL inhibitor), Tof (JAK/STAT inhibitor), and Bez (PI3K/mTOR inhibitor) (Materials and Methods).

Fig. 5.

DRUG-NEM analysis on two ALL patient samples. (A) Table showing all lineage and nonlineage markers used in the study. (B, Top) 3D scatterplot of pooled UPN1 and UPN7 manually gated cells corresponding to malignant cells derived from gating out potential T and myeloid cells respectively color coded by the cPARP expression. (Bottom) Corresponding distribution of the cells in the top row across all treatment conditions color coded here as blue (Basal), black (BEZ), orange (Das), and green (Tof) showing a random distribution. (C) Heatmaps corresponding to lowly expressed cPARP cells from all seven subpopulations derived using CCAST showing normalized FCs before (Basal) and after treatment. Notice the strong down-regulation effect of 4EBP1 by BEZ across major subgroups. (D) Bar plot showing the distribution of best DRUG-NEM (down FC) predictions for 30 random samples from patients UPN1 (i) and UPN7 (iii), respectively, with the mode on BEZ + Das. The associated dominant DRUG-NEM networks (ii and iv) for both patients are different, and most target effects are associated with BEZ (UPN1) and Das (UPN7), respectively.

DRUG-NEM identified intratumoral signaling-response heterogeneity in the ALL samples.

The DRUG-NEM ALL results for 2 of the 30 patient samples (UPN1 and UPN7) are summarized in Fig. 5 B–D. The samples were manually gated to capture live malignant cells. The top row of Fig. 5B shows the 3D scatterplot of the two patient samples, based on three manually selected markers (which differs for UPN1 and UPN7) and color-coded by cPARP expression. Note that even after manual gating to remove the apoptotic cells, there is still evidence of cPARP heterogeneity in each sample. The bottom row of Fig. 5B shows the cells are randomly distributed across all treatment conditions color-coded here as blue (Basal), black (Bez), orange (Das), and green (Tof) for UPN1 and UPN7, respectively.

To account for intratumor heterogeneity, we initiated DRUG-NEM with a minimum of five subpopulations based on exploratory clustering with SPADE (13) (Fig. S5) and then applied CCAST to identify and match seven cell subpopulations across the three inhibitors and basal (pretreatment) conditions for each patient sample (Fig. 5C). The CCAST-derived decision trees that define the subpopulations for UPN1 and UPN7 are shown in Fig. S6. The similar percentages of cells for subpopulations across all conditions (basal and treatment following the three inhibitors) provide evidence of stability in the subpopulation distributions (Fig. S7A). Note that the larger sized subpopulations predominately show down-regulation of p4EBP1 by Bez in both samples (Fig. 5C). This phosphorylated oncogenic protein operates downstream of the PI3K/AKT/mTOR kinase signaling pathway, and its down-regulation signifies the inhibition of this particular pathway by Bez. Interestingly, a greater number of diverse effects to all three inhibitors are found in the smaller sized subpopulations.

For both UPN1 and UPN7, DRUG-NEM predicted the best drug combination as BEZ + Das, where the desired effects were based on a decrease in FC, denoted as Down FC (Fig. 5 D, i and iii, respectively). For both patients, BEZ + Das was the most frequent top ranking strategy based on 30 different DRUG-NEM runs, where each run consisted of about 10,000 cells that were density-dependent down-sampled from the original data (13). Note the most frequent drug NEM differed for both patients (Fig. 5 D, ii and iv, respectively), yet after scoring, the BEZ + Das combination was the highest ranking treatment strategy for both patients.

Validation of DRUG-NEM by showing consistency between predicted and observed drug-combination ranking on two ALL patient samples, UPN1 and UPN7.

To validate the combination of BEZ + Das for UPN1 and UPN7, all two-drug combinations were analyzed together with the single drugs by CyTOF using the same panel (Fig. 5A). The actual top-ranked treatment strategy based on the maximal sum of desired effects following all drug combination responses was compared with the top-ranked prediction from DRUG-NEM, which was derived from the single-drug responses alone. The DRUG-NEM analysis was performed using the same sampling scheme as before with 30 runs. For each run, the number of mismatches between the actual versus predicted top scoring treatment strategy was compared under the DrugNEM versus the Independence scoring metrics, assuming down-regulated desired effects. Out of the 30 runs, the number of mismatches using the DrugNEM versus Independence metric was 1 versus 21 for UPN1 and 5 versus 9 for UPN 7 (Fig. S7 B, i and ii, first row, labeled “Down FC”), demonstrating DrugNEM produced the least mismatches for both patients.

Extensions of DRUG-NEM illustrated on ALL patient samples, UPN1 and UPN7.

We consider three extensions of DRUG-NEM. First, we address the possibility that the user does have prior knowledge on the desired effects. In the examples above, we assumed the desired effect was down-regulation of the intracellular markers, referred to as Down FC. Here we consider two more potential desired effects: (i) the intracellular signaling effects estimated from the odds of increasing down-regulation derived from a weighted T-statistic (Down T-stat) and (ii) the intracellular effects associated with up-regulation of death markers (e.g., cPARP) (Up Death Marker). In 3. Sensitivity Analysis of DRUG-NEM on Prior Knowledge of Desired Intracellular Effects on Two ALL Patient Samples, UPN1 and UPN7 and Fig. S7B, we report the number of mismatches under these different desired effects and show that in each case DrugNEM outperformed Independence scoring. In addition, we show DRUG-NEM performs better using one of these priors compared with considering any effect (i.e., no prior) (Fig. S7C). In the absence of an appropriate prior for the desired effects, we propose the use of the odds ratios to compare the maximum DRUG-NEM scores under different assumptions of desired effects, described in 4. Generalizing DRUG-NEM to Estimate the Most Likely Desired Effects Without Prior Knowledge, 5. Illustrating the Selection of Desired Effects in Absence of Prior Knowledge, and Fig. S8. Next, we show that DRUG-NEM results are robust to slight variations in the lineage marker distribution due to drug perturbation by bootstrapping the underlying subpopulations (3. Sensitivity Analysis of DRUG-NEM on the Characterization of Subpopulations on ALL Patient Samples and Fig. S7 D and E). Finally, we show that DRUG-NEM can be extended to optimize different responses in different cell types, opening the possibility for optimizing drug combinations based on desired intracellular responses in malignant cells and possibly a different set of desired effects in nonmalignant cells (7. DRUG-NEM Jointly Applied to Malignant and Nonmalignant Subpopulations and Fig. S9).

Application of DRUG-NEM on 30 ALL patient samples.

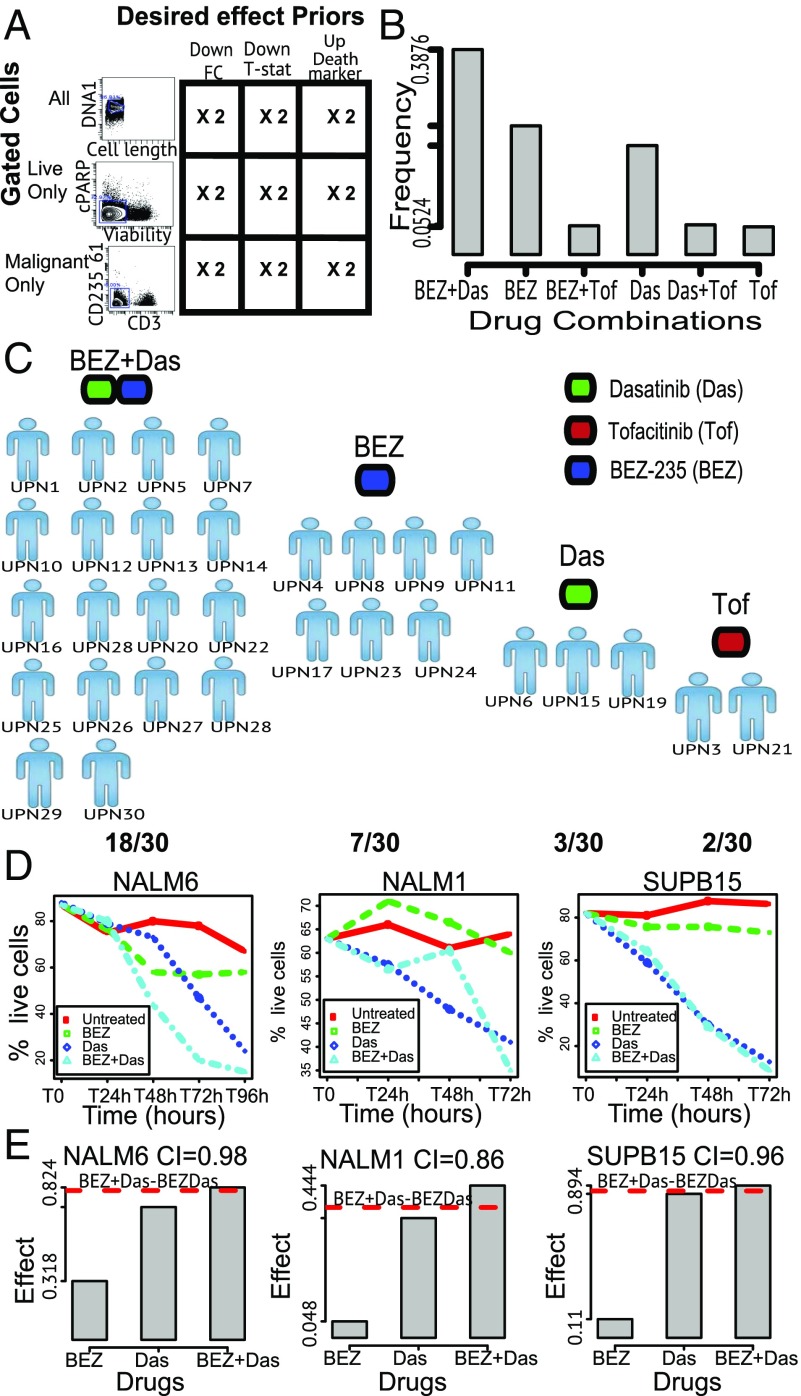
When we applied DRUG-NEM to 30 ALL patient samples, we accounted for additional variability by applying DRUG-NEM after three different gating strategies: (i) “All,” denoting the entire sample including live and death cells; (ii) “Live only,” denoting the manually gated live cells; and (iii) “Malignant cells,” denoting the process of manually gating to enrich for malignant white blood cells (blasts), devoid for normal cells, such as T and myeloid cells. The gating strategies are summarized in Fig. 6A. We considered all three desired priors described above (Down FC, Down T-stat, and Up Death Marker). We repeated the down-sampling twice. In total, for each patient sample, we have 18 different conditions (3 Gating Strategies × 3 Desired Effects Prior × 2 Down-Sampling Replicates). Adding to these analyses, the results from no prior weighting yielded a total of 36 runs per patient.

Fig. 6.

DRUG-NEM analysis on 30 ALL patient samples and viability analysis of ALL cell lines. (A) Cross-classification table showing the DRUG-NEM study design for each ALL sample between three different gated cells and three different desired effects. Each DRUG-NEM analysis was repeated twice on down-sampled data of about 10,000 cells per FCS file to account for sample variation. (B) Bar plot showing the distribution of top DRUG-NEM predictions for all 30 patients with BEZ + Das having a 39% chance of being selected as the best drug combination. (C) Distribution plot showing the patient-specific optimal drug combination predictions by DRUG-NEM. The single dominant two-drug strategy (BEZ + Das) for 60% of patients may not be optimal for all patients. (D) Line survival plots showing the average time varying percentages of live cells. (E) Bar plot illustration of drug effectiveness in terms of bliss independence for all three cell lines showing a potential BEZ + Das synergistic effect in terms of combination index (CI) with the strongest effect occurring in the NAM1 cell line (CI = 0.86). The dotted red line shows the theoretical expected additive effect for BEZ + Das.

To determine if the BEZ + Das prediction by DRUG-NEM for UPN1 and UPN7 above can be generalized, we analyze the top ranking predicted strategy across all 30 patients. We summarize the top predictions across the 30 patients in a bar plot shown in Fig. 6B showing the distribution of results from a total of 1,080 DRUG-NEM analyses (30 patients × 36 conditions per patient). Interestingly, although BEZ + Das had a 39% chance of being selected as the best drug combination, in roughly 45% of the runs, BEZ alone or Das alone was top ranking. Fig. S10A summarizes distribution of the DRUG-NEM network models across all 1,080 analyses. Fig. 6C shows the DRUG-NEM patient-specific predictions indicating that except for two patients (UPN3 and UPN21), a strategy including BEZ alone, Das alone, or BEZ + Das is optimal for 93% of the patients, with BEZ + Das as top ranking in 60% of the patients (Fig. S10B). In summary, this analysis suggests while there may be a single dominant two-drug strategy (BEZ + Das) for the vast majority of ALL patients, that strategy may not be optimal for all patients.

Viability analysis of BEZ alone, DAS alone, and the BEZ–Das combination on three ALL cell lines.

Because BEZ + Das was selected as the optimal two-drug combination across the vast majority of the ALL patient samples, we tested the effect of BEZ + Das by performing two independent viability assays on three independent ALL-related cell lines, treating the cells with both the single inhibitors and combination of BEZ + Das and observing the cell growth over a period of at least 72 h (see Dataset S1). The three cell lines tested were (i) the NALM6 cell line, which is a precursor (pre)-B human cell line derived from an adult ALL relapsed patient (33); (ii) the NALM1 cell line, a non-T, non-B human leukemia cell line (NALM-1) (34); and (iii) the SUP-B15 cell line, derived from a Ph + ALL child (35). Fig. S10C shows the stacked bar plots corresponding to the relative frequency of cells that were alive, dead, or committed to early apoptosis after treating the cell lines for 3 d using viability assays. The biggest decrease in cell viability can be observed over time for all cell lines using both drugs compared with the single-drug conditions with almost all of the cells killed in the SUP-B15 cell line after 72 h (Fig. 6D). The survival curves are derived from average survival values of each cell line treatment condition at optimal doses (Materials and Methods). BEZ + Das consistently achieved the most cell kills after 72 h compared with the single drugs. With the effect measured as cell death, we use the CI [1. Optimizing Drug Combinations Using Expected Additive Independent Effects (Independence Scoring Metric)] to investigate the presence of a synergistic effect (CI < 1), additive effect (CI = 1), or antagonist effect (CI > 1) for the BEZ + Das effect. Under Bliss independence, Fig. 6E illustrates and quantifies the drug effectiveness of BEZ + Das across all three cell lines. The synergistic effect is strongest in the NALM1 cell line, with a CI value of 0.86. In summary, the ALL analysis shows that analyzing intratumor heterogeneity in terms of single-cell signaling responses may prove to be an additional tool for guiding combination treatment decisions for the individual patient.

Discussion

Single-cell technologies enable the possibility for personalized combination cancer therapies that account for ITH. We introduced an algorithm, DRUG-NEM, that identifies top ranking drug combinations based on a short-term single-cell perturbation response when an individual tumor sample is screened against a panel of single drugs. We demonstrate DRUG-NEM using a single-cell technology, CyTOF, to determine effects of drugs on intracellular markers. The major assumption underlying DRUG-NEM is that changes in intracellular signaling markers serve as a surrogate for drug effectiveness. It is worth noting that while short-term intracellular signaling changes are not guaranteed evidence of long-term cell fate such as cell death, several studies (8–10) including our analysis (Fig. S8 A and B) show such an association can exist. Continued work in this area is fueled by the limited ability to establish a long-term drug response on primary samples. Given that the identification of such intracellular biomarkers is an active area of research, DRUG-NEM leverages these short-term surrogate endpoints to single drugs to identify drug combinations that account for intratumoral signaling heterogeneity.

DRUG-NEM is composed of four steps: (i) identify the subpopulations that make up the tumor and may respond differently to treatment, (ii) estimate the effects associated with a desired response, (iii) reconstruct a drug NEM that integrates the drug effects across all subpopulations to capture subsetting relationships among individual drug effects, and (iv) using the drug NEM, score the drug combinations by prioritizing the minimum number of drugs that in combination have the greatest number of desired intracellular effects. In a simulation analysis, we showed that drug combinations scored by assuming drug nested effects outperformed those based on the additivity assumption of independent drug effects, particularly when the effects of the drugs are not disjointed.

DRUG-NEM analysis on HeLa cells predicted TRAIL and MEK inhibitor as the optimal combination after analyzing the CyTOF-based single-cell intracellular perturbations with TRAIL and three different inhibitors. This result was validated based on viability studies of all drug combinations together with TRAIL. Admittedly, this result is influenced by the selected markers used to infer the response. The markers in the HeLa analysis were based on expert knowledge of pathways implicated in TRAIL’s mechanism of action and resistance. The HeLa analysis also highlights the performance of DRUG-NEM when intracellular markers are used to identify the subpopulations. While DRUG-NEM was conceptualized assuming lineage markers would be available to identify the subpopulations, lineage markers may not be available (or known) that can best define the subpopulations. While an extensive analysis on the use of intracellular markers for identifying the subpopulations is warranted, we showed that the use of intracellular markers for identifying the subpopulations on the HeLa cells produced a more accurate prediction of the drug combinations than assuming the cell line lacked intratumoral signaling heterogeneity.

The application of DRUG-NEM on 30 ALL patient drug–response CyTOF single-cell data found ABL/Src and PI3k/mTOR inhibitors as the best combination therapy for 60% of the patients. The use of the mTOR inhibitor is consistent with the finding that targeting mTOR is a promising strategy for cancer therapy by strongly suppressing 4EBP1 phosphorylation. Such an inhibitor has been shown to be a potent cytotoxic agent against leukemia cells and enhance the efficacy of the TKIs such as Imatinib and Das in Ph + acute leukemia models (36). In addition, the combination of ABL/Src inhibitor and PI3k/mTOR inhibitor was validated using viability assays on three ALL cell lines.

In the ALL analysis, we explored the properties of DRUG-NEM with an extensive sensitivity analysis, assessing the robustness of several aspects of the algorithm, including gating, weighting, and down-sampling. DRUG-NEM was robust in this context within reasonable variations related to gating and down-sampling. We demonstrated that the DRUG-NEM results are robust to slight variations in the lineage marker distribution used to determine pre- and posttreatment subpopulations. For this analysis, we assumed the desired effects were down-regulation of intracellular markers because many of these markers were associated with signaling drug targets. When we assumed that the desired effects were associated with up-regulation of death markers, the most optimal drug strategy was unchanged. In the absence of any prior knowledge for choosing the desired effects, we explored the use of DRUG-NEM to inform the best choice of desired effects. We proposed choosing the desired effects that maximize the DRUG-NEM score based on odds ratios for alternative desired effects assumptions.

To date, accounting for single-cell signaling heterogeneity in drug response for an individual tumor in a high-throughput manner is a relatively unexplored area. DRUG-NEM provides a formalism that addresses this area. Because DRUG-NEM leverages single-cell data, DRUG-NEM can be extended to optimize different responses in different cell types, opening the possibility for optimizing drug combinations based on desired intracellular responses in malignant cells and a different set of desired effects among the nonmalignant cells (Fig. S9). Moreover, the intracellular signaling panel can be extended to quantify potential unwanted off-target effects, which can also be incorporated in the effects matrix and weighted as undesired effects, enabling simultaneous optimization for reduced toxicity effects.

DRUG-NEM provides a broad analytical framework that can be expanded. First, DRUG-NEM can be applied to a larger number of drugs. We demonstrated DRUG-NEM on a small number of drugs (four drugs on the HeLa cell line and three drugs on 30 ALL samples) as a proof of concept. As the number of drugs increases (>5), more efficient search and ranking algorithms will need to be implemented (8. DRUG-NEM on Large Networks). Given the large number of potential combinations when choosing from a large number of drugs, DRUG-NEM’s ranked combinations may be used to prioritize drug combinations for further testing. Second, DRUG-NEM can be adapted to different logical rules. The current scoring implementation of DRUG-NEM assumes an OR relationship between drugs in alternative paths to integrate drug combination effects. Adaptation of the Boolean NEM (37) within the framework of DRUG-NEM, which requires drug combination data to incorporate logic combinations of desired effects when integrating other molecular data types, may be used to score Boolean drug combinations as well as refine the drug combination ranking distribution. Furthermore, it is possible on a longer time scale that one or more drugs may induce new subpopulations that were not present in the baseline condition. Such a scenario will require an adaptive strategy, which includes updating the subpopulation identification step, potentially requiring modeling of dynamic nested effects (19).

In summary, DRUG-NEM is a framework using single-cell technologies that measure intracellular perturbations to optimize drug combination strategies while accounting for ITH. It can be adapted to incorporate complementary molecular data to ultimately achieve more effective therapy for individual cancer patients.

Materials and Methods

Deidentified pediatric ALL bone marrow specimens were obtained under informed consent from Pediatric Clinic University of Milan Bicocca (Monza, Italy) for 30 primary diagnostic patient samples. Use of these samples was approved by the institutional review board in both Italy and Stanford. All relevant ethical regulations were followed in this study. MCM measurement and data preprocessing was performed using mass-tag cellular barcoding (MCB) as described previously by Bodenmiller et al. (7). We assume that the data have already been preprocessed using standard analytic steps for MCM data to remove spurious events and then transformed using Arcsinh function with cofactor 1 (11).

HeLa Clonogenic Assay Analysis.

HeLa cells were plated at a density of 2,000 cells per well in triplicates in the presence or absence of Mek (20 $\mu$M), pP38 MAPK (20 $\mu$M), and PI3K (2.5 $\mu$M) inhibitors for 1 h, followed by treatment with TRAIL (20 $\mu$M) for 24 h. After TRAIL treatment, drug-treated media was replaced with fresh growth media (DMEM) and cells were allowed to grow for about a week before colony counting. Note that the same concentrations were used for the CyTOF data analysis.

ALL Cell Line Survival Assay Analysis.

ALL cell lines were grown in suspension in RPMI medium supplemented with 10% serum for a period of at least 72 h in the presence or absence of Bez (1 uM) and Das (100 nM) individually and in combination. Trypan Blue, Ann V FITC, and 7AAD stainings were used to obtain live, dead, and early apoptotic cell numbers and percentage viability. The above concentrations were used for performing the single- and double-drug CyTOF data analysis including 100 nM of Tof that was not used in the survival assays.

Availability of Supporting Datasets and Algorithms.

All supplementary data (S3–S9) can be downloaded from ccsb.stanford.edu/research/core.html.

DRUG-NEM Algorithm.

In the following sections, we provide a detailed description of DRUG-NEM as a four-step algorithm: (i) population identification, (ii) estimation of desired effects, (iii) nested effect modeling, and (iv) score-rank analysis to prioritize combination therapy.

Step 1: DRUG-NEM uses a decision tree to automatically gate out apoptotic cells in each subpopulation and averages out the expression of each signaling protein across the remaining cells.

For each subpopulation, DRUG-NEM gates out the cells in which apoptosis has been initiated using a prespecified death marker or by selecting the most statistical significant death marker among others using the CCAST algorithm by Anchang et al. (15). This step filters out apoptotic cells and leaves nonapoptotic cells whose signaling is taken to be informative of a preapoptotic response. We denote the signaling expression measurements for each marker $M_i$ from drug $S_j$ condition on subpopulation $k$ as $M_{ij|k}$. Note that all of the cells for each marker in each subpopulation will form replicate data under each treatment. This allows for averaging the signaling marker expressions from each subpopulation and statistically testing for differential treatment effects for each marker using linear models.

Step 2: DRUG-NEM uses “limma” to estimate the probability of drug intracellular signaling effects for each subpopulation.

DRUG-NEM uses the probability (or log-odds) of each measured intracellular signaling marker being differentially expressed after drug treatment in each subpopulation $k$. These probabilities can be easily estimated using linear models (16). More specifically for each subpopulation, the limma package in Bioconductor uses Empirical Bayes estimates (B-statistic) derived from a moderated T-statistic for a particular marker $M_i$ with the variance component estimated across all of the markers. DRUG-NEM uses the B-statistic (B) output from limma, which is the log odds that the marker is differentially expressed (16) to derive the probability $E_{ij|k}$ of a marker $M_i$ being differentially expressed under drug $S_j$ condition on subpopulation $k$. Assuming $B_{ij|k}$ and $E_{ij|k}$ correspond to the log odds and probability estimates, respectively, for marker $M_i$ to be differentially expressed after drug treatment $S_j$ in subpopulation $k$,

$$log\left(\frac{E_{ij|k}}{1-E_{ij|k}}\right)=B_{ij|k}.$$ [1]

This implies $E_{ij|k}=\frac{\exp (B_{ij|k})}{1+\exp (B_{ij|k})}$. Without prior knowledge, by defining our estimated intracellular signaling effect probabilities for each subpopulation as our desired effect, we create an input for the nested effect modeling part of the DRUG-NEM algorithm as a 2D effect data matrix, denoted as E with the intracellular signaling markers assigned to the rows and the drug labels assigned as columns. DRUG-NEM can also incorporate prior related information by weighting each intracellular signaling effect $E_{ij|k}$ to generate a new effect data matrix representing the desired effect matrix required for drug combination scoring.

Estimating desired effects using down-regulated intracellular signaling effects.

Assuming $w_{ij|k}$ represents the weight for down-regulation associated with intracellular signaling marker $M_i$ under drug $S_j$ in subpopulation $k$ and can take only values 0 or 1, then without changing the notation for our desired effect matrix (E), $E_{ij|k}=w_{ij|k}{E}_{ij|k}$ and a drug NEM can be applied on this weighted 2D matrix, E. Also, the log (odds) measure from Eq. 1 is related to a moderated T-statistic (16). Assuming the odds of a desired effect is associated with negative T-statistic, we can equally generate discrete desired probabilities for each marker $M_i$ by setting $w_{ij|k}=1$ if $T_{ij|k}<0$ and 0 otherwise, where $T_{ij|k}$ represents the corresponding T-statistic associated with marker $M_i$ to be differentially expressed after drug treatment $S_j$ in subpopulation $k$. In a parametric setting, we can also approximate $log(\frac{E_{ij|k}}{1-E_{ij|k}})$ as $-T_{ij|k}$ to derive desired effects associated with the odds of down-regulation. We denote both processes as Down FC and Down T-stat, respectively.

Estimating desired probability effects using up-regulation of death markers (Up Death Marker).

Biologically, eventual cell death is expected to be associated with cells whose intracellular signaling effect correlates with an increase in expression of death markers. In practice, since our model requires effect probabilities, we again use the moderated T-statistic, which is also related to B for a given death marker $M_i$ denoted here as $T_i$. Assuming up-regulation (positive T-statistic) of the death marker is associated with the odds of cell death compared with a negative score, a logistic function on $T_i$ is used to generate the effect probabilities. Also, B is derived from a logistic function representing the probability of intracellular signaling effect. Under independence assumptions, we consider the bivariate effects ($B,T_i$) as a random variable derived from a bivariate distribution with independent logistic marginals given by

$$F(b,t_i)=\frac{1}{1+e^{-b}+e^{-t_i}+e^{-(b+t_i)}}for-\mathrm{\infty }<(b,t_i)<+\mathrm{\infty }.$$ [2]

The joint probability is then used as input for drug nested effects modeling and drug combination scoring. Under such a scenario, $E_{ij|k}=F_{ij|k}$.

Step 3: DRUG-NEM uses NEMs to generate a graphical model of drugs representing the relationships between drugs and markers across subpopulations.

DRUG-NEM builds on the NEMs. We briefly introduced the notion of NEMs in Results. The NEM methodology is implemented in the bioconductor r package nem and cran packages nessy or ddepn (18). NEMs were first proposed for the analysis of nontranscriptional signaling networks (21). Following refs. 17, 21, the perturbed players in the signaling pathway are called S-genes, and the players that show expression changes in response to perturbation are called E-genes. In summary, an NEM is a directed and possibly cyclic network that connects the S-genes with the edges representing subset relationships.

Within the context of DRUG-NEM, we define S-genes as drug interventions and E-genes as targeted intracellular signaling markers. If we denote the single-drug interventions by $S=S_1,\mathrm{\dots },S_n$, a directed edge from $S_1$ to $S_2$ indicates that intracellur signaling markers affected by the drug $S_2$ are also affected by drug $S_1$. This defines a subset relationship on pairs of drugs, and thus, transitive relationships are expected for more than two drugs mathematically represented as a transitively closed graph or adjacency matrix that defines a partial order on the drugs $S$ (38). Assuming that the effect data E is a 2D data matrix with number of rows of E representing $m$ independent effect vectors associated with $m$ markers, closely following the formulism of NEM in ref. 21, a NEM model consists of the transitively closed graph $\mathrm{\Phi }$ and the parameters for the allocation of specific desired effects to drugs denoted as E-marker positions $\mathrm{\Theta }$. Fig. S1 gives complete model parameterization for four drugs with all E marker effect positions for six different NEM models. Specifically, $\mathrm{\Theta }={\{{\theta }_i\}}_{i=1}^m$ with ${\theta }_i\in \{1,\mathrm{\dots },n\}$ and ${\theta }_i=j$ if $M_i$ is attached to $S_j$. NEM was extended in refs. 19 and 39 by including an additional node denoted by $\oplus$, which is not connected to any of the drug intervention schemes. E-markers can be linked to this node, if their effect pattern does not match any of the ${\theta }_i$ in $\varphi$. Markers linked to the $\oplus$ node are usually excluded from the model.

Estimating model parameters of the DRUG-NEM model conditioned on the effect data.

Here we provide a brief overview of how the likelihood of the model is calculated and maximized given the estimated effect data matrix E. A given network $\mathrm{\Phi }$ is usually scored by estimating the posterior probability given the data E, $P(\mathrm{\Phi }|E)$. According to Bayes’ rule, the posterior probability can be written as

$$P(\mathrm{\Phi }|E)=\frac{P(E|\mathrm{\Phi })P(\mathrm{\Phi })}{P(E)},$$ [3]

where $P(E)$ is a normalization constant that does not depend on $\mathrm{\Phi }$. Consequently, the marginal likelihood $P(E|\mathrm{\Phi })$ together with the network prior $P(\mathrm{\Phi })$ play the central role in the inference. An exhaustive search on all network structures only depends on scoring each network by the marginal likelihood. Assuming we have the effect data E, the marginal likelihood involves marginalization over the whole parameter space $\mathrm{\Theta }$.

$$P(\mathrm{\Phi }|E)={\int }_{\mathrm{\Theta }}P(E|\mathrm{\Phi },\mathrm{\Theta })P(\mathrm{\Theta },\mathrm{\Phi })d\mathrm{\Theta }=\frac{1}{n^m}\prod _{i=1}^m\sum _{j=1}^{n}P(E_i|\mathrm{\Phi },{\theta }_i=j).$$ [4]

The marginal likelihood $P(E|\mathrm{\Phi },\mathrm{\Theta })$ is based on the assumption of conditional independence of effects given the network $\mathrm{\Phi }$ and the fact that each effect associated with each marker is linked to exactly one node in the network. Our goal is to find the maximum a posterior (MAP) estimate for $P(\mathrm{\Phi },\mathrm{\Theta }|E)$ given by

$$(\widehat{\mathrm{\Phi }},\widehat{\mathrm{\Theta }})=\underset{\mathrm{\Phi },\mathrm{\Theta }}{\arg \hspace{0.17em}\max }\hspace{0.17em}P(\mathrm{\Phi },\mathrm{\Theta }|E).$$ [5]

In an exhaustive setting, once we maximize the graph $\mathrm{\Phi }$, we can also maximize the E-marker positions $\mathrm{\Theta }$. Given a network model $\mathrm{\Phi }$, the posterior probability for an edge between drug $S_j$ and an E-marker $M_i$ is derived (21). Alternatively, $\mathrm{\Theta }$ and $\mathrm{\Phi }$ can be maximized together (39), or their optimal parameters can be estimated by a Bayesian MAP approach (40). In most cases, $\mathrm{\Theta }$ is treated as nuisance parameters that are integrated out (17, 19, 21, 28) to make predictions on the perturbation space. The ultimate goal of the study is to optimize drug combinations by using the drug nested desired effects. Scoring of drug combinations requires parameter estimates from the maximized drug network model $(\widehat{\mathrm{\Phi }},\widehat{\mathrm{\Theta }})$.

Step 4: Scoring functions for ranking drug combinations.

We present two approaches to score and prioritize drug combinations given the drug effect data E. The first approach based on additivity of independence effects is illustrated in SI Text, and the following method is based on NEM’s network parameters.

DRUG-NEM uses the maximum conditional posterior probabilities to score and rank drug combinations (DrugNEM metric).

For scoring a single-drug combination, we use the maximum of the posterior weights, $E_{ic}^{\ast }=max(P({\theta }_{i=j}|{\widehat{\mathrm{\Phi }}}_c,E,j\in c))$ as an estimate of desired effects from a given drug NEM $\widehat{\mathrm{\Phi }}$ associated with each intracellular signaling marker $M_i$ under each drug combination indexed by c, where $c\in \mathrm{\wp }(S=1,\mathrm{\dots },n)/\mathrm{\varnothing }$ corresponds to an element of the power set of all combinations generated from the index set $\{1,\mathrm{\dots },n\}$ for drugs $S_1,\mathrm{\dots },S_n$ with $r$ corresponding to the $r^{th}$ element in $c$ and $\left|c\right|$ the cardinality of $c$. We sum over all posterior probabilities associated with union of markers in the combination to determine the score for a given combination denoted as $F(c)$. For a given nested effects network $\widehat{\mathrm{\Phi }}$, if we denote the set of markers associated with drug $S_j$ as $A_j$, the union set of markers for a given drug combination indexed by c with r corresponding to the $r^{th}$ element in c is determined using sequences of index families of sets. For example, given a combination indexed by $c=\mathrm{1,2}$, where ${\widehat{\mathrm{\Phi }}}_c$ forms a subgraph of $\widehat{\mathrm{\Phi }}$ with ${\widehat{\mathrm{\Phi }}}_{\{1\}}\subseteq {\widehat{\mathrm{\Phi }}}_{\{\mathrm{1,2}\}}$ and $\{A_{\{1\}}\}\subseteq \{A_{\{\mathrm{1,2}\}}\}$, the smallest set containing each element of $A_r$ corresponds to the supremum of a sequence of index sets given by $sup{\{A_c\}}_c=A_{\{1\}}\cup A_{\{\mathrm{1,2}\}}=A_{\{\mathrm{1,2}\}}.F(\{\mathrm{1,2}\})={\sum }_{i\in sup{\{A_{\{\mathrm{1,2}\}}\}}_{\{\mathrm{1,2}\}}}{E}_{i\{\mathrm{1,2}\}}^{\ast }$, which corresponds to the sum of the union of all desired effects associated with all markers attached to ${\widehat{\mathrm{\Phi }}}_{\{\mathrm{1,2}\}}$.

For ranking a set of drug combinations, for a given set of drugs $S_1,\mathrm{\dots },S_n$, indexed as $\{1,\mathrm{\dots },n\}$, the total number of drug combinations corresponds to the cardinality of $\mathrm{\wp }(S=1,\mathrm{\dots },n)/\mathrm{\varnothing }$ given by $\left|\mathrm{\wp }(S=1,\mathrm{\dots },n)\right|/\mathrm{\varnothing }=2^n-1$. For simplicity we denote this as $\left|\mathrm{\wp }(S)\right|$. If we let $X_1,X_2,\mathrm{\dots },X_{\left|\mathrm{\wp }(S)\right|}$ be the scores for each drug combination estimated by $F(c)$; a nondecreasing ranking of the scoring distribution for these drug combinations is given by $X_{(1)}\le X_{(2)}\le \mathrm{\dots }\le X_{(\left|\mathrm{\wp }(S)\right|)}$,where $X_{(r)}$ is the $r^{th}$ smallest value in the distribution for $r=\mathrm{1,2},\mathrm{\dots },\left|\mathrm{\wp }(S)\right|$ and the optimal drug combination is given by $\arg (X_{(\left|\mathrm{\wp }(S)\right|)})$, corresponding to the combination with the maximum order score. For DRUG-NEM, $X_{(1)}\le X_{(2)}\le \mathrm{\dots }\le X_{(\left|\mathrm{\wp }(S)\right|)}$ under certain graph structures is expected to produce ties even under noisy data (e.g., Fig. S1F). Under this particular model, the nested structure breaks the tie, forcing $\arg (X_{(\left|\mathrm{\wp }(S)\right|)})$ in this case to $S_1$. In practice, we identify all drug combinations having a score of $X_{(\left|\mathrm{\wp }(S)\right|)}$. This corresponds to a new index family of elements of $\left|\mathrm{\wp }(S)\right|$ denoted here as $R_{X_{(\left|\mathrm{\wp }(S)\right|)}}$, where $R_{X_{(\left|\mathrm{\wp }(S)\right|)}}=\{c|c\in \mathrm{\wp }(S),X_{(\left|\mathrm{\wp }(S)\right|)}=F(c),\forall c\}$. The optimal combination from a tie is then given by $\{c|\left|c\right|=min\{|d|,\forall d\in R_{X_{(\left|\mathrm{\wp }(S)\right|)}}\}\}$.