Integrating effects of species composition and soil properties to predict shifts in montane forest carbon–water relations

Significance

This research focuses on how species composition and soil properties interact to control carbon fixation and water loss in California’s montane forests. Two conclusions arise: (i) The amount of carbon fixed per unit of water lost via transpiration varies widely among forest stands depending on dominant tree species and their inherent leaf characteristics, and (ii) different parent materials and stages of soil development regulate the effect of climate on water-use efficiency and productivity of trees across altitudinal gradients. Taken together, dynamic biological processes related to species composition and relatively inert physicochemical properties that characterize soil development can be combined to anticipate changes in forest carbon and water balances.

Abstract

This study was designed to address a major source of uncertainty pertaining to coupled carbon–water cycles in montane forest ecosystems. The Sierra Nevada of California was used as a model system to investigate connections between the physiological performance of trees and landscape patterns of forest carbon and water use. The intrinsic water-use efficiency (iWUE)—an index of CO₂ fixed per unit of potential water lost via transpiration—of nine dominant species was determined in replicated transects along an ∼1,500-m elevation gradient, spanning a broad range of climatic conditions and soils derived from three different parent materials. Stable isotope ratios of carbon and oxygen measured at the leaf level were combined with field-based and remotely sensed metrics of stand productivity, revealing that variation in iWUE depends primarily on leaf traits (∼24% of the variability), followed by stand productivity (∼16% of the variability), climatic regime (∼13% of the variability), and soil development (∼12% of the variability). Significant interactions between species composition and soil properties proved useful to predict changes in forest carbon–water relations. On the basis of observed shifts in tree species composition, ongoing since the 1950s and intensified in recent years, an increase in water loss through transpiration (ranging from 10 to 60% depending on parent material) is now expected in mixed conifer forests throughout the region.

Globally, it is estimated that montane forest watersheds provide water for over 4 billion people (1). In California, as many as 20 million people rely on montane forest watersheds for drinking water (2, 3). In California’s Sierra Nevada, recent changes in climate have caused alterations of forest species composition and productivity (4, 5). As in other montane systems, rising temperatures are now expected to force tree species migration to higher altitudes (6) in tandem with shifting physiologically optimal climate zones (7, 8). To the extent this occurs, forest watersheds, which currently provide ∼68% of the water that fills California’s reservoirs, could see >20% decreases in river flow due to increasing tree cover and a proportional increase in water loss through transpiration (3). This contribution, however, can vary widely across forest stands because of interacting biological and environmental factors that make predicting shifts in forest function difficult, leading to uncertain impacts on terrestrial carbon and water cycles.

Foremost among sources of uncertainty are interactions between soils and plants across altitudinal gradients. Specifically, properties that depend on the slow process of soil development from parent material weathering (e.g., nutrient content and water-holding capacity) influence growth and water use of individual trees (9, 10), exerting a bottom-up control on the distribution and composition of forest ecosystems (11, 12). For the particular case of Sierra Nevada forests, altitudinal gradients of soil development that arise from diverse parent materials delineate mosaics throughout landscapes where different vegetation types coexist (12, 13). Given that gradients of soil development can constrain the physiological performance of trees as well as the composition of forests (14) a hierarchical approach is needed to anticipate their effect on forest carbon and water uptake (15). The present study makes such an assessment by combining stable isotope measurements of individual trees with stand-level soil and climate data across altitudinal transects that span different forest types on the west slope of the Sierra Nevada (Fig. 1).

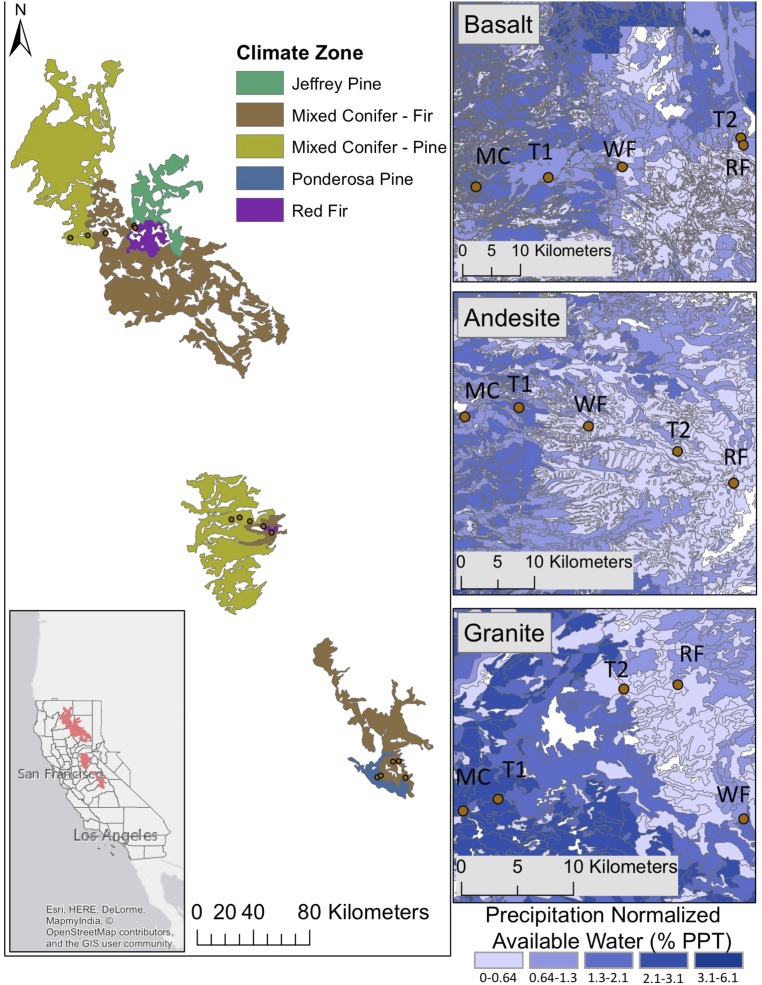
Fig. 1.

Field site locations within California and their associated climate zones (CALVEG attribute CVNAME). Each field area transitions from an MC or ponderosa pine forest toward a fir-dominated forest with red fir at the top of the transects. Maps on the right are blown up to show the gradient of plant available water down to 150 cm in soil (SSURGO) and normalized to mean annual precipitation. Stands (15 total, five per transect) with lower precipitation have greater water storage relative to incident precipitation. Climate zones (five total, repeated within each transect) MC, T1, WF, T2, and RF increase in elevation in that order.

Transects which share a common gradient of tree cover and species composition were replicated on three different parent materials to test how soil development—characterized by weathering of the parent rock into secondary minerals and smaller particle sizes (16)—modulates physiologically controlled carbon–water relations (Fig. 2). Carbon isotope ratios (δ¹³C) of leaf cellulose were used to calculate differences in intrinsic water-use efficiency (iWUE)—defined as the ratio of net CO₂ assimilation (A) to stomatal conductance (g_s) (17)—of nine dominant tree species common to all transects. Cellulose δ¹³C ratios can be used to infer iWUE because both leaf transpiration and isotopic fractionation of carbon are controlled by g_s (18). Estimated iWUE was then combined with climate data to calculate differences in water use in changing forest landscapes. Since δ¹³C ratios vary with changes in either A or g_s, independent measurements of oxygen isotope ratios (δ¹⁸O) of cellulose were used to separate these effects on iWUE. After accounting for differences in water source and vapor pressure deficit (VPD), δ¹⁸O ratios of leaf cellulose vary in tandem with transpiration (19, 20). This occurs because any increase in g_s leads to a proportional decrease in ¹⁸O evaporative enrichment of leaf water that is maintained by high transpiration rates (21). At the same time, an increase in g_s can lead to increases in ¹³C discrimination by sustaining high intercellular CO₂ levels (22). To further support this interpretation, leaf carbon-to-nitrogen (C:N) content—a key factor affecting leaf photosynthetic rates (23)—was measured to control for potential effects of nitrogen availability on iWUE (e.g., refs. 23 and 24).

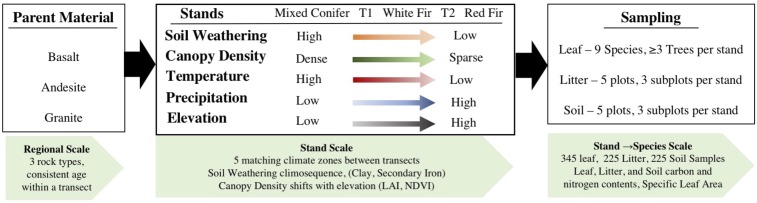
Fig. 2.

The sampling design is shown starting with regional scale variables on the left, stand scale properties in the middle, and plant scale on the right, based on the scale at which each property was measured. Transects were established on different parent materials (BS, AN, and GR) selected for their prevalence across the Sierra Nevada and for their contrasting mineralogical properties that result from differences in weatherability. At the stand scale, a number of dynamic climatic and ecosystem variables represent general trends associated with elevational gain at all transects. Soil weathering was measured as clay content, secondary iron (Fe_d), and as a function of a pedogenic energy (E_ped). Canopy density was measured by hemispherical photography used to calculate LAI, which was compared with stand-level NDVI, a satellite-based measure of greenness and productivity. Climate variables were derived from the PRISM model (26). Tree-level variables, such as isotopic composition and nitrogen content, were measured to help understand resource limitation and photosynthetic capacity across the gradient. Taken together, these variables were used to investigate how species traits and soil properties affect productivity and water-use efficiency of trees and forests throughout the region.

In cases where leaf-to-air VPD (LAVD) is known, the actual amount of water transpired per unit of CO₂ assimilated can be calculated from iWUE estimates (25). Here, this calculation was done using stand-level VPD obtained from available datasets (26) and assumed constant among leaves of coexisting trees at any given stand. Data generated through this approach permitted comparison of the effect of shifting species composition on forest water balance across different parent materials while also controlling for differences in climate and atmospheric pressure. Specifically, the following three hypotheses were tested. (H_i) Significant differences in iWUE occur across the elevation gradient beyond those expected from changes in climate and atmospheric pressure, which are known to influence leaf gas exchange (i.e., water-use efficiency increases with elevation due primarily to differences in species composition and soil development). (H_ii) Within a forest stand iWUE varies significantly and predictably among coexisting tree species as a function of leaf traits that influence carbon and water exchange (i.e., broadleaf species have lower iWUE than conifers). (H_iii) For a specific tree species iWUE varies significantly and predictably across the landscape as a function of parent material and stage of soil development (i.e., water-use efficiency varies as a function of geology, but is highest when soil development is lowest). Finally, on the basis of empirical support found for all three hypotheses, statistical models were developed to predict changes in water use relative to carbon assimilation using species composition, soil properties, and their interaction as predictors.

Results

δ¹³C Values and iWUE.

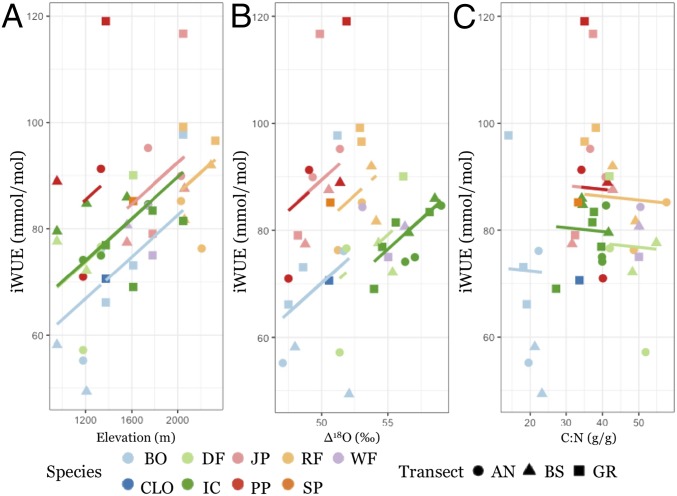
In agreement with H_i, cellulose δ¹³C values varied widely within and across species but increased consistently with elevation (Fig. 3A). On average, cellulose δ¹³C increased ∼2‰ per 1,000-m elevation, which exceeds expected increases due to a natural decline in temperature and oxygen partial pressure with altitudinal gain (∼0.8‰; ref. 9). After controlling for atmospheric CO₂ concentration and δ¹³C values, a strong increase in iWUE tracked changes in species composition from low to high altitudes (Fig. 4A), an observation that is in agreement with H_ii. When treated as categorical variables, both species composition and soil development as well as their interaction had significant effects on iWUE (Table 1). Among 22 continuous variables that represent species and soils effects, the strongest correlations with cellulose δ¹³C-derived iWUE were found for specific leaf area (24%), leaf-area index (LAI, 16%), VPD (13%), and pedogenic energy (12%). In contrast, there was no detectable effect of precipitation on iWUE (SI Appendix, Fig. S4) due to the dominant effect of species and soil properties. These results further support H_ii and are in agreement with H_iii, which is also supported by estimates of water loss. This point is illustrated in Fig. 5, where water use standardized by division (i.e., iWUE divided by VPD; Eq. 5) is shown for low-efficiency (dark blue) and high-efficiency (light blue) species that coexist in mixed conifer (MC) forests. In this example, if pine trees were to be replaced with broad-leaf trees, intrinsic differences in water-use efficiency (on average iWUE differs by 28–80% among species depending on transect; Fig. 4) would translate into a 10–60% increase in water loss per any given amount of carbon assimilated (Fig. 5), with the low and high ends of this spectrum corresponding to andesite (AN)- and granite (GR)-derived soils, respectively.

Fig. 3.

Leaf cellulose δ¹³C and δ¹⁸O values of all sampled trees by transect (shapes)—AN, BS, and GR—and species (color). Regressions were performed on all data points yielding positive correlations with elevation isotopic values. Regression models for the trends are as follows: (A) y = 0.0026x − 29.97, R²_adj = 0.32, P < 0.0001 and (B) y = 0.0011x + 41.40, R²_adj = 0.015, P = 0.012. Species abbreviations are as follows: BO, black oak/Quercus kelloggii; CLO, canyon live oak/Quercus chrysolepis; DF, Douglas fir/Pseudotsuga menziesii; IC, incense cedar/Calocedrus decurrens; JP, Jeffrey pine/Pinus jeffreyi; PP, ponderosa pine/Pinus ponderosa; RF, red fir/Abies magnifica; SP, sugar pine/Pinus lambertiana; and WF, white fir/Abies concolor.

Fig. 4.

Measured iWUE averaged by species at each sampled forest stand and plotted in relation to elevation (A), ∆¹⁸O values (B), and C:N ratios (C). Different species are shown in different colors and parent material in different shapes as described in Fig. 3. Clustering is apparent at the species level with species effects shown as solid regression lines. The final observed versus predicted mixed-effect model including species:parent material interactions is shown in SI Appendix, Fig. S6. These plots indicate that increasing iWUE with elevation is primarily due to differences in species traits and associated effects on transpiration, as inferred from carbon and oxygen isotope fractionations. In contrast, leaf C:N content has a weak association with iWUE. See SI Appendix, Table S4 for model coefficients and random intercepts and SI Appendix, Table S5 for R codes.

Table 1.

Test of H_i, H_ii, and H_iii using linear mixed-effects models to show significant elevation, species, and parent material effects on iWUE

Model	Random effects	Fixed effects	Significance	AICc	Adjusted R2
Hi	Species	Elevation	<0.0001	2,831	0.28
Hii	Parent material	Species	<0.0001	2,774	0.30
Hiii	Species	Parent material	<0.0001	2,812	0.30
Interaction	NA	Species × parent material	<0.0001	2,776	0.36

All hypotheses are supported and species effects emerge as dominant. SI Appendix, Table S1 shows effect sizes for each these terms. AICc, corrected Akaike information criterion; NA, not applicable.

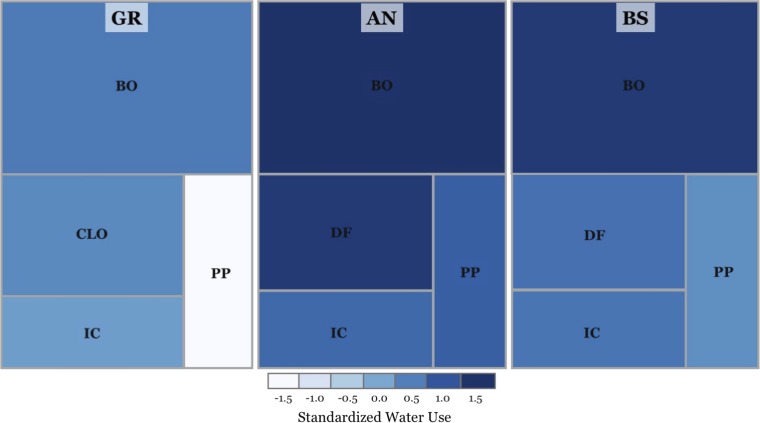
Fig. 5.

Graphic representation of standardized water use for dominant tree species present in MC stands AN, BS, and GR transects. In this schematic representation, increasing color intensities represent decreasing water-use efficiency, such that each incremental step (from light to dark blue) corresponds to a 10–15% increase in water loss through transpiration per unit of carbon assimilated during photosynthesis. Standardized water use is inferred from iWUE (divided by VPD; Eq. 5) and scaled for ease of comparison with a mean of zero and SD of 1. The area of each square is proportional to the average specific leaf area of each species (SI Appendix, Table S3), which generally corresponds to water use (i.e., species with high leaf area tend to have low efficiency). The effect of parent material can be visualized as variation in color intensity within each of the selected species: BO, black oak/Quercus kelloggii; CLO, canyon live oak/Quercus chrysolepis; DF, Douglas fir/Pseudotsuga menziesii; IC, incense cedar/Calocedrus decurrens; and PP, ponderosa pine/Pinus ponderosa. In this example, which is based on observations of compositional change in forests located at altitudes where the selected species cooccur, the expansion of broad-leaf trees into conifer-dominated stands could represent >10% increase in water transpired in forests on AN- and BS-derived soils and up to 60% increase in water loss through transpiration in forests on GR-derived soils.

δ¹⁸O Values.

Unlike δ¹³C values, we did not find a consistent increase in cellulose δ¹⁸O values with elevation (Fig. 3B). However, this lack of correlation is obfuscated by the accompanying changes in the δ¹⁸O values of source water. The effect of source water across sites was corrected for, revealing a significant relationship with elevation for the oxygen isotope fractionation of leaf cellulose (i.e., ∆¹⁸O values) (SI Appendix, Fig. S5). Moreover, a strong positive relationship was apparent when average ∆¹⁸O values were correlated with average iWUE for each species and parent material (Fig. 4B). It is important to note that no apparent relationship was found between ∆¹⁸O, LAI, VPD, or other hydrological parameters, whereas parent material and clay content were significant predictors of ∆¹⁸O variability (R² = 0.08, P < 0.0001 and R² = 0.04, P < 0.0001, respectively). However, species differences accounted for the largest portion of the variability (SI Appendix, Figs. S1 and S6).

Leaf, Litter, and Soil Quality.

Litter C:N ratios showed no trend with elevation, but soil N content decreased with elevation across all parent materials (R² = 0.09, P < 0.0001). Significant differences in litter and soil C:N were observed between parent materials (SI Appendix, Table S2), which explained 11.4% and 8.9% of the variation in litter and soil C:N across all stands, respectively. However, unlike ∆¹⁸O values, leaf C:N ratios show a small influence over iWUE even when controlling for species by assigning distinct intercepts to species-specific trends (Fig. 4C and SI Appendix, Table S4).

Stand Productivity.

Measurements of LAI, normalized differential vegetation index (NDVI; Eq. 7 and Materials and Methods), and actual evapotranspiration (aET) were used as metrics of stand productivity and water loss. As expected, LAI, NDVI, and aET were inversely correlated with elevation (R² = 0.64, 0.39, and 0.64, respectively, P < 0.0001) and showed an inverse relationship with iWUE and a positive relationship with δ¹⁸O values of leaf cellulose (Table 2). A time series of NDVI to January 1999 using MODIS (Moderate Resolution Imaging Spectroradiometer) data showed that all stands have stable productivity except at the highest elevation [red fir (RF)-dominated stands] in the basalt (BS) transect, which burned in 2012 and has since persisted at a relatively lower NDVI steady state. All metrics of stand productivity had an inverse relationship with seasonality (SD NDVI), indicating that the link between climate and productivity is dependent on seasonal intensity as much as annual input.

Table 2.

Summary statistics for correlations of all measured variables and iWUE

Group	iWUE predictor	Effect size	Adjusted R2	Significance
Soil development	Clay	−4.7	0.08	<0.0001
	Fed	−4.1	0.06	<0.0001
	Eped	−5.6	0.12	<0.0001
	SWS	−3.9	0.06	<0.0001
Productivity	LAI	−6.5	0.16	<0.0001
	NDVI	−3.3	0.04	0.0003
	VPD maximum	−5.9	0.13	<0.0001
Soil and litter quality	C:N litter	0.50	0	0.56
	%N litter	0.40	0	0.65
	%N soil	−0.10	0	0.91
	%C soil	−0.40	0	0.65
	Feo	0.05	0	0.95
Seasonality	Temperature	−5.5	0.11	<0.0001
	Precipitation	1.7	0.01	0.05
	cvPPT	−0.97	0	0.27
	RUN	4.0	0.06	<0.0001
	RCH	−1.4	0	0.11
	SD NDVI	1.1	0	0.21
Other	Elevation	5.8	0.12	<0.0001
	SLA	−7.2	0.19	<0.0001
Categorical	Species		0.24	<0.0001
	Parent material		0.02	0.01
	Climate zone		0.13	<0.0001

The relationships are separated into major categories that are expected to effect iWUE. All variables were standardized to a mean of 0 and SD of 1 before analysis and related to untransformed iWUE values.

Soil Development.

Clay content and Fe_d decreased consistently with increasing elevation in BS stands (e.g., from 62.5 to 6.8% and 58.7 to 9 g/kg; SI Appendix, Fig. S2 and Table S2). The GR transect carries a different pattern, as GR contains relatively little weatherable Fe (27). Estimates of E_ped decreased with elevation and precipitation by an average of 33% from RF to MC stands across all transects. As a result, soil water storage (SWS) decreased with elevation across all transects regardless of parent material differences (R² = 0.63, P < 0.0001).

Climatic and Hydrologic Indicators.

Temperature and elevation were closely related across all sites (ranging from 5.8 to 13.9 °C between 2,325 and 954 m, respectively; SI Appendix, Fig. S3), as would be expected in a typical orographic gradient. However, while precipitation and elevation are correlated, their relationship is weak (R² = 0.21, P < 0.0001) and, as mentioned above, had no effect on iWUE. Among transects, precipitation peaked at different elevations (SI Appendix, Table S2), reflecting latitudinal patterns in seasonal rainfall. Last, the coefficient of variation of monthly precipitation (cvPPT) and SD NDVI were used as a metrics of seasonality (28), ranging from 3.5 to 8.4% and 5.2 to 15.6%, respectively. Although these variables were not found to correlate well with δ¹³C or iWUE, SD NDVI was strongly related to LAI (SI Appendix, Table S2, R² = 0.83, P < 0.0001) and cvPPT to state of soil development (Fe_d, SI Appendix, Fig. S2, R² = 0.88, P < 0.0001).

Discussion

Summary of Hypotheses Testing.

It has long been established that gas exchange between leaves and the atmosphere varies globally with air temperature and oxygen partial pressure, leading to decreasing carbon isotope discrimination from CO₂ to plant tissue with increasing elevation (9). In montane forest ecotones, declines in carbon isotope discrimination are expected to be stronger than those caused by changes in temperature or oxygen partial pressure alone (H_i) due to changes in tree species composition (H_ii) and soil development gradients (H_iii) that lead to increasing iWUE from low to high altitudes. We found support for each of these hypotheses in California’s montane forests. First, we identified increases in iWUE across a ∼1,500-m elevation gradient that overwhelms those caused by changes in temperature and atmospheric pressure alone. Second, we found that iWUE increases with elevation due primarily to differences in abundance and species-specific leaf traits of nine dominant tree species. Third, we found a significant modulating effect of soil development and parent material on species iWUE trends with elevation. Taken together, these observations were used to estimate the potential impact of species range shifts on forest water balance at various parent materials and stages of soil development as follows.

Species Effects on iWUE.

The major driver of iWUE variability was specific leaf area (SLA), which ranges from ∼70 to 260 g⋅cm⁻² on average among the studied species (SI Appendix, Table S3). The effect of SLA on leaf gas exchange can be understood based on the strong influence of this trait, which generally integrates the effects of leaf thickness and mesophyll conductance on intercellular to atmospheric CO₂ concentrations (i.e., c_i/c_a, Eq. 3) and transpiration (29). Here, diverse multispecies forest stands are dominated by species with inherently high SLA at low elevation sites. This is consistent with a well-established tradeoff between productivity and efficiency observed for many different functional groups across biomes (e.g., refs. 30–32). Briefly, interspecific differences in SLA overwhelm any effects of SLA plasticity in determining differences in photosynthetic gain per water loss via transpiration. As a result, high-SLA species tend to dominate in competitive environments where water and other soil resources are abundant. Conversely, low-SLA species tend to dominate in environments where soil resources are scarce and maximizing efficiency over productivity is more advantageous, a pattern that holds true from tropical to alpine forest ecotones (e.g., refs. 33–35). Importantly, we observed increasing iWUE with elevation within and across species, always in association with independently measured oxygen isotope discrimination (Δ¹⁸O). Cellulose Δ¹⁸O changed in tandem with declines in Δ¹³C; therefore, differences in iWUE are attributed to a decreasing trend in g_s. In contrast, nitrogen availability and leaf C:N ratios show only weak influence over iWUE across species and stands. Overall, multiple lines of evidence indicate that forests at high elevations are subject to greater stress than those at low elevations, primarily from water availability. Crucially, this elevation effect was modulated by parent material, which is consistent with the expectation of water availability-driven tree growth in poorly developed montane soils. Moving down the elevation gradient, leaf C:N data suggest increasing competition for N driven by increasing productivity (e.g., LAI). Thus, low-elevation sites appear to face greater N limitation and less water stress than high-elevation sites, which is in agreement with changes in leaf traits of dominant forest species which favor competitive growth over water-use efficiency (WUE) at low elevations.

Soil Development Effects on iWUE.

It is important to note that iWUE was found to have a remarkably weak relationship with precipitation (SI Appendix, Fig. S4; P = 0.05, R² = 0.01), yet, when plotted against elevation, iWUE was found to match trends in soil development (Fig. 4 and Table 2). This is also reflected in gradients of stand productivity, which is lowest at high elevations due to the harsh climate and intensified seasonality. Productivity is here represented by LAI, a measure of canopy density, and NDVI (Eq. 7 and Materials and Methods), a remotely sensed measure of canopy greenness. The productivity gradient exacerbates competition for soil N at lower elevation sites, leading to different physiological limitations between low and high elevations. As a result, the physiologically controlled trade-off between productivity and efficiency described above is also manifested at the landscape level. We argue that this trade-off reflects differences soil development, as it displays clear trends with elevation and parent materials. Generally, we see highly weathered clay rich soils in the warmest parts of the transects and poorly developed sandy soils at high elevations. Low-elevation soils support the least efficient yet most productive systems, with the highest water-holding capacity and smallest water losses to recharge (RCH) and runoff (RUN) (Fig. 1 and SI Appendix, Fig. S4 and Table S2). Although this observation is consistent with previous montane conifer studies, previous research has focused on physiological indicators of these gradients, rather than environmental drivers (23, 36). As soil development determines not only hydrologic partitioning but also field capacity and SWS (37–39), it is an inertial force which integrates the impact of climate through long periods of time. Conversely, the flora of specific climate zones tend to be tuned to the local physical and chemical properties that influence carbon–water dynamics from trees to ecosystems. The result is a biological inertia, which makes it difficult and more challenging for species shifts to occur. Macroscale evidence of this phenomenon has been observed by Huang et al. (40), where the velocity of vegetation productivity (i.e., the rate of change of productivity over time) is shown to lag behind changes in climate. Our empirical observations and statistical models show similar spatial contrasts, which support the notion that interactions between species composition and soil properties, particularly those related to water or nutrient deficiencies, exert dominant control on forest ecosystem function.

A Case Study of Shifting Forest Composition and Function.

A central conclusion of this study is that variation in leaf traits and interactions between species composition and parent material are primary factors influencing variation in carbon and water cycles across montane landscapes. This can be visualized in Fig. 5, where the color scheme that represents water use matches previously reported average differences in species leaf area (41)—represented by box sizes according to values shown in SI Appendix, Table S3—and reveals considerable within-species variation as a function of parent materiel. On the basis of these findings, historical baselines and recent surveys of forest composition can be used to evaluate the potential impact of species range shifts on water-use efficiency and its dependency on soil properties throughout the landscape. A classic case study by Ansley and Battles (42) provides an example where significant changes in the contribution of dominant tree species to the productivity of Sierra Nevada MC forests were recorded from 1957 to 1996. Consistent with reports from other alpine regions (6), Ansley and Battles found increasing density of broad-leaf species into areas previously dominated by ponderosa pine trees, a trend that has accelerated in recent decades due to human disturbances and climate warming (8). When combined with standardized water use—calculated here for the same dominant species commonly found at altitudes where mixed forests occur—the observed migration of broad-leaf trees toward higher altitudes is expected to cause a 10–60% increase in water loss through transpiration, depending on parent material (Fig. 5). It should be noted that this is a conservative estimate that assumes a similar level of productivity for newly established relative to preexisting forest stands. If productivity increases or if tree species migration proceeds to higher altitudes, as observed at the upper treeline of other montane regions (6, 43), an opening of transpiration “floodgates” could significantly affect Sierra Nevada watersheds, which depend on RCH and RUN of alpine systems as the source of most of the water that fills California reservoirs (3).

Summary and Future Directions.

This research exemplifies the need to understand how proximal factors, such as soil parent material and species composition, interact with distal factors, such as atmospheric pollution and climatic regime shifts, to influence essential services provided by forest ecosystems. Montane forests are particularly sensitive to climatic and atmospheric changes, which have been shown to alter the distribution of major primary producers along altitudinal gradients. Such alterations can have cascading impacts on ecosystem function, threatening vulnerable water resources that are often regarded as slow to respond to climatic change. Additional steps toward predicting the effects of species migration on regional hydrologic regimes are warranted; specifically, promising areas for future research include the use of pedogenic thresholds to delineate the limits of biogeographical and biogeochemical responses to global environmental change and data-enabled models to connect local management (e.g., silvicultural practices) to the regional stability of forest composition and function.

Materials and Methods

Description of Study Sites.

California’s Sierra Nevada and Cascade mountains provide a diversity of well-defined bioclimatic zones which overlie several different geological formations. We selected study sites spanning ∼1,500 m of elevation gain characterized by average annual precipitation ranging from 947 to 1,626 mm (increasing with elevation and latitude) and mean annual temperature ranging from 13.9 to 5.8 °C (from low to high elevations). Three transects were identified to isolate the effect of distinct parent materials: AN, BS, and GR. A total of 45 stands were selected (15 per transect) to represent five different altitudes or climatic zones replicated in each transect, with five sites per stand, each with three subsites, totaling 225 sampling locations (Fig. 2). At the lowest elevation, sampling was conducted at stands characterized by deep highly weathered soils and MCs, at intermediate elevation stands were characterized by poorly developed soils and white firs (WF), and at the highest elevation shallow skeletal soils and RFs predominated. Forest stands at these three main climatic zones of contrasting soil development and species dominance were replicated in each transect, using the same sites described in previous soil characterization studies (44, 45). In addition to these three main climatic zones, two stands were selected at intermediate altitudes, transition 1 (T1) between MC and WF and transition 2 (T2) between WF and RF.

Sampling Design.

A hierarchical approach was used to assess coupled carbon and water dynamics at the leaf, species, and stand levels across climatic zones (altitude) and lithological zones (transects of different parent materials) (Fig. 2). First, leaf cellulose δ¹³C ratios were used as an index for iWUE (i.e., A/g_s) for nine coexisting tree species across forest elevation gradients on three different parent materials. Second, leaf cellulose δ¹⁸O ratios were compared with those of source water (i.e., precipitation) and combined with air-to-cellulose ¹³C discrimination (Δ¹³C) to distinguish A from g_s, thus separating the effect of water use from that of CO₂ assimilation. This interpretation is based on the well-supported assumption that ¹⁸O fractionation (Δ¹⁸O) represents a direct response to transpiration regulation (21). Additionally, interpretation of carbon and oxygen isotope data was supported by measurements of C:N ratios in leaves, litter, and soil, which are known to correlate with photosynthetic capacity (23, 25), and thus could cause divergences in iWUE among stands or species. Field sampling was done in the months of August and September 2014, at the end of the growing season and before fall rains began. The number of samples collected at each stand was determined using an a priori test of statistical power, anticipating three potential predictors: climate, soil type, and species effects, and a moderate statistical power of 0.8 (46). Briefly, at each of the five altitudinal sites at each transect an area of ∼1 ha with no apparent disturbance was chosen. At each of these stands nine dominant tree species were identified and sampled whenever present (Fig. 2). At least three individual trees randomly distributed through the stand (>50 m apart) with no apparent damage to the trunk or canopy were sampled for each species at each stand. For each individual tree, three branches and attached new growth needles were taken to represent the most recent growth season. Branches were sampled 2–5 m above the ground level and always from sun-exposed south-facing canopies. Fifteen litter samples were taken from randomly selected sites at each stand. Additionally, the underlying topsoil (0–10 cm) was collected. Soil and litter replicates were taken no closer than 10 m apart and never under the cover of one individual tree. At each stand, hemispherical photos were taken using a Nikon Coolpix 4500 camera with a Nikon FC-E8 181° hemispherical lens on a north-oriented level tripod 1.5 m above the ground. Photos were processed using Gap Light Analyzer to calculate LAI, integrating at the 60° zenith angle (47, 48). To characterize species-specific differences in leaf traits we used average values of specific leaf area (SLA), that is, the ratio between leaf area and mass, for each dominant species as provided by ref. 41.

Sample Processing.

Leaves, litter, and soil were dried at 60 °C for 1 wk until steady dry weight was reached. Leaves were lightly washed and ground to a fine powder using a coffee grinder. Alpha-cellulose was extracted from leaf samples by acetic acid–nitric acid digest (49). Woody material was removed from litter, which was then dried for 1 wk at 60 °C and ground to 1 mm using a Wiley mill. Soils were sieved to 2 mm and kept this way for further particle size analysis, while subsamples of each soil were ground to a fine powder in a ball mill for isotopic and elemental analysis. Particle size distributions of soils at MC, WF, and RF stands were gathered from previous studies at the sites (45). For sites unique to this study (T2 and T1) the modified pipette method was used, which employs Stokes law to approximate the settling time of soil particles (50). Soil samples were analyzed for mineral composition by selective dissolution using acid oxalate and citrate dithionite to extract short-range order and reduced iron, respectively. Extracts were analyzed colorimetrically for iron content after chelation with ferrozine (51).

Stable Isotope Analysis and Interpretation.

Stable isotope ratios are reported using delta (δ) notation. In Eq. 1, the generic relationship is shown, where y is the atomic mass of the heavy isotope, X is the atom of interest, and R_sample and R_standard are the measured ratios of the sample and a reference standard, where results are reported in per-mil (i.e., 1/1,000, or ‰) values. Values are reported with reference standards calibrated to Vienna Belemnite of the Pee Dee formation for δ¹³C and the Vienna Standard Mean Ocean Water for δ¹⁸O. Leaf cellulose samples are prepared individually in tin or silver capsules for C or O analysis (EA Consumables), respectively. For carbon, samples are introduced with an autosampler into a PDZ Europa ANCA-GSL elemental analyzer (Sercon Ltd.) with a combustion chamber packed with chromium oxide and silvered copper oxide and held at 1,000 °C to ensure complete combustion. Following combustion, the gas is reduced using reduced copper in a second reactor at 650 °C. Helium carrier gas then transfers analytes through a magnesium perchlorate water trap and into a Carbosieve molecular sieve GC column at 65 °C to separate gasses before they are introduced into a PDZ Europa 20–20 isotope ratio mass spectrometer (Sercon Ltd.). Long-term precision for the instrument is 0.2‰ for δ¹³C measurements. For oxygen samples, silver capsules are analyzed using an elementar PyroCube interfaced to an Isoprime VisION mass spectrometer (Elementar Analysensysteme GmbH). Samples are pyrolized to CO in a reactor containing glassy carbon, graphite felt, and lamp black at 1,400 °C. An adsorption trap isolates CO from N₂, which is then analyzed in the mass spectrometer. δ¹⁸O measurements had a precision of 0.16‰.

$${\delta }^{y}X=(\frac{R_{\text{sample}}}{R_{\text{standard}}}-1).$$ [1]

Isotope ratios of carbon were used to calculate iWUE of each sample following standard methods. Beginning with raw δ¹³C measurements, Eqs. 2–4 are used to calculate iWUE, or the millimoles of carbon assimilated per mole of water lost. Eq. 2 is used to calculate isotopic discrimination relative to the source (atmospheric CO₂):

$${\mathrm{\Delta }}^{13}\mathrm{C}=({\mathrm{\delta }}^{13}{\mathrm{C}}_a-{\mathrm{\delta }}^{13}{\mathrm{C}}_p)/(1+\frac{{\mathrm{\delta }}^{13}{\mathrm{C}}_p}{\mathrm{1,000}}),$$ [2]

where subscripts a and p denote air and plant δ¹³C, respectively. Eq. 3 relates ∆¹³C from Eq. 2 to diffusive and photosynthetic fractionation constants (a: 4.4‰ and b: 27‰) and CO₂ partial pressures inside the leaf (c_i) and in the atmosphere (c_a):

$${\mathrm{\Delta }}^{13}\mathrm{C}=a+(b-a)\frac{c_i}{c_a}.$$ [3]

Finally, Eq. 4 relates these parameters to iWUE by using the scaling factor 1.53, which is the ratio of diffusivity of water vapor to CO₂. This is defined as the ratio of net photosynthetic rate (A) to stomatal conductance (g_s) (18). To calculate iWUE, Δ¹³C from Eq. 2 is used in Eq. 3 along with constants a and b to calculate c_i/c_a. This is then substituted into Eq. 4, yielding iWUE:

$$\text{iWUE}=\frac{\text{A}}{\text{gs}}=\frac{c_a(1-\frac{c_i}{c_a})}{1.53}.$$ [4]

When LAVD is known, the actual amount of water lost via transpiration can be estimated from iWUE measurements (26). Here, to estimate relative differences in water use, stand-level maximum VPD was obtained from existing datasets (27) and assumed constant for all coexisting trees at any given stand (SI Appendix, Table S2) to generate a normalized index for actual WUE, here termed “standardized water use”:

$$\text{WUE}=\frac{\text{A}}{E}=\frac{\text{iWUE}}{\text{VPD}}.$$ [5]

It is important to note that using a single VPD value to compare water use among coexisting species is a conservative approach that minimizes interspecific differences relative to intensified LAVD gradients that may occur due to leaf morphology (e.g., when broad leaves and needles are compared). Furthermore, this standardized index of water use is based on ∆¹³C and iWUE calculations that incorporate a steady decrease in c_a with altitude at a rate of 9.5% per 1,000-m elevation gain from a 400-ppm baseline at sea level (52). Thus, environmental changes that would otherwise inflate iWUE values (9) are controlled for in this calculation, allowing direct comparisons among colocated species as well as among species that occur across the altitudinal gradient on different parent materials (Fig. 2).

Calculation of Δ¹⁸O (Eq. 6 below) is equivalent to the calculation in Eq. 2 above, substituting δ¹⁸O of plant material, and using δ¹⁸O source water (sw) estimated by the Online Isotopes in Precipitation Calculator (53). Interpretation of Δ¹³C/Δ¹⁸O is based on recent models which show that this relationship normalizes carbon isotope discrimination to the impact of stomatal conductance (19, 54). This interpretation was aided by analysis of trends in VPD obtained from PRISM (26), which accounts for differences in leaf to air pressure gradients (55):

$${\mathrm{\Delta }}^{18}\mathrm{O}=({\mathrm{\delta }}^{18}{\mathrm{O}}_{sw}-{\mathrm{\delta }}^{18}{\mathrm{O}}_p)/(1+\frac{{\mathrm{\delta }}^{18}{\mathrm{O}}_p}{\mathrm{1,000}}).$$ [6]

Stand-Level Data.

The normalized difference vegetation index (NDVI) is calculated from satellite measurements of visible and infrared light. Additionally, the SD NDVI was calculated for the year 2014, which represents the magnitude of the annual NDVI cycle. Eq. 7 is used to calculate NDVI, where NIR is MODIS band 2 (841–876 nm) and Red is MODIS band 1 (620–670 nm). Annual data were downloaded and processed; values represent annual averages for 2014, smoothed with temporal interpolation to remove the effect of unperceivable cloud and aerosol distortion using the MODIStools package for R (56). Values are derived from the MODIS Terra satellite, which captures images at 250-m-resolution grid cells every 16 d. Each stand is represented by a 2.25-km² grid consisting of 81 cells:

$$\text{NDVI}=\frac{\text{NIR}-\text{Red}}{\text{NIR}+\text{Red}}.$$ [7]

Stand-level 30-y normal (1981–2010) of monthly and annual hydrologic variables were derived from the USGS CA Basin Characterization Model, a downscaled climate model that is merged with soil parameters from the SSURGO database. Here, we test potential evapotranspiration , aET, SWS, RCH, and RUN, all measured in millimeters and found to vary significantly across sites (SI Appendix, Fig. S2), as hydrologic variables expected to affect iWUE. Even though it is possible that plants draw water from below the SSURGO limit (2 m) the model includes adaptations to include bedrock hydrology and landscape topography, available in 270-m-grid cell raster format (39).

Soil Development Model.

To evaluate the effect of soil development on iWUE, soil texture, secondary iron (dithionite extractable iron, Fe_d), and oxalate extractable iron (Fe_o) were measured and related to plant-derived isotopic data. In addition, pedogenic energy input (E_ped) was calculated using models calibrated at the same study sites (37) and SWS was obtained from the CA Basin Characterization Model (39). As in previous studies, soil development is defined as the weathering of parent material into secondary minerals and finer texture. Soil properties that change with development stage are evaluated from an energetic perspective. Briefly, this model calculates pedogenic potential of a soil system based on energy inputs from precipitation and primary productivity, which results in a gradient of relative development measured in kilojoules per square meter per year and represented as E_ped in the text. Details of the calculation, assumptions, and applications specifically designed for different parent materials can be found in Rasmussen et al. (57) and Rasmussen and Tabor (58). Other soil development variables (e.g., clay and pedogenic iron) were directly measured and discussed under sample preparation above.

Statistics.

Significant interactions were detected between species and parent material; as a result, each combination was separated for analysis. To compare stands, measurements within a stand were treated as replicates and averaged and displayed in SI Appendix, Table S2. To measure uncertainty, measured variable SDs are calculated, while for some variables (e.g., satellite data, CA Basin Characterization Model) SDs are provided by models as their spatial resolution is too coarse to produce a range of values for each stand. All data presented in tables and figures are untransformed data, data are normal, and model residuals passed checks for independence of error. Last, as litter and soil data were balanced 1:1, but multiple leaf points exist per litter/soil measurement, a different dataset was generated to compare those points so that all data could be included; this results in eliminating certain values with no leaf data and duplicating some litter/soil data for values with multiple associated leaf points. All statistical analyses were performed using R Studio environment to run R statistical computing software.