Structural characterization of a non-heme iron active site in zeolites that hydroxylates methane

Significance

Understanding the structure of iron active sites that form in zeolites is critical to understanding the extreme reactivity of Fe-zeolite catalysts, which show promise in important industrial applications. This study defines the geometric structure of an Fe-zeolite active site that cleaves the inert C–H bond of methane at room temperature to form methanol. The high reactivity of this site derives from a constrained coordination geometry enforced by the rigid matrix of the catalyst. This insight into the relationship between catalyst structure and function is an important step toward cost-effective methanol fuels and chemical feedstocks derived from natural gas.

Abstract

Iron-containing zeolites exhibit unprecedented reactivity in the low-temperature hydroxylation of methane to form methanol. Reactivity occurs at a mononuclear ferrous active site, α-Fe(II), that is activated by N₂O to form the reactive intermediate α-O. This has been defined as an Fe(IV)=O species. Using nuclear resonance vibrational spectroscopy coupled to X-ray absorption spectroscopy, we probe the bonding interaction between the iron center, its zeolite lattice-derived ligands, and the reactive oxygen. α-O is found to contain an unusually strong Fe(IV)=O bond resulting from a constrained coordination geometry enforced by the zeolite lattice. Density functional theory calculations clarify how the experimentally determined geometric structure of the active site leads to an electronic structure that is highly activated to perform H-atom abstraction.

The direct catalytic conversion of methane to methanol would enable more efficient use of our natural gas resources. Currently, conversion of methane to methanol requires extreme reaction conditions and proceeds through the intermediacy of syngas, leading to significant energy waste. The main challenges here are (i) cleaving the inert 104 kcal/mol C–H bond of methane and (ii) preventing overoxidation, which is thermodynamically favored. Metallozeolites are heterogeneous catalysts that show remarkable performance in this application. Molecular active sites are present in both Cu- and Fe-zeolites that perform selective partial methane oxidation. The reduced active site in Fe-zeolites, α-Fe(II), is activated by N₂O to form the reactive intermediate α-O, which hydroxylates methane rapidly at room temperature (1). Magnetic circular dichroism (MCD) studies showed α-O is a mononuclear high-spin (S = 2) square pyramidal Fe(IV)=O species with an electronic structure that is highly activated toward H-atom abstraction (2). The same study defined the reduced precursor site α-Fe(II) as a mononuclear high-spin (S = 2) square planar Fe(II) species. It was proposed that the activated electronic structure of α-O derives from a constrained coordination geometry enforced by the zeolite lattice. This raised a parallel to metalloenzymes, which use geometric constraints to activate their metal sites for function, generating what are known in biology as entatic states (2, 3).

In the current study, we performed two synchrotron-based measurements—X-ray absorption spectroscopy (XAS) and nuclear resonance vibrational spectroscopy (NRVS) (4)—leading to geometric structural data on the methane hydroxylating active sites in Fe-zeolites. This has enabled quantitative comparison of α-O to other mononuclear Fe(IV)=O intermediates, clarifying how its geometric structure leads to an exceptionally activated electronic structure. In NRVS, synchrotron radiation is tuned into the vibrational sidebands of the 14.4 keV Mössbauer transition of the ⁵⁷Fe nucleus. The resulting NRVS data, reported as a partial vibrational density of states (PVDOS) spectrum, contain contributions solely from normal modes that involve displacement of the absorbing ⁵⁷Fe nucleus [This is because NRVS intensity scales with the mass-weighted displacement of the ⁵⁷Fe nucleus, m_Fe(Δr_Fe)², in a normal mode at a given frequency.] (In this context, “intensity” refers to the amplitude of the normalized density of states derived from the raw NRVS data.) (4). Here, NRVS methodology developed on Fe(IV)=O intermediates in model complexes (5, 6) and metalloenzymes (7) is applied to α-Fe(II) and α-O. NRVS data, interpreted with the aid of frequency calculations performed on experimentally validated density functional theory (DFT) models, provide selective insight into the structure and bonding of these <0.3 wt % Fe active sites bound to a dominant aluminosilicate matrix. [In principle, selectivity can also be achieved using resonance Raman spectroscopy; however, this requires a sample with an intense absorption feature that is stable under laser radiation. High spin ferrous centers such as α-Fe(II), are therefore not accessible.] As NRVS and XAS are bulk techniques, all Fe sites (active and inactive) contribute spectroscopic signals. Samples of zeolite beta (BEA) with low iron loadings (0.3 wt %) leading to >70–80% active sites (as quantified by Mössbauer spectroscopy; see Supporting Information) were therefore required to gather reliable data. From extended X-ray absorption fine structure (EXAFS), the Fe=O bond of α-O appears unremarkable compared with other mononuclear Fe(IV)=O intermediates. However, NRVS reveals significant differences related to spin state, the lack of a trans axial ligand, and the presence of lattice constraints on the iron active site. With the aid of DFT calculations, the unique structural features of α-O evident from NRVS are correlated to related Fe(IV)=O model systems to define the α-O electronic structure that enables rapid H-atom abstraction from the strongest aliphatic C–H bonds.

Results and Discussion

Structural Characterization of α-Fe(II).

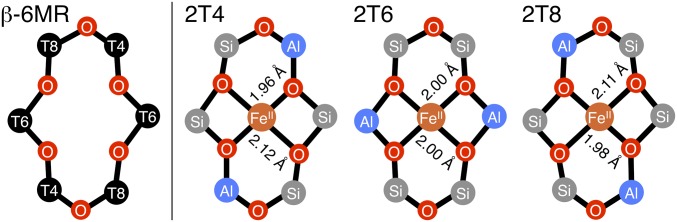
β-Type six-membered ring (β-6MR) motifs containing two Al T-sites (anionic AlO₄⁻ tetrahedra) have been identified as the location of α-Fe(II) formation in the BEA lattice (Fig. 1) (2). From literature on the distribution of Al in high-silica zeolite lattices (Si/Al > 10), three configurations of these Al T-sites are possible within a β-6MR (2, 8, 9). Schematic representations of the corresponding square planar S = 2 Fe(II)-bound β-6MRs are shown in Fig. 1 (including bond lengths from DFT in ref. 2). These are labeled according to the position of Al substitution within the β-6MR [i.e., the 2T8 model has two Al at the two T8 positions (Fig. 1, Right); other Al configurations, including mixed T-site pairs (e.g., T4/T6) involve Al–O–Si–O–Al or Al–O–Al sequences that are not present in high-silica BEA lattices]. (8, 9) In the 2T4 and 2T8 sites, the Fe(II) center is bound by one pair of anionic _SiO_Al ligands and one pair of neutral _SiO_Si ligands. In the 2T6 model, Fe(II) is bound by four anionic _SiO_Al ligands. This difference in first coordination sphere results in a 25–30 kcal/mol stabilization of the 2T6 model relative to the 2T4/2T8 sites (2). Diffuse reflectance UV-visible, Mössbauer, and variable-temperature, variable-field (VTVH)-MCD data together show a single type of α-Fe(II) site exists in Fe(II)-BEA, and from VTVH-MCD zero-field splitting parameters coupled to CASPT2 calculations it was inferred that this single site most closely resembles the 2T6 model (2). To evaluate this model, we used Fe K-edge XAS and NRVS to gain direct insight into the geometric structure of α-Fe(II) in Fe-BEA.

Fig. 1.

(Left) Schematic of a β-6MR in zeolite beta, including T-site numbering scheme (ring A1 in ref. 2). Three configurations of two Al T-sites are allowed in a β-6MR. The Fe(II)-bound sites—labeled according to the position of Al—are shown (Right), along with Fe-O_lattice bond lengths from DFT (2). Atoms are omitted for clarity. Adapted with permission from ref. 2 (Copyright 2016, Nature Publishing Group).

Fe K-Edge XAS of α-Fe(II).

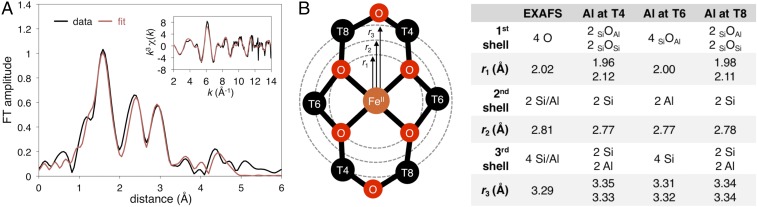
Fe K-edge XAS spectra were collected from a sample of Fe(II)-BEA containing 73% α-Fe(II) (from Mössbauer; see Table S1). The X-ray absorption near edge structure (XANES) region of the spectrum shown in Fig. S1A contains weak pre-edge transitions (1s → 3d) and a pronounced rising edge transition (1s → 4p) characteristic of high-spin Fe(II) in a square planar ligand field (10–13). Analysis of the XANES region is presented in SI Fe K-Edge XANES of Fe-BEA. The k³-weighted EXAFS spectrum of Fe(II)-BEA is shown in Fig. 2A, Inset, along with the corresponding Fourier transform taken from 2 ≤ k ≤ 14 Å⁻¹ (data in black, fit in red). Key EXAFS scattering interactions are shown Fig. 2B. From the EXAFS fit (see Table S2 for details), the first coordination shell of α-Fe(II) contains four oxygen scatterers at 2.02 Å (r₁ in Fig. 2A). Similar Fe–O bond lengths are seen in other structurally defined S = 2 square planar Fe(II)O₄ sites from X-ray diffraction (12–14). There is a second shell at 2.81 Å containing the two T6 T-atoms that bind Fe(II) (r₂). Finally, at 3.29 Å, there is a third shell containing the four T4/T8 T-atoms (r₃). The T-atom scattering interactions at r₂ = 2.81 Å and r₃ = 3.29 Å are direct evidence that α-Fe(II) forms in β-6MRs. Comparing the experimental data to theory, the three models in Fig. 2B have average Fe–O_lattice bond lengths (2.00–2.04 Å) that are comparable to each other and to the experimental value of 2.02 Å. Fitting EXAFS data with two pairs of first-shell oxygen scatterers (instead of four equivalent oxygen scatterers) did not clarify this ambiguity or improve the error of fit (35%). EXAFS is therefore not sufficiently sensitive to resolve the distribution of Al within the active site. However, the distribution of Al could be evaluated directly from NRVS data [see NRVS of α-Fe(II)].

Fig. 2.

(A) k³-weighted EXAFS spectrum of Fe(II)-BEA (Inset, black) with fit in red. The Fourier transforms of the 2 ≤ k ≤ 14 Å⁻¹ region of EXAFS (black) and fit (red) is shown in the main figure. (B) Key EXAFS scattering interactions for a square planar Fe(II) site bound to a β-6MR (Left), with a comparison of the EXAFS geometry of α-Fe(II) to DFT models with different distributions of Al (2T4, 2T6, and 2T8). The experimental data require a fit with all three shells. See Table S2 for parameters of the full fit, including all scattering paths, Debye–Waller factors, and E₀. The reported EXAFS distances have an error of ±0.03 Å (27).

NRVS of α-Fe(II).

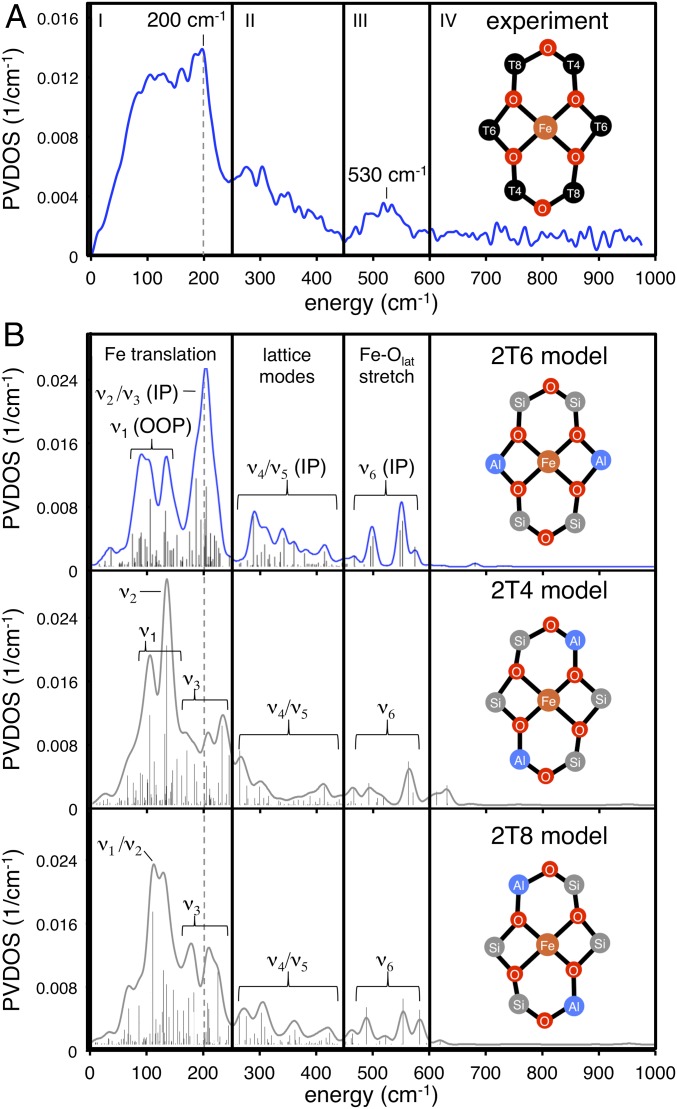
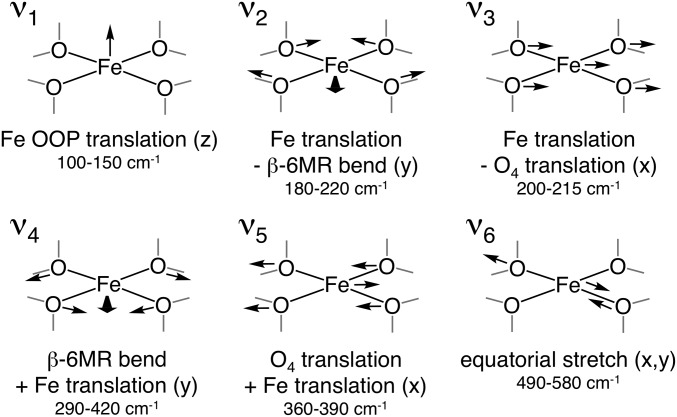
The NRVS PVDOS spectrum of α-Fe(II) shown in Fig. 3A (73% purity from Mössbauer; see Table S1) contains four distinct regions. In region I (0–250 cm⁻¹), there is a plateau with a peak on the high-energy side at ca. 200 cm⁻¹. Region II (250–450 cm⁻¹) contains a descending slope. In region III (450–600 cm⁻¹), there is a broad feature centered at ∼530 cm⁻¹, and there is no NRVS intensity for α-Fe(II) in region IV (600–1,000 cm⁻¹). The simulated NRVS spectra of the 2T6, 2T4, and 2T8 models are shown in Fig. 3B. (These are 133-atom models that incorporate a double 6MR motif, as well as a full additional layer of T-atoms beyond the 6MR core; see ref. 2 for details.) There are significant differences in the distribution of simulated NRVS intensity in region I for these models. The 2T4 and 2T8 spectra have intense low-frequency peaks (120–130 cm⁻¹) followed by lower-intensity plateaus from 150 to 250 cm⁻¹. This intensity distribution is inverted in the 2T6 spectrum, where there is diminished intensity at low frequency and an intense peak at higher frequency (200 cm⁻¹). NRVS is therefore sensitive to the configuration of Al within the active site, and the experimental data in Fig. 3A allow the assignment of α-Fe(II) to the 2T6 model. [Previous studies show a single α-Fe(II) site is present, ruling out mixed contributions from 2T4, 2T6, and 2T8 (2). However, the presence of 27% spectator Fe(II) may contribute to deviations between the experimental data and simulations in Fig. 3.] To understand this sensitivity to Al distribution, features in the simulated spectra were assigned to specific normal modes of a planar FeO₄ core (Fig. 4). A planar five-atom core bound to a rigid support has 15 vibrational degrees of freedom (translational and rotational degrees of freedom become vibrations upon coupling to the zeolite lattice). Eight of these 15 vibrations involve motion of the ⁵⁷Fe nucleus and will in principle be NRVS-active. However, only the normal modes shown in Fig. 4 involve sufficient Fe motion to be observed in the experimental data. For all models, the same three vibrations contribute in region I (ν₁, ν₂, and ν₃ in Fig. 4). Contributions from out-of-plane (OOP) translational motion of the iron atom (ν₁) are found between 50–150 cm⁻¹. For the 2T6 model, ν₁ appears as a split feature due to mixing with multiple zeolite lattice modes. We note that in the presence of an axial ligand (e.g., in α-O, discussed above), this OOP iron motion is redistributed into modes involving stretching of the axial Fe–L bond, resulting in diminished NRVS intensity in the low-frequency region associated with OOP Fe translation. For α-Fe(II), the large amount of intensity associated with ν₁ therefore reflects the vacant axial positions of this square planar active site. For the 2T4 and 2T8 models, there is additional intensity in the 120–130 cm⁻¹ region that derives from in-plane (IP) equatorial bending motion (ν₂ in Fig. 4). Calculations show this vibration occurs at higher frequency for the 2T6 model (185 cm⁻¹ versus ∼130 cm⁻¹ for the 2T4/2T8 models) because placing Al at the T6 positions results in a higher force constant for the β-6MR deformation coupled to ν₂. The ν₂ NRVS mode is therefore sensitive to the distribution of Al within the active site, explaining the higher frequency of the intensity maximum in region I for the 2T6 model. Finally, for all models, there is intensity in the 150–250 cm⁻¹ region that derives from IP translation of the FeO₄ unit (ν₃ in Fig. 4). Like ν₁, the ν₃ intensity is distributed across a number of zeolite lattice modes. Moving up in frequency to region II, the 2T6 model reproduces the experimental distribution of NRVS intensity, but reasonable agreement is also seen for the 2T4 and 2T8 models. Intensity in region II derives from deformations of the β-6MR mixed with higher-frequency IP motions of the FeO₄ core (ν₄ and ν₅ in Fig. 4). Whereas ν₂ and ν₃ in region 1 involve concerted motion of the iron atom with equatorial motion of the _SiO_Al ligands, ν₄ and ν₅ involve motion of the iron atom against the equatorial _SiO_Al ligands. Vibrations in region II involve minimal iron motion and therefore contribute limited NRVS intensity. The features in region III correspond to antisymmetric stretching of the equatorial Fe–O_lattice bonds (ν₆ in Fig. 4). For the 2T6 model, these motions couple to two T-site stretching modes of the β-6MR and as a result appear as a pair of x, y degenerate features in the simulated spectrum at ∼500 and ∼550 cm⁻¹ that broaden into one peak centered at ∼530 cm⁻¹ in the experimental spectrum. Similar features are seen in region III for the 2T4 and 2T8 models. Finally, all three models show essentially no intensity in region IV, in agreement with experiment.

Fig. 3.

Experimental NRVS spectrum of Fe(II)-BEA (A), along with the DFT-simulated spectra of the 2T6 (B, Top), 2T4 (B, Middle), and 2T8 (B, Bottom) models of α-Fe(II).

Fig. 4.

Key NRVS-active modes of the planar FeO₄ core of α-Fe(II) and their DFT-predicted frequencies for the 2T6 model of the active site. The x and y directions are defined by the long and short axes (respectively) of the β-6MR.

The correlation of experimental and simulated NRVS spectra—particularly from region I—provides direct evidence that the distribution of Al within the active site most closely resembles the 2T6 model. This demonstrates a distinct advantage of NRVS over EXAFS, which could not reliably discriminate different distributions of Al [discussed in Fe K-Edge XAS of α-Fe(II)]. The experimental and simulated (2T6) NRVS spectra of α-Fe(II) serve as a reference for the NRVS spectroscopy of α-O in the following section.

Structural Characterization of α-O.

Past VTVH-MCD studies of α-O showed this is a mononuclear S = 2 [FeO]²⁺ site with ground state spin Hamiltonian parameters that are similar to known S = 2 Fe(IV)=O species (2). However, the bonding interaction between the reactive oxygen and the iron center has not been probed directly. We therefore pursued XAS and NRVS studies to define the geometric structure of α-O that leads to high reactivity.

Fe K-Edge XAS of α-O.

Fe K-edge XAS spectra were collected from a sample of N₂O-activated Fe-BEA containing 70% α-O (from Mössbauer spectroscopy; see Table S1). The XANES region of the spectrum shown in Fig. S1B contains 1s → 3d pre-edge transitions whose energies are consistent with other S = 2 Fe(IV)=O sites (15–17). Analysis of the XANES region is presented in SI Fe K-Edge XANES of Fe-BEA. These pre-edge features are unusually intense – estimated to be at least 55 units for pure α-O [versus 20–30 for a ‘typical’ Fe(IV)=O complex (17)]. This high pre-edge intensity reflects high Fe 3d/4p mixing due to the presence of a short Fe(IV)=O bond with no trans axial ligand (see EXAFS below and SI Fe K-Edge XANES of Fe-BEA) (10, 18). The main edge of α-O shifts up by ∼2 eV relative to α-Fe(II), consistent with oxidation from Fe(II) to Fe(IV).

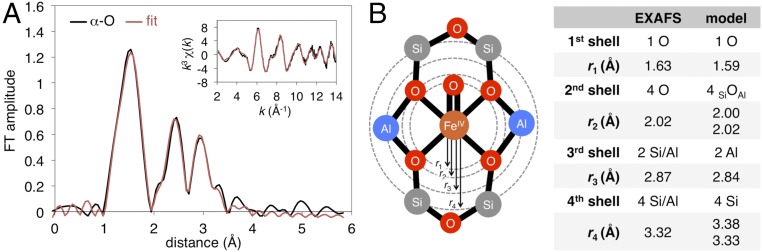
The k³-weighted EXAFS spectrum of N₂O-activated Fe-BEA is shown in Fig. 5A, Inset, along with the corresponding Fourier transform taken over 2 ≤ k ≤ 14 Å⁻¹ (black curves). Parameters associated with the fit (red curves in Fig. 5A) are shown in Fig. 5B (see Table S2 for details), along with comparison with the geometry of the 2T6 DFT model of α-O. Like α-Fe(II), the first coordination sphere of α-O contains four O scatterers at 2.02 Å (r₂ in Fig. 5B) corresponding to the four equatorial _SiO_Al ligands. The fit requires an additional O scatterer at 1.63 Å (r₁) that is not present in α-Fe(II), confirming the presence of a short Fe=O bond in α-O. The Fe=O scattering path does not appear as a distinct peak in the Fourier transform due to its overlap with the path at 2.02 Å; however, its presence is responsible for the additional intensity in the 1–2 Å region, and this scattering path is required to fit the experimental data (see Fig. S2 for details). It is interesting that the Fe=O bond of α-O appears fairly unexceptional in EXAFS given its extreme reactivity (17). (We note that NRVS data presented below are consistent with a somewhat shorter 1.61 Å Fe=O bond, which is, however, within the 0.03 Å error of EXAFS.) At larger distances in the EXAFS data, there are scattering interactions associated with T-atoms of the β-6MR. The Al T-atoms (T6) that mediate Fe binding appear at 2.87 Å, while the remaining four Si T-atoms are observed at 3.32 Å. The positions of these Al and Si T-atoms are shifted only slightly relative to α-Fe(II), where they appear at 2.81 Å and 3.29 Å (respectively). Oxidation of α-Fe(II) to α-O is therefore associated with only minimal changes to the equatorial ligand field of the Fe center, and to the geometry of the β-6MR.

Fig. 5.

(A) Comparison of α-O EXAFS data (black) to the fit (red) summarized in B: key EXAFS scattering interactions for α-O, with comparison of the experimental geometry from EXAFS to 2T6 DFT model of α-O (table). See Table S2 for parameters of the full fit, including Debye–Waller factors and E₀. The reported EXAFS distances have an error of ±0.03 Å (28).

NRVS of α-O.

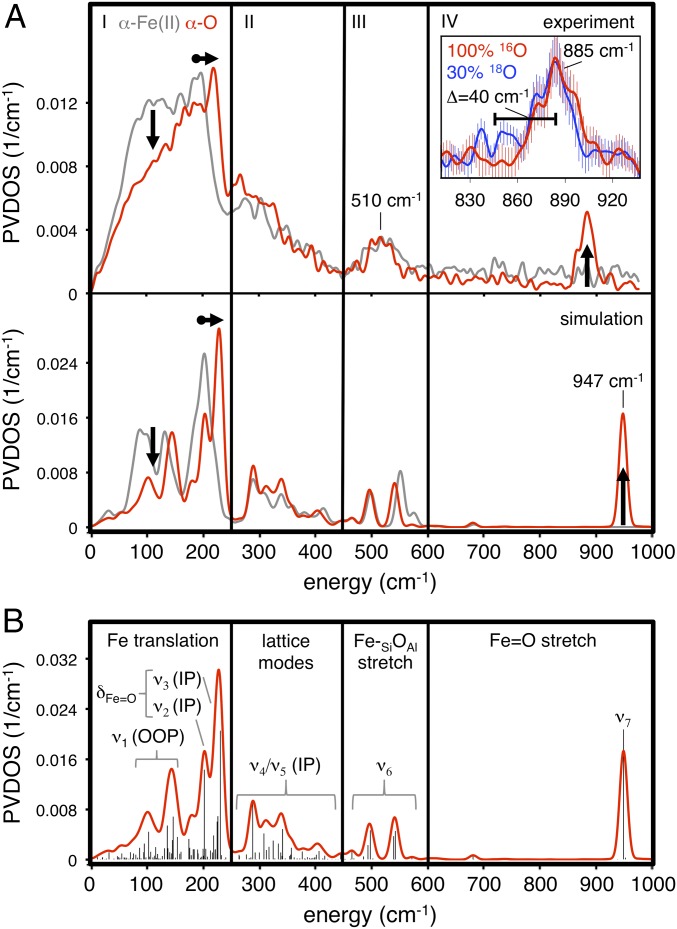
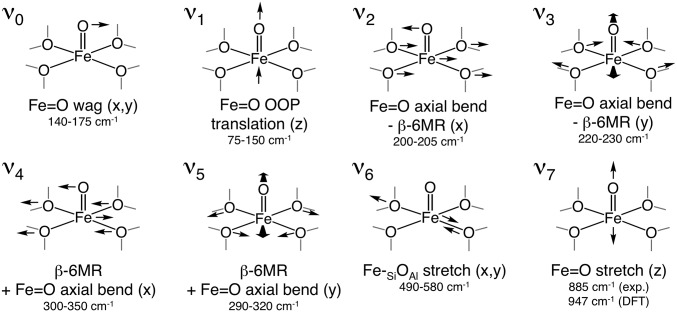
The NRVS PVDOS spectrum of α-O (83% purity; Table S1) is shown in Fig. 6A (red curves). Data from α-Fe(II) are included for comparison (gray curves, reproduced from Fig. 3). Comparing α-Fe(II) and α-O in region 1, there is a loss of intensity from 50 to 150 cm⁻¹, as well as a shift in the intensity maximum from 200 cm⁻¹ up to ca. 225 cm⁻¹. There are minimal changes in regions II and III. However, in region IV, a feature appears for α-O at 885 cm⁻¹ that was not present for α-Fe(II). As shown in Fig. 6A, Inset the 885-cm⁻¹ feature exhibits a ∼40-cm^{−1 16/18}O isotope shift following ∼30% ¹⁸O exchange with ¹⁸O₂ (see supporting NRVS and mass spectrometery data presented in Fig. S3). This is the only isotope-sensitive NRVS vibration resolved for α-O (within the 8-cm⁻¹ resolution of the experiment). The changes observed in α-O relative to α-Fe(II) are reproduced by the simulated NRVS spectra of the 2T6 models of α-O and α-Fe(II) shown below the experimental data in Fig. 6A. To understand these changes, features in the simulated NRVS data were assigned to normal modes of the O=FeO₄ core of α-O (Figs. 6B and 7). Intensity in the 50–150 cm⁻¹ region correlates to OOP translation of the Fe=O unit (ν₁ in Fig. 7). The intensity of OOP Fe translation is diminished for α-O relative to α-Fe(II) due to the presence of the axial oxo ligand, which redistributes intensity associated with OOP Fe motion away from ν₁ and into the Fe=O stretch (ν₇). The most intense NRVS feature of α-O, observed at 220–225 cm⁻¹, is associated with axial bending of the Fe=O unit coupled to equatorial motions of the FeO₄ core (ν₂ and ν₃ in Fig. 7). For α-Fe(II), the peak maximum associated with the analogous motions of the FeO₄ core is observed at lower frequency (200 cm⁻¹). The 20–25 cm⁻¹ frequency increase for α-O, seen experimentally and reproduced by calculations (right-facing arrows in Fig. 6A) is due to mixing with the low-energy Fe=O wag (ν₀ in Fig. 7). For other Fe(IV)=O sites characterized by NRVS, the most intense features are also (trans) axial bends, but these appear between 350–400 cm⁻¹ (region II) (5–7). From DFT analysis presented in SI Analysis of the Low-Frequency Axial Bend of αO, the ∼150-cm⁻¹ decrease in axial bend frequency seen experimentally for α-O is largely due to lattice constraints on the motions of its equatorial ligands.

Fig. 6.

(A) Comparison of experimental (Top) and simulated (Bottom) NRVS spectra of α-O (red) and α-Fe(II) (gray), with key changes indicated. The ¹⁶O/¹⁸O isotope sensitivity of the 885-cm⁻¹ feature is shown (Inset). (B) Simulated spectrum, with assignments to normal modes of α-O shown in Fig. 7.

Fig. 7.

Key NRVS-active modes of the O=FeO₄ core of α-O and their DFT-predicted frequencies for the 2T6 model of the active site.

Moving up in frequency to region II, the vibrations of α-O and α-Fe(II) are comparable. Features here correspond to β-6MR modes mixed with IP vibrations of the FeO₄ unit (ν₄/ν₅ in Figs. 4 and 7). The NRVS features in region III, due to Fe-_SiO_Al stretching, are similar for α-Fe(II) and α-O (ν₆ in Figs. 4 and 7). The similarity between α-Fe(II) and α-O across regions I–III indicate these sites have comparable equatorial ligand fields, complementing EXAFS data, which show equivalent Fe–_SiO_Al bond lengths for α-Fe(II) and α-O (Figs. 2 and 5). The 510-cm⁻¹ equatorial M-L stretching frequency of α-O is comparable to other mononuclear Fe(IV)=O intermediates characterized by NRVS (6, 7). Finally, in region IV, α-O shows a feature at 885 cm⁻¹ that is not present in α-Fe(II). This is the only isotope-sensitive feature of α-O (Fig. S3), shifting down by ∼40 cm⁻¹ in α-¹⁸O (Fig. 6A). This confirms the 885-cm⁻¹ vibration is the Fe=O stretch of the oxo ligand. From Badger’s rule, an experimental 885-cm⁻¹ Fe=O stretch correlates to a 1.61-Å Fe=O distance (19), in agreement with the EXAFS distance of 1.63 ± 0.03 Å. The simulated α-¹⁸O spectrum in Fig. S3 reproduces the experimental isotope sensitivity (∆¹⁸O = 41 cm⁻¹ computationally). The DFT functional used here (B3LYP) systematically overestimates Fe=O stretching frequencies by ∼50 cm⁻¹ (5, 6). (However, as shown in Fig. S4J, the predicted distribution of NRVS intensity in regions 1–2 is fairly insensitive to the choice of functional, with variations under <20 cm⁻¹. The M–L stretching modes in region III vary by ∼30 cm⁻¹ depending on the choice of functional.) Accounting for this systematic error, the DFT-predicted frequency of 947 cm⁻¹ scales to ∼895 cm⁻¹, in reasonable agreement with experiment. The 885-cm⁻¹ band is the highest-frequency Fe(IV)=O stretch yet observed (17). This confirms the presence of an unusually strong Fe=O bond in α-O, a key factor leading to high reactivity (2).

Structural Contributions to Fe(IV)=O Reactivity.

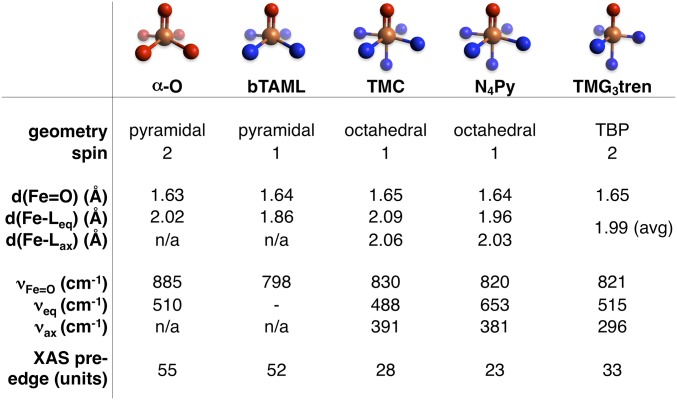
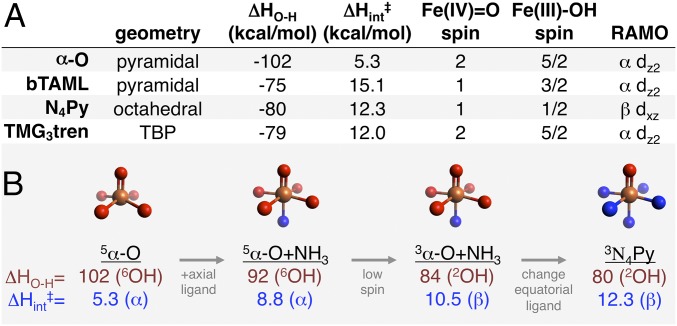
The experimentally determined structural parameters of α-O from XAS/NRVS are compared with data from four relevant mononuclear non-heme Fe(IV)=O intermediates in Fig. 8. The high-frequency 885-cm⁻¹ Fe=O stretch of α-O is consistent with an unusually strong Fe=O bond. However, the equatorial M–L bond distances and stretching frequencies of α-O (2.02 Å and 510 cm⁻¹, respectively) are similar to TMC, N₄Py, and TMG₃tren. The equatorial ligand field of α-O is therefore unremarkable except for stabilizing an S = 2 ground state. However, α-O is the first S = 2 intermediate with a vacant trans axial position. DFT calculations were performed on the intermediates in Fig. 8 to clarify how the equatorial and axial ligand fields of α-O tune the Fe=O bond. From analysis presented in SI Comparison of Fe(IV)=O Bonding, the Fe=O σ bond of α-O is uniquely covalent due to weak donation of the β-6MR into d_z2. This is significant with respect to reactivity, as covalency leads to low-lying unoccupied Fe=O frontier molecular orbitals with high oxo 2p content that are activated for H-atom abstraction (2, 7, 17, 20, 21).

Fig. 8.

Comparison of the experimental geometric structural parameters of α-O from NRVS/EXAFS to other mononuclear Fe(IV)=O intermediates [bTAML (18), TMC (6, 28, 29), N₄Py (6, 30, 31), and TMG₃tren (5, 16, 32)]. Fe, tan; O, red; N, blue; TBP, trigonal bipyramidal.

α-O is unique among mononuclear Fe(IV)=O intermediates in its ability to hydroxylate the C–H bond of methane rapidly at room temperature, with reactivity significantly exceeding the binuclear 2Fe(IV) intermediate Q of soluble methane monooxygenase (22) (see SI Comparison of Fe/O C–H Oxidation Rates for details). DFT calculations summarized in Fig. 9A were performed to understand this difference in reactivity. For H-atom abstraction, the reaction enthalpy reflects the difference in bond dissociation energy for the cleaved C–H bond and product O–H bond. Focusing on the driving force for O–H bond formation (ΔH_O-H), the ΔH_O-H of α-O (102 kcal/mol) is predicted to be 20–25 kcal/mol greater than the other intermediates [∼75–80 kcal/mol, in agreement with available experimental OH bond strengths from N₄Py (23) and bTAML (18)]. Correcting for these differences in ΔH_O-H using Marcus theory (24, 25), the intrinsic activation enthalpy (ΔH_int^‡) for α-O abstracting an H-atom from CH₄ is ≤1/2 that of the other intermediates in Fig. 9A. From comparisons presented in SI Comparison of Fe(IV)=O Reactivity by DFT , the spectroscopically defined structural features of α-O that impart high reactivity are (i) a vacant trans axial position, which increases both the Fe(IV)/Fe(III) reduction enthalpy (tunes up ΔH_O-H) and oxo 2p content of the reactive FMO (tunes down ΔH_int^‡); (ii) a moderately weak equatorial ligand field leading to a high spin ground state [exchange stabilization of the redox-active molecular orbital on the S = 2 surface, which mostly affects ΔH_O-H by increasing the Fe(IV)=O reduction enthalpy]; and (iii) the presence of zeolite lattice constraints that enforce this otherwise unstable combination of a vacant trans axial position and high-spin Fe(IV)=O electronic structure. This defines the entatic state of α-O, originally proposed in ref. 2.

Fig. 9.

(A) Comparative reactivity of mononuclear Fe(IV)=O intermediates from DFT, including driving forces for O–H bond formation (ΔH_O-H) and estimated intrinsic barriers for H-atom abstraction from CH₄ (ΔH_int^‡; see SI Materials and Methods). Also included are the spin states of the Fe(IV)=O reactants and Fe(III)-OH products, as well as the redox-active molecular orbital (RAMO) that ultimately accepts the electron following H-atom transfer. (B) Correlation of α-O to N₄Py, with intermediate steps illustrating the effects of adding a trans axial ligand and then moving to an S = 1 ground state. Correlations to bTAML and TMG₃tren are presented in Fig. S6.

Conclusion.

NRVS methodology developed on mononuclear non-heme iron model complexes and metalloenzymes has provided a detailed structural characterization of an iron active site in a zeolite. In this application, NRVS offers a number of advantages over other “traditional” techniques (XAS, IR, and Raman). This is evident from the NRVS vibrations of α-Fe(II) and α-O, which reflect their coordination geometries, the nature of their lattice-derived ligand (_AlO_Si versus _SiO_Si—not distinguishable by EXAFS), and the presence of lattice constraints on the active site. We anticipate this technique will prove useful in future studies of intermediates formed during the selective hydroxylation of methane and benzene, and in the selective catalytic reduction of NO_x.

Geometric structural parameters from spectroscopy have enabled quantitative comparison of α-O to other Fe(IV)=O intermediates. The unprecedentedly high 885-cm⁻¹ Fe=O stretch of α-O reflects an unusually strong Fe=O bond. DFT calculations calibrated against experimental data show that the combination of a moderately weak equatorial ligand field and vacant trans axial position (enforced by zeolite lattice constraints) tunes up the covalency of the Fe=O bond. This leads to reactive FMOs with high oxo 2p content (resulting in high intrinsic reactivity), as well as a large Fe(IV)/Fe(III) reduction enthalpy (resulting in a large driving force for O–H bond formation)—factors that render α-O highly activated for H-atom abstraction.

Materials and Methods

Zeolite samples were prepared as described in ref. 2. XAS data were collected at beamlines 7-3 and 9-3 at the Stanford Synchrotron Radiation Lightsource (SSRL) under ring operating conditions of 500 mA over an energy range of 6,785−7,876 eV (k = 14 Å⁻¹). NRVS spectra were collected at the Advanced Photon Source (APS) in Argonne, at beamline 3-ID-D. DFT calculations were performed using the Gaussian 09 software package (26). Details on sample preparation and spectroscopic experiments are included in SI Materials and Methods.