Individual Variability of the System-Level Organization of the Human Brain

Abstract

Recent functional magnetic resonance imaging-based resting-state functional connectivity analyses of group average data have characterized large-scale systems that represent a high level in the organizational hierarchy of the human brain. These systems are likely to vary spatially across individuals, even after anatomical alignment, but the characteristics of this variance are unknown. Here, we characterized large-scale brain systems across two independent datasets of young adults. In these individuals, we were able to identify brain systems that were similar to those described in the group average, and we observed that individuals had consistent topological arrangement of the system features present in the group average. However, the size of system features varied across individuals in systematic ways, such that expansion of one feature of a given system predicted expansion of other parts of the system. Individual-specific systems also contained unique topological features not present in group average systems; some of these features were consistent across a minority of individuals. These effects were observed even after controlling for data quality and for the accuracy of anatomical registration. The variability characterized here has important implications for cognitive neuroscience investigations, which often assume the functional equivalence of aligned brain regions across individuals.

Introduction

The human cortex is organized into a number of large-scale, spatially distributed systems consisting of multiple interacting cortical areas. These systems can be described in vivo using a functional magnetic resonance imaging (fMRI)-based technique known as resting-state functional connectivity (RSFC), which relies on the observation that in the absence of any task, spatially distant regions of cortex exhibit highly correlated patterns of blood oxygen level-dependent (BOLD) activity (Biswal et al. 1995); this is posited to at least partly reflect the statistical history of interactions between regions (Dosenbach et al. 2007). RSFC-based approaches have consistently identified around 10–17 brain systems that replicate across multiple datasets and analysis strategies (Power et al. 2011; Yeo et al. 2011) and correspond with task coactivation patterns (Smith et al. 2009). The spatial characterization of these systems has enabled the identification of plausible links between brain organization and cognitive function (Dosenbach et al. 2007; Laird et al. 2011).

However, these previous descriptions of cortical systems have been derived from data averaged across many individuals. While RSFC correlation patterns calculated in single individuals are broadly reliable across people (Shehzad et al. 2009), some degree of interindividual variability can nonetheless be observed in these patterns (Mueller et al. 2013). Furthermore, recent work has shown how the locations of cortical areas—which are believed to subdivide large-scale brain systems (Sejnowski and Churchland 1989)—can vary substantially across individuals (Amunts et al. 2000; Caspers et al. 2006, 2008; Malikovic et al. 2007), even after precise surface-based anatomical alignment (Fischl et al. 2008; Van Essen et al. 2012). It is likely that such variability might also be present in the system-level organization of individual brains, as recent findings have suggested (Harrison et al. 2015), though this variability has not been comprehensively described. Such variability could be an important consideration for system-based RSFC analyses that test for differences in node-to-node connectivity strength across individuals.

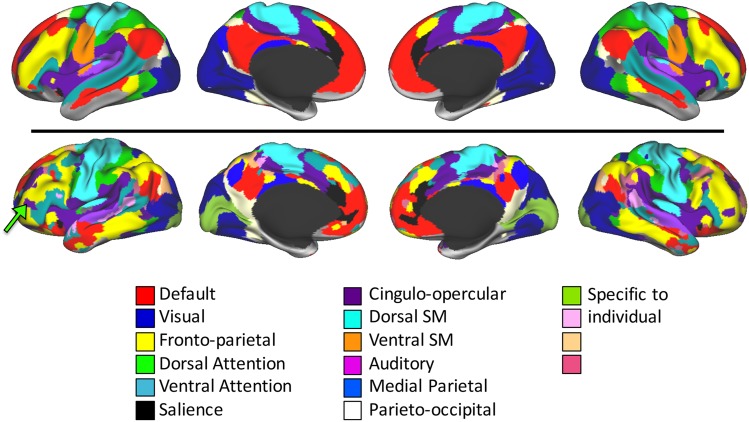
We have recently described the system-level organization of a single highly sampled human subject (Laumann et al. 2015), which helps identify the types of individual variability in cortical systems that may be present in a population. Several notable features can be observed by comparing this individual's system map with a group-level system map [Fig. 1, modified from Laumann et al. (2015)]. First, the individual's map contains almost all of the same systems as the group map. Second, the discrete, discontiguous patches of each system, hereafter referred to as “system patches,” observed in the group are generally also present in the individual. Third, some system patches in the individual are larger or smaller than equivalent patches in the group. Fourth, the individual has a number of small system patches that cannot be matched to anything in the group map. Instead, these patches appear to be connected to “alternate” systems, compared with the systems present at that location in the group map. For example, the individual's map has a Cingulo-opercular patch in left anterior inferior frontal gyrus (Fig. 1, green arrow); nothing similar exists in the group map. Taken together, these observations suggest that while the group-level systems correspond well with brain systems defined in the individual, the individual-specific systems also contain distinct features that may be important for interpreting system-level analyses of individuals.

Figure 1.

The system-level organization of a single subject (bottom) is similar to the organization of a group average (top), with almost all of the same systems present in the same general configuration. However, the patches of the individual's systems are variously expanded and contracted, as well as physically shifted along the cortex relative to the group average systems. Furthermore, the individual's system map has numerous small topological features not present in the group average (for example, a patch of the Cingulo-opercular system in anterior inferior frontal gyrus; see green arrow). Adapted from Laumann et al. (2015).

Ultimately, it is difficult to draw definitive conclusions about individual variability from the study of a single individual. Thus, in the present study, we characterized individual variability in RSFC systems across two independent groups of healthy adults. We applied a template-matching procedure to identify brain systems in individuals. Following our previous observations of a single subject's brain system (Laumann et al. 2015), we examined the degree to which individuals' brain systems (1) had similar topologies to group-level systems; (2) had variability in the sizes of system patches; and (3) had regions that were consistently identified across a substantial minority of subjects as connected to “alternate” systems, relative to the group average.

Methods

We acquired two independent resting-state fMRI datasets: Dataset 1, a large group of healthy young adults that we used to create system templates and to investigate patterns of system variability (n = 120); and Dataset 2, a second large group of healthy young adults that we used to replicate findings from Dataset 1 (n = 108).

Details of the data acquisition, preprocessing, functional connectivity processing, and surface creation and mapping procedures follow closely the procedures described in Gordon et al. (2014) and can be found in Supplementary Material.

Group Average System Map

The group average system map we used has been previously described (Laumann et al. 2015) and can be seen in the top panel of Figure 1. Briefly, the group average full connectivity matrix was calculated for Dataset 1 by correlating the timecourses of every (cortical and subcortical) gray matter point with every other gray matter point, applying the Fisher z-transformation to the resulting correlation matrix, and averaging these matrices across subjects. This resulted in a 66 697 × 66 697 group average connectivity matrix. We then applied the Infomap algorithm for community detection in graphs to the resulting matrix (Rosvall and Bergstrom 2008), removing connections within 20 mm of each other. System assignments were computed at a range of correlation thresholds selected for specific edge sparseness. Systems with 400 or fewer gray matter points were considered unassigned and eliminated from consideration. A “consensus” assignment was then derived by collapsing across thresholds (Gordon et al. 2014). We then removed from consideration: (1) small communities that were only present at a single threshold, (2) communities that did not appear to correspond to brain systems described in previous work (Smith et al. 2009; Power et al. 2011; Yeo et al. 2011), and (3) subcortical voxels, which do not tend to robustly sort into systems unless specialized methods are employed (Zhang et al. 2008; Buckner et al. 2011; Greene et al. 2014).

Template Matching for System Identification in Individual Subjects

In principle, system identification could be conducted in individual subjects by applying an unsupervised clustering or community detection procedure to single-subject correlation matrices, such as the Infomap procedure described above [as in Laumann et al. (2015)]. However, here we are testing the presence and localization of known brain systems in individuals, rather than attempting the data-driven discovery of unknown systems. Thus, we have developed a procedure to identify systems in individual subjects using previously described group average systems as priors for a template-matching procedure.

To derive a connectivity template for each system in the group average system map, we calculated the average timecourse across cortical vertices within that entire system for each subject. Then, we correlated that timecourse against all other gray matter timecourses to obtain a system connectivity map. We then applied the Fisher z-transformation and averaged these maps across subjects for each system (see Supplementary Fig. 1 for system connectivity maps). Finally, we thresholded and binarized each of these averaged maps at the top 5% of connectivity strengths (as calculated across systems), which was Z(r) ≥ 0.383. This binarization was done because a brain region's network membership is most typically identified based on the regions with which it has strong positive connections [in line with graph theory-based approaches, as reviewed in Bullmore and Sporns (2009) and Sporns (2014)]. These binarized maps serve as templates for individual subject matching.

To match each cortical vertex in each subject to a template, we first correlated the vertex's timecourse with all other gray matter timecourses in that subject's data, Fisher z-transformed the resulting connectivity map, and then thresholded and binarized the resulting map at the top 5% of connectivity values (as calculated across vertices). This resulted in a binarized map of regions with high connectivity to the chosen cortical vertex. We then calculated the Dice coefficient of overlap between the binarized vertex connectivity map and each binarized template map, excluding from the calculation all vertices within 20 mm geodesic distance from the selected vertex, in order to prevent matches from being driven by purely local connectivity (Power et al. 2011). The template with the highest overlap was judged to be the best match, and that template's system identity was assigned to that vertex in that subject.

Finally, contiguous surface patches of a given system identity that were smaller than 100 mm² were removed, as such patches are smaller than the approximate effective resolution of our data (originally 4 mm isotropic voxels, smoothed 6-mm full-width at half-maximum on the cortical surface). Neighboring system identities were “grown” into the removed regions one vertex at a time until the region was filled. See Supplementary Figure 2 for individual system maps resulting from the template-matching procedure.

Matching Group-Level System Patches to Subject-Level System Patches

The discrete pieces of subject-level system maps (“system patches”) can be expected to vary across subjects, both in their position on the cortical surface and in their size (Frost and Goebel 2012). However, despite this variance, these system patches can visually be compared between an individual and the group based on their spatial position and overall shape. To directly compare subject-level system maps with the group-level system map, we developed an automated procedure to match the patches of the subject- and group-level systems in a way that is robust to slight displacements that would be expected by individual variability.

We first identified discrete system patches of at least 100 mm² in the group system map. For each of these group system patches, we then matched the most similar system patch in each individual subject. This matching was performed by attempting to minimize the total geodesic distance from all vertices in the group patch to the closest vertex in each candidate individual patch with the same system identity. Overlapping points would thus have distances of zero, whereas points that did not overlap the template would have increasing distances, depending on their proximity to the group patch. This distance-based approach thus indexes the spatial similarity between two local, binarized maps by testing for proximity rather than overlap.

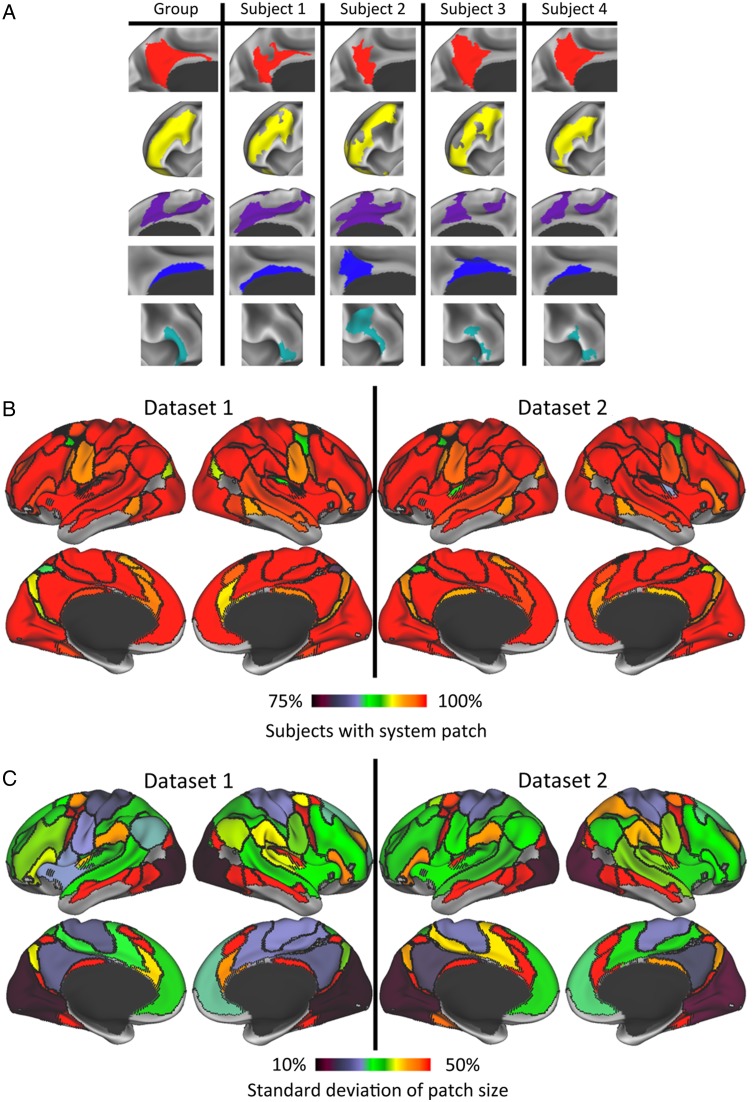
We conducted patch-to-patch matching that minimized this distance metric by using a variant of the classic Hungarian assignment algorithm (Bourgeois and Lassalle 1971) that allows many-to-one assignments (Dondeti and Emmons 1996), because individual subject patches were sometimes spatially discontinuous (e.g., the medial patches of the Cingulo-opercular system in Fig. 2A). Matches with a mean distance greater than 20 mm were disallowed. Figure 2A shows examples of individual subject system patches that were matched to group patches.

Figure 2.

(A) Examples of matches between group-level system patches (left column) and system patches in 4 individual subjects (right columns). From top to bottom are displayed matched patches in Default, Fronto-parietal, Cingulo-opercular, Medial Parietal, and Ventral Attention systems. (B) Most group average system patches are present in the vast majority of subjects. Group average system patches (see Fig. 1 for systems) are demarcated by black outlines and are colored according to the number of subjects in Dataset 1 (left) and Dataset 2 (right) who had a matching system patch. Orange–red colors indicate that greater than 95% of subjects had a matching patch. (C) Variance in sizes of subject-level system patches, relative to the group-level system patches, was largest in relatively small patches and lowest in primary visual and motor regions. For Dataset 1 (left) and Dataset 2 (right), group-level systems are demarcated by black outlines and are colored according to the standard deviation of the patch sizes, expressed as a percent of the group-level patch sizes. Green and hotter colors indicate that the patch's size variance was greater than 30% of the group patch size.

Assessment of Variance in System Patch Sizes

To assess how variable the sizes of system patches were, we calculated the surface area of each subject-level system patch as a percentage of the surface area of the group-level matched patch (this normalization prevents observed variance being driven primarily by patch size). For each group-level patch, we then calculated the standard deviation across subjects of the matched subject-level patch sizes, including only subjects who had a patch matching that group-level patch. This analysis was conducted for Datasets 1 and 2 separately.

We then tested whether there were interdependencies among the observed patch size variability, such that knowing the size of one system patch could predict something about the sizes of other patches. For this analysis, we first combined Datasets 1 and 2, and then, for each pair of group-level system patches, we correlated the sizes of the matched subject-level patches against each other, restricting the analysis to all subjects who had successful matches for both patches. We Bonferroni-corrected the observed P-values from these correlations for multiple comparisons.

Finally, to determine whether any observed interdependencies between system patch sizes were related to the network structure of the systems, we tested whether size interdependencies were related to the connectivity strengths between those system patches. For each subject, we calculated the connectivities between all successfully matched system patches as the Fisher z-transformed correlations between the patches' average timecourses; we averaged these connectivity strengths across subjects to create a group average connectivity matrix. We then tested whether the average connectivity strengths predicted patch size relationships by correlating the values in the (Fisher z-transformed) patch size correlation matrix against the values in the group average connectivity matrix, separately for within- and between-system relationships.

Identification of Regions with Variable System Identities Across Subjects

We conducted several analyses to investigate the intersubject variability of the system identities found at each cortical vertex. First, we identified the modal system identity across subjects at each cortical vertex. We then tested whether some vertices had an “alternate” system identity (i.e., a different identity from the one present at that vertex in the group-level system map), and whether that alternate identity was shared across a substantial minority of subjects. In particular, we tested whether the second most common system identity was present in at least 10%, 15%, 20%, 25%, 30%, 35%, and 40% of subjects. This analysis was conducted for Datasets 1 and 2 separately. As results from the two datasets were very similar (see Supplementary Fig. 4), they were combined for subsequent analyses to increase power.

Identification and Characterization of Regions with Variable System Identities Across Subjects

Results from the previous analysis indicated that the majority of intersubject variability in system identity occurred very near system borders, suggesting variability in the location of these systems on the cortical sheet. However, variability in system identity was also observed in a few regions that were not near system borders. In other words, for some subjects, a region in the middle of a group average system patch had a different system identity, similar to our previous observations (Laumann et al. 2015). Such system variability in these regions cannot easily be attributed to simple displacement of system patches along the cortical surface (due to, e.g., mis-registration, or to anatomical variability in the location of cortical areas relative to cortical features used for registration), as they are too far away from other regions in the system.

We identified these variable regions as contiguous patches of cortical vertices that (1) had a substantial number of subjects with the same “alternate” system identity (i.e., not the identity of the group system at that vertex), and (2) were at least 8 mm away from the nearest border of that alternate system in the group system map (so that, e.g., a variable region representing the Default system could be near a Fronto-parietal/Ventral Attention system border, as long as it was far from any Default system borders). We then eliminated patches of variable cortical vertices that (1) did not span at least 100 mm² of cortex, (2) appeared to trace the contours of the nearest system border (likely reflecting border variability that extended beyond 8 mm), and (3) were in regions known to have low signal-to-noise (SNR) ratios [defined as regions with mean BOLD signal <750, consisting primarily of orbitofrontal cortex and anterior temporal lobe; see Ojemann et al. (1997) and Wig et al. (2014)]. We stress that many of the parameter choices here are relatively arbitrary (e.g., the number of subjects with alternate systems; the size of variable regions; and the distance from system borders). These parameters were chosen because they identify a relatively small number of the most variable regions, but they could be adjusted to identify more, smaller regions with fewer variable subjects. Accordingly, we do not claim to have precisely characterized all brain systems in all subjects, but rather to have provided a reasonable and conservative description of particularly variable regions.

To test whether the identification of an “alternate” system in each region reflects meaningful differences in connectivity patterns, we characterized each subject as either having the alternate system identity in that region, or not having the alternate system. This characterization was done by calculating whether at least 50% of the region's surface area in the subject's system map contained the alternate system identity. We then compared subjects with alternate system connectivities against those with common system connectivities in two different ways.

First, we examined whether the “alternate” system identified in the variable regions reflected a categorical distinction in the patterns of correlation observed in different subjects [e.g., as suggested by Laumann et al. (2015), Fig. 7] or a continuous gradation in correlation patterns [perhaps reflecting regions participating in multiple systems, as suggested by Yeo et al. (2014)]. We reasoned that if different subjects had categorically different systems in the region, the subjects' system-level connectivities would be distributed in a bimodal pattern. On the other hand, if the variability was related to mixed signals from multiple systems, connectivity would be distributed in a unimodal pattern. For each subject, in each variable region, we calculated the mean timecourse of all the vertices in the region with the alternate identity (if the subject was classified as having the alternate system in the region) or the common identity (if the subject was classified as having the common identity). We then correlated this timecourse against the mean timecourse of the remaining regions of the brain with the common identity, as well as against the mean timecourse of the remaining regions of the brain with the alternate identity. These correlation values were then Fisher z-transformed. This procedure produced the connectivity strength between the variable region and the common system for each subject, as well as between the variable region and the alternate system. The difference between these two values in a given subject reflects how closely the variable region is associated with the common system versus the alternate system. Thus, we examined the distributions of these connectivity differences for evidence of bimodality, suggesting a categorical as opposed to a continuous distinction of these systems in the variable region across subjects.

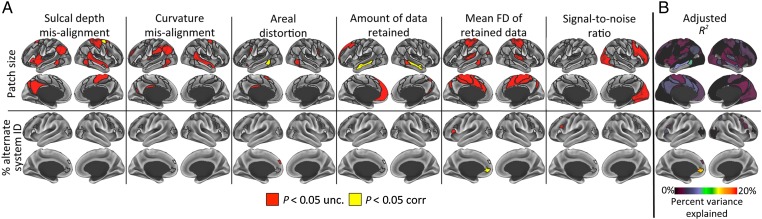
Figure 7.

Estimates of variability in subject-level systems are significantly affected by confound variables, but these variables explain a low percent of variance. (A) Multiple regressions reveal significant effects of 6 possible confound variables (columns) on patch size (top row) and the percent surface areas of region that were assigned to an alternate system identity (bottom row). Red indicates significance at P < 0.05 uncorrected; yellow indicates significance at P < 0.05 Bonferroni-corrected for multiple comparisons. Regressions were only calculated for a priori regions (group system patches in the top row; variable regions in the bottom row). (B) The percent of the total variance in the size of each patch (top) and the percent surface area assigned to an alternate system (bottom) explained by the confound variable regressions. The confound variables explained >10% of the total variance in only one region.

Second, we examined the effect of multiple system representation on connectivity patterns seeded from the variable regions as a whole. We calculated the region's connectivity maps for each subject by correlating the average timecourse of the whole region against the timecourses of every other cortical vertex and applying the Fisher z-transformation. The connectivity maps from subjects with the alternate identity were compared with the maps from subjects with the common identity using a two-sample t-test. Results were corrected for multiple comparisons (including the number of regions tested) by employing a two-dimensional surface-based version of the approach described by Nichols and Holmes (2002) and Hayasaka and Nichols (2004), in which group labels of subject connectivity maps are permuted and the maps are entered into t-tests to generate a null distribution of variously sized patches. This approach established the correction threshold at T > 3.85, with the cluster extent threshold varying between 42.2 and 45.0 mm² for the various regions tested; this corresponded to an overall corrected level of P < 0.05. We note that this analysis does not represent the testing of an independent hypothesis, but rather is used to validate that differences observed in template-matched systems actually reflect reliably different connectivity patterns.

Controlling for Inadequate Surface Registration and Data Quality

It is possible that observed variability in system identity might be driven at least in part by inadequate registration of cortical surfaces. The surface registration procedure registers individual subjects to a template that has substantially less anatomical detail than the individuals; as a result, many gyral and sulcal features in a given individual may not be precisely matched with anything on the template. This could reduce intersubject agreement in regions with poor registration of features. Furthermore, connectivity estimates could be affected by the amount each surface point had to be deformed to match the template. For each subject, we assessed feature alignment at each vertex in three ways: (1) by calculating the absolute difference between the subject's registered cortical curvature map and the template curvature map; (2) by calculating the absolute difference between the subject's registered sulcal depth map and the template sulcal depth map; and (3) by calculating the amount that the surface represented by each vertex was distorted in the registration process (the “areal distortion” of the vertex).

Similarly, it is possible that variability in system identities might be driven in part by reduced data quality, which could introduce noise that would reduce the accuracy of the template-matching procedure. The precision of connectivity estimates may be reduced for a number of reasons, including insufficient data (Anderson et al. 2011; Laumann et al. 2015); the existence of artifacts driven by small residual motion effects that may still exist in the data even after scrubbing frames with head motion (Power et al. 2014); or low SNR in a given brain region. Thus, for each subject, we assessed data quality in three ways: (1) by counting the number of frames remaining after scrubbing; (2) by calculating the mean frame-wise displacement (FD; a summary measure of frame-to-frame motion) in the frames remaining after scrubbing; and (3) by calculating the temporal SNR ratio in each vertex as the mean of the BOLD signal across timepoints divided by the standard deviation of that signal.

We combined Datasets 1 and 2 and performed a series of tests to determine whether any of these 6 possible confound variables—(1) curvature mis-alignment, (2) sulcal depth mis-alignment, (3) areal distortion, (4) number of frames, (5) mean FD, and (6) SNR ratio—affected the system variability we are measuring. First, for each group-level patch, we conducted a multiple regression across subjects to determine whether any of the 6 confound variables predicted the size of the patch. Significant effects of each variable were corrected for the number of regions tested. Second, we tested whether these confound variables affected the identification of variable regions far from system borders. We conducted a similar multiple regression across subjects testing whether the percent of each variable region assigned to an “alternate” system identity was predicted by the 6 confound variables (averaging vertex-wise values within each variable region to get a single value for each region). Third, we tested whether the observed patch size interdependencies were maintained following confound variable regression. Fourth, we tested whether the confound variables drove any observed differences in connectivity maps of the variable regions between subjects with and without the alternate system identity. For each region's connectivity map in each subject, we regressed out the confound variables in a vertex-wise fashion, and we repeated the two-sample t-tests of RSFC maps described above.

Results

Topological Similarity of Individual Systems to Group-Level Systems

We examined the general topological similarity between the group system map and the individual system maps by calculating the percentage of subjects who had a patch matching each group-level patch. We observed that the majority of group-level system patches were identifiable in almost every subject, in both datasets (Fig. 2B). In Dataset 1, 49 of 68 group-level patches (72.1%) were identified in at least 95% of individual subjects. These common system patches tended to be relatively large, and together covered 94.0% of the portion of the cortical surface that had group-level system identities. Similarly, in Dataset 2, 56 of 68 group-level patches (82.4%) were identified in at least 95% of individual subjects, covering 95.9% of the cortical surface with group-level systems. These results indicate that the majority of group-level system patches, covering a very large percentage of cortex, tend to be present in almost every individual, suggesting strong topological similarities between individuals and the group-level systems (though, notably, these matched patches did not have identical sizes, shapes, or positions across individuals; see below). Across both datasets, small patches appeared to be identified less frequently, possibly because some subjects had versions of these patches smaller than the minimum size threshold set in our analysis.

Variance of System Patch Sizes

We examined how variable the size of each system patch was across individuals. Figure 2C shows the standard deviation of patch sizes across subjects (expressed as a percentage of the group average patch size). In both datasets, we observed high size variance in small patches and in patches near low-SNR regions. Among larger patches, moderate variance was observed in lateral prefrontal, lateral parietal, lateral temporal, and medial prefrontal cortex. Lowest size variance was observed in the occipital Visual system patch, the Dorsal and Ventral Somatomotor system patches, and the posterior medial Default system patch.

Interdependence of System Patch Sizes

Given that there is variability in the sizes of system patches, a natural question follows: does knowing the size of one system patch predict something about the sizes of other patches? For example, do system patches expand randomly and independently, or do all of the patches of a given system expand together? Do particular patches or systems compete with one another for cortical real estate, such that expansion of one predicts contraction of another?

We examined relationships between system patch sizes and found 91 significant correlations between patch sizes at P < 0.05, Bonferroni-corrected for multiple comparisons (Fig. 3A). The majority of these significant relationships (67.0%) were positive. Notably, every single positive relationship was between patches within the same system, whereas every single negative relationship was between patches in different systems. The within-system positive relationships suggest that coordinated expansion occurs within a given system, independent of expansion in other systems (see Fig. 3B for an example). Furthermore, these relationships were observed to be more robust in systems with stronger within-network connectivity (see Supplementary Fig. 3).

Figure 3.

The sizes of system patches are correlated across subjects, such that system patches within networks tend to be expanded/contracted together, relative to the group-level patches, whereas patches in different networks can expand/contract in opposite directions. (A) Matrix indicating cross-correlations between the sizes of all system patches, correlated across subjects. Patches are sorted by system membership (Fig. 1). Hot colors indicate positive correlations, which occur exclusively within systems, whereas cool colors indicate negative correlations, which occur exclusively between systems. Black indicates that the correlation did not achieve significance at P < 0.05 after Bonferroni correction. (B) Examples of coordinated expansion of the Cingulo-opercular system. From top to bottom, 3 subjects with, respectively, a small system across all patches, a medium-sized system, and a large system. (C) Examples of negative relationships between patch sizes. From top to bottom, three subjects with, respectively, a large Dorsal but a small Ventral Somatomotor system; two moderately-sized systems; and a small Dorsal but a large Ventral Somatomotor system.

In contrast, the between-system negative relationships suggest that some systems expand into specific cortical regions usually represented by other systems (see Fig. 3C for an example). Broadly, these negative relationships tended to be stronger between systems that have stronger cross-network connectivity (see Supplementary Fig. 3); furthermore, the most significant negative relationships were between patches that were physically adjacent, such as between Visual and Dorsal Attention systems (which are adjacent in the lateral occipital lobe), and between Dorsal and Ventral Motor systems (adjacent in the central sulcus).

Most Common System Identity at Each Cortical Vertex

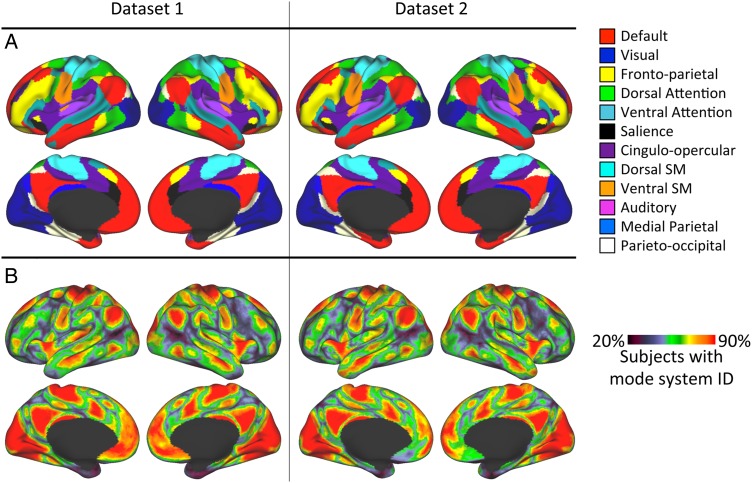
Across subjects, the map of the system most commonly observed at each vertex was highly similar to the community detection-derived template map, in both Datasets 1 and 2 (Fig. 4A), indicating that the template-matching approach accurately recapitulates the template. We further calculated the number of subjects with the mode template identity at each cortical vertex. In both datasets, we observed large expanses of the cortex where greater than 90% of subjects had the same system identity (Fig. 4B). Regions with more variable system identities primarily appeared at the borders between systems.

Figure 4.

Mode system identities recapitulate the original group average system map, and in some cortical regions are present in large proportions of subjects. (A) The most common system identity at each vertex, in Dataset 1 (left) and Dataset 2 (right). (B) At each vertex, the percentage of subjects who had the most common system identity, in Dataset 1 (left) and Dataset 2 (right). Red coloring indicates that greater than 90% of subjects had the mode system identity.

Cortical Regions with Consistent, Alternate System Identities Across Subjects

We identified cortical vertices in which a significant percentage of subjects had the same “alternate” system identity (i.e., different from the group-level system identity at that vertex), and we varied that threshold from 10% to 40% of subjects (see Supplementary Fig. 4). The resulting maps of alternate system identity were very similar for both Datasets 1 and 2; as a result, we combined the two datasets for subsequent analyses.

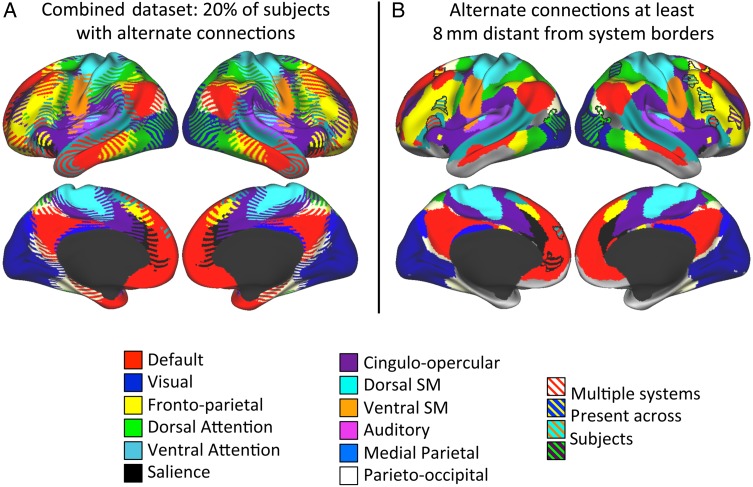
We observed that most of the regions with consistent, alternate systems present in some subjects were very near system borders. This can be most easily observed in the map requiring at least 20% of subjects to have an alternate identity (Fig. 5A, left). In total, 85.2% of the cortical surface area in which alternate connections were present in this map was within 8 mm of a border between group-level systems. Furthermore, the presence of alternate systems near the border between two given systems was generally due to many subjects having the “other” system at each point (e.g., a point near a Default/Cingulo-opercular border that is part of the Default system in most subjects, but that is Cingulo-opercular in a minority). In other words, this was driven by shifts in the borders between systems in individual subjects.

Figure 5.

Most regions with consistent alternate system identities in at least 20% of subjects are primarily near group average system borders, but some are far from those borders. (A) Striped colors indicate all vertices where at least 20% of subjects in the combined dataset (Datasets 1 and 2) had the same alternate system identity, with one color in the stripes representing the modal identity and the others representing alternate identities. (B) Striped colors indicate regions of at least 100 mm² that had consistent alternate system identities in at least 20% of subjects (as in the left panel) and that were also at least 8 mm from the borders of that group average alternate system. Fourteen such regions (outlined in black) can be observed (see Table 1 for details).

However, we also observed a few regions that had alternate connections in a large minority of subjects, but were not near system borders. The alternate connections in these regions cannot easily be explained by shifts in borders. To examine this phenomenon, we identified regions in the 20% map in which every point was at least 8 mm from the borders of the group-level system map and which had a surface area of at least 100 mm². We found 14 regions that met these criteria; see Figure 5B and Table 1 for a complete description of these variable regions.

Table 1.

Cortical regions >8 mm from system borders that had variable system identities across individuals

Region number	Group-level system identity	Alternate system identity	Location	Centroid coordinates (MNI)	Size (mm2)	Subjects with >50% alternate system identity (%)
1	Default	Fronto-parietal	Left superior frontal gyrus	−22 17 50	184	23.7
2	Default	Fronto-parietal	Right superior frontal gyrus	24 10 49	259	18.9
3	Default	Fronto-parietal	Left anterior inferior frontal sulcus	−22 58 3	120	16.2
4	Default	Ventral Attention	Left anterior superior frontal gyrus	−4 56 34	149	17.5
5	Default	Salience	Left ventromedial prefrontal cortex	−9 48 1	195	20.6
6	Visual	Dorsal Attention	Left lateral occipital lobe	−39 −78 11	649	17.1
7	Visual	Dorsal Attention	Right lateral occipital lobe	40 −76 8	1014	21.1
8	Fronto-parietal	Ventral Attention	Left posterior inferior frontal sulcus	−38 13 25	126	21.5
9	Fronto-parietal	Ventral attention	Right posterior middle frontal gyrus	42 5 44	152	20.2
10	Fronto-parietal	Ventral Attention	Right posterior inferior frontal sulcus	38 17 25	208	18.4
11	Fronto-parietal	Cingulo-opercular	Right anterior middle frontal gyrus	39 44 14	193	19.7
12	Dorsal Attention	Visual	Right superior parietal lobule	26 −55 53	187	27.2
13	Ventral Attention	Default	Left inferior frontal gyrus	−52 24 8	324	20.2
14	Ventral Attention	Default	Right inferior frontal gyrus	55 26 10	120	22.8

To evaluate whether these regions represent truly distinct systems, we characterized the distribution of connectivity to common versus alternate systems. For the majority of regions, the distributions of connectivity differences suggest a bimodal distribution (see Supplementary Fig. 5), though in some regions the distributions are not well enough separated to make this unambiguously clear. This result suggests a categorical rather than a continuous connectivity difference between vertices with different system identities.

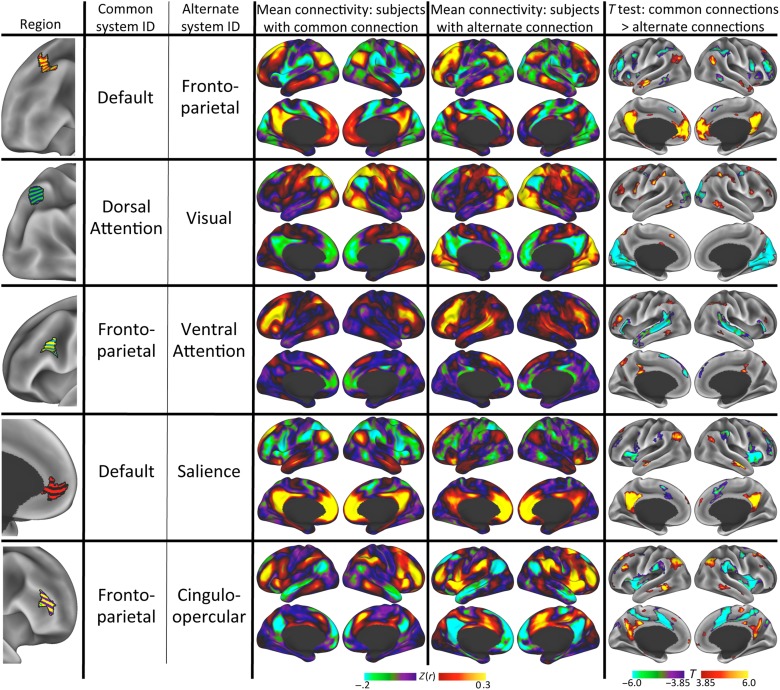
Finally, to evaluate whether, across subjects, the presence of varying systems in these variable regions affected region-seeded connectivity patterns, we compared the connectivity patterns of these regions in subjects with the alternate identity against those in subjects without the alternate identity. For each region, we observed large and reliable connectivity differences between subjects with substantial alternate-network vertices in the region and subjects without; these differences invariably conformed with the putative system differences identified by the template-matching procedure (see Fig. 6 for effects seeded from example regions; see Supplementary Fig. 6 for all regions). This result indicates that these regions, which are far from average system borders, are connected with different large-scale systems in different individuals.

Figure 6.

Connectivity patterns seeded from regions with “alternate” system identities differ between subjects who had the common system in the region and subjects who had the alternate system. Column 1 (leftmost): Visual representation of the region. Column 2: Identity of most common (modal) system. Column 3: Identity of the alternate system present at each vertex in at least 20% of subjects. Column 4: Average connectivity pattern seeded from the region for subjects who had <50% of the vertices in the region identified as the alternate system. Column 5: Average connectivity pattern seeded from the region for subjects who had >50% of the vertices in the region identified as the alternate system. Column 6: Vertex-wise two-sample t-test illustrating differential connectivity between subjects with the common system (hot colors) and subjects with the alternate system (cool colors), thresholded at P < 0.05 corrected for multiple comparisons. See Supplementary Figure 6 for additional regions.

Effect of Inadequate Surface Registration and Data Quality on System Variability Estimates

We used multiple regressions to test whether a variety of confound variables (including inadequate registration of cortical features such as sulcal depth and curvature, amount of distortion induced by the registration procedure, amount of data remaining after motion scrubbing, mean FD of retained data, and SNR ratio of retained data) influences estimates of patch sizes or regions with multiple system identities across subjects. We found that the sizes of a number of regions were influenced by these confound variables. The sizes of multiple large patches in Default, Fronto-parietal, and Cingulo-opercular systems were predicted by the confound variables at P < 0.05 uncorrected (Fig. 7A, top row). Additionally, at P < 0.05 corrected, the amount of data retained predicted the sizes of two Default patches in lateral temporal cortex (near low-SNR regions); sulcal depth mis-alignment predicted the size of one small superior frontal Dorsal Attention patch; and areal distortion predicted the size of one small lateral temporal Dorsal Attention patch. However, none of these multiple regressions explained as much as 10% of variance in the size of any system patch (Fig. 7B, top).

We further observed that after regressing out the confound variables, 94.5% of significant relationships between patch sizes remained significant after correction and in the same direction (see Supplementary Fig. 7A), suggesting that the observed interdependencies were not driven by known registration or data quality effects.

We also found that the percent of the variable region identified as an “alternate” system was influenced by mean FD in the left inferior frontal gyrus at P < 0.05 uncorrected and in the left ventromedial prefrontal cortex at P < 0.05 corrected; by the amount of areal distortion in the left anterior superior frontal gyrus at P < 0.05 uncorrected; and by SNR in the left middle frontal gyrus at P < 0.05 uncorrected (Fig. 7A, bottom row). Of all regions, the regression explained greater than 10% of the variance only in the left ventromedial prefrontal region (adjusted R² = 0.15; Fig. 7B, bottom).

Finally, we observed that after regressing the confound variables out of subject-level connectivity maps seeded from these regions, we still observed large and highly significant connectivity differences between subjects with alternate-network identity in the region and subjects without; these effects were almost identical to the effects observed before the confound variable regression (see Supplementary Fig. 7B).

Discussion

Large-Scale Brain Systems Vary Across Individuals

In this work, we investigated the individual variability of large-scale brain systems in two large, independent groups of healthy adults. We described several notable findings resulting from these analyses. First, we showed that the majority of group-level system patches, covering a very large percentage of the cortex, were observed in at least 95% of individual subjects. This suggests that the group system map provides a valid description of the system topology that is common across individuals. While the smaller group system patches were somewhat less reliably present across subjects, we believe this is likely due to the low effective resolution of the data (and our resulting methodological choice to remove small patches in individual system maps), preventing us from reliably measuring small features in individuals.

Second, we observed that the sizes of the discrete system patches could vary across individuals, with many patches having a standard deviation of over 30% of the group-level patch size. This agrees with previous work describing substantial individual variability in the sizes of cytoarchitectonically defined cortical areas (Van Essen et al. 2012). Of course, the system patches measured here do not strictly correspond to architectonically defined cortical areas. However, cortical areas in general, as defined via a combination of architectonic anatomy, connectivity, and function (Felleman and Van Essen 1991), are believed to be the discrete units of the cortex which interact to form the large-scale systems identified here (Sejnowski and Churchland 1989), and thus the system patches may be presumed to vary in similar ways. Indeed, it appears that many of the regions of greatest system variability in the present work (e.g., posterior inferior frontal gyrus and inferior frontal sulcus; anterior inferior parietal lobule; and posterior lateral temporal cortex; Fig 5A) correspond with cytoarchitectonically defined cortical areas shown to have particularly large individual variability in size and position (respectively, BA44, Fischl et al. 2008; the opercular subdivision of anterior inferior parietal lobule, Caspers et al. 2008; human occipital cortex area 5, Malikovic et al. 2007).

Third, we observed that individual subjects have areas of cortex with “alternate” system identities compared with the group-level system present in the same region (see Supplementary Fig. 2 for examples). These regions of alternate system identity were most often observed near the borders of the group-level systems (Figs 4B and 5A). Furthermore, the alternate systems present near these borders were consistent across subjects and appeared to reflect intersubject variability in the position of the border, suggesting that the boundaries of individual-level systems could be variably translated along the cortical sheet. This observation of intersubject variability in the location of functionally similar units agrees with previous work, demonstrating that the locations of functional responses can vary along the cortical surface across individuals, even after the subjects' cortical surfaces were aligned using a registration procedure similar to the one employed in the present work (Frost and Goebel 2012).

Fourth, we observed several regions far from system borders that had consistent, alternate system identities across subjects. In at least 20% of subjects, we observed (1) Ventral Attention patches in the posterior lateral prefrontal cortex and left anterior dorsomedial prefrontal cortex; (2) a Dorsal Attention patch in the lateral occipital cortex; (3) a Salience patch in the ventromedial prefrontal cortex; and (4) a Default patch in the inferior frontal gyrus, among others (Fig. 5B and Table 1). This finding may help explain some of the apparent inconsistencies in previous descriptions of the brain's group average system organization. For example, the systems previously described using two different approaches (Power et al. 2011; Yeo et al. 2011) are mostly convergent, but do demonstrate some divergence. In the 17-system parcellation described by Yeo et al. (2011), there is a system similar to the Dorsal Attention system identified in Power et al. (2011) and here, except that it also extends substantially into lateral occipital cortex. Similarly, the parcellation in Yeo et al. (2011) describes a system much like the Ventral Attention system described here, except that it also extends some distance into the anterior dorsomedial prefrontal cortex. Notably, these two features coincide with regions described as having alternate connectivity patterns in a minority of individuals in the present work (examples 1 and 2 above). We speculate that the subject sample characterized in Yeo et al. (2011) may have had a higher proportion of subjects with those alternate connectivity patterns than the sample used here, allowing those features to emerge in the group average.

Taken together, these results may help contextualize previous findings showing that, in group average data, various regions demonstrated reduced system segregation, such that they participated in multiple networks (Yeo et al. 2014). Like the present results, these regions were primarily near system borders, but a few were far from such borders. The present results suggest that these regions of reduced segregation may actually be driven by variability in the systems present across subjects; when averaged, these multiple systems would appear to have aspects of each system, and would thus appear less segregated. It is not clear whether reduced system segregation of the type described by Yeo et al. (2014) would be observable in individuals.

Findings Expand Previous Work Describing Individual Variability in RSFC Patterns

This work validates and extends several previous observations about how the systems observed in a single, highly sampled subject differed from those observed from a group average (Laumann et al. 2015; Fig. 1). That work indicated that the single subject had systems that (1) included almost all of the discrete patches observed in the group systems, (2) were variously enlarged or reduced relative to the group systems, (3) had system borders that were sometimes translated along the cortical sheet relative to the group systems, and (4) contained unusual topological features—small patches of an “alternate” system embedded inside large system patches—that were not observed in the group system map. These findings have now been fully replicated in the present work.

This work also extends previous work describing cross-subject variability in RSFC, which found high variability in lateral frontal cortex, occipito-temporal cortex, and temporal–parietal junction (Mueller et al. 2013; Laumann et al. 2015). The present work generally replicates those findings, while providing additional specificity and descriptive power about the nature of the variability present. For example, by looking at Figure 5A, we can observe that (1) variance observed in the posterior lateral frontal cortex appears to be due to the fact that, in some subjects, the Dorsal Attention, Default, and/or Ventral Attention systems intrude into the posterior lateral prefrontal Fronto-parietal patch; (2) variance in the temporal–parietal junction is driven by variable borders at the juxtaposition of Fronto-parietal, Cingulo-opercular, Default, and Ventral Attention systems; and (3) variance in occipito-temporal cortex is driven by variable borders at the confluence of a large number of systems, including Visual, Dorsal Attention, Default, Ventral Attention, Parieto-occipital, Cingulo-opercular, and Fronto-parietal.

Variability in Brain Systems Has Important Implications for RSFC Research

A large proportion of modern research using RSFC techniques investigates the connectivity of a priori seed regions (either those regions' connectivity to other regions, or the voxel-wise whole-brain connectivity maps of those regions) and uses a general linear model (GLM) to test whether the strength of this connectivity measure differs between groups of interest, or is parametrically associated with some behavioral variable. This approach implicitly assumes that the seed region represents the same object in two given subjects, and that the resulting connectivity measure thus varies continuously between subjects. However, the present work demonstrates that across subjects, the same seed region may be a member of different systems (Fig. 5), and that the connectivity of that seed appears to vary categorically between subjects (Fig. 6 and see Supplementary Fig. 5), as previously demonstrated in a single subject (Laumann et al. 2015; Satterthwaite and Davatzikos 2015). Interpreting “weaker” connectivity of a given seed becomes more challenging in this situation, and it is dubious whether such connectivity strengths should be entered into a GLM. Indeed, individual differences in the system identity of a given seed may be a substantial source of unexplained variance that could impair the ability to detect actual relationships between connectivity strength and behavior or group membership, as previous work has speculated (Wang and Liu 2014).

A GLM-based approach to seed-derived RSFC analysis should still be viable as long as there is some confidence that the seeds tested really are part of the same system in almost every subject. Figure 4B shows regions (in red) where subjects showed little variance in system identity. The connectivity of most other seed locations may be confounded by individual variability in system identity.

Interdependencies of System Patches Illustrate How Systems Vary Across Individuals

We observed a large number of significant interdependencies in system patch sizes (Fig. 3A). The majority of these relationships were positive correlations between patches of the same system. This finding suggests that, in a given individual, patch size differences relative to the group average tend to occur across an entire system, such that many pieces of the system are larger (or smaller) than the group average system. This effect was most obvious in the Cingulo-opercular system (see Fig. 3B for examples), possibly suggesting a tighter interdependence of patches within that system than within other systems, though this possibility would need to be tested more rigorously.

This analysis also revealed a smaller number of negative correlations of region sizes between patches in different systems, most frequently between systems physically adjacent to each other. This finding suggests that the relative expansion of one system reduces the amount of cortex available to other systems (as it must), and furthermore, that this reduction is not distributed evenly across all other systems, but that adjacent, connected systems in particular surrender cortical real estate to that expansion (Fig. 3C and see Supplementary Fig. 3).

There are two possible explanations for the observed variances in the size of system patches. The first is that it is driven by variance (i.e., relative expansion or contraction) in the sizes of the systems' constituent cortical areas (Van Essen et al. 2012). The second possibility is that expanded systems actually appropriate cortical areas that normally serve other systems. It is not clear which of these possibilities is more likely to explain the variance in systems we observe here. Indeed, these possibilities may not be mutually exclusive; each may explain some aspect of the observed variance. For example, the push–pull relationship between Dorsal and Ventral Somatomotor systems (Fig. 3C) may be best explained by areal size variation, as it seems unlikely that a cortical area devoted to hand somatomotor processing in one individual would be devoted to mouth processing in another. On the other hand, the specific topological anomalies observed in the middle of large system patches (as in Fig. 5B) cannot be the result of expanded areas, as there is no adjacent patch of the same system, and so may be best explained by areas connecting with different systems in different individuals.

Individual Variability in System Identity Does Not Appear to be Strongly Driven by Anatomical Mis-alignments or Data Quality

In principle, observed individual differences in brain organization may be caused by artifactual effects driven by inadequate intersubject registration (Frost and Goebel 2012) or by motion-related artifact (Power et al. 2012, 2014). In the present study, we used surface-based alignment for intersubject registration, and we used stringent motion controls as recommended in Power et al. (2014). However, we cannot assume that our correction methods are perfect; some individual variance may be driven by residual differences in cortical surfaces, in motion below the threshold for correction, in the amount of data used for analysis, or in the quality of the retained data. We tested whether the individual variability we observed was affected by these possible confounds, and we found a number of significant effects (Fig. 7). However, few effects survived correction for multiple comparisons. Furthermore, the amount of variance explained by the confound variables was low, and regressing out the effects of these variables did not affect our estimates of dependencies between patch sizes or connectivity pattern differences (see Supplementary Fig. 7). We conclude that these confound variables may slightly influence individual variability in system identities, but they do not drive the majority of effects described here.

In contrast, it is possible that some of the variability across individuals described here may be confounded, at least in part, by within-individual variability. Connectivity estimates of a given individual may vary from scan to scan or even minute to minute, potentially reflecting temporary state effects (e.g., drowsiness or anxiety) rather than replicable functional/anatomic variance. While the present study cannot estimate this within-individual variability, as we do not have repeated scans on our subject, we note that previous work (Laumann et al. 2015) demonstrated that the magnitude of within-subject variability is much smaller, and localized to different regions of the brain, than between-subject variability. This suggests that the majority of effects described here likely result from between- rather than within-individual variability.

Conclusion

Here, we characterized the variability of brain system topologies across individuals. We demonstrated that systems derived in individuals have similar topologies as systems derived from a group average dataset, but that system features were variable in size and position in individuals. Furthermore, we demonstrated the presence of additional topological features in individuals that were not present in the group-level systems, but were consistent across a substantial minority of individuals. We also illustrated how the presence of these features can give rise to divergent connectivity estimates from the same seed region in different subjects.

This last observation may present challenges for studies that assume the functional equivalence of anatomically registered regions, as it may represent a substantial, unexplained source of variance in the connectivity patterns across individuals. If a given subject is observed to have, for example, relatively weak functional connectivity between prefrontal and parietal nodes of the Fronto-parietal system, does that subject truly have a disrupted system? Or is the system intact, but translated along the cortical surface away from the group average-derived system node? Parsing anatomical/topological variability from functional variability in this fashion may be critical for interpretation of observed effects.

Furthermore, if ideas postulating the equivalence of brain network architecture during the resting state and during tasks (Fox and Raichle 2007; Smith et al. 2009) are correct, then the same concerns are likely to be relevant for task fMRI studies. Specifically, “lower activation” in a given subject could indicate either a reduced functional response or a translation of the activated region away from the peak of the group average response or the a priori region of interest. Given the present findings, it is possible that an RSFC-based approach for deriving individualized functional regions of interest, like the techniques presented here, may improve the accuracy of activation estimates made in task-based studies. Future work may examine the feasibility of this approach.

These concerns may point to the need for a functional alignment approach that does not attempt to register subjects into a common anatomical space, because even the most advanced alignment procedures (e.g., Robinson et al. 2014) will fail to find a registration warp that can align two subjects who have topologically dissimilar features (Wang and Liu 2014; Harrison et al. 2015). Previous work has proposed alignment into a purely functional space (Sabuncu et al. 2010; Haxby et al. 2011); future versions of such approaches may be improved by using the system maps identified here as priors to assist in functional registration.

Finally, we note that the functional significance of the variability observed here is not yet clear. One possibility is that some aspects of this variability—for example, the size of a system, or the presence or absence of a particular system feature—may be predictive of variability in cognitive performance. Alternately, it is possible that these varying system configurations may represent a diverse but equivalently effective set of possible brain systems—in other words, that these systems are degenerate, such that equivalent performance may be enabled by many different possible system configurations (Tononi et al. 1999; Price and Friston 2002). Such possibilities remain to be investigated in future work.

Authors' Contributions

E.M.G. and S.E.P. conceived the experimental questions. B.A., E.M.G., and T.O.L. preprocessed the data. E.M.G. and T.O.L. designed the analyses with feedback from B.A. and S.E.P. E.M.G. implemented the analyses and wrote the paper. B.A., S.E.P., and T.O.L. edited the paper.

Supplementary Material

Supplementary material can be found here.

Funding

This work was supported by the National Institutes of Health (grant numbers NS061144 to S.E.P., MH100872 to T.O.L., and MH091657 to David Van Essen), the McDonnell Foundation (Collaborative Action Award to S.E.P.), and the Simons Foundation (Award 95177 to S.E.P.).