Electrophysiological Responses in the Ventral Temporal Cortex During Reading of Numerals and Calculation

Abstract

Recent evidence suggests that specific neuronal populations in the ventral temporal cortex show larger electrophysiological responses to visual numerals compared with morphologically similar stimuli. This study investigates how these responses change from simple reading of numerals to the active use of numerals in an arithmetic context. We recorded high-frequency broadband (HFB) signals, a reliable measure for local neuronal population activity, while 10 epilepsy patients implanted with subdural electrodes performed separate numeral reading and calculation tasks. We found that calculation increased activity in the posterior inferior temporal gyrus (ITG) with a factor of approximately 1.5 over the first 500 ms of calculation, whereas no such increase was noted for reading numerals without calculation or reading and judging memory statements. In a second experiment conducted in 2 of the same subjects, we show that HFB responses increase in a systematic manner when the single numerals were presented successively in a calculation context: The HFB response in the ITG, to the second and third numerals (i.e., b and c in a + b = c), was approximately 1.5 times larger than the responses to the first numeral (a). These results provide electrophysiological evidence for modulation of local neuronal population responses to visual stimuli based on increasing task demands.

Introduction

In daily life, one must frequently recognize numerals and use them in arithmetic calculations, such as simple additions. Calculation involves multiple processes in the brain (Dehaene and Cohen 1995), including representations of numerosity in the parietal and frontal regions, which have been widely investigated in both humans and nonhuman primates [for reviews see Ansari (2008) and Nieder and Dehaene (2009)]. In comparison, the neuronal basis for the visual identification of numerical symbols, including numerals, is less widely studied. Visual numeral representations were assumed to be localized in the ventral visual system, with direct connections to parietal and frontal areas involved in numerical cognition (Dehaene et al. 2004). Functional imaging and electrophysiological studies confirmed ventral temporal activation during tasks that involved visual processing of numerals or calculation (Allison et al. 1994; Park et al. 2012), for a review see Arsalidou and Taylor (2011). More recent evidence from intracranial electrophysiological recordings in human subjects suggests that specific neuronal populations within the ventral temporal cortex located in the posterior inferior temporal gyrus (ITG) show preferential responses to numerals compared with morphologically and semantically similar stimuli (Shum et al. 2013).

To date, it remains unclear whether ITG responses to visual numerals reflect only visual encoding (digit recognition) or the active use of these symbols in a given cognitive function such as calculation. For instance, while the current evidence suggests that the ITG plays a role in reading single numerals, it remains to be determined if visual numerals will elicit different neuronal activity when the same numerals are simply read or used in the context of calculation. Do additional neuronal populations get recruited in the ITG or are distinct responses elicited? There is precedence from studies in patients with ventral temporal lesions in whom reading or recognition of single numerals is not affected while they suffer from a significant functional deficit in reading multiple numerals for the purpose of calculation (Cohen and Dehaene 1995).

Understanding how task demands influence the processing of visual symbols is essential for understanding the function of ventral temporal cortex (Price and Devlin 2003; Dehaene and Cohen 2011; Vogel et al. 2014). We designed the present study to understand how calculation influences the processing of visual numerals in the ITG. Intracranial recordings in humans have shown how task aspects influence local neuronal responses to words in which later responses (>300 ms) can increase or decrease dependent on semantic and mnemonic aspects or repetition (Halgren et al. 2006; McDonald et al. 2010). If calculation requires additional neuronal computation in the ITG during equations, we therefore expect that responses to equations increase over time, whereas responses to numerals do not change or decrease. Direct cortical recordings (also known as electrocorticography, ECoG) in patients implanted with subdural electrodes in subtemporal areas allowed us to measure neuronal population responses to passive and active processing of numerals, with a high anatomical fidelity and temporal resolution in each individual brain.

Methods

Subjects and Procedure

Ten subjects (4 females, all right-handed, average age 37 years, range 23–48) who suffered from intractable epilepsy gave informed consent to participate in this study. Three subjects were implanted with electrodes on the left hemisphere and 7 with electrodes on the right hemisphere. During ECoG monitoring, experiments were performed while subjects sat comfortably in their bed and stimuli were presented on a laptop screen using the psychtoolbox (http://psychtoolbox.org/). The laptop was placed 60 cm from the subject's eyes at chest level. Screen resolution was 1280 × 800. Subjects signed informed consent and the study was approved by the Stanford University IRB.

Two experiments were performed. Experiment I was performed to measure the level of ECoG neuronal population responses in the ITG while viewing numerals passively and during calculations. Experiment II was performed to determine the time course of calculation-related influences on ECoG responses in the ITG.

Experiment I

Subjects performed 2 tasks (Fig. 2A) on separate occasions to measure indices for number selectivity. Control stimuli accounted for semantic and phonological processing and components of decision-making.

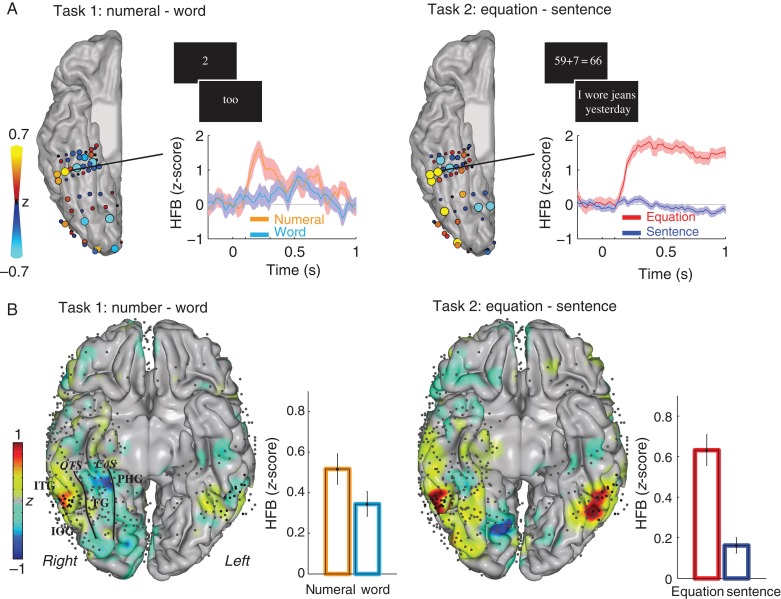
Figure 2.

(A) During Experiment I, subjects performed 2 tasks. In the first task (left), subjects read numerals or words aloud, and in the second task (right), subjects viewed equations and sentences silently and pressed a button to indicate if a given equation or sentence was correct or incorrect. The difference in HFB response amplitude from 100 to 500 ms after stimulus onset between reading numerals versus words (task 1) and equations versus sentences (task 2) for one representative subject (S1) in shown in A. Size and color of recording sites parallel the difference in z-scored HFB response. The traces of the z-scored HFB response for the indicated electrode are shown for each task (the shaded area is the standard error). (B) The difference between numerals versus words (task 1) and equations versus sentences (task 2) from 100 to 500 ms after response onset across all subjects. Z-values for the difference between the conditions are controlled for electrode density and plotted on an MNI brain. Gray dots are the ECoG electrodes, and black dots were located on the posterior ITG (based on individual subject's anatomy), also see Figure 1. The bar graphs show the average responses (±standard error) for the electrodes on the posterior ITG. Different anatomical areas in ventral temporal cortex are indicated by the following abbreviations: ITG, inferior temporal gyrus; IOG, inferior occipital gyrus; PHG, parahippocampal gyrus; FG, fusiform gyrus; OTS, occipital temporal sulcus; CoS, collateral sulcus.

In the first task, subjects were visually presented with 20 numerals, 20 number words, and 20 nonnumber words in a random order, one at a time (white font, Times, Size 90, on a black background, and stimulus height ∼2 degrees of visual angle). Subjects were instructed to read each stimulus aloud. Stimuli were presented until a response was given after which the experimenter pressed a button. The minimum stimulus presentation time was 835 ms and the intertrial interval (after the button press) was 500 ms. Only numerals and nonnumber words were used for analysis; the numerals were 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 14, 16, 20, 28, 30, 40, 50, and 90 and words were hero, won, too, tree, for, hive, sex, heaven, aid, pine, thin, elephant, fortress, sustain, plenty, celebrate, dirty, shorty, nifty, and naughty. Data from this task in 7/10 of subjects have been previously reported (Shum et al. 2013).

In the second task, numerical equations and memory sentences were visually presented (white font, Times, Size 90, on a black background, and stimulus height ∼2 degrees of visual angle) in a random order. Subjects were instructed to press a button to indicate whether each sentence or equation was true or false. The intertrial interval was 200 ms. Equations were additions of a two-digit and a one-digit numeral (e.g., 16 + 4 = 20; n = 40–48 equations, dependent on the task length). Sentences were episodic memory statements (n = 100–240 sentences). Data from this task (pertaining other regions of the brain) have been reported before (Dastjerdi et al. 2011; Foster et al. 2012).

Experiment I compares early and late ECoG responses during calculation and while reading single digits. Since more digits were presented on the screen during calculation than during the numeral reading condition, differences in activity can be due to the number of stimuli on the screen and eye movements necessary to process these stimuli. The second experiment was designed to account for these potential confounds and directly compare ITG responses to the same visual input with and without calculating.

Experiment II

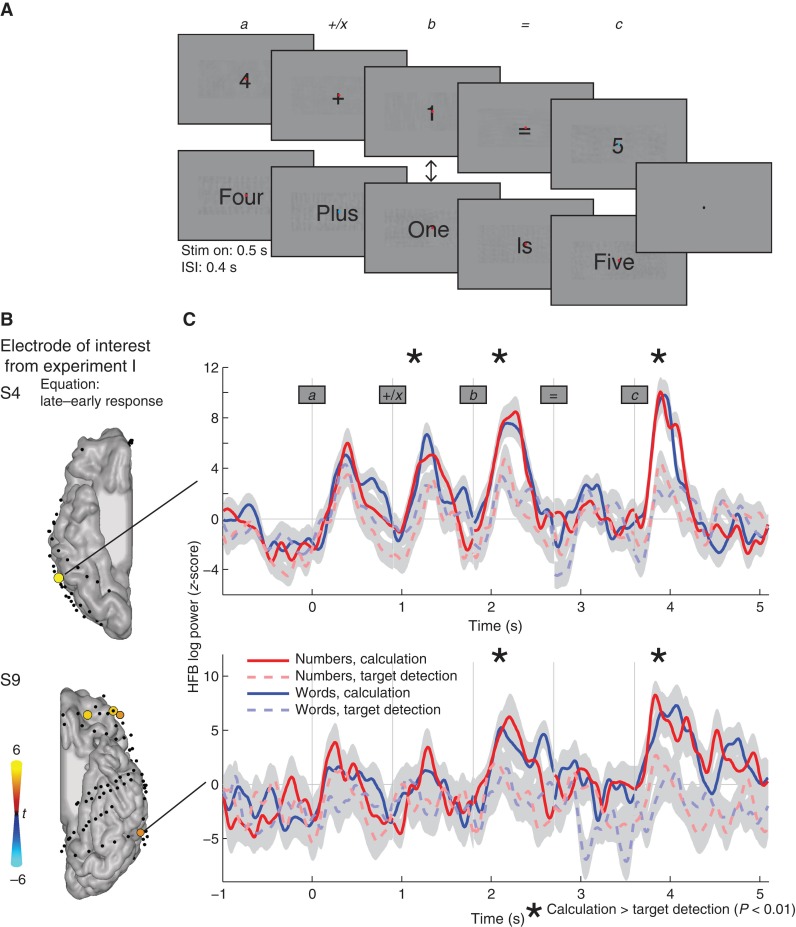
In the second experiment, we presented single digits to investigate the stages at which cognitive context of calculation influences visual number processing (Fig. 4A). Three subjects performed this experiment. Equations ($a{}^{\circ }b=c$), in which the stimulus $a\in \{2,3,4,5,\text{or their number word equivalent}\}$, the stimulus $b\in \{1,2,3,4,5,\text{or their number word equivalent}\},$ and the operator ${\hspace{0.17em}}^{\circ }\in \{+,\times \}$ were shown in rapid serial visual presentation, with each stimulus shown for 500 ms and separated by 400 ms interstimulus interval. Equations consisted of either number stimuli (e.g., 2 + 3 = 5) or number word stimuli (e.g., two plus three is five). In half of the trials stimulus b was presented in the opposite form of stimulus a (e.g., 2 + three = 5 or two plus 3 is five).

Figure 4.

In Experiment II, single digits or number words were presented in sequence. Subjects were either instructed to press a button when the dot in the center of the screen changed color (referred to as passive viewing or target detection) or to report whether the equation answer was correct (active calculation). Additionally, the second numeral stimulus (b) was either a numeral (50%) or number word (50%) independent of the previous stimuli. (B) Rendered results in subjects S4 and S9 from the first experiment show that the HFB response increases significantly during the late minus the early time interval during equations (P < 0.05 Bonferroni-corrected). Increases are shown in red–yellow and decreases are shown in blue–cyan. The electrodes that showed a significant increase in activity during equations were selected for the HFB traces in C. Changes in HFB power over the course of calculation (solid lines) and passive viewing (dashed lines) are presented in C. Stars indicate a statistically significant increase during calculation compared with passive viewing (P < 0.05, main effect of instruction in the ANOVA). No significant differences were found between numbers and number words. The shaded area indicates ±1 standard error.

A 2 × 2 design was used, with one instruction factor and one stimulus factor. The stimulus factor varied from numerals to number words and the instruction factor varied from calculation to target detection. The instruction changed every 4 trials as follows. Throughout the task, a small red fixation dot was displayed in the center of the screen that turned blue during stimuli in a random manner. In half of the trials, the subject was instructed to simply press the button when the fixation dot turned blue (target detection, ignore the equation). In the other half of the trials, the instruction was to indicate if the equations were correct or incorrect (calculation, ignore the dot). After the response, the intertrial interval was 3 s.

ECoG Recording and Preprocessing

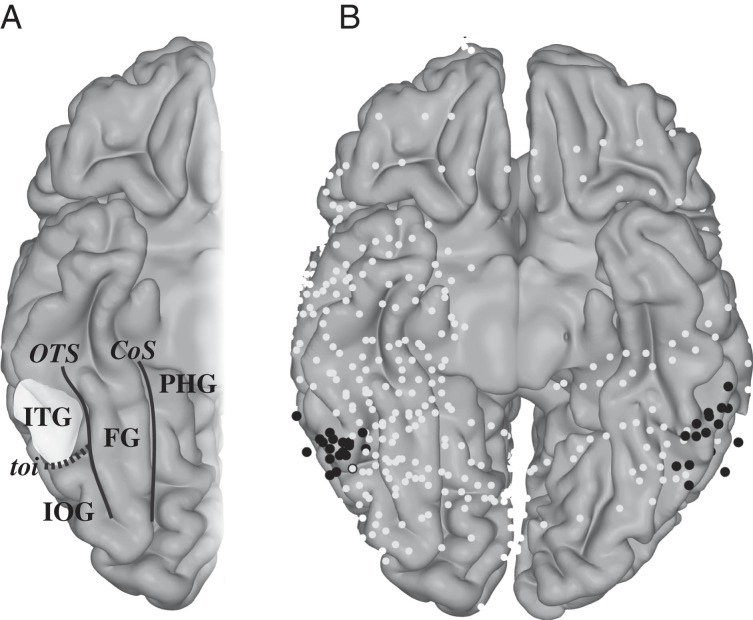
In each patient, signals were recorded from 76 to 126 electrodes (AdTech Medical Instrument Corp.) with different strips and grid configurations and 5 or 10 mm interelectrode distance. All electrodes had a measurement surface of 2.3 mm diameter. Figure 1 shows the electrode locations on the ventral temporal surface in all subjects (also see Supplementary Figure 1). To localize electrodes, a computed tomography (CT) scan was acquired after electrode implantation and coregistered with a preoperative structural MRI scan. Electrodes were localized from the CT scan and visualized on the MRI with an accuracy of ±5 mm (median 2.6 mm) as described previously (Hermes et al. 2010). ECoG signals were recorded at 3052 Hz through a 128-channel recording system made by Tucker Davis Technologies (http://www.tdt.com). Electrodes that showed large artifacts or epileptic activity, as determined by the patient's neurologist (J.P.), were excluded from analysis (5–29 electrodes per patient). Off-line, data were re-referenced to the common average and down sampled to 1000 Hz for computational purposes. In addition to the exclusion of electrodes, epochs containing potential artifacts, such as large jumps in the data, were excluded from analyses. Electrodes that were located on the posterior ITG, as previously shown to show a preferential response to numerals, were localized in all individual subjects (Fig. 1 and Supplementary Figure 1).

Figure 1.

Schematic of the ventral temporal cortex. (A) Different anatomical areas: ITG, inferior temporal gyrus; IOG, inferior occipital gyrus; PHG, parahippocampal gyrus; FG, fusiform gyrus; OTS, occipital temporal sulcus; CoS, collateral sulcus; toi, temporal occipital incisures. The ITG location where visual numeral responses were found before (Shum et al. 2013) is highlighted. (B) ECoG electrodes plotted on an MNI brain: Black electrodes were located on the posterior ITG based on the anatomy in individual subjects (Supplementary Fig. 1).

ECoG Analysis

We measured high-frequency broadband (HFB) changes, as this signal has been shown to be a good index of local spiking activity (Manning et al. 2009; Miller et al. 2009; Ray and Maunsell 2011). A third-order Butterworth filter was used in bands of 5 Hz from 70 to 115 Hz and 125 to 150 Hz (leaving out the 120-Hz harmonic of the 60 Hz line noise). We calculated the envelope of each of these filtered signals by a Hilbert transform and calculated the log power. The mean log power was subtracted from each band, thus whitening the spectrum, and averaged across all bands to compute the HFB estimate. Since the ECoG power spectrum has a 1/f shape, the whitening of the spectrum makes sure that the lower frequencies do not dominate the HFB estimate. This HFB estimate was then resampled at 100 Hz and this entire trace was z-scored with respect to a baseline period: $X_{z-\mathrm{score}}={\displaystyle \frac{X-\text{mean(}{X}_{\mathrm{baseline}})}{\text{std(}{X}_{\mathrm{baseline}})}.}$ The baseline for Experiment I (tasks 1 and 2) was the 200-ms interval before the start of each trial. The baseline for Experiment II consisted of a 1000-ms interval before the start of the first stimulus of the equation.

For Experiment I, numeral and equation responses were compared as follows. First, HFB responses were averaged over time from 100 to 500 ms after stimulus onset, and each condition was compared with its task-specific control (numeral vs. nonnumber words in task 1 and calculation vs. memory sentences in task 2) to show that neuronal population responses in the posterior ITG previously reported during number reading (Shum et al. 2013) are also observed while solving equations. Second, HFB responses were averaged over time from 100 to 300 ms after stimulus onset and from 300 to 500 ms after stimulus onset. We tested whether there was a significant change in the response level over time. All results in individual subjects are reported at P < 0.05 Bonferroni-corrected for the number of electrodes. At the group level, statistical tests were performed on the responses from electrodes on the posterior ITG (N = 37); similar results were found when responses were first averaged per subject (N = 10).

For Experiment II, we first tested whether there was a significant effect of instruction (calculate vs. not calculate) or stimulus (number or number word) for each of the 5 stimuli in the equation. HFB responses were averaged over time from 200 to 500 ms after stimulus onset and a 2 × 2 ANOVA was performed, with one instruction factor and one stimulus factor. The interaction or main effect was considered significant if P < 0.05, Bonferroni-corrected for multiple comparisons across the number of stimuli (5 stimuli: 3 numbers and 2 operators).

Results

Two experiments were performed to investigate whether the neuronal population responses to visual numerals in higher-order visual regions are altered by the cognitive demand of calculation. As a measure of neuronal population response, we used the power of HFB activity (70–150 Hz) because this frequency range in the ECoG signal is tightly coupled to the population firing rate (Manning et al. 2009; Miller et al. 2009; Ray and Maunsell 2011) and fMRI BOLD responses (Logothetis et al. 2001; Lachaux et al. 2007; Hermes et al. 2012). Furthermore, changes in the HFB power show a striking spatial and functional selectivity, providing the best metric of local cortical activation from these signals.

Experiment I: Neuronal Responses to Numerals and Equations Compared With Words and Sentences

First, we replicate previous findings that the posterior ITG shows a preferential response to numerals over words (Shum et al. 2013). Figure 2A,B (left panels) shows the spatial distribution of HFB activity for numerals compared with words. The difference in HFB activity between numerals and words peaks in the ITG: The MNI coordinates of the peak of the smoothed comparison between numerals and words in the right hemisphere were 57, −51, and −17. Across the 37 electrodes on the posterior ITG from all subjects, the HFB response to numerals was significantly larger than the response to words [paired t-test, t₍₃₆₎ = 3.6, P < 0.001].

In addition, across the 37 electrodes on the posterior ITG, the HFB response to equations was significantly larger than the response to memory sentences [paired t-test, t₍₃₆₎ = 7.0, P < 0.001, Figure 2A,B right panels]. Figure 2A,B (right panels) shows the spatial distribution of HFB activity for equations compared with sentences, peaking on the posterior ITG: The MNI coordinates of the peak in the right hemisphere were 57, −53, and −24.

In task 2 (calculation and memory sentences), the average reaction time (±standard deviation) was 1.50 s (±0.10 s) for the sentences and 1.38 s (±0.12 s) for the equations. For the equations, the average percent correct was 84% (for subjects S1–S10, respectively, 55%, 85%, 95%, 70%, 98%, 85%, 90%, 93%, 75%, and 89%).

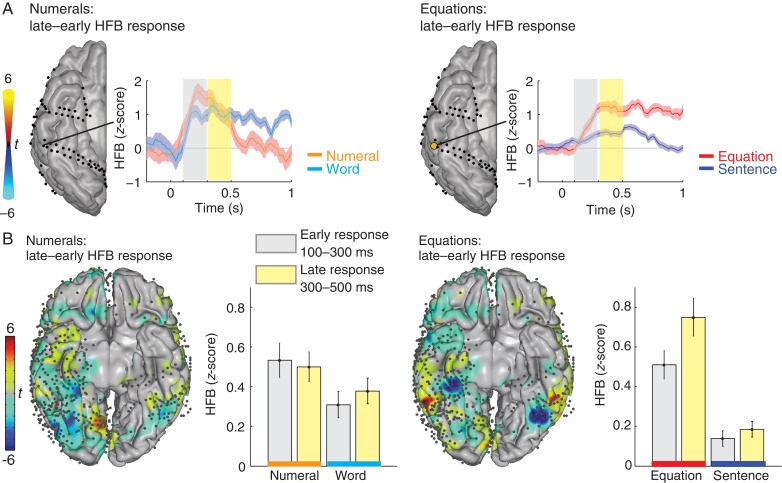
Experiment I: Neuronal Responses to Equations on the Posterior ITG Change Over Time

We investigated how HFB responses change within the first 500 ms after stimulus onset. Responses were averaged for 100–300 and 300–500 ms. Figure 3A shows for one example subject that the response to numerals did not change between these 2 time intervals. However, the response to equations increased significantly in the late time interval in a posterior ITG electrode (P < 0.05 Bonferroni-corrected). In individual subjects, this pattern was found in at least 1 electrode on the posterior ITG in 8 of 9 subjects (89%) with electrodes in this area (see Supplementary Fig. 1). Figure 3B shows the results in the group and the average across all electrodes in the posterior ITG. During reading numerals, activity remained similar for early and late time windows. During calculation, activity increased in the posterior ITG. In the electrodes on the posterior ITG, there was a significantly larger response to numerals compared with words (ANOVA, F_1,144 = 5.55, P < 0.05), but no significant change between early and late time intervals (ANOVA, F_1,144 = 0.06, P = 0.81). However, there was both a significant larger response to equations compared with sentences (ANOVA, F_1,144 = 50.40, P < 0.001) and a significant increase in the late time window (300–500 ms) compared with early time window (100–300 ms) (ANOVA, F_1,144 = 4.68, P < 0.05). The increase in activity during equations was about 1.5 times larger from 300–500 compared with 100–300 ms.

Figure 3.

HFB responses change over time. (A) Left: for one example subject, the difference in the HFB response to numerals in early (gray: 100–300 ms) and late (yellow: 300–500 ms) time windows shows no significant differences in any inferior temporal electrode. Right: the difference in the HFB response to equations in early (100–300 ms) and late (300–500 ms) time windows shows a significant increase in a posterior ITG electrode. T-values are plotted on the cortical surface; only electrodes that show a significant difference between early and late windows (P < 0.05 Bonferroni-corrected) are shown in color. (B) The left panel shows the difference between the late minus early HFB responses to numerals rendered on an MNI brain (red: late > early and blue: early > late). Across all subjects, there are no clear areas that show a significant increase during number reading. The bar graphs show the average responses across the electrodes on the posterior ITG (±standard error). The right panel shows the difference between the late minus early HFB responses to equations rendered on an MNI brain (red: late > early and blue: early > late). Across all subjects, the posterior ITG shows a significant increase during equations in the late time window. The bar graphs show the average responses across the electrodes on the posterior ITG (±standard error).

Experiment II: Sequential Viewing of Numerals During Arithmetic Processing and Passive Viewing

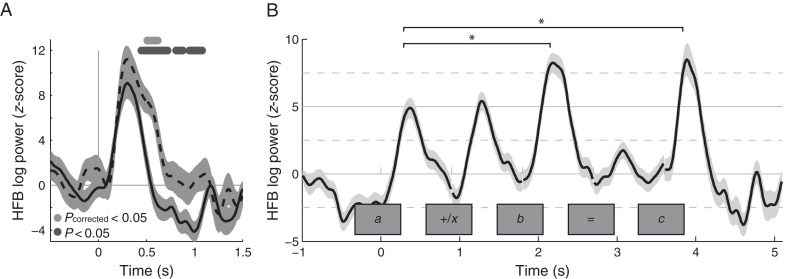
Experiment I showed that HFB activity in neuronal populations in the posterior ITG increased over time during equations, but it did not study the temporal pattern of these increased responses. The second experiment was designed to investigate how these responses develop over the course of calculation and to directly compare the same visual input with and without calculation. Three subjects participated in Experiment II (S2–159 trials, S4–240 trials, and S9–80 trials). The ITG electrodes of interest were localized based on findings from Experiment I: Electrodes had to show a significantly larger HFB response in the late window (300–500 ms) compared with the early window (100–300 ms) during calculation. In only 2 of the 3 subjects, electrodes of interest were found: One electrode in the ITG in each subject (S4 and S9, Fig. 4B) showed increases over time, and these are considered for further analyses (other electrodes, that do not show an increase over time during equations in Experiment I, are also not expected to show such a pattern during sequential viewing of the stimuli in an equation, see Supplementary Fig. 2).

HFB responses were calculated for the ITG electrodes of interest for the active calculation and passive viewing of numerals and number words (Fig. 4C), where stimuli of the form $a{}^{\circ }b=c$, were presented sequentially. Responses were then averaged for 200–500 ms after stimulus onset. The results were highly consistent between the 2 sites in the 2 subjects. HFB activity was significantly larger during calculation compared with target detection for stimulus b and c, but not for stimulus a (Fig. 4C, main effect of calculation, ANOVAs, P < 0.01, corrected for multiple comparisons across the 5 stimuli). There were no significant differences between numerals and number words, and no significant interactions.

Experiment II: The ITGs Responses Differ Between Correct and Incorrect Answers in an Equation

Equations elicit multiple processes that can result in the increased responses. The previous analysis found that the HFB response to the second number (b) and the answer (c) in the equations was increased during calculation compared with passive viewing. The answer in the equation can be correct or incorrect and correct answers might be more expected than incorrect answers. Functional MRI studies have shown that expectancy can increase responses in ventral temporal cortex to unexpected items during oddball tasks (Yoshiura et al. 1999; Marois et al. 2000). Moreover, other tasks that manipulate expectancy have shown that fMRI responses are increased when items do not match what is expected (errors) (Summerfield and Egner 2009; Egner et al. 2010). Therefore, response increases to the answer could potentially be driven by the incorrect answers, because these incorrect answers are less expected, rather than to cognitive task demands during calculation. To control for this, we performed 2 analyses. First, we explored whether the response to the (unexpected) incorrect answers was larger compared with correct answers. Second, we excluded the incorrect answers and tested whether the response to correct answers was increased over the response to the first number in the equation. If responses to correct answers are still increased over the response to the first numeral, factors other than expectancy are likely to modulate the response to the answer. To test whether expectancy effects were present, we tested if the HFB activity during the stimulus c was increased for incorrect (unexpected) versus correct (expected) stimuli. We thus compared the HFB response after the presentation of stimulus c from those trials when a correct answer c was presented and the subject's response was correct (hits) to the HFB response to incorrect answers c, where the subject indicated that the answer was incorrect (correct rejections). Second, we tested whether HFB responses increased during the equation during the hit trials (stimuli b and c compared with a). Subject S4 responded to the equations by button presses and scored 96% correct. Subject S9 responded verbally and scored only 55% correct, but the verbal responses indicated that the subject was engaged in the calculation task. As shown in Figure 5, the first analysis revealed that HFB responses were significantly larger for incorrect answers in subject S4 (multiple t-tests across time points, P < 0.05 Bonferroni-corrected). In subject S9, the same trend was found (multiple t-tests across time points, P < 0.05 uncorrected). This shows that the increased response during the answer c could be partially explained by increased responses for incorrect equations.

Figure 5.

(A) HFB changes during correct (solid) and incorrect (dashed) answers (i.e., the last digit c) averaged for subject S4, from the same site as in Figure 4 combining numbers and number words. Dots indicate that the HFB changes were significantly larger during incorrect answers (by a t-test dark gray dots = P < 0.05 uncorrected, light gray dots = P < 0.05 corrected for all time points tested by Bonferroni correction). (B) HFB changes during calculation averaged across the 2 subjects (S4 and S9), combining numbers and number words. Only correct answers are shown for the last digit c. Significant increases were noted during the second and third numeral (b and c) compared with the first numeral (a). The shaded area indicates ±1 standard error.

To test whether the increased HFB activity during the answer was fully explained by expectancy effects to incorrect answers, we compared HFB response levels for stimuli b and c to a, only including correct equations. Expectancy effects cannot be present during b (before the answer is known) and should only lower responses to correct answers c. Figure 5B shows the average responses across both subjects for the calculation condition with only the correct equations. During the calculation condition, the size of the responses to the second and third numeral stimuli (b and c) was significantly larger (∼1.5 times) than the response to the first numeral stimulus a (fixed-effects ANOVA, F_2,296 = 11.35, P < 0.001, with Tukey's honest significant difference criterion as a post hoc test). These results show that the stimulus-locked HFB increases in the ITG over the course of the equation cannot be explained only by expectancy, and other aspects of calculation play a significant role.

Discussion

We reported recently that a specific location within the human ventral temporal cortex has selective responses to visual numerals compared with morphologically similar false fonts or letters or phonologically identical number words or phonologically similar nonnumber words, and that this level of functional specificity was observed in a small area within the posterior ITG, which we called the visual numeral area (Shum et al. 2013). Here, we extend these findings by showing that calculation influences the responses in the posterior ITG and that neuronal population activity increases during arithmetic function, such as simple addition.

We found that responses in the posterior ITG increase by a factor of approximately 1.5 during the course of calculation. Several analyses were utilized to address why responses to visual numerals in the ITG increased in the context of calculation. The number of stimuli presented on the screen or eye movements made to process these stimuli could not explain this increase in local neuronal activity.

In the first experiment, we noted an increase in local neuronal activity from 300–500 compared with 100–300 ms during calculation and not during number reading. This increase in activity over time could either be due to an increase in a response that is sustained during the entire calculation, or to a phasic increase in a transient response to each digit. In 2 subjects, we show that the response to single visual numerals increased in a phasic manner during calculation, and not during passive viewing. Rather than a baseline effect, the increased phasic activity we found is more likely to be partially driven by the stimulus.

Over the course of an equation, we noted similar increases in activity for both numerals and number words. The increased ITG responses observed in the equation context were thus not limited to numerals only, but extended to number words. The effect of calculation was thus not as specific to the visual stimulus as the visual responses without calculation that we noted before (Shum et al. 2013). However, this observation is in line with previous studies that have discussed the degree to which the activity of the visual word form area in the ventral temporal cortex is modulated by tasks other than visual word presentation (Price and Devlin 2003; Dehaene and Cohen 2011; Vogel et al. 2014). Our results show that the cognitive demands of calculation, rather than features of visual stimuli alone, influenced the activity of the posterior ITG during calculations.

These findings suggest that the ITG is influenced by activity in other brain regions with increasing task demands. Representations of numerosity in parietal and frontal brain regions are well investigated in both humans and nonhuman primates (Ansari 2008; Nieder and Dehaene 2009; Dastjerdi et al. 2013; Harvey et al. 2013; Vansteensel et al. 2014). White matter pathways connect ventral temporal cortex to these parietal and frontal regions (Yeatman et al. 2013). A previous fMRI study showed that, during calculation, ventral temporal regions show increased functional connectivity with parietal regions (Park et al. 2012). Moreover, a number area is present in the ITG in blind subjects, and shows connectivity with parietal and frontal areas (Abboud et al. 2015). Our results show that increased neuronal population response during calculation could be due to an increase in network interactions between the ITG and other regions of the brain that are engaged during a demanding cognitive task.

The responses in inferior temporal cortex can be modulated by multiple higher-order cognitive demands (Gilbert and Li 2013), such as the computational operations of calculation, attention, or memory. Previous studies of attention (both fMRI studies in humans and single-cell recordings in monkeys) have often shown an increase in baseline activity in ventral temporal cortex (Chelazzi et al. 1993, 1998; Kastner et al. 1999; Giesbrecht et al. 2006). An increase in general visual attention to the presented stimuli during the attention-demanding calculation condition should have resulted in an increased response to all numbers in the equation (a, b, and answer c in $a{}^{\circ }b=c$), and to the nonnumber stimuli. As noted, the increased responses were seen only for the second and third numerals (b and c) and not the other visual forms. This pattern is more specific than a general attentional effect: The pattern is specific for the numerals in the equation and evolves over time.

Increasing memory load may also be a contributing factor in shaping the neuronal population responses in the ITG, since calculation requires keeping several items in memory. There is evidence that visual short-term memory capacity is behaviorally correlated with calculation performance in children (Rosselli et al. 2006). Functional MRI studies have also reported sustained responses in ventral temporal cortex for the maintenance of items in short-term memory (Ranganath and D'Esposito 2005). Finally, HFB power, as computed in our study, has been shown to increase with working memory load (Howard et al. 2003; Mainy et al. 2007). Future work is needed to disentangle the differential role of mathematical processing versus attention and memory effects, for example subjects could be instructed to simply keep numerals in memory, without calculation, and asked whether the cue was one of the previous 2 numerals.

Previous studies have shown that lesions in the left inferior temporal cortex cause problems with reading multiple digits or performing addition tasks without affecting the reading of single digits as much (Cohen and Dehaene 1995). An electrocortical stimulation study also showed that reading sequences of 2 digit numerals was specifically impaired when stimulating the left ITG, while sentence reading was unaffected (Roux et al. 2008). The anatomical location of increased responses in the ITG during calculation is highly similar to the location of sites noted by Roux et al. (2008). We show that calculating with multiple digits increases activity in the ITG compared with reading digits. Future studies will have to determine whether the disturbance of the ITG has behavioral effects for calculation and not for reading.

Visual word responses are often reported to be larger on the left compared with the right hemisphere (Cohen et al. 2000). Increased responses to visual numerals in the context of equations were noted in both the left and right ITG. However, all subjects were implanted with unilateral electrode arrays and we cannot resolve the lateralization of these responses in single-subject level or study whether these effects were larger on the left or right hemisphere.

In conclusion, we replicated previous work showing selective responses to visual numerals in the ITG (Shum et al 2013), and extended these results by showing that this response is strongly modulated by arithmetic processing. As proposed in the triple code model of numerical cognition (Dehaene et al. 2004), neuronal populations in the ITG are part of the information-processing network involved in arithmetic function.

Supplementary Material

Supplementary material can be found here.

Funding

This work was supported in part by the National Institutes of Health Grant 1R01 NS0783961 and US National Science Foundation (BCS1358907) grant to J.P., Stanford NeuroVentures Program to J.P., and the National Institutes of Health Grant T32-EY20485 to D.H. and the National Institute of Mental Health Grant K99-MH103479 to B.L.F.