FUNNEL-GSEA: FUNctioNal ELastic-net regression in time-course gene set enrichment analysis

Abstract

Motivation

Gene set enrichment analyses (GSEAs) are widely used in genomic research to identify underlying biological mechanisms (defined by the gene sets), such as Gene Ontology terms and molecular pathways. There are two caveats in the currently available methods: (i) they are typically designed for group comparisons or regression analyses, which do not utilize temporal information efficiently in time-series of transcriptomics measurements; and (ii) genes overlapping in multiple molecular pathways are considered multiple times in hypothesis testing.

Results

We propose an inferential framework for GSEA based on functional data analysis, which utilizes the temporal information based on functional principal component analysis, and disentangles the effects of overlapping genes by a functional extension of the elastic-net regression. Furthermore, the hypothesis testing for the gene sets is performed by an extension of Mann-Whitney U test which is based on weighted rank sums computed from correlated observations. By using both simulated datasets and a large-scale time-course gene expression data on human influenza infection, we demonstrate that our method has uniformly better receiver operating characteristic curves, and identifies more pathways relevant to immune-response to human influenza infection than the competing approaches.

Availability and Implementation

The methods are implemented in R package FUNNEL, freely and publicly available at: https://github.com/yunzhang813/FUNNEL-GSEA-R-Package.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Microarrays and RNA-seq have made simultaneous expression profiling of thousands of genes across several experimental/clinical conditions widely accessible. However, interpreting the profiles from such large numbers of genes remains a key challenge. An important conceptual advance in this area was the shift from a focus on differential expression of single genes to testing sets of biologically related genes (Mootha et al., 2003; Subramanian et al., 2005). Here gene sets are typically defined a priori to include genes that share some common biologically relevant properties (e.g. members of the same metabolic pathway, having a common biological function, presence of a binding motif etc.). In addition to the advantage in interpretability, another benefit of analyzing gene sets instead of individual genes is that small changes in gene expression are unlikely to be captured by conventional single-gene approaches, especially after correction for multiple testing (Mootha et al., 2003).

Due to these advantages, gene-set hypothesis testing has become a popular research area and many methods have been developed (Dinu et al., 2007; Jiang and Gentleman, 2007; Kim and Volsky, 2005; Luo et al., 2009; Oron et al., 2008; Saxena et al., 2006; Wu et al., 2010; Wu and Smyth, 2012; Yaari et al., 2013) in recent years to improve the original GSEA procedure (Subramanian et al., 2005). For example, some recently developed gene set tests such as CAMERA (Wu and Smyth, 2012) and its extension (Yaari et al., 2013) include adjustments for inter-gene correlation. Such adjustments are necessary because inter-gene correlation can increase the false discoveries of many differential expression tests (Qiu et al., 2005, 2013, 2014; Qiu and Yakovlev, 2006, 2007) and gene-set tests (Breslin et al., 2004; Dørum et al., 2009; Wu and Smyth, 2012) substantially and render the results highly variable.

Another under-developed area is time-course gene set analyses. Although some inferential tools (Conesa et al., 2006; Luan and Li, 2004; Park et al., 2003; Sohn et al., 2009; Storey et al., 2005; Wu and Wu, 2013) are available for detecting temporally significant genes, only a handful existing methods are specifically designed for time-course gene set analyses (Hejblum et al., 2015; Nueda et al., 2009; Wang et al., 2008, 2009a,b; Zhang et al., 2011) based on generic analytical tools such as linear mixed effect regression (Wang et al., 2008, 2009a,b), principal component analysis (PCA, Nueda et al., 2009), and B-splines (Hejblum et al., 2015).

Increasingly, personalized approaches are applied to transcriptome analyses to study subject-specific responses. Unlike genetically identical mice, transcriptomic studies across human population have revealed that human subjects exhibit large variation in responses to biological conditions across subjects. Large between-subject variation can reduce the statistical power significantly in a standard cross-sectional study. This problem can be mitigated by incorporating subject-specific information (e.g. baseline measurements before intervention or infection in a longitudinal analysis (Thakar et al., 2015; Tsang et al., 2014). Moreover, to quantify the heterogeneity of subject-specific responses may be an important aspect of a study (Henn et al., 2013; Wu and Wu, 2013). This consideration has led to the development of the single sample GSEA (Barbie et al., 2009) that uses the differences in empirical cumulative distribution functions of gene expression ranks inside and outside the gene set to calculate sample-specific enrichment statistics.

In this study, we propose a new method based on functional PCA (FPCA, Ramsay and Silverman, 2005). It can detect arbitrary non-constant trends in time-course data analysis and is superior to several competing omnibus tests based on B-splines (Sohn et al., 2009; Storey et al., 2005), mainly because eigen-functions selected by FPCA form an orthogonal functional basis that explains more L²-variation of the entire transcriptome than any other basis. Moreover, FPCA is applied to each subject separately to improve the ability to identify subject-specific variations. Population-based inference can then be made by aggregating P-values across subjects with a suitable meta-analysis tool such as Fisher’s combined probability test (Fisher, 1963).

The availability of high-quality gene sets from publicly accessible databases, such as MSigDB (Liberzon et al., 2011) and KEGG pathways (Kanehisa and Goto, 2000) is critical for the success and popularity of gene set tests. Because pathway definitions in the public repositories are typically curated from many studies therefore not context-specific, there is a remarkable overlap in these gene sets. For example, we use 186 CP:KEGG biological pathways provided from MSigDB database in this study. These pathways consist of 5267 unique genes, and 2278 (or 43.3%) of them belong to two or more pathways. Ignoring this overlap overweighs the importance of genes shared by multiple sets and increases the dependence of hypothesis tests, thus reduces statistical power and induce spurious type I error and instability of inferences at the gene set level (Gordon et al., 2007; Qiu et al., 2005; Qiu and Yakovlev, 2006, 2007).

Moreover, we and others have studies context-specific activations of pathways (Hartmann et al., 2015; Katanic et al., 2016; Lee et al., 2011; Segal et al., 2003), which are more pertinent to various immune and stress responses in both human and yeast models. It will be difficult to design follow-up experiments if the significance of selected gene sets is largely driven by generic associations that are not specific to the biological conditions of interest.

To address this issue, we developed a weighting method based on functional elastic-net regression to assess the functional similarities between a given gene and the sets to which it belongs. By design, we let the weights pertinent to one gene sum up to one; so that this gene is not over-counted in gene-set-level analyses. We also developed a generalized Mann-Whitney U (MWU) test for gene-set-level inferences, which incorporates both inter-gene correlation and the weights determined by the functional elastic-net regression. With the proposed method, we will be able to estimate condition-specific importance of genes in the pathways, which will facilitate future empirical investigations.

Dubbed as FUNNEL-GSEA (FUNctioNal ELastic-net regression in Gene Set Enrichment Analysis) or simply FUNNEL, our method utilizes recent advances in functional data analysis and is the first method to directly account for the overlapping genes by decomposing them into fractions (weights) in gene-set-specific manner. In this study, we demonstrate that FUNNEL has better statistical power and uniformly better receiver operator characteristics (ROC) curves than two major competing methods, CAMERA (Wu and Smyth, 2012) and TcGSA (Hejblum et al., 2015). The original CAMERA parametric test is designed for detecting linear trend only; with appropriately selected summary statistic, CAMERA can be extended for non-linear trends using its non-parametric test. Furthermore, we apply FUNNEL to temporal gene expression data collected from human subjects challenged with live influenza viruses to show increased sensitivity and identification of pathways more informative in describing the differences of two phenotypic groups (symptomatic and asymptomatic subjects) at the molecular level.

2 Materials and methods

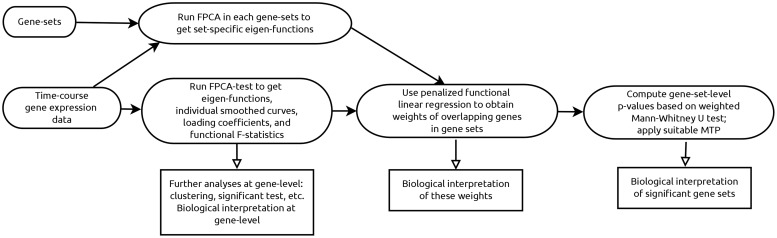
Our method, FUNNEL-GSEA, consists of three components: (i) A gene-level summary statistic based on FPCA test (Ramsay and Silverman, 2005; Wu and Wu, 2013). (ii) A weighting method to decompose overlapping genes based on functional elastic-net regression. (iii) A generalized MWU test that incorporates both weights and inter-gene correlation to test significant gene sets. These components are described in the following subsections.

2.1 A gene-level summary statistic based on FPCA

Let $y_{ij}$ be the pre-processed (i.e. normalized and log-transformed) expression level for the $i$th gene at the $j$th sampling time point. The observed data can be modeled as

$$y_{ij}=x_i\left(t_j\right)+{\mathrm{ϵ}}_{ij},\hspace{0.17em}\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{ }i=1,\dots ,m;\mathrm{ }j=1,\dots ,n,$$

where $x_i(\cdot )$ is unknown gene-specific function of time, and ${ϵ}_{ij}$ is random noise. After subtracting the mean expression over time for each gene, we apply FPCA across all the centered expression values. The estimated per-gene expression curve is represented as

(1)

where ${\widehat{\mathrm{\mu }}}_i$ is the temporal sample mean expression; ${\widehat{\mathrm{\varphi }}}_l\left(t\right)$ is the $l$th eigen-function; and ${\widehat{\xi }}_{il}$ is the functional principal component (FPC) score that quantifies how much ${\widehat{x}}_i\left(t\right)$ can be explained by ${\widehat{\mathrm{\varphi }}}_l\left(t\right)$. Empirical evidences show that the first three eigen-functions (L = 3) explain about 86% of total variance of the real data (see Supplementary Material Section S1), and thus can represent the overall expression pattern of a given gene set. This high-level of variance explained by just a few eigen-genes is very common in FPCA analyses of time-course gene expression data (Qiu et al., 2015b; Wu et al., 2014; Wu and Wu, 2013). As a comparison, we performed standard PCA in the time direction on the same expression data. Top 3 principal components only explain about 53% of total variance and it would require at least 8 principal components to explain about 86% of variance (see Supplementary Material Section S1). The main reason that FPCA is much more efficient than PCA in explaining data variation is that FPCA uses roughness penalty to achieve smoothness of temporal functions; in doing so it ‘borrows information’ across time points and reduces a large proportion of spurious variation pertaining to the i.i.d. measurement error.

For time-course gene expression data, a temporally differentially expressed gene can be defined as a gene with significant non-constant expression pattern across time points. In other words, we want to test the following hypotheses

$$H_{i0}:x_i\left(t\right)={\mathrm{\mu }}_i\hspace{0.17em}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{s}\mathrm{u}\mathrm{s}\hspace{0.17em}{H}_{i1}:x_i\left(t\right)\ne {\mathrm{\mu }}_i,\hspace{0.17em}\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{ }t\in \left[t_1,t_n\right].$$

Under $H_{i0}$, $x_i\left(t\right)$ is estimated by a function with constant value ${\widehat{\mathrm{\mu }}}_i$ (the sample mean expression for the $i$th gene); under $H_{i1}$, ${\widehat{x}}_i\left(t\right)$ defined in Equation (1) is used instead. We use the following functional $F$-statistic to summarize the information contained by each gene over time:

$$F_i=\frac{\mathrm{R}\mathrm{S}{\mathrm{S}}_i^0-\mathrm{R}\mathrm{S}{\mathrm{S}}_i^1}{\mathrm{R}\mathrm{S}{\mathrm{S}}_i^1},$$

where $\mathrm{R}\mathrm{S}{\mathrm{S}}_i^0$ and $\mathrm{R}\mathrm{S}{\mathrm{S}}_i^1$ are the residual sum of squares under the null and alternative hypotheses, respectively. This summary statistic can be viewed as a ‘signal-to-noise’ ratio for functional data. The larger $F_i$ is, the more significant the $i$th gene is.

2.2 Decomposing overlapping genes based on functional elastic-net regression

We use the following concurrent functional linear model to decompose an overlapping gene between gene-sets

(2)

Here ${\mathcal{K}}_i$ is the set of gene sets where the $i$th gene belong; ${\mathrm{\beta }}_{l,i}^k$, $l=\mathrm{1,2}\dots L,\mathrm{ }k\in {\mathcal{K}}_i$, is the linear coefficient w.r.t. ${\widehat{\mathrm{\varphi }}}_l^k\left(t\right)$, the $l$th eigen-function obtained from performing FPCA on the $k$th gene set. ${\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\mathrm{a}\mathrm{l}}_i^k\left(t\right)={\sum }_{l=1}^L{\mathrm{\beta }}_{l,i}^k{\widehat{\mathrm{\varphi }}}_l^k\left(t\right)$ represents the temporal signal of the $i$th gene attributed to the $k$th gene set; and ${\mathrm{ϵ}}_i\left(t\right)$ is the noise function that cannot be explained by any gene set.

We denote the set of eigen-functions $\{{\widehat{\mathrm{\varphi }}}_l^k\left(t\right),\mathrm{ }l=\mathrm{1,2}\dots L,\mathrm{ }k\in {\mathcal{K}}_i\}$ as a vector of functions ${\widehat{\mathit{\varphi }}}_i\left(t\right)$; the set of linear coefficients $\{{\beta }_{l,i}^k,l=\mathrm{1,2}\dots L,\mathrm{ }k\in {\mathcal{K}}_i\}$ in Equation (2) as a vector$\mathrm{ }{\mathit{\beta }}_i$, which can be estimated by the following optimization problem

$${\widehat{\mathit{\beta }}}_i=\underset{{\mathit{\beta }}_i}{\min }\mathrm{O}\mathrm{B}\mathrm{J}\left({\mathit{\beta }}_i\right|x_i\left(t\right),{\widehat{\mathit{\varphi }}}_i\left(t\right)),\mathrm{ }\mathrm{O}\mathrm{B}\mathrm{J}\left({\mathit{\beta }}_i\right|x_i\left(t\right),{\widehat{\mathit{\varphi }}}_i\left(t\right))={\Vert x}_i\left(t\right)-{\widehat{\mathit{\varphi }}}_i{\left(t\right)}^{\mathrm{T}}{\mathit{\beta }}_i{\Vert }^2+{\mathrm{\lambda }}_1{\Vert \mathit{\beta }}_i{\Vert }_1+{\lambda }_2\Vert {\mathit{\beta }}_i{\Vert }^2.$$

Here ${\mathrm{\lambda }}_1$ is the LASSO (Tibshirani, 1996) penalty coefficient and ${\lambda }_2$ is the ridge (L²) penalty coefficient. We need LASSO penalty because sparcity in ${\widehat{\mathit{\beta }}}_i$ enhances the biological interpretability. We also need ridge penalty to account for possible collinearity problems because some genes are shared by many gene sets, which implies that a large number of covariates (eigen-functions) may be used in regression. Besides, although eigen-functions pertain to one gene set are independent by construction, there may be high correlation between certain eigen-functions estimated from different gene sets. In this case, adding ridge penalty can make the parameter estimation more stable.

By using the terminology from multivariate regression, we call the above optimization problem as functional elastic-net regression (Zou and Hastie, 2005). Most currently available penalized functional linear regression methods (Goldsmith et al., 2012) focus on using Tikhonov regularization (semi-positive-definite penalty) to achieve smoothness and computational stability of functional linear regression. Model selection methods such as LASSO and group SCAD (Fan and Li, 2001; Wang et al., 2007) regularization were recently used in functional linear regression but most of them (Collazos et al., 2016; Gertheiss et al., 2013; James et al., 2009; Lee and Park, 2012; Matsui and Konishi, 2011) are developed for standard functional regression model (functional covariates and scalar responses). Model selection methods for historical functional linear models (of which the concurrent model is a special case) were studied in (Harezlak et al., 2007; Matsui et al., 2009). These methods involve computational expensive fitting techniques that are not necessary for concurrent functional regression model. In this study, we took a different approach based on an equivalence relationship between the penalized concurrent functional regression and a standard multivariate regression. This approach is computationally efficient and highly flexible. Technical details of this approach can be found in Supplementary Material Section S2. The selection of the penalty coefficients can be found in Supplementary Material Section S6.

Once ${\widehat{\mathit{\beta }}}_i$ is estimated, we define the estimated weight for the $i$th gene in the $k$th gene set to be

$${\widehat{w}}_{i,k}:=\frac{{\sum }_{l=1}^L({\widehat{\mathrm{\beta }}}_{l,i}^k{)}^2}{{\sum }_{k\in {\mathcal{K}}_i}{\sum }_{l=1}^L({\widehat{\beta }}_{l,i}^k{)}^2}.$$

We assign ${\widehat{w}}_{i,k}=1$ if gene $i$ belongs to the $k$th gene set only. Due to the use of LASSO penalty, in some cases both the numerator and denominator may be zero, in which case we assign ${\widehat{w}}_{i,k}=0$. The weighting vector of the $k$th pathway is denoted by ${\mathbf{w}}_k=\{w_{i,k},i\in {\mathcal{I}}_k\}$, where ${\mathcal{I}}_k$ is the set of genes in this gene set.

2.3 Weighted MWU test with correlation

The MWU test is a rank-based non-parametric test that can be used in a competitive GSEA to test whether the median of gene-level summary statistics ($F_i$) sampled from the testing gene set is significantly greater than the median of $F_i$ sampled from the rest of the genome (called the background genes). Unlike the setting of classical MWU test in which all observations are assumed to be independent, genes are known to be correlated with each other, especially within one biological pathway. Consequently, the classical MWU test must be adapted to accommodate with such correlation. As a special case, CAMERA assumes that genes in the testing gene set share a common pairwise correlation $\mathrm{\rho }$ (interchangeable correlation structure) and the background genes remain independent. In this study, we further extended the modified MWU test used in CAMERA to allow the use of weights, which reflect the empirical membership of the overlapping genes assigned to the test gene set.

Suppose we want to test the $k$th gene set which contains $m_1$ member genes. We denote the number of background genes as $m_2=m-m_1$. We define the weighted MWU statistic for this gene set as

$$r_{i,k}≔\sum _{i\mathrm{\text{'}}=1}^{m_2}{I}_{F_i>F_{i\mathrm{\text{'}}}},\hspace{0.17em}{\mathrm{U}}_k\left({\mathbf{w}}_{\mathrm{k}}\right):=\sum _{i=1}^{m_1}{w}_{i,k}{r}_{i,k}=\sum _{i=1}^{m_1}{w}_{i,k}\sum _{i\mathrm{\text{'}}=1}^{m_2}{I}_{F_i>F_{i\mathrm{\text{'}}}}.$$

It is worth noting that applying weights to the Mann-Whitney style of ranks is not equivalent to applying weights to the Wilcoxon style of ranks, which are the ranks of observations in both samples. Under the assumption of interchangeability, it is easy to show that under $H_0$

$$\mathbb{E}\left({\mathrm{U}}_k\left({\mathbf{w}}_{\mathrm{k}}\right)\right)=\sum _{i=1}^{m_1}{w}_{i,k}\mathbb{E}\left(r_{i,k}\right)=\frac{m_1^{\mathrm{*}}{m}_2}{2},\hspace{0.17em}{m}_1^{\mathrm{*}}:=\sum _{i=1}^{m_1}{w}_{i,k}.$$

Here $m_1^{\mathrm{*}}$ can be considered as the effective sample size of the testing gene set. We also compute the variance of ${\mathrm{U}}_k\left({\mathbf{w}}_{\mathrm{k}}\right)$ under $H_0$ as

$$\mathrm{V}\mathrm{a}\mathrm{r}\left({\mathrm{U}}_k\left({\mathbf{w}}_{\mathrm{k}}\right),\mathrm{\rho }\right)=\frac{m_2}{2\pi }\left[c_1\right({\mathbf{w}}_k\left)\right(\frac{\pi }{2}+\left(m_2-1\right)\frac{\pi }{6})+c_2\left({\mathbf{w}}_k\right)\left(\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{s}\mathrm{i}\mathrm{n}\frac{\rho +1}{2}+(m_2-1)\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{s}\mathrm{i}\mathrm{n}\frac{\rho }{2}\right)],$$

where $\mathrm{\rho }$ is the inter-gene correlation; $c_1\left({\mathbf{w}}_k\right)$ and $c_2\left({\mathbf{w}}_k\right)$ are two constants depending on weights ${\mathbf{w}}_k$ only. More details can be found in Supplementary Material Section S3.

Because $F_i$ is signless (the larger $F_i$, the more significant), we apply a one-sided $t$-test based on the following standardized weighted rank sum statistic

$$T_k=\frac{{\mathrm{U}}_k\left({\mathbf{w}}_{\mathrm{k}}\right)-\mathbb{E}\left({\mathrm{U}}_k\right({\mathbf{w}}_{\mathrm{k}}\left)\right)}{\mathrm{V}\mathrm{a}\mathrm{r}({\mathrm{U}}_k({\mathbf{w}}_{\mathrm{k}}),\mathrm{\rho }{)}^{\frac{1}{2}}}.$$

Similar to CAMERA, we set the degrees of freedom of the $t$-distribution to $n-1$, to reflect the precision with which $\rho$ is estimated. Our test reduces to CAMERA’s MWU test when ${\mathbf{w}}_k\equiv \mathbf{1}$; which further reduces to the usual MWU test when $\mathrm{\rho }=0$.

As a summary, we illustrate the overall structure of FUNNEL-GSEA in Figure 1.

Fig. 1.

An illustration of the FUNNEL-GSEA analysis pipeline

2.4 Human influenza infection data

Gene expression data of human influenza infection (Huang et al., 2011; Woods et al., 2013) were downloaded from Gene Expression Omnibus (Edgar et al., 2002) series GSE52428. A total of 17 (9 symptomatic and 8 asymptomatic) subjects infected by influenza A H3N2/Wisconsin virus were studied. Whole transcriptome expression data had been sampled at 16 time points from one day before the infection till 5 days after the infection. Gene expressions were log2-transformed and filtered based on inter-quantile range (IQR ≥ 0.3). After non-specific filtering, ∼10 000 genes were reported for each subject. These gene expressions were standardized by the z-score transformation.

2.5 Simulations

Simulated data were generated by a linear mixed effect model with 16 time points (as in the real data) and 5000 genes with two (small and large) noise variance parameters. These genes were grouped into 90 synthesized pathways such that 3000 of them belong to a single pathway and the rest 2000 are shared by more than one pathway. 18 out of these 90 pathways were assigned with true signals generated from linear combinations of three designed signal patterns, to represent linear trend, sinusoid trend, and late (linear) response, respectively. We simulated cases with small and large variance. The simulation was repeated for 20 times for each case. Technical details of these simulated data, as well as some additional simulations based on biological signals and correlation structures more general than the interchangeable structure can be found in Supplementary Material Section S5.

3 Results

3.1 Large proportion of genes are shared by multiple gene sets

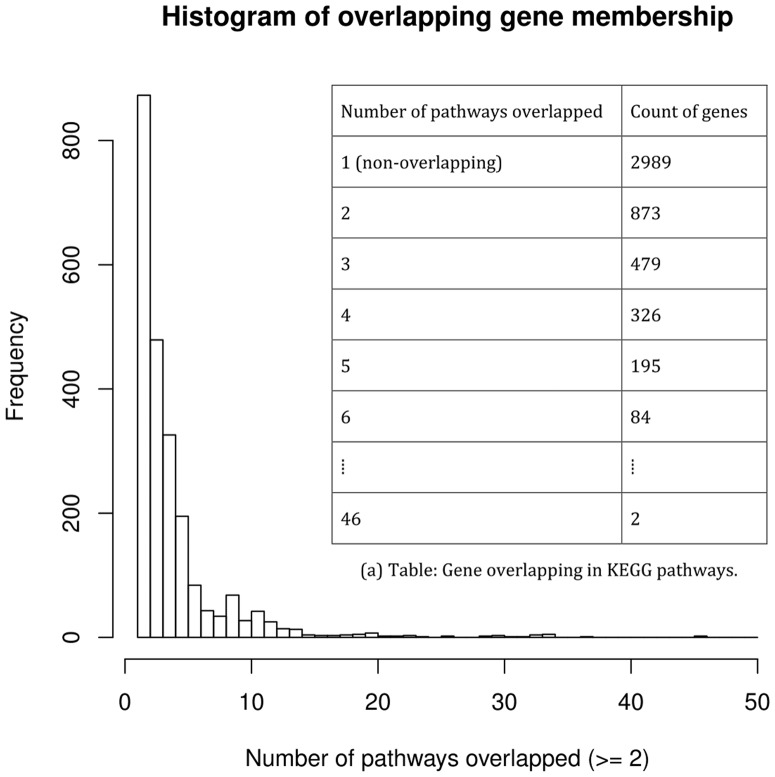
Functionally related genes in specific gene sets or pathways are static instances derived frequently by curation and recently by meta-analysis (Ruparelia et al., 2015; Tan et al., 2014). The overlap between these gene-sets is inevitable given modular topology of biological response. For example, NFkB related genes can be induced upon stimulation by several cytokines. However, exact instance of activation of NFkB regulated genes in a specific infection might not be derived by all the cytokines that can activate those genes. Specifically, we use 186 pathways from MSigDB (category CP:KEGG), which have 5267 unique genes. Among them, 2278 (or 43.3%) genes belong to two or more pathways; the two most-overlapped genes (MAPK1 and MAPK3) belong to 46 pathways (see Fig. 2 for more details).

Fig. 2.

Distribution of overlapping genes among KEGG pathways curated by MSigDB. Each bin in the histogram represents one row in Table (a). In total, 5267 unique genes pooled from 186 CP:KEGG pathways are used in this illustration. Among them, 2278 (or 43.3%) genes belong to two or more pathways; the two most-overlapped genes (MAPK1 and MAPK3) belong in 46 pathways

3.2 Estimating the empirical membership (weights) of overlapping genes

Given a gene associated with multiple gene sets, its context-specific activation could be indeed mediated by all the gene sets, only one of the gene sets, or none of the gene sets. Virtually all currently available gene set tests simply assume that the overlapping genes are activated by all gene sets to which they belong. This practice is equivalent to always assign ${\widehat{w}}_{i,k}=1$ for estimated weights and is henceforth called the naïve method. In order to evaluate weight assignment, we developed simulated data sets where the real membership of each gene to its gene-sets ($w_{i,k}$) is known using a linear mixed effect model (see Section 2 and Supplementary Material Section S5). The mean squared error (MSE) of the empirical membership (weights) estimated by FUNNEL averaged across 20 replications was 0.13 for the small variance simulations and 0.18 for the large variance simulations. Here ${\mathrm{M}\mathrm{S}\mathrm{E}}_{\mathrm{s}\mathrm{i}\mathrm{m}}$ for each simulation is defined as

where $N={\sum }_{i=1}^{2000}\left|{\mathcal{K}}_i\right|$, and $\mathrm{M}\mathrm{S}\mathrm{E}=\hspace{0.17em}{\sum }_{\mathrm{s}\mathrm{i}\mathrm{m}\hspace{0.17em}=\hspace{0.17em}1}^{20}{\mathrm{M}\mathrm{S}\mathrm{E}}_{\mathrm{s}\mathrm{i}\mathrm{m}}/20$ is averaged over 20 replications.

To put the accuracy of weight estimation in context, we took a closer look at genes that are shared by two pathways and compare the MSEs associated with FUNNEL with the naïve method. For the clarity of discussion, we consider binary weights (provide MSE at binary level) and dichotomize the estimated weights to be zero if ${\widehat{w}}_{i,k}<0.2$ and one if ${\widehat{w}}_{i,k}\ge 0.2$. The results for the small variance case are listed as follows (see Supplementary Tables S1 and S2 for the large variance case).

• Case I. On average (over 20 repetitions), 495.9 genes belong to two insignificant gene sets that do not carry any true temporal signals (true weight $w_{i,k}$ = (0,0)). FUNNEL correctly assigned zero weights 82% of times (MSE_FUNNEL = 0.18 and MSE_naïve = 1).

• Case II. On average, 267.75 genes belong to one significant and one insignificant pathways (true weights $w_{i,k}$ = (0,1) or (1,0)). FUNNEL assigned the correct weights 83% of times (MSE_FUNNEL = 0.17 and MSE_naïve = 0.5).

• Case III. On average, 13.35 genes belong to two significant gene sets. Because the true weight are in continuous scale, we only report the MSE for the continuous estimates for this case: MSE_FUNNEL = 0.20 and MSE_naïve = 0.26.

In summary, FUNNEL was able to estimate the true weights better than the naïve method in all cases.

3.3 Performance of gene set tests in simulation studies

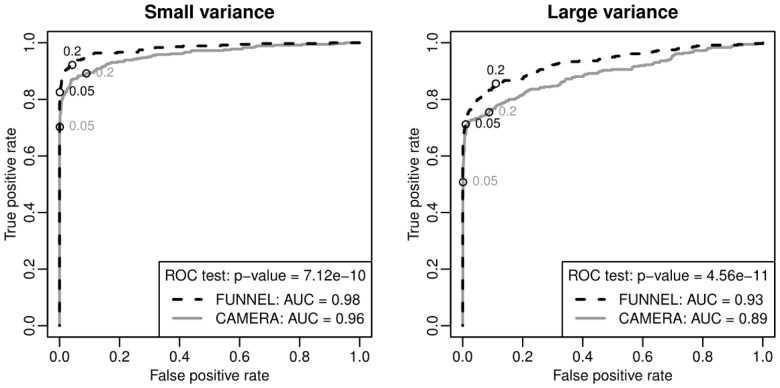
Once weights are estimated, we apply the weighted MWU test with correlation (see Section 2) to test the significance of 90 synthesized pathways. Table 1 summarizes the statistical power and type I error for FUNNEL and CAMERA for both small and large variance cases. We find that FUNNEL always has better statistical power than CAMERA. Next, we conduct receiver operating characteristic (ROC) analyses for both methods. Figure 3 shows that the ROC curves of FUNNEL dominate that of CAMERA uniformly. In both small and large variance cases, the area under the ROC curve (AUC) of FUNNEL is larger than that of CAMERA, and such differences are significant based on a non-parametric AUC test (DeLong et al., 1988).

Table 1.

Mean (STD) of statistical power and type I error at 5% significance level for FUNNEL and CAMERA in 20 replicates of simulation

		Small variance	Large variance
FUNNEL	Power	0.825 (0.049)	0.714 (0.049)
	Type I error	0.001 (0.003)	0.010 (0.013)
CAMERA	Power	0.703 (0.049)	0.508 (0.101)
	Type I error	0.001 (0.003)	0.001 (0.004)

Fig. 3.

ROC curves of FUNNEL (black, dashed) and CAMERA (grey, solid) for different signal to noise levels. ROC curves were plotted for small (left) and large (right) variances in the noise level of the simulated data (see Section 2 for the details). ROC curve of FUNNEL dominates that of CAMERA in both cases. The differences of AUC in both cases are highly significant based on the AUC test

Next, we compare the performance of TcGSA on the same set of simulation data. Unlike FUNNEL or CAMERA, TcGSA is a self-contained gene set test; so the comparison is only exploratory. Out of the 90 synthesized pathways, TcGSA identifies all of them being significant, irrespective of whether the pathways have true signal or not. The potential reasons for such poor performance may include technical failures [such as convergence problem in the likelihood model and size limitation of gene set, which is documented in (Hejblum et al., 2015)], and the ignorance of overlapping among pathways.

3.4 Analyses of time-course H3N2 infection data

The time-course gene expression data used in our study were collected from 9 symptomatic and 8 asymptomatic subjects infected by influenza A H3N2/Wisconsin virus (see Section 2). We apply FUNNEL and CAMERA to test the significance of 186 KEGG-derived pathways provided by MSigDB for each subject. We use functional $F$-statistic as the gene-level summary statistic for both procedures. For CAMERA, gene-set-level inference is made by the Wilcoxon rank sum test with adjustment for correlation. We use the same correlation estimates and the degrees of freedom in both FUNNEL and CAMERA (see Supplementary Material Section S4). The resulting subject-level $P$-values are combined by Fisher’s combined probability test (Fisher, 1963) for each (symptomatic and asymptomatic) group. After applying Bonferroni procedure to control for the familywise error rate (FWER) at 0.05 level, FUNNEL is able to identify 32 significant pathways from the symptomatic group (n = 9) which include pathogen recognition receptor signaling pathways such as the Cytosolic DNA sensing, NOD-like receptor signaling, RIG-I-like receptor signaling, and Toll-like receptor signaling pathways. Adaptive immune response related pathways such as the B cell receptor signaling and T cell receptor signaling pathways are also significant. All of the above pathways are significant in 6 or more (≥67%) number of symptomatic subjects. For the asymptomatic group (n = 8), FUNNEL identifies 22 significant pathways, including the B cell receptor signaling, Antigen processing and presentation, and Ribosome pathways. Fewer subjects (≤50%) in the asymptomatic group show activation of the above pathways. We present a heatmap of -log10-transformed $P$-values for the 32 significant pathways selected from the symptomatic subjects in Figure 4. In contrast, CAMERA only identifies four pathways with very general biological functions (the Glutathione metabolism, Ribosome, Proteasome and Primary immunodeficiency pathways) for the symptomatic group and seven (the Oxidative phosphorylation, Ribosome, Spliceosome, Proteasome, Protein export, B cell receptor signaling and Parkinsons disease pathways) for the asymptomatic group. We also list top 30 most significant (ranked by adjusted P-values) pathways selected by CAMERA for the symptomatic group in Supplementary Material Section S7 for a more holistic comparison. In conclusion, FUNNEL has improved sensitivity to identify relevant pathways than CAMERA.

Fig. 4.

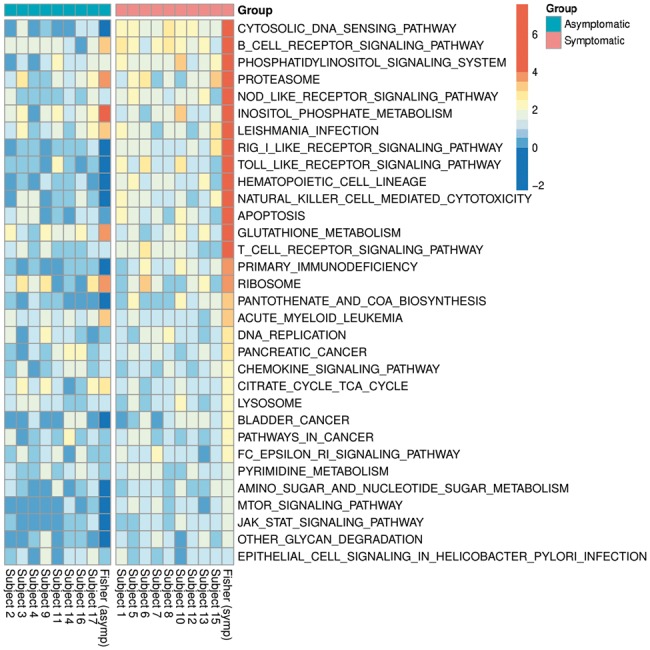
A Heatmap of -log10-transformed P-values for all 32 significant CP:KEGG pathways selected by FUNNEL (ordered by adjusted Fisher’s P-values for the symptomatic group). The P-values computed from individual subjects were combined by Fisher’s combined probability test in each group. Bonferroni procedure for multiple testing adjustment was applied to the combined Fisher’s P-values to control for FWER. Many of these pathways listed here, such as the B-, T-cell receptor signaling, NOD-like signaling, RIG-like receptor signaling, Toll-like receptor signaling, Chemokine signaling, JAK-STAT signaling, FC-Epsilon-RI signaling, MTOR signaling pathways are well documented immune signaling pathways that send signals that lead to the activation of various cell-specific immune activities (Color version of this figure is available at Bioinformatics online.)

Next, we applied TcGSA to the real data. Out of 186 pathways tested, 23 (12%) have problematic pathway size as reported by TcGSA and another 74 (40%) fail to converge. For the symptomatic group, 139 pathways (many with the above technical issues) are significant after controlling for FDR at 0.05 level by the Benjamini-Yekutieli procedure implemented in TcGSA.

3.5 The utility of estimated empirical memberships

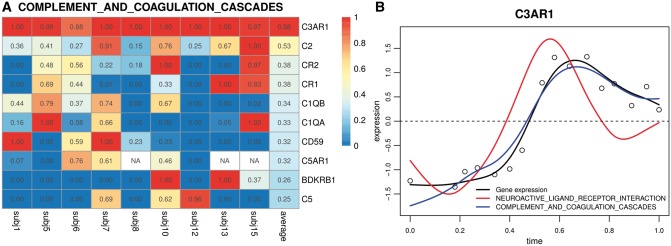
We illustrate the utility of the empirical memberships (weights) estimated from penalized functional linear regression in Figure 5. Shown in Figure 5A are the color-coded empirical memberships of top 10 overlapping genes with the largest average weights in the Complement and coagulation cascades pathway, estimated from nine symptomatic subjects. We can see that C3AR1 is assigned to Complement and coagulation cascades pathway almost exclusively for all subjects. According to MSigDB, C3AR1 can potentially be assigned to two pathways: the Neuroactive ligand-receptor interaction and Complement and coagulation cascades pathway. We found that the temporal pattern of C3AR1 resembles the Complement and coagulation cascades pathway most closely (Fig. 5B). This empirical evidence suggests that while C3AR1 can potentially be activated by diseases related to neuro-active ligand receptors such as thyroid hormone resistance syndrome (Cheng, 2005) and woolly hair (Shimomura et al., 2008, 2009, 2010), it is exclusively activated by the Complement and coagulation cascades pathway for the specific biological condition (H3N2/Wisconsin influenza infection) of the study.

Fig. 5.

(A) Estimated weights. Empirical memberships (weights) of genes in the Complement and coagulation cascades pathway estimated from applying the penalized functional linear regression analysis to all symptomatic subjects. 10 overlapping genes with the largest average estimated weights are shown in this figure. NA cells are due to genes being removed by the non-specific filtering criterion (IQR < 0.3). (B) Temporal expression pattern of C3AR1 (black circles/curve) from Subject 7. This gene belongs to two CP:KEGG pathways: the Neuroactive ligand-receptor interaction (red curve) and Complement and coagulation cascades (blue curve) (Color version of this figure is available at Bioinformatics online.)

4 Discussion

Time-series gene expression data have gained popularity in recent years due to their application in the translation studies. Identifying early changes in the gene-expression that are predictive of future responses to the diseases, infections or vaccinations can be predicted by applying advanced mathematical modeling tools such as high-dimensional differential equations (Lu et al., 2011; Qiu et al., 2015a; Wu et al., 2013, 2014), dynamic Bayesian network (Perrin et al., 2003; Zou and Conzen, 2005), or Granger’s model (Lozano et al., 2009; Shojaie and Michailidis, 2010) to study the dynamic and causal relationship between genes based on changes of expressions over many time points. Unlike group comparisons, advanced inferential tools such as non-parametric regression (Müller, 2012) and functional data analysis are required to detect biological signals presented in the form of non-linear temporal trends of gene expression profiles most efficiently. Only a handful gene set analysis methods are designed to detect arbitrary non-linear temporal trend at this moment and there are much room for improvement. For example, TcGSA (Hejblum et al., 2015) has an option to use either cubic polynomials or natural cubic splines to model non-linear temporal trends. However, TcGSA assumes the same trend among all genes in a set, which is unrealistic in many situations. PCA-maSigFun, developed by Nueda et al. (Nueda et al., 2009), does have the ability to account for possible heterogeneity inside a gene set; but its use of standard PCA and linear regression is suboptimal for time-course data with complex non-linear patterns. On the other hand, CAMERA (Wu and Smyth, 2012) is a generic GSEA framework that can be used in time-course gene expression analysis as well. CAMERA adjusts for inter-gene correlation in the gene-set-level inference; is more efficient than procedures based on permuting samples; and is more flexible and robust than approaches based on estimating or approximating the correlation matrix (Nam, 2010; Wang et al., 2008, 2009a). That being said, CAMERA’s performance depends largely on the efficiency of the summary statistics used to capture temporal trends. In FUNNEL-GSEA, we use functional PCA to capture arbitrary and possibly heterogeneous non-linear trends within gene sets, which is known to be more efficient than competing methods such as splines (Sohn et al., 2009; Storey et al., 2005).

Although our method is designed with a focus on subject-specific analyses; group-level results can be obtained by a suitable meta-analysis method. We choose to combine individual P-values by Fisher’s combined probability test in this study because it allows the detection of gene sets that are activated by influenza infection with subject-specific expression patterns, which is more flexible than those competing approaches that depend on detecting common expression patterns across all subjects. This approach also enables us to study the heterogeneity of subject-level responses, e.g. in Figures 4 and 5A. Although Fisher’s combined probability test is arguably the most widely used meta-analysis procedure, we will explore other meta-analysis options that have better protection against type I error in the future.

GSEA facilitates comparisons across independent studies performed on different platforms and techniques by assembling gene-sets from available data-sets in the public repositories. The problem of overlapping gene-sets is exacerbated when these data are obtained under different experimental conditions. For example, C3AR1 is a protein coding gene that could be assigned to the Neuroactive ligand-receptor interaction and Complement and coagulation cascades pathway; yet within the context of influenza viral infection, empirical evidences show that it is almost entirely driven by the Complement and coagulation cascades pathway. To our best knowledge, no currently available GSEA methods has the ability to assign conditional pathway memberships to overlapping genes like C3AR1, and they simply count the summary statistics of overlapping genes in all gene sets to which they may belong in gene-set analyses. This naïve practice can inflate type I error if overlapping genes are signal-carrying genes assigned to irrelevant pathways, and/or reduce statistical power when many irrelevant null genes are assigned to an informative pathway. FUNNEL-GSEA assigns weights (empirical pathway membership) of overlapping genes based on penalized functional linear regression that reflects the functional similarities between overlapping genes and the gene sets they belong to. Such empirical memberships are more specific and relevant to the experimental conditions than generic associations provided by public databases. Furthermore, we require weights pertain to one gene to sum up to one; so that this gene is not over-counted in gene-set-level analyses.

We also want to discuss the applicability of functional data analysis, which is designed for continuous data, to RNA-seq-based expression data (Garber et al., 2011; Mortazavi et al., 2008; Wang et al., 2009b). Unprocessed RNA-seq reads are discrete random variables that are commonly represented by the negative binomial model (Anders and Huber, 2010; Hardcastle and Kelly, 2010; Robinson et al., 2010) or NBP model (Di et al., 2011). Several recent studies (Law et al., 2014; Rapaport et al., 2013; Ritchie et al., 2015) show that pre-processing techniques such as non-specific filtering, normalization, and log transformation can greatly reduce the granularity of raw reads so that analytic tools designed for continuous high-throughput data have comparable or even better performance on these data as compared with specialized tools based on discrete models. We believe this is largely due to the removing of genes with very low reads in modern gene expression analysis pipelines such as DESeq2 (Love et al., 2014) and LIMMA (Smyth, 2005). The remaining genes have large numbers of reads that can be well approximated by continuous distributions such as the normal distribution (after log2 transformation). In the future, we plan to extend FUNNEL-GSEA so that it has an option to use summary statistics that are designed for discrete time-course models to summarize gene-level information; then use standard PCA and linear regression to assign weights for overlapping genes. Such an extension may be more suitable for un-normalized and un-filtered time-course RNA-seq data.

Funding

This work is supported in part by Respiratory Pathogens Research Center (NIAID contract number HSN272201200005C), the University of Rochester Center for AIDS Research (NIH 5 P30 AI078498-08), the University of Rochester CTSA award number UL1 TR002001 from the National Center for Advancing Translational Sciences of the National Institutes of Health and PhRMA informatics research starter award.

Conflict of Interest: none declared.