Comprehensive Morpho-Electrotonic Analysis Shows 2 Distinct Classes of L2 and L3 Pyramidal Neurons in Human Temporal Cortex

Abstract

There have been few quantitative characterizations of the morphological, biophysical, and cable properties of neurons in the human neocortex. We employed feature-based statistical methods on a rare data set of 60 3D reconstructed pyramidal neurons from L2 and L3 in the human temporal cortex (HL2/L3 PCs) removed after brain surgery. Of these cells, 25 neurons were also characterized physiologically. Thirty-two morphological features were analyzed (e.g., dendritic surface area, 36 333 ± 18 157 μm²; number of basal trees, 5.55 ± 1.47; dendritic diameter, 0.76 ± 0.28 μm). Eighteen features showed a significant gradual increase with depth from the pia (e.g., dendritic length and soma radius). The other features showed weak or no correlation with depth (e.g., dendritic diameter). The basal dendritic terminals in HL2/L3 PCs are particularly elongated, enabling multiple nonlinear processing units in these dendrites. Unlike the morphological features, the active biophysical features (e.g., spike shapes and rates) and passive/cable features (e.g., somatic input resistance, 47.68 ± 15.26 MΩ, membrane time constant, 12.03 ± 1.79 ms, average dendritic cable length, 0.99 ± 0.24) were depth-independent. A novel descriptor for apical dendritic topology yielded 2 distinct classes, termed hereby as “slim-tufted” and “profuse-tufted” HL2/L3 PCs; the latter class tends to fire at higher rates. Thus, our morpho-electrotonic analysis shows 2 distinct classes of HL2/L3 PCs.

Introduction

The temporal cortex is considered to have important cognitive functions (Mirz et al. 1999; Fortier et al. 2011). In humans, the temporal neocortex is especially thick (2773 μm) compared with monkeys (2300 μm) or rodents (969 μm) (see Mohan et al. 2015, and DeFelipe et al. 2002). Layers 2 and 3 (L2/L3) which receive input from Layer 4 and send their output to Layer 5/6, are considered to play a key role in intrinsic cortical computation (Callaway 2004; Douglas and Martin 2004; Feldmeyer 2012; Constantinople and Bruno 2013; Li et al. 2014). In the human temporal cortex, L2/L3 was found to be particularly thick (949 ± 179 μm, Mohan et al. 2015), which implies that it might endow the human neocortex with enhanced computational capabilities. The major building block of L2/L3 are the pyramidal cells, which in rodents consist of at least 70–80% of its total number of cells (Nieuwenhuys 1994).

L2/L3 pyramidal neurons from the human temporal cortex (HL2/L3 PCs) possess several unique features. Recent fine-scale anatomical studies on these neurons have demonstrated that they are large, in terms of total dendritic length and number of dendritic branches (Mohan et al. 2015). The dendrites of these cells are decorated with a large number of dendritic spines (~25 000–30 000 spines per neuron, Benavides-Piccione et al. 2013; DeFelipe et al. 2002; Defelipe 2011). Dendritic spines are the main targets for excitatory synapses; their large number per neuron implies that L2/L3 pyramidal neurons in humans are part of a densely connected network. In addition, dendritic spines are key elements in memory and learning processes (Yuste 2010), suggesting that L2/L3 neurons and the networks that they form are endowed with enhanced memory capacity.

What are the biophysical characteristics of L2/L3 pyramidal neurons from the human temporal cortex? To answer this question, experiments on living human brain tissue are needed; however, this kind of tissue is only available in a few laboratories worldwide and is obtained after brain surgery. Thus, there is scant information about the biophysical properties of human neocortical neurons (Inda et al. 2006; Köhling and Avoli 2006; Szabadics et al. 2006; Molnár et al. 2008; Verhoog et al. 2013; Testa-silva et al. 2014; Tian et al. 2014; Varga et al. 2015; Wang et al. 2016). Recently, our team demonstrated that HL2/L3 PCs have distinctive biophysical features (Eyal et al. 2016) including the fact that their specific membrane capacitance, C_m is ~0.5 μF/cm², half the conventional value (1 μF/cm²). We showed that such C_m values have important implications for signal transfer and information processing at both the neuron and the network level. However, unlike in rodents (Mason and Larkman 1990; Elston et al. 2001; Marx and Feldmeyer 2013; Staiger et al. 2014; Qi et al. 2015; Van Aerde and Feldmeyer 2015), very little is known either about the morphology or the physiology of human cortical pyramidal neurons (Elston et al. 2001, 2005; Fernandez-Gonzalez et al. 2017).

Here, we employed our recently developed feature-based characterization scheme to demonstrate that morphologically, many features of HL2/L3 PCs show a gradual depth dependency (such as a gradual increase with depth in the total dendritic surface area, the number of branches and horizontal field span). Using a novel topological method (Kanari et al. 2016, 2017), we found that HL2/L3 PCs fall into 2 distinct classes we dub “slim-tufted” and “profuse-tufted” HL2/L3 PCs. These 2 morphological types are also distinctive in their I/F relationship. Moreover, HL2/L3 PCs express a prominent “sag” in response to hyperpolarizing currents, possibly suggesting that these cells express hyperpolarization-activated cyclic nucleotide-gated (HCN) channels (Magee 1998). We also found that the mean cable length of human neurons is independent of depth, in contrast to the physical mean length. Interestingly, we found a subpopulation of deep neurons that have large diameters and large R_m values, both of which compensate for their long dendrites. We discuss the functional implications of our results and compare our results to those obtained for L2/L3 pyramidal neurons in rodents.

Materials and Methods

Electrical Recordings of Human L2/L3 Pyramidal Cells (Acute Living Slices)

All procedures on human tissue were performed with the approval of the Medical Ethical Committee (METc) of the VU University Medical Centre (VUmc), with written informed consent by patients involved to use brain tissue removed for the treatment of their disease for scientific research, and in accordance with Dutch license procedures and the declaration of Helsinki (VUmc METc approval “kenmerk 2012/362”). Slices of human temporal cortex were cut from neocortical tissue that had to be removed to enable the surgical treatment of deeper brain structures for epilepsy or tumors. In all patients (20–57 years of age), the resected neocortical tissue was located outside the epileptic focus or tumor, and displayed no structural/functional abnormalities in preoperative MRI investigations. After resection, the neocortical tissue was placed within 30 s in ice-cold artificial cerebrospinal fluid (aCSF) slicing solution which contained in (mM): 110 choline chloride, 26 NaHCO3, 10 D-glucose, 11.6 sodium ascorbate, 7 MgCl₂, 3.1 sodium pyruvate, 2.5 KCl, 1.25 NaH₂PO₄, and 0.5 CaCl₂—300 mOsm, saturated with carbogen gas (95% O₂/5% CO₂) and transported to the neurophysiology laboratory, which is located 500 m from the operating room. The transition time between resection of the tissue and the start of preparing slices was less than 15 min. Neocortical slices (350–400 μm thickness) were prepared in ice-cold slicing solution, and were then transferred to holding chambers filled with aCSF containing (in mM): 126 NaCl; 3 KCl; 1 NaH₂PO₄; 1 MgSO₄; 2 CaCl₂; 26 NaHCO₃; 10 glucose—300 mOsm, bubbled with carbogen gas (95% O₂/5% CO₂). Here, slices were stored for 20 min at 34 °C, and for at least 30 min at room temperature before recording. Whole-cell, patch clamp electrophysiology recordings were then made from human L2/L3 pyramidal neurons as described previously (Verhoog et al. 2013; Testa-silva et al. 2014). In short, we used standard, uncoated borosilicate glass pipettes (glass thickness 0.64 mm) with fire-polished tips (4.0–6.0 MΩ resistance) filled with intracellular solution containing (mM): 110 K-gluconate; 10 KCl; 10 HEPES; 10 K₂ Phosphocreatine; 4 ATP-Mg; 0.4 GTP, biocytin 5 mg mL⁻¹ (pH adjusted with KOH to 7.3; 280–290 mOsm). Recordings were made using a MultiClamp 700B amplifier (Axon Instruments), sampling at 10–50 kHz and low-pass filtering at 3–30 kHz. Recordings were digitized with an Axon Digidata 1440A and acquired using pClamp software (Axon). Recording aCSF was the same solution as the aCSF in which slices were stored. Recording temperature was 32–35 °C.

3D Reconstructions of Human and Mouse L2/L3 Pyramidal Cells (Acute Living Slices)

Sixty morphologies of human L2/L3 cells, residing at depths of 409–1192 μm below the pia, and 14 morphologies of mouse L2/L3 cells from depths of 222–493 μm were reconstructed in 3D using Neurolucida software (Microbrightfield), using a 100× oil objective (1.4 N.A.). Dendritic diameters were incorporated into the morphological reconstruction using Neurolucida (Microbrightfield) by manually setting the diameter of the line segments during reconstruction of the biocytin-filled neurons. Reconstructions were standardized for both human and mouse reconstructions. The value for dendritic diameter was subsequently extracted for individual segments from the digital files. Dendritic segments are assumed to be truncated cones, with initial and end diameters. The surface area is the area of this dendritic cone, not including the end caps. Additional details regarding the reconstruction methods can be found in Mohan et al. (2015).

For a subset of neurons used in this study, the axons were also reconstructed (Mohan et al. 2015); these axons were not included in the analysis performed in the present study.

In this work, dendritic spines were only considered when building cable models of human neurons (Figs 6 and 7). In these models, the spine membrane area was incorporated globally using the F factor as in Rapp et al. (1992) (and for human neurons, as in Eyal et al. 2016). In this work, Eyal et al. computed the F factor to be 1.9, based on detailed data from human cingulate cortex and human temporal cortex (Benavides-Piccione et al. 2013). These data are based on 2 post-mortem samples from 2 human males (aged 40 and 85) in which the neurons and dendritic spines were reconstructed in 3D using high-resolution confocal microscopy. To the best of our knowledge, this is the most accurate data about human spines in neocortical pyramidal cells available today. However, we do not yet know whether the density and the size of dendritic spines in human neurons are depth-dependent or if there is any difference in spine density between slim-tufted and profuse-tufted neurons. Thus, for the modeling part of this work, we used F = 1.9 for all of our neuron models.

Figure 6.

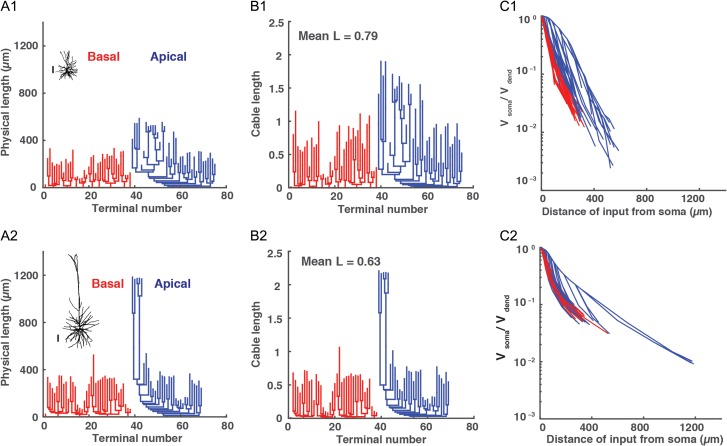
Physical and electrotonic dendritic structure of superficial versus deep HL2/L3 PCs. (A1 and A2) Morphology and dendrogram, in physical units, of HL2/L3 superficial (471 μm from pia, cell #2 in Fig. 1) and deep (1148 μm from pia, cell #54 in Fig. 1) exemplar neurons, respectively. Red denotes basal tree and blue the apical tree. Scale bar is 100 μm for both neurons. (B1 and B2) Dendrogram, in cable units, for the neurons in A1 and A2, respectively. These dendograms were calculated assuming R_i = 200 Ωcm, C_m = 0.5 μF/cm² whereas τ_m was extracted for each cell from its experimental transients (Fig. 5B, inset). (C1 and C2). Steady voltage attenuation factor from the dendrites (V_dend) to the soma (V_soma) for the neurons in A1 and A2, respectively.

Figure 7.

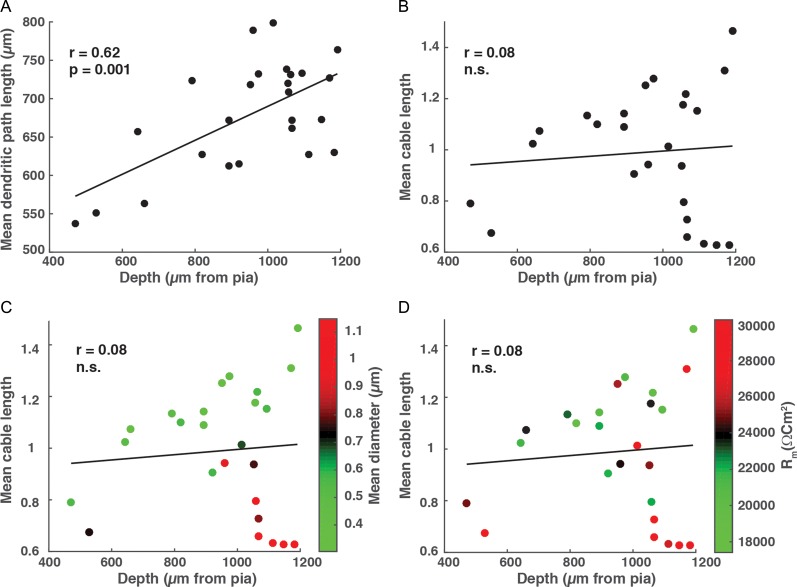
Physical and electronic length of HL2/L3 PCs. (A) The mean physical length of all dendritic paths as a function of depth. (B) The mean cable length of all paths as a function of depth; this length was calculated assuming R_i = 200 Ωcm, C_m = 0.5 μF/cm² whereas τ_m was extracted for each cell from its experimental transients (Fig. 5B, inset). (C) Same as in B, but neurons are colored according to their mean diameter. Note the group of deep cells with large diameters (red circles). (D) Same as in B but neurons are colored according to their respective R_m values. Note the deep cells with large R_m (red circles).

Morphological Features

The 32 morphological features used for the present study are listed in Table 2. These features are the natural ones to consider when characterizing dendritic morphologies. These 32 features were extracted for each of the 60 human and 14 mouse L2/L3 pyramidal neurons in our database using both the Pneumatk and NeuroM packages in Python developed by the Blue Brain Project (Juan Palacios, Lida Kanari, Eleftherios Zisis, Mike Gevaert). NeuronM is available in https://github.com/BlueBrain/NeuroM.

Table 2.

The 32 features used for the morphological analysis

Feature number	Feature description
1	Maximal radial distance of apical tree from soma (μm)
2	Maximal path length of apical tree from soma (μm)
3	Vertical field span of apical tree (μm)
4	Total length of apical tree (μm)
5	Maximal branch order in apical tree
6	Number of branches in apical tree
7	Mean length of nonterminal apical branches (branches between 2 consecutive bifurcations) (μm)
8	Horizontal field span of apical tree (μm)
9	Total surface area of apical tree (μm2)
10	Total volume of apical tree (μm3)
11	Trunk diameter of apical tree (μm)
12	Mean length of terminal apical branches (branches between final bifurcation and dendritic termination) (μm)
13	Mean diameter of apical tree (μm)
14	Ratio between the horizontal and vertical field span of apical tree
15	Density of apical tree—ratio between the volumes of the apical tree and of a rectangular cuboid surrounding it
16	Total length of basal tree (μm)
17	Number of branches in basal tree
18	Maximal radial distance of basal tree from soma (μm)
19	Mean trunk diameter of basal tree (μm)
20	Total surface area of basal tree (μm2)
21	Maximal path length of basal tree from soma (μm)
22	Horizontal field span of basal tree (μm)
23	Total volume of basal tree (μm3)
24	Mean length of terminal basal branches (branches between final bifurcation and dendritic termination) (μm)
25	Maximal branch order in basal tree
26	Number of basal trees
27	Vertical field span of basal tree (μm)
28	Density of basal tree—ratio between the volumes of the basal tree and of a rectangular cuboid surrounding it
29	Ratio between the horizontal and vertical field span of basal tree
30	Mean diameter of basal tree (μm)
31	Mean length of nonterminal basal branches (branches between 2 consecutive bifurcations) (μm)
32	Mean soma radius (μm)

Features related to the apical tree are numbered 1–15; features related to the basal tree are numbered 16–31 and Feature 32 is related to the soma. Radial distance (Feature #1, Feature #18) is the Euclidean distance from the soma to each section terminal. The total length (Feature #4, Feature #16) is the sum of all the section lengths of the neurite. The path length (Feature #2, Feature #21) is the length of the path from a terminal to the soma. The center of the soma is defined as the mean of all the soma points. The mean radius of the soma is defined as the mean distance of all the soma points from the center. For further documentation see https://github.com/BlueBrain/NeuroM.

Extraction of Biophysical Features

Electrical features were extracted from voltage responses to long hyperpolarizing and depolarizing somatic current injections of various amplitudes (Table 3). Features 1–8 were extracted from the responses to 150% supra-threshold depolarizing current. Spikes were detected by a crossing of a voltage threshold (0 mV). We defined the beginning of the spike by detecting the maximum of the second derivative in the rising phase of the spike. The end of the spike was defined as the minimum voltage following the spike. The following features were defined:

1. Mean AP amplitude: Mean amplitude of the set of spikes that occurred during the current step. The amplitude of a spike was defined as the difference between the voltage at the beginning and the peak of the spike.

2. Mean AP half-width: Mean half-width of the set of spikes that occurred during the current step. The half-width of a spike was defined as the amount of time from the first crossing (in the upward direction) of the half-height voltage value to the second crossing (in the downward direction) of this value. The half-height voltage is the voltage at the beginning of the spike plus half the spike amplitude.

3. Mean AP rise time: The mean rise time of the set of spikes that occurred during the current step. The rise time was defined as the amount of time from the beginning to the peak of the spike.

4. Mean AHP (after-hyperpolarization) depth: The mean AHP depth of the set of spikes that occurred during the current step. The AHP depth (relative to rest) was defined as the difference between the voltage at the end of the spike and the resting membrane potential.

5. First spike latency: The amount of time from the current onset to the peak of the spike.

6. Spike frequency: The firing rate of the neuron during the current step.

7. ISI-CV: Coefficient of variation (standard deviation divided by the mean) of the distribution of ISIs (inter-spike interval).

8. Mean ISI: The mean of the distribution of ISIs.

9. Threshold current for spike generation: The minimal current that elicited a spike.

10. Membrane time constant, τ_m: This is estimated through exponential fit to the recovery of the voltage response following a step hyperpolarizing current (Fig. 5B, inset). To capture the slowest (membrane) time constant, the exponential fit to the voltage trace was calculated after a delay of 10 ms from the start of voltage recovery. The fitted time constant should be considered as the “effective membrane time constant” as an active I_h current might be involved in this estimate (Fig. 5B).

11. Input resistance, R_N: estimated by the linear fit of the I/V curve.

12. Sag ratio: defined as: $100\left(\frac{V_{\mathrm{ss}}-V_{\min }}{V_{\mathrm{rmp}}-V_{\min }}\right)$, where $V_{\mathrm{ss}}$ is the voltage at steady-state, $V_{\min }$ is the minimum value reached after the beginning of the current injection and $V_{\mathrm{rmp}}$ is the voltage at the resting membrane potential.

Table 3.

The 14 features used for the biophysical and cable analysis with their corresponding values

Feature number	Feature description	Mean	SD
1	Mean AP amplitude at 150% threshold current (mV)	85.09	5.24
2	Mean AP half-width at 150% threshold current (ms)	1.26	0.42
3	Mean AP rise time at 150% threshold current (ms)	0.76	0.15
4	Mean AHP depth relative to rest at 150% threshold current (mV)	15.39	3.63
5	First spike latency at 150% threshold current (ms)	28.85	12.29
6	Spike frequency at 150% threshold current (Hz)	12.72	5.62
7	ISI-CV at 150% threshold current	0.37	0.22
8	Mean ISI 150% threshold current (ms)	94.64	48.67
9	Threshold current (Ithresh) for spike generation (pA)	267.20	118.52
10	Membrane time constant, τm (ms)	12.03	1.79
11	Input resistance, RN (MΩ)	47.68	15.26
12	Sag ratio (%)	16.60	8.16
13	Resting membrane potential (mV)	−85.1	3.19
14	Mean cable length, L	0.99	0.24

Neurons analyzed are marked in asterisks in Figure 1. Features related to AP shape are numbered 1–4; features related to AP firing are numbered 5–9. Feature #14 is analyzed separately in the cable analysis section. See “Materials and Methods” section for further details.

Figure 5.

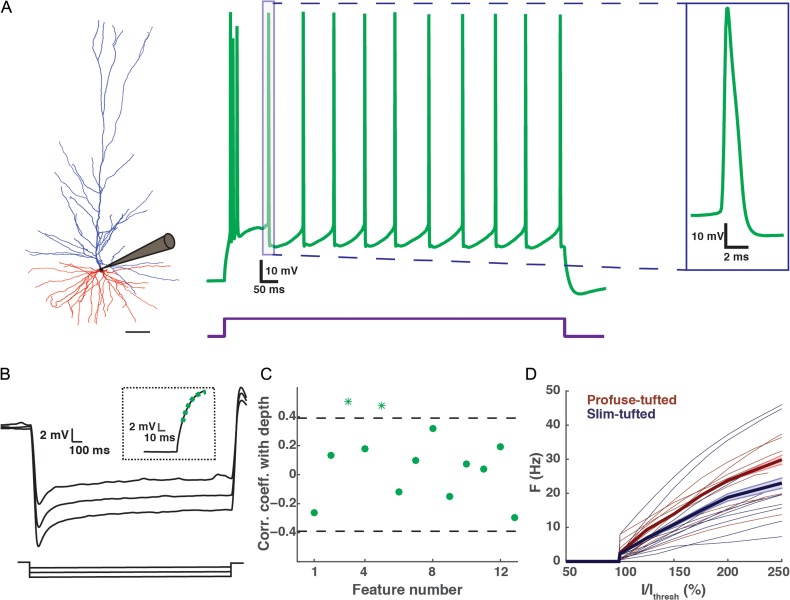
Biophysical features of HL2/L3 PCs. (A) Left, a 3D reconstructed exemplar HL2/L3 cell (1063 μm from pia, cell #44 in Fig. 1). Scale bar is 100 μm. Middle, voltage response to a depolarizing step current for the cell at left. The current step (450 pA) was 150% larger than the threshold current. Right, zoom-in into an individual spike (demarcated by box in middle trace). (B) Voltage responses to hyperpolarizing step currents of −250, −200, −150 pA for cell #59 shown in Figure 1. Inset shows the exponential fit (green dashed line) to the voltage response (black line) following the termination of the −250 pA current step. This fit was used to estimate the membrane time constant, τ_m (see “Materials and Methods” section). (C) Correlation coefficient with depth for 13 biophysical features (Table 3). Features with a significant correlation coefficient (P < 0.05) are marked with an asterisk (outside of the dashed lines). Most biophysical features are depth-independent. (D) Normalized I/F curves for the profuse-tufted (dark red) and slim-tufted (dark blue) pyramidal cells. The thicker lines are the mean of each class respectively; the shaded area is the respective standard error. Note that the profuse class tends to fire at higher rates. Normalization is to the minimal current (I_thresh) that generated a spike.

Software

Analysis was carried out by custom software programmed in Matlab. The electrotonic dendrograms in Figure 6B1,B2 and the scaled mouse neuron in Figure 8D were constructed using the TREES toolbox (Cuntz et al. 2010), and the compartmental modeling simulations of 3D reconstructed neurons shown in Figure 6C1,C2 were run using NEURON 7.4 (Carnevale and Hines 2006).

Figure 8.

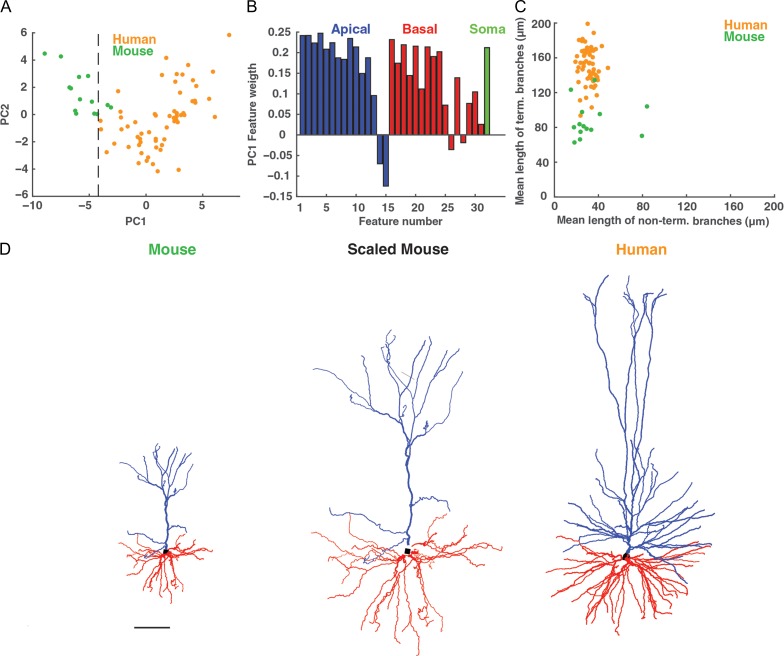
Human versus mouse L2/L3 pyramidal cells from the temporal cortex. (A) PCA of morphological features of human (n = 60, orange) as well as mouse (n = 14, green) cells; the first principal component (PC1) and the second principal component (PC2) are based on the 32 morphological features for human and mouse cells combined (Table 2). Black dashed line separates the 2 cell populations well. (B) The weight of the contribution of each of the 32 features to the first principal component. Apical dendrite features are marked in blue, basal dendrite features in red and the somatic feature in green. (C) Plot of the nonterminal branches versus the terminal branches of the basal tree for human (orange) and mouse (green) neurons. Note the distinctly elongated terminal branches in human neurons. (D) Visual comparison of original exemplar mouse neuron (left), whose dendritic branches are stretched by a factor of 2 (middle), and an original human (right) L2/L3 exemplar pyramidal neuron (cell #41 in Fig. 1). Scale bar 100 μm.

Data Analysis and Statistics

Principal component analysis

Principal component analysis (PCA; Duda et al. 2001) was used to determine the prominent components of the variability in the data by calculating the eigenvectors of the covariance matrix.

Statistical Tests

To calculate the correlation between features and depth we used the Pearson correlation coefficient. To correct for multiple correlations the Benjamini & Hochberg procedure (Benjamini and Hochberg 1995) was used to control for the false discovery rate (FDR) of a family of hypothesis tests with a FDR of 0.05. To compare the apical and basal trees and compare between the biophysical features of the 2 classes (“slim-tufted” and “profuse-tufted”) we used the 2-sample Kolmogorov–Smirnov test (K–S test), a nonparametric hypothesis test.

Topological Morphology Descriptor

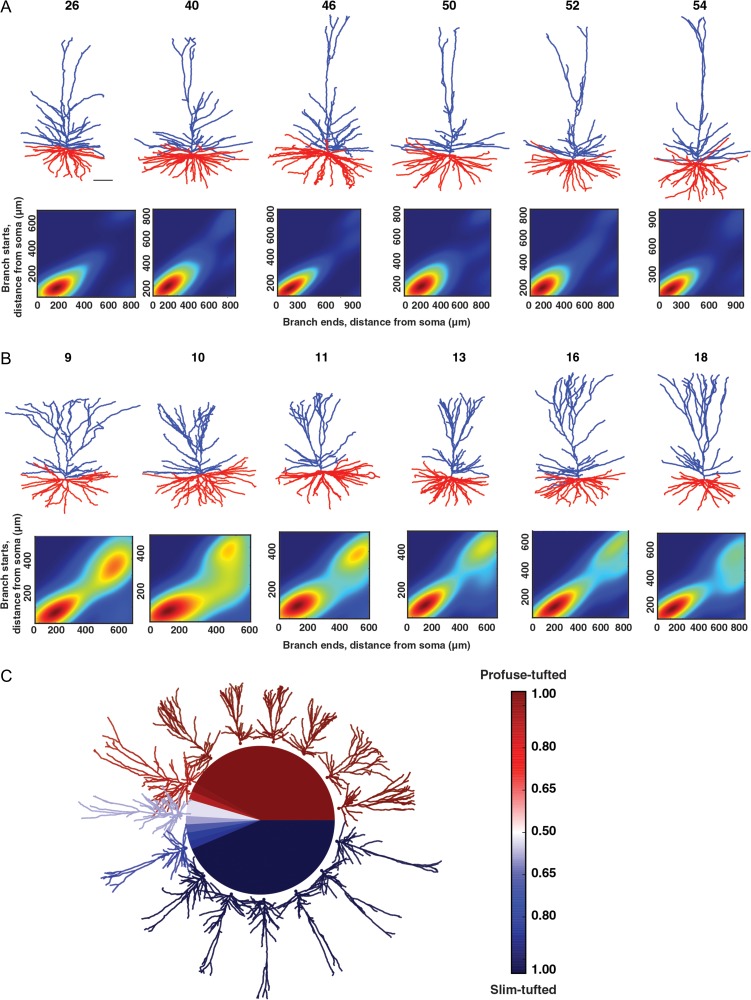
We generated the topological profile of a neuron from its branching structure (the detailed method is described in Kanari et al. 2016, 2017). The algorithm takes the branch points and the termination points of a tree as input as well as their connectivity, and produces a set of intervals on the real line known as a persistence diagram (Carlsson 2009). Each interval is a pair of real numbers that encodes the “lifetime” of a single branch in the underlying structure; the first (y-axis) represents the distance from the soma to the starting point of the branch and the second (x-axis) represents the distance from the soma to the end point of the branch. The persistence images (Fig. 4A,B) are the density plots generated from the persistence diagram, where the intensity of the color corresponds to the density of points in the persistence diagram.

Figure 4.

Examples of the 2 classes (“slim-tufted” and “profuse-tufted”) in HL2/L3 PCs. (A) Top, six 3D reconstructed exemplars of a slim-tufted HL2/L3 cell, cell numbers are as in Figure 1. Scale bar is 100 μm. Bottom, density plot of the cells on top (see “Materials and Methods” section). (B) Top, six 3D reconstructed exemplars of the profuse-tufted HL2/L3 cell, cell numbers are as in Figure 1. Bottom, density plot of the cells on top. (C) Illustration of the separation of the 2 classes. The colors represent the probability of each neuron to be classified as a certain type: dark blue indicates slim-tufted; dark red indicates profuse-tufted.

Classification of HL2/L3 PCs

For the classification, we used an open-source tool developed in Scikit-learn: Machine Learning in Python (Pedregosa et al. 2011). The persistence images (Fig. 4A,B) were used as input to the classifier. We initially trained the classifier with the persistence images of the 48 apical trees that were clearly distinguishable. Then we assigned the remaining 8 cells to classes according to the assessment of the classifier (Fig. 4C). We cross-validated the results of the classifier by a leave-one-out method (Evgeniou et al. 2004) based on a Decision Tree classifier. The accuracy of the classifier was measured by the percentage of correct assignments of the persistence images into classes. The accuracy of the classifier, based on the leave-one-out cross-validation, was ~90%. To control for the performance of the classifier, we randomized the labels of the cells and repeated the previous experiment. The accuracy of the classifier for the randomized data set was ~50%.

Results

Morphological Properties

Depth Dependent

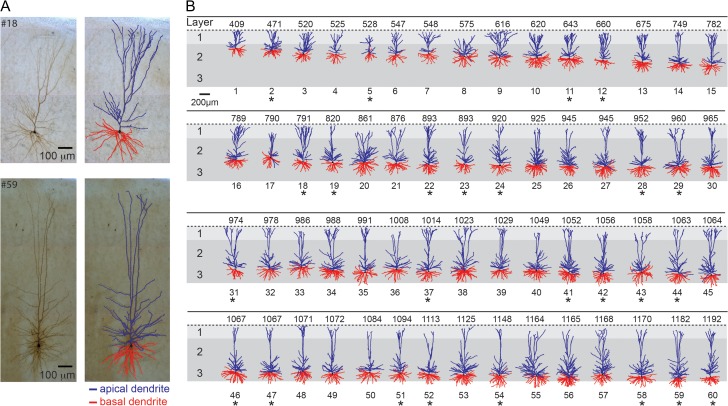
The data set of 60 morphologies from the human neocortex used in this study is shown in Figure 1. All the neurons used for the morphological analysis in the present study were human L2/L3 pyramidal neurons from the medial temporal cortex (Brodmann area 21). The considerable variability in dendritic size and shape can be seen in the figure, with a clear increase in the length of the apical tree with increasing distance from the pia.

Figure 1.

Sixty 3D reconstructed Layers 2 and 3 pyramidal cells from the human temporal cortex arranged according to somatic depth with respect to pia surface. (A) Two exemplar cells (top, cell #18, bottom, cell #59; left biocytin filled; right 3D reconstruction). Apical dendrites are indicated in blue and basal dendrites in red. (B) Database used for the morphological analysis conducted in the present study. The numbers on top of each cell indicate the depth from the pia in μm. The 25 neurons that were also characterized physiologically are marked by an asterisk.

Table 1 summarizes the basic morphological features used for comparing apical to basal dendrites. As shown in Table 1, the total surface area (apical + basal) of L2/L3 human dendrites is about 35 000 μm² on average. The mean length of the nonterminal branches is much longer for the apical tree (69.35 ± 13.62 μm) as compared with the basal tree (31.06 ± 5.97 μm, P < 0.0001, n = 60, K–S test). By contrast, some morphological features (e.g., the diameter) of the 2 trees are not significantly different (P = 0.63, n = 60, K–S test).

Table 1.

Representative morphological features and corresponding values for the 60 reconstructed HL2/L3 PCs

Feature	Mean	SD
Features of the apical tree
Total surface area (μm2)	20 125	10 168
Mean diameter (μm)	0.78	0.29
Mean length of nonterminal branches (μm)	69.35	13.62
Mean length terminal branches (μm)	162.31	21.97
Features of the basal tree
Total surface area (μm2)	16 207	8699
Mean diameter (μm)	0.74	0.29
Mean length of nonterminal branches (μm)	31.06	5.97
Mean length terminal branches (μm)	150.58	21.30

The complete list of 32 morphological features used in this study are shown in Table 2.

For a systematic analysis of our morphological database of HL2/L3 PCs, we used the set of 32 features extracted from each of the 60 neurons in our database (Table 2). We separated the features into 2 major groups composed of the features for the apical tree (#1–#15) and the basal tree (Features #16–#31). We added a single feature related to the soma (Feature #32); namely, the mean soma radius.

Interestingly, the majority of the morphological features exhibited a gradual depth-dependent change. Therefore, we sorted the features in descending order according to their correlation with the cell's depth in the cortex (order of features as in Table 2). Note that we sorted the features separately for the apical tree and for the basal tree.

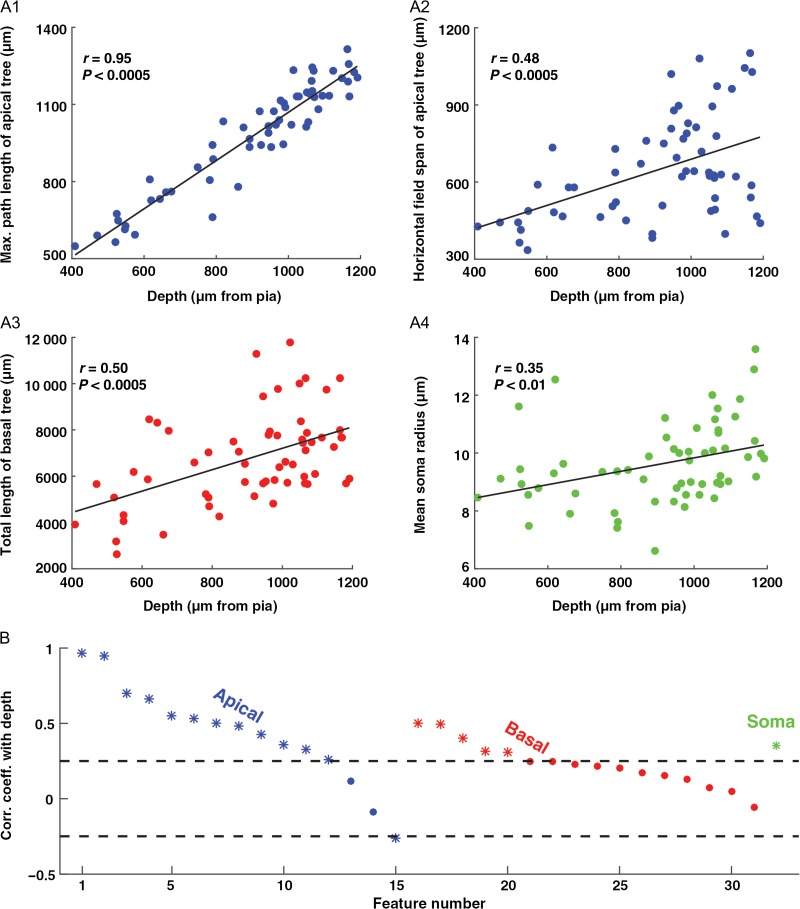
Figure 2A depicts 4 representative features that show the gradual depth-dependent change. Since all cells reached the pia (Fig. 1), it is not surprising that the maximal path length of the apical tree was strongly correlated with depth (Fig. 2A1, Feature #2, r = 0.95, P < 0.0005, n = 60). However, other features, perhaps unexpectedly, showed a significant positive correlation with cortical depth, such as the horizontal field span of the apical tree (Fig. 2A2, Feature #8, r = 0.48, P < 0.0005, n = 60), the total length of the basal tree (Fig. 2A3, Feature #16, r = 0.50, P < 0.0005, n = 60) and the mean soma radius (Fig. 2A4, Feature #32, r = 0.35, P < 0.01, n = 60).

Figure 2.

Many of the morphological features of HL2/L3 PCs display a gradual depth-dependent change. (A1–A4) Four representative features that showed a gradual depth-dependent change. The continuous line is the linear regression fit. (B) Correlation coefficient for all 32 features with depth. The features are separated into 3 groups: apical tree features (#1–#15, blue), basal tree features (#16–#31, red), and a single somatic feature (#32, green); see Table 2 for feature definitions. In each group, the features are sorted in descending order according to the correlation coefficient value with depth. Features with a significant correlation coefficient (P < 0.05) are marked with an asterisk (outside the dashed lines).

Figure 2B depicts the correlation coefficients between the feature values and the depths of the cells. Features with a significant correlation coefficient (P < 0.05) are marked with an asterisk. Notably, most of the features displayed a positive correlation with depth. In fact, out of the 32 features used, 18 showed a significant positive correlation with depth and nearly all of the remaining features showed a weak positive correlation. Note that at chance level only ~2 features (5% of 32) would have a P-value of less than 0.05. After correcting for multiple correlations (see “Materials and Methods” section), 17 features showed a significant positive correlation with depth.

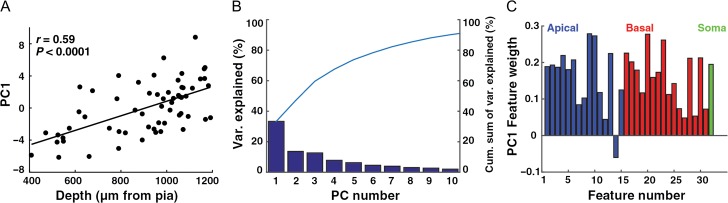
Next, we performed PCA (see “Materials and Methods” section) using all 32 features (Table 2) to test the correlation between the linear combination of the features and depth. Figure 3A shows the first principal component values for all cells as a function of depth. Note the high correlation between the first principal component score and depth (r = 0.59, P < 0.0001, n = 60), indicating that depth dependency is a major component accounting for the variability in the data. Figure 3B shows the fraction of variability represented by each of the first 10 principal components. Over 30% of variance was captured by the first principal component and about 90% of the variance was captured by the first 10 principal components.

Figure 3.

PCA of HL2/L3 PCs morphological features. (A) The first principal component score (PC1, based on 32 morphological features) as a function of the depth from pia. (B) Percentage of variance captured by each of the first ten principal components. The line displays the cumulative sum of the variance captured. (C) The weight of the contribution of each of the 32 features to the first principal component. Apical dendrite features are marked in blue, basal dendrite features in red and the somatic feature in green.

The weight of the contribution of each of the 32 features to the first principal component is shown in Figure 3C. Features related to the apical dendrite are shown in blue and features related to the basal dendrites are in red; the soma feature is in green (Feature #32). Interestingly, the distribution is broad, with various features carrying substantial weight, both for those related to the apical dendrite and to the basal dendrites (e.g., the total surface area of apical tree, Feature #9 and the total surface area of basal tree, Feature #20). Together, these results demonstrate that many morphological features contribute strongly to the main source of variability in the data; namely, the depth-dependent change in morphological properties.

Morphological Classification

From work in rodents it is known that neocortical layers can contain multiple subtypes of pyramidal neurons (Hallman et al. 1988; Mason and Larkman 1990). In order to examine the possibility that there were distinct morphological classes in HL2/L3 PCs we employed the Topological Morphology Descriptor (TMD) method for encoding the spatial structure of a branching morphology (see “Materials and Methods” section). On the first run of this method we found 4 cells that clearly did not have a tuft that could be distinguished from the oblique branches. Because of the limited group size of these cells, they were excluded from the analysis. Next, the topological analysis of the apical trees of HL2/L3 PCs revealed the existence of 2 distinct morphological classes which we dubbed the “slim-tufted” (Fig. 4A) and the “profuse-tufted” (Fig. 4B) pyramidal cells.

The slim-tufted neurons are characterized by the low density of the tuft branches whereas the profuse-tufted have a significantly higher density of tuft branches. Both types display a high density of oblique branches proximal to the soma. Using the TMD method it was straightforward to distinguish between 24 cells in each class (48 cells altogether); 8 additional cells were not obviously belonging to either of these classes. By training a classifier (Decision Tree in “Materials and Methods” section) on the 2 obvious classes, the classifier did label each of the unresolved cells (n = 8) into 1 of these 2 classes (Fig. 4C). The final result thus yielded 2 distinct groups of 27 slim-tufted, 29 profuse-tufted, and n = 4 neurons that did not have a clear tuft (total n = 60). Generally, the profuse-tufted neurons tended to be located more superficially than the slim-tufted neurons. However, the classes were not completely separated by depth (Supplementary Fig. 1A).

To assess the performance of the classifier we cross-validated the proposed grouping using the leave-one-out method (Evgeniou et al. 2004). The proposed grouping was shown to be stable with respect to the Decision Tree classifier with an estimated accuracy of ~90%, as opposed to a randomization of the groups, which resulted in ~50% accuracy (see “Materials and Methods” section).

Finally, we examined if the slim-tufted and the profuse-tufted classes exist in L2/L3 PCs from mouse temporal cortex. Based on our limited data (n = 14) these 2 classes of neurons could not be found in mouse, suggesting that these 2 types are unique types in the L2/L3 of the human cortex. Note that both groups of neurons (mouse and human) were sampled across the full L2/L3 range, came from adult subjects and the same methodology was used for both samples, including biocytin filling, histological processing, and reconstruction methods (Mohan et al. 2015).

Biophysical Properties

Depth Independent

We next examined the biophysical features of the human L2/L3 pyramidal neurons. In this analysis, we used our database of electrical recordings from 25 human neurons, which were included in the morphological analysis above (cells marked with asterisks in Fig. 1).

To characterize the biophysical characteristics of HL2/L3 PCs, we analyzed the responses of these neurons to hyperpolarizing and depolarizing somatic current injections (Fig. 5). Typically, a brief high frequency burst of spikes appears at the start of the supra-threshold current pulse; the following spikes appear to be highly regular (Fig. 5A). A zoom into an individual spike is shown on the right of Figure 5A. Figure 5B depicts the voltage responses to hyperpolarizing step currents. Inset shows the exponential fit (green dashed line) to the voltage response (black line) following the termination of a current step. For each neuron, the membrane time constant, τ_m (Feature #10) was estimated from an exponential fit to the recovery of the voltage response following a step hyperpolarizing current (Fig. 5B inset and see “Materials and Methods” section).

Table 3 summarizes the 14 biophysical features used in this study (Feature #14, the mean cable length, L, is analyzed separately in the cable analysis bellow). Note that the comparison between the different spike features was made at 150% threshold current. However, the conclusions drawn below are also valid for 175% threshold current (not shown). The values for these biophysical features in human L2/L3 pyramidal cells (e.g., the mean AP half-width and AP amplitude) are well within the range of L2/L3 pyramidal neurons in rodents (Staiger et al. 2014). However, one interesting feature worth noting from Table 3 is the appearance of a sag in the voltage response to long hyperpolarizing current injections (Feature #12). This contrasts with L2/L3 rodent pyramidal neurons in the somatosensory cortex, which show only very small sag (Larkum et al. 2007; but see, however, Van Aerde and Feldmeyer 2015 who found a subpopulation of L3 pyramidal cells that do display larger sag of ~12%). In human L2/L3 pyramidal neurons the sag is prominent, similar to that found in L5 rat pyramidal neurons (Zhu 2000; Larkum et al. 2007; Van Aerde and Feldmeyer 2015). These results suggest that HCN channels might be present in L2/L3 human pyramidal neurons (see “Discussion” section).

In the morphological analysis above we found that many features showed a gradual depth-dependent change. We therefore tested whether this was also the case for the biophysical features. Figure 5C presents the correlation coefficient for the feature value and the depth of the cells. In contrast to the morphological features, there was no correlation with depth for most of the biophysical features; only Feature #3 (mean AP rise time) and #5 (first spike latency) showed a slight correlation with depth. One unexpected finding was that the input resistance (R_N, Feature #11) was not correlated with depth. One expects that neurons with smaller surface areas (more superficial neurons) should have larger R_N. However, we found that neurons with smaller surface areas tend to have smaller τ_m (namely, a smaller specific membrane resistivity, R_m, and consequently a smaller R_N than expected if R_m were constant for all cells, Supplementary Fig. 2A). Other correlations between various biophysical features are depicted in Supplementary Figure 2B,C.

Biophysical Classification

Next, we compared the biophysical features of the slim-tufted and the profuse-tufted neurons found in the morphological analysis. Figure 5D shows the normalized I/F curves of the 24 HL2/L3 PCs profuse-tufted (dark red curves) and slim-tufted (dark blue curves) neurons. The 25th neuron that was measured physiologically did not have a tuft. The threshold current differs among these cells; however, when normalized by the threshold current (I_thresh), the average I/F curves clearly distinguish between these 2 classes (thick dark blue and dark red lines). The profuse-tufted class tends to fire at higher rates than do the neurons belonging to the slim-tufted class. Indeed, at I/I_thresh of 125, 150, and 175%, the firing rate was statistically different between the 2 classes (K–S test, P < 0.05; the number of cells with I/I_thresh of 200% was too small for a reliable statistical test). The result of Figure 5D suggests that the 2 morphological classes that were found in this work are also 2 separate biophysical classes in term of their I/F curves. This assertion should be further validated on a larger data set when it becomes available. Note, however, that other biophysical features (shown in Table 3) do not show significant difference between the slim-tufted and the profuse-tufted neurons (K–S test, P > 0.05).

Cable Length

The cable properties of dendrites determine the integrative properties of the neurons (Rall 1959). The cable properties of neurons are affected by both their morphology and biophysical properties. In this section, we focus on a key cable parameter of HL2/L3 PCs dendrites; namely L, their electrotonic length. L is defined as, L = x/λ (in dimensionless units, Rall 1959), where x is the physical length of the dendritic branch and λ is its space constant $\mathrm{\lambda }=\sqrt{({\mathrm{d}\cdot \mathrm{R}}_{\mathrm{m}})/(4{\cdot R}_i)}$ where d is the diameter of the dendritic branch, R_m is the specific membrane resistance (in Ωcm²) and R_i is the specific axial resistivity (in Ω cm). We define the mean cable length of a neuron as the mean cable length of all (apical + basal) paths from the soma to the dendritic terminals. In our calculation, the axial resistivity, R_i was assumed to be 200 Ωcm and R_m was estimated from the experimental membrane time constant, τ_m (Fig. 5B, inset) using the specific membrane capacitance, C_m of 0.5 μF/cm² of human cortical neurons reported before (Eyal et al. 2016). As in the previous sections, we examined hereby the dependence of L on the depth from pia as well as whether it differs between the slim-tufted and the profuse-tufted neurons. We did not find significant differences in the value of L between these 2 classes (K–S test, P > 0.05) and thus proceeded to explore below its depth dependency.

Figure 6A1 and A2 depict the physical dendrograms of a superficial and a deep neuron, respectively. As expected, the deeper neuron was longer in physical units. Surprisingly, when comparing the electrotonic length of both neurons, the physically longer deeper neuron was, on average, shorter in cable units (Fig. 6B1,B2, 0.79 x/λ versus 0.63 x/λ for the superficial and deep neurons, respectively). Moreover, for the cells shown in Figure 6, the steady-state voltage attenuation factor from dendrites to soma was larger, on average, for the superficial versus the deep neuron; 54.64 versus 20.20 respectively (Fig. 6C1,C2, respectively). This finding suggests that the electrical compactness (and integration properties) of small and large HL2/L3 PCs is comparable, despite the considerable difference in the physical length of their dendrites (see “Discussion” section).

Figure 7A shows the mean physical length of the dendritic tree for the 25 HL2/L3 PCs (marked in asterisks in Fig. 1) as a function of its depth from the pia. As expected, there was a high correlation between physical length and depth (n = 25, r = 0.62, P < 0.001). However, the mean cable length, L, of these neurons was not correlated with depth (Fig. 7B, n = 25, r = 0.08, P > 0.5). Two parameters could account for this result: the dendritic diameter might be larger for deep cells, and/or $R_m$ might be larger for these cells. Figure 7C clearly shows that some of the deeper neurons (red circles) that were electronically short indeed had larger mean diameters. For these neurons, their larger diameter partially compensated for their longer dendrites, resulting in relatively small L values. Figure 7D demonstrates that several deep neurons also had large R_m values and, consequently, had relatively short electronic lengths. Note that the relative impact of the larger R_m for the deep neurons in scaling their respective L values was smaller than that of the mean diameter (compare the range of the color scale in Fig. 7C vs. D). Examination of the top right-most group of cells in Figure 7B–D shows that there is a population of deep neurons with particularly large average L values that resulted from small corresponding dendritic diameters and relatively small $R_m$ values.

On Human Versus Mouse L2/L3 Pyramidal Cells from Temporal Cortex

We utilized the same 32 features as in Table 1 to compare human and mouse L2/L3 pyramidal neurons in the temporal cortex. As expected, the dendritic tree of the HL2/L3 PCs was significantly larger than that of the mouse. However, the dendritic diameter was similar in mouse and human cells (Supplementary Fig. 3A). Unlike in L2/L3 in the human temporal cortex (as well as in L2/L3 pyramidal neurons in rat barrel cortex, Staiger et al. 2014), mouse L2/L3 neurons from the temporal cortex do not show a significant gradual change with depth in most of their morphological features (Supplementary Fig. 3B). We further applied PCA and found a clear separation between human and mouse neurons based on all 32 morphological features. As shown in Figure 8A, the first principal component, separated both groups well. Over 40% of the variance was captured by the first principal component and many features carried substantial weight in the first principal component (Fig. 8B). Note that a complete separation between the mouse and human neurons was found when using a spectral k-means algorithm (Uw et al. 2001) (not shown).

We also examined whether human neurons were morphologically just a “scaled” version of mouse neurons; this does not seem to be the case (Fig. 8D). First, HL2/L3 PCs are not just longer, but they have significantly more branches in both the apical and basal trees (Mohan et al. 2015). Moreover, interestingly, we found that human terminal branches were particularly long compared with the terminal branches in mouse. Yet, the nonterminal branches were similar in human and mouse cells (Fig. 8C). From this result, it is clear that human L2/L3 neurons are not a simple linear stretch of mouse L2/L3 neurons. Further analyzes should be conducted to determine the structural rule for “transforming” HL2/L3 PCs into the respective mouse neurons. It is important to note that this comparison was based on the morphological properties of the neurons. As demonstrated above in the cable analysis, from a functional viewpoint, the morphological properties only provide a partial perspective thus making it crucial to compare the biophysical and cable properties of both groups. In any case, many elongated, thin basal dendrites as found here in human L2/L3 pyramidal neurons constitute independent computational “subunits”, and have been argued to enhance the computation repertoire of the neuron (Poirazi and Mel 2001; Polsky et al. 2004).

Discussion

Using several cluster analysis methods, as well as cable theory, we analyzed a large data set of human L2/L3 pyramidal cells from the temporal cortex. This yielded a systematic description of the morphological, biophysical, and cable properties of HL2/L3 PCs.

Since these data were taken from tissue removed after brain surgery (treatment of deep tumors and/or epileptic seizures) there is ample justification in inquiring the extent to which these cells were healthy. First, the neocortical tissue we study is always well away from the epileptic focus or tumor, so never part of the disease. Microglia and other inflammatory markers are at normal levels in this tissue, and the cytoarchitecture of the tissue is normal. Pathologists of our hospital label this tissue as “normal tissue”. Moreover, we compare parameters in patient groups with different disease backgrounds (sclerosis, glioma, meningitis, and cavernoma). These groups receive very different medications (see for instance Table 1 in Mohan et al. 2015). When the parameter overlaps between different groups, we conclude that it generalizes across disease backgrounds. Finally, if the epilepsy has a role in the parameter, one would expect that the severity of the disease would play a role. Therefore, we quantify the potential influence of the disease history on the parameter by correlating the parameter against the number of years of epilepsy of the patient and the seizure frequency. These numbers widely vary between patients, from 1 to 50 years of epilepsy and from 1 to 400 seizures per month (see Fig. 4 in Mohan et al., 2015). When there is no correlation between disease severity and the parameter, we conclude that the epilepsy has little to do with the parameter value. Further details are presented in Mohan et al. (2015).

In this study, we found that throughout the particularly thick L2/L3 (949 ± 179 μm) in the already thick human temporal cortex (2773 μm), cell bodies that are close to the pia have small apical trees and overall, about half of the dendritic length and surface area as compared with the deep neurons; these measurements were obtained for the 5 most superficial neurons and the 5 deepest neurons in Figure 1. When averaging the dendritic length of the entire 60 HL2/L3 PCs cells in our data set, the average length was 14 793 μm; hence, almost 3 times larger than the L2/L3 pyramidal cells from the rodent temporal cortex, and actually closer to the value found in L5 rodent pyramidal cells from the somatosensory cortex (an average of 12 758 μm) (Hay et al. 2013). Despite the considerable differences between superficial and deep HL2/L3 PCs, our key morphological finding is that most of the 32 morphological features used here (Table 2) show a gradual depth-dependent change (Figs 2 and 3).

In general, the apical tree of cortical pyramidal cells reaches the pia, enabling these cells at all depths to receive inputs that target Layer 1 (mostly cortico-cortical bundles and input from secondary thalamic nuclei). Inputs to Layer 1 were recently shown to regulate robustness to sensory inputs (Egger et al. 2015). Furthermore, the dependence of various features on depth (e.g., of total dendritic length, number of branches, and horizontal filed span of dendrites) might suggest that L2/L3 cells at different depths sample differently the input sources arriving to these layers. Also, deeper cells (with longer total dendritic length and surface area) receive more synapses (about twice assuming that the synaptic density/unit length is identical at all depths) and are more likely to serve as “hub neurons” as compared with superficial neurons (Gal et al. 2017). Interestingly, it was also shown that morphological variability of the dendritic tree in the cortical tissue ensures that the average synaptic properties are robust to changes at the local network level as compared with the case where all neurons are similar to each other (Ramaswamy et al. 2012). This might be another functional consequence of the large morphological variability of HL2/L3 PCs (see also Reimann et al. 2017).

By implementing a new method to characterize the global topology of neurons we identified 2 distinct morphological types of L2/L3 neurons in the human temporal cortex which we dubbed “profuse-tufted” and “slim-tufted” pyramidal neurons (Fig. 4). These 2 M-types also show a significant difference in their I/F curves; the profuse-tufted fire at higher rates (Fig. 5D). In contrast, based on our limited data (n = 14) of L2/L3 PCs from mouse temporal cortex, these 2 classes of neurons could not be found (but see Van Aerde and Feldmeyer 2015 showing that in L3 in rat medial prefrontal cortex there are several electro-morphological subtypes).

We would like to emphasize that our approach revealed 2 morphologically different cell-types and in parallel found that the I/F curves were cell-type specific. The finding of these 2 cell-types could have implications beyond the I/F curves. For example, the excitability of the apical tufts could differ between these classes (perhaps showing e.g., NMDA spikes in one class and not/less so in the other class), and/or in the properties of the back and/or forward propagation of electrical signals along the dendrites. Other features that might also differ among these classes could be their spine density, wiring diagrams between cell-types, etc. These are important questions for future studies.

It is tempting to speculate that these 2 cell-types in HL2/L3 PCs are comparable to the 2 excitatory cell-types in Layer 5 of the rodents; that is, the slender and thick tufted pyramidal cells (Hallman et al. 1988; Mason and Larkman 1990), which have been found in the somatosensory, visual, auditory, motor, and prefrontal cortices (Hübener et al. 1990; Gao and Zheng 2004; Morishima and Kawaguchi 2006; Larsen et al. 2007; Sakata and Harris 2009; Meyer et al. 2010; Oberlaender et al. 2012; Van Aerde and Feldmeyer 2015). In rodents, these 2 types of neurons are thought to be the main output cells of these cortices, and presumably project to different regions (Alloway 2008; Groh et al. 2008; Aronoff et al. 2010; Meyer et al. 2010; Oberlaender et al. 2011; Narayanan et al. 2015). Studies have also shown that thick and thin tufted neurons differentially increase their firing activity depending on the behavioral state of the animal (de Kock et al. 2007; de Kock and Sakmann 2009). Whether the slim-tufted and the profuse-tufted neurons that we found in human L2/L3 also project to different regions should be tested, perhaps using the whole tissue taken out during surgery, which includes subcortical regions as well. We stress that we gave new names to these human L2/L3 pyramidal cells to avoid potential confusion with the 2 L5 pyramidal cell-types found in rodents.

We further analyzed whether the patient parameters were different between the 2 groups. Four parameters were compared: the age of epilepsy onset, seizure frequency, the total number of seizures, and years of epilepsy. None of the 4 patient parameters corresponded to the clustering of individual morphologies into slim-tufted and profuse-tufted pyramidal cells (Supplementary Fig. 1B–F). Thus, the 2 groups of cells are not related to the patient parameters.

We next examined the biophysical features of human L2/L3 neurons using 14 biophysical features, both passive and active (see Table 3). In contrast to the morphological features, human L2/L3 pyramidal neurons did not show gradual depth-dependent changes for most of the biophysical features (Fig. 5C). Interestingly and counter-intuitively, we found that the input resistance of the neurons did not correlate with the surface area of the cells. However, the membrane time constant did correlate (but not strongly) with the surface area (Supplementary Fig. 2A).

We also analyzed more fully than ever before the active biophysical properties of HL2/L3 PCs (Table 3). The properties of individual spikes for HL2/L3 PCs (mean half-width of 1.26 ± 0.42, mean spike amplitude of 85.09 ± 5.24, Table 3) were typical of the cortical pyramidal cells of rodents (Staiger et al. 2014). Interestingly, HL2/L3 PCs show a prominent sag in the voltage response to long current injections (Table 3, Feature #12), unlike the L2/L3 pyramidal neurons from sensory cortices in rodents (Larkum et al. 2007; but see however Van Aerde and Feldmeyer 2015 who found a subpopulation of L3 pyramidal cells that do display larger sag of ~12%). The sag voltage is an indication of the presence of HCN channels. In L5 pyramidal cells, HCN channels are located almost exclusively in the apical dendritic tree (Williams and Stuart 2000; Berger et al. 2001; Lörincz et al. 2002; Kole et al. 2006; Harnett et al. 2015). These channels are active at resting membrane potentials, further activated with hyperpolarization and deactivated with depolarization. The reverse voltage-dependence of HCN channels suggests a regulating role in which its main function is to oppose changes in membrane potential (Wahl-Schott and Biel 2009). Moreover, HCN channels play an important role in various dendritic computations and temporal summation and act as a spatial filter that preferentially dampens distal inputs (Magee 1998; Williams and Stuart 2000; Harnett et al. 2015). HCN channels were also shown to have a behavioral role in controlling spatial working memory (Wang et al. 2007) and long term synaptic plasticity (Nolan et al. 2004). Hence, HCN channels may endow human L2/L3 neurons with potentially greater computation properties than in the corresponding neurons in the mouse.

We also computed the cable length, L, of HL2/L3 PCs, which is a feature that combines both morphological and biophysical properties. Unlike the physical length, which correlated with depth, the mean cable length of the neurons was depth independent. Some of the deeper neurons had a larger diameter and a larger specific membrane resistivity, both of which can be interpreted as compensating for the expected marked voltage attenuation in long dendrites (Figs 6 and 7). This compensation resulted in a comparable voltage attenuation along the dendritic tree in both the small (near pia) and large (deeper) HL2/L3 PCs. Our passive cable analysis showed very large voltage attenuations from distal dendrites in the entire HL2/L3 PCs population (Fig. 6C1 and C2); we therefore predict that active mechanisms (e.g., dendritic Ca²⁺ spikes and NMDA spikes) operate in these cells in order to compensate for this large voltage attenuation, as is found in rodents (Larkum et al. 2009; Chen et al. 2011; Xu et al. 2012; Major et al. 2013; Smith et al. 2013; Grienberger et al. 2015; Takahashi et al. 2016). The characterization of the membrane properties of human dendrites constitutes a crucial experimental challenge for the near future.

Our study provides a first systematic multi-feature analysis of the morphological, biophysical, and passive cable properties of human Layers 2 and 3 pyramidal neurons. We found 2 distinct morpho-electrotonic types within this population, which we termed “slim-tufted” and “profuse-tufted” pyramidal neurons. It would also be important to further characterize additional building blocks (the various neuron types, Wang et al. 2015) composing the human cortex which, in many ways, enable the unique cognitive capabilities found in humans.

Supplementary Material

Supplementary data are available at Cerebral Cortex online.

Funding

I.S. was supported by grant agreement no. 604102 “Human Brain Project” and by a grant from the Gatsby Charitable Foundation. H.D.M. received funding for this work from the Netherlands Organization for Scientific Research (NWO; VICI grant), ERC StG “BrainSignals”, and EU H2020 grant agreement no. 604102 “Human Brain Project”. Part of this project was supported by Hersenstichting Nederland (grant HSN 2010(1)-09) to C.P.J.D.K.