The Excess Chemical Potential of Water at the Interface with a Protein from Endpoint Simulations

Abstract

We use endpoint simulations to estimate the excess chemical potential of water in the homogeneous liquid and at the interface with a protein in solution. When the pure liquid is taken as the reference, the excess chemical potential of interfacial water is the difference between the solvation free energy of a water molecule at the interface and in the bulk. Using the homogeneous liquid as an example, we show that the solvation free energy for growing a water molecule can be estimated by applying UWHAM to the simulation data generated from the initial and final states (i.e., “the endpoints”) instead of multi-state free energy perturbation simulations because of the possible overlaps of the configurations sampled at the endpoints. Then endpoint simulations are used to estimate the solvation free energy of water at the interface with a protein in solution. The estimate of the solvation free energy at the interface from two simulations at the endpoints agrees with the benchmark using 32 states within a 95% confidence interval for most interfacial locations. The ability to accurately estimate the excess chemical potential of water from end point simulations facilitates the statistical thermodynamic analysis of diverse interfacial phenomena. Our focus is on analyzing the excess chemical potential of water at protein receptor binding sites with the goal of using this information to assist in the design of tight binding ligands.

Introduction

The excess chemical potential of a solvent molecule at the interface with a solute is the difference between the free energy of insertion of the solvent molecule at the interface and insertion in the bulk far from the solute. It is equivalent to the potential of mean force (pmf) to move a solvent molecule from the bulk to the interface. The excess chemical potential has a direct part which corresponds to the potential energy of interaction of the solvent molecule with the solute, and an indirect part, a free energy, corresponding to the difference between the pmf and the direct part. Analysis of the excess chemical potential is key to understanding interfacial phenomena and to the statistical thermodynamics of solutions.^1–27 Recently we have shown how knowledge of the excess chemical potential of hydrating waters at the interface of protein-ligand binding sites can be used to inform the design of tighter binding ligands.²⁸ In principle the evaluation of the excess chemical potential of interfacial water molecules requires sampling over intermediate states as a tagged water molecule with fixed position and orientation is coupled into the solution. In this article we show that the excess chemical potential of water can often be estimated accurately using data from just the two endpoints of the coupling process (the pure liquid and the solution) obviating the need for simulating the intermediate states. This observation will facilitate the use of the methods described in reference [²⁸] to analyze solvent effects on protein-ligand binding, as well as the further development of end point methods based on density functional theory^7,27,29 for estimating the excess chemical potential of solutes in solution. Although this paper focuses on analyzing the excess chemical potential of water at the protein-water interface, the endpoint simulations can be applied to facilitate the statistical thermodynamic analysis of diverse interfacial phenomena, which is essential to understand many chemical and biophysical phenomena such as ion channel gating, protein folding and self-assembly of membrane proteins.^14,30,31; and is also relevant to applications in the energy industry including such phenomena as the transport of electrolytes through pores.³²

Methodology and Simulations

Methodology

The potential of mean force to move a tagged water molecule from the bulk to the position x in solution WT (x), namely, the excess chemical potential of a water molecule at x, can be estimated by the difference between the solvation free energy for growing a water molecule at x, ΔF (x) and the solvation free energy for growing a water molecule in the bulk ΔF (∞) (or the pure liquid ΔF⁽⁰⁾)

$$WT(\mathbf{x})=\mathrm{\Delta }F(\mathbf{x})-\mathrm{\Delta }F(\mathrm{\infty })\approx \mathrm{\Delta }F(\mathbf{x})-\mathrm{\Delta }{F}^{(0)}$$ (1)

Here x includes the coordinates of the oxygen atom of the tagged water molecule (x, y, z) and the orientation of the tagged water molecule (α, β, γ). The solvation free energy for growing a water molecule in solution (or the bulk) can be estimated by free energy perturbation (FEP) simulations.^33–40 As shown in Fig. 1, M independent parallel simulations are run for the solution with a tagged water molecule fixed at x. Each simulation follows the Hamiltonian (potential) function

$$H_i(\mathbf{x},\{\overrightarrow{x}\})=U_{uv}(\{\overrightarrow{x}\})+E_{u\overline{v}}(\mathbf{x},{\gamma }_i)+U_{vv}(\{\overrightarrow{x}\})+E_{v\overline{v}}(\mathbf{x},\{\overrightarrow{x}\},{\gamma }_i),$$ (2)

where $\{\overrightarrow{x}\}$ are the coordinates of the other water molecules; $E_{u\overline{v}}(\mathbf{x},{\gamma }_i)$ is the soft-core interaction energy between the tagged water molecule fixed at x and the solute at the ith γ-state; and $E_{v\overline{v}}(\mathbf{x},\{\overrightarrow{x}\},{\gamma }_i)$ is the soft-core total interaction energy between the tagged water molecule and the other water molecules at the ith γ-state. $E_{u\overline{v}}(\mathbf{x},{\gamma }_i)$ and $E_{v\overline{v}}(\mathbf{x},\{\overrightarrow{x}\},{\gamma }_i)$ change from zero to $U_{u\overline{v}}(\mathbf{x})$ and $U_{v\overline{v}}(\mathbf{x},\{\overrightarrow{x}\})$ respectively when γ_i changes from zero to one, where $U_{u\overline{v}}(\mathbf{x})\equiv E_{u\overline{v}}(\mathbf{x},1)$ and $U_{v\overline{v}}(\mathbf{x},\{\overrightarrow{x}\})\equiv E_{v\overline{v}}(\mathbf{x},\{\overrightarrow{x}\},1)$ are the full interaction energies. $U_{uv}(\{\overrightarrow{x}\})$ is the interaction energy between the solute and the other (untagged) water molecules; and $U_{vv}(\{\overrightarrow{x}\})$ is the total interaction energy of all the other (untagged) water molecules with each other. In this study the solute is rigid and always fixed in the solution, therefore the full interaction energy between the solute and the fixed tagged water molecule $U_{u\overline{v}}(\mathbf{x})$ is a constant.

Figure 1.

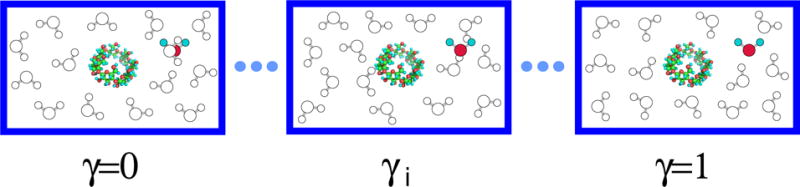
Slow growth of a tagged water molecule in solution. During the simulation at the γ = 0 state, the interaction energy between the tagged water molecule and the other water molecules $E_{v\overline{v}}(\mathbf{x},\{\overrightarrow{x}\},{\gamma }_i=0)$ and the interaction energy between the tagged water molecule and the solute $E_{u\overline{v}}(\mathbf{x},{\gamma }_i=0)$ are both zero. Therefore, the tagged water molecule can overlap with other water molecules. When the value of γ increases from zero to one, $E_{v\overline{v}}(\mathbf{x},\{\overrightarrow{x}\},{\gamma }_i)$ and $E_{u\overline{v}}(\mathbf{x},{\gamma }_i)$ increase from zero to $U_{v\overline{v}}(\mathbf{x},\{\overrightarrow{x}\})$ and $U_{u\overline{v}}(\mathbf{x})$ respectively. In this study, the simulations at different γ-states are independent. Both the solute and the tagged water molecule are fixed in the solution.

The unbinned weighted histogram analysis method (UWHAM) is an algorithm to estimate the free energy differences and density of states from the data generated by multi-state simulations.^41–44 Suppose M parallel simulations in the canonical ensemble are run at M states and X_i is the ith observation. The probability of observing X_i at the αth state is

$$P_{\alpha }(X_i)~\frac{q_{\alpha }({\{\overrightarrow{x}\}}_i)}{Z_{\alpha }}=\frac{\exp \{-{\beta }_{\alpha }{E}_{\alpha }({\{\overrightarrow{x}\}}_i)\}}{Z_{\alpha }},$$ (3)

where $q_{\alpha }({\{\overrightarrow{x}\}}_i)=\exp \{-{\beta }_{\alpha }{E}_{\alpha }({\{\overrightarrow{x}\}}_i)\}$ is the unnormalized probability; ${\{\overrightarrow{x}\}}_i$ are the coordinates of the microstate X_i; β_α = 1/(k_BT_α) is the inverse temperature of the αth state; $E_{\alpha }({\{\overrightarrow{x}\}}_i)$ is the potential energy of the microstate X_i at the αth state; and Z_α is the partition function of the αth state. The UWHAM estimate of the density of states Ω(u_i) and the partition function Z_α are obtained by solving the coupled equations:

$$\begin{gathered} {\widehat{Z}}_{\alpha }={\displaystyle \sum _{i=1}^N{q}_{\alpha }(u_i)\widehat{\Omega }(u_i)} \\ \widehat{\Omega }(u_i)=\frac{1}{{\displaystyle {\sum }_{\kappa =1}^M{N}_{\kappa }{\widehat{Z}}_{\kappa }^{-1}{q}_{\kappa }(u_i)}}, \end{gathered}$$ (4)

where N_κ is the number of observations observed at the κ state; $N={\displaystyle {\sum }_{\kappa =1}^M{N}_{\kappa }}$ is the total number of observations; u_i is the reduced (energy) coordinate of the microstate X_i; and the hat on ${\widehat{Z}}_{\alpha }$ and $\widehat{\Omega }$ denotes the most likely estimate of the true value given the discrete data set sampled from the distributions at each of the γ-states.

To study the statistical thermodynamics of growing a tagged water molecule in solution, we define the effective density of states Ω(x; U^tot) as the total probability of observing the microstates that satisfy:

• the sum of interaction energies $U_{u\overline{v}}+U_{v\overline{v}}$ equals U^tot.

at the reference state (γ = 0 state) when the tagged water molecule is fixed at x. Namely,

$$\Omega (\mathbf{x},U^{\mathit{tot}})={\displaystyle \int d\{\overrightarrow{x}\}\delta (U^{\mathit{tot}}-[U_{u\overline{v}}(\mathbf{x})+U_{v\overline{v}}(\mathbf{x},\{\overrightarrow{x}\})])\exp \{-\beta H_0(\{\overrightarrow{x}\})\}},$$ (5)

where $\delta (U^{\mathit{tot}}-[U_{u\overline{v}}(\mathbf{x})+U_{v\overline{v}}(\mathbf{x},\{\overrightarrow{x}\})])$ is the delta function which satisfies the identity

$${\displaystyle {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}d{U}^{\mathit{tot}}\delta (U^{\mathit{tot}}-[U_{u\overline{v}}(\mathbf{x})+U_{v\overline{v}}(\mathbf{x},\{\overrightarrow{x}\})])=1,}$$ (6)

and H₀ is the Hamiltonian function of the reference state (γ = 0 state)

$$H_0(\{\overrightarrow{x}\})=U_{uv}(\{\overrightarrow{x}\})+U_{vv}(\{\overrightarrow{x}\}).$$ (7)

Here γ is the coupling parameter for the intermolecular interaction of the tagged water molecule with the others. The biasing potential for the ith γ-state is $E_{u\overline{v}}(\mathbf{x},{\gamma }_i)+E_{v\overline{v}}(\mathbf{x},\{\overrightarrow{x}\},{\gamma }_i)$. The free energy difference between the γ = 0 and γ = 1 states is

$$\begin{gathered} \mathrm{\Delta }F(\mathbf{x})=-k_{B}T\ln \left(\frac{Z_1}{Z_0}\right) \\ =-k_{B}T\ln \frac{{\displaystyle \int d\{\overrightarrow{x}\}\exp \{-\beta [H_1(\mathbf{x},\{\overrightarrow{x}\})-H_0(\{\overrightarrow{x}\})]\}\exp \{-\beta H_0(\{\overrightarrow{x}\})\}}}{{\displaystyle \int d\{\overrightarrow{x}\}\exp \{-\beta H_0(\{\overrightarrow{x}\})\}}} \\ =-k_{B}T\ln \frac{{\displaystyle \int d\{\overrightarrow{x}\}{\displaystyle {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}d{U}^{\mathit{tot}}{e}^{-\beta [H_1-H_0]}\delta (U^{\mathit{tot}}-[U_{u\overline{v}}(\mathbf{x})+U_{v\overline{v}}(\mathbf{x},\{\overrightarrow{x}\})])e^{-\beta H_0}}}}{{\displaystyle \int d\{\overrightarrow{x}\}{\displaystyle {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}d{U}^{\mathit{tot}}\delta (U^{\mathit{tot}}-[U_{u\overline{v}}(\mathbf{x})+U_{v\overline{v}}(\mathbf{x},\{\overrightarrow{x}\})])e^{-\beta H_0}}}} \\ =-k_{B}T\ln \frac{{\displaystyle \int \Omega (\mathbf{x},U^{\mathit{tot}})\exp (-\beta U^{\mathit{tot}})d{U}^{\mathit{tot}}}}{{\displaystyle \int \Omega (\mathbf{x},U^{\mathit{tot}})d{U}^{\mathit{tot}}}}, \end{gathered}$$ (8)

where Z₀ and Z₁ are the partition functions of the γ = 0 and γ = 1 states respectively. Because both the solute and the tagged water molecule are fixed, the interaction energy between the tagged water molecule and the solute at the γ = 1 state $U_{u\overline{v}}\equiv \epsilon$ is a constant. Eq.(8) can be simplified as

$$\mathrm{\Delta }F(\mathbf{x})=\epsilon -k_{B}T\ln \frac{{\displaystyle \int \Omega (\mathbf{x},U_{v\overline{v}})\exp (-\beta U_{v\overline{v}})d{U}_{v\overline{v}}}}{{\displaystyle \int \Omega (\mathbf{x},U_{v\overline{v}})d{U}_{v\overline{v}}}}.$$ (9)

The UWHAM estimates of the probability of observing the reduced coordinate $U_{v\overline{v}}$ at the γ = 0 and γ = 1 states are

$${\widehat{P}}_0(U_{v\overline{v}})=\frac{\widehat{\Omega }(U_{v\overline{v}})}{{\widehat{Z}}_0}$$ (10)

and

$${\widehat{P}}_1(U_{v\overline{v}})=\frac{\widehat{\Omega }(U_{v\overline{v}})\exp \{-\beta (U_{v\overline{v}}+\epsilon )\}}{{\widehat{Z}}_1}$$ (11)

respectively.

Simulations

The simulations in this study were performed using the GROMACS 5.1.2 simulation package with the Amber99SB force field. The soft-core interactions implemented in GROMACS (see Chapter 4.5.1 of the Reference Manual Version 5.1.2 of GROMACS) were used for the free energy perturbation simulations. All the simulations were run at 300 K with constant volume and used the leap-frog (SD) integrator as the thermostat. The step size is 1 fs although the SHAKE constraint algorithm was applied. One data point was recorded every 0.1 ps. When estimating the solvation free energy for growing a water molecule in pure solvent, the Coulombic interaction and van der Waals interaction between the tagged water molecule and the other water molecules were gradually turned off together using 24 γ-states in the FEP simulations. The chosen γ values are (0.0, 0.005, 0.02, 0.05, 0.075, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5, 0.55, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9, 0.95, 1.0). For the pure solvent with TIP3P water model, the system contains 1, 410 water molecules in a cubic box of side 3.484 nm. Each independent simulation lasted 20 ns. For the pure solvent with the SPC/E water model, the system contains 1, 000 water molecules in a cubic box of side 3.106 nm. Each independent simulation lasted 20 ns. Before estimating the solvation free energy for growing a water molecule in a solution containing one Factor Xa (FXa) molecule,⁵¹ the chain A of FXa molecule and the coordinated calcium ion (PDB: 1MQ5) were solvated in a cubic box of side 8.029 nm with 15, 951 water molecules. To neutralize the system, three chloride ions have been added to the system. In the FEP simulations, the Coulombic interactions between the tagged water molecule and the other molecules were turned off first with 12 γ_e values: (0.0, 0.05, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0). Then the van der Waals interactions were turned off with 21 γ_v values: (0.0, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5, 0.55, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9, 0.95, 1.0). Each independent simulation lasted 10 ns except the one at the γ = 0 state, which has been kept running for 100 ns so that the simulation data can also be used for endpoint calculations.

Results and Discussion

By setting $U_{u\overline{v}}(\mathbf{x})$ and $U_{uv}(\{\overrightarrow{x}\})$ to zero, Eq.(2)–(9) can also be applied to the homogeneous solution to estimate the solvation free energy for growing a solvent molecule in pure solvent ΔF⁽⁰⁾, which is required for estimating the excess chemical potential of water in inhomogeneous solutions (see Eq.(1)). To estimate the solvation free energy of inserting (growing) a water molecule in a box of pure solvent ΔF⁽⁰⁾, we ran simulations of pure water with a tagged water molecule at a fixed location at each of the 24 γ-states, and each simulation lasted 20 ns. (Note that fixing the tagged water molecule is not necessary in this calculation because the tagged water molecule is in a homogeneous environment). Then the simulation data were UWHAMed to obtain the free energy difference between the γ = 0 and γ = 1 states. Since a water molecule is relatively small compared with the simulation box, water-size cavities are observed around position x during the independent simulation at the γ = 0 state because of the fluctuations of water density.^23,45–48 In those configurations, the virtual water molecule (the tagged water molecule at the γ = 0 state) does not overlap with any other water molecules. Therefore, the probabilities of observing those configurations at the γ = 1 state are non-trivial. In other words, the configurations generated at the γ = 0 and γ = 1 states (endpoints) have some (small) overlap without introducing any intermediate γ-states. Because of this, the UWHAM estimate of the solvation free energy calculated from two independent simulations at the endpoints is a close approximation compared with the UWHAM estimate calculated from the 24 independent simulations when the tagged water molecule is progressively inserted into the homogeneous solution. Note that UWHAM (or MBAR)⁴⁹ is equivalent to the Bennett acceptance ratio method (BAR) when there are only two γ-states in the system. And the UWHAM equations are the asymptotically unbiased estimators of the equilibrium distributions and free energy differences.⁴¹ As shown in Table. 1, for the TIP3P water model, the solvation free energy for growing a tagged water molecule in pure solvent estimated from FEP simulations using 24 γ-states is −6.18 ± 0.02 kcal/mol. The estimate is −6.03 ± 0.19 kcal/mol when only the data from the γ = 0 and γ = 1 states are UWHAMed. When using the SPC/E water model, the difference between these two estimates is also as small as 0.16 kcal/mol.

Table 1.

Solvation free energy (kcal/mol) for growing a water molecule in pure solvent

# of states	24	2	γ = 0	γ = 1
ΔF(0)(TIP3P)	−6.18±0.02	−6.03±0.19	−3.3	−9.8
ΔF(0)(SPC/E)	−6.81±0.02	−6.97±0.14	−3.7	−11.9

In Fig. 2, we plot the probability densities of the interaction energy between the tagged water molecule and the other water molecules $U_{v\overline{v}}$ in pure solvent at the γ = 0 and γ = 1 states when the TIP3P water model is used. The histograms in Fig. 2 are the UWHAM estimates based on the 24 independent simulations according to Eq.(10) and (11). As shown in these pictures, $U_{v\overline{v}}$ at the γ = 1 state has visible probability density in the region from −35 kcal/mol to −5 kcal/mol, and the probability density peaks at a value ~ −20 kcal/mol. In contrast, the probability density of $U_{v\overline{v}}$ at the γ = 0 state spreads over a much boarder region with a peak at a value ~ 10 kcal/mol and a long decreasing tail on the positive side. The insert in Fig. 2b shows the overlap of the probability density of $U_{v\overline{v}}$ at the γ = 0 and the γ = 1 states. The overlap is critical for UWHAM to converge and obtain the free energy difference between these two endpoints.

Figure 2.

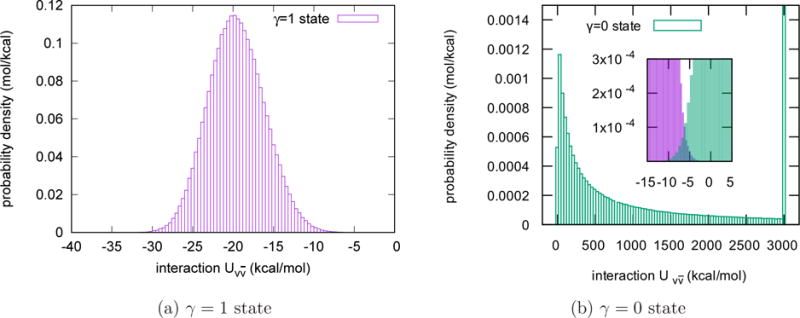
Probability density of $U_{v\overline{v}}$ at the γ = 0 state and the γ = 1 state for the homogeneous liquid. The probability density of $U_{v\overline{v}}$ at the γ = 0 state spreads over a much boarder region than at the γ = 1 state. Note that $U_{v\overline{v}}$ at the γ = 0 state has a long decreasing tail. The last bin on the right side of the figure (b) includes all the observations whose $U_{v\overline{v}}$ is larger than 3000 kcal/mol. The total probability in the last bin is 52.0%. The insert shows the overlap of the probability density of $U_{v\overline{v}}$ at the γ = 0 and the γ = 1 states.

Fig. 3a shows the estimates of the density of states ${\Omega }^{(0)}(u_{v\overline{v}})$ of the TIP3P water model obtained by the UWHAM procedure using the data from 24 γ-states compared with the corresponding result obtained from the two endpoint simulations. The two estimates are in very good agreement. Notice that the right side of the density of states histogram beyond −5 kcal/mol. Compared with Fig. 2a, the microstates in these bins have very small probabilities to be observed at the γ = 1 state, but they constitute the large majority of states in the histogram of the density of states. The last data point on the right side of the density of states shown in Fig. 3a, which includes all the microstates for which the the interaction energy between the tagged water molecule and the other water molecules $u_{v\overline{v}}$ is larger than 50 kcal/mol, has total probability as large as 93.8%.

Figure 3.

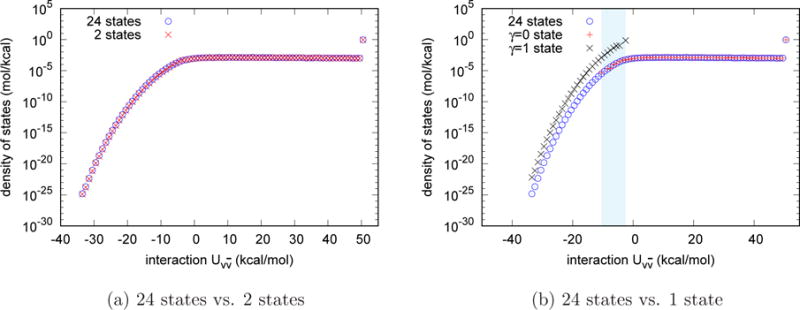
Comparison of the estimates of the density of states for the homogeneous liquid (using the TIP3P water model). In both pictures the density of states estimated from the simulations at 24 γ-states is the benchmark. (a) The density of states estimated from the two endpoint simulations agrees with the benchmark very well. (b) The density of states estimated from the simulation at the γ = 0 state matches the benchmark for more repulsive values of $U_{v\overline{v}}$ but does not agree with the benchmark data where $U_{v\overline{v}}$ is smaller than −10 kcal/mol. The density of states estimated from the simulation at the γ = 1 state does not agree with the benchmark. The shady area shows the overlap of density of states estimated from the γ = 0 and that estimated from γ = 1 states.

As discussed above, when we decrease the number of γ-states from 24 to 2, the estimate of the solvation free energy for growing a tagged water molecule in pure water ΔF⁽⁰⁾ only changes from −6.18 kcal/mol to −6.03 kcal/mol for the TIP3P water model. However, the estimate of ΔF⁽⁰⁾ becomes significantly worse when using only the data from one γ-state and Zwanzig’s free energy perturbation equation³³

$$\mathrm{\Delta }F(A\to B)=F_B-F_A=-k_{B}T\ln {\langle \exp \left(-\frac{E_B-E_A}{k_{B}T}\right)\rangle }_A.$$ (12)

In Eq.(12), E_A and E_B denote the potential energies of a configuration evaluated by the Hamiltonian function of state A and state B respectively. The angle brackets denote an ensemble average. As shown in Table. 1, we found ΔF⁽⁰⁾ = −3.3 kcal/mol by only using the simulation data obtained at the γ = 0 state, and ΔF⁽⁰⁾ = −9.8 kcal/mol by only using the data obtained at the γ = 1 state. This phenomenon is well known.⁵⁰

It is easy to understand this phenomenon by rewriting Eq.(9) in its discrete form

$$\mathrm{\Delta }{F}^{(0)}=-k_{B}T\ln \frac{{\displaystyle {\sum }_{i=1}^{N_0+N_1}{\Omega }^{(0)}(U_{v\overline{v}}[i])\exp (-\beta U_{v\overline{v}}[i])}}{{\displaystyle {\sum }_{i=1}^{N_0+N_1}{\Omega }^{(0)}(U_{v\overline{v}}[i])}},$$ (13)

and supposing there are N₀ and N₁ observations observed at the γ = 0 and γ = 1 states respectively. Note that the probability density of the numerator is plotted in Fig. 2a. Therefore, the data points obtained from the simulation at the γ = 1 state are the major contribution of the numerator in Eq. (13). The data in the first and second group together determine the normalization, namely, the factor ${\Omega }^{(0)}(U_{v\overline{v}}[i])/{\displaystyle {\sum }_{i=1}^{N_0+N_1}{\Omega }^{(0)}(U_{v\overline{v}}[i])}$. According to Eq.(10), we used the probability density of $U_{v\overline{v}}$ obtained from the independent simulation at the γ = 0 state $P_0(U_{v\overline{v}})$ to estimate the density of state ${\Omega }^{(0)}(u_{v\overline{v}})$, and the results are plotted in Fig. 3b. As can be seen, the density of states estimated from the γ = 0 state agrees with the density of states estimated from 24 independent simulations, but no data were sampled where the interaction energy $U_{v\overline{v}}$ is smaller than −10 kcal/mol so the density of states is estimated to be zero in this region. According to Eq.(11), we reweighted the probability density of $U_{v\overline{v}}$ obtained from the independent simulation at the γ = 1 state $P_1(U_{v\overline{v}})$ to estimate the density of states ${\Omega }^{(0)}(u_{v\overline{v}})$, and the results are plotted in Fig. 3b. As can be seen, the density of states estimated from the γ = 1 states has data points where the interaction energy $U_{v\overline{v}}$ is smaller than −10 kcal/mol, but it does not agree with the density of states estimated from 24 γ-states because of the incorrect normalization. The shaded area in Fig. 3 shows the overlap of the density of states estimated from the γ = 0 and the density of states estimated from the γ = 1 state.

Next we have applied endpoint simulations to estimate the solvation free energy for growing a water molecule in a solution contains one protein molecule Factor Xa (FXa)⁵¹ and 15, 951 TIP3P water molecules. Unlike in pure solvent, the water density in inhomogeneous liquids depends on the position and orientation of the water molecule x:

$$\rho (\mathbf{x})=\rho (\mathrm{\infty })\exp \{-\frac{WT(\mathbf{x})}{k_{B}T}\}=\rho (\mathrm{\infty })\exp \{-\frac{\mathrm{\Delta }F(\mathbf{x})-\mathrm{\Delta }F(\mathrm{\infty })}{k_{B}T}\},$$ (14)

where ρ(∞) is the water density in the bulk. As explained previously, water-size cavities generated by water density fluctuations around x at the γ = 0 state are essential for the overlap of the configurations observed at the γ = 0 and γ = 1 states. For the favorable positions (ΔF (x) < ΔF (∞)) in solution, it usually requires longer simulations at the γ = 0 state than for the unfavorable positions (ΔF (x) > ΔF (∞)) to obtain converged estimates of ΔF (x) by endpoint simulations.

Fig. 4 shows the dependence of the average number of water molecules on the direct interaction between the water molecule and FXa. The histogram is constructed based on the 500 snapshots of a 5 ns MD simulation. As can be seen, the direct interaction ε ranges from ~ −25 kcal/mol to ~ +10 kcal/mol. We chose 21 positions at the interface from the MD trajectory to test endpoint calculations of the solvation free energy of water molecules at those locations. The direct interactions between the tagged water molecules and the solute at those positions are approximately evenly distributed between the minimum and the maximum values observed. To obtain benchmarks with better precision, we ran FEP simulations using 32 γ-states for each position. Each independent simulation lasted 10 ns except the one at the γ = 0 state which lasted 100 ns. For each chosen position, a total number of 4, 100, 000 data points were UWHAMed to obtained the free energy difference between the γ = 0 and γ = 1 states as the benchmark using all 32 γ-states. The data generated at the γ = 0 and γ = 1 states were used for the endpoint calculations. We also measured the overlap between the γ = 0 and γ = 1 states based on the endpoint calculations. The overlap is defined as

$$S={\displaystyle \sum _{i=1}^{N}min\{w_0(u_i),w_1(u_i)\}},$$ (15)

where N = 1, 100, 000 is the total number of data points observed at the γ = 0 and γ = 1 states; u_i is the ith data point; w₀(u_i) and w₁(u_i) are the normalized UWHAM weight of the observation u_i at the γ = 0 and γ = 1 state respectively. The summation in Eq.(15) is a quantification of the overlap between the probability density of observing each observation at the γ = 0 and the γ = 1 states (see the insert of Fig. 2b).^52,53

Figure 4.

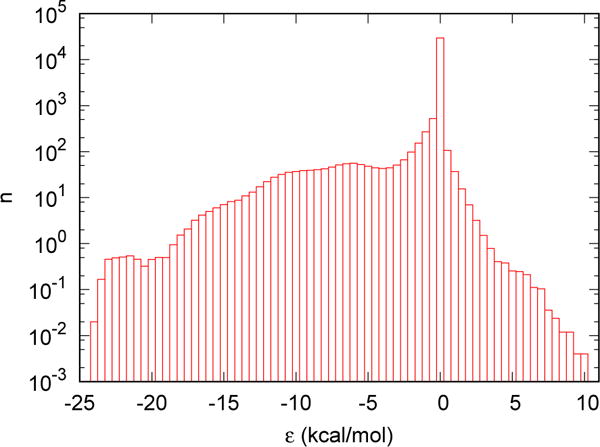
The average number of water molecules with direct interaction between the tagged water molecule and the solute in a solution containing 1 protein molecule (Factor Xa) and 15951 TIP3P water molecules.

The 32-states benchmark, the overlap of the data ensembles at the endpoints, and the results of endpoint calculations are shown in Table. 2. The positions shown with white background in Table. 2 have relatively large overlap (about two orders larger than 1.0e − 6) between the data ensembles at the γ = 0 and γ = 1 states. For these positions, the solvation free energy of the tagged water molecule can be estimated by only using the first 10 ns data points at the γ = 0 and γ = 1 states (see Supporting Information for the results). The positions shown with gray background in Table. 2 have relatively small overlap (about the same order as 1.0e − 6). The data set which includes 100 ns of sampling at the γ = 0 states and 10 ns of sampling at the γ = 1 state are required to estimate the solvation free energy of growing a water molecule at these positions. As can be seen, for positions in both categories, the UWHAM estimates of the solvation free energy of the tagged water molecule agree with the benchmark within 95% confidence interval. However, even UWHAMing the 10 ns data points at the γ = 1 state and the 100 ns data points at the γ = 0 state is insufficient sampling to estimate the solvation free energy for the two positions (#4 and #20). For these two challenging positions, we found that UWHAM analysis converges after including the data of one intermediate γ-state (see Supporting Information for details). Note that these 21 positions are chosen so that their direct interactions ε are approximately evenly distributed between the minimum and the maximum values observed. They are not chosen randomly from the frames of the 5 ns long MD trajectory. Table. 3 shows the estimates of the excess chemical potential WT and the indirect part ω = (WT − ε) based on the solvation free energies estimated by end point calculations.

Table 2.

Solvation free energy (kcal/mol) for growing a water molecule in a solution containing one protein molecule (Factor Xa) and 15951 water molecules. The data in the ΔF (32 states) column are the benchmarks. The ΔF (2 states) column shows the estimates when the 10 ns simulation data at the γ = 1 state and the 100 ns simulation data at the γ = 0 state are UWHAMed. The uncertainties marked with star are the lower limits of the uncertainty. The details of uncertainty evaluation are provided in Supporting Information.

#	ε	ΔF (32 states)	ΔF (2 states)	Overlap (10−6)
1	−22.68	−13.84 ± 0.09	−14.0 ± 0.5*	7.5e + 00
2	−21.01	−12.7 ± 0.17*	−13.3 ± 0.4*	3.4e + 00
3	−19.09	−11.0 ± 0.4*	−11.8 ± 0.4*	2.1e + 00
4	−17.47	−12.7 ± 0.13*	–	~ 0
5	−16.16	−11.40 ± 0.07	−11.9 ± 0.4*	2.0e + 00
6	−14.44	−10.36 ± 0.03	−10.51 ± 0.11	3.7e + 02
7	−12.76	−11.43 ± 0.08	−10.7 ± 0.6*	3.2e + 00
8	−11.11	−9.033 ± 0.014	−9.00 ± 0.15	9.1e + 01
9	−9.63	−8.782 ± 0.016	−8.87 ± 0.12	1.4e + 02
10	–7.83	−9.095 ± 0.013	−9.06 ± 0.07	4.9e + 02
11	−6.40	−7.774 ± 0.017	−7.67 ± 0.13	8.1e + 01
12	−5.78	−8.895 ± 0.012	−8.92 ± 0.09	1.6e + 02
13	−4.74	−5.765 ± 0.011	−5.85 ± 0.08	1.3e + 02
14	−4.19	−5.66 ± 0.02	−5.82 ± 0.14	8.2e + 01
15	−2.08	−9.33 ± 0.06	−9.26 ± 0.09	1.2e + 03
16	−0.015	−6.013 ± 0.010	−6.02 ± 0.08	2.9e + 02
17	1.04	−4.731 ± 0.015	−4.61 ± 0.12	9.9e + 01
18	3.14	−6.200 ± 0.013	−6.19 ± 0.13	1.6e + 02
19	5.29	−4.578 ± 0.014	−4.46 ± 0.08	5.9e + 02
20	7.04	−11.0 ± 0.12*	–	~ 0
21	8.94	−8.60 ± 0.14	−7.7 ± 0.6*	3.5e + 00

Table 3.

Excess chemical potential WT and indirect part ω. The excess chemical potentials are estimated based on the end point calculations, where WT = ΔF (2 states)−(−6.18 kcal/mol). The indirect part is the difference between the excess chemical potential WT and the direct part ε, namely, ω = (WT − ε).

#	ε	ΔF (2 states)	WT	ω
1	−22.68	−14.0 ± 0.5*	−7.82	14.86
2	−21.01	−13.3 ± 0.4*	−7.12	13.89
3	−19.09	−11.8 ± 0.4*	−5.62	13.47
4	−17.47	–	–	–
5	−16.16	−11.9 ± 0.4*	−5.72	10.44
6	−14.44	−10.51 ± 0.11	−4.33	10.11
7	−12.76	−10.7 ± 0.6*	−4.52	8.24
8	−11.11	−9.00 ± 0.15	−2.82	8.29
9	−9.63	−8.87 ± 0.12	−2.69	6.94
10	−7.83	−9.06 ± 0.07	−2.88	4.95
11	−6.40	−7.67 ± 0.13	−1.49	4.91
12	−5.78	−8.92 ± 0.09	−2.74	3.04
13	−4.74	−5.85 ± 0.08	0.33	5.07
14	−4.19	−5.82 ± 0.14	0.36	4.55
15	−2.08	−9.26 ± 0.09	−3.08	−1.00
16	−0.015	−6.02 ± 0.08	0.16	0.18
17	1.04	−4.61 ± 0.12	1.57	0.53
18	3.14	−6.19 ± 0.13	−0.01	−3.15
19	5.29	−4.46 ± 0.08	1.72	−3.57
20	7.04	–	–	–
21	8.94	−7.7 ± 0.6*	−1.52	−10.46

The direct and indirect parts of the excess chemical potential of water carry the thermodynamic signatures characteristic of hydrophobic and hydrophilic hydration; this information can be used in a semi-quantitative way to assist in the process of designing tighter binding ligands to proteins. Two of the interfacial water locations listed in Table. 2 and 3 (waters #11 and #13) are located at the active binding site of Factor Xa. We recently reported the results of an analysis of the thermodynamic signatures of these and other active site waters (see Eq.[A11] in the appendix of reference [²⁸]). While waters #11 and #13 both have quite favorable interaction energies with the protein receptor site which are hydrophilic in nature, for water #13 the indirect solvent-solvent contribution to the PMF almost completely cancels the direct interaction, and therefore the density is close to the bulk at this location. The consequences of this for ligand design are discussed in reference [²⁸]. The remaining waters listed in Table. 2 and 3 are at the interface with Factor Xa, but not at the receptor binding site. We expect that many features of the thermodynamic signatures of interfacial waters shown in Table. 2 and 3 are not specific to Factor Xa, but are general features which characterize the protein-water interface; including the range of direct interaction energies, both the magnitude and sign, and the extent to which the indirect term, partially or completely cancels the direct contribution (e.g. waters # 13, #14, and #18 have direct and indirect terms which almost completely cancel). It is interesting to note that waters are hydrating charged residues at both the most favorable (ε = −22 kcal/mol) and least favorable (ε = +8.9 kcal/mol) ends of the distribution. At the most favorable end of the distribution of direct interaction energies (e.g. water #1), the thermodynamic signature of the water is characteristic of a high density solvent region in proximity to a charged site on a solute. At the most repulsive end of the distribution of direct interaction energies (e.g. waters #18 - #21), these waters are in proximity to a pair of charged residues or a very polar and charged residue. The indirect contribution to the pmf is very favorable, while the direct interaction is dominated by a short range electrostatic repulsion. Water #21 as an example, interacts unfavorably with both the negatively charged Glu 76 and Glu 80. The solvation characteristics of these waters are interesting in that they are not typical of either hydrophilic or hydrophobic hydration; they appear to correspond to locations which bridge the hydration shells of two charged residues or a charged and polar residue. We will provide a more detailed analysis of the thermodynamic signatures of waters at the protein interface in a future communication.

Conclusion

In summary, this article introduced the use of endpoint simulations together with UWHAM to estimate the excess chemical potential of a tagged water molecule WT (x), in the pure liquid and at the protein-water interface. First, we reviewed how UWHAM is used to estimate the solvation free energy of a tagged water molecule when it is coupled into the solution by simulating a series of intermediate states explicitly. Next using the homogeneous solution (pure water) as an example, we showed that endpoint simulations can be used to obtain the solvation free energy of a tagged water molecule without the need to simulate the intermediate states explicitly. This is possible because the relatively small size of a water molecule facilitates overlaps in the phase space between the simulations at the γ = 0 and γ = 1 states. Then we showed that endpoint simulations can be used to estimate the excess chemical potential of solvating waters at the interface of a protein. The solute we chose as an example, the protein FXa, was one we recently used²⁸ to illustrate how knowledge of the excess chemical potential of interfacial waters can be used to help design tighter binding ligands. We found that for most of the interfacial water locations, the solvation free energies and excess chemical potentials estimated based on a 10 ns simulation at the γ = 1 state and a 100 ns simulation at the γ = 0 state agree with the 32-states benchmark within the 95% confidence interval. For two locations, it was challenging to obtain the solvation free energy of a tagged water molecule just from the endpoint simulations alone. For those positions, accurate estimates can be obtained by inserting one intermediate γ-state.