ancGWAS: a post genome-wide association study method for interaction, pathway and ancestry analysis in homogeneous and admixed populations

Abstract

Motivation: Despite numerous successful Genome-wide Association Studies (GWAS), detecting variants that have low disease risk still poses a challenge. GWAS may miss disease genes with weak genetic effects or strong epistatic effects due to the single-marker testing approach commonly used. GWAS may thus generate false negative or inconclusive results, suggesting the need for novel methods to combine effects of single nucleotide polymorphisms within a gene to increase the likelihood of fully characterizing the susceptibility gene.

Results: We developed ancGWAS, an algebraic graph-based centrality measure that accounts for linkage disequilibrium in identifying significant disease sub-networks by integrating the association signal from GWAS data sets into the human protein–protein interaction (PPI) network. We validated ancGWAS using an association study result from a breast cancer data set and the simulation of interactive disease loci in the simulation of a complex admixed population, as well as pathway-based GWAS simulation. This new approach holds promise for deconvoluting the interactions between genes underlying the pathogenesis of complex diseases. Results obtained yield a novel central breast cancer sub-network of the human interactome implicated in the proteoglycan syndecan-mediated signaling events pathway which is known to play a major role in mesenchymal tumor cell proliferation, thus providing further insights into breast cancer pathogenesis.

Availability and implementation: The ancGWAS package and documents are available at http://www.cbio.uct.ac.za/~emile/software.html

Contact: emile.chimusa@uct.ac.za, Nicola.Mulder@uct.ac.za

Supplementary information: Supplementary data are available at Bioinformatics online.

1 Introduction

Genome-wide Association Studies (GWAS) have successfully identified genetic variants in human populations, however many authors have pointed out that GWAS may not detect genetic variants with low or moderate risk, which don’t reach the intrinsic genome-wide significance cut-off (5.00e − 08) (Cantor etal., 2010; Zhang etal., 2014). Today, only a few common variants have been linked to disease and the associated loci explain only a small fraction of the genetic risk (Zhang etal., 2014). Because the effect of a gene polymorphism may be small, GWAS may fail to detect a significant signal if the effect of a variant in another gene is not taken into account (Cantor etal., 2010). Since complex diseases are typically caused by multiple factors, including multiple genes, through gene–gene interactions (Jia etal., 2010), single-marker-based analysis in GWAS may generate false negative and inconclusive results (Jia et al., 2010; Peng etal., 2008). Currently the challenges facing GWAS include: (i) the translation of associated loci into suitable biological hypotheses, (ii) the well-known problem of missing heritability (Cantor et al., 2010; Chimusa etal., 2012) and (iii) the understanding of how multiple modestly associated loci within genes interact to influence a phenotype (Peng etal., 2008).

Detecting the underlying genetic etiology of the disease can be difficult, as it may involve a single gene or interactions between two or more genes. Recent studies have demonstrated that there is a relationship between gene function and phenotype, and that functionally related genes are more likely to interact (Wang etal., 2015a). Alternatively, the effect can be at the phenotypic level, where a pair of genes can interact to produce a specific phenotype (Zhang etal., 2014). Interactions can play critical roles in the cause of disease, therefore standard GWAS analysis alone is insufficient to examine the complex genetic structure of complex diseases (Zhang etal., 2014). The challenge of gene–gene interaction methods is that the large number of multi-locus genotype combinations generated from large numbers of genetic variants may leads to the so-called ‘curse of dimensionality’ problem (Bellman, 1961). Recently, gene-set based methods have been used to examine gene sets, particularly in the form of biological pathways or grouping genes by cellular functions or functional groups, using GWAS datasets (O’Dushlaine etal., 2009; Wang etal., 2010). These methods search for significantly enriched gene sets collected from predefined canonical pathways or functional annotations such as Gene Ontology (GO) terms. However, these approaches have limitations, such as (i) the requirement for strong disease-specific background knowledge, (ii) the incomplete annotation of pathways or GO annotations in the current knowledgebase (Jia etal., 2010) and (iii) the results might be limited to a priori knowledge, thus, making it difficult to identify a meaningful combination of genes (Peng etal., 2008). Because risk genes may differ in different individuals, but may still lie in the same pathway (Cantor etal., 2010; Wang etal., 2015a), the protein–protein interaction (PPI) network based approach was recently introduced. This approach has been shown to largely overcome some of the limitations in its flexibility in setting the components of a gene set (Cantor etal., 2010; Jia et al., 2010; Peng etal., 2008). Examining the combined effects of genes by detecting genetic signals beyond single gene polymorphisms may increase our ability to fully characterize the susceptible genes and unravel the pathogenesis of disease (Liu et al., 2010; Wang etal., 2015a). These existing network-based approaches are mostly based on combining p-values from standard GWAS for correlated SNPs into an overall significance level for a gene, and combining P-values for the genes in a pathway into an overall significance level to investigate the association of a pathway with the disease (Zhang etal., 2014). However, in many cases, SNPs within genes and genes within pathways are correlated, and these methods do not account for this dependency, but rather assume genes or SNPs to be independent and uniformly distributed under a null hypothesis, which may lead to erroneous results. In addition, most of these network-based approaches do not account for topological properties of biological networks, which may lead to meaningless sub-networks (Mazandu and Mulder, 2011).

Here, we present a method, ancGWAS that leverages PPI network information, local ancestry (in the case of admixed populations) and Linkage Disequilibrium data to mine GWAS results. ancGWAS introduces flexibility in estimating gene- and sub-network-specific ancestry using the inferred local ancestry from ancestry inference approaches such as in (Baran etal., 2012). From different simulation results, we demonstrate that ancGWAS holds promise for comprehensively examining the interactions between genes underlying the pathogenesis of genetic diseases and also underlying ethnic differences. In addition, we applied ancGWAS to a GWAS data set from postmenopausal women of European ancestry with invasive breast cancer (Hunter etal., 2007). Our result yielded an interesting central breast cancer sub-network of the human interactome implicated in the proteoglycan syndecan-mediated signaling events pathway.

2 Materials and methods

We present an algebraic graph-based method (ancGWAS) that leverages the topological analysis of the PPI network to (i) identify hub genes, and use their topological properties, (ii) identify the most meaningful and significant sub-networks, (iii) account for the correlation that exists between SNPs within or between genes and genes within pathways and (iv) estimate gene- and sub-network-specific ancestry. Figure 1 summarizes the work-flow of the ancGWAS approach and more details are provided in the following sections.

Fig. 1.

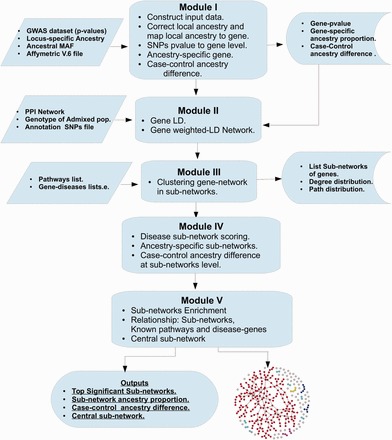
Work-flow of the ancGWAS approach, providing an overview of the inputs, modules and outputs

2.1 Assignment of ancestry, P-values and LD from SNPs to genes

SNPs, their associated local ancestry, ancestral population minor allele frequencies and GWAS P-values are assigned to a given gene if they are located within the gene’s downstream or upstream region. The dependency between genes is complex and is due to many factors (Liang and Wen-Hsiung, 2007) between closely located SNPs. LD can be observed due to functional interactions where even genes from different chromosomes can jointly confer an evolutionary selected phenotype or can affect the viability of potential offspring. To capture such information and to exploit the topological structure of PPI network for identifying informative sub-networks, we weight the PPI network with LD estimated from genotype data of the population under study. This is accomplished by computing an overall LD from pairwise LD between SNPs at each given pair of interacting genes. In this manner, the PPI network is weighted with a correlation estimated from the population genotype data. This should efficiently break down the PPI network into different sub-networks (see the section below) and help in combining p-value approaches that account for dependency of neighbouring genomic markers within/between genes.

Assuming sets of SNPs $S^a={\left\{s_i\right\}}_{i=1,2,\dots ,m}$ and $S^b={\left\{s_j\right\}}_{j=1,2,\dots ,n},\hspace{0.17em}{s}_i\ne s_j$, for $i=1,2,\dots ,m$, and for $j=1,2,\dots ,n$ are assigned to genes a and b; the pairwise LD of SNPs between a and b are independent and are computed using the r² measure (Kristin etal., 2002) from non-admixed population genotype data. In the case of an admixed population, the admixture LD is computed following the model in (Pickrell etal., 2012). The distribution of the LD is not normal, thus from ($s_i\ne s_j$) we compute the average z-transforms of LD from all possible combinations of pairs of SNPs between genes a and b. The z-transforms of LD are normally distributed with mean 0 and variance 1 (Choi, 1977). We compute the combined LD between two genes a and b as follows,

$$r_{ab}=\tanh \left(\frac{{\displaystyle \sum _{i\ne j}^{n*m}{\tanh }^{-1}}\left({\text{LD}}_{s_i{s}_j}\right)}{n*m}\right).$$ (1)

The combined LD is used as the weight of the edge between a and b genes in the PPI network. The computation of Eq. (1) may generate values close to zero (but not exactly zero) for unlinked SNPs, particular for the genotype data of non-admixed populations, where SNPs at genes across chromosomes or even on the same chromosome are not at all linked. After weighting the gene (node) with summary statistics from GWAS results and local ancestry; and the edges of PPIs with LD data, the next section introduces the method for breaking and clustering the network into different sub-networks.

2.2 Searching for sub-networks using centrality measures

Genes interact in large networks in all living organisms, and some genes in the network are more important or central than others (Liang and Wen-Hsiung, 2007). Highly connected genes in PPI networks can be functionally important and the removal of such nodes is related to lethality (Liang and Wen-Hsiung, 2007). Here we introduce four centrality measures (see more details in Supplementary Text S1) to account for the topological analysis of the PPI network. We consider our edges- and nodes-weighted PPI network as an undirected network, $G=\left(V,E\right)$, where V is the set of n genes as nodes and E is the set of edges as interactions found between genes weighted using gene-correlation. To break down the graph G into sub-networks, we analyse the general properties of G and quantify the usefulness of each gene in G using their centrality scores; closeness, betweenness, degree or eigenvector. These different centrality measures and the procedure for identifying central genes and associated sub-networks based on these centrality scores are described in the supplementary Text S1.

2.3 Statistical methods for combining P-values at the gene and sub-network level

Here we discuss our approach to rule out the statistical significance from SNPs within a given gene/sub-network. Combined P-value approaches are commonly utilized for meta-analysis (Han and Eskin, 2011) and neighbouring genomic markers in genetic association studies, and have a long history (Folks, 1984). Under the null hypothesis, the P-values P_i, $\left(i=1,\dots ,L\right)$ for a test-statistic with a continuous null distribution are uniformly distributed in the interval $\left[0,1\right]$. In this framework, a parametric cumulative distribution function F is chosen and the P-values are transformed into quantiles according to $q_i=F^{-1}(p_i),\hspace{0.17em}\left(i=1,\dots ,L\right)$. The combined test statistic $C^P={\sum }_{i=1}^L{q}_i$ is a sum of independent and identically distributed random variables q_i each of which follows the corresponding probability density function for F. To account for the independent assumption of P-values and the correlation of P-values among neighboring genomic markers, we implement both the Stouffer–Liptak (Liptak, 1958) and Fisher’s Combined probability (Fisher, 1958) methods (refer to Supplementary Text S2) accounting for spatial correlations among SNPs within a gene or SNPs within a given sub-network. We apply a similar algorithm to the Benjamini–Hochberg (Benjamini and Hochberg, 1995) false-discovery correction method (Supplementary Text S2) on summary statistics from both Stouffer–Liptak and Fisher’s Combined probability methods to control the influence of possible type I error and account for gene/sub-network difference the number of associated SNPs.

2.4 Method for combining local ancestry at gene and sub-network level

Case–control admixture mapping has recently been advertised as a promising strategy for identifying regions that contribute to both shared and population-specific difference in disease susceptibility. Admixture mapping has been applied to some admixed populations such as Puerto Rican and Mexican populations (Torgerson etal., 2012). However, similarly to standard GWAS, both approaches are based on single-marker-based analysis. Because complex diseases are caused by several factors, such as multiple genes through gene–gene interactions and gene–environment interactions (Zhang etal., 2014), both approaches mentioned above may generate false negative results. To take advantage of the combined effects of all SNPs in a particular gene and genes within a sub-network, here we combine the effect of locus-specific ancestry of SNPs within a gene/sub-network in estimating sub-network- or gene-specific ancestry (see Supplementary Text S3 for more details). The unknown true gene-specific ancestry at gene j from the kth ancestral population, μ_jk, is estimated using the maximum likelihood approach, and together with its variance ν_jk are approximated by

$${\widehat{\mu }}_{jk}=\frac{{\displaystyle \sum _{m=1}^L{W}_{mk}}{\varphi }_{mk}}{{\displaystyle \sum _{m=1}^L{W}_{mk}}}\text{and}{\widehat{\nu }}_{jk}=\frac{1}{{\displaystyle \sum _{m=1}^L{W}_{mk}}}$$ (2)

where ${\varphi }_{mk}$ is the average locus-specific ancestry from the kth ancestry of SNP $m\in \{1,2,\dots ,L\}$ associated with a given gene (or to a combined set of SNPs associated with each gene within a sub-network) and W_mk its inverse variance (precision). We test case–control ancestry difference at gene or sub-network level using a naive admixture mapping approach and computing the p-value using the importance sampling approach. Let ${\Theta }_{jk}^{+}$ and ${\Theta }_{jk}^{-},\hspace{0.17em}(j=1,\dots ,N$) be the gene-specific ancestries (for N genes within a given sub-network) estimated from n₁ samples of cases and from n₂ samples of controls. Assuming $|{\Theta }_{jk}^{+}-{\Theta }_{jk}^{-}|\ne 0,\hspace{0.17em}(j=1,\dots ,N)$, thus let Γ_j be the rank pairs from smallest to largest absolute difference within a sub-network. We use the Wilcoxon signed-rank statistic $\mathcal{W}=|{\sum }_j^{N}sign\left({\Theta }_{jk}^{+}-{\Theta }_{jk}^{-}\right).{\Gamma }_j|$ (Wilcoxon, 1945), a non-parametric test of the null hypothesis that the gene-specific ancestries from cases and controls are the same against an alternative hypothesis. Because N increases, the sampling distribution of $\mathcal{W}$ converges to a normal distribution (Wilcoxon, 1945), therefore we construct our weighted z-score as follows,

$$Z_{\mathcal{W}}=\frac{\left(\mathcal{W}-0.5\right){\displaystyle \sum _j^N|}{\rho }_{jk}^{+}-{\rho }_{jk}^{-}|}{{\sigma }_{\mathcal{W}}\sqrt{{\displaystyle \sum _j^N|}{({\rho }_{jk}^{+})}^2-{({\rho }_{jk}^{-})}^2|}}$$ (3)

where, ${\sigma }_{\mathcal{W}}=\sqrt{\frac{N(N+1)(2N+1)}{6}},\hspace{0.17em}{\rho }_{jk}^{+}$ and ${\rho }_{jk}^{-}$ are the posterior probabilities estimated from cases and controls (Supplementary Text S4). The sign is an odd mathematical function that extracts the sign of a real number (Supplementary Text S4). The p-value can be calculated from enumeration of all possible combinations of $\mathcal{W}$, given N.

2.5 Characterization of enriched sub-networks

Here we aim to identify the association between each sub-network (obtained from our network-based clustering approach) S_i, $(i=1,\dots ,T)$ within $n_1,\dots ,n_T$ genes and human pathway $P_j\in \mathcal{P}$ the set of human pathways. We obtained 1047 annotated pathways from (Zhang etal., 2012) and collected more than 107 annotated pathways from the KEGG, BioCarta and Ambion GeneAssist Pathway Atlas pathway databases. We downloaded genomic coordinates for all genes from the NCBI ftp-server ftp://ftp.ncbi.nih.gov and retained only entries for the human reference sequence. We assign the SNPs located within a gene or less than 40 kb distance up/downstream of the gene. Let α be the number of genes in the intersection between genes within S_i and genes within the pathway P_j. Let β be the number of genes in the intersection between genes within S_i and those in the union of all pathways P_k for $k=1,\dots ,J$. Let $N^{*}$ be the number of genes in the intersection between genes in the pathway P_j and those in the union of all pathways P_k for $k=1,\dots ,J$ with $k\ne j$, and $M^{*}$ be the total number of genes in all pathways P_k for $k=1,\dots ,J$. We compute the statistic of significance of overlap between sub-network S_i of n_t genes and a given pathway P_j using the z-score $(Z_S)$, which employs the binomial proportions test (Berger etal., 2007),

$$Z_S=\left(\frac{\alpha }{N^{*}}-\frac{\beta }{M^{*}}\right)/\sqrt{\frac{\frac{\beta }{M^{*}}.\left(1-\frac{\beta }{M^{*}}\right)}{M^{*}}}$$ (4)

3 Results

3.1 Evaluating ancGWAS

Firstly, we evaluated ancGWAS using the data of a 4-way admixed population simulated from 162 samples of North-west Europe (CEU), 140 Yoruba (YRI), 82 Guraji indian (GIH) and 80 Chinese (CHB) within two disease loci associated with the IL23R gene in the chromosomal region $1p31.3$ and two other disease loci associated with the SLC2A1 gene in the chromosomal region $1p34.2$ (simulation detail in Supplementary Text S5). We conducted the association analysis on the causal simulated data set by applying EMMAX (Kang etal., 2010), which accounts for both population stratification and hidden relatedness. EMMAX could not identify any significant SNPs, and failed to significantly identify the simulated disease loci at SNPs rs841404 (P-values = 2.84e − 05), rs2297977 (P-values = 1.10e − 05), rs790633 (P-value = 0.002) and rs6664119 (P-value = 0.002) (Supplementary Table S1). However, ancGWAS, in which the effect of several SNPs are combined within a gene (see also Supplementary Text S6), detects the simulated disease gene SLC2A1 (P-value = 2.98e − 12 and IL23R (P-value = 2.16e − 04 based on Stouffer–Liptak statistics) and interestingly other genes interacting with SLC2A1 or IL23R which were not of genome-wide significance from the standard GWAS are now significant after combining effects of different SNPs within a gene (Supplementary Table S1). Both our modified Stouffer–Liptak statistical and Fishers combined probability tests produce similar results, with no evidence of type I error (Supplementary Fig. S1).

We additionally analysed the ancestry of the GWAS data set from causal simulation of a 4-way admixed population and compared it to the true locus-specific ancestry generated from that particular simulation. We noted from our simulation (Supplementary Text S5) that the ancestry-specific minor allele frequencies from the correct proxy ancestral populations (Chimusa et al., 2013; Pasaniuc etal., 2013) of the admixed population may serve to correct the local ancestry bias along the genome of the admixed individuals. We tested for unusual case–control difference in ancestry under the null hypothesis at the gene level using a modified Wilcoxon signed-rank statistic. The reported Wilcoxon P-values and its q-values in Supplementary Table S1 suggest a significant signal of unusual difference in YRI ancestry from case and control samples at the IL23R locus (57%, P-value = 5.21e − 08, q-value = 0.0005), consistent with our simulation framework.

To fully characterize the susceptible genes and determine the genetic structure of the simulated disease at the biological pathway level, we conducted sub-network-specific association analysis using ancGWAS. We built an LD-weighted network of 21 429 pair-wise gene–gene interactions using the z-score method. We assessed whether there is an opportunity of using topological properties of the network as a factor for clustering. Supplementary Figure S2 shows that the network exhibits scale-free topology, meaning that the degree distribution of genes approximates a power law $P(k)=k^{-\gamma }$, where $\gamma \approx 2.19$ is the degree exponent obtained by fitting the model using the least-square approach. This indicates that most genes have few interacting partners but some have many and are crucial for the robustness of the network. In addition it also shows that the network has a small world property, suggesting that the spread of information in the network is achieved through an average of 7.01 steps, which corresponds to the average shortest communication in the network. We computed the cut-off for each centrality measure (Supplementary Text S1), and the intersection of the top genes from each measure were considered to be the set of central nodes (hubs). To break down the network into sub-networks, we ran the searching algorithm described in Supplementary Text S1. Using network centrality measures, we identified all the central genes (hubs) by applying the cut-off for each centrality measure, and the intersection of the top genes from each measure were considered to be the set of central genes (Mazandu and Mulder, 2011).

We assessed the significance of each sub-network using the Stouffer–Liptak statistical and Fishers combined probability tests. We adjusted the latter statistics using the Benjamini–Hochberg false-discovery correction. To make sure that the score of a sub-network did not occur by chance, we applied a permutation test based on the bootstrap. Our implemented bootstrap method adjusts for the dependency of P-values using a non-degenerate correlation matrix and computes the related q-values (Supplementary Text S2). Supplementary Table S2 displays the top 20 sub-networks ranked by p-values and the overlap of each sub-network with known biological pathways. 11 genes, including our simulated disease-genes and their interacting genes, overlap between the top sub-network and the metabolism pathway. From these top 20 sub-networks (Supplementary Table S2), we identified the central sub-network (Fig. 2) as the sub-network that has the connected hubs and overlapping genes with the rest of top 19 sub-networks and performed enrichment analysis as described in Section 2. This central sub-network was found to be associated with the Integrin family cell surface interactions pathway (z-score of overlap, $Z\_w$ = 1.6). The overlapping set of genes includes our simulated disease genes (SLC2A1 and IL23R) and some of their interacting genes. In addition, results of the causal simulation data set (Supplementary Table S3) demonstrate evidence of unusual case–control difference in YRI ancestry in one of these top 20 sub-networks, consistent with the simulation. Finally, SLC2A1 and UBC are the hubs of the central sub-network (Fig. 2) and both genes are interacting (Wu etal., 2009). This highlights the benefit of characterizing susceptible genes beyond standard GWAS and demonstrates the ability of ancGWAS (i) to examine the combined effects of genes by detecting genetic signals beyond a single SNP and (ii) to elucidate the interactions between genes underlying the pathogenesis of a simulated complex disease that could not be detected in a standard GWAS analysis.

Fig. 2.

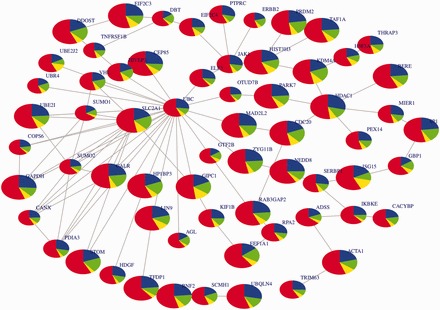
Central sub-network from the top 20 ranked sub-networks on the causal simulation data of a 4-way admixed population. The central sub-network in this figure is highly connected and related to the Integrin family cell surface interactions pathway (z-score of overlap = 1.6). The size of a node denotes its statistical significance from small to large. Nodes are coloured according to the ancestry proportions: red = YRI (Yoruba ancestry), blue = CEU (European ancestry), green = CHB (Chinese ancestry) and yellow = GIH (Gujarati Indian ancestry)

Next, to determine whether the ancGWAS approach is calibrated, we evaluated ancGWAS using a null simulated data set without any simulated causal SNPs of a 4-way admixed population (see Supplementary Text S6). We conducted the association analysis on this simulated data by using EMMAX. As expected, from the top 19 SNPs displayed in Supplementary Table S4, no genome-wide significance was observed. We applied ancGWAS to the resulting GWAS data set, but when combining effects of different SNPs within a gene, the result was still not significant (Supplementary Table S4), although the top genes are associated with the top SNPs observed in the standard GWAS analysis. In addition, no significant results were observed at the sub-network level (Supplementary Table S5). At both gene and sub-network levels (Supplementary Tables S4 and Supplementary Data), the Wilcoxon signed-rank statistical test of unusual case–control difference in ancestry did not show any statistical significance either. Overall, both the causal and null simulation of a 4-way admixed population suggest that the approaches developed in ancGWAS protect against false positives, and can unravel signals of ancestry difference in disease risk.

Finally, we evaluated ancGWAS using a simulated pathway-based GWAS data set (detail of simulation in Supplementary Text S5). The standard single-marker-based association analysis using EMMAX in Supplementary Table S6, failed to significantly identify our three weak simulated interactive disease-associated loci with very weak genetic effects (rs2834287 associated with ATP5O, rs507238 associated with ATPIF1 and rs2250305 associated with BTG3). We thus used a pathway-based approach in ancGWAS to analyse the combined effect of all SNPs within a gene and genes within a pathway, to detect the simulated interactive disease genes with very weak genetic effects in the up-regulated aged mouse hypothalamus pathway. We retained the resulting top 20 sub-networks, and for each sub-network, we computed the number of genes overlapping between each sub-network and the up-regulated aged mouse hypothalamus pathway (AGED_MOUSE_HYPOTH_UP), which is our simulated pathway. Supplementary Table S7 displays the result of ancGWAS, which was able to identify the up-regulated aged mouse hypothalamus pathway, among the 20 top sub-networks with 5 overlapping genes.

3.2 Application to CGEMS breast cancer data

We conducted an association analysis using data from the CGEMS Breast Cancer study (see Supplementary Text S7), which included 1145 postmenopausal women of European ancestry with invasive breast cancer (Hunter etal., 2007) and 1142 controls. We conducted GWAS analysis based on the typed data set and imputed missing SNPs using the 1000 Genomes reference panel (McVean etal., 2012). Results from both GWAS on typed and genome-wide imputation data did not yield any significant association signal with breast cancer (Supplementary Table S8). To account for possible interacting cancer disease SNPs and moderate risk that did not reach genome-wide significance in the standard GWAS, we applied ancGWAS to the resulting GWAS data set containing 528 169 SNPs. We identified a central sub-network (Fig. 3) and applied enrichment analysis to it (see Supplementary Text S7 for more details). 63 genes from the central sub-network overlapped those from the proteoglycan syndecan-mediated signaling events pathway (z-score of overlap, Z$\_w$ = 12.9). The overlap of the central sub-network (Fig. 3) and this pathway includes 15 known or previously identified breast cancer genes (Supplementary Table 9) including BRCA1, TGFBR1, BRCA2, FANCA, MTR, MRPL19, CASP8, IGFBP3, IGFBP1, VEGFA, IGF1, ATR, XRCC3, FGFR2, CHEK2. This is an important result, illustrating the benefit of incorporating both the association signal from a standard GWAS and the human PPI network for testing the combined effects of SNPs and searching for significantly enriched sub-networks for complex diseases.

Fig. 3.

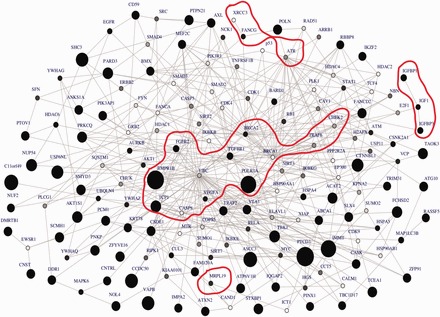
Central sub-network of breast cancer. The size of a node denotes its significance with size increasing with significance. Dark nodes or nodes inside a contour denote previously identified breast cancer associated genes or genes interacting with known breast cancer genes

3.3 Comparing ancGWAS with dmGWAS

It is challenging to compare different pathway analysis methods because of the lack of accurate knowledge of complex traits and the incomplete human protein interaction network (Wang etal., 2015a). Most of these methods do not accept a user-defined network, only accept a short list of SNPs or genes, or use VEGAS (Liu etal., 2010) to map SNPs to genes, such as EW_dmGWAS, iPINBPA and PINBPA (Wang etal., 2015a,b). This makes it impossible to directly compare these methods to ancGWAS. Additional to GWAS summary statistics, and although ancGWAS can use any weighted biological network, it uses case–control genotype data sets to construct the weights of the network, which current post-GWAS approaches do not account for. dmGWAS (Jia etal., 2010; Wang etal., 2015b) is currently the most popular network-based approach that uses a similar strategy to ancGWAS for mapping SNPs to genes and analysing GWAS data sets at the gene and sub-network level. This makes it the most appropriate tool to compare against ancGWAS and enables a reasonable comparison between these two approaches. The dmGWAS method uses the dense module searching algorithm for identifying modules or sub-networks in massive networks. Their searching algorithm is based on a greedy algorithm that searches for dense modules using two parameters: (i) the numerical parameter d, is the constraint distance for which any node with a shortest path to another node greater than this cut-off, will not be considered as an interacting neighbour, (ii) the parameter r, which obstructs restriction on the score of the module (sub-network), and has a considerable effect on the result. Although the new version of dmGWAS may use the edge-weighted PPI network, the greedy searching algorithm and strategy used in both (Jia etal., 2010; Wang etal., 2015b) don’t consider the topological properties of biological networks. This may lead to less meaningful modules or sub-networks (Mazandu and Mulder, 2011). Furthermore, the accuracy and performance of dmGWAS relies on the choice of these parameters (Jia etal., 2010; Wang etal., 2015b). Supplementary Table S10, provides a comparison of technical components implemented in both ancGWAS and dmGWAS.

Because dmGWAS was not designed for admixed populations, we firstly applied both ancGWAS and dmGWAS to the simulated pathway-based GWAS data set (Supplementary Text S5) to compare their ability to detect the simulated interactive disease genes with very weak genetic effects in the up-regulated aged mouse hypothalamus pathway. We retained the top 20 sub-networks from each approach. For each sub-network from both approaches, we computed the number of genes overlapping between each sub-network and the up-regulated aged mouse hypothalamus pathway (simulated pathway). The top 3 sub-networks from ancGWAS include the simulated disease genes ATP5O, ATPIF1 and BTG3 while sub-networks from dmGWAS had no overlaps with the simulated disease genes (Fig. 4). This indicates that the top sub-networks from ancGWAS are more enriched disease genes than those obtained from dmGWAS. The advantage of ancGWAS may be due to the usage of the topological structure of the network and network communication to break down the network into different sub-networks, as shown previously in Wang etal. (2015a). We also applied both methods to the breast cancer GWAS data (Supplementary Text S5). The top sub-networks from both methods are associated with proteoglycan syndecan-mediated signaling events pathway. However, the numbers of overlapping known breast cancer disease genes with these top sub-networks from ancGWAS are greater than those from dmGWAS (see Supplementary Table S9 and Supplementary Text S8 for more details).

Fig. 4.

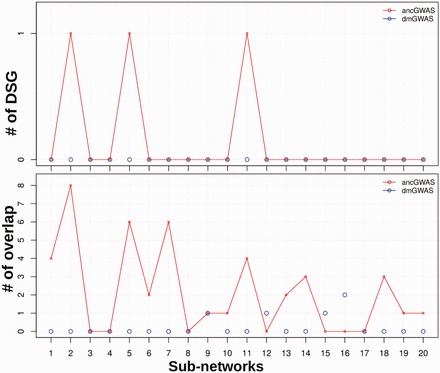
Comparing dmGWAS and ancGWAS. (A) Number of overlaping genes between the top sub-networks from dmGWAS and ancGWAS and the simulated disease-susceptibility genes (DSG). (B) Number of overlapping genes between top sub-networks from dmGWAS and ancGWAS and the entire disease pathway (AGED_MOUSE_HYPOTH_UP). Line plot is ancGWAS and circle plot is dmGWAS

4 Discussion

We introduced ancGWAS, a post GWAS method based on an algebraic graph-based approach that leverages the topological analysis of the PPI network to (i) identify hub genes, and use their topological properties, (ii) identify the most meaningful and significant genes or sub-networks relevant to a disease and those underlying ethnic difference in disease risk in the case of admixed populations and (iii) account for the correlation that exists between SNPs within or between genes and genes within pathways. ancGWAS integrates the association signal from standard GWAS data, the local ancestry for admixed populations and the SNP LD into the human PPI network. In addition, ancGWAS also handles other user-defined weights such as topological weight. ancGWAS introduces flexibility in estimating gene- and sub-network-specific ancestry using the inferred local ancestry from ancestry inference approaches such as in (Baran etal., 2012). When ruling out the gene- and sub-network-specific ancestry, the proposed method corrects for possible bias in the inferred local ancestries obtained from current approaches of local ancestry inference (Chimusa et al., 2012; Pasaniuc etal., 2013). In addition, it tests for case–control unusual difference in ancestry at the gene and sub-network level using the corrected local ancestry of admixed populations.

We have done 3 types of simulation to test ancGWAS (i) causal simulation (with some causal SNPs) on a 4-way admixed population to test if ancGWAS can recover the GWAS signal and ancestry differences, (ii) null simulation (without disease SNPs) on a 4-way admixed population to test if ancGWAS produces a false signal or type I error and (iii) pathway-based simulation with weak disease effect to test ancGWAS’s ability to recover interactive disease genes within a pathway. All simulated data sets are available with the ancGWAS package, at http://www.cbio.uct.ac.za/ancGWAS.

Our results from the causal simulation of a 4-way admixed population; and the data set of invasive breast cancer demonstrated that ancGWAS can recover weak and moderate association signals from standard GWAS results by leveraging effects of all SNPs within a gene and sub-network to unravel signals of possible disease associated genes or pathways (further discussion in Supplementary Text S9). Although our statistical methods account for false discovery, we assessed the ability of ancGWAS to control both type I and II errors based on null simulation with no causal loci and causal simulation of disease loci in the simulation of an admixed population, respectively. In these assessments, no false positive/negative signals were identified (Supplementary Tables S1 and Supplementary Data). Moreover, ancGWAS can detect ancestry differences in admixed data as shown in Figure 2, which displays candidate ancestry difference at the gene/sub-network level. However, our current method cannot perform allelic tests of association directly from the data, controlling for differences in gene/sub-network-specific ancestry (candidate peaks), as this is very challenging due to gene–gene interactions (or considering sub-networks of iterative genes). This would mean a large number of multi-locus genotype combinations generated from large numbers of genetic variants, leading to the so-called ’curse of dimensionality’ problem (Bellman, 1961). Inferring accurate local ancestry is also challenging (Chimusa et al., 2014; Pasaniuc etal., 2013) and currently we do not have access to a phenotypic data set of an admixed population. Otherwise it would be interesting to apply the proposed approach to such a population to evaluate the performance of this approach in identifying the pathways associated with a disease. The lack of accurate knowledge of complex traits and the incomplete human protein interaction network makes it challenging to directly compare the results from different pathway analysis methods. Nevertheless, we used a GWAS data set of invasive breast cancer (Supplementary Text S8) to compare ancGWAS to dmGWAS. These results have shown that ancGWAS identified more cancer associated genes in its results than dmGWAS, and holds promise for deconvoluting the interactions between genes underlying the pathogenesis of complex diseases. dmGWAS recently released a new feature (Wang etal., 2015b) that uses gene expression profiles for edge weights (Wang etal., 2015b). However, because the new dmGWAS still uses the same greedy searching algorithm to break down the biological network into sub-networks, it still doesn’t take advantage of the topological properties of biological networks like ancGWAS does.