NRGC: a novel referential genome compression algorithm

Abstract

Motivation: Next-generation sequencing techniques produce millions to billions of short reads. The procedure is not only very cost effective but also can be done in laboratory environment. The state-of-the-art sequence assemblers then construct the whole genomic sequence from these reads. Current cutting edge computing technology makes it possible to build genomic sequences from the billions of reads within a minimal cost and time. As a consequence, we see an explosion of biological sequences in recent times. In turn, the cost of storing the sequences in physical memory or transmitting them over the internet is becoming a major bottleneck for research and future medical applications. Data compression techniques are one of the most important remedies in this context. We are in need of suitable data compression algorithms that can exploit the inherent structure of biological sequences. Although standard data compression algorithms are prevalent, they are not suitable to compress biological sequencing data effectively. In this article, we propose a novel referential genome compression algorithm (NRGC) to effectively and efficiently compress the genomic sequences.

Results: We have done rigorous experiments to evaluate NRGC by taking a set of real human genomes. The simulation results show that our algorithm is indeed an effective genome compression algorithm that performs better than the best-known algorithms in most of the cases. Compression and decompression times are also very impressive.

Availability and Implementation: The implementations are freely available for non-commercial purposes. They can be downloaded from: http://www.engr.uconn.edu/~rajasek/NRGC.zip

Contact: rajasek@engr.uconn.edu

1 Introduction

Next-generation sequencing (NGS) techniques reflect a major breakthrough in the domain of sequence analysis. Some of the sequencing technologies available today are massively parallel signature sequencing, 454 pyrosequencing, Illumina (Solexa) sequencing, SOLiD sequencing, ion semiconductor sequencing, etc. Any NGS technique produces abundant overlapping reads from a DNA molecule ranging from tiny bacterium to human species. Modern sequence assemblers construct the whole genome by exploiting overlap information among the reads. As the procedure is very cheap and can be done in standard laboratory environments, we see an explosion of biological sequences that have to be analysed. But before analysis the most important prerequisite is storing the data in a permanent memory. As a consequence, we need to increase physical memory to cope up with this increasing amount of data. By 2025, between 100 million and 2 billion human genomes are expected to have been sequenced, according to Stephens et al. (2015). The storage requirement for this data alone could be as much as 2–40 exabytes (one exabyte being 10¹⁸ bytes). Although the recent engineering innovation has sharply decelerated the cost to produce physical memory, the abundance of data has already outpaced it. Besides this, the most reliable mechanism to send data instantly around the globe is using the Internet. If the size of the data is huge, it will certainly create a burden over the Internet. Network congestion and higher transmission costs are some of the side-effects. Data compression techniques could help alleviate these problems. A number of techniques can be found in the literature for compressing general-purpose data. They are not suitable for special purpose data like biological sequencing data. As a result, the standard compression tools often fail to effectively compress biological data. In this context, we need specialized algorithms for compressing biological sequencing data. In this article, we offer a novel algorithm to compress genomic sequences effectively and efficiently. Our algorithm achieves compression ratios that are better than the currently best performing algorithms in this domain. By compression ratio we mean the ratio of the uncompressed data size to the compressed data size.

The following two versions of the genome compression problem have been identified in the literature:

1. Referential Genome Compression. The idea is to utilize the fact that genomic sequences from the same species exhibit a very high level of similarity. Recording variations with respect to a reference genome greatly reduces the disk space needed for storing any particular genomic sequence. The computation complexity is also improved quite a bit. So, the goal of this problem is to compress all the sequences from the same (or related) species using one of them as the reference. The reference is then compressed using either a general purpose compression algorithm or a reference-free genome compression algorithm.

2. Reference-free Genome Compression. This is the same as Problem (i) stated above, except that there is no reference sequence. Each sequence has to be compressed independently. In this article we focus on Problem (i). We propose an algorithm called NRGC (Novel Referential Genome Compressor) based on a novel placement scheme. We divide the entire target genome into some non-overlapping segments. Each segment is then placed onto a reference genome to find the best placement. After computing the best possible placements, each segment is then compressed using the corresponding segment of the reference. Simulation results show that NRGC is indeed an effective compression tool.

The rest of this article is organized as follows: Section 2 has a literature survey. Section 3 describes the proposed algorithm and analyzes its time complexity. Our experimental platform is explained in Section 4. This section also contains the experimental results. Section 5 presents some discussions. Section 6 concludes the study.

2 A survey of compression algorithms

We now briefly introduce some of the algorithms that have been proposed to compress genomic sequences using a reference from the same species. In referential genome compression, the goal is to compress a large set S of similar sequences potentially coming from similar species. The basic idea of referential genome compression can be defined as follows. We first choose the reference sequence R. The selection of R can be purely random or it can be chosen algorithmically. All the other sequences $s\in S-R$ are compressed with respect to R. The target T (i.e. the current sequence to be compressed) is first aligned onto the reference R. Then, mismatches between the target and the reference are identified and encoded. Each record of a mismatch may consist of the position with respect to the reference, the type (e.g. insertion, deletion or substitution) of mismatch, value and the matching length.

Brandon et al. (2009) have used various coding techniques such as Golomb [Golomb et al. (1966)], Elias [Peter et al. (1975)] and Huffman [Huffman et al. (1952)] to encode the mismatches. Wang et al. (2011) have presented a compression program, GRS, which obtains variant information by using a modified Unix diff program. The algorithm GReEn [Pinho et al. (2012)] employs a probabilistic copy model that calculates target base probabilities based on the reference. Given the base probabilities as input, an arithmetic coder was then employed to encode the target. Recently, an algorithm called ERGC (Efficient Referential Genome Compressor) [Saha et al. (2015)] has been introduced which is based on a reference genome. It employs a divide and conquer strategy. Another algorithm, namely, iDoComp [Ochoa et al. (2014)] has been proposed recently which outperforms some of the previously best-known algorithms such as GRS, GReEn and GDC. GDC [Deorowicz et al. (2011)] is an LZ77-style compression scheme for relative compression of multiple genomes of the same species. In contrast to the algorithms mentioned above, Christley et al. (2009) have proposed the DNAzip algorithm. It exploits the human population variation database, where a variant can be a single-nucleotide polymorphism or an indel (an insertion and/or a deletion of multiple bases). Some other notable algorithms that employ VCF (Variant Call Format) files to compress genomes have been given by Deorowicz et al. (2013) and Pavlichin et al. (2013). Next, we provide a brief outline of some of the best-known algorithms in the domain of referential genome compression. An elaborate summary can be found in Saha et al. (2015).

GRS at first finds longest common subsequences between the reference and the target genomes. It then employs the Unix diff program to calculate a similarity score between the two sequences. Based on the similarity score, it either encodes the variations between the reference and target genomic sequences using Huffman encoding or the reference and target sequences are divided into smaller blocks. In the latter case, the computation is then restarted on each pair of blocks. The performance of GRS degrades sharply if the variation is high between the reference and target genomes. GDC can be categorized as an LZ77-style [Ziv et al. (1977)] compression algorithm. It is mostly a variant of RLZopt [Shanika et al. (2011)]. It finds the matching subsequences between the reference and the target by employing hashing where RLZopt employs suffix array. GDC is referred to as a multi-genome compression algorithm. From a set of genomes, it cleverly detects one (or more) suitable genome(s) as reference and compresses the rest based on the reference. An arithmetic encoding scheme is introduced in GReEn. At the beginning, it computes statistics using the reference and an arithmetic encoder is then used to compress the target by employing the statistics. GReEn uses a copy expert model which is largely based on the non-referential compression algorithm XM [Cao et al. (2007)]. iDoComp is based on suffix array construction and entropy encoder. Through suffix array it parses the target into the reference and an entropy encoder is used to compress the variations. The most recent algorithm ERGC divides both the target and the reference sequences into parts of equal size and finds one-to-one maps of similar regions from each part. It then outputs identical maps along with dissimilar regions of the target sequence. Delta encoding and PPMD lossless compression algorithm are used to compress the variations between the reference and the target genomes. If the variations between the reference and the target are small, it outperforms all the best-known algorithms. But its performance degrades when the variations are high.

As referential genome compression is based on finding similar subsequences between the reference and the target genomes, some existing algorithms such as MUMmer [Kurtz et al. (2004)] or BLAST [Altschul et al. (2004)] can be used to find the maximal matching substrings. The acronym ‘MUMmer’ comes from ‘Maximal Unique Matches’, or MUMs. MUMmer is based on the suffix tree data structure designed to find maximal exact matches between two input sequences. After finding all the maximal matching substrings, an approximate string aligner can be used to detect the variations.

3 Materials and methods

We can find all the variations between the reference and target genomic sequences by employing any exact global alignment algorithm. As the time complexity of such an algorithm is typically quadratic, it is not computationally feasible. So, every referential genome compression algorithm employs an approximate string matcher which is greedy in nature. Although genomic sequences of two individuals from the same species are very similar, there may be high variations in some regions of genomes. This is due to the large number of insertions and/or deletions in the genomic sequences of interest. In this scenario, greedy algorithms often fail to perform meaningful compressions. Either they can run indefinitely to search for common substrings of meaningful length or output compressed data of very large size. Taking all of these facts into consideration, in this article we propose a novel referential genome compression algorithm which is based on greedy placement schemes. Our algorithm overcomes the disadvantages of the existing algorithms effectively.

There are three phases in our algorithm. In the first phase, we divide the target genome T into a set of non-overlapping segments $t_1,t_2,t_3\dots ,t_n$ of length L each (for some suitable value of L). We then compute a score for each segments t_i corresponding to each possible placement of t_i onto reference genome R employing our novel scoring algorithm. The scores computed in the first phase are then used to find a non-overlapping placement of each t_i onto R in the second phase. This task is achieved using a placement algorithm that we introduce. Finally in the third phase, we record the variation between each segment t_i and the reference genome R by employing our segment compression algorithm. More details of our algorithm are provided next.

3.1 Computing scores

At the beginning, the target genome T is divided into a set of non-overlapping segments $t_1,t_2,t_3\dots ,t_n$ each of a fixed length L where L is user defined. As the genomic sequence can be composed of millions to billions of base pairs and can contain large insertions and/or deletions along with mutations, finding the best possible placement of t_i onto R is not trivial. In fact, an exact algorithm will have a quadratic time complexity to compute the best possible placements for all the t_is. Let $\left|R\right|$ and $\left|T\right|$ be the lengths of R and T, respectively. The time complexity of an exact algorithm could be $O(|R\left|\right|T|)$ which is extremely high. There is a trade-off between the time an algorithm takes and the accuracy it achieves. We accomplish a very good balance between these two by carefully formulating the scoring algorithm. This is done by employing fingerprinting and an ordered lengths of the fragments. We randomly generate a small substring F of length l where $4\le l\le 6$ considering only A, C, G and T characters. F serves as a barcode/fingerprint in this context. Each possible occurrence of F is then collected from R. As we know the position of each occurrence of F at this point, we can build an ordered lengths of the fragments by clipping the sequence at known fingerprint positions. Following the same procedure stated we can compute the ordered lengths of the fragments for each t_i by employing the same F. Suppose there are no errors (either indels or substitutions) in R and T. In this scenario for any given ordered fragment lengths of a segment t_i, in general, there should exist a subset of matching ordered fragment lengths in the reference R. This information helps to place a segment t_i onto R. But in reality errors could occur due to deletions of some fingerprint sites or a change in some fragment lengths (due to insertions). A novel scoring algorithm is thus introduced to quantify the errors.

Let $A=t_1^i,t_2^i,t_3^i,\dots ,t_q^i$ be the ordered fragment lengths of segment t_i from T and $B=r_s,r_{s+1},r_{s+2},r_{s+3},\dots ,r_{m-s+1}$ be the ordered fragment lengths of a particular region of R. The region is stretched from sth fragment to $(m-s+1)\text{th}$ fragment. The score of t_i for this particular region is computed as in Equation (1).

$$\text{Score}(t_i)=\left|\sum _{j=1}^{q_i}{t}_j^i-\sum _{j=s}^{m-s+1}{r}_j\right|+P*\text{MFS},$$ (1)

where P and MFS are the penalty factor and number of missed fingerprint sites, respectively. Penalty term P is user defined and should be very large. Details of our scoring algorithm follow. Let $r_1,r_2,r_3,\dots ,r_m$ be the ordered fragment lengths of the reference R. Let $t_1^i,t_2^i,t_3^i,\dots ,t_q^i$ be the ordered fragment lengths computed from any segment t_i. The individual scores are then computed by matching $t_1^i$ with r₁, $t_2^i$ with r₂, $t_3^i$ with r₃, and so on. In other words, we compute a score for $t_1^i$ by matching it with r_j for each possible value of i where $1\le j\le m$. In brief, the inputs of the scoring algorithm are ordered fragment lengths of the reference genome R and ordered fragments lengths of each non-overlapping segment t_i where $1\le i\le n$. As m and q are the number of ordered lengths of the reference genome R and a segment t_i, respectively, there will be $(m-q+1)$-matching scores for each t_i. Each score is calculated by incrementing the position by one until all the $(m-q+1)$-steps are used. In this context, position refers to the length of a particular fragment in R. So, the first position refers to the first fragment, the second position refers to the second fragment, and so on. After aligning the ordered fragment lengths of a segment t_i to a particular position of the reference R, we greedily detect the number of fragment lengths of t_i that coincide reasonably well with the ordered fragment lengths of R and the number of missed fingerprint sites. We then calculate a matching score of that particular position by employing Equation (1). We calculate all the $(m-q+1)$ scores of each segment t_i following the same procedure stated above.

A detailed pseudocode is supplied in Algorithm 1. The run time of our greedy scoring algorithm is O(mnq), where m is the number of fragments in the reference genome R, n is the number of segments of target genome T and q is the maximum number of fragments in any segment t_i.

3.2 Finding placements

Our placement algorithm utilizes the matching scores for each segment t_i to correctly place it onto the reference genome R. The algorithm takes a score list of a particular segment t_i and an ordered fragment lengths of R as input. If m is the number of ordered fragment lengths computed from R and n is the number of non-overlapping segments of target T, then the number of scores associated with each segment t_i will be $m-n+1$. The algorithm proceeds as follows: at first the matching scores associated with t_i are sorted in increasing order. Hence, the first position of the sorted list of t_i contains the minimum score among all the scores. As the penalty factor is very large, this matching score is the best score for placing this particular t_i anywhere in R.

The case stated above outlined an expected ideal case. But sometimes it is not possible to place t_i by considering the least score. If the placements cause to share some regions of R by more than one segment, the placement strategy is not valid at all. To avoid the collision we first try to place t₁; Next we attempt to place t₂, and so on. When we try to place any segment t_i, we check whether the starting and/or ending fragments of segment t_i overlap with any of the already placed segments. If there is such an overlap, we discard this placement and move onto the next segment in the sorted list to correctly place it onto R.

A detailed pseudocode is supplied in Algorithm 2. Let m be the number of fragments in the reference genome R, and n be the number of segments from target T. Intuitively, the number of matching scores of each segment t_i is at most O(m). As the matching score is an integer, sorting matching scores of each segment t_i takes at most O(m) time. So, the execution time of lines 1–5 in Algorithm 2 is O(mn). Sorting segments with respect to starting position of fragments takes O(n) time (line 6). In the worst case, detecting the overlaps (lines 7–14) takes $O(n\hspace{0.5em}\text{log}\hspace{0.5em}n)$ time. As $n\ll m$, the run time of Algorithm 2 is O(mn).

3.3 Recording variations

This is the final stage of our algorithm NRGC. Let $t_1,t_2,t_3,\dots ,t_q$ be the segments of T that are placed onto the segments $r_1,r_2,r_3,\dots ,r_q$ of R, respectively. The algorithm proceeds by taking one segment at a time. Consider the segment t₁. At first t₁ and r₁ are divided into s equal parts, i.e. $t_1=t_1^1{t}_2^1{t}_3^1\dots t_s^1$ and $r_1=r_1^1{r}_2^1{r}_3^1\dots r_s^1$, respectively. The variations of $t_1^1$ with respect to $r_1^1$ is computed first, variations of $t_2^1$ with respect to $r_2^1$ is computed next, and so on. Let $(r\prime ,t\prime )$ be processed at some point in time. At first, the algorithm decomposes $r\prime$ into overlapping substrings of length k (for a suitable value of k). These k-mers are then hashed into a hash table H. It then generates k-mers from $t\prime$ one at a time and hashes the k-mers into H. This procedure is repeated until one k-mer collides with an entry in H. If a collision occurs we align $t\prime$ onto $r\prime$ based on this particular colliding k-mer and extend the alignment until we find any mismatch between $r\prime$ and $t\prime$. We record the matching length, the starting position of this stretch of matching in the reference genome R and the mismatch. If no collision occurs, we decompose $r\prime$ into overlapping substrings of length $k\prime$ where $k\prime <k$ and follow the same procedure stated above. At this point we delete the matching sequences from $r\prime$ and $t\prime$ and align the rest using the same technique as described above. As there could be large insertions in the target genome T, we record the unmatched sequence of T as a raw sequence. The procedure is repeated until the length of $r\prime$ or $t\prime$ becomes zero or no further alignment is possible.

The information generated to compress the target sequence is stored in an ASCII-formatted file. After having processed all the segments of R and the corresponding segments in T, we compress the starting positions and matching length using delta encoding. The resulting file is further compressed using PPMD lossless data compression algorithm. It is a variant of prediction by partial matching (PPM) algorithm and an adaptive statistical data compression technique based on context modelling and prediction. It predicts the next symbol depending on n previous symbols. This method is also known as prediction by Markov Model of order n. The rationale behind the prediction from n previous symbols is that the presence of any symbol is highly dependent on the previous symbols in any natural language. The Huffman and arithmetic coders are sometimes called the entropy coders using an order-(0) model. On the contrary PPM uses a finite context Order-(k) model. Here, k is the maximum context that is specified ahead of execution of the algorithm. The algorithm maintains all the previous occurrences of context at each level of k in a table or trie with associated probability values for each context. For more details the reader is referred to Moffat et al. (1990). Some recent implementations of PPMD are effective in compressing text files containing natural language text. The 7-Zip open-source compression utility provides several compression options including the PPMD algorithm. Details of the algorithm are shown in Algorithm 3.

Consider a pair of parts r and t (where r comes from the reference and t comes from the target). Let $\left|r\right|=\left|t\right|=\ell$. We can generate k-mers from r and hash them in $O(\ell k)$ time. The same amount of time is spent, in the worst case, to generate and hash the k-mers of t. The number of different k-values that we try is a small constant and hence the total time spent in all the hashing that we employ is $O(\ell k)$. If a collision occurs, then the alignment we perform is greedy and takes only $O(\ell )$ time. After the alignment recording the difference and subsequent encoding also takes linear (in $\ell$) time. If no collision occurs for any of the k-values tried, t is stored as such and hence the time is linear in $\ell$. Put together, the run time for processing r and t is $O(\ell k)$. Extending this analysis to the entire target sequence, we infer that the run time to compress any target sequence T of length n is O(nk) where k is the largest value used in hashing.

3.4 Parameters configuration

There are several user-defined parameters and these can be found in the code for the proposed algorithm NRGC. Almost all of the experiments were done using default parameters. The most important parameter of the algorithm is the segment size. In the first phase of NRGC, the target genome is decomposed into a set of non-overlapping segments of fixed size L. In our experimental evaluations, we have fixed L as 500K. Users can change this value using an interface provided. A rule of thumb is: if the variations between the reference and the target genomes are small, L can be small otherwise it should be large. The penalty term P was set to 9999. In the third phase, NRGC builds hash buckets by decomposing the sequences into overlapping k-mers. The set of k-values used in the experiment was $K=\{11,12,13\}$.

Fingerprint/barcode was set to a default string ‘ACTAC’ throughout the experiments. User can change it to any fingerprint/barcode string using the application interface. It is also permitted that application itself can generate fingerprint of user-defined fixed size. In this case, NRGC randomly selects alphabets from A, C, G and T with equal probability and builds a barcode string of user-defined length. It then computes the number of times the fingerprint found in the reference genome. This process is repeated several times and the most occurring fingerprint is chosen for ordered fragment length generation.

4 Results

4.1 Experimental environment

We have compared our algorithm with the best-known algorithms existing in the referential genome compression domain. In this section we summarize the results. All the experiments were done on an Intel Westmere compute node with 12 Intel Xeon X5650 Westmere cores and 48 GB of RAM. The operating system running was Red Hat Enterprise Linux Server release 5.7 (Tikanga). NRGC compression and decompression algorithms are written in standard Java programming language. Java source code is compiled and run by Java Virtual Machine (JVM) 1.6.0.

4.2 Datasets

To measure the effectiveness of our proposed algorithm, we have done a number of experiment using real datasets. We have used hg19, hg18 release from the UCSC Genome Browser, the Korean genomes $KOREF\_20090131$ (KOR131 for short) and $KOREF\_20090224$ (KOR224 for short) [Ahn et al. (2009)], and the genome of a Han Chinese known as YH [Levy et al. (2008)]. To show the effectiveness of our proposed algorithm NRGC, each dataset acts as a reference. When a particular dataset is chosen to be the reference the rest act as targets. By following this procedure any bias related in using a particular reference is omitted. We have taken chromosome 1–22, X and Y chromosomes (i.e., a total of 24 chromosomes) for comparison purposes. Please, see Table 1 for details about the datasets we have used.

Table 1.

Datasets used in the experiments

Dataset	Species	No. of chromosomes	Retrieved from
hg19	Homo sapiens	24	ncbi.nlm.nih.gov
hg18	Homo sapiens	24	ncbi.nlm.nih.gov
KO224	Homo sapiens	24	koreangenome.org
KO131	Homo sapiens	24	koreangenome.org
YH	Homo sapiens	24	yh.genomics.org.cn

4.3 Outcomes

Next, we discuss details on the performance evaluation of our proposed algorithm NRGC in terms of both compression and CPU elapsed time. We have compared NRGC with three of the four best performing algorithms namely GDC, iDoComp and ERGC using several standard benchmark datasets. GReEn is one of the state-of-the-art algorithms existing in the literature. But we could not compare GReEn with our algorithm. The site containing the code of GReEn was down at the time of experiments. Although run time and compression ratio of ERGC were impressive, it did not perform meaningful compression when the variation between target and reference is large. It performs well when the variation between target and reference is small which is not always the case in our experiments. In fact, NRGC is a superior version of ERGC. GDC, GReEn, iDoComp and ERGC are highly specialized algorithms designed to compress genomic sequences with the help of a reference genome. These are the best performing algorithms in this area as of now.

Effectiveness of various algorithms including NRGC is measured using several performance metrics such as compression size, compression time, decompression time, and so on. Gain measures the percentage improvement in compression achieved by NRGC when compared with iDoComp and ERGC. Comparison results are shown in Tables 2 and 3. Clearly, our proposed algorithm is competitive and performs better than all the best-known algorithms. Memory consumption is also very low in our algorithm as it processes one and only one part from the target and reference sequences at any time. Please, note that we do not report the performance evaluation of GDC for every dataset, as it ran for at least 3 h but did not complete the compression task for some datasets. We refer to it in this article as Time Limit Exceeded (or TLE in short).

Table 2.

Performance evaluation of four algorithms using various metrics

				GDC			iDoComp			ERGC			NRGC
Dataset	Reference	Target	A.Size	R.Size	C.Time	D.Time	R.Size	C.Time	D.Time	R.Size	C.Time	D.Time	R.Size	C.Time	D.Time
D1	hg19	hg18	2,996	24.42	68.76	0.54	5.15	20.65	2.55	131.34	13.93	2.22	14.85	14.25	2.09
		KO131	2,938	TLE	TLE	TLE	78.79	21.73	12.51	247.15	16.93	2.21	46.04	16.36	2.10
		KO224	2,938	TLE	TLE	TLE	77.74	37.78	28.96	268.38	18.08	2.15	43.54	16.49	2.27
		YH	2,987	TLE	TLE	TLE	79.68	41.83	31.87	190.59	16.58	2.12	33.04	14.54	2.06
D2	hg18	hg19	3,011	24.42	68.76	0.54	6.10	31.68	2.41	299.45	18.56	2.22	12.37	14.70	1.84
		KO131	2,938	TLE	TLE	TLE	65.03	35.75	11.65	13.46	8.39	1.51	36.89	14.55	1.95
		KO224	2,938	TLE	TLE	TLE	68.58	26.80	11.63	12.03	7.85	1.35	37.780	14.94	2.02
		YH	2,987	TLE	TLE	TLE	64.16	21.41	11.04	7.52	10.10	2.16	27.64	14.32	1.98
D3	KO224	hg19	3,011	TLE	TLE	TLE	195.19	22.36	11.61	443.15	21.45	2.19	28.90	14.90	2.09
		hg18	2,996	TLE	TLE	TLE	200.91	19.86	12.07	18.79	10.17	1.42	30.69	14.37	2.11
		KO131	2,938	11.57	80.49	0.83	6.57	27.91	1.68	5.98	7.23	1.41	7.95	13.72	1.99
		YH	2,987	31.08	68.05	0.52	29.02	37.05	3.56	8.81	14.01	2.07	21.96	13.82	1.94
D4	YH	hg19	3,011	TLE	TLE	TLE	37.11	22.55	13.02	433.41	20.14	2.13	27.11	15.22	1.87
		hg18	2,996	TLE	TLE	TLE	34.18	48.18	12.26	17.22	7.25	1.37	27.61	14.23	2.05
		KO131	2,938	36.28	73.66	0.53	19.16	25.01	4.41	13.05	8.14	1.37	27.99	14.47	1.94
		KO224	2,938	31.08	68.05	0.52	16.02	37.21	3.90	11.57	7.89	1.29	28.66	14.42	1.95

Note: Best values are shown in bold face. A.Size and R.Size refer to Actual Size and Reduced Size in MB, respectively. C.Time and D.Time refer to the Compression Time and Decompression Time in minutes, respectively.

Table 3.

Performance evaluation of three algorithms using various metrics

		iDoComp			ERGC			NRGC			Gain
Dataset	A.Size	R.Size	C.Time	D.Time	R.Size	C.Time	D.Time	R.Size	C.Time	D.Time	iDoComp	ERGC
D1	11,859	241.36	121.99	75.89	816.23	65.52	8.70	137.47	61.64	8.52	43.04%	83.16%
D2	11,874	203.87	115.64	36.73	332.46	44.90	7.24	114.68	58.51	7.79	45.22%	65.51%
D3	11,932	431.69	107.18	28.92	476.73	52.86	7.09	89.50	56.81	8.13	79.27%	81.23%
D4	11,883	106.47	132.95	33.59	475.25	43.42	6.16	111.37	58.34	7.81	−4.60%	76.57%

Note: Best values are shown in bold face. A.Size and R.Size refer to Actual Size in MB and Reduced Size in MB, respectively. C.Time and D.Time refer to the Compression Time and Decompression Time in minutes, respectively

At first consider the dataset D₁. In this case we consider the hg19 human genome as the reference. Targets include hg18, KO131, KO224 and the YH human genome. iDoComp performs better in compressing the hg18 genome by employing hg19 as the reference. In all the other cases, NRGC performs better in compressing KO131, KO224 and YH than all the other algorithms of interest. In fact, NRGC compresses approximately two times better than iDoComp for those particular genomes. NRGC is also faster than iDoComp in terms of both compression and decompression times. Please, see Table 2 for more details. Now consider the overall evaluation for dataset D₁ given in Table 3. The total size of the target genomes is 11 859 MB. NRGC algorithm compresses it to 137.47 MB corresponding to a compression ratio of 86.26. On the other hand, iDoComp achieves a compression ratio of 49.13. Specifically, the percentage improvement NRGC achieves with respect to iDoComp is 43.04%. Compression and decompression times of NRGC are almost $2\times$ and $9\times$ less than those of iDoComp. Note that we did not include the performance evaluation of GDC as in most of the cases it fails to compress the data within 3 h. The average performance of ERGC is poor. The percentage improvement NRGC achieves over iDoComp is 83.16%.

Next consider the dataset D₂. In this case, we consider the hg18 human genome as the reference and the rest as targets. iDoComp performs better in compressing the hg19 genome; in all the other cases, NRGC performs better in terms of compression and elapsed times. In fact, NRGC compresses approximately $1.5-2.0\times$ better than iDoComp for those particular genomes (e.g. KO131, KO224 and YH). NRGC is also faster than iDoComp in terms of both compression and decompression times. Please, see Table 2 for more details. Now consider the overall performance for the dataset D₂ given in Table 3. The percentage improvements NRGC achieves with respect to ERGC and iDoComp are 65.51% and 45.22%, respectively. Compression and decompression times of NRGC are also very impressive compared with iDoComp and comparable with ERGC. For the D₃ dataset the percentage improvements NRGC achieves over ERGC and iDoComp are 81.23% and 79.27%, respectively. The compression achieved by NRGC on the D₄ dataset is slightly lower than that of iDoComp. Please, see Figure 1 for visual details of different evaluation metrics.

Fig. 1.

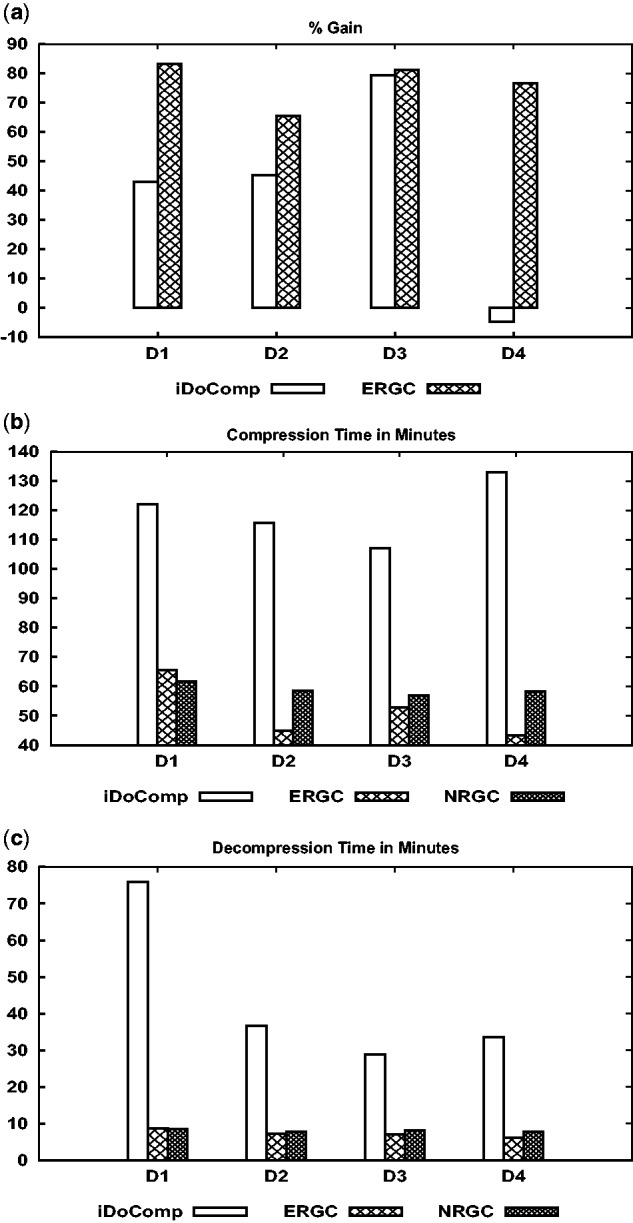
Performance comparisons of iDoComp, ERGC and NRGC methods

5 Discussion

Our proposed algorithm is able to work with any alphabet used in the genomic sequences of interest. Other notable algorithms existing in the domain of referential genome compression can perform compression only with a restricted set of alphabets used for genomic sequences, e.g. $\sum =\{A,a,C,c,G,g,T,t,N,n\}$. These characters are most commonly seen in biological sequences. But there are several other valid characters frequently used in clones to indicate ambiguity about the identity of certain bases in sequences. In this context, our algorithm is not restricted with the limited set of characters found in ∑. NRGC also differentiates between lower-case and upper-case letters. GDC, GReEn and iDoComp can identify the difference between upper-case and lower-case characters defined in ∑ but algorithms such as GRS or RLZ-opt can only handle upper-case alphabet from ∑. iDoComp replaces all the character in the genomic sequence with N that does not belong to ∑. Specifically, NRGC compresses the target genome file regardless of the alphabets used and decompresses the compressed file that is exactly identical to the target file. GDC, iDoComp and ERGC perform the similar job. But GReEn does not include the metadata information and outputs the sequence as a single line instead of multiple lines, i.e. it does not encode the line-break information.

The difference between two genomic sequences can be computed by globally aligning them as the sequences in the query set coming from the same species are similar and of roughly equal size. Let R and T denote the reference and target sequences, respectively, as stated above. The time complexity of a global alignment algorithm is typically $O(|R\left|\right|T|)$, i.e. quadratic in terms of the reference and target lengths. Global alignment is solved by employing dynamic programming and thus is a very time and space intensive procedure specifically if the sequences are very large. In fact, it is not possible to compute the difference between two human genomes using global alignment in current technology. Instead if we divide the reference and target into smaller segments and globally align the corresponding segments, the time and space complexities seem to be improved. But there are two shortcoming in this approach: (i) it still is quadratic with respect to segment lengths and (ii) because of large insertions and/or deletions in the reference and/or target, the corresponding segments may come from different regions (i.e. dissimilar). To quantify this issue, we propose a placement scheme which efficiently finds the most suitable place for a segment in the reference. The segment is then compressed by our greedy variation detection algorithm.

From the experimental evaluations (please see Table 2), it is evident that ERGC performs better than GDC, iDoComp and NRGC in 9 out of 16 datasets. It is also not restricted to the alphabets defined in ∑. But the main limitation of ERGC is that it performs better only when the variations between the reference and the target genomes are small. If the variations, i.e. insertions and/or deletions are high between the reference and the target, its performance degrades dramatically. As hg19 contains large insertions and/or deletions, ERGC fails to perform a meaningful compression while using this genome as the reference or the target. On the contrary, NRGC performs better than ERGC (and other notable algorithms) on an average (please see Table 3). This is due to the fact that NRGC can handle large variations between the reference and target genomes. The main difference between NRGC and ERGC is that NRGC at first finds a near optimal placement of non-overlapping segments of target onto the reference genome and then records the variations. On the other hand, ERGC tries to align the segments contiguously and due to its look-ahead greedy nature it fails to align the segments when there are large insertions and/or deletions in the reference and/or the target genomes. In this scenario, ERGC concludes that the segments could not be aligned and stores them as raw sequences.

As discussed previously, our proposed algorithm NRGC runs in three phases. At first, it computes a score for each of the non-overlapping segments. These segments are then aligned onto the reference genome in the second phase using the scores computed in the first phase. After finding the best possible alignment, NRGC records the variations in the final phase. We provide the time elapsed in each phase in Table 4. Computing scores takes less time compared to alignment and record variation phases. This is due to the fact that the placement procedure performs sorting twice and searches for a non-overlapping placement for each segment. The execution time can be reduced by restricting the search within certain regions of the reference genome. The third phase performs k-mer production, hash table generation and recording variations. This is why it also consumes higher CPU cycles than the first phase.

Table 4.

Phase-wise time decomposition of NRGC

Dataset	Reference	Target	First phase	Second phase	Third phase	Total
D1	hg19	hg18	2.39	5.23	6.62	14.25
		KO131	2.63	5.30	8.42	16.36
		KO224	2.81	5.63	8.04	16.49
		YH	2.10	5.38	7.05	14.54
D2	hg18	hg19	2.25	5.02	7.42	14.70
		KO131	2.40	5.29	6.84	14.55
		KO224	2.46	5.44	7.03	14.94
		YH	2.02	5.41	6.88	14.32
D3	KO224	hg19	2.12	5.83	6.94	14.90
		hg18	2.43	5.41	6.52	14.37
		KO131	2.46	5.40	5.85	13.72
		YH	1.97	5.33	6.52	13.83
D4	YH	hg19	2.20	5.99	7.03	15.22
		hg18	2.39	5.41	6.42	14.23
		KO131	2.40	5.45	6.61	14.47
		KO224	2.38	5.39	6.64	14.42

Note: CPU-elapsed times are given in minutes.

6 Conclusions

In this article, we have proposed a novel referential genome compression algorithm. We employ a scoring-based placement technique to quantify large variations among the genomic sequences. NRGC runs in three stages. At the beginning the target genome is divided into some segments. Each segment is then placed onto the reference genome. After getting the most suitable placement we further divide each segment into some non-overlapping parts. We also divide the corresponding segments of the reference genome into the same number of parts. Each part from the target is then compressed with respect to the corresponding part of the reference. A wide variety of human genomes are used to evaluate the performance of NRGC. It is evident from the simulation results that the proposed algorithm is indeed an effective compressor compared with the state-of-the-art algorithms existing in the current literature.

Funding

This work was supported in part by the following grants: NIH R01-LM010101 and NSF 1447711.

Conflict of Interest: none declared.