Accurate estimation of isoelectric point of protein and peptide based on amino acid sequences

Abstract

Motivation: In any macromolecular polyprotic system—for example protein, DNA or RNA—the isoelectric point—commonly referred to as the pI—can be defined as the point of singularity in a titration curve, corresponding to the solution pH value at which the net overall surface charge—and thus the electrophoretic mobility—of the ampholyte sums to zero. Different modern analytical biochemistry and proteomics methods depend on the isoelectric point as a principal feature for protein and peptide characterization. Protein separation by isoelectric point is a critical part of 2-D gel electrophoresis, a key precursor of proteomics, where discrete spots can be digested in-gel, and proteins subsequently identified by analytical mass spectrometry. Peptide fractionation according to their pI is also widely used in current proteomics sample preparation procedures previous to the LC-MS/MS analysis. Therefore accurate theoretical prediction of pI would expedite such analysis. While such pI calculation is widely used, it remains largely untested, motivating our efforts to benchmark pI prediction methods.

Results: Using data from the database PIP-DB and one publically available dataset as our reference gold standard, we have undertaken the benchmarking of pI calculation methods. We find that methods vary in their accuracy and are highly sensitive to the choice of basis set. The machine-learning algorithms, especially the SVM-based algorithm, showed a superior performance when studying peptide mixtures. In general, learning-based pI prediction methods (such as Cofactor, SVM and Branca) require a large training dataset and their resulting performance will strongly depend of the quality of that data. In contrast with Iterative methods, machine-learning algorithms have the advantage of being able to add new features to improve the accuracy of prediction.

Contact: yperez@ebi.ac.uk

Availability and Implementation: The software and data are freely available at https://github.com/ypriverol/pIR.

Supplementary information: Supplementary data are available at Bioinformatics online.

1 Introduction

In a titration curve, the isoelectric point (pI) is the value at which the overall net surface charge of a macromolecular polyprotic species equals zero. Protein pI values are amongst the most widely determined and widely reported quantities in all of biochemistry and proteomics. The pI is obtained as essentially incidental information during isoelectric focusing (IEF) experiments, free flow electrophoresis (FFE), capillary electrophoresis, and in-gel electrophoresis experiments using IPG strips (Audain et al., 2014; Ramos et al., 2008). Electrophoresis-based separation of proteins and peptides in both free-flow and gel systems has been adapted to a wide variety of proteomics platforms in order to reduce the complexity of the studied proteome (Ramos et al., 2008, 2011). In addition to the resolution and dynamic range of the fractionation technique, combining the electrophoretic separation of proteins with mass spectrometry analysis provides an orthogonal analytical method for improving protein identification in different workflows (Perez-Riverol et al., 2013).

Assuming a protein to be denatured, theoretical calculation of the pI is typically rapid, requiring only the sequence as input (Cargile et al., 2004). Most techniques exploit tabulated pK_a values for the different ionizable amino acid residues; such values are assumed to be constant regardless of structural context (Maldonado et al., 2010). Many authors have reported different values for the pK_as of protein side chains and most of them are derived from measurements of side chains in isolated amino acids or from model compounds; as well as values derived from ionizable side chains in situ (Bjellqvist et al., 1993; Lengqvist et al., 2011). As many such alternative theoretical methods have been proposed, the calculation of protein pI values is in urgent need of benchmarking, since its accuracy remains largely untested. Extant comparison has been exiguous, using very small datasets (Patrickios and Yamasaki, 1995), peptides rather than proteins (Cargile et al., 2004; Lengqvist et al., 2011) or has reported poor accuracy (Henriksson et al., 1995; Patrickios and Yamasaki, 1995).

We have previously described the database PIP-DB (Bunkute et al., 2015), a collection of proteins, with associated experimentally determined pI values, as collated from the literature (Bunkute et al., 2015). In this paper, we use PIP-DB as a gold standard reference for comparison, and describe the benchmarking of protein pI prediction. We also include a peptide dataset to evaluate the performance of pI prediction methods when estimating peptide pIs, due to the importance of properly assessing the accuracy of such prediction. As previously we combine different methods with different parameter values. Specifically, we evaluated five isoelectric point prediction algorithms: Iterative (Maldonado et al., 2010; Patrickios and Yamasaki, 1995), Bjellquivst (Bjellqvist et al., 1993; Cargile et al., 2008), Cofactor (Cargile et al., 2008), SVM (Perez-Riverol et al., 2012) and Branca (Branca et al., 2014); using, where appropriate, a set of alternate values for ionizable amino acid side chain pK_as.

2 Methods

Five different isoelectric point prediction algorithms were evaluated: Iterative (Maldonado et al., 2010; Patrickios and Yamasaki, 1995), Bjellquivst (Bjellqvist et al., 1993; Cargile et al., 2008), Cofactor (Cargile et al., 2008), SVM (Perez-Riverol et al., 2012) and Branca (Branca et al., 2014). The iterative model only considers the contribution of individual pK_a values to the Henderson-Hasselbach equation (Patrickios and Yamasaki, 1995). The Bjellquivst (Bjellqvist et al., 1993) algorithm is based on determining the pK_a differences between closely related amino acids, and it was the first algorithm to propose a different pK_a value depending on the amino acid position in the sequence. The Cofactor algorithm (Cargile et al., 2008) accounts for the effect of adjacent amino acids ±3 residues away from a charged aspartic or glutamic acid and the C-terminus, as well as applying a correction term to the corresponding pK_a values. Perez-Riverol and co-workers (Perez-Riverol et al., 2012) proposed a support vector machine approach to predict the isoelectric point of peptides in electrophoretic experiments based on amino acid sequences and AAIndex properties. The Branca method (Branca et al., 2014) uses pK_a value correction considering the influence of neighboring ionizable groups up to six residues away, multiplying each correction factor by the charged fraction of the neighboring ionizable group before applying it to the initial pK_a value. It also introduces the use of a statistical correction factor that depends on the number and type (Asp or Glu) of carboxylic acid side chains in the sequence.

Different pK_a values were evaluated for each method: for the iterative algorithm we include multiple pK_a sets reported previously (Supplementary Information, Table 1). The Bjellquivst method was evaluated using different pK_a correction factors for C- and N-terminus (Calibrated (Gauci et al., 2008), Expasy (Gasteiger et al., 2003), Skoog and default (Bjellqvist et al., 1993)). The algorithms Cofactor and SVM were evaluated using the default values reported in the corresponding publications. The Branca algorithm was used with the flag pKconstants_plain set, and without considering additional chemical modification in the polypeptide sequence (for example, peptides derivatized with iTRAQ or TMT reagents). Detailed information of each estimation method can be found in Supplementary Information S1.

Table 1.

Benchmark statistics for peptides and protein

	Peptide		Protein
Method	R 2	RMSD	R 2	RMSD
SVM	0.96	0.21	0.59	1.28
ITERATIVE_GRIMSLEY	0.96	0.27	0.54	1.45
BJELL_DEFAULT	0.96	0.28	0.58	1.37
ITERATIVE_RODWELL	0.96	0.31	0.58	1.47
BJELL_CALLIBRATED	0.96	0.32	0.59	1.41
BJELL_EXPASY	0.96	0.33	0.60	1.41
ITERATIVE_THURLKILL	0.96	0.36	0.57	1.50
COFACTOR	0.86	0.44	0.57	1.39
ITERATIVE_SILLERO	0.96	0.46	0.58	1.52
ITERATIVE_TOSELAND	0.95	0.47	0.53	1.41
ITERATIVE_EMBOSS	0.96	0.48	0.57	1.54
BRANCA	0.85	0.51	–	–
BJELL_SKOOG	0.93	0.66	0.57	1.47
ITERATIVE_SOLOMON	0.93	0.71	0.57	1.48
ITERATIVE_LEHNINGER	0.93	0.71	0.57	1.48
ITERATIVE_PATRICKIOS	0.42	1.63	0.15	2.73

Pearson correlation (R²) and root-mean-square deviation (RMSD) for methods and each pK_a set. The best combination (higher R² and low RMSD) was obtained using the support vector machine algorithm for peptides, and the Bjellquivst algorithm with the Expasy pK_a set for proteins.

2.1 pIR R-package

To facilitate analysis of isoelectric point prediction for peptides and proteins, an R package (pIR) was developed using standard best practices for bioinformatics software development (Leprevost et al., 2014; Perez-Riverol et al., 2014). It provides several datasets used in the current study with the corresponding experimental and predicted isoelectric point values. It also provides a framework for reproducible analysis, allowing correlation and RMSD analysis of the predicted values; plot visualization and data processing (outlier removal, null value detection). pIR was implemented in R version ≥2.13.0 and is available from URL: https://github.com/ypriverol/pIR.

2.2 Datasets

For the protein analysis, PIP-DB (Bunkute et al., 2015) (version 1.0), which contains curated protein pI literature data, was used to determine the accuracy of isoelectric point calculation. All proteins where sequence data was available were retrieved from PIP-DB with the corresponding experimental isoelectric point.

For the peptide analysis, a previously published dataset was used (Heller et al., 2005). We utilized the PeptideProphet score to filter out low-confidence peptides from the dataset. In summary, a cellular extract of Drosophila Kc167 cells was fractionated in an isoelectric focusing Off-GEL device using 15 fractions. The tryptic proteome is separated using the isoelectric point and the experimentally derived pI values are reported with the final results. The identified peptides were analyzed with two different database search engines, namely PHENYX and SEQUEST, together with PeptideProphet, which is a popular post-processing peptide identification tool: a final list of 6529 peptides were used for the present study (Heller et al., 2005).

In addition, we have analyzed the impact of common post-translational modifications on isoelectric point estimation using a third dataset, as published previously by Gauci et al. (2008). This experimental dataset was obtained using online TiO2 enrichment in combination with in-gel peptide IEF of a Zebrafish embryo lysate. It contains sub-populations of phosphorylated and N-terminal acetylated peptides whit the corresponding experimental pI values associated.

3 Results

3.1 Isoelectric point estimation of protein sequences

Initially, PIP-DB (Bunkute et al., 2015) was divided into two subsets: proteins with several experimental pI values and proteins with a single experimental pI value (called unique proteins hereafter). Figure 1 shows the protein distribution by isoelectric point for both sets. The second group (proteins with only one pI value) contains 1066 proteins, most of which are from acid fractions (pH range 3.0–6.0).

Fig. 1.

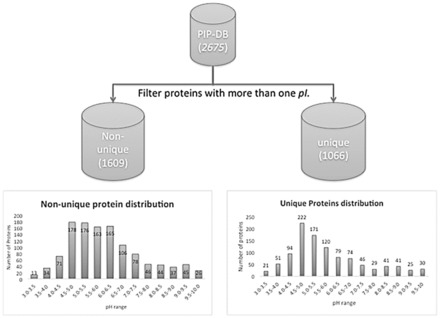
Composition of isoelectric points from PIP-DB (2675 proteins) for the two datasets: unique proteins (proteins with only one isoelectric point value, 1066 proteins); and non-unique proteins (proteins with two or more pI experimental values, 1609). The chart shows the protein number versus pH distribution for both subsets (pH range 3.0–10)

As PIP-DB contains legacy data, not all entries were deemed useful. Initially, we isolated entries with a single measured isoelectric point rather than entries with multiple pI values or a range of values. Estimation of theoretical pI values was undertaken on the unique protein subset. Pearson correlation coefficients and root-mean square deviation (RMSD) values were used to evaluate the performance of the methods in predicting pI.

Table 1 summarizes the correlation coefficients and RMSD values achieved for each evaluated algorithm. The overall correlation between the experimental and theoretical pI values varied between R²= 0.60 (Bjellquivst—Expasy pK_a set) and R²= 0.15 (Iterative-Patrickios pK_a set). The lowest RMSD value was for the SVM algorithm (RMSD = 1.28). Most of the algorithms performed poorly when predicting protein pI, with a correlation coefficient between 0.55 and 0.58.

Figure 2 shows the correlation between the experimental value and the predicted values for five different methods. The correlation in the basic fractions (pI > 7.5) is inferior compared to the complete dataset. Compared to previous studies with peptides (Perez-Riverol et al., 2012), the best correlation is obtained in the neutral range (5.0–7.0 pH) where fewer proteins are observed. Interestingly, the algorithms based on machine learning techniques, such as those of Cargile et al. (Cofactor) and Perez-Riverol et al. (SVM), show a similar correlation compared with the Iterative and Bjellquivst methods: 0.58 and 0.57. These results are consistent with the nature of machine learning algorithms, such as support vector machines and genetic algorithms, which depend critically on the quality and size of training datasets (Larranaga et al., 2006; Perez-Riverol et al., 2012).

Fig. 2.

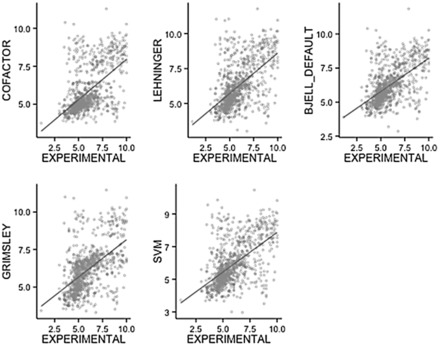
Experimental versus theoretical isoelectric point of proteins from PID-DB. Five different combinations of methods and pK_a values and algorithms were used. The x-axis corresponds to the experimental isoelectric point range of 3–10 and the y-axis is the corresponding calculated values

These algorithms were developed for peptide-mixture prediction where a large number of peptides can be used to train the model (Perez-Riverol et al., 2012). The recently developed Branca algorithm cannot be used to compute protein isoelectric points as it was only optimized for peptides with K or R at their C-terminus: it fails for proteins that do not have a basic C-terminus. This low correlation between experimental and predicted values demonstrated that only certain of the algorithms could be used for in silico studies of the isoelectric point distribution in proteomes, such as those by Wu et al. (2006) and Carugo (2007).

Figure 3 shows the distribution of experimental isoelectric points and predicted distributions for several algorithms. The distribution of the experimental values only shows similarity to the theoretical distribution of the SVM (Perez-Riverol et al., 2012), Bjellquivst (Bjellqvist et al., 1993) and Iterative (with Lehninger pK_a set) algorithms. We explored the correlation between the theoretical and experimental isoelectric point of proteins for the complete PIP-DB database (Supplementary Information S2, Fig. 1) using four pK_a sets (DEFAUT, Expasy, CALIBRATED and SKOOG). The correlation for the CALIBRATED and Expasy pK sets is negative (R²= −0.017) for the entire PIP-DB. In contrast to peptides, over 50% of the proteins in our dataset have more than one experimental pI (Table 2), making it difficult to study this property properly, due to the historic use of poor analytical methods, together with protein denaturation and fragmentation (Ramos et al., 2012).

Fig. 3.

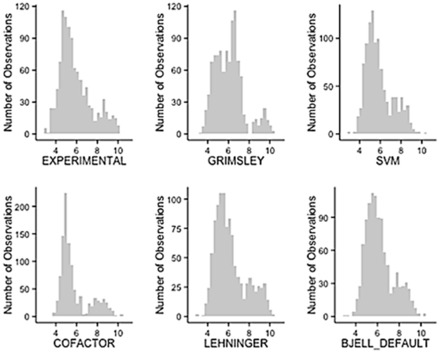
Distribution of isoelectric point for different methods and the experimental distribution. The y-axis is the number of proteins for the corresponding isoelectric point value (x-axis)

Table 2.

Protein occurrence in PIP-DB

Occurrences	1	2	3	4	5	6	7	8	9	10	11	12	13	15	>15
Number of proteins	1042	183	81	41	30	21	14	8	4	5	3	3	2	1	8

Over 50% of proteins are found with at least 2 experimental isoelectric point value associated.

A potential use of pI prediction algorithms is the possibility to detect outliers from experimental data and detect possible incorrect assignment at the protein and peptide level (Perez-Riverol et al., 2011). The number of outliers also can be use as quality assessment metric of the separation technique (Ramos et al., 2011). If the algorithm is more accurate it tends to predict more outliers and possible false-positive identifications assignments. Figure 4 shows the distribution of outliers and non-outliers, of four of the pI algorithms under study. The SVM-based algorithm proposed by Perez-Riverol and co-workers in 2012 predicted the percentage of outliers, especially in the neutral and basic regions, where the method out-performs the other algorithms.

Fig. 4.

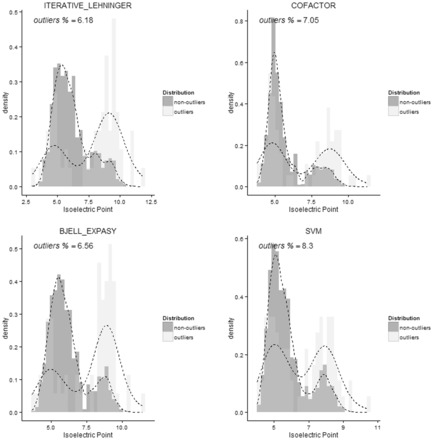
Distribution of outliers and non-outliers populations of the PIPDB portion evaluated. An outliers is defined if: Abs(pI_experimental – pI_theoretical) ≥ SD (pI_theoretical)

3.2 Isoelectric point estimation of peptide sequences

Results seen for the peptide dataset are markedly different: a high correlation was observed for most methods (Table 1). Although the top seven methods all show the same correlation R²= 0.96, the best result is the SVM method (Perez-Riverol et al., 2012) which has the lowest RMSD (0.21). Figure 5 shows the average pI and standard deviation from IEF fractions from the peptide dataset analyzed. The largest standard deviation was found in the 5–7 pI range. The best correlation is always observed in the acid fractions (Fig. 4). In this region, most of the methods generated a good estimate for the peptides, with a pI between 4.0 and 5.0, where the lowest RMSD was obtained. Similar to the results obtained on PIP-DB analysis, the Iterative method used with the Patrickios pK_a set fails fully in the complete dataset.

Fig. 5.

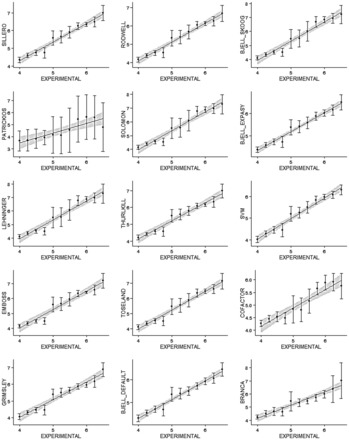
Experimental versus theoretical isoelectric point for 11 different peptide fractions of an OFF-GEL electrophoresis experiment (Heller dataset)

The Bjellquivst algorithm shows a higher number of outliers (black dots) in the basic fractions compare with the SVM algorithm (Supplementary Information S2, Fig. 2). Outlier (peptide with deviant pI) detection is highly dependent on both the accuracy of the pI estimation and the quality of the electrophoretic experiment (Ramos et al., 2011). Predicted pIs can be applied to remove less likely identified peptides and to curate the final protein identification result lists in a shotgun proteomics experiment (Perez-Riverol et al., 2011). Importantly an outlier may not necessarily imply an estimation error, but may indicate the presence of one or more posttranslational modifications (Lengqvist et al., 2011).

Interestingly, no major changes in the correlation values are observed when different pK_a sets are used with the Bjellqvist method, 0.95–0.96; this suggests that most of the pK_as values published after Bjellqvist (Bjellqvist et al., 1993) only perform better in certain analytical settings (Table 1). A similar trend is observed for the Iterative method; this again suggests that none of the sets of pK_a values is optimal or is necessarily superior to any other, and in most cases different pK_a values should be used for different calculations. The cofactor method (Fig. 4) performs more poorly than most of the algorithms as it was designed to study acid fractions only (Cargile et al., 2008). The recent Branca algorithm also exhibited a poor performance on this dataset (R²= 0.85, Table 1). It was also designed and trained to study peptides in acid fractions by adding corrections to the original pK_a sets proposed by Bjellquivst. For this reason, in basic ranges the algorithm has a low correlation coefficient and a high RMSD value (Fig. 4).

In contrast, other methods such as SVM, Bjellqvist and Iterative (with certain pK_a sets) show better behavior throughout the fractions analyzed. The confidence intervals indicating the ability to predict near to an ideal performance (pI_experimental versus pI_predicted) are closest for these last algorithms.

3.3 Isoelectric point estimation of modified peptides

Post-translational and experimentally induced peptide modifications can shift peptide pI compared to the values estimated for the unmodified sequence in two ways: (i) by introducing charged groups or (ii) by neutralizing charged groups (Ramos et al., 2011). The results presented in Section 3.2, show for most of the algorithms, a good correlation between the predicted and experimental pI values of peptides on a ‘non-modified’ dataset. However, an extended analysis taking into account post-translational modifications such as phosphorylation and N-terminal acetylation will provide a more accurate representation of a real electrophoretic experiment. Figures 6 and 7 show the experimental pI values versus the predicted phosphopeptide and acetylated peptide pI and also the non-modified variants for several pI algorithms, with a previously reported dataset (Gauci et al., 2008). The best correlation was obtained when the modification was considered during the estimation of the theoretical pI, increasing the correlation from 0.4 to 0.9 for most of the algorithms (Supplementary Information S3), demonstrating the dramatic effect of post-translational modifications on pI estimation.

Fig. 6.

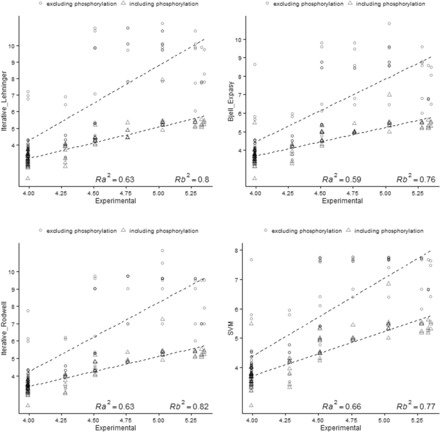
Correlation between predicted pI versus experimental pI. The plots show the correlation obtained if Phosphorylation is exclude (○) or include (Δ) in the pI calculation. R_a and R_b denote the correlation coefficients excluding and including the modification in the estimation respectively. The pK_a and pK_b values of 1.2 and 6.5 for phosphorylation S and T were used to consider the phosphorylation effect in the pI estimation

Fig. 7.

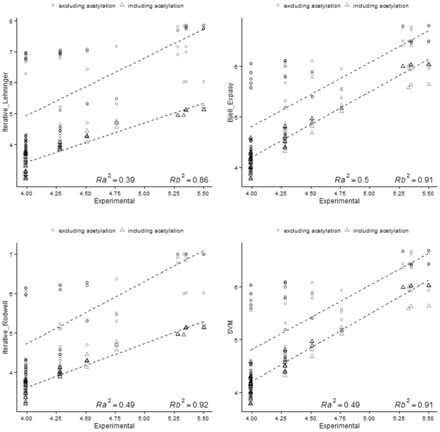
Correlation between predicted pI versus experimental pI. The plots show the correlation obtained if N-terminal acetylation is exclude (○) or include (Δ) in the pI calculation. R_a and R_b denote the correlation coefficients excluding and including the modification in the estimation respectively. The pI of the N-terminal acetylated peptides was calculated by omitting the pK values of the N-terminal residue in the peptide sequence

When the N-terminus of a peptide is acetylated, a positive charge is lost, decreasing the overall charge of the peptide (Gauci et al., 2008; Lengqvist et al., 2011). Correspondingly, phosphorylation affects the charge of a peptide by adding a negatively charged group (Halligan, 2009; Ramos et al., 2011). Figure 7 shows that the impact of acetylation is more predominant to phosphorylation, making results poorer if acetylation is not take into account. If those PTMs are not considered during predictions and in silico studies, the final results can be completely different to the real experiment, especially, the acetylation due the distribution of Lysine and N-terminally in tryptic proteomes (Perez-Riverol et al., 2011).

4 Discussion

Our benchmarking comparison constitutes a strong blind test, since no method is in any way optimized for this particular data set and all the proteins and corresponding isoelectric points were collected from different sources and correspond to distinct analytical settings. The present study demonstrates that the algorithms from Bjellqvist et al. and Perez-Riverol et al. represent the most accurate algorithms overall for computing protein isoelectric points. The results also demonstrate that when other pK_a sets are employed no significant differences were seen for the Bjellqvist et al. approach, and most of the small differences observed can be related to specific analytical conditions specific to the experiment. The poor performance of all evaluated algorithms for the single value protein dataset is alarming. There are several possible explanations for this behaviour. The dataset was evaluated using a variety of methods over many decades. Thus the intrinsic variation will arise both from true biological variation (the presence of unknown processed or truncated proteins or proteins with charged post-translational modifications, etc.) and other errors introduced by a gallimaufry of different experimental protocols, each with distinct and incommensurable calibration. The low correlation between experimental and predicted values throws serious doubt on the veracity of many theoretical studies of isoelectric point distributions in whole proteomes, such as the studies by Wu et al. (2006) and Carugo (2007), and any arguments made on that basis. An alternative exegesis posits that PIP-DB must contain a large number of annotation errors, as introduced during database construction, which seriously contaminates the result. This is clearly possible, if highly unlikely.

In IEF gels or SDS-PAGE experiments, it is common to find the same polypeptide instance through multiple experimental fractions, due to diffusion phenomena, or from uneven cutting during band excision across of the gel. In addition, the peptides or proteins could have precipitated out of solution during migration from the well to the appropriate pH in the gel.

Possible aggregation and degradation could contribute to enhance inappropriate focalization, making it difficult to correctly interpret the results obtained. It has also been shown that not only the amino acid composition but also its subsequent modification can influence the accurate estimation of the isoelectric point, e.g. common modifications such as phosphorylation and acetylation which might lead to the shielding of surface charges (as previously described in Section 3.3). PIP-DB illustrates this complex scenario as shown in the Table 3. It contains multiple proteins that may be ‘detectable’ in both acid and basic region, showing a wide focalization zone. Most pI prediction methods do not take into account such ‘artifacts’ and will thus fail to make accurate estimates.

Table 3.

Proteins with a wide focalization zone in PIP-DB

Protein	Occurrences	Focalization zone size*
gi|15924609	3	3.5
sp|P09616	5	3.5
sp|Q02161	3	3.5
sp|Q3T0P6	3	3.65
sp|P12019	3	3.7
tr|Q9N102	4	3.79
sp|P00750	2	3.8
sp|P23141	3	3.8
sp|Q8WVB3	28	3.8
tr|Q9XDT2	2	3.9
sp|P31211	6	4.0
sp|P00558	3	4.05
tr|Q6LBH1	30	4.08
sp|O00142	3	4.1
gi|2506195	2	4.2
sp|P24735	6	4.3
tr|Q9AJM4	2	4.3
sp|P06746	4	4.35
sp|P55056	2	4.39
sp|P01139	3	4.8
sp|P54819	10	4.8
sp|P00480	5	4.85
sp|P13233	23	4.9
sp|P14518	5	4.9
tr|E5GC51	8	6.4

* Defined by the difference between the maximal and minimal pI experimental value found for the protein in PIP-DB.

These results also highlight the need for a complete and customizable tool that can provide all available algorithms and pK_a sets for isoelectric point analysis. The machine-learning algorithms, especially the SVM-based algorithm, showed a superior performance when studying peptide mixtures. In general, learning-based pI prediction methods (such as Cofactor, SVM and Branca) require a large training dataset and their resulting performance will strongly depend of the quality of that data. Even though Cofactor and Branca algorithms are based on learning approaches, it is not possible to retrain these algorithms with different datasets. In this sense, the SVM approach shows more ‘flexibility’ in pI computation, and this feature can improve prediction accuracy. In contrast with Iterative methods, machine-learning algorithms have the advantage of being able to add new features to improve prediction. Considering the amount of pK_a sets reported to date, use of the Iterative approach provides a good opportunity to find some variant that fits well with particular experimental conditions. In the near future, new algorithms and bioinformatics tools should be able to provide a way of choosing different pK_a sets and thus obtain more accurate prediction for a given analytical setting. The SVM and Cofactor methods should only be used where a high number of sequences are studied and can thus be used to train the algorithms. We observed notable fluctuations in pI predictions for Iterative methods on a small dataset, showing this method to be sensitive to small changes in the amino acid pK_a values used. Moreover, the algorithm fails when certain pK_a values are missing. We envisage that more algorithms based on machine learning, including new additional features, should be explored allowing the development of fast, accurate and reliable pI calculation algorithms for use in future protein and peptide proteomic analysis.

Funding

Y.P-R. is supported by the BBSRC ‘PROCESS’ grant [BB/K01997X/1].

Conflict of Interest: none declared.