Dual-Phase ADC Modelling of Breast Masses in Diffusion-Weighted Imaging: Comparison with Histopathologic Findings

Abstract

Objective

To investigate the diagnostic value of dual-phase apparent diffusion coefficient (ADC) compared to traditional ADC values in quantitative diffusion-weighted imaging (DWI) for differentiating between benign and malignant breast masses.

Materials and Methods

Diffusion-weighted images of pathologically confirmed 88 benign and 85 malignant lesions acquired using a 3.0T MR scanner were analyzed. Small region-of-interests focusing on the highest signal intensity of lesions were used. Lesion ADC estimates were obtained separately from all b-value images (ADC; b=50, 400 and 800s/mm²), lower b-value images (ADC_low; b=50 and 400s/mm²) and higher b-value images (ADC_high; b=400 and 800s/mm²). A set of dual-phase ADC (dpADC) models were constructed using ADC_low, ADC_high and a perfusion influence factor ranging from 0 to 1.

Results

Strong positive correlation is observable between ADC and all dpADCs (ρ=0.80–1.00). Differences in ADC and dpADCs between the benign and the malignant lesions are all significant (p<0.05). In detecting malignancy, traditional lesion ADC provides a good performance (AUC=89.9%) however dpADC_0.5 (dpADC with a factor of 0.5) accomplishes a better performance (AUC=90.8%). At optimal thresholds, ADC achieves 94.1% sensitivity, 72.7% specificity and 83.2% accuracy while dpADC_0.5 leads to 92.9% sensitivity, 79.5% specificity and 86.1% accuracy.

Conclusion

Dual-phase ADC modelling may improve the accuracy in breast cancer diagnosis using DWI. Further prospective studies are needed to justify its benefit in clinical setting.

Introduction

Diffusion-weighted imaging (DWI) utilizes diffusion signal attenuated due to the random microscopic motion of water molecules influenced by cell density, membrane integrity, tissue microstructure, perfusion and diffusion heterogeneity within the tissue (1). When compared with benign lesions and healthy tissue, more restricted water mobility of malignant lesions engenders slower attenuation of the diffusion signal captured from a set of images acquired with different degrees of diffusion weighting (reported as b-value) (2).

Quantitative diagnosis of cancer from DWI relies on metrics computed as the parameters of a “signal attenuation” model fitted to the diffusion signal data. The need for reliable and precise metrics motivates new studies on development of advanced models for better fittings to the diffusion signal data or advanced methods for optimized estimation of diffusion metrics (3). There exist several advanced exponential signal attenuation models such as stretched exponential (4), bi-exponential (known as intravoxel incoherent motion) (5), statistical (6) and kurtosis (7) capable of describing complex diffusion processes of the breast tissue. However, the parameters derived from these models are difficult to estimate and quite complex for use in diagnosis. For instance, physiological basis of the heterogeneity index of the stretched exponential model is reported to be uncertain and likewise pseudo-diffusion coefficient of the biexponential model is thought to be unreliable (8). On the other hand, these models involve several parameters that complicate both the diffusion estimation process and the diffusion weighted imaging protocol. To get accurate diffusion estimates, the initial value and the limits for any model parameter should be determined very carefully and an appropriate optimization method should be employed (9). To reach consistent numerical solutions, the number of b-values of the diffusion weighted imaging protocol must set to be more than the number of parameters in the model and large number of b-values would lengthen the imaging time remarkably making it unmanageable in clinical practice. These challenges promote the use of a mono-exponential model, that offers only one free parameter (namely apparent diffusion coefficient) estimated from two different b-value images with simplicity and high reproducibility, as the traditional model in diagnostic DWI in clinical practice (10).

Diffusion-weighted imaging and the use of apparent diffusion coefficient has been reported to be a very beneficial technique adjunct to dynamic contrast-enhanced imaging in diagnosis of breast cancer using magnetic resonance (MR) imaging (11, 12). While DWI holds potential to improve the detection and biological characterization of breast cancer (13), apparent diffusion coefficient (ADC) is capable of reflecting breast tissue cellularity, fluid viscosity, membrane permeability, macromolecular structures, microvascularity and lesion blood flow (14). Benign lesions have higher ADC than malignant lesions, especially the invasive carcinomas mainly due to their less compact cellularity (15). However, overlap between the ADC estimates from benign and malignant breast lesions motivate new studies to improve the performance of ADC in distinguishing benign lesions from malignant lesions.

The b-value set used during diffusion weighted imaging has an impact on the fitting performance of the mono-exponential model and on the diagnostic performance of ADC consequently (16). The lowest b-value is set to be sufficiently high so as the model can describe the diffusion signal data appropriately (b≥50s/mm² is usually used) while the highest b-value should be chosen so as to provide adequate suppression of water signal from normal fibroglandular tissue and maximum breast lesion visibility (17) (The use of b≥800s/mm² is usually recommended (18, 19)). Incorporating more than two b-values into the imaging protocol has been reported to provide more precise sampling of the diffusion signal and consistent ADC estimates (20, 21).

Diagnostic performance of ADC is also influenced by the methods used during image analysis and computation. A smaller region-of-interest (ROI) focusing on the highest signal intensity for the lesion is reported to have a better differential value for ADC when compared with a larger ROI for the overall lesion, especially in discrimination of invasive carcinomas (22). Normalized ADC (also called ADC ratio) calculated from the ratio of the lesion ADC to a reference tissue ADC (usually ipsilateral glandular breast tissue) is illustrated to make some improvements in the overall performance of ADC (23–25). Two separate ADCs from a lesion, one estimated from low b-value images and the other estimated from high b-value images, are demonstrated to be potentially more useful than a single lesion ADC in assessing the non-Gaussian water diffusion in vivo that is more closely related to the advanced models (26). In this study, we introduce dual-phase ADC modelling that integrates two separate ADCs, one from low b-value images and the other from high b-value images, and evaluate the utility of the modeling for breast masses in comparison with the histopathologic findings in quantitative DWI.

Materials and Methods

Patient Population

A total of one hundred seventy-three lesions (88 benign and 85 malignant) from 173 women aged 18–78 years (mean, 46 years), who underwent standard breast MRI including diffusion weighted imaging to clarify uncertain clinical, mammographic, sonographic findings or to assess preoperative staging of patients with known malignancies, have been retrospectively enrolled in this study. Written informed consent was obtained from each woman and local ethics committee approval was received. All findings were verified by histopathological examination. Average lesion size was 18.2±8.1mm. The benign lesions were 45 fibroadenomas, 14 columnar cell changes, 8 fibroses, 6 adenoses, 5 abscesses, 5 apocrine metaplasias and 5 other benign changes. The malignant lesions were 61 invasive ductal carcinomas, 9 invasive lobular carcinomas, 8 ductal carcinomas in situ, 3 invasive mucinous carcinomas, 1 invasive apocrine carcinoma, 1 medullary carcinoma, 1 medullary like carcinoma and 1 liposarcoma.

Breast MR Imaging Protocol

Breast MR imaging was performed by a 3T MR scanner (Magnetom Verio, Siemens Healthcare, Erlangen, Germany) using a dedicated 16-channel breast coil while patients were lying in prone position. At first, T2-weighted images were acquired using an axial turbo spin-echo with 70ms echo time (TE), 4100ms repetition time (TR), 448×381 matrix size, 320mm field of view (FOV), 3mm slice thickness. Next, diffusion-weighted images were captured in the axial plane using a 2D spin-echo echo-planar imaging (EPI) sequence at three b-values (b=50, 400 and 800s/mm²) with the following parameters: 86ms echo time, 9700ms repetition time, 90° flip angle, 3 averages, 82×192 matrix size, 155×360mm FOV and 4mm slice thickness (leading to an in-plane resolution of 1.9×1.9×4mm³). Finally, axial dynamic contrast-enhanced MR images were taken using 3D volumetric interpolated breath-hold (VIBE) imaging sequence with the following parameters: 1.77ms echo time, 5.01ms repetition time, 10° flip angle, 512×512 matrix size, 340mm FOV and 1mm slice thickness. During and immediately after the bolus injection of contrast agent Gadobutrol (0.1mmol/kg Gadovist®, Bayer Schering Pharma, Berlin, Germany) or Gadoterate Meglumine (0.1mmol/kg Dotarem®, Guerbet, Villepinte, France), one pre-contrast and six postcontrast bilateral images were acquired with a temporal resolution of 88 seconds.

Image Evaluation and ROI Delineation

All images acquired during imaging were transferred to workstation and evaluated by two experienced radiologists (with 4 and 17 years of experience in breast MRI, respectively) using Syngo. Via 3D reading and advanced visualization software (Siemens Healthcare, Erlangen, Germany) installed on the workstation. Both radiologists were blinded to pathology during evaluation. The radiologists first analyzed the dynamic contrast-enhanced images to localize lesions. The radiologists next evaluated each localized lesion on diffusion-weighted images and manually placed a region of interest (ROI) with consensus on the diffusion-weighted image with b=800s/mm² with care to include only the solid portion of the lesion with the highest signal intensity, excluding the necrotic and the cystic regions. All ROIs were defined to be circular with a diameter of 5mm. For each ROI placed, average signal intensity for each b-value of the diffusion-weighted imaging protocol given by the software was recorded for use to estimate apparent diffusion coefficients.

Dual-phase Apparent Diffusion Coefficient Modelling

Dual-phase ADC modelling integrates the two ADC estimates: ADC_low from lower b-value images (b=50–400s/mm²) and ADC_high from higher b-value images (b=400–800s/mm²) by using the following formula introduced in this study:

$${\text{dpADC}}_{\text{pf}}=\text{pf}\times {\text{ADC}}_{\text{low}}+(1-\text{pf})\times {\text{ADC}}_{\text{high}}$$ (1)

Here pf is “perfusion” influence factor that ranges from 0 to 1. When pf is set to 0, the influence of ADC_low is omitted giving dpADC₀ = ADC_high. In contrast, if pf is set to 1, the influence of ADC_high is omitted and dpADC_1.0=ADC_low. ADC_low is influenced by perfusion mostly and diffusion in a certain degree while ADC_high reflects diffusion only. By voluntarily modifying the value of pf, different dual-phase ADC models can be obtained. The apparent diffusion coefficient can be estimated by using the mono-exponential model and the average signal intensity for an ROI recorded for n-th b-value of the diffusion-weighted image, S(b_n):

$$\text{S}({\text{b}}_{\text{n}})=\text{S}({\text{b}}_{\text{1}})\times {\text{exp}}^{-{\text{b}}_{\text{n}}\times \text{ADC}}$$ (2)

In this study, ADC estimates were obtained for all breast lesions separately by using average signal intensity values from all b-value images (ADC; b=50, 400 and 800s/mm²), from only lower b-value images (ADC_low; b=50 and 400s/mm²) and from only higher b-value images (ADC_high; b=400 and 800s/mm²). The estimations were performed using our own in-house developed computer software based on MatLab (Mathworks, Natick, MA) implementing a nonlinear fitting method based on the Trust-Region-Reflective least squares algorithm with the same pre-set initial value and the same limits for the ADC parameter (initial value=1.5×10⁻³mm²/s, upper and lower limits=3.0×10⁻³mm²/s and 0.3×10⁻³mm²/s, respectively) (Figure 1).

Figure 1. a–c.

A 48-year-old woman with a benign lesion (a fibroadenoma) finding on the left breast and (a) the ROI placed for the lesion (solid red line contour) on the diffusion-weighted image at b=800mm²/s. (b) Plots for the average signal intensity measurements recorded and for the results of the nonlinear fittings obtained (ADC=1.64×10⁻³mm²/s, ADC_low=1.73×10⁻³mm²/s and ADC_high=1.42×10⁻³mm²/s) and (c) Plot for the dpADC computed for a specific “perfusion” influence factor

Statistical Analysis

Systematic difference in ADC and dpADC of the lesions were tested using Wilcoxon signed-ranks test. Spearman’s rho (ρ) was used to test correlation between lesion dpADC and lesion ADC. Absolute relative difference between dpADC and ADC was measured using

$${\mathrm{\Delta }}_{\text{rel}}=\frac{\left|\text{dpADC-ADC}\right|}{\text{ADC}}\times 100$$ (3)

Systematic differences in ADC and dpADC between benign and malignant lesions were tested using Mann-Whitney U-test. Diagnostic performance was assessed by plotting the receiver operating characteristic (ROC) curves and calculating the areas under the ROC curves (AUC). A p value of <0.05 was considered to be statistically significant.

Optimal thresholds for ADC and dpADC were determined by applying Youden statistics to the results of ROC analysis while considering improvements in both sensitivity and specificity. The classification performances of the optimal thresholds were assessed using sensitivity (Se), specificity (Sp), positive predictive value (PPV) and accuracy (Ac). All statistical analyses were performed using SPSS software for Windows (version 23; SPSS, Chicago, IL).

Results

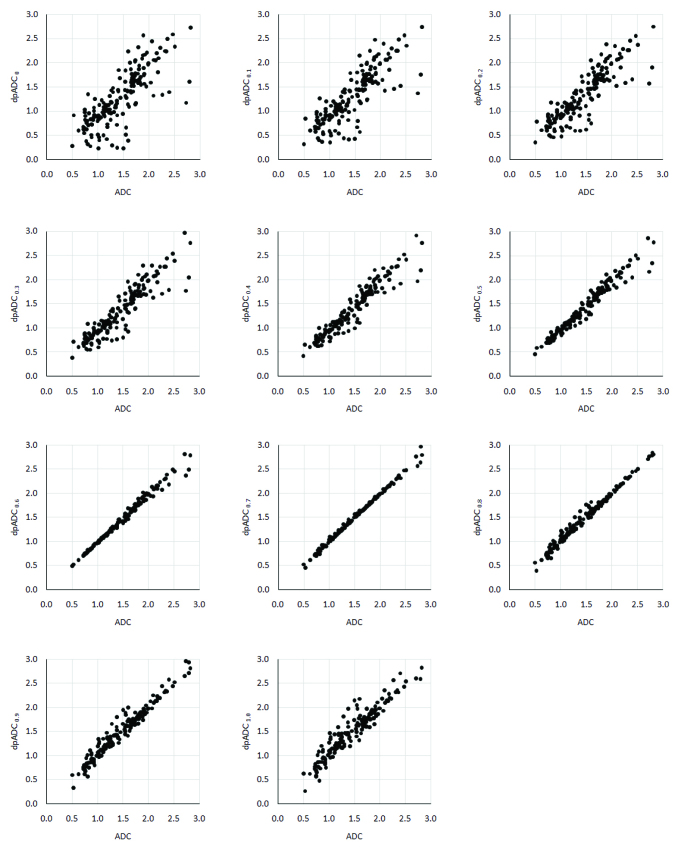
Dual-phase apparent diffusion coefficient models using a set of perfusion influence factor (pf) and overall dual-phase ADC values (dpADC) estimated by the models from all breast lesions enrolled in this study are seen in Table 1. dpADC is at its minimum when pf is set to zero while dpADC is at its maximum when pf is set to one showing that dpADC is directly proportional to the perfusion influence factor: an increase in the factor leads to an increase in dpADC. ADC estimate from all lesions is 1.47±0.51×10⁻³mm²/s and a very similar value of 1.47±0.52×10⁻³mm²/s is obtained by the dpADC model with a pf of 0.7 leading to the lowest absolute relative difference among all the dpADC models studied (Δ_rel=1.6%). However, there are systematic difference in ADC and dpADC from all the models, but significant positive correlations are present between ADC and dpADC at all (p<0.05). Strong correlations exist between ADC and dpADC obtained by the models using pf values of 0, 0.1 and 0.2 (ρ=0.80–0.90) but the rest of the models offer very strong correlations (ρ=0.90–1.00) (Figure 2). Table 2 shows the ADC and dpADC estimates from the benign and the malignant lesions. Independent of the perfusion influence fraction considered during modelling, low dpADC values indicate malignancy as in traditional ADC case. The differences in dpADC estimates between benign and malignant lesions from all the models are significant (p<0.05).

Table 1.

Dual-phase ADC models and lesion dpADC with respect to perfusion influence factor and corresponding correlations and relative differences between dpADC and ADC

Model	pf	dpADC	ρ	Mean Δrel(%)
dpADC0	0	1.31±0.61	0.80	20.4
dpADC0.1	0.1	1.33±0.58	0.85	17.4
dpADC0.2	0.2	1.36±0.56	0.88	14.3
dpADC0.3	0.3	1.38±0.54	0.93	11.3
dpADC0.4	0.4	1.40±0.52	0.96	8.2
dpADC0.5	0.5	1.43±0.51	0.99	5.2
dpADC0.6	0.6	1.45±0.51	1.00	2.1
dpADC0.7	0.7	1.47±0.51	1.00	1.6
dpADC0.8	0.8	1.49±0.52	0.99	4.0
dpADC0.9	0.9	1.52±0.53	0.97	7.1
dpADC1.0	1.0	1.54±0.55	0.94	10.1

Mean±SD in 10⁻³mm²/s, overall ADC is (1.47 0.52)x10⁻³mm²/s

All statistical values are significant (p<0.05)

pf: perfusion influence factor; dpADC: dual-phase ADC; ρ: spearman’s rho; Δ_rel: absolute relative difference

Figure 2.

Plots for the ADC estimates with respect to dpADC estimates by the model using a pf of (a) 0, (b) 0.1, (c) 0.2, (d) 0.3, (e) 0.4, (f) 0.5, (g) 0.6, (h) 0.7, (i) 0.8, (j) 0.9 and (k) 1.0 from all lesions

Table 2.

Benign and malignant lesion dpADCs

Model	Benign Lesion	Malignant Lesion
dpADC0	1.68±0.56 a	0.92±0.38
dpADC0.1	1.70±0.52	0.95±0.35
dpADC0.2	1.72±0.49	0.98±0.33
dpADC0.3	1.73±0.46	1.00±0.31
dpADC0.4	1.75±0.45	1.04±0.30
dpADC0.5	1.76±0.44	1.07±0.30
dpADC0.6	1.78±0.43	1.10±0.30
dpADC0.7	1.80±0.44	1.13±0.32
dpADC0.8	1.81±0.45	1.16±0.34
dpADC0.9	1.83±0.48	1.19±0.34
dpADC1.0	1.84±0.51	1.23±0.40

^aMean±SD in 10⁻³mm²/s

All statistical values are significant (p<0.05)

dpADC: dual-phase ADC; ADC: apparent diffusion coefficient

Results of the ROC analyses of ADC and dpADC in differentiation of malignant lesions from benign lesions are as presented in Table 3. The dpADC models using a pf value of 0.2, 0.3, 0.4, 0.5 or 0.6 provides better performance (AUC≥90.0%) when compared to ADC (AUC=89.9%). Among these models, the model dpADC_0.5 that enrolls a perfusion influence fraction of 0.5 stands out in terms of its highest diagnostic accuracy (AUC=90.8%).

Table 3.

Diagnostic performance of dpADC and of ADC (in %)

	AUC	SE	95% Confidence Interval of AUC
			Lower Bound	Upper Bound
dpADC0.5	90.8	2.2	86.4	95.2
dpADC0.4	90.7	2.3	86.3	95.2
dpADC0.3	90.6	2.3	86.2	95.1
dpADC0.6	90.3	2.3	85.7	94.8
dpADC0.2	90.0	2.4	85.3	94.7
ADC	89.9	2.4	85.3	94.5
dpADC0.7	89.7	2.4	85.0	94.3
dpADC0.1	89.1	2.5	84.2	94.0
dpADC0	88.1	2.6	82.9	89.9
dpADC0.8	88.0	2.5	83.0	93.2
dpADC0.9	86.2	2.7	80.8	91.5
dpADC1.0	84.1	3.0	78.3	89.9

ADC: apparent diffusion coefficient; dpADC: dual-phase ADC; AUC: area under the curve; SE: standard error

Diagnostic performances of ADC and dpADC form the models for optimal thresholds determined are listed in Table 4 and the corresponding plots for sensitivity, specificity and accuracy of the models are seen in Figure 3. ADC achieves 94.1% sensitivity, 72.7% specificity, 76.9% positive predictive value and 83.2% accuracy due to 5 false-negative and 24 false-positive detections (29 false detections in total) at an optimal threshold of 1.61×10⁻³mm²/s. Among the dpADC models, dpADC₀ offers low sensitivity (77.6%) but the highest specificity (87.5%) meanwhile dpADC_0.5 and dpADC_0.6 provide the highest sensitivity (92.9%) but lower specificities (79.5% and 78.4%, respectively). However, the best performance is given by dpADC_0.5: 92.9% sensitivity, 79.5% specificity, 81.4% positive predictive value and 86.1% accuracy due to 6 false-negative and 18 false-positive detections (24 false detections in total) at an optimal threshold of 1.50×10⁻³mm²/s. These results show that when compared to ADC, dual-phase ADC can provide almost the same sensitivity but considerably higher specificity that improves the positive predictive value and the accuracy.

Table 4.

Classification performance of dpADC and of ADC

	Thresholda	False Detections	Se	Sp	PPV	Ac
dpADC0.5	1.50	24 [18b+6b]	92.9	79.5	81.4	86.1
dpADC0.6	1.54	25 [19+6]	92.9	78.4	80.6	85.5
dpADC0.2	1.29	26 [14+12]	85.9	84.1	83.9	85.0
dpADC0.3	1.33	26 [14+12]	85.9	84.1	83.9	85.0
dpADC0.4	1.44	26 [18+8]	90.6	79.5	81.1	85.0
dpADC0.1	1.35	28 [10+18]	88.2	79.5	80.6	83.8
ADC	1.61	29 [24+5]	94.1	72.7	76.9	83.2
dpADC0.7	1.53	29 [12+17]	85.9	80.7	81.1	83.2
dpADC0	1.13	30 [19+11]	77.6	87.5	85.7	82.7
dpADC0.8	1.40	33 [18+15]	78.8	83.0	81.7	80.9
dpADC0.9	1.42	35 [21+14]	75.3	84.1	82.1	79.8
dpADC1.0	1.47	37 [21+16]	75.3	81.8	80	78.6

^aIn 10⁻³ mm²/s

^bNumber of false positives and cNumber of false negatives

ADC: apparent diffusion coefficient; dpADC: dual-phase ADC; Se: sensitivity; Sp: specificity; PPV: positive predictive value; Ac: accuracy

Figure 3.

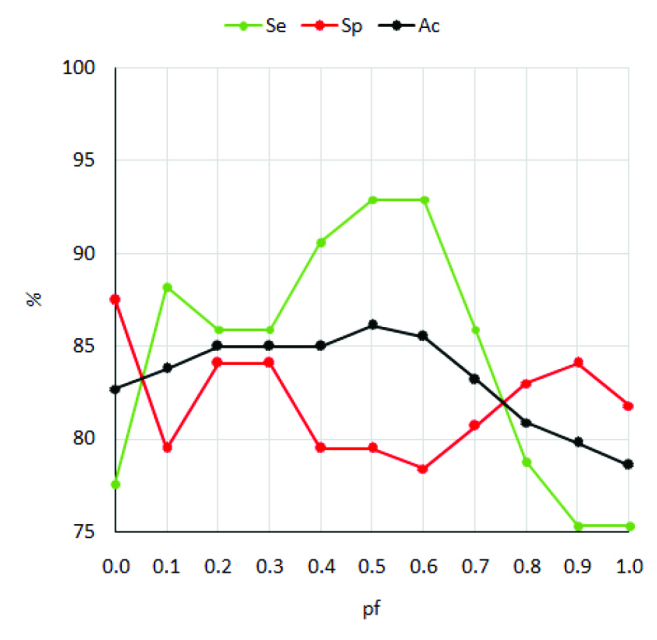
Plots for the sensitivity, specificity and overall accuracy of the dpADC models

Discussion and Conclusion

Challenges in quantitative diagnosis of breast cancer from diffusion-weighted imaging (DWI) motivate new studies to develop enhanced methods focusing on better modelling of the diffusion signal data and on enhancing the diagnostic performance of diffusion coefficients from the models. This study introduces a dual-phase apparent diffusion coefficient modeling that may improve the dialogistic performance of traditional ADC in breast cancer.

The dual-phase apparent diffusion coefficient model integrates two separate ADCs: one from low b-value images (b=50–400s/mm²) and the other from high b-value images (b=400–800s/mm²) of DWI. The model estimates a single diffusion coefficient value (dpADC) by summing the two ADCs weighted by a perfusion influence factor. The value of the factor may range from 0 to 1 and different dpADC estimates can be obtained by using different factor values. In the current study, analyses are performed using the factor values of 0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9 and 1.0.

A meta-analysis of thirteen studies evaluating the diagnostic performance of ADC in quantitative breast DWI from 964 lesions (615 malignant and 349 benign) demonstrates that pooled mean ADC from malignant lesions is significantly lower than that of benign lesions that may range from 0.87 to 1.61×10⁻³mm²/s and the recommended ADC threshold for cancer diagnosis may vary from 0.90 to 1.76×10⁻³mm²/s (27). In the current study, ADC estimations are performed by nonlinear fitting the mono-exponential model to average lesion signal intensity data to ensure high precision in the estimates (use of commonly preferred linear fitting complemented with log transformation in ADC estimations is reported to lower the precision (28)). The mean malignant lesion ADC and the optimal ADC threshold for cancer diagnosis are found to be 1.12×10⁻³mm²/s and 1.61×10⁻³mm²/s, respectively, all in agreement with the literature. The optimal ADC threshold leads to misclassification of 29 lesions (24 benign and 5 malignant lesions) from 173 lesions (88 malignant and 85 benign) analyzed.

Mean dpADC from the malignant lesions is significantly lower than that of benign lesions independent of the perfusion influence factor used in the model that demonstrates a possible use of dual-phase ADC modelling in cancer diagnosis. The dual-phase ADC model with a perfusion influence factor of 0.5 offers the best performance among all the models. From this model, the mean malignant lesion dpADC is 1.07×10⁻³mm²/s and the optimal dpADC threshold for cancer diagnosis is 1.50×10⁻³mm²/s. The model misclassifies 24 lesions (18 benign and 6 malignant lesions) from the 173 breast lesions analyzed.

One invasive ductal carcinoma, 1 liposarcoma, 1 ductal carcinoma in situ and 2 invasive mucinous carcinoma are misclassified by both ADC and dpADC. Use of dpADC lead to misclassification of one invasive lobular carcinoma additionally. On the other hand, 5 fibroadenomas, 4 abscesses, 3 adenoses, 2 columnar cell changes, 3 fibroses and 1 intraductal papilloma are misclassified by both ADC and dpADC. Use of ADC resulted in misclassification of other 6 benign lesions: 3 fibroadenomas, 1 abscess, 1 apocrine metaplasia and 1 columnar cell change. Dual-phase ADC modelling reduces the number of false-positive detections remarkably.

Some precautions should be considered for dpADC. Although dpADC of malignant lesions is significantly lower than that of benign lesions, mucinous carcinoma can reveal high dpADC values and can be misdiagnosed as benign while papilloma, abscess and fibrosis may demonstrate low dpADC values and therefore can be misdiagnosed as cancer. These shortcomings can be due to the underlying pathophysiology of these specific lesions. The mucinous carcinoma is among the malignant lesions, but it may reveal low cellularity and with relatively high-water content (29). Also, abscess, papilloma, and fibrosis are the benign lesions that may exhibit high cellularity (30). The current study imaging protocol schedules DWI before DCE-MRI scan and in the case of DWI immediately after DCE-MRI, presence of contrast agent in the tissue may lead to an artificial increase in dpADC from malignant lesions (A similar artificial increase has been recognized for ADC (30)).

During this retrospective study, a dedicated post-processing software has been developed and used to obtain the two separate ADC estimates within the dual-phase ADC model. However, the vendor-specific software packages installed on the main MR consoles are equipped with functionality to obtain different ADC maps (3) and can be set-up with little effort to obtain the maps required for dpADC modelling. This would facilitate the use of dpADC in clinic practice.

There are some limitations of the current study. The clinical utility of the dpADC for multi-centers and the repeatability and reproducibility of the dpADC from different brand MR scanners are questionable since this study enrolls breast lesions imaged using a 3.0T MR scanner at a single center. Small region-of-interests are placed for the breast lesions manually. This process requires utmost attention and experience especially for the lesions obscured with architectural distortion and if not performed precisely, may lead to a great variability in dpADC. The value of dpADC is calculated using two different ADC estimates and three different b-value images from DWI. More precise calculations can be accomplished with more number of images acquired with well selected b-values (20, 21). The current study has been designed to assess the best dpADC model in differentiating the breast masses using DWI only. Its use in clinical setting and value in multiparametric imaging complemented with dynamic contrast-enhanced MR imaging should be evaluated with further prospective studies.

In conclusion, dual-phase ADC modelling can provide almost the same sensitivity but considerably better specificity than traditional ADC calculations. Thus, dual-phase ADC modelling can improve the diagnostic accuracy of quantitative DWI in differentiating breast cancers from benign lesions. Requiring acquisition of only three different b-value images and benefiting from easy-to-setup ADC mapping tools installed on the main MR console, dpADC based evaluations can be easily adoptable to current imaging and evaluation protocols. Further prospective studies considering multiple institutions and multiple scanners are needed to justify its benefit in clinical setting and its value in diagnosis of breast lesions.