Feasibility Study of Compton Cameras for X-ray Fluorescence Computed Tomography with Humans

Abstract

X-ray fluorescence imaging is a promising imaging technique able to depict the spatial distributions of low amounts of molecular agents in vivo. Currently, the translation of the technique to preclinical and clinical applications is hindered by long scanning times as objects are scanned with flux-limited narrow pencil beams. The study presents a novel imaging approach combining x-ray fluorescence imaging with Compton imaging. Compton cameras leverage the imaging performance of XFCT and abolish the need of pencil beam excitation. The study examines the potential of this new imaging approach on the base of Monte-Carlo simulations. In the work, it is first presented that the particular option of slice/fan-beam x-ray excitation has advantages in image reconstruction in regard of processing time and image quality compared to traditional volumetric Compton imaging. In a second experiment, the feasibility of the approach for clinical applications with tracer agents made from gold nano-particles is examined in a simulated lung scan scenario. The high energy of characteristic x-ray photons from gold is advantageous for deep tissue penetration and has lower angular blurring in the Compton camera. It is found that Doppler broadening in the first detector stage of the Compton camera adds the largest contribution on the angular blurring; physically limiting the spatial resolution. Following the analysis of the results from the spatial resolution test, resolutions in the order of one centimeter are achievable with the approach in the center of the lung. The concept of Compton imaging allows to distinguish to some extend between scattered photons and x-ray fluorescent photons based on their difference in emission position. The results predict that molecular sensitivities down to 240 pM/l for 5 mm diameter lesions at 15 mGy for 50 nm diameter gold nano-particles are achievable. A 45-fold speed up time for data acquisition compared to traditional pencil beam XFCT could be achieved for lung imaging on cost of a small sensitivity decrease.

1. Introduction

Computed tomography (CT) provides valuable anatomic information of a patient anatomy and is indispensable in oncology for diagnosis, staging, treatment planning, and therapeutic assessment of cancer (Kuang et al 2013). While CT can provide the highest spatial resolution, it lacks functional and molecular information. Conventional MI modalities, such as SPECT and PET, use radioactive isotopes combined with specifically engineered biochemistry to provide biomarkers of functional metabolism. Both modalities are used since decades in clinical diagnoses and have proven to be reliable and highly specific tools in patient care. They have high molecular sensitivity but limited spatial resolution. Furthermore, the production of tracers and patient management is extensive and limited due to radioactivity and lifetime of the isotopes.

In x-ray fluorescence CT (XFCT), target regions are labeled with high atomic number probes and irradiated with x-rays. When electrons in the inner shells of the probes are removed via interactions with x-rays, characteristic x-ray fluorescent (XF) photons or Auger-electrons are emitted. Energy-resolving detectors can measure the XF photons which provides information about the distribution and concentration of the tracer agents in the target regions (Kuang et al 2014). Nanoparticles (NP) made for example from Au, Gd, Ba, I, or Hf are attractive labels for tracer molecules due to the highly penetrating XF radiation emitted from these elements. They can be functionalised by conjugation with peptides or antibodies to target pathologic structures. Compared to PET and SPECT tracers, the synthesis, storage, and patient administration time are not limited and also slow biological processes can be monitored over whole treatment cycles. In comparison to dual-energy or spectral CT, which identifies the same high atomic number probes by increased absorption in projection direction of the x-ray beam, much higher molecular sensitivities are possible in XFCT. The molecular sensitivity is also higher than in fMRI and overcomes depth-penetration limitations in opto-acoustics and other optical modalities such as optical microscopy, optical coherence tomography, and diffuse optical tomography. The most compelling property of XFCT and spectral CT is the spatial resolution. Furthermore, the XFCT resolution is mainly limited by instrumentation challenges rather than physical limits as in PET and SPECT. All these advantages render XFCT as a highly promising candidate for a future modality in clinical molecular imaging.

Recent XFCT work by several groups (Pratx et al 2010, Cong et al 2011, Kuang et al 2013, Kuang et al 2014, Bazalova et al 2014, Ren et al 2014, Feng et al 2014, Ahmad, Bazalova, Xiang and Xing 2014, Ahmad, Pratx, Bazalova and Xing 2014, Sjölin and Danielsson 2014, Bazalova-Carter et al 2015, Ahmad et al 2015) have shown that XFCT can have theoretical molecular sensitivities down to 10 pM for 10 nm diameter AuNPs (Ahmad, Bazalova, Xiang and Xing 2014). Gold concentrations down to 2.5 mg/ml were experimentally detectable with a clinical x-ray source at 14 mGy in a proof of concept setup (Ahmad et al 2015). Animal studies with a HPGe detector and monochromatic x-rays were able to detect 23.8 μg/ml of I-IMP in vivo (Takeda et al 2008). However, limitations in acquisition speed restrain the modality from fast translation to clinical applications. Previous approaches for XFCT utilized pencil beams from x-ray sources or synchrotrons to image XF probes. For L-shell XFCT, usually bench-top sources with energies up to 62 keV were used (Manohar et al 2013, Bazalova-Carter et al 2015), while several studies for K-shell XF were conducted with collimated clinical x-ray sources (Kuang et al 2013, Kuang et al 2014, Ahmad, Pratx, Bazalova and Xing 2014). As pencil beam excitation limits the acquisition speed of the modality to an unmanageable scan time for clinical applications, we propose to realize XFCT imaging with fan-beam and cone-beam excitation.

When large volumes are irradiated with fan- or cone-beams, the spatial information of XF emission must be recovered through some means at the x-ray detector. Jones and Cho used detector collimation similar to SPECT (Jones and Cho 2011). However, this limits the imaging sensitivity. In our alternative approach, we propose using Compton cameras to recover spatial information without the loss of sensitivity associated with collimation. The use of CCs for XFCT imaging poses an intriguing and promising method, as the excitation principle in XFCT allows to choose arbitrary emission volumes. This additional information is beneficial for image reconstruction.

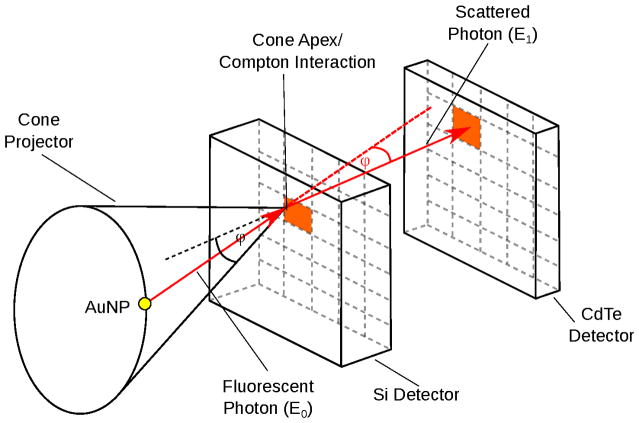
CCs are energy resolving 3D-positioning detectors which usually consist of at least two x-ray detection stages of different material. At least two interactions of a photon event are required to restrict the emission point to a cone surface as it is illustrated in Fig. 1 (Motomura et al 2008). In this scenario, it is advantageous when the first detector stage consists of a low Z material to have a higher probability for a Compton interaction than for a photo absorption. For the second stage instead, a high Z material is desirable to have a higher probability for a photo absorption. The two detector stage approach is particular necessary for lower photon energies as photon absorption is more probable for lower energies. For the typical energies in XFCT, a promising material for the second stage is CdTe (Watanabe et al 2009) and CZT (He et al 1996). For higher energies (> 200 keV), it is also possible to build CCs from a single material (Du et al 2001).

Figure 1.

Principle of Compton imaging. The energy and position measurement of two separate interactions restricts the emission to a cone surface.

Following Compton kinematics, the emission of the XF photons can be restricted to a cone surface. The cone angle is correlated to the energy measurement of the two interactions by (Chinn et al 2006, Wilderman et al 1998):

$$cos(\phi )=1-m_e{c}^2(\frac{1}{E_1}-\frac{1}{E_0}),$$ (1)

where E₁ is the photon energy after the first interaction and E₀ is the energy of the incoming photon. Experimental studies of CCs for lower γ-energies were done with Si-detectors (Meier et al 2002) and for higher energies with Ge-strip detectors (Motomura et al 2008).

This study aims to demonstrate the feasibility of human XFCT with Compton camera detectors. The imaging system performance is analyzed in terms of spatial resolution, scan time, and molecular sensitivity in clinical imaging scenarios. XFCT imaging with a CC is simulated by Monte-Carlo radiation transport. For fan beam excitation, the data distinguishes from other applications with CCs and its advantages in image reconstruction will be studied. The feasibility of the approach will be examined using imaging simulation of lesions in the human lung. Current detector technology, in particular realistic energy resolution, was simulated to demonstrate feasibility.

2. Methods

2.1. XFCT Simulation Setup

The efficiency of a CC to detect the XF signal of high atomic number probes is studied with the simulation toolkit Geant4 (Agostinelli et al 2003). As in previous XFCT studies, the efficiency to detect characteristic K-shell XF photons of gold is examined. Gold is a suitable element for this study as it has the highest emission energy among the high atomic number probes which are proposed for XFCT. Higher photon energy has the advantage of larger penetration depth and better angular resolution for CCs. The different XF emission lines for gold generated by the Livermore library within Geant4 are listed in Table 1.

Table 1.

Characteristic XF emission energies of gold atoms.

Type	Kβ2	Kβ1	Kα2	Kα1	Lγ1	Lβ2	Lβ1	Lα2	Lα1
Energy (keV)	78.226	77.8157	69.038	67.184	13.4225	11.5869	11.4753	9.7098	9.6213

The kinematics of Compton scattering inherits a higher energy transfer to the scatter electron for larger scatter angles. As a consequence, back-scatter photons have lower energies than forward scattered photons. It was shown (Ahmad, Bazalova, Xiang and Xing 2014, Sjölin and Danielsson 2014) that the angular dependence of the scatter background allows to increase signal to noise ratio in optimized angular setups. In the optimized setup used in the current study, only K_β photons are reconstructed which are measured in a detector back-orientation. For a mono-energetic source, only multiple- or Rayleigh scattered photons can disturb the signal of the high energetic K_β XF photons, as single scattered primary photons from the x-ray source have lower energies than the XF photons. The statement about improved sensitivity of a back-scatter setup even holds for polychromatic sources as the amount of primary scatter photons is substantially reduced.

As implication of these findings, all simulation setups which consider scatter background are performed with detectors arranged in back-scatter configuration. The image reconstructions are in these cases performed only for events in the energy window of the K_β XF photons. The K_β XF energies of 77.8 keV and 78.2 keV are low in comparison to applications like SPECT (e.g. ^99mTc-140 keV) or high gamma-ray emission imaging (e.g. ⁸⁵Sr-514 keV, ⁶⁵Zn-1.115 MeV) (Motomura et al 2008). High energy resolution is necessary in the XF energy range to reach practicable molecular sensitivity because XF photons must be distinguished from primary Compton scattered photons and other background sources. Hence, the simulation study is performed assuming energy resolutions of state-of-the-art detectors.

2.2. Phantoms

The imaging capabilities of the CC approach are studied in various phantoms and simulation settings. Each is described below.

2.2.1. Excitation Geometry Phantom

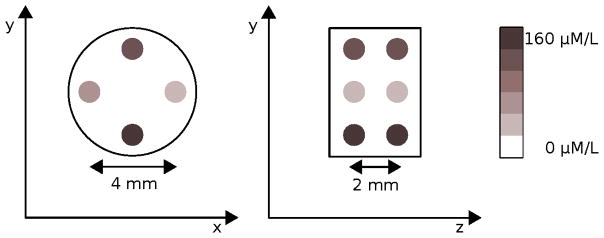
The first scenario is an idealized setup with a reconstruction phantom which will demonstrate the performance differences between cone-beam and fan-beam excitation. A cylindrical 5 mm diameter water phantom with eight spherical 1 mm diameter gold regions is used for the excitation geometry performance setup. The spheres are grouped in two sets where each set consist of four spheres with gold concentrations of 160 μM/1, 80 μM/1, 40 μM/1, and 20 μM/1 assuming 50 nm diameter gold nano-particles. The two sets are placed 2 mm apart in the axial direction. Within each set, the transaxial separations on the main axes are 4 mm, each. A schematic drawing of the phantom is illustrated in Fig. 2.

Figure 2.

Transversal and sagittal view on the excitation geometry phantom with the eight target regions with four different AuNP concentrations.

2.2.2. Lung Lesion Model

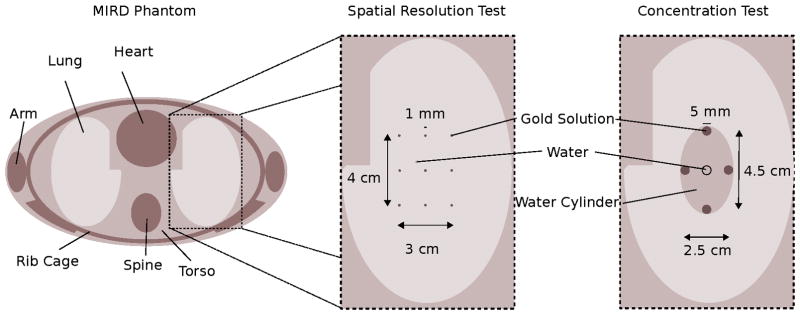
The clinical scenario models a lung scan of the Medical Internal Radiation Dose (MIRD) phantom (Snyder et al 1969). The MIRD phantom is an anthropomorphic phantom with simplified mathematical descriptions of the organ structures and homogeneous organ materials to accelerate Monte-Carlo simulations. The MIRD phantom implementation in Geant4 is accessible in the application source code (Guatelli et al 2006). Target volumes for spatial resolution- and concentration-tests, which will be described in the next sections, are based on this MIRD phantom model and are placed in the center of the right lung volume. A transverse view of the excitation plane together with the different target volumes is shown in Fig. 3.

Figure 3.

Cross-sectional view on the MIRD phantom of the excitation plane. The inlets present the zoom on the lung region where either the spatial resolution or the concentration phantom is placed.

2.2.3. Spatial Resolution Test

For the spatial resolution analysis, nine spherical target regions are placed in a grid pattern in the lung center. The grid spacing is 1.5 cm in the x- and 2 cm in the y-direction, respectively. The target regions are spheres with a diameter of 1 mm. With respect to the expected spatial resolution, the targets can be interpreted as point sources. The regions are made of different gold water mixtures with a high gold concentration of around 320 μM/1. The high concentrations are required to generate sufficient statistics for reconstruction.

2.2.4. Concentration Test

The concentration phantom should demonstrate the molecular detectability limit. For this purpose, a 3 cm×5 cm×l mm diameter elliptical water cylinder is spiked with four 5 mm diameter cylindrical target regions on the outer rim of the water cylinder with a horizontal target distance of 2.5 cm and a vertical target distance of 4.5 cm. The large target distances are chosen to mitigate influences related to spatial resolution constraints. The gold concentrations in the target regions are 240 pM/1, 320 pM/1, 560 pM/1, and 640 pM/1 of 50 nm diameter gold nano-particles. For comparison, the 240 pM/1 concentration equates to 0.015% weight per volume (w/v) or 150 μg/ml.

2.3. Detectors

2.3.1. Idealized Setup

For the excitation geometry analysis, the phantom is placed in the center of a spherical shell detector with a 50 cm radius and nearly 4πangular coverage including an inlet and outlet for primary x-ray beam. The detection material is a 6 mm thick Si layer. In the data processing, the scatter contribution is neglected and energy and spatial blurring are disabled in order to isolate the distortion due to excitation geometry.

2.3.2. Lung Lesion Setup

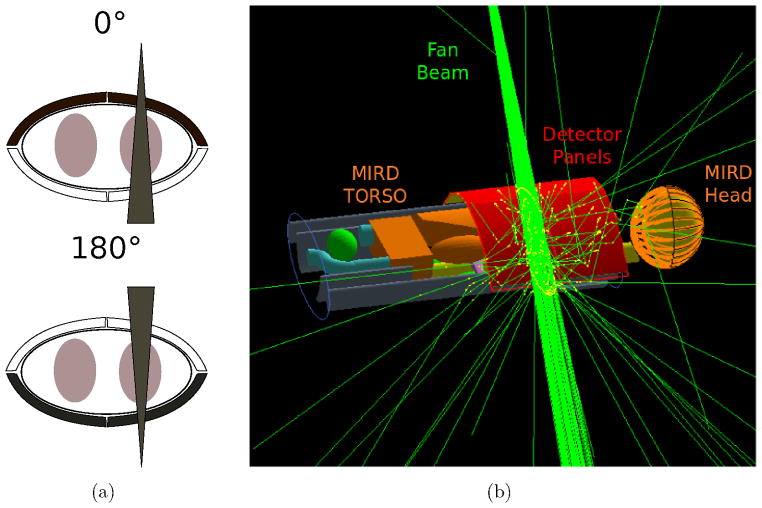
For the clinical scenario with the MIRD phantom, the CC consists of four 16×26 cm² detector panels which are placed in two different setups with beam orientations from the front and the back of the thorax as shown in Fig 4(a). The setups are in an optimized back-scatter configuration to reduce the amount of scatter photons (Ahmad, Bazalova, Xiang and Xing 2014, Sjölin and Danielsson 2014). An example of the 0° setup together with the MIRD phantom and the fan beam is illustrated in Fig. 4(b). The detector is a dual layer detector with a Si and a CdTe stage. The thickness of the Si layer is optimized to 3 mm as thicker layers lead to more double Compton events. The CdTe stage is a 2 mm thick detector absorbing the vast majority of the K_β XF photons. The energy and spatial resolution of the detectors are modeled with Gaussian distributions. For the CdTe detector, the FWHM of the energy resolution is set to 880 eV which is also chosen as the energy window to include the scatter contamination in the data. The FWHM of the energy resolution for the Si layer is set to 140 eV. The FWHM of the spatial resolutions of both detectors are set to 100 μm to be comparable to the Timepix3 chip (Gromov et al 2011).

Figure 4.

Detector and beam orientation used in the clinical scenario (a). Black detector panels are enabled. Simulation setup for the lung scan is shown in (b) with four carved CC panels in back-scatter orientation drawn in red.

2.4. X-ray Sources

All simulations are executed with a point source placed 1 m away from the center of the FOV to be comparable with existing CBCT system geometries. The x-ray source emits mono-energetic photons to show the physical limit of the approach and to keep simulation processing times manageable. The x-ray energy is set to 82 keV which is slightly above the excitation threshold for photo-electric K-shell absorption in gold.

2.4.1. Idealized Setup

The photons are emitted in the direction of a fan beam with an opening angle of 0.5° in the imaging plane. The x-ray source is translated in 50 μm steps across the full 7.5 mm long FOV of the phantom. To approximate cone-beam excitation, all output files are combined to generate the 3D dataset, while the dataset of each slice is used for the 2D reconstruction. More details on the reconstruction are given in section 2.7.

2.4.2. Lung Lesion Setup

The fan-beam for the clinical scenario has an axial extent of about 1.2 mm at the phantom center. In this volumetric excitation mode, dose calculations are possible which are taken out for water regions of the same size as the according target regions close to the lung center. The MIRD phantom is irradiated from two directions as shown in Fig. 4(a). The source is translated by 8.5 cm in the transverse direction to be located over the lung center. The opening angles of the fan beam are 2.6° for the resolution- and concentration-phantom respectively. This equates to a transaxial beam width of 4.5 cm at the iso center.

2.5. Event Selection

All events which have at least two interactions with one Compton scattering in the sandwich detector are written to a binary output file. The events with an energy in correspondence to one of the K_β spectral lines are selected for image reconstruction. When background scatter photons are taken into account, the events within the energy window according to the selected energy resolution around the K_β XF energies are selected. In a measurement, the energy of the incoming photon is not directly determined but rather its energy deposition is measured. For example, photons could undergo two Compton interactions and escape the detector volume which would not be recognized in a real measurement. To quantify the amount of different event types, a separate simulation setup was build where a pencil beam with 10M photons with an energy of 78 keV irradiates the CC face on. The different event types are reported in section 3.2 and are considered respectively in the data processing of the lung lesion model.

In the simulation, the events are stored with ideal spatial and energy response of the detector. To model the behavior of a realistic detector, spatial and energy blurring are induced by Gaussian noise models in a post-simulation processing with two random number generators.

2.6. Angle Error

The error of the cone angle in Compton reconstruction depends on three components (Singh 1983):

$$tan(\mathrm{\Delta }\phi )=tan(\mathrm{\Delta }{\phi }_1)+tan(\mathrm{\Delta }{\phi }_2)+tan(\mathrm{\Delta }{\phi }_3)$$ (2)

where Δφ₁ is the error induced by the energy resolution, Δφ₂ is the error induced by the Doppler effect, and Δφ₃ is the error induced by the spatial resolution of the detector. The spatial resolution has a minor impact on the angle error as Si and CdTe detectors in this energy range are quite thin and have therefore usually excellent spatial resolution. Within the clinical scenario, the FWHM of the Gaussian model for the spatial resolution was fixed to 100 μm in all spatial directions.

2.6.1. Energy Resolution

The error induced by the energy resolution can simply be obtained by error propagation of equation (1). Derivation of the expression leads to (Du et al 2001):

$$\mathrm{\Delta }{\phi }_1=\frac{{(1+\alpha (1-cos(\phi )))}^2}{E_0\alpha sin(\phi )}\mathrm{\Delta }E$$ (3)

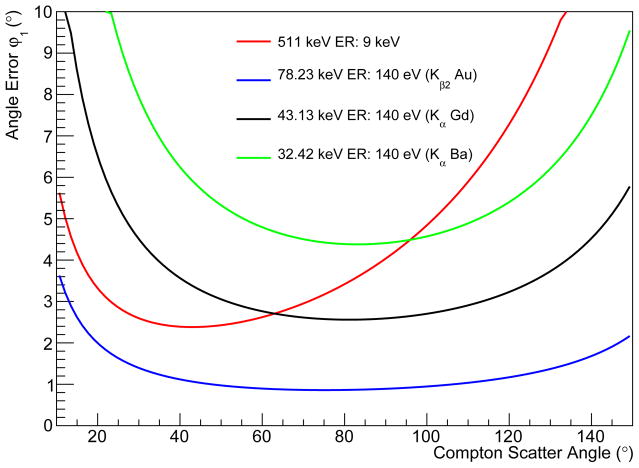
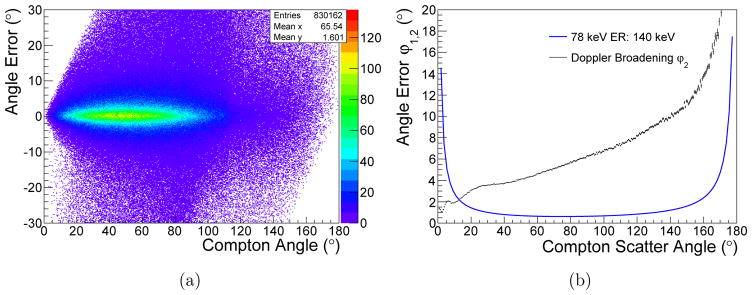
with α = E₀/m_ec². The angle error was calculated for the K energies of three high atomic number probes, namely Au, Gd, and Ba with a hypothetical energy resolution of 140 eV as shown in Fig. 5.

Figure 5.

Distribution of the angle uncertainty due to the limited energy resolution of the detector calculated for the K-lines of the isotopes Au, Gd, and Ba. The detector energy resolution is assumed to be 140 eV FWHM. The distributions are also compared to the detection of 511 keV photons with a CZT detector with an energy resolution of 9 keV (Du et al 2001).

2.6.2. Doppler Broadening

The derivation of equation (1), assumes an electron at rest which is only valid in first approximation. In detail, bonded electrons have a finite momentum in connection to their spin and orbit relation. The angle error is proportional to the impulse of the electron along the scatter vector k = k₁ − k₀ (Du et al 2001). At a fixed Compton angle, the error is mainly defined by the so called Compton profile which can be numerically calculated by using Hartee-Fock wavefunctions (Biggs et al 1975). It was presented elsewhere (Uche et al 2011) that the theoretical calculations are well described by the implementation of Doppler broadening in Geant4. In order to discuss the magnitude of Δφ₂ for the specific application of XFCT with CCs, the proposed sandwich CC is irradiated frontally with a mono-energetic 78 keV beam in an additional simulation. The error induced by Doppler broadening is determined by subtracting the geometrical Compton angle (available in simulation) from the angle calculated from equation (1).

2.7. Image Reconstruction

The image reconstruction is performed with a list-mode MLEM algorithm with cone-projector on a GPU (Pratx et al 2009, Pratx and Levin 2011). Within the reconstruction the cone angle of each voxel is calculated given the cone apex and cone axis of each list-mode event. Each voxel is weighted based on the deviation between the calculated cone angle and the cone angle information in the listmode data. As the calculation of the cone angle is a simple processing, it is a suitable task for the GPU since the parallelization boosts reconstruction times significantly compared to sequential processing.

One advantage of XFCT imaging in combination with CCs is that it is possible to excite tracer molecules in a well defined region. In our example, the probe region is excited in thin axial planes and the reconstructed images are 2D slices. This 2D reconstruction of fan-beam excitation differs from conventional CC reconstruction as the emission plane is usually not known. The 3D reconstruction, instead, equates the common reconstruction for SPECT imaging and resembles in this study a cone-beam excitation. To make the images comparable for the data analysis, the 150 images of the 2D reconstruction are stacked.

In the clinical scenarios, the uncertainty of angular blurring is modeled appropriately in the simulation. It is possible to compensate the angular error to some extent in image reconstruction by adapting the kernel function for the cone projector which determines the weight for each voxel in regard to a single event. Explicitly, the system matrix is calculated as follows:

$$a_{ij}=e^{-{(\mathrm{\Delta }cos{\phi }_{ij})}^2{\sigma }_{\mathit{cone}}}$$ (4)

where Δcos φ_ij is the deviation of the cosine of the cone angle in voxel i and the cosine of the measured angle of event j. The PSF parameter σ_cone invokes the kernel function. A high value for the PSF parameter means a high angular precision while low values represent larger blurring. The PSF models the impact of all three spatial resolution degrading effects from equation (2).

Within the reconstruction, no attenuation correction is performed and only cone angles below 89° are processed. The reconstruction parameters for the different experiments are listed in Table 2.

Table 2.

Reconstruction Parameters

Phantom	Voxels	FOV (mm3)	Iterations	PSF Parameter
Reconstruction Phantom (2D)	150×150×1	7.5×7.5×0.05	80	1.5e7
Reconstruction Phantom (3D)	150×150×150	7.5×7.5×7.5	80	1.5e7
Spatial Resolution Phantom	200×200×40	100×100×20	400	700
Concentration Phantom	200×200×1	100×100×0.5	200	700

2.8. Figures of Merit

The different figures of merit which are used in the analysis of the reconstructed images are defined as follows:

Contrast ratio:

$$\text{CR}=\frac{\mid {\mu }_{\mathit{ROI}}-{\mu }_{\mathit{bkg}}\mid }{{\mu }_{\mathit{bkg}}}$$ (5)

Contrast to noise ratio:

$$\text{CNR}=\frac{\mid {\mu }_{\mathit{ROI}}-{\mu }_{\mathit{bkg}}\mid }{{\sigma }_{\mathit{bkg}}}$$ (6)

Signal to noise ratio:

$$\text{SNR}=\frac{{\mu }_{\mathit{ROI}}}{{\sigma }_{\mathit{ROI}}}$$ (7)

where μ_ROI and σ_ROI are the average voxel intensity and the standard deviation of the voxel intensity within the region of interest (ROI) or the background region, respectively. For the excitation geometry phantom the background region is defined as a 0.5 mm rim around each target region.

The spatial resolution is also evaluated by reporting the full-width-at-half-maximum (FWHM) or the full-width-at-tenth-maximum (FWTM) of line profiles in reconstructed images in all spatial directions.

The spatial accuracy is furthermore determined with the Dice coefficient which is calculated as follows:

$$\text{DC}=\frac{2\mathrm{\sum }{v}_{\mathit{ROIs}}}{\mathrm{\sum }{v}_{\overline{\mathit{ROIs}}}+2\mathrm{\sum }{v}_{\mathit{ROIs}}}$$ (8)

where υ_ROIs is the intensity of the voxels inside the ROIs and $v_{\overline{\mathit{ROIs}}}$ the intensity of voxels outside of the ROIs.

3. Results

3.1. Excitation Geometry Analysis

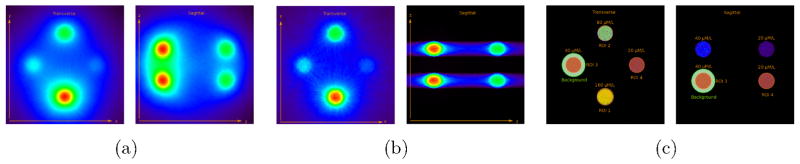
The comparison of the reconstruction of the datasets from the cone- and fan-beam excitation shows that both 2D and 3D reconstruction converge to a FWHM of 1 mm. In axial direction, it is found that the spatial resolution for the fan-beam acquisition is only limited by the axial fan beam spread and the stepping size as shown in Fig. 6(b). It is also visible that the spatial resolution for the 2D reconstruction is significantly better than for the 3D reconstruction after the first iteration.

Figure 6.

Images obtained from the reconstruction phantom after one iteration. Compared are the 3D reconstruction (a, cone-beam excitation) to the 2D reconstruction (b, fan-beam excitation). The origin of the XF photons is shown together with the ROIs (c).

In the simulation, 1.5×10¹⁰ photons were tracked which produced 2.7 M detected XF photon events. The processing time of the reconstruction is a factor of 44 smaller for all slices in 2D than in 3D; yielding a processing time for the whole dataset of ~1 h for 80 iterations in 2D.

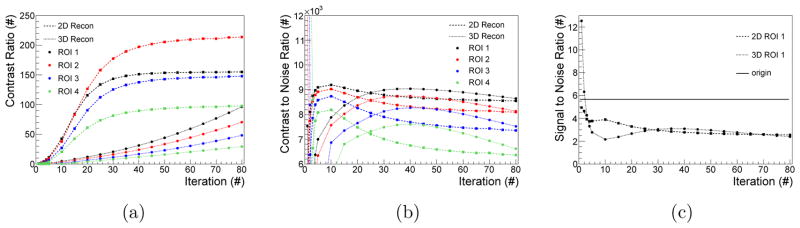
The CRs for the two different reconstruction methods are shown in Fig. 7(a). The analysed ROIs and the background region of ROI three are indicated in Fig. 6(c) together with the true origin of the detected XF photons. For the 2D reconstruction, the CRs of all ROIs converge after approximately 40 iterations. The 3D reconstruction does not reach convergence after 80 iterations. The CR in each ROI is between 60%–303% larger for the 2D reconstruction than in the 3D reconstruction after 80 iterations. Because of the excessive computational demand, it was not possible to assess the final CR at convergence for 3D reconstructions from cone-beam excitation.

Figure 7.

Analysed figures of merit determined for 80 iterations in 2D and 3D reconstruction. CR (a) and CNR (b) are compared for all ROIs while the SNR (c) is evaluated for the representative ROI 1.

The CNRs for the different ROIs are illustrated in Fig. 7(b); reporting the best performance of the reconstruction at 10 iterations for the 2D reconstruction and at 40 iterations for the 3D reconstruction. The corresponding CNRs are 2%, 3%, 6%, and 8% larger for ROI 1 to ROI 4 in 2D reconstruction compared to 3D reconstruction.

The SNR values of ROI 1 are displayed in Fig. 7(c). For the 3D reconstruction, the SNR reaches a local maximum at 35 iterations similar to the local maximum of the CNR. The high SNR for low iterations follows from the low spatial resolution characteristic at the beginning of the reconstruction. The 2D reconstruction possesses also a local maximum at 10 iterations as the CNR and is 26% larger than the local maximum of the 3D reconstruction.

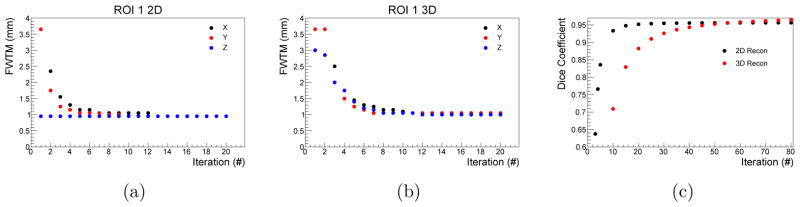
The analysis of the FWTM and the Dice coefficient are illustrated in Fig. 8. It is visible in Fig. 8(a) that the FWTM in axial direction is already around 1 mm in the first iterations while the two other directions have a characteristic exponential convergence. In the 3D reconstruction, the exponential convergence is observed for all space directions. The Dice coefficient converges for the 2D reconstruction after approximately 15 iterations while the 3D reconstruction requires 45 iterations to reach the same value (Fig. 8(c)). After 60 iterations, the Dice coefficient of the 3D reconstruction slightly exceeds the value from the 2D reconstruction.

Figure 8.

FWTM of ROI 1 and Dice coefficient calculated for different iterations. The results are compared for each spatial direction between the 2D (a) and 3D (b) reconstruction. The Dice coefficient shows faster convergence for the 2D reconstruction (c).

Following the superior performance in contrast and faster convergence of the fan-beam excitation, 2D reconstruction is pursued for the remainder of this work with exception for the spatial resolution test.

3.2. Occurrence of Different Event Types

The probability for the different event types to occur in the proposed detector design is given in Table 3. The fraction of Compton events is about 9.5% which is the event type required for image reconstruction. This means that the amount of useful XF events is significantly reduced in comparison to XFCT imaging with pencil beams or volumetric excitation with collimators. However, the scatter reduction characteristics of the CC approach promises better molecular sensitivities at least for clinical applications. This will be discussed in more detail in section 4.

Table 3.

Fraction of interaction types in the detector for incident x-rays.

Event Type	Compton Events	Photo Interactions	Photo Effects in Si	Photo Effect in CdTe	Single Compton Interactions	Transversed Photons
Contribution (%)	9.5	84.5	5.8	78.7	3.4	2.6%

The different types of Compton events are listed in Table 4. 48.4% of the events are the common case with one interaction in the Si layer and one interaction in the CdTe layer. The event types marked have either a huge angular uncertainty or can not be identified by a real detector. Hence, the events are rejected in the data processing of the studies presented below. The residual events have more than two interactions but they can be used in image reconstruction when the first two interactions can be resolved. For 17.7% of the events, all interactions happen in the Si layer. In these cases the energy window is adapted in accordance of the energy resolution of the Si detector.

Table 4.

Type of events within the identified Compton events.

Event Type	1 CI in Si PE in CdTe	2 CI in Si PE in CdTe	1 CI in CdTe PE in CdTe	1 CI in Si 1 CI in CdTe PE in CdTe	PE in Si	More than 3 interactions	Escaping Compton Events†
Contribution (%)	48.4	6.3	16.9*	1.8	17.7	2.1	6.8*

Compton interaction (CI), photoelectric effect (PE),

^*problematic events,

^†events without photo-electric event but at least two interactions in the detector (Rayleigh or Compton).

3.3. Doppler Broadening

The spread of the angular error induced by Doppler broadening in the Si layer in dependence of the Compton scatter angle is shown in Fig. 9(a). The comparison of the mean error to the angle error induced by the limited energy resolution is presented in Fig. 9(b). At 90°, the angular error of Doppler broadening is about six times larger than from the energy resolution.

Figure 9.

Angle error induced by Doppler broadening in dependence of the Compton scattering angle for 78 keV photons in the sandwich Si-CdTe CC (a). In (b), the average angle error induced by Doppler broadening is compared to the angle error caused by energy blurring.

3.4. Spatial Resolution Test

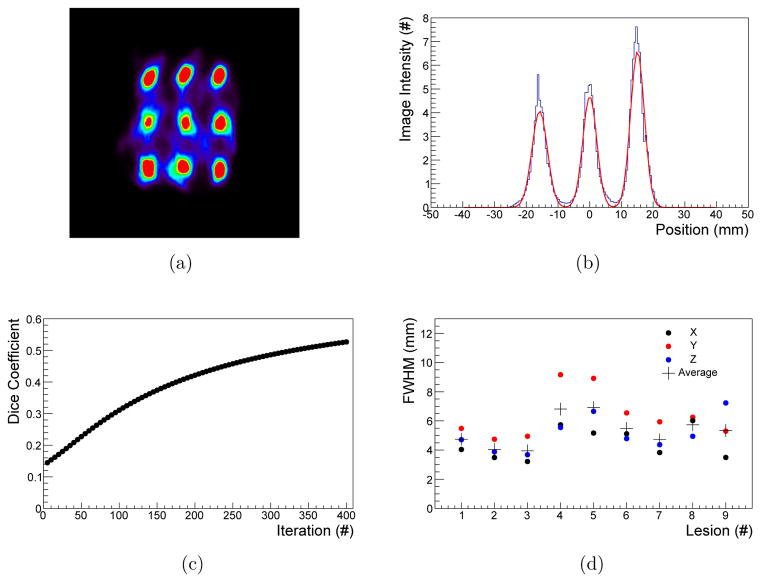
The spatial resolution phantom was irradiated with 9.2 × 10¹⁰ photons, leading to a water dose of approximately 34 mGy for a 1 mm diameter water sphere close to the lung center. The images were reconstructed with up to 400 iterations and the nine ROIs are clearly distinguishable as shown in Fig. 10(a). It is found that the reconstruction with a PSF value of 700 leads to good FWHM values with a low amount of background artifacts.

Figure 10.

Central slice of the spatial resolution phantom reconstructed at 7 mGy (a). Line profile fitted with Gaussian functions of the middle three ROIs (b). Convergence of the Dice coefficient for ROIs with 6 mm diameter (c) and FWHM of the individual ROIs of iteration 400 (d).

The target regions are completely separated as illustrated for the line profile of the first three ROIs in Fig. 10(b). The Dice coefficient increases from an initial value of 0.14 after five iterations to 0.53 after 400 iterations as shown in Fig. 10(c). It is visible that the reconstruction has not converged after 400 iterations. The FWHM for the individual regions and each spatial direction are shown in Fig. 10(d). Details on the mean FWHM for each spatial orientation together with their minimum and maximum after 400 iterations are listed in Table 5.

Table 5.

Mean FWHM of the nine ROIs after iteration 400 for individual space directions.

Direction	X (mm)	Y (mm)	Z (mm)	Global (mm)
Mean	4.5 ± 1.1	6.4 ± 1.6	5.1 ± 1.2	5.3 ± 1.4
Maximum [Number of ROI]	6.0 [8]	9.2 [4]	7.2 [9]	9.2 [4]
Minimum [Number of ROI]	3.2 [3]	4.7 [2]	3.7 [3]	3.2 [3]

3.5. Concentration Test

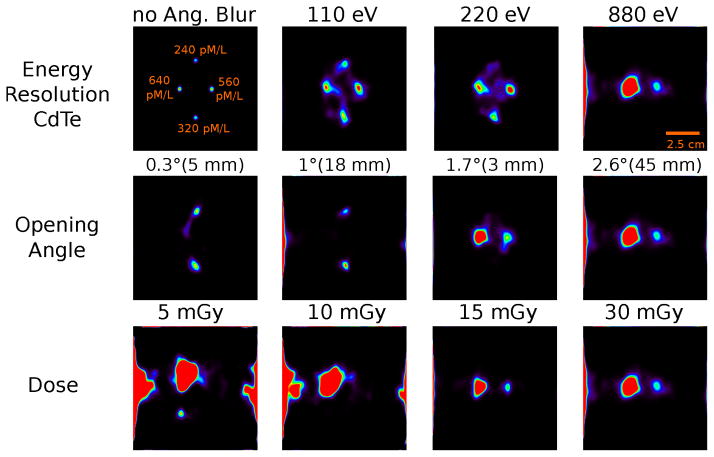
The simulation of the concentration phantom involved a dose of 30 mGy in a 5 mm region at the center of the lung using 1.1 × 10¹¹ photons. Reconstructed images with different analysis parameters are shown in Fig. 11. The upper row emphasizes the influence of the angular blurring and the scatter content induced by the energy resolution of the CdTe stage in the CC. The first image shows the reconstruction from pure XF photon events without any angular blurring to illustrate the true position and concentration of the lesions. In the other images, angular blurring is enabled and different amount of scatter events are added in dependence of the energy resolution of the CdTe detector for a fan-beam opening angle of 2.6°. For the energy resolution of 110 eV, all four target regions are visible but slightly displaced. The signal intensity of the 560 pM/l exceeds the signal amplitude of the 640 pM/l source which indicates a non-uniform spatial distribution of scatter events.

Figure 11.

Images of the concentration phantom reconstructed for different data set analysis parameters after 200 iterations. The angular blurring and CdTe energy resolution influence is shown in the upper row while the variation of the scatter contribution due to the opening angle of the fan beam is presented in the middle row (fan beam width at iso-center indicated). The lower row displays images for different target doses for a 2.6° opening angle of the fan-beam and a CdTe energy resolution of 880 eV.

For the images with detector energy resolutions of 220 eV and 880 eV, the scatter content increases which leads to a disappearance of the 240 pM/l target for the 220 eV energy resolution and of the 320 pM/l target for the 880 eV energy resolution.

The second row of Fig. 11 shows images reconstructed for fan-beam opening angles of 0.3°, 1°, 1.7°, and 2.6° for a CdTe energy resolution of 880 eV. For the first two angles, only the two low concentration targets are irradiated. While both regions are visible for the 0.3° and 1° opening angles, the scatter content in the both datasets is significantly different; causing the different signal amplitudes. As soon as the excitation beam covers the higher gold concentration lesions, as shown in the 1.7° image, the lower gold concentration regions are not detectable anymore. In the 2.6° opening angle image, the larger scatter contamination causes a signal amplitude variation compared to the 1.7° image which also indicates that the scatter distribution is not uniform. Additionally, a scatter signal is visible on the left image frame for the largest opening angle.

The dataset was subdivided to show the detectability dependence for different target doses. The reconstructed images for 5, 10, 15, and 30 mGy after 200 iterations are shown in the lower row of Fig. 11. While the 5 mGy and 10 mGy images show only distorted concentration distributions, the two high gold concentration targets are only visible in the 15 mGy and 30 mGy images. Obviously, there is no further image quality gain for doses above 15 mGy.

We conclude from the analysis that target concentrations down to 560 pM/1 can be reliable detected for a fan beam opening angle of 2.6° and a CdTe energy resolution of 880 eV.

3.6. Scanning Time Estimation

The scanning time states one of the biggest challenges for pencil beam XFCT imaging with high resolution settings. To estimate the scanning time of the concentration phantom, the photon spectra calculation software for tungsten anodes SpekCalc is used (Poludniowski et al 2007). A typical x-ray spectrum optimized for Au XFCT with 110 kVp and 0.8 mm, 1 mm, and 1 mm thin beryllium, aluminum, and copper filters was modeled. A water absorption of 40 mm was set to mimic the influence from the torso and concentration phantom. SpekCalc estimates a output dose of 6.9 μGy/mAs at the lung center. Assuming a tube current of 200 mA for typical clinical x-ray sources, a dose rate of 1.38 mGy/s at iso-center is given.

The fan beam with the 2.6° opening angle has a lateral extent of 4.5 cm at the lung center, leading to a scanning time of around 11 min for a dose of 20 mGy for a single slice in pencil beam excitation when a 1 mm diameter pencil beam is stepped along the 4.5 cm. For the CC approach, the scanning time is reduced to 15 s which makes whole lung scans in an order of 1 h possible. Taken the results from the opening angle analysis of the concentration phantom into account, the scanning time reduction comes on the cost of a small sensitivity decrease in the order of 2.

4. Discussion

The comparison of the fan and cone beam excitation unveils several advantages of 2D reconstruction which equates to fan-beam excitation. The most important advantages are the dramatically reduced reconstruction time, early convergence, and higher contrast ratios. As 2D reconstruction in SPECT is only possible with less attractive heavily collimated setups, 2D reconstruction is a unique appealing option for XFCT. The faster convergence was proven for the CR, CNR, SNR, the Dice coefficient and the FWTM. The fast processing time is highly demanded, as it is inevitable that a huge amount of scatter events needs to pass the reconstruction step. A slight advantage for the 3D reconstruction is found for a large number of iterations according to the Dice coefficient analysis which is may only given for the examined phantom geometry. It was presented above that the fraction of scatter events scales with the size of the fan beam’s opening angle. The opening angle is proportional to the irradiation field size and it is expected that the scatter amount is dependent on the field size and independent from the excitation geometry. Following this assumption and the results of the analysis, fan-beams with larger angles are preferred over cone-beams to speed up scanning times, as 2D reconstruction is mainly superior to 3D reconstruction.

The analysis of the spatial resolution phantom shows that lesion separations below 1.5 cm in x- and z-direction and 2 cm in y-direction are possible, respectively. For higher iterations, FWHM of point like targets below 6 mm are accessible which makes the approach comparable to clinical resolutions achieved in PET imaging. The better spatial resolution in x- and z-direction is attributed to the elliptic shape of the human torso. Events with cone axis more parallel to the x- or z-direction improve the spatial resolution in the y-direction. In this setup, these events are on a larger detector target distance which leads to the decreased spatial resolution. The spatial resolution test was also performed with 2 mm diameter targets with lower gold concentrations. The results were similar which shows that further target size reduction doesn’t improve spatial resolution. The overall spatial resolution is mainly restricted by Doppler broadening within the Si stage of the CC. In principle, the spatial resolution can be improved by using detector materials made of elements with smaller electron shells. E.g. diamond detectors would be an alternative, but the energy resolutions of such detectors are not sufficient yet for this application.

The molecular sensitivity is dependent on the size of the NPs which is connected to the tracer molecule. It was shown that gold NPs with a diameter of 50 nm are internalized at a faster rate compared to larger (74–100 nm) or smaller (15–30 nm) diameters (Chithrani et al 2006). Considering the lowest concentrations of 240 pM/l and 560 pM/l detectable at 0.3° and 2.6° opening angles at 15 mGy for this nano-particle size, good molecular sensitivity can be achieved.

The study shows that the CC is able to distinguish scatter from XF photon events to some degree which is especially emphasized in the lung scan as surface scatter is spatially separated from the XF photons. In this specific setup, it is expected that the approach gives the better molecular sensitivity compared to pencil beam XFCT and collimated cone-beam XFCT at comparable irradiation dose. The event analysis emphasized that only 9.5% of XF photon interactions are useful for image reconstruction. While this lowers sensitivity, the scatter reduction capability compensates on the other side. Given the large scatter to XF ratio of 16 to 175 in the concentration phantom for opening angles from 0.3° to 2.6°, it is a reasonable assumption that the molecular sensitivity is improved for XFCT with CCs in this case. However, we have shown that in a mouse size phantom concentrations of 0.001% are detectable at 2 mGy with pencil beam XFCT (Ahmad, Bazalova, Xiang and Xing 2014) which is 15 times lower than achieved in this study. In mouse size phantoms much less scatter is present and the scatter reduction capability of the CC approach is also drastically reduced due to the relative high angular blurring. This states that highest sensitivity is not attributable to a single XFCT approach but rather depends on the imaging task. Therefore, it is requested that comparable studies between all three XFCT approaches with varying phantom sizes are taken out in the future.

The focus of this study is related to the speed up of the scan time capability of the CC approach. We have presented that good molecular sensitivity can be achieved including 45 fold scanning time reduction. The improvement in scanning time can also be achieved with fan-beam or cone-beam excitation combined with collimators. Probably higher molecular sensitivities are accessible with CCs, as effective collimation absorbs the majority of XF photons. This is especially true for pin hole collimators utilized in special configurations to reduce scatter content. However, collimator approaches include much lower detector complexity and 3D excitation is possible without additional reconstruction load. Hence, high speed low sensitivity XFCT is possible with the collimator approach.

It was shown in MC simulations for XFCT with collimators that a spatial resolution of about 1 mm is achievable for doses in the cGy range for mouse size objects and similar gold concentrations as presented here (Jones and Cho 2011). While the CC approach is not able to achieve as good as spatial resolution than the collimator approach due to the physical limitations, the method is appropriate to achieve comparable molecular sensitivity at more acceptable clinical doses.

A possible extension for image reconstruction is to process only voxels which are affected by the exciting fan-beam geometry. With this approach the spatial resolution can be boosted by using smaller fan-beam angles. In an extreme scenario of this approach, the excitation beam is limited to a narrow pencil beam. In this pencil beam setup, the high and unrestricted spatial resolution of standard XFCT is preserved. The additional information of the CC is used similar to time-of-flight information in PET imaging to restrict the emission position along the line of response defined by the excitation beam. This boosts image contrast as well as molecular sensitivity. However, the scanning times are the same as in standard XFCT in this measurement mode.

Another potential application for XFCT is nano-particle enhanced radiation therapy (Hainfeld et al 2004) where XFCT imaging would provide extremely relevant information for dose calculations and quality assurance when combined with on-board imaging (OBI) systems of clinical linear accelerators. If these molecular OBI (OBMI) systems are established, the XF method would be used to optimize tumor positioning. Tumor specific markers can be used to outline the target region and its orientation more precisely than the low contrast images from CBCT systems.

In the given example the MIRD phantom is only irradiated from two projection angles to simplify the data analysis. This induces a large dose on the patients surface which can be avoided by rotating the source around the patient. However, it was found that irradiation from 90° or 270° causes a lot of forward scatter in the detector. This makes large areas of the detector insensitive for XF photons. Conclusively, balanced partial arc protocols need to be devised to optimize the dose to sensitivity ratio and to provide more uniform dose distributions.

When standard clinical CT scanners are upgraded with CCs, molecular information can be retrieved during standard scans in radiology without any additional dose exposure for the patient. This procedure can spare additional Gamma or PET imaging and spares radiation dose for the patient.

When polychromatic x-ray sources are used, it has to be mentioned that the dose has to be approximately increased by an order of magnitude to reach the same molecular sensitivity as with a monochromatic source. Increased dose requires longer scanning and image reconstruction time which has to be taken into account when translated to a real application.

Nevertheless, high molecular sensitivities at doses commonly used in radiology can be achieved at synchrotron sites or with compact light sources (CLS) which are able to provide mono-energetic x-ray beams.

5. Conclusion

The study showed that the combination of XFCT and Compton scatter imaging is a valid path to realize molecular imaging with nano-particle tracers for clinical diagnosis. For the first time, the impact of plane excitation compared to volume emission in Compton image reconstruction was investigated. The results hold that plane excitation improves reconstruction time as well as image quality.

A physical limitation for the spatial resolution is given by Doppler broadening in the CC which also restricts the scatter reduction capability and molecular sensitivity which was quantified for a lung scan example in this work. The spatial resolution analysis promises FWHM of point-like sources around 5.3 mm in proximity of the lung center. Following the geometry of this study, the scanning time of XFCT can be reduced by a factor of 45 with the use of CCs. Hence, imaging of a single slice can be reduced from 11 min to 15 s.

A detectability limit of 560 pM/l gold concentration for this scan time accelerated scenario was presented for 5 mm diameter lesions close to the lung center.