Abstract
In designing an ERP study, researchers must choose how many trials to include, balancing the desire to maximize statistical power and the need to minimize the length of the recording session. Recent studies have attempted to quantify the minimum number of trials needed to obtain reliable measures for a variety of ERP components. However, these studies have largely ignored other variables that affect statistical power in ERP studies, including sample size and effect magnitude. The goal of the present study was to determine whether and how the number of trials, number of participants, and effect magnitude interact to influence statistical power, thus providing a better guide for selecting an appropriate number of trials. We used a Monte Carlo approach to measure the probability of obtaining a statistically significant result when testing for (1) the presence of an ERP effect, (2) within-participant condition differences in an ERP effect, and (3) between-participant group differences in an ERP effect. Each of these issues was examined in the context of the error-related negativity (ERN) and the lateralized readiness potential (LRP). We found that doubling the number of trials recommended by previous studies led to more than a doubling of statistical power under many conditions. Thus, when determining the number of trials that should be included in a given study, researchers must consider the sample size, the anticipated effect magnitude, and the noise level, rather than relying solely on general recommendations about the number of trials needed to obtain a “stable” ERP waveform.
Introduction
Event-related potentials (ERPs) are small relative to other signals in the EEG and therefore are not typically visible on a single trial. Instead, ERPs are isolated from the EEG by averaging over many instances of a particular type of event. Averaging increases the signal-to-noise ratio of the data by reducing the contribution of any voltage fluctuations that are not time-locked to the event of interest, allowing the event-related brain activity to become larger than the noise. The signal-to-noise ratio improves as a function of the square root of the number of trials included in the average (Luck, 2014). All else being equal, the more trials that are included in the average, the better the quality of the data. However, there are practical limits on the number of trials that can be presented in an experiment. For example, participants can become fatigued or fidgety if an experiment is too long, which can increase the noise level in the data and negatively impact performance on the task. Thus, it is necessary to optimize the number of trials included in an experiment by balancing the tradeoff between the quality of the data (which impacts the ability to detect a significant effect) and the amount of time and resources spent collecting the data.
The decision about how many trials to include in a given ERP experiment has typically been made on the basis of tradition or anecdotal evidence from previous research. More recently, studies have attempted to provide specific, data-driven guidelines for how many trials should be included in an ERP experiment. These studies have examined several widely used ERP components, including the error-related negativity (ERN), error positivity (Pe), N100, N200, vertex positive potential (VPP)/N170, mismatch-negativity (MMN), feedback-related negativity (FRN), late positive potential (LPP), and P300 (Cohen & Polich, 1997; Duncan et al., 2009; Fischer, Klein, & Ullsperger, 2017; Huffmeijer, Bakermans-Kranenburg, Alink, & van IJzendoorn, 2014; Larson, Baldwin, Good, & Fair, 2010; Marco-Pallares, Cucurell, Münte, Strien, & Rodriguez-Fornells, 2011; Olvet & Hajcak, 2009; Pontifex et al., 2010; Rietdijk, Franken, & Thurik, 2014; Segalowitz & Barnes, 1993; Steele et al., 2016; Thigpen, Kappenman, & Keil, 2017). The general approach of these studies has been to take the data from an experiment with a particular number of trials and simulate experiments with smaller numbers of trials by subsampling from the original dataset. This makes it possible to determine the minimum number of trials that are required to obtain an ERP that is as stable and reliable as the ERP from the available full sample of trials. The similarity between averages with different numbers of trials has been quantified in a variety of ways, such as by comparing the correlation among the ERPs or measuring the internal reliability of the averages (e.g. Olvet & Hajcak, 2009). Some studies have also focused on how the number of trials used to calculate an ERP affects its psychometric properties, including test-retest reliability (Huffmeijer et al., 2014; Larson et al., 2010; Segalowitz & Barnes, 1993), internal consistency (Thigpen et al., 2017), and reliability across different age groups (Marco-Pallares et al., 2011; Pontifex et al., 2010). The overall goal of these studies has been to determine the minimum number of trials necessary to obtain a reliable version of the particular ERP component examined.
For large ERP components, these studies have generally concluded that a relatively small number of trials is adequate. For example, several studies have concluded that stable grand-average ERPs can be obtained with 10 or fewer trials for the ERN (Larson et al., 2010; Olvet & Hajcak, 2009; Pontifex et al., 2010; Steele et al., 2016; see Fischer et al., 2017 for a recommendation of at least 15 trials). This conclusion was based on the calculated stability of the ERN, generally defined as a high correlation between ERPs averaged over relatively few trials and ERPs averaged using more trials. However, as noted by Gehring, Liu, Orr, and Carp (2012, p. 278), “this does not speak to the ability of standard analyses to find between-condition or between-group differences.” This point has also been made by a recent study, in which the ability to detect a between-groups difference on the ERN was examined as a function of the number of trials included in the ERP average and the error rate across groups (Duncan et al., 2009; Fischer et al., 2017). The study by Fischer et al. (2017) offered some initial evidence that specific recommendations that are based on tests of ERP stability may not be appropriate as guidelines for detecting differences between groups. Specifically, they found that larger numbers of trials were necessary to obtain appropriate statistical power to detect significant differences between groups compared with number-of-trial estimates obtained from a simple examination of stability.
This is a significant issue, as it is not the goal of most ERP studies to determine whether an ERP component is present or absent. Instead, the aim of most ERP studies is to determine whether an ERP differs across individuals, conditions, and/or groups. Such studies typically examine much smaller differences than simple comparisons of correct versus error trials (for the ERN) or rare versus frequent trials (for the P300). Thus, a critical question concerns how the number of trials (along with the sample size and effect size) impacts the ability to detect statistically significant between-condition or between-group effects. In other words, statistical power for the effect of interest is usually the most important consideration when determining the number of trials necessary for a given ERP study, yet this has not been examined by most of the previous work in this area. Framing this issue in terms of statistical power is particularly important given recent demonstrations that neuroscience studies tend to be underpowered, creating the double-pronged problem of decreased likelihood of detecting an effect and overestimation of effects that are detected (Button et al., 2013; Groppe, 2017).
An important conclusion that one might draw from previous studies of the number of trials is that ERP researchers can collect data from relatively small numbers of trials without any practical cost to data quality (Cohen & Polich, 1997; Duncan et al., 2009; Fischer et al., 2017; Huffmeijer et al., 2014; Larson et al., 2010; Marco-Pallares et al., 2011; Olvet & Hajcak, 2009; Pontifex et al., 2010; Rietdijk et al., 2014; Segalowitz & Barnes, 1993; Steele et al., 2016; Thigpen et al., 2017). For example, a researcher may read that “P300 amplitude stabilizes with approximately 20 target trials for all conditions” (Cohen & Polich, 1997, p. 249) or that the “ERN and Pe may be accurately quantified with as few as six to eight commission error trials across the life span” (Pontifex et al., 2010, p. 767). The researcher who reads such statements may then assume that there is no point in obtaining any more than 20 trials in a P300 study or 6–8 trials in an ERN study, even if more trials could be reasonably obtained. However, most previous research on this topic has not directly examined the effect of the number of trials on statistical power or assessed whether this interacts with the sample size and the effect magnitude1. Therefore, the guidelines from these previous studies may lead our hypothetical researcher to underestimate the number of trials needed to obtain statistically significant effects. As a result, considerable time and resources may be wasted conducting studies that have little chance of yielding significant effects. On the other hand, if there truly is little or no value in including more than 20 trials per condition in a P300 experiment or more than 6–8 error trials per condition in an ERN experiment, then this would allow researchers to design studies that would be infeasible with larger numbers of trials. Thus, it is important to determine whether other aspects of experimental context need to be considered when determining the optimal number of trials for a given study.
The Current Study
The primary goal of the current study was therefore to explore the effect of the number of trials on statistical power and how this interacts with the sample size and effect magnitude. If the number of trials required to obtain statistically significant results varies widely depending on these other factors, then this will undermine the idea that we can use simple guidelines for the number of trials in an ERP experiment that can be applied broadly across very different types of studies. This is a vitally important issue for determining how future ERP studies are designed.
To address this issue, we systematically manipulated three key factors that play a role in determining statistical power: the number of trials contributing to the averaged ERP, the sample size, and the effect magnitude. We examined the influence of these factors on the probability of obtaining a statistically significant result (1) when testing for the presence of an ERP effect (e.g., a difference in ERN amplitude between error trials and correct trials), (2) when testing for within-participant differences across conditions in an ERP effect, and (3) when testing for between-groups differences in an ERP effect. To address these questions, we used a Monte Carlo approach to simulate experiments with various numbers of trials, numbers of participants, and effect magnitudes by subsampling trials and participants from a large data set. By simulating 1000 experiments for each given set of parameters, we were able to estimate the probability of obtaining a statistically significant result (i.e., the statistical power) for each combination of parameters. Our goal was not simply to show that each of these factors impacts statistical power, but instead to determine how they interact in determining power. In other words, we examined how the effect of increasing the number of trials per participant depends on the sample size and the effect magnitude. This made it possible to determine whether it is valid to assume that the point at which it is no longer worth increasing the number of trials is relatively constant across studies or, alternatively, whether different studies require substantially different numbers of trials to achieve the same level of statistical power.
To preview the results, we found that statistical power increased as the number of trials per participant increased, even beyond the point needed to achieve a “stable” ERP waveform. For example, statistical power more than doubled when we increased the number of trials from 8 to 16 in simulated ERN experiments with small effects and small numbers of participants. Generally speaking, increasing the number of trials was most helpful at low and intermediate levels of statistical power (which, in turn was determined by the size of the effect and the number of participants). However, when power was already high with a relatively small number of trials (because of a large effect size or large number of participants), increasing the number of trials yielded relatively little increase in power (a ceiling effect).
Methods
ERP Components
We focused on two ERP components, the error-related negativity (ERN) and the lateralized readiness potential (LRP). The ERN was selected because it is a robust effect that has recently been the subject of several reliability studies (Fischer et al., 2017; Larson et al., 2010; Olvet & Hajcak, 2009; Pontifex et al., 2010; Steele et al., 2016). The LRP was selected because it is typically a smaller effect and requires a relatively large number of trials to detect, thus allowing a broader range of trial counts and effect magnitudes to be examined. These two ERP effects were also selected because they can be isolated using a single task, allowing us to use data from a single experiment for all analyses, thereby eliminating differences in data quality, noise level, participant alertness, etc., across analyses. The data set included a relatively large number of participants (N = 40), making it possible to examine a broad range of sample sizes.
The ERN is typically observed in response-locked waveforms as more negative voltage on error trials relative to correct trials (for a recent review, see Gehring et al., 2012). ERN onset is closely tied to the execution of the error (within ~50 ms) and is maximal at fronto-central electrode sites. The difference in amplitude between error trials and correct trials is relatively large (typically 5–15 μV), and is often quantified with a relatively small number of error trials (which is sometimes necessary given the relatively small number of errors that participants make in the tasks that are commonly used to elicit the ERN).
The lateralized readiness potential (LRP) is an ERP that is associated with the selection and preparation of a lateralized manual response (see Eimer, 1998; Smulders & Miller, 2012 for reviews). It is a negative-going deflection observed at electrode sites over motor cortex and is larger at electrode sites contralateral to the response hand compared with the ipsilateral sites. The LRP can be seen in both stimulus-locked or response-locked averages, and it typically onsets shortly before a response is made; in the current study, we focus on stimulus-locked LRP waveforms as a contrast for the response-locked ERN analysis. The neural activity associated with response preparation can be isolated by taking advantage of the contralateral organization of motor processing in the brain. Specifically, the LRP is isolated by subtracting activity recorded at electrode sites ipsilateral to the response hand from activity recorded at electrode sites contralateral to the response hand. This yields just the activity related to preparation of the motor response. Unlike the ERN, the LRP is a relatively small component (typically 1–4 μV), and it is usually quantified using averages of between 50–100 trials per response hand (Smulders & Miller, 2012).
Participants
Forty undergraduate students between the ages of 18 and 30 with normal color perception and no history of neurological injury or disease were tested (25 female). Of these 40 participants, 8 participants were excluded from the ERN analyses for having too few (<16) artifact-free error trials, leaving 32 participants; 1 participant was excluded from the LRP analyses for having an error rate over 50%, leaving 39 participants. The study was approved by the University of California, Davis Institutional Review Board (IRB), and participants received monetary compensation.
Stimuli and Task
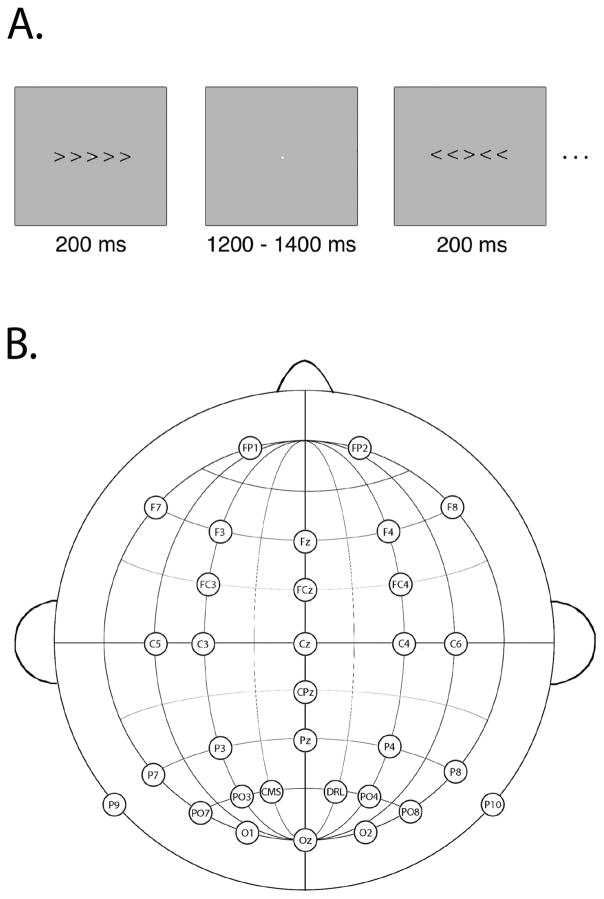
Participants completed a modified version of the Eriksen flanker task (Eriksen & Eriksen, 1974)2. An example stimulus display is presented in Figure 1a. Each trial consisted of a set of five arrowhead stimuli presented for 200 ms in black on a light grey background. Each arrowhead subtended 1 × 1° of visual angle. The central arrowhead was designated the target stimulus, and participants made either a left-hand or right-hand button press on a Logitech gamepad corresponding to the direction of the central arrowhead. The flanking arrowheads either pointed in the same direction (congruent trials) or the opposite direction (incongruent trials) as the target stimulus, resulting in four sets of stimuli: ≪≪<, ≫≫>, ≪>≪, and ≫<≫. The directions of the target and flankers were chosen randomly on each trial, with leftward and rightward pointing targets each occurring on half of the trials, and congruent and incongruent flankers each occurring on half of the trials. Stimuli were presented over a continuously visible central white fixation point (.15° visual angle), with a jittered stimulus onset asynchrony of 1400–1600 ms (rectangular distribution, average of 1500 ms). Participants completed 400 trials with a participant-controlled break provided every 40 trials to allow participants to rest their eyes. To ensure an adequate number of error trials, feedback was presented during the break screens reading “Try to respond a bit faster” if the error rate from the preceding block was below 10%, or “Try to respond more accurately” if the error rate from the preceding block exceeded 20%; if the error rate was between 10–20%, a message of “Good job!” was presented.
Figure 1.
Panel A: Example stimulus display for modified Eriksen flanker task. Panel B: The electrode recording montage.
EEG Recording and Processing Procedures
The continuous EEG was recorded using a Biosemi ActiveTwo recording system (Biosemi B.V., Amsterdam, the Netherlands). The electrodes were mounted in an elastic cap using a subset of the International 10/20 System sites (FP1, FP2, F3, F4, F7, F8, FC3, FC4, C3, C4, C5, C6, P3, P4, P7, P8, P9, P10, PO3, PO4, PO7, PO8, O1, O2, Fz, FCz, Cz, CPz, Pz, and Oz; see Figure 1b). A common mode sense electrode was located at site PO1, with a driven right leg electrode located at site PO2. The horizontal electrooculogram (EOG) was recorded from electrodes placed lateral to the external canthi and was used to detect horizontal eye movements; the vertical EOG was recorded from an electrode placed below the right eye and was used to detect eyeblinks and vertical eye movements. The EEG and EOG were low-pass filtered using a fifth order sinc filter with a half-power cutoff at 204.8 Hz and digitized at 1024 Hz with 24 bits of resolution. The single-ended EEG and EOG signals were converted to differential signals offline, referenced to the average of the left and right mastoids.
Signal processing and analysis was performed in Matlab using EEGLAB toolbox (Delorme & Makeig, 2004) and ERPLAB toolbox (Lopez-Calderon & Luck, 2014). The EEG was downsampled to 256 Hz and high-pass filtered with a cut-off of 0.1 Hz (noncausal Butterworth impulse response function, half-amplitude cut-off, 12 dB/oct roll-off). Portions of EEG containing large muscle artifacts or extreme voltage offsets (identified by a semi-automatic ERPLAB algorithm) were removed, as well as all break periods longer than two seconds. Independent component analysis (ICA) was then performed for each participant to identify and remove components that were clearly associated with eyeblinks as assessed by visual inspection of the waveforms and the scalp distributions of the components (Jung et al., 2000). The ICA-corrected EEG data were segmented for each trial as follows. For the ERN, trials were segmented beginning 600 ms prior to the onset of the response and continuing for 400 ms post-response; baseline correction was performed using the −400 to −200 ms window prior to response onset. For the LRP, trials were segmented beginning 200 ms prior to the onset of the stimulus through 800 ms post-stimulus; baseline correction was performed using the 200 ms prior to stimulus onset.
Trials containing artifacts were removed by means of automated ERPLAB algorithms, including voltage offsets greater than +/−200 μV, and eye movements larger than 0.1 degree of visual angle that were detected using the step function described by Luck (2014). For the stimulus-locked LRP, trials that contained an eyeblink during the presentation of the stimulus were also excluded. Trials with RTs less than 200 ms or greater than 1000 ms were excluded from all analyses. Trials with incorrect behavioral responses were excluded from the LRP analysis.
Time windows and measurement sites were chosen a priori on the basis of prior research (see Gehring et al., 2012; Smulders & Miller, 2012). To isolate the ERN, correct trials and error trials were averaged separately, and an error-minus-correct difference wave was created. ERN amplitude was quantified as the mean amplitude from 0–100 ms relative to the response at electrode Fz. The LRP was isolated by creating separate ERP waveforms for the hemisphere that was contralateral to the response and the hemisphere that was ipsilateral to the response, collapsed across compatible and incompatible conditions. From these waveforms, contralateral-minus-ipsilateral difference waveforms were created, averaged across left- and right-hand responses. LRP amplitude was measured from the difference waves as the mean amplitude from 300–500 ms at electrode C3/4.
Monte Carlo Analyses
We conducted three sets of simulated experiments. For each, Monte Carlo analyses were used to simulate a large number of experiments by randomly sampling subsets of trials and participants from our data set. Student’s t test was used to determine whether a given simulated experiment resulted in a significant difference between conditions (using paired t tests) or between groups (using independent-samples t tests). To estimate the probability obtaining a statistically significant effect (alpha = .05) for a given combination of parameters (sample size, number of trials, and effect magnitude), 1000 experiments were simulated for each combination. For all analyses, we used real data collected from our participants. For the within-participant and between-participant analyses, we added artificial effects so that the true effect magnitudes would be known (see Kiesel, Miller, Jolicœur, & Brisson, 2008; Smulders, 2010; Ulrich & Miller, 2001 for similar approaches). This approach is ideal because it uses a combination of real EEG data (so that the noise properties are realistic) and artificially induced experimental effects (so that the actual truth is known).
Results
Noise Levels and Basic ERP Results
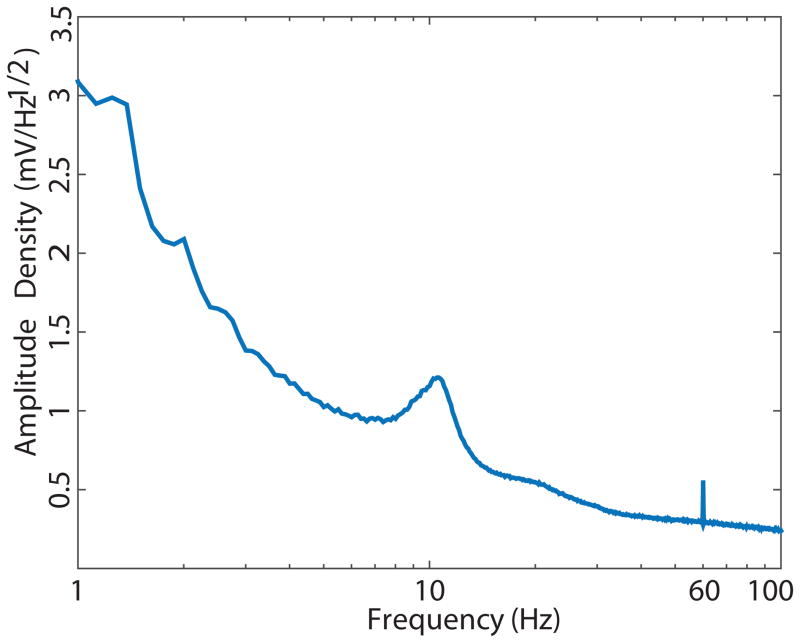
The quality of the EEG data impacts the ability to detect a statistically significant result, and we therefore quantified the noise level of our data. The noise level differs across experiments as a function of the laboratory environment, including the EEG equipment used, the electrical shielding in the testing space, the electrode impedances, and the temperature and humidity of the recording environment (Kappenman & Luck, 2010). To quantify the noise level in our data set, we computed the amplitude density at each frequency ranging from 1 to 100 Hz using the fast Fourier transform (FFT). Although the raw EEG contains both signal and noise, the noise is much larger than the signal, especially at very low and very high frequencies, so the amplitude at a given frequency provides an approximate measure of the noise at that frequency. To provide one set of noise quantifications for both the ERN and LRP, FFTs were calculated using the full data set (N=40). FFTs were computed on zero-padded 5-second segments of the continuous EEG with 50% overlap, after downsampling and applying a high-pass filter as described above. Segments containing large artifacts (over 200 μV) were excluded, and then the amplitude spectrum was averaged across segments, electrode sites, and participants. The resulting grand average amplitude density spectrum is shown in Figure 2.
Figure 2.
Amplitude density as a function of frequency, calculated from Fast Fourier transforms (FFTs) of data from all epochs, electrodes, and participants in the data set. A log scale is used for frequency to make it easier to visualize the lower frequencies.
Additional methods of visualizing data quality for each ERP component are described in detail below (see Figures 3 and 4).
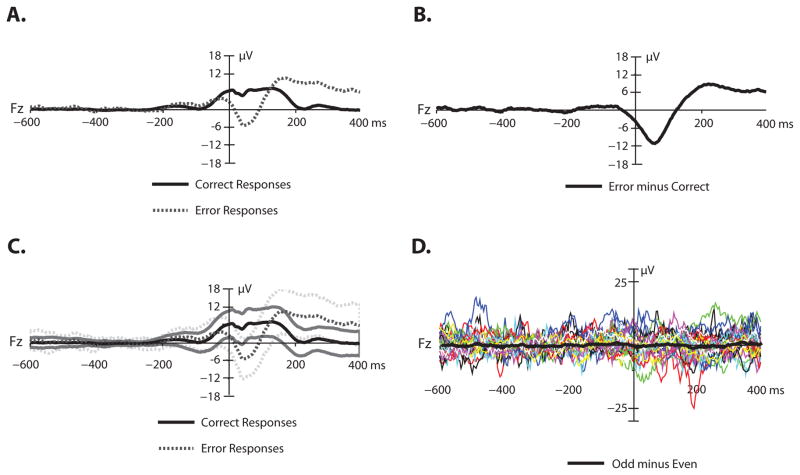
Figure 3.
ERN waveforms. Panel A: Response-locked grand average ERP waveforms for error and correct trials at electrode Fz. Panel B: Response-locked grand average difference waveform (error minus correct trials). A low-pass filter was applied offline before plotting (non-causal Butterworth impulse response function, half-amplitude cutoff = 30 Hz, 12 dB/oct roll-off). Panel C: Response-locked grand average ERP waveforms for error and correct trials at electrode Fz. Standard error of the mean is indicated by shaded lines. Panel D: Plus-minus averages for the error trials, which remove the ERP signal but leave the noise. The grand average noise waveform is superimposed in bold on the individual participant noise waveforms.
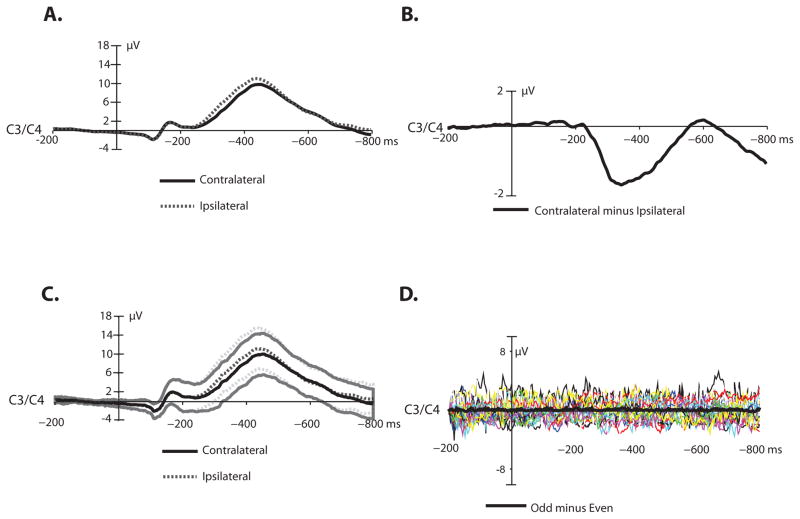
Figure 4.
LRP waveforms. Panel A: Stimulus-locked grand average contralateral and ipsilateral ERP waveforms collapsed across electrodes C3 and C4. Panel B: Stimulus-locked grand average difference waveform (contralateral minus ipsilateral trials). A low-pass filter was applied offline before plotting (non-causal Butterworth impulse response function, half-amplitude cutoff = 30 Hz, 12 dB/oct roll-off). Panel C: Stimulus-locked grand average contralateral and ipsilateral waveforms at electrode C3/4. Standard error of the mean is indicated by shaded lines. Panel D: Plus-minus averages for the LRP, which remove the ERP signal but leave the noise. The grand average contralateral-minus-ipsilateral noise waveform is superimposed in bold on the individual participant noise waveforms.
ERN
Figure 3A shows the grand average ERP waveforms for correct and incorrect trials, averaged across all participants included in the ERN analyses (N=32 with at least 16 artifact-free error trials); the error-minus-correct difference waveform is shown in Figure 3B. Consistent with the large ERN literature, error responses elicited a larger negative deflection than correct responses, beginning shortly before response onset and continuing for about 100 ms post-response. A paired t test indicated that this was a significant difference (t(31) = 8.56; p < 0.0001; η2 = 0.7). The average error-minus-correct mean amplitude difference was −8.02 μV (SEM = 0.93). Panel C shows the average standard error of the mean. That is, the standard error of the mean across trials was calculated for each participant at each time point in each ERP waveform, and these values were then averaged across participants.
To visualize the noise level more directly, we implemented the plus-minus averaging approach (Schimmel, 1967). This approach subtracts the ERP while leaving the noise by inverting the waveform on half of the trials. Specifically, all artifact-free error trials for each participant in the ERN analysis were separated into two sets for averaging, with one average for odd-numbered trials and one for even-numbered trials. The average waveform for odd-numbered error trials was then subtracted from the waveform for even-numbered error trials for each participant. This effectively cancels the ERP signal, which should be equivalent between odd-numbered and even-numbered trials, but leaves the noise (which is just as large whether or not the waveform is inverted). Figure 3D overlays the single-participant plus-minus averages as well as the average across participants for the error trials.
LRP
Figure 4A shows the grand average contralateral and ipsilateral waveforms, averaged across all participants included in the LRP analyses (N=39); the contralateral-minus-ipsilateral difference waveform is shown in Figure 4B. Consistent with previous LRP studies, activity at electrode sites contralateral to the response hand elicited a larger negative voltage deflection than electrode sites ipsilateral to the response hand, and this effect was present from approximately 300 – 500 ms after stimulus onset. A paired t test indicated that this was a significant difference (t(38) = 10.98; p < 0.0001; η2 =0 .76). The average contralateral-minus-ipsilateral mean amplitude difference was −1.31 μV (SEM = 0.12). Figure 4C shows the average standard error of the mean, and Figure 4D shows the plus-minus average as a means of visualizing the noise.
Internal Reliability
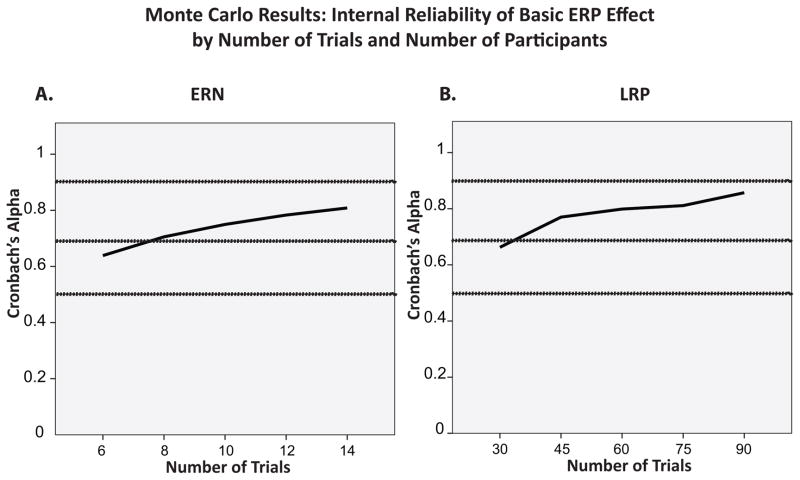
To assess the internal reliability of the ERN and LRP as a function of the number of trials and the sample size, we computed Cronbach’s alpha. Specifically, for each combination of parameters, we calculated Cronbach’s alpha for each participant. We then averaged the resulting values across participants within a simulated experiment and across all 1000 simulated experiments for each combination of number of trials and sample size. The results are plotted in Figure 5. These results replicate the findings of previous studies (Fischer et al., 2017; Larson et al., 2010; Olvet & Hajcak, 2009; Pontifex et al., 2010; Steele et al., 2016), and suggest that to achieve high internal reliability (Cronbach’s alpha values of .7–.9), 8 trials is sufficient for the ERN and 45 trials is sufficient for the LRP. However, the goal of the present study was to determine whether statistical power is improved by increasing the number of trials beyond this level, which is addressed in the following sections.
Figure 5.
Panel A: Internal reliability of the ERN at Fz as a function of number of trials in the Monte Carlo simulations, measured by Cronbach’s alpha. Panel B: Internal reliability of the LRP at C3/4 as a function of number of trials and sample size in the Monte Carlo simulations, measured by Cronbach’s alpha. Both panels show values for N=32, the largest sample size tested in our Monte Carlo analyses. Values of Cronbach’s alpha above .9 are indicative of excellent internal reliability, between .7 and .9 of high internal reliability, between .5 and .7 of moderate internal reliability, and below .5 of low internal reliability (Hinton Perry, Brownlow, McMurray, & Cozens, 2004).
Probability of obtaining a statistically significant ERP effect
Our first set of Monte Carlo analyses assessed the probability of detecting the presence of a significant ERN or LRP (which is a “low bar” for assessing the number of trials). Subsequent analyses will focus on detecting within- or between-group differences in ERP and LRP amplitude.
We simulated experiments with varying numbers of trials and numbers of participants. In our ERN analyses, we simulated experiments with 6, 8, 10, 12, and 14 artifact-free error trials, as well as with all available error trials (mean: 50.29; range: 16 – 87). For the LRP analyses, we simulated experiments with 30, 45, 60, 75, and 90 artifact-free trials, as well as with all available trials (range: 91 – 195). For each number of trials, we simulated experiments with 12, 16, 20, 24, 28 and 32 participants.
ERN
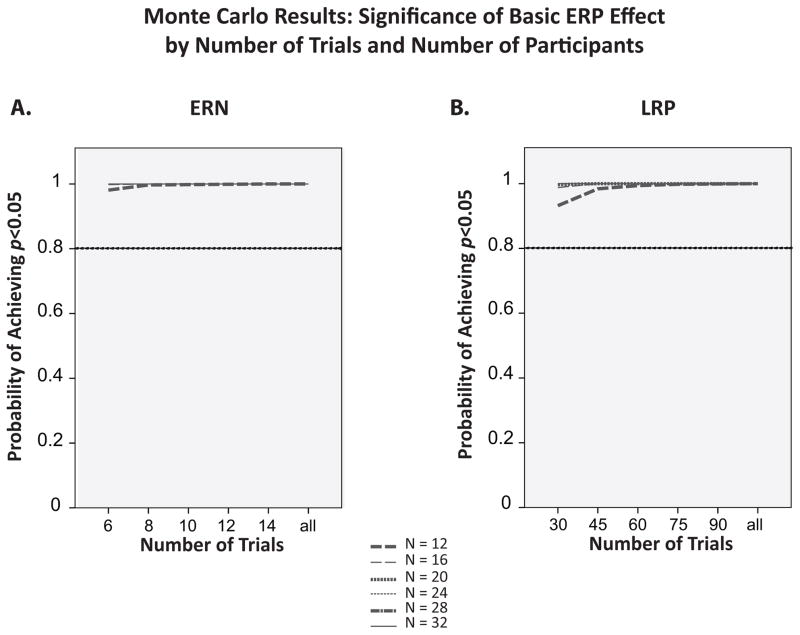
Figure 6a shows the probability of obtaining a significant ERN (i.e., a non-zero difference in amplitude between error trials and correct trials) as a function of the number of trials included in the error-trial averages. The correct-trial averages included all available trials (because the number of correct trials is typically so great that it does not meaningfully impact the results). The statistical power for determining whether error and correct trials differ in ERN amplitude was extremely high even with a small number of trials and a small number of participants, so variations in these factors had very little impact on statistical power (a ceiling effect). However, very few studies are designed to simply determine whether the ERN differs between error trials and correct trials, so these findings do not indicate that most experiments could use the minimum number of trials and participants examined here.
Figure 6.
Panel A: Probability of obtaining a significant ERN (difference between the ERP on error versus correct trials) as a function of number of trials and sample size in the Monte Carlo simulations. Panel B: Probability of obtaining a significant LRP (difference between the contralateral versus ipsilateral ERP waveforms) as a function of number of trials and sample size in the Monte Carlo simulations.
LRP
Figure 6b shows the probability of obtaining a significant LRP (difference between activity contralateral vs. ipsilateral to the response) as a function of the number of trials and the sample size. As with the ERN, power was at ceiling for this simple comparison, so varying the number of trials and participants had very little effect.
Detecting significant effects in within-participant experiments
We next simulated experiments in which each participant is tested in two conditions, allowing us to assess the probability of detecting the presence of a within-participants condition difference. These simulations would be analogous to an experiment examining, for example, differences in ERN amplitude under conditions of low versus high emotional arousal, where the same participants experience both the low- and high-arousal conditions. To simulate an effect of a known size in the magnitude of the ERN, we randomly divided each participant’s error trials into two sets of 8 errors each (8 errors per set being the maximum possible, because some participants had as few as 16 artifact-free error trials). To simulate this effect with 16 trials, we used the well-validated bootstrap approach (Di Nocera & Ferlazzo, 2000; Efron & Tibshirani, 1994), in which each participant’s error trials are divided into two sets of 16 trials each, sampling with replacement from the 16 available trials. In other words, we sampled 16 trials with replacement from the 16 available trials for a given participant to create the trials for one simulated condition, and then we repeated this process with a new random sample of 16 trials to create the trials for the other simulated condition. It has been well established that sampling with replacement in this manner provides a good approximation of sampling without replacement from an infinite population of trials (Singh, 1981). To simulate a difference of X μV between the two groups of waveforms, a voltage of ½X was subtracted from the mean amplitude from 0–100 ms post-response at electrode Fz from one set of waveforms and added to the other (e.g., to simulate a 4 μV difference between conditions, 2 μV was added to one set of trials and subtracted from the other).
In these simulations, we are assuming that all participants respond equivalently to the experimental manipulation and that all of the variance is a result of (1) the finite number of trials being averaged together and (2) condition-independent individual differences in ERN amplitude. In real experiments, some variance will also arise from individual differences in the response to the experimental manipulation. However, when the number of trials is small, most of the variance presumably comes from noise in the single-trial EEG data that is not eliminated. A particularly high degree of inter-trial variability might be expected for experiments in which stimuli are not identical within a condition (e.g., language experiments in which different words comprise the stimuli for a given condition). We would also expect some additional variance to arise from differences across participants in biophysical factors (e.g., cortical folding patterns) (Luck, 2014). Thus, for the sake of simplicity, we chose to ignore individual and inter-trial differences in the size of the experimental effect in the present simulations.
We simulated experiments with differences of 1, 2, 3, 4, 5, 6, and 7 μV in the magnitude of the ERN between conditions. For each simulated experiment, the error trials in the two conditions differed in amplitude by this amount (plus or minus noise), and we determined whether the observed difference was statistically significant (comparing just the error trials for the two conditions). This procedure was then iterated 1000 times with different random selections of trials and participants so that we could estimate the probability of obtaining a significant difference between conditions with a given number of trials and participants.
For the LRP, we conducted an analogous analysis by randomly dividing each participant’s trials into two sets of 45 trials or two sets of 90 trials (sampling with replacement) and computing the contralateral minus ipsilateral difference for each to simulate two different LRP conditions. These simulations would be analogous to an experiment examining, for example, differences in LRP amplitude between congruent and incongruent trials in a flankers task. Voltage was subtracted from the mean amplitude from 300–500 ms at electrode C3/4 for one set of waveforms and added to the other (as described above), with simulated differences of 0.25, 0.5, 0.75, 1, 1.25, 1.5, and 1.75 μV between the two LRP conditions. We then performed a statistical comparison to determine whether the difference waves were significantly different in amplitude between the two simulated conditions.
In both the ERN and LRP analyses, we assessed sample sizes of 12, 16, 20, 24, 28 and 32 participants for each simulated difference in effect magnitude and number of trials. Thus, we factorially varied the number of trials, the number of participants, and the magnitude of the difference across conditions.
ERN results
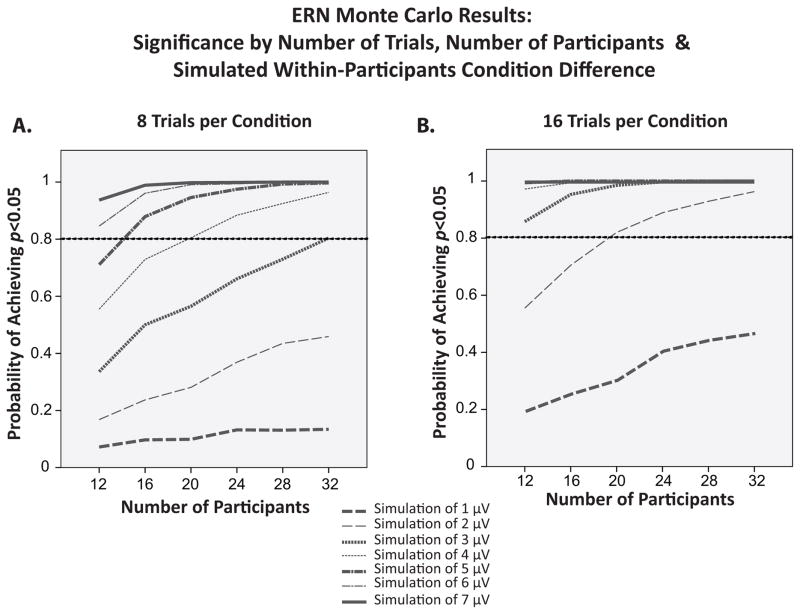
Figure 7 shows the probability of obtaining a statistically significant difference in ERN amplitude between two conditions (i.e., the statistical power) as a function of the number of trials, the number of participants, and the magnitude of the condition difference. All three factors interactively influenced the probability of obtaining a significant result. With 16 trials per condition, power was high (above .8), independent of the number of participants as long as the experimental effect was at least 3 μV. With only 8 trials per condition, however, power for detecting a 3 μV effect increased dramatically as the number of participants increased, reaching .8 only when the experiment included 32 participants. With a fairly typical N of 20 participants, power for detecting this 3 μV effect rose from only approximately .5 with 8 error trials to nearly 1.0 with 16 error trials. Similarly, with a relatively large N of 32 participants, power for detecting a somewhat smaller 2 μV effect rose from approximately .4 with 8 error trials to above .9 with 16 error trials. Thus, doubling the number of trials can more than double the statistical power under some conditions.
Figure 7.
Probability of obtaining a significant within-participants difference in ERN amplitude between two conditions as a function of number of trials and sample size in Monte Carlo simulations of experiments with between-condition differences of 1–7 μV. Note that for this analysis, sample size is plotted on the X-axis.
With a small (but very plausible) difference of 1 μV between conditions and only 8 error trials per participant, power to detect the difference between conditions was low and increased very gradually as the number of participants increased from 12 to 32. This suggests that an extraordinarily large number of participants would be needed to reliably detect small differences in ERN amplitude with only 8 error trials per participant. However, power for detecting this 1 μV effect rose steadily as the number of participants increased when the experiment included 16 error trials per participant, suggesting that reasonable levels of power could be achieved with a realistic number of participants.
Thus, although 8 trials was sufficient to obtain high levels of internal reliability (defined as Cronbach’s alpha > .7) and was sufficient to yield acceptable levels of power for detecting very large between-condition differences in ERN amplitude, increasing the number of trials to 16 dramatically increased the statistical power to detect small- or medium-sized differences in ERN amplitude. More broadly, statistical power was determined interactively by the number of trials, the number of participants, and the magnitude of the between-condition amplitude difference.
LRP results
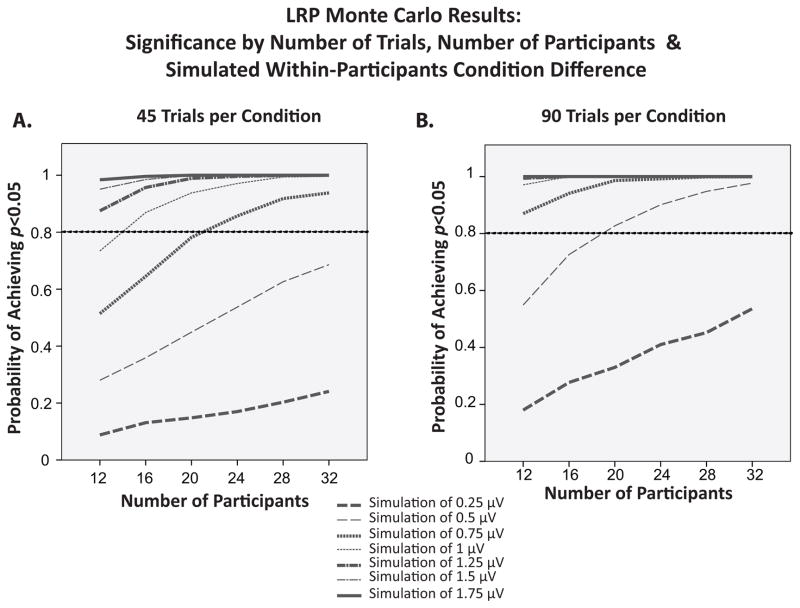
Figure 8 shows the probability of obtaining a statistically significant difference in LRP amplitude between two conditions as a function of the number of trials, the number of participants, and the magnitude of the difference between the simulated conditions. The results closely paralleled the ERN results shown in Figure 7, with all three factors interacting to determine statistical power. With an effect of 1.5–1.75 μV that approximately doubles the LRP amplitude, the power to detect the effect was near ceiling no matter whether the experiment included 45 or 90 trials per participant, even with only 12 participants. However, increasing the number of trials from 45 to 90 approximately doubled the statistical power under certain conditions (e.g., when the simulated experiment involved 20 participants and the conditions differed by 0.5 μV). Thus, increasing the number of trials beyond the number needed to achieve high internal reliability led to substantial increases in statistical power for detecting small-to-medium differences in LRP amplitude.
Figure 8.
Probability of obtaining a significant within-participants difference in LRP amplitude between two conditions as a function of number of trials and sample size in Monte Carlo simulations of experiments with between-condition differences of 0.25–1.75 μV. Note that for this analysis, sample size is plotted on the X-axis.
Detecting significant differences between groups
To assess the probability of detecting the presence of a between-groups difference in the ERN and LRP, we conducted a third set of Monte Carlo analyses. To simulate a between-participants difference in the magnitude of the ERN, we divided our sample into randomly selected groups of 16 participants each. To simulate a larger sample size of 32 participants per group, we used the bootstrap approach and randomly divided our sample into two groups of 32 participants each, sampling with replacement from the 32 available participants. Again, this is a well-validated approach that provides a good approximation of sampling without replacement from an infinite population of participants (Di Nocera & Ferlazzo, 2000; Efron & Tibshirani, 1994). To simulate a difference of X μV between the two groups, a voltage of ½X was subtracted from the average error-minus-correct difference in mean amplitude in the ERN time window for each participant in one group and added to this difference for each participant in the other group (e.g., to achieve a 4 μV group difference, 2 μV was added to the amplitudes for one group of participants and subtracted from the other). We simulated experiments with 1, 2, 3, 4, 5, 6, and 7 μV differences in the magnitude of the between-groups difference. The analogous simulations for the LRP used differences of 0.25, 0.5, 0.75, 1, 1.25, 1.5, and 1.75 μV; the appropriate voltages were added to or subtracted from the mean contralateral-minus-ipsilateral difference for each participant, and then the resulting difference scores were submitted to the statistical analyses. For the ERN, we simulated experiments with 6, 8, 10, 12, 14 error trials, and all available error trials. For the LRP, we simulated experiments with 30, 45, 60, 75, 90 trials, and all available trials. Variations in the number of trials were factorially combined with variations in the number of participants (16 or 32 per group) and variations in the between-group amplitude differences.
ERN
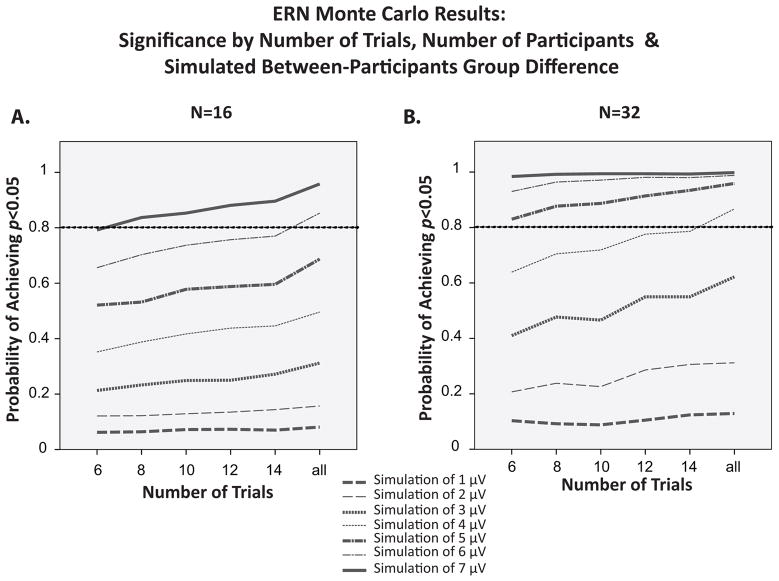
Figure 9 shows the probability of obtaining a statistically significant between-groups difference in ERN amplitude (the statistical power) as a function of the number of error trials, the number of participants, and the magnitude of the difference between groups. All three factors interacted to determine the statistical power, although the interactions were not as strong as for the within-participants manipulations shown in Figure 7. With 16 participants per group, power increased slowly but steadily as the number of trials increased unless the effect was so small that power was near floor. With 32 participants per group, power was near ceiling independent of the number of trials for extremely large between-group differences of 6–7 μV, increased slowly but steadily as the number of trials increased for moderate between-group differences, and remained near floor independent of the number of trials for very small between-group differences.
Figure 9.
Probability of obtaining a significant difference in ERN amplitude between two groups as a function of magnitude of the difference and sample size in Monte Carlo simulations of experiments with group differences of 1–7 μV.
LRP
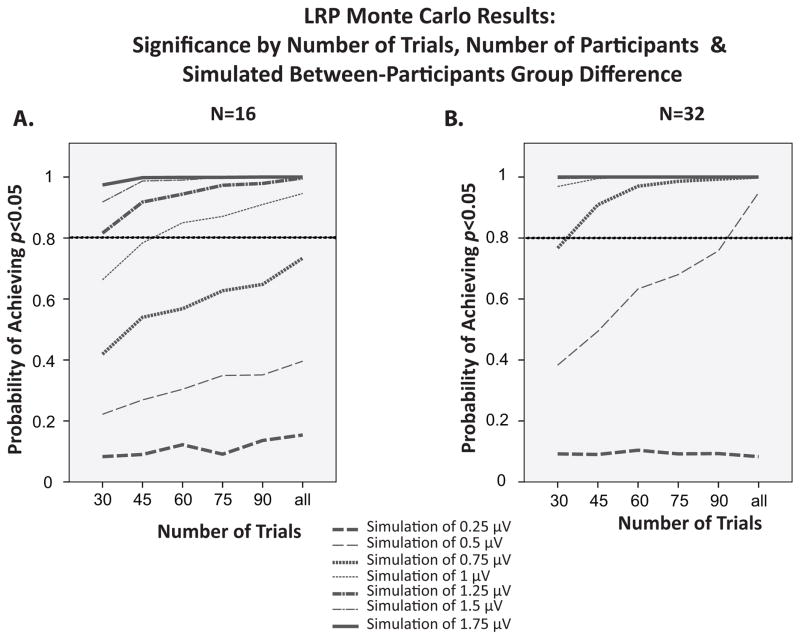
Figure 10 shows statistical power for between-group differences in LRP amplitude as a function of the number of trials, the number of participants, and the magnitude of the difference between groups. As was observed for the within-participant simulations shown in Figure 8, there were substantial interactions between these factors in the between-group simulations. With very small or very large group differences, power remained at floor or ceiling, respectively, as the number of trials or number of participants increased. For intermediate group differences, however, power increased substantially as the number of trials or participants increased. For example, the power to detect a 0.5 μV group difference increased dramatically as the number of trials increased when each group contained 32 participants. In addition, power saturated rapidly as the number of trials increased for effects of 0.75 μV or greater with 32 participants per group, whereas power increased steadily with the number of trials for group differences of 0.5–1.25 μV with 16 participants per group.
Figure 10.
Probability of obtaining a significant difference in LRP amplitude between two groups as a function of magnitude of the difference and sample size in Monte Carlo simulations of experiments with group differences of 0.25–1.75 μV.
Discussion
Probability of obtaining a statistically significant ERP component
In our first set of simulations, we examined how the systematic manipulation of number of trials and sample size impacted the likelihood of observing a statistically significant overall ERN or LRP effect. That is, for the ERN we examined the likelihood of finding a statistically significant amplitude difference between error trials and correct trials; for the LRP, we examined the likelihood of finding a statistically significant amplitude difference between the hemispheres contralateral versus ipsilateral to the response hand. Consistent with previous work (Fischer et al., 2017; Larson et al., 2010; Olvet & Hajcak, 2009; Pontifex et al., 2010; Steele et al., 2016), the ERN proved to be a robust effect that was reliably observed even when relatively few trials were included in the average (see Figure 6a). In addition, the internal reliability of the ERN reached the “high” range (.7 – .9) with only 8 error trials, which also replicates prior results (Olvet & Hajcak, 2009).
The LRP also proved to be a robust effect. All combinations of sample size and numbers of trials yielded acceptable likelihoods of statistical significance for determining that an LRP was present, and 45 trials was sufficient to yield “high” levels of internal reliability.
However, it is rarely the goal of an experiment to simply detect the presence of an ERP. Rather, most ERP experiments are aimed at assessing differences between conditions and/or between groups of participants, which tend to be much subtler effects. Therefore, we conducted simulations to investigate whether and how the number of trials interacted with the number of participants and the magnitude of the effect to determine the ability of an experiment to detect within-participants condition differences and between-participant group differences.
Detecting within-participant condition differences
Our second set of simulations examined statistical power for detecting differences in ERN or LRP amplitude across conditions in within-participant experiments. We found clear evidence that power was interactively determined by the number of trials, the number of participants, and the magnitude of the between-condition difference. Although high internal reliability was obtained for large-sized effects with 8 trials for the ERN and 45 trials for the LRP, doubling the number of trials led to substantial increases in the power to detect small- and medium-sized effects. Indeed, with some combinations of parameters, doubling the number of trials effectively doubled the statistical power. However, when the differences in amplitude between conditions were very large, power was already near ceiling with a small number of trials, and increasing the number of trials had very little impact on power under these conditions. Such large effects are rare, however, and for the effects that are common in within-participant experiments on the ERN and LRP, increasing the number of trials beyond 8 ERN trials and 45 LRP trials will typically yield substantial increases in statistical power. With even larger numbers of trials, one would eventually reach a point where power reached asymptote and further increases in the number of trials would have little impact, but the present data set did not have enough trials to determine this point. Likewise, increasing the number of participants generally improved statistical power, but had little impact when the differences in amplitude between conditions were very large, particularly when the number of trials was large.
Detecting group differences
Our third set of simulations examined how statistical power in between-group designs varied as a function of the number of trials, the number of participants, and the magnitude of the group difference. For the LRP, we again found strong interactions among these factors. Power increased substantially as the number of trials increased as long as the magnitude of the group difference was not so large that power was at ceiling or so small that power was at floor. However, the impact of increasing the number of trials was not as large for the between-group simulations as it was for the within-participant simulations. The effect of increasing the number of trials was even weaker for the between-group ERN simulations, where doubling the number of trials typically increased the statistical power by .2 or less. This does not appear to be a result of an asymptote: Increasing the number of trials appeared to produce a gradual but steady increase in power. Thus, there would be value in increasing the number of trials in such experiments, but large numbers of trials might be necessary to reach acceptable levels of power. By contrast, increasing the number of participants had a relatively dramatic impact on statistical power, for both the ERN and the LRP. Doubling the number of participants from 16 to 32 substantially increased power, particularly when the simulated group difference in amplitude was in the intermediate range.
It should be noted that the simulated groups in the present study did not differ in either noise level or true score variance, as may occur in real world between-group experiments. For example, in comparing a patient group with a control group, greater noise levels may be present in the patient data than in the control data, and the patients may also be intrinsically more variable than the controls above and beyond any differences in EEG noise. Such differences in variance between groups may impact the effect that the number of trials, number of participants, and effect magnitude have on statistical power. This is an important direction for future research to explore. In addition, our analyses focused on simulations of very simple situations, in which the mean voltage from a known time window was compared across two conditions or two groups. It would be useful for future work to ask how the number of trials impacts more complex designs and analytical approaches such as multifactor interactions, mass univariate analyses (Groppe, Urbach, & Kutas, 2011), and mixed-effect modeling (Tibon & Levy, 2015).
It should also be noted that the effects of the number of trials on statistical power could be viewed in terms of changes in effect size (e.g., Cohen’s d, which divides the mean difference between conditions or groups by a measure of within-condition or within-group variability). As the number of trials decreases, the variability increases, which produces a decrease in both effect size and statistical power.
The present study does not indicate why the effect of increasing the number of trials was often greater for within-participant designs than for between-participant designs (or whether this would generalize to other ERP components, other paradigms, and other design and analysis parameters). We speculate that the key factor is the proportion of variance that is a result of having a finite number of trials and the proportion that is a result of stable individual differences. If the main source of variance is the number of trials, then increasing the number of trials should produce a large decline in error variance and therefore a large increase in statistical power. If, in contrast, there are large stable differences among participants, then increasing the number of trials will have a proportionally smaller impact on the error variance and statistical power. Within-participant designs minimize the impact of stable individual differences (by factoring out differences across individuals in their average scores), and so a greater proportion of the error variance will typically be driven by the number of trials. This is just speculation at this point, and additional research is needed to determine all the factors that determine the extent to which increasing the number of trials will increase statistical power.
Conclusions
Collectively, these analyses demonstrate how several factors have an impact on statistical power in ERP studies, including number of trials, sample size, and effect magnitude, as well as interactions among these factors. These results provide clear evidence that there is no single answer to the question of how many trials are needed in an ERP study, even in the context of a single ERP component in a single experimental paradigm. Indeed, the number of trials required to achieve acceptable levels of statistical power varied substantially depending on the sample size, the effect magnitude, and whether a within-participant or between-group design was used.
Although there is no simple answer to the question of how many trials that should be included in a given ERP experiment, the present study does make it possible to draw two practical conclusions (although simulations of other paradigms and other components are necessary before we can be fully certain that the present results are generalizable). First, unless power is near floor or ceiling, increasing the number of trials almost always produces appreciable increases in power. Power does not saturate at 8 trials in an ERN experiment or at 45 trials in a LRP experiment for the effect magnitudes that most experiments are designed to detect. Thus, it is usually worth increasing the number of trials if there is little cost to doing so.
Second, the extent to which power can be increased by increasing the number of trials appears to be greater in within-participant designs than in between-group designs. In within-participant studies, it will often be worth the effort to increase the number of trials (assuming that this does not lead to fatigue or other factors that might decrease the quality of the data). In between-group studies, however, increasing the number of trials may have only a modest impact, and increasing the number of participants may be a more efficient way to increase power. For example, we found that doubling the number of trials in within-participant simulations more than doubled the statistical power under many conditions, but doubling the number of participants typically had a smaller impact. By contrast, doubling the number of participants typically had a much larger effect than doubling the number of trials in our between-group simulations.
There are additional factors that were not examined in this study that are also likely to influence the optimal number of trials and sample size for a given study, including data quality, experimental paradigm, and participant population. Therefore, although our simulations provide estimates of the power that would be achieved with a specific number of trials, number of participants, and magnitude of effect, we caution researchers against extrapolating these specific values to other studies that differ in data quality, paradigm, and participant population. For example, our participants were all undergraduate students in a highly selective university, and power would likely be lower for studies with a more heterogeneous population. Indeed, the present study should make it clear that, despite an ever-expanding number of studies that recommend specific numbers of trials for specific ERP components, there is no single number that can answer this question. Instead, the field needs a power calculator that can indicate the expected power for a given study when given the number of trials, number of participants, anticipated difference in amplitude between conditions or groups, and the noise level of the raw EEG. We hope the present study is a step in that direction.
Acknowledgments
This research was made possible by NIH grant R01 MH087450 to S.J.L.
Footnotes
In this paper, we use the term sample size to refer to the number of participants in a study (and not the number of trials sampled from the hypothetical population of trials for each participant). We use the term effect magnitude to refer to the absolute size of an effect in microvolts (as opposed to the term effect size, which typically refers to a quantity that is scaled by the amount of variability). As the number of trials per participant increases or decreases, this will change the effect size for a given effect magnitude. For example, a 1 μV effect might lead to an effect size of 0.8 (Cohen’s d) with a large number of trials and 0.4 with a small number of trials, and this in turn would impact the statistical power.
In addition to the experiment described in the present manuscript, participants completed five additional short ERP tasks in the same testing session. The data from these tasks will be published separately.
References
- Button KS, Ioannidis JP, Mokrysz C, Nosek BA, Flint J, Robinson ES, Munafò MR. Power failure: why small sample size undermines the reliability of neuroscience. Nature Reviews Neuroscience. 2013;14(5):365–376. doi: 10.1038/nrn3475. [DOI] [PubMed] [Google Scholar]
- Cohen J, Polich J. On the number of trials needed for P300. International Journal of Psychophysiology. 1997;25(3):249–255. doi: 10.1016/s0167-8760(96)00743-x. [DOI] [PubMed] [Google Scholar]
- Di Nocera F, Ferlazzo F. Resampling approach to statistical inference: bootstrapping from event-related potentials data. Behavior Research Methods. 2000;32(1):111–119. doi: 10.3758/bf03200793. [DOI] [PubMed] [Google Scholar]
- Duncan CC, Barry RJ, Connolly JF, Fischer C, Michie PT, Näätänen R, … Van Petten C. Event-related potentials in clinical research: guidelines for eliciting, recording, and quantifying mismatch negativity, P300, and N400. Clinical Neurophysiology. 2009;120(11):1883–1908. doi: 10.1016/j.clinph.2009.07.045. [DOI] [PubMed] [Google Scholar]
- Efron B, Tibshirani RJ. An introduction to the bootstrap. Boca Raton, USA: CRC press; 1994. [Google Scholar]
- Eimer M. The lateralized readiness potential as an on-line measure of central response activation processes. Behavior Research Methods, Instruments, & Computers. 1998;30(1):146–156. [Google Scholar]
- Fischer AG, Klein TA, Ullsperger M. Comparing the error-related negativity across groups: The impact of error- and trial-number differences. Psychophysiology. 2017 doi: 10.1111/psyp.12863. n/a-n/a. [DOI] [PubMed] [Google Scholar]
- Gehring WJ, Liu Y, Orr JM, Carp J. The Error-Related Negativity (ERN/Ne) In: Luck SJ, Kappenman ES, editors. The Oxford handbook of event-related potential components. Oxford University Press; 2012. [Google Scholar]
- Groppe DM. Combating the scientific decline effect with confidence (intervals) Psychophysiology. 2017;54(1):139–145. doi: 10.1111/psyp.12616. [DOI] [PubMed] [Google Scholar]
- Groppe DM, Urbach TP, Kutas M. Mass univariate analysis of event-related brain potentials/fields I: A critical tutorial review. Psychophysiology. 2011;48(12):1711–1725. doi: 10.1111/j.1469-8986.2011.01273.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hinton Perry R, Brownlow C, McMurray I, Cozens B. SPSS Explained. New York: Routledge; 2004. [Google Scholar]
- Huffmeijer R, Bakermans-Kranenburg MJ, Alink LR, van IJzendoorn MH. Reliability of event-related potentials: The influence of number of trials and electrodes. Physiology & behavior. 2014;130:13–22. doi: 10.1016/j.physbeh.2014.03.008. [DOI] [PubMed] [Google Scholar]
- Kiesel A, Miller J, Jolicœur P, Brisson B. Measurement of ERP latency differences: A comparison of single-participant and jackknife-based scoring methods. Psychophysiology. 2008;45(2):250–274. doi: 10.1111/j.1469-8986.2007.00618.x. [DOI] [PubMed] [Google Scholar]
- Larson MJ, Baldwin SA, Good DA, Fair JE. Temporal stability of the error-related negativity (ERN) and post-error positivity (Pe): the role of number of trials. Psychophysiology. 2010;47(6):1167–1171. doi: 10.1111/j.1469-8986.2010.01022.x. [DOI] [PubMed] [Google Scholar]
- Luck SJ. An introduction to the event-related potential technique. MIT press; 2014. [Google Scholar]
- Marco-Pallares J, Cucurell D, Münte TF, Strien N, Rodriguez-Fornells A. On the number of trials needed for a stable feedback-related negativity. Psychophysiology. 2011;48(6):852–860. doi: 10.1111/j.1469-8986.2010.01152.x. [DOI] [PubMed] [Google Scholar]
- Olvet DM, Hajcak G. The stability of error-related brain activity with increasing trials. Psychophysiology. 2009;46(5):957–961. doi: 10.1111/j.1469-8986.2009.00848.x. [DOI] [PubMed] [Google Scholar]
- Pontifex MB, Scudder MR, Brown ML, O’Leary KC, Wu CT, Themanson JR, Hillman CH. On the number of trials necessary for stabilization of error-related brain activity across the life span. Psychophysiology. 2010;47(4):767–773. doi: 10.1111/j.1469-8986.2010.00974.x. [DOI] [PubMed] [Google Scholar]
- Rietdijk WJ, Franken IH, Thurik AR. Internal consistency of event-related potentials associated with cognitive control: N2/P3 and ERN/Pe. PloS one. 2014;9(7):e102672. doi: 10.1371/journal.pone.0102672. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schimmel H. The (±) Reference: Accuracy of Estimated Mean Components in Average Response Studies. Science. 1967;157(3784):92–94. doi: 10.1126/science.157.3784.92. [DOI] [PubMed] [Google Scholar]
- Segalowitz SJ, Barnes KL. The reliability of ERP components in the auditory oddball paradigm. Psychophysiology. 1993;30(5):451–459. doi: 10.1111/j.1469-8986.1993.tb02068.x. [DOI] [PubMed] [Google Scholar]
- Singh K. On the asymptotic accuracy of Efron’s bootstrap. The Annals of Statistics. 1981:1187–1195. [Google Scholar]
- Smulders FT. Simplifying jackknifing of ERPs and getting more out of it: retrieving estimates of participants’ latencies. Psychophysiology. 2010;47(2):387–392. doi: 10.1111/j.1469-8986.2009.00934.x. [DOI] [PubMed] [Google Scholar]
- Smulders FT, Miller J. The lateralized readiness potential. In: Kappenman E, Luck S, editors. The Oxford handbook of event-related potential components. 2012. pp. 209–229. [Google Scholar]
- Steele VR, Anderson NE, Claus ED, Bernat EM, Rao V, Assaf M, … Kiehl KA. Neuroimaging measures of error-processing: Extracting reliable signals from event-related potentials and functional magnetic resonance imaging. NeuroImage. 2016;132:247–260. doi: 10.1016/j.neuroimage.2016.02.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thigpen NN, Kappenman ES, Keil A. Assessing the internal consistency of the event-related potential: An example analysis. Psychophysiology. 2017;54(1):123–138. doi: 10.1111/psyp.12629. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tibon R, Levy DA. Striking a balance: analyzing unbalanced event-related potential data. Frontiers in psychology. 2015;6 doi: 10.3389/fpsyg.2015.00555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ulrich R, Miller J. Using the jackknife-based scoring method for measuring LRP onset effects in factorial designs. Psychophysiology. 2001;38(5):816–827. [PubMed] [Google Scholar]