Adaptive and Selective Time-Averaging of Auditory Scenes

Summary

To overcome variability, estimate scene characteristics, and compress sensory input, perceptual systems pool data into statistical summaries. Despite growing evidence for statistical representations in perception, the underlying mechanisms remain poorly understood. One example of such representations occurs in auditory scenes, where background texture appears to be represented with time-averaged sound statistics. We probed the averaging mechanism using “texture steps” – textures containing subtle shifts in stimulus statistics. Although generally imperceptible, steps occurring in the previous several seconds biased texture judgments, indicative of a multi-second averaging window. Listeners seemed unable to willfully extend or restrict this window but showed signatures of longer integration times for temporally variable textures. In all cases the measured timescales were substantially longer than previously reported integration times in the auditory system. Integration also showed signs of being restricted to sound elements attributed to a common source. The results suggest an integration process that depends on stimulus characteristics, integrating over longer extents when it benefits statistical estimation of variable signals, and selectively integrating stimulus components likely to have a common cause in the world. Our methodology could be naturally extended to examine statistical representations of other types of sensory signals.

Introduction

Sensory receptors measure signals over short timescales, but perception often entails combining these measurements over much longer durations. In some cases, this is because the structures that we must recognize are revealed gradually over time. In other cases, the presence of noise or variability means that samples must be gathered over some period of time in order for quantities of interest to be robustly estimated. Although much is known about integration over space via receptive fields of progressively larger extent in the visual system [1, 2], less is known about analogous processes in time.

Integration plays a fundamental role in the domain of textures – signals generated by the superposition of many similar events or objects. In vision and touch, texture often indicates surface material (bark, grass, gravel etc.) [3]. In audition, textures provide signatures of the surrounding environment, as when produced by rain, swarms of insects, or galloping horses [4–7]. Whether received by sight, sound, or touch, textures are believed to be represented in the brain by statistics that summarize signal properties over space or time [8–11].

Statistical representations, in which signals are summarized with aggregate measures that pool information over space or time, are believed to contribute to many aspects of perception [2, 12–24], but texture is a particularly appealing domain in which to study them. Textures are rich and varied, ubiquitous in the world, relevant to multiple sensory systems, and arguably the only type of signal that is well described (at present) by biologically plausible models that are signal-computable (i.e., that operate on actual sensory signals and as such can be applied to arbitrary input; Figure 1A). Moreover, the proposed integration operation for texture is simple: the statistics believed to underlie texture perception can all be written as averages of sensory measurements of various sorts [5, 8]. In sound, this averaging occurs over time.

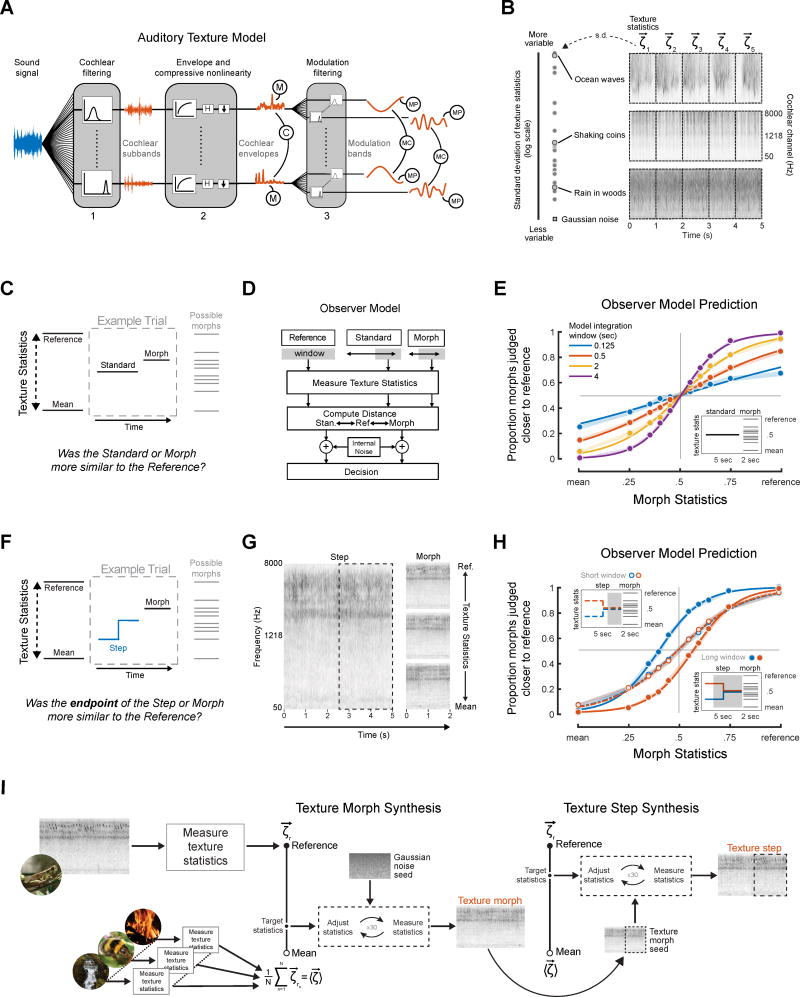
Figure 1. Sound texture: statistics, modeling, and stimulus generation.

(A) Auditory texture model [5]. Statistics are measured from an auditory model capturing the tuning properties of the peripheral and subcortical auditory system in three stages. The statistics measured from this model include marginal moments and pair-wise correlations at different stages of the model. (B) Variability of statistics in real-world textures. Left panel shows the standard deviation of texture statistics measured from multiple 1s excerpts of each of a set of 27 textures used in the subsequent experiments. Right panel shows spectrograms of 5 s excerpts of example textures (ocean waves, shaking coins, and rain in the woods). Dashed lines denote borders of 1s segments from which statistics were measured. Some real-world textures have statistics that are quite stable at a time scale of 1s (also evident in the consistency of the visual appearance of 1s spectrogram segments), while others exhibit variability (and would only produce stable estimates at longer timescales). (C) Schematic of texture discrimination experiment trial structure. Listeners judged whether the standard or the morph was most similar to a reference texture. (D) Observer model. The model averaged statistics within a rectangular window extending from the endpoint of the trial stimuli and compared them to the statistics of the reference texture. The model and stimulus generation assumed a Euclidean metric within each class of statistics (see Methods). (E) Texture discrimination by the observer model using four different window sizes. Plot shows the proportion of morphs judged closer to reference as a function of the morph statistics (drawn from the line between the mean and reference statistics). Model results suggest task could be performed with a wide range of analysis windows. The slopes of the psychometric functions were determined in part by noise added at the decision stage of the model (see Methods). Here and elsewhere, shaded regions show SEM obtained via bootstrap (10,000 samples). (F) Schematic of step discrimination trial structure. Listeners judged whether the step or the morph was most similar to a reference texture. Listeners were told that the step stimulus would undergo a change, and to base their judgments on the end of the stimulus. (G) Spectrograms of example step experiment stimuli for the “swamp insects” reference texture. The step occurs 2.5s from the endpoint. The morph examples have statistics from the reference, midpoint and mean. (H) Performance of the observer model on a texture step experiment using two different window sizes. When the integration window extends beyond the step (solid lines, bottom right inlay) the observer model exhibits a difference in the point of subjective equality between conditions, but not otherwise (dashed lines, top-left inlay). (I) Synthesis of texture morphs and steps. A reference texture was passed to the auditory model, which measured its texture statistics and generated target texture statistics at intermediate points along a line in the space of statistics between the reference texture statistics and the mean statistics of a large set of textures. Synthesis began with Gaussian noise and adjusted the statistics to the target values. Texture steps were created by further adjusting a portion (dashed region) of a texture morph to match the statistics of another point on the line between the reference and mean texture.

See also Figure S1 and S2 and Table S1.

The goal of this paper was to characterize the extent and nature of the averaging mechanism. We posed three questions. First, is there a particular temporal extent over which averaging occurs? Second, does this extent depend on the intrinsic timescales of the signal being integrated? Third, is information averaged blindly within an integration window, or is it subject to perceptual grouping?

It was not obvious a priori what sort of averaging processes to expect. Longer term averages are more robust to variability and noise, but run the risk of pooling together signals with distinct statistical properties. Moreover, textures vary in the timescale at which they are stationary (i.e., at which they have stable statistics), reflected in the variability of their statistics (Figure 1B). Some textures, such as dense rain, have statistics that are stable over even short timescales, and that could be reliably measured with a short-term time-average. But others, such as ocean waves, are less homogeneous on local time scales despite being generated by a process with fixed long-term parameters. In the latter case, a longer averaging window might be necessary to accurately measure the underlying statistical properties. It thus seemed plausible that an optimal integration process would vary in the timescale of integration depending on the nature of the acoustic input. An additional complexity is that textures in real-world scenes typically co-occur with other sounds, raising the question of whether texture statistics are averaged blindly over all the sound occurring within some window.

We developed a methodology to probe the averaging process underlying texture perception using synthetic textures whose statistics underwent a subtle shift at some point during their duration. The rationale was that judgments of texture should be biased by the change in statistics if the stimulus prior to the change is included in the average. By measuring the conditions under which biases occurred, we hoped to characterize the extent of averaging and its dependence on signal statistics and perceptual grouping.

Results

The logic of our main task was to measure the statistics ascribed to one texture stimulus by asking listeners to compare it to another (Figure 1C). The stimuli were intended to resemble natural sound textures and thus varied in a high-dimensional statistical space previously found to enable compelling synthesis of naturalistic textures [5, 7, 9]. To render the discrimination of such high-dimensional stimuli well-posed, we defined a line in the space of statistics between a mean texture stimulus and a reference texture and generated stimuli from different points along this line (that thus varied in their perceptual similarity to the reference texture). The reference texture was defined by the statistics of a particular real world texture; the “mean” texture was defined by the average statistics of 50 real-world textures. To familiarize listeners with the dimension of stimulus variation, the mean and reference stimulus were presented repeatedly prior to a block of trials based on the reference. On each trial, they were asked to judge which of two stimuli was most similar to the reference. This design was chosen because presenting the reference on each trial would have produced prohibitively long trials.

To ensure that the task could be performed as intended using time-averaged statistics, we implemented an observer model (Figure 1D). The model measured statistics from each experimental stimulus using an averaging window extending for some duration from the end of the stimulus and chose the stimulus whose statistics were closest to those of the reference. Figure 1E shows the result of the model performing the task for a range of different averaging window durations. The “standard” was fixed at the midpoint of the statistics continuum, whereas the “morph” varied from trial to trial between the reference and mean texture, never with the same statistics as the standard. Here and in the subsequent experiments, the results are expressed as psychometric functions, plotting the proportion of trials on which the morph was judged closer to the reference as a function of the morph statistics.

As expected, the proportion of trials on which the morph was chosen increased as the morph statistics approached the reference, with the point of subjective equality at the midpoint on the statistic continuum (Figure 1E). This result confirms that the task can be performed using statistics measured from the stimuli but also that above-chance performance can be obtained for a range of window durations.

In order to assess the extent over which statistics were averaged by the human auditory system, we asked listeners to compare a texture whose statistics underwent a change mid-way through their duration (“steps”) to a texture whose statistics were constant (“morphs”; Figure 1F). Because the extent of integration was not obvious a priori, and because it was not obvious whether listeners would retain only the most recent estimate of the statistics of a signal, they were told that the first stimulus would undergo a change, and that they should base their judgments on the end of the stimulus. We envisioned that if listeners incorporated the signal preceding the step into their statistic estimate, the estimate would be shifted away from the endpoint statistics, biasing discrimination judgments. Figure 1G displays a spectrogram of an example texture step and three morphs for the “swamp insects” reference texture (see Figure S1 for visualizations of the statistic changes in step stimuli). In practice, we used several different reference textures per experiment, and the experiments were divided into blocks of trials based on a particular reference.

Figure 1H shows the result of the model performing the texture step discrimination task with two different averaging windows extending from the end of the stimulus. When the averaging window included the step, the psychometric functions were shifted in the direction of the step, as intended. We tested whether human listeners would exhibit similar biases and, if so, over what timescales.

Textures were synthesized using an extended version of the McDermott and Simoncelli [5] sound synthesis procedure, in which Gaussian noise was shaped to have particular values for a set of statistics. Statistics were measured from a model of the peripheral auditory system that simulated cochlear and modulation filtering [25] (Figure 1A). The statistics employed included marginal moments and pairwise correlations measured from both sets of filters; each class of statistics is necessary for realistic texture synthesis [5] and thus is perceptually significant. Steps were generated by first synthesizing a morph for the starting values of the step statistics and then running the synthesis procedure again on the latter part of the signal to shift the statistics to the end values of the step (Figure 1I). This avoided stimulus discontinuities not necessitated by the change in statistics.

Although the stimuli were generated from target statistic values that underwent a discrete step, statistics must be measured over some temporal extent, and thus, the statistics measured from a signal at different points in time inevitably exhibit a gradual transition from the value before the step to the value after the step (Figure S2). However, this gradual transition is strictly a consequence of averaging the stimulus before and after the step location – the stimulus itself was not biased by the step, as shown by the statistics measured by windows immediately adjacent to the step (Figure S2). Bias in perceptual judgments is thus diagnostic of the inclusion of the stimulus prior to the step.

Experiment 1: Step size selection

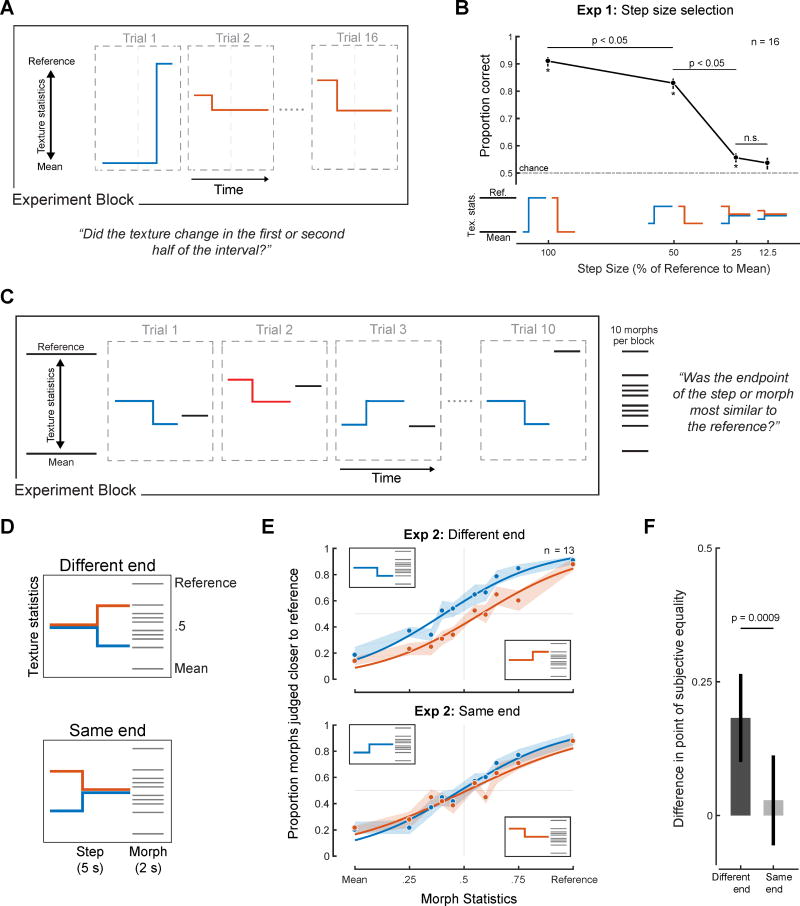
Because it seemed plausible that task performance might be affected by audible changes in the stimulus, we sought to use texture steps that were difficult to detect (but that were otherwise as large as possible, to elicit measurable biases). We conducted an initial experiment to determine an appropriate step size. Steps were generated in either the first or second half of a 5s texture stimulus, and listeners were asked to identify whether the step occurred in the first or second half (Figure 2A). Steps of 25% were difficult to localize (Figure 2B), and this step magnitude was selected for use in subsequent step experiments.

Figure 2. Design and results of Experiments 1 and 2 (Step size selection and task validation).

(A) Schematic of Experiment 1 block and trial structure. Listeners heard a texture step and judged whether a change occurred in the first or second half of the stimulus. The step was positioned at either 25% or 75% of the stimulus duration. (B) Localization performance of human listeners vs. step size. Error bars show SEM, obtained via bootstrap. Asterisks indicate significant differences from chance (t-test, two-tailed, p < 0.05). p values between data points indicate result of paired t-tests between conditions. (C) Schematic of Experiment 2 (testing task compliance). Listeners judged whether the step or the morph was most similar to a reference texture. Listeners were informed that the first stimulus (the step) could undergo a change and to base their judgments on the end of that stimulus. (D) Schematics of experimental conditions. (E) Results of Experiment 2. Shaded regions show SEM of individual data points, obtained by bootstrap. Solid lines plot logistic function fits. (F) Difference between fitted points of subjective equality for the upward and downward step conditions (computed separately for the same start and same end conditions). Here and elsewhere, error bars show bootstrapped 95% confidence intervals on the difference, obtained by bootstrap.

See also Figure S3 and S7.

Experiment 2: Task validation

The other requirement of our experimental design was that listeners base their judgment on the end of the step interval. We evaluated compliance with the instructions by comparing discrimination for steps presented at either the beginning or end of the stimulus (Figure 2C&D). If listeners used the endpoint of the step interval as instructed, their judgments should differ substantially for the two different end conditions but less so for the two same end conditions, assuming the entire stimulus does not contribute to listeners’ judgments.

As shown in Figure 2E, the psychometric functions for the different end conditions were offset, whereas those for the same end conditions were not. The offset in the psychometric functions was quantified as the difference in the point of subjective equality (Figure 2F), which was significantly different from zero for the Different End conditions (p < 0.0001, via bootstrap), but not for the Same End conditions (p = 0.15). These results suggest listeners were indeed able to follow the instructions and used the endpoint of the step interval when making judgments.

Experiments 3–5: Effect of stimulus history on texture judgments

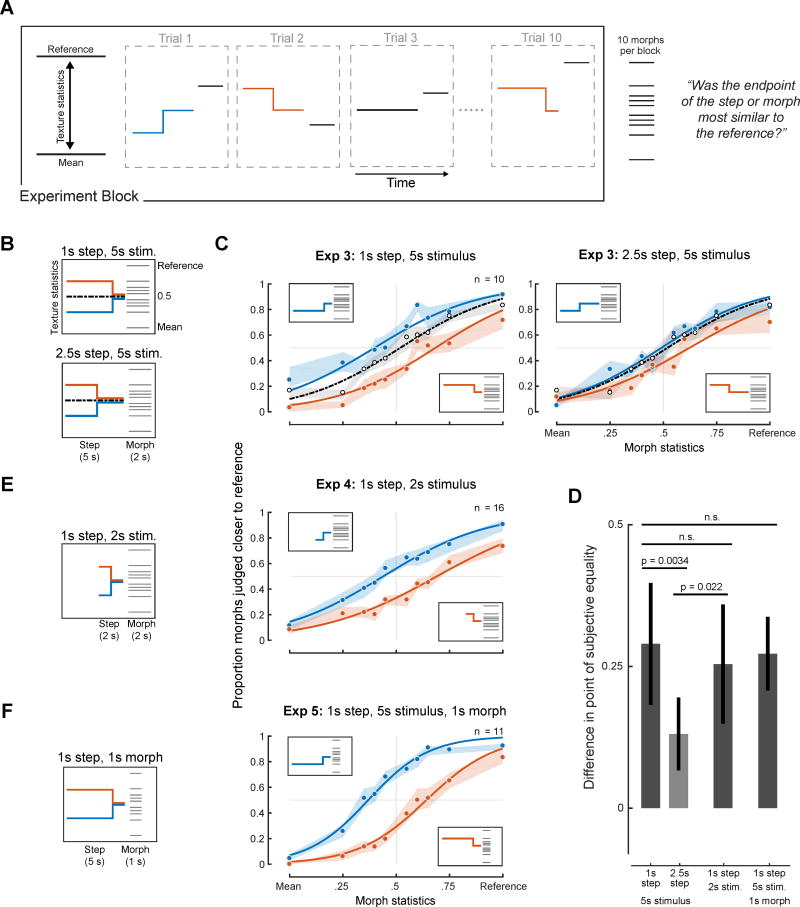
Having established that listeners could perform the task, we turned to the main issue of interest: the extent of the stimulus history included in texture judgments. As an initial assay we positioned the step at two different points in time (either 1s or 2.5s from the endpoint, Figure 3A&B). The step moved either toward or away from the reference, with an endpoint midway between the mean and reference texture. The experiment also included a baseline standard condition with constant statistics at the midpoint between the reference and mean texture, for which no bias was expected.

Figure 3. Design and results of Experiments 3–5 (Effect of texture step on texture discrimination).

(A) Schematic of block and trial structure used in Experiment 3. (B) Schematic of stimulus conditions of Experiment 3. (C) Results of Experiment 3. Here and elsewhere, shaded regions show SEM of individual data points obtained by bootstrap and curves plot logistic function fits. (D) Difference between points of subjective equality for the upward and downward step conditions (computed separately for the different conditions of Experiments 3–5). Error bars show 95% confidence intervals on the difference, obtained by bootstrap. (E) Results of Experiment 4 (with 2s step stimuli). (F) Results of Experiment 5 (with 1s morph stimuli).

See also Figure S3.

The baseline condition with constant statistics (black curve) yielded the expected psychometric function with a point of subjective equality at the midpoint of the statistic continuum (Figure 3C). By contrast, the psychometric functions for the step conditions were offset in either direction, indicating that the stimulus history beyond the step influenced listeners’ judgments despite the instructions to base their judgments on the step endpoint. The bias (again quantified as the difference in the point of subjective equality for the two step directions) was statistically significant for both the 1s steps (Figure 3D; p<0.0001; via bootstrap) and 2.5s steps (p<0.0001), but was significantly reduced in the latter condition (p=0.0034). The bias was also slightly asymmetric (greater for the red than blue curves, p<0.0001 for 2.5s step; see Figure S3 for bias measurements for individual step directions), suggesting that listeners incorporated more of the stimulus history for one step direction than the other. We will return to this latter issue in Experiment 7 and 8. Overall, however, the results are consistent with integration over the course of a few seconds.

Although one interpretation of the multi-second integration evident in Experiment 3 is that it reflects an obligatory perceptual mechanism, the results could also in principle be explained by a decision strategy. Two possibilities seemed particularly worth addressing. The first is that upon being instructed that the step stimulus would undergo a subtle change, listeners may have assumed that the change would most likely happen mid-way through the stimulus, and accordingly listened to roughly the last half of the 5s stimulus when making their judgments. A second possibility was that listeners monitored the step stimulus for an extent comparable to the 2s duration of the morph stimulus to which the step was compared. Both of these strategies would have produced integration over several seconds in Experiment 3, but would predict different integration extents if stimulus duration was varied.

To explore whether listeners were simply monitoring the last half of the step stimulus, we repeated Experiment 3 with a two-second step stimulus with a step at 1s (Figure 3E). If listeners based judgments on the last half of the stimulus, the 1s step should yield similar results to the 2.5s step from Experiment 3. By contrast, if integration was due to a perceptual process that was largely independent of the stimulus duration, results should instead be similar to the 1s step from Experiment 3. As shown in Figures 3D & 3E, the bias from the 1s step in the two-second stimulus was indistinguishable from that of the 1s step in the five-second stimulus of Experiment 3 (p=0.51), and significantly different from that of the 2.5s step in Experiment 3 (p=0.022). These results are consistent with a perceptual mechanism of fixed extent rather than a decision strategy based on the stimulus duration.

To assess the effect of the morph duration we also repeated the 1s step conditions of Experiment 3 using a one-second morph stimulus (Figure 3F). The biases measured here were again indistinguishable from those measured with a comparison stimulus twice as long (p=0.76).

Both of these experiments indicate that the extent of the stimulus that influences texture judgments seems to be relatively independent of the stimulus durations. This is consistent with the idea that the averaging is perceptual in origin, and not strongly subject to strategies employed by the listener.

Experiment 6: Can integration be extended?

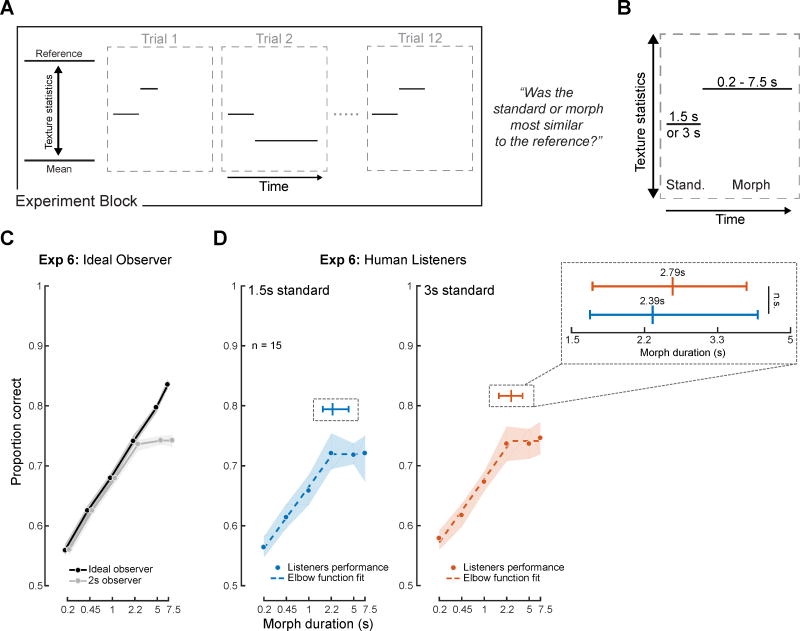
The results of Experiments 3–5 suggest that listeners integrate over several seconds to estimate texture statistics even when warned that the signals were changing and that they should attend to their endings. To further explore the extent to which integration was obligatory, we investigated whether listeners could instead extend integration when it would benefit performance. We designed an alternative task in which listeners were presented with two texture excerpts generated from constant statistic trajectories: a “standard” excerpt of a fixed duration, and a morph whose duration varied from 0.2 to 7.5 seconds and whose statistics could either be closer or further from the reference with equal probability (Figure 4A&B). Listeners again judged which of the two sounds was more similar to a reference texture, and the sounds were again generated from statistics drawn from the line between the mean and reference statistics.

Figure 4. Design and results of Experiment 6 (Effect of texture duration).

(A) Schematic of block and trial structure. Listeners judged which of two stimuli was most similar to a reference texture. The Standard had constant statistics and duration within blocks; the Morph varied in duration across trials and took on one of two statistic values. (B) Across blocks, the standard took durations of either 1.5 or 3s. The morph varied in duration within a block, taking on one of six values from 0.2s to 7.5s. The standard was always generated from statistics at the midpoint of the mean-reference continuum, whereas the morph was generated from either the 25% or the 75% point on the continuum. (C) Performance of observer models (run on experimental stimuli) as a function of probe duration. Performance of ideal observer (integrating over entire available stimulus; black) increased with probe duration because statistical estimates become more accurate as more samples are available for averaging. An otherwise identical model with a 2s analysis window placed at the end of each stimulus (gray) showed a performance plateau once the probe duration exceeded the analysis window. The two model curves are slightly offset in the horizontal dimension to make them both visible. Error bars show SEM obtained via bootstrap (over stimuli). (D) Performance of human listeners vs. morph duration. Shaded region indicates SEM of individual data points, obtained via bootstrap. Dashed line shows piecewise linear “elbow” function fit. Insets plot the median elbow point and 95% confidence intervals on the elbow point (via bootstrap).

See also Table S2.

We reasoned that statistical estimation should benefit from averaging over the entire morph duration, such that an ideal observer would improve continuously as the duration increased (Figure 4C, black curve). But if listeners were constrained by an integration window of fixed duration and retained only its most recent output for a given stimulus, performance might be expected to plateau after the probe duration exceeded it (Figure 4C, gray curve). We used two different standard durations (1.5 and 3 seconds, fixed within blocks) to verify that integration over the morph was not somehow determined by the duration of the sound it was being compared to. A fixed standard duration was used to avoid prohibitively long trials, which would otherwise have occurred if both stimuli varied in duration.

As shown in Figure 4D, performance increased with duration of the morph interval up to 2 seconds, but then plateaued, with no improvement for the longest two durations used. Results were similar for both standard durations. We assessed the location of the plateau by fitting an elbow function [26] to the data, bootstrapping to obtain confidence intervals on the elbow point (Figure 4D, top inset). The best-fitting elbow points were 2.39 and 2.79s (for 1.5s and 3s standards, respectively, which were not significantly different, p=0.96). This finding is consistent with the idea that listeners cannot average over more than a few seconds, at least for the textures we used here, even when it would benefit their performance. The results provide additional evidence for a perceptual integration mechanism whose temporal extent is largely obligatory and not under willful control.

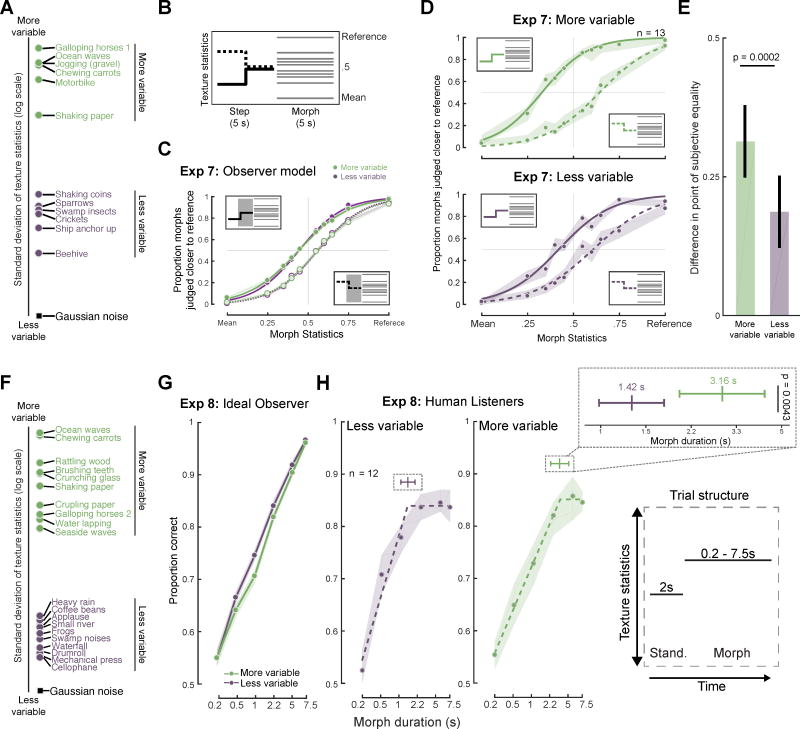
Experiments 7 & 8: Effect of texture variability on temporal integration

Although Experiments 3–6 were suggestive of an averaging mechanism whose temporal extent was relatively fixed, there was some reason to think that integration might not always occur over the same timescale. In particular, optimal estimation of statistics should involve a tradeoff between the variability of the estimator (which decreases as the integration window lengthens) and the likelihood that the estimator pools across portions of the signal with distinct statistics (which increases as the integration window lengthens). Because textures vary in their stationarity, the window length at which this tradeoff is optimized should also vary. For highly stationary textures, such as dense rain, a short window might suffice for stable estimates, whereas for less stationary textures, such as the sound of ocean waves, a longer window could be better. We thus explored whether the timescale of integration might vary according to the variability of the sensory signal.

We first evaluated the variability of a large set of textures by measuring the variation in statistics measured in 1s analysis windows (Figure 5A). We selected the six textures with maximum variability and the six with minimum variability for use as reference textures in an experiment. We then repeated the step discrimination paradigm of Experiment 3 with a step at 2.5s (Figure 5B).

Figure 5. Results of Experiment 7 & 8 (Effect of texture variability).

(A) Variability in texture statistics measured across 1-s windows for the 12 reference textures from Experiment 7. Variability of Gaussian noise statistics is provided for comparison. (B) Schematic of stimuli for Experiment 7 (step discrimination). (C) Results from observer model plotted separately for more and less variable textures. The model used a 3s averaging window for both sets, and showed similar biases, illustrating that the results need not differ between the stimulus sets. Here and elsewhere, shaded regions show SEM obtained via bootstrap and curves plot logistic function fits. See Figure S4 for observer model results for additional analysis window durations. (D) Results from human listeners, plotted separately for more variable (upper panel) and less variable (lower panel) textures. (E) Difference between points of subjective equality between upward and downward step conditions. (F) Variability in texture statistics for the 10 reference textures from Experiment 8 (discrimination of textures varying in duration). (G) Results from observer model integrating over the entire duration of the morph interval. The shaded region shows SEM obtained via bootstrap. (H) Performance of human listeners vs. duration, plotted separately for less and more variable textures. Dashed lines show piecewise linear “elbow” function fits. Top inset shows inflection points of piecewise linear functions fit to data for the two texture groups (with 95% confidence intervals). Bottom inset shows trial structure.

See also Figure S3, S4 and S5 and Table S3.

To underscore the fact that integration times need not be different for the two sets of textures, we ran our observer model on the experiment using a single fixed analysis window (of 3s). The model yielded similar biases for both texture sets (Figure 5C; see Figure S4 for comparable results with other window durations). It was thus plausible that human listeners might also exhibit comparable biases for the two sets of stimuli.

Unlike the model results obtained with a fixed averaging window, the bias in human listeners was substantially larger for the textures that were more variable (p = 0.0002, Figure 5D&E). This result suggests that more of the stimulus history is incorporated into statistic estimates for the more variable textures, and is consistent with an averaging process whose temporal extent is linked to the temporal variability of the texture. It also appears that the degree of bias for the more homogeneous textures is greater than that observed in Experiment 3 for the 2.5s condition (non-significant trend: p = 0.087). Although the participants were different between experiments, this difference could indicate that the extent of averaging adapts to the local context, such that the presence of highly variable textures within the experiment could affect the extent of averaging in the blocks with less variable textures.

As a further test of the effect of texture variability, we conducted a second experiment, in this case replicating the design of Experiment 6, again using two sets of textures that clustered at opposite ends of the spectrum of variability (Figure 5F). An ideal observer model produced similar results for the two sets of textures (Figure 5G), but human listeners did not: the dependence of performance on the probe duration was different for the two groups of textures, with discrimination appearing to plateau at a longer probe duration for the more variable textures (Figure 5H). To quantify this effect, we again fit piecewise linear “elbow” functions to the data (Figure 5H, top inset). The elbow points of the best fitting functions were 1.42s and 3.16s for the less and more variable textures, respectively, and were significantly different (p=0.0043, via bootstrap).

This finding replicated when the results of Experiment 6 were re-analyzed, splitting the textures into more and less variable groups. Even though these textures were distinct from those of Experiment 8, and were not selected for their statistic variability, it was again the case that discrimination performance plateaued at longer durations for more variable textures (Figure S5). Longer integration for more variable textures is also consistent with the asymmetric results in Experiment 3 (in which history-induced biases were larger for steps in one direction than the other). As shown in Figure S2, the statistics of the step closer to the reference were more variable than those of the step closer to the mean (larger error bars for the red compared to the blue curve, due to the reference textures in that experiment being more variable than the mean texture). No such asymmetry is evident in Experiment 7, but that may be because the differences across textures were much larger than in Experiment 3, swamping any effect of the step direction.

Overall, the results provide converging evidence for an averaging process that pools information over a temporal extent that depends on the signal variability.

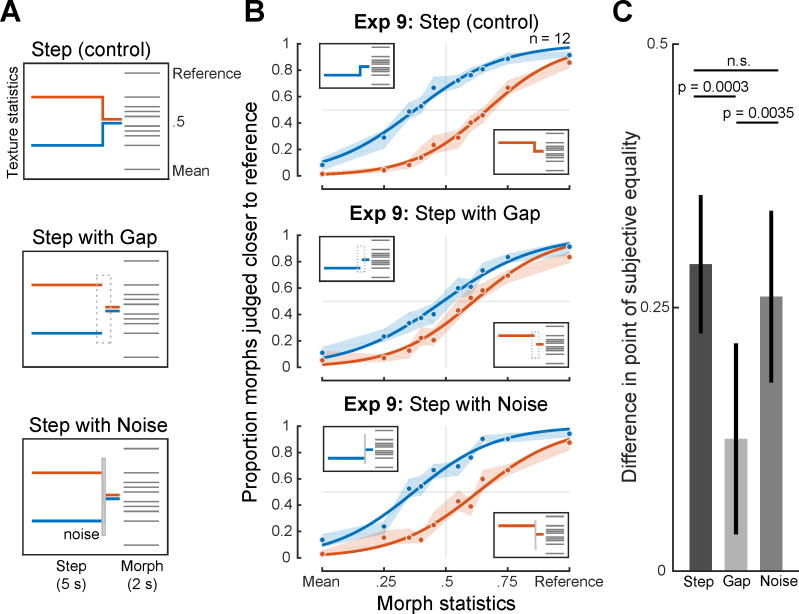
Experiment 9: Effect of stimulus continuity on texture integration

The apparent presence of an averaging window raised the question of whether the integration process operates blindly over all sound that occurs within the window, or whether integration might be restricted to the parts of the sound signal that are likely to belong to the same texture. We explored this issue by introducing audible discontinuities in the step stimulus immediately following the statistic change. We hypothesized that the discontinuity might cause the history prior to it to be excluded from or down-weighted in the averaging process.

We created three variants with a step positioned 1s from the endpoint (Figure 6A). The first condition preserved continuity at the step (as in Experiment 3), whereas the second condition replaced the texture immediately following the step with a silent gap (200ms in duration). A third condition tested the effect of perceptual rather than physical continuity by filling the gap with a spectrally matched noise burst that was substantially higher in intensity than the texture, causing the texture to sound continuous [27, 28]. Listeners were again instructed to base their judgments on the endpoint of the step stimulus.

Figure 6. Results of Experiment 9 (Effect of texture continuity).

(A) Schematic of stimuli. The gap condition included a 200ms silent gap positioned immediately following the step (1s from the endpoint of the step interval). The noise burst condition replaced the gap with a 200ms spectrally matched noise, the intensity of which was set to produce perceptual continuity between the texture before and after it. (B) Results for the three conditions. The shaded regions show SEM of individual data points obtained via bootstrap and solid lines plot logistic function fits. (c) Difference between points of subjective equality for the upward and downward steps for each condition (with bootstrapped 95% confidence intervals).

See also Figure S3, S6 and S7.

As shown in Figure 6B, the gap (middle panel) substantially reduced the bias produced by the step compared to the continuous (top panel) or noise burst (bottom panel) conditions. This reduction was statistically significant in both cases (gap versus continuous: p = 0.0003; gap versus noise burst: p = 0.0035; Figure 6C). By contrast, the biases measured for the continuous step and noise burst conditions were not significantly different (p = 0.46). These results are consistent with the idea that the integration process underlying texture judgments is partially reset by discontinuities attributed to the texture but not by those attributed to other sources, as though integration occurs preferentially over parts of the sound signal that are likely to have been generated by the same process in the world.

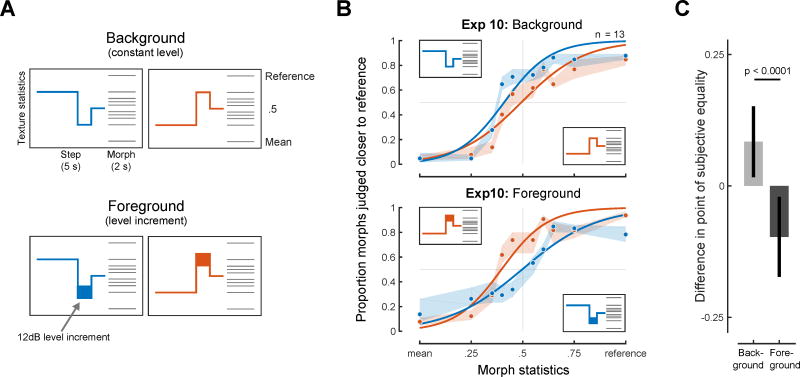
Experiment 10: Effect of foreground/background on texture grouping

The finding that integration appears to occur across an intervening noise burst (Experiment 9) raised the question of whether such extraneous sounds are included in the texture integration process. Textures in auditory scenes are often superimposed with other sound sources, as when a bird calls next to a stream, or a person speaks during a rainstorm. Are such sounds excluded from the integration process?

To test whether foreground sounds embedded in a texture are excluded from integration, we extended our texture step paradigm. Stimuli were generated with three segments (producing two steps, at 2s and 1s from the endpoint). In the “Background” condition, the segments were all the same intensity and appeared to all be part of the same continuous background texture (Figure 7A, top panel). In the “Foreground” condition, the level of the second segment was 12dB higher than the other segments (Figure 7A, bottom panel). The level increment caused the middle segment to perceptually segregate from the other two segments, which were heard as continuing through it [27, 28]. The segment statistics were chosen such that integration over several seconds would yield biases in opposite directions depending on whether the middle segment was included in the integration, as confirmed with observer models that integrated blindly or that excluded the middle segment (Figure S6). Listeners were told that the step interval might undergo a change in loudness, and that they should in all cases base their judgments on the endpoint of the step stimulus.

Figure 7. Results from Experiment 10 (Exclusion of foreground sounds from texture integration).

(A) The step stimulus for the background condition was composed of 3 segments with different statistics, creating steps 2s and 1s from the endpoint of the step interval. The grouping of the second segment with the other two was manipulated by increasing the level of the second segment by 12dB (indicated by thicker line in the Foreground schematic). The level increment caused the second segment to be heard as a distinct foreground sound, “behind” which the other segments perceptually completed. (B) Results for Background and Foreground step conditions. Shaded regions show SEM of individual data points obtained via bootstrap and solid lines plot logistic function fits. (C) Difference between points of subjective equality for the two step directions for the two conditions (with bootstrapped 95% confidence intervals).

See also Figure S3 and S6.

Without the level increment, listeners’ judgments exhibited a bias toward the statistics of the middle segment (Figure 7B, top), consistent with its inclusion in the averaging process used to estimate texture statistics. However, the bias was reversed when the middle segment was higher in level than its neighbors (Figure 7B, bottom; the biases in the two conditions were significantly different: p<0.0001, Figure 7C). This pattern of results is consistent with what would be expected if the middle segment was excluded from the integration, and if integration extended across the middle segment to include part of the first segment (consistent with Experiment 9). These results provide further evidence that texture integration is restricted to sounds that are likely to have come from a similar source. Overall, the results of Experiments 9 and 10 indicate that texture perception functions as part of auditory scene analysis, concurrent with the grouping or streaming of sound sources.

Discussion

Textures, be they visual, auditory, or tactile, are believed to be represented with statistics – averages over time and/or space of sensory measurements. We conducted a set of experiments on sound textures to probe the nature of the averaging process. We found that the judgments of human listeners were biased by subtle changes in statistics that occurred in the previous several seconds, implicating an integration process over this extent (Experiments 3–5). This effect was present even though participants were instructed to attend to the end of the stimulus and were warned that the stimulus would undergo changes. When given the opportunity to average over more than a few seconds (Experiment 6), listeners did not appear able to do so. However, the biasing effects of the stimulus history were more pronounced when textures were more variable, suggesting that the integration process occurs over longer extents in the presence of higher stimulus variability, perhaps as needed to achieve stable statistic estimates (Experiment 7 & 8). We also found that biasing effects were diminished when there was a salient change (silent gap) in the texture (Experiment 9), as though the integration process partially resets itself in such conditions. Lastly, texture integration appears to occur across foreground sounds that interrupt a texture (Experiment 9), but to exclude such foreground sounds from the calculation of the texture’s statistics (Experiment 10). The results indicate an integration process extending over several seconds that compensates for the temporal complexity of the auditory input, and that appears to be inseparable from auditory scene analysis.

Evidence for perceptual integration

One natural question is whether these effects might be attributed to a cognitive decision strategy on the part of the listener rather than a perceptual mechanism. There was some reason a priori to think that listeners would be constrained to base their judgments on time-averaged statistics – previous experiments suggest that listeners can discriminate texture statistics, but not the details that give rise to those statistics [9]. We employed textures taken from those prior studies, and used similar stimulus durations, making it likely that listeners were similarly limited to statistical judgments in our tasks. However, listeners might in principle be able to control the temporal extent over which statistics were computed depending on the stimulus and task, in which case the integration extent would reflect their strategy rather than the signature of a perceptual mechanism.

Several lines of evidence suggest that this is not the case. First, listeners were told to base their judgments on the end of the step stimulus, and did so (Experiment 2), but were nonetheless biased by stimulus features several seconds in the past. Moreover, the extent of integration appeared to be approximately invariant to stimulus duration (Experiment 4), and to the duration of the comparison stimulus (Experiment 5), even though these manipulations might have been expected to cause listeners to adjust the extent of integration were it under willful control. Second, in a distinct experiment paradigm, listeners were unable to integrate over longer periods of time even when it would have benefitted their performance (Experiments 6 and 8). This limitation is suggestive of a mechanism that constrains the information accessible to listeners. Moreover, the integration extent evident in these latter experiments was roughly comparable to that suggested by the step experiments (Experiments 3–5 and 7) even though different integration strategies would have been optimal for each experiment. The fact that a similar integration timescale emerged from two different types of experiment gives support to a single sensory process that limits texture judgments.

One consequence of multi-second, obligatory integration is that sensitivity to changes in statistics should be limited – an averaging window blurs together the statistics on either side of a change. Experiment 1 provided evidence that this was the case for the steps that we used: listeners could not localize the step to one half of the stimulus or the other. We performed an additional experiment in which listeners simply had to detect the presence of a step at the stimulus midpoint. Results were comparably poor provided steps were modest in amplitude (Figure S7). The detection of larger steps might leverage salient signal discontinuities that accompany pronounced statistic changes. Consistent with this notion, performance improved when a gap was inserted at the step location (Figure S7; see also Experiment 9).

The perception of stimuli longer than the texture integration window merits further exploration. Do listeners retain any sense of drift in statistical properties when they change over time [29]? One presumptive advantage of a limited averaging window is to retain some sensitivity to such changes. We know that listeners can retain estimates of texture statistics for multiple discrete excerpts, because they must in order to perform the discrimination tasks used here and elsewhere [9]. But it also appears that listeners do not always retain distinct estimates from different time points within the same statistical process (otherwise they would have shown some improvement with duration beyond a few seconds in Experiment 6) [30]. It thus remains to be seen how the temporal evolution of a changing statistical process is represented.

Effects of variability on time-averaging

Although the integration process underlying listeners’ judgments appeared not to be subject to willful control, its temporal extent showed signs of depending on the stimulus variability. One possibility is that different statistics have different integration times, and that different statistics are used for discrimination depending on the texture. For instance, more variable textures tend to have more power at slow modulations, which are plausibly measured over longer timescales than faster modulations [31]. Under this account, the variation in integration extent suggested by our experiments need not reflect an active process of adaptation to stimulus variability. One piece of evidence that appears inconsistent with this idea is that the bias for less variable textures in Experiment 7 was somewhat greater than that in Experiment 3, potentially because the most variable textures influenced integration on other blocks of trials. It thus remains possible that stimulus variability is sensed (e.g. by monitoring the stability of internal statistic estimates), and that it influences the extent of integration for individual statistics. Regardless of the mechanism, the effects of variability on integration suggest a potential general principle for time-averaging that could be present in other domains where statistical representations are used [14–21, 23, 24].

Temporal integration in the auditory system

Although our experiments represent the first attempt (to our knowledge) to measure an integration window for texture, there has been longstanding interest in temporal integration windows for other aspects of hearing. Loudness integration is perhaps most closely analogous to the averaging that seems to occur for texture, and is believed to reflect a nonlinear function of stimulus intensity averaged over a window of a few hundred milliseconds [32–35]. Integration also occurs in binaural hearing, on a similarly short timescale [36]. The integration process we have characterized for sound texture seems noteworthy in that it is quite long relative to typical timescales in the auditory system (though it is comparable to integration times proposed in parts of the visual system) [37].

We use the term integration here to refer specifically to averaging operations. In this respect the phenomena we study appear distinct from other examples in which prior context can change the interpretation of a stimulus [38–41]. In most such cases the representation of the current stimulus remains distinct from that of the past, and the effects seem better described either by history-dependent changes to the stimulus encoding (e.g. via adaptation) and/or by inference performed on the current stimulus with respect to the distribution of prior stimulation [42, 43]. Such prior distributions can be learned over substantial periods of time, and in this respect appear distinct from texture representations, which represent the momentary statistics of a sound source by averaging over a local temporal neighborhood. It is plausible that similar contextual effects occur with texture, i.e. that the longer-term statistical history [44] influences statistical estimates of the current stimulus state.

Apart from the (substantial) interactions with scene analysis phenomena (Experiments 9 and 10), our results are well described by a simple averaging window operating on a biologically plausible auditory model (Fig. S6). However, the averaging time scales implicated by our experiments are quite long relative to receptive fields in the auditory cortex (which are rarely longer than a few hundred milliseconds) [45–47]. To our knowledge the only phenomenon in the auditory system that extends over multiple seconds is stimulus-specific adaptation [44, 48–53]. Adaptation is widespread in sensory systems, and may also scale with stimulus statistics [54] but its computational role remains unclear. Whether adaptation could serve to compute quantities like texture statistics is an intriguing question for future research.

Although we have suggested an averaging “window” of several seconds, we still know little about the shape of any such window. Systematic exploration of the effects of steps at different time lags could help to determine whether different parts of the signal are weighted differently. And as noted above, there need not be a single window – texture is determined by many different statistics, some of which might pool over longer windows than others, potentially depending on their intrinsic variability. Our results suggest a rough overall integration time constant of several seconds, but this could represent the net effect of different integration windows for different statistics. This issue could be investigated by generating steps that are restricted to particular statistics. We also note that the apparent sophistication of the averaging (excluding distinct foreground sounds, for instance) renders the metaphor of a “window” limited as a description of the integration process.

Texture perception and scene analysis

Our results indicate that texture integration is intertwined with the process of segregating an auditory scene into distinct sound sources. We found that a silent gap was sufficient to substantially reduce the influence of the stimulus history, suggestive of an integration process that selectively averages those stimulus elements likely to be part of the same texture. We also found evidence that concurrent foreground sounds are not included in the estimate of texture statistics when there is strong evidence that they should be segregated from the texture. Texture integration thus seems to be restricted to texture “streams”, which may be critical for accurate perception of textures in real-world conditions with multiple sound sources.

Relation to statistical representations in other sensory modalities

The results presented here seem likely to have analogs in statistical representations in other modalities [14–20, 24]. Visual texture representation is usually conceived as resulting from averages over spatial position [10, 11], but similar computational principles could be present for spatial averaging. Visual textures also sometimes occur over time, as when we look at leaves rustling in the wind [55], and the time-averaging evident with sound textures could also occur in such cases [16]. Tactile textures, where spatial detail is typically registered by sweeping a finger over a surface, also involve temporal integration [56, 57], the basis of which remains uncharacterized. In all these cases, the experimental methodology developed here could be used to study the underlying mechanisms.

STAR Methods

CONTACT FOR REAGENT AND RESOURCE SHARING

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Richard McWalter (mcwalter@mit.edu).

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Participants were recruited from a university job posting site and had self-reported normal hearing. Experiments were approved by the Committee on the Use of Humans as Experimental Subjects at the Massachusetts Institute of Technology. Participants completed the required consent form (overseen by the Danish Science-Ethics Committee or the Committee on the Use of Humans as Experimental Subjects at the Massachusetts Institute of Technology) and were compensated with an hourly wage for their time. Participant demographics were slightly different for each experiment and are provided below in sections for each experiment.

METHOD DETAILS

Auditory Texture Model

To simulate cochlear frequency analysis, sounds were filtered into subbands by convolving the input with a bank of bandpass filters with different center frequencies and bandwidths. We used 4^th-order gammatone filters as they closely approximate the tuning properties of human auditory filters and, as a filterbank, can be designed to be paraunitary (allowing perfect signal reconstruction via a paraconjugate filterbank). The filterbank consisted of 34 bandpass filters with center frequencies defined by the equivalent rectangular bandwidth (ERB_N) scale [59] (spanning 50Hz to 8097Hz). The output of the filterbank represents the first processing stage from our model (Figure 1A).

The resulting “cochlear” subbands were subsequently processed with a power-law compression (0.3) which models the non-linear behavior of the cochlea [60]. Subband envelopes were then computed from the analytic signal (Hilbert transform), intended to approximate the transduction from the mechanical vibrations of the basilar membrane to the auditory nerve response. Lastly, the subband envelopes were downsampled to 400Hz prior to the second processing stage.

The final processing stage filtered each cochlear envelope into amplitude modulation rate subbands by convolving each envelope with a second bank of bandpass filters. The modulation filterbank consisted of 18 half-octave spaced bandpass filters (0.5 to 200Hz) with constant Q = 2. The modulation filterbank models the selectivity of the human auditory system and is hypothesized to be a result of thalamic processing [25, 45, 61]. The modulation bands represent the output of the final processing stage of our auditory texture model.

The model input was a discrete time-domain waveform, x(t), usually several seconds in duration (~5s). The texture statistics were computed on the cochlear envelope subbands, x_k(t), and the modulation subbands, h_k,n(t), where k indexes the cochlear channel and n indexes the modulation channel. The windowing function, w(t), obeyed the constraint that Σ_tw(t) = 1.

The envelope statistics include the mean, coefficient of variance, skewness and kurtosis, and represent the first four marginal moments. The marginal moments capture the sparsity of the time-averaged subband envelopes. The moments were defined as (in ascending order)

$${\mu }_k=\sum _{t}w(t)x_k(t)$$

$$\frac{{\sigma }_k^2}{{\mu }_k^2}=\frac{{\sum }_{t}w(t){(x_k(t)-{\mu }_k)}^2}{{\mu }_k^2},$$

$${\eta }_k=\frac{{\sum }_{t}w(t){(x_k(t)-{\mu }_k)}^3}{{\sigma }_k^3},$$

$$K_k=\frac{{\sum }_{t}w(t){(x_k(t)-{\mu }_k)}^4}{{\sigma }_k^4},k\in [1\dots 34]\text{ in each case}.$$

Pair-wise correlations were computed between the eight nearest cochlear bands. The correlation captures broadband events that would activate cochlear bands simultaneously [5, 62]. The measure can be computed as a square of sums or in the more condensed form can be written as

$$c_{\mathit{\text{jk}}}=\frac{{\sum }_{t}w(t)(x_j(t)-{\mu }_j)(x_k(t)-{\mu }_k)}{{\sigma }_j{\sigma }_k},j,k,\in [1\dots 34]$$

$$\mathit{\text{such that }}(k-j)=[1,2,3,4,5,6,7,8].$$

To capture the envelope power at different modulation rates, the modulation subband variance normalized by the corresponding total cochlear envelope variance was measured. The modulation power (variance) measure takes the following form

$${\sigma }_{k,n}=\frac{{\sum }_{t}w(t){(b_{k,n}(t)-{\mu }_{k,n})}^2}{{\sigma }_k^2},k\in [1\dots 34],n\in [1\dots 18].$$

Lastly, the texture representation included correlations between modulation subbands of distinct cochlear channels. Some sounds feature correlations across many modulation subbands (e.g. fire), whereas others have correlations only between a subset of modulation subbands (ocean waves and wind, for instance, exhibit correlated modulation at slow but not high rates [5]). These correlations are given by

$$c_{\mathit{\text{jk}},n}=\frac{{\sum }_{t}w(t)(b_{j,n}(t)-{\mu }_{j,n})(b_{k,n}(t)-{\mu }_{k,n})}{{\sigma }_{j,n}{\sigma }_{k,n}},$$

$$j\in [1\dots 34],(k-j)=[1,2],n\in [\mathrm{3\; 5\; 7\; 9\; 11\; 13}].$$

The texture statistics identified here resulted in a parameter vector, ζ, which was used to generated the synthetic textures.

Texture Stimuli Synthesis

Synthetic texture stimuli were generated using a variant of the McDermott and Simoncelli (2011) synthesis system. The synthesis process allowed for the generation of distinct exemplars that possessed similar texture statistics by seeding the synthesis system with different samples of random noise. The original system was modified (Figure 1I) to facilitate the generation of “texture morphs” (sound textures generated from statistics sampled at points along a line between two textures) and “texture steps” (sound textures that underwent a change in their statistics at some point during their duration).

First, sound texture statistics were measured from 7-s excerpts of real-world texture recordings. The measured statistics comprised the mean, coefficient of variation, skewness, and kurtosis of the Hilbert envelope of each cochlear channel, pair-wise correlations across cochlear channels, the power from a set of modulation filters, and pair-wise correlations across modulation bands [5]. Statistics were measured from 50 real-world texture recordings (Table S1). Statistics from individual real-world recordings, ζ_ref were used to synthesize “reference” textures. The statistics of all 50 recordings were averaged to yield the statistics, ζ_mean, from which the “mean” texture was synthesized. In practice the envelope mean statistics for the mean texture were replaced with those of the reference texture in order to avoid spectral discontinuities in the texture step stimuli. The measured statistics were imposed on a random noise seed whose duration depended on the stimulus type.

Texture morphs were generated by synthesizing a texture from a point along a line in the space of statistics between the mean and the reference (ζ_Δ1 = Δ₁ζ_ref + (1 − Δ₁)ζ_mean), using Gaussian noise as the seed.

Texture steps were generated such that their statistical properties changed at some point in time by stepping from one set of texture statistics to another. The process began by synthesizing a texture from one set of statistics, ζ_Δ1, usually set to a point along a line in the space of statistics between the mean and the reference (ζ_Δ1 = Δ₁ζ_ref + (1 − Δ₁)ζ_mean), using Gaussian noise as the seed. We then passed the synthesis system a second set of statistics, typically a different point along the same line in the space of statistics, ζ_Δ2, and the previous synthetic texture as the seed. The two resulting synthetic textures were then windowed (with rectangular windows) and summed to create a texture step with the transition in the desired location. This synthesis process minimized artifacts that might otherwise occur by simply concatenating texture segments generated from distinct statistics – the seeding procedure helped ensure that the degree and location of amplitude modulations at the border between segments with distinct statistics were compatible. We were thus able to generate textures whose statistics varied over time, yet had no obvious local indication of the change in statistics. In practice the changes in the statistics were difficult to notice (as demonstrated in Experiments 1 and 11). Moreover, this approach ensured that the statistics on either side of the step were unbiased by the signal on the other side, as verified in Figure S2.

Texture Metric

Our stimulus generation and modeling assumed a Euclidean metric for each statistic class. We adopted this metric because discovering the perceptually correct metric seemed likely to be intractable given the high dimensionality of the statistic space. The metric we used seemed like the simplest possibility a priori, and so we used it in pilot psychophysical experiments. These pilot experiments suggested that stimuli spaced regularly according to a Euclidean metric produce pretty reasonable psychometric functions, and that texture steps in opposite directions that were equal-sized according to a Euclidean metric produced approximately equal biases (though not always, as is evident in Experiment 3). This suggests that even though the metric we used is surely not exactly right, it was sufficient for our purposes.

Observer Model

We created an observer model to quantify the effect of an integration window on texture discrimination. The model instantiated the hypothesis that stimuli are discriminated by comparing statistics computed by averaging nonlinear functions of the sound signal over some temporal window. We emphasize that the model was stimulus-computable – it operated on the actual sound waveforms used as experimental stimuli.

The model (Figure 1D) measured the texture statistics of the two stimuli in each trial of the experiment using an averaging window extending backward in time for some duration that was applied to the output of the auditory model described above. The model compared these measured statistics to the statistics of the reference texture (measured in the same way from a 5s sound waveform). The step and morph stimuli were generated from statistics on the line between the mean and reference texture statistics, but because the observer model computed statistics over finite windows, the measured statistics were always displaced from the line to some extent due to measurement error from the finite sample. To determine which stimulus was closer to the reference, the statistics of the step (ζ⃗_step) and morph (ζ⃗_morph) were thus projected onto the line between the statistics of the mean (ζ⃗_mean, also measured from a 5s waveform) and reference (ζ⃗_ref) texture:

$${\overrightarrow{\zeta }}_{\mathit{\text{ref}},i}^{\prime }={\overrightarrow{\zeta }}_{\mathit{\text{ref}},i}-{\overrightarrow{\zeta }}_{\mathit{\text{mean}},i}$$

$${\overrightarrow{\zeta }}_{\mathit{\text{step}},i}^{\prime }={\overrightarrow{\zeta }}_{\mathit{\text{step}},i}-{\overrightarrow{\zeta }}_{\mathit{\text{mean}},i}$$

$${\overrightarrow{\zeta }}_{\mathit{\text{step}},i}^{″}=\frac{{\left({\overrightarrow{\zeta }}_{\mathit{\text{step}},i}^{\prime }\right)}^T{\overrightarrow{\zeta }}_{\mathit{\text{ref}},i}^{\prime }}{{\left({\overrightarrow{\zeta }}_{\mathit{\text{ref}},i}^{\prime }\right)}^T{\overrightarrow{\zeta }}_{\mathit{\text{ref}},i}^{\prime }}{\overrightarrow{\zeta }}_{\mathit{\text{ref}},i},$$

$${\overrightarrow{\zeta }}_{\mathit{\text{morph}},i}^{\prime }={\overrightarrow{\zeta }}_{\mathit{\text{morph}},i}-{\overrightarrow{\zeta }}_{\mathit{\text{mean}},i}$$

$${\overrightarrow{\zeta }}_{\mathit{\text{morph}},i}^{″}=\frac{{\left({\overrightarrow{\zeta }}_{\mathit{\text{morph}},i}^{\prime }\right)}^T{\overrightarrow{\zeta }}_{\mathit{\text{ref}},i}^{\prime }}{{\left({\overrightarrow{\zeta }}_{\mathit{\text{ref}},i}^{\prime }\right)}^T{\overrightarrow{\zeta }}_{\mathit{\text{ref}},i}^{\prime }}{\overrightarrow{\zeta }}_{\mathit{\text{ref}},i},$$

where i denotes the class of texture statistics (mean, coefficient of variation, skew, kurtosis, cochlear correlation, modulation power, modulation correlation).

Because the different classes of statistic (envelope mean, variance, skewness, and kurtosis; cross-envelope correlation; modulation power; cross-band modulation correlation) have different units and cover different ranges, the procedure described above was performed separately for each class, each time normalizing by the distance of the reference to the mean $({\overrightarrow{\zeta }}_{\mathit{\text{ref}},i}^{\prime })$ for that statistic class. The mean and reference texture statistics were always substantially different (in part because they were always fairly high-dimensional), such that we never observed stability issues with this normalization process. These normalized distances were then summed across classes as follows:

$$d_{\mathit{\text{step}}}=\frac{1}{L}\sum _i\frac{{({\sum }_k|{\zeta }_{\mathit{\text{ref}},i,k}^{\text{'}}-{\zeta }_{\mathit{\text{step}},i,k}^{"}{|}^2)}^{1/2}}{{({\sum }_k|{\zeta }_{\mathit{\text{ref}},i,k}-{\zeta }_{\mathit{\text{mean}},i,k}{|}^2)}^{1/2}}+n_i,$$

$$d_{\mathit{\text{morph}}}=\frac{1}{L}\sum _i\frac{{({\sum }_k|{\zeta }_{\mathit{\text{ref}},i,k}^{\text{'}}-{\zeta }_{\mathit{\text{morph}},i,k}^{"}{|}^2)}^{1/2}}{{({\sum }_k|{\zeta }_{\mathit{\text{ref}},i,k}-{\zeta }_{\mathit{\text{mean}},i,k}{|}^2)}^{1/2}}+n_i,$$

where d is the distance to the reference texture statistics $({\overrightarrow{\zeta }}_{\mathit{\text{ref}},i}^{\prime })$, i is the statistic class, L is the number of statistic classes, k indexes over statistics within a class, and n was Gaussian noise added to match the observer model’s overall performance to that of human listeners. The model then chose the smaller of the two distances {d_step, d_morph}.

The amplitude of the added noise was selected by averaging the behavioral data from many 1s step conditions (because we had the most data for this condition) across experiments (N=41 participants in total) and fitting the observer model’s psychometric function. The noise affected the slope of the psychometric function, but not the bias, and thus did not directly affect the main quantity of interest. The decision to weight each statistic class equally was arbitrary, but respected previous findings that each statistic class contributes to texture judgments [5].

To evaluate optimal performance characteristics for the duration experiment (Figure 4C), we implemented a related ideal observer model. The structure of the ideal observer was similar to the observer model described above, with the exception that the ideal observer operated on the entire length of the experimental stimulus, and that the statistics of the reference and mean texture were measured from 7.5s excerpts, equal to the longest morph duration.

Experiments 9 (effect of noise burst and silent gap) and 10 (exclusion of foreground elements from texture integration) utilized stimuli with large signal discontinuities and thus necessitated a modified observer model to ensure that the measured statistics could be projected onto a line between the reference and mean texture. The observer model included a standard automatic gain control (AGC) to adjust the level of the incoming signal [63]. The AGC operated on the cochlear envelopes of the auditory texture model and adjusted their level to that of the reference texture. The cochlear envelope level was adjusted with a time-varying gain that depended on the signal level estimated over a local time window:

$$y_k(t)=g_k(t)x_k(t),\text{where }{g}_k(t)=g_{k,\mathit{\text{target}}}/x_{k,\mathit{\text{avg}}}(t)$$

where y_k(t) is the envelope of the k^th cochlear channel following gain control, x_k(t) is the envelope of the k^th cochlear channel prior to gain control, g_k is the gain, g_k,target is the target level (the mean of the reference texture envelope), and x_k,avg(t) is the cochlear envelope amplitude averaged over a local time window:

$$x_{k,\mathit{\text{avg}}}(t)=[1-\alpha ]x_{k,\mathit{\text{avg}}}(t-1)+\alpha x_k(t),$$

where α determines the extent of averaging over time (α = 20 · ΔT, where ΔT is the sample period, which was 2.5ms in our implementation).

The AGC prevented the large differences in level produced by the 12dB increment of the foreground condition from dominating the statistical measurements. The observer model was also modified to analyze only the portions of the step interval with non-zero values (to prevent the level differences introduced by the gap from dominating the statistical measurements). This was implemented with a window function in each statistical measurement that applied positive weight only to non-zero portions of the signal.

We compared this “blind” observer model (which measured statistics from all non-zero portions of the signal falling within a fixed integration window of 2.5s) to an “oracle” model. The oracle model averaged statistics over only selected portions of the signal specified by the experimenter as those potentially selected as belonging to the same sound source (indicated by the gray regions in the insets of the right column of Figure S6). We emphasize that only the “blind” model was signal-computable; the oracle model required the specification of the signal segments to be averaged. The oracle model is included only to demonstrate that selective averaging could produce the observed experimental results were there a way to implement the selection.

Experimental Procedures – Sound Presentation

The Psychophysics Toolbox for MATLAB [58] was used to play sound waveforms. All stimuli were presented at 70 dB SPL with a sampling rate of 48 kHz in a soundproof booth (Industrial Acoustics). For experiments conducted at MIT, sounds were played from the sound card in a MacMini computer over Sennheiser HD280 PRO headphones. For experiments conducted at DTU, sounds were played from an RME FireFace UCX sound card over Sennheiser HD650 headphones.

Experimental Procedures – General Logic

Most of the experiments involved asking participants to compare two texture excerpts. The stimuli varied in a high-dimensional statistical space, and to render their discrimination well-posed, we defined a line in the space of statistics between a mean texture stimulus and a reference texture. The reference texture was defined by the statistics of a particular real-world texture, and the “mean” texture by the average statistics of 50 real-world textures, altered so that it was spectrally matched to the corresponding reference texture to prevent discontinuities at texture steps. This latter constraint was achieved by setting the cochlear envelope mean statistics to those of the reference. Stimuli were generated from statistics drawn from different points along this line, and thus varied in their perceptual similarity to the reference texture. The discrimination tasks required listeners to judge which of two textures was more similar to the reference.

In principle we could have presented the reference on each trial (e.g. in an “ABX” design), but were concerned that this would yield exhaustingly long trials. We thus instead opted to block trials into groups corresponding to a particular reference texture, and to familiarize participants with the mean and reference textures prior to each block. The mean texture was intended to help define the dimension along which the textures would vary. Participants were given the option of listening to the mean and reference texture again whenever they wanted during the experiment. In practice most took advantage of this during the initial stages of the experiment. We note also that because the trials were grouped by reference texture, successive trials tended to reinforce the sound of the reference and mean. In practice participants reported little difficulty remembering the reference to which the stimuli were to be compared.

Experimental Procedures – Step Discrimination Paradigm

We used two main texture discrimination paradigms. In the first, we measured the influence of a step in texture statistics at different points in time on judgments of the end state of a texture (as a measure of whether the step was included in the estimation process).

Stimuli

The first stimulus (the “step”) consisted of a texture that started at one position along the mean-reference continuum and stepped to another position at some point in time. In most experiments this stimulus began at either 25% or 75% of the distance between mean and reference, and stepped to the midpoint between reference and mean (e.g. Figure 3B).

The second stimulus on a trial (the “morph”) was generated with statistics drawn from one of 10 positions on the line between the mean and the reference (indicated by the relative position along the line: 0 - mean, 0.25, 0.35, 0.4, 0.45 0.55, 0.6, 0.65, 0.75, and 1 - reference). The morph duration was fixed within an experiment, typically to two seconds. The step and morph were always separated by an inter-stimulus-interval of 250 ms.

Six reference textures (recordings of bees, sparrows, shaking coins, swamp insects, rain, and a campfire) were used in all step experiments except for Experiments 7 and 10. These textures were selected because they were perceptually and statistically unique and produced relatively realistic synthetic exemplars.

The specific stimuli used on a trial were randomly drawn from pre-generated stimuli for each condition and reference texture. Steps were drawn from a discrete set of exemplars. Morphs were a randomly selected excerpt from a longer pre-generated signal.

Procedure

Trials were organized into blocks corresponding to a particular reference texture. Each block presented one trial for each of the 10 morph positions paired with a randomly selected step stimulus. Each step condition occurred once with each morph position for each reference texture across the experiment, but were otherwise unconstrained within a block. The order of the blocks was always random subject to the constraint that two blocks with the same reference texture never occurred consecutively.

Participants selected the interval that was most similar to the reference texture. They were informed that the step interval could change over time and were instructed to use the endpoint when comparing the two intervals. Feedback was not provided.

Prior to beginning the experiment, participants completed a practice session consisting of 6 blocks (six reference textures) of 6 trials intended to familiarize listeners with the texture discrimination task. Unlike in the main experiment, the stimuli in the practice trials never contained a step. The first stimulus always had statistics at the midpoint between the reference and mean, and the second stimulus had statistics drawn from one of six positions (0, 0.25, 0.4, 0.6, 0.75, 1 on the continuum from the mean to the reference). Both stimuli were 2s in duration. Feedback was given following each trial.

Data Exclusion

We excluded the data from poorly performing participants with an inclusion criterion that was neutral with respect to the hypotheses: we required participants to perform at least 85% correct when the morph was set to its most extreme values (with the statistics of the reference or mean) for at least one of the step conditions. On average, 82.0% of subjects met the inclusion criteria.

Experimental Procedures – Varying Duration Discrimination Paradigm

The second main discrimination paradigm required listeners to discriminate texture excerpts that varied in duration but whose statistics were fixed over time. The idea was that discrimination should improve with duration up to any limit on the extent over which averaging could occur.

Stimuli

Stimuli were again generated from statistics drawn from the line between a reference real-world texture recording and a mean texture whose statistics were averaged across 50 real-world texture recordings but that was spectrally matched to the reference. The first stimulus (the “standard”) was fixed in duration within a condition, and was generated from statistics drawn from the midpoint of the mean-reference continuum. The second stimulus (the “morph”) varied in duration (either 0.2, 0.45, 1, 2.2, 5, 7.5-s) and had statistics set to either the 25% or 75% point on the mean-reference continuum. The inter-stimulus-interval was 250 ms. The reference textures varied across experiments due to the demands of the designs (described below).

Procedure

Trials were again blocked by the reference texture. Each block consisted of 12 trials: one for each of the 6 probe durations at each of the two morph statistic values. Trials were randomly ordered within blocks, and the block order was random subject to the constraint that two blocks from the same reference texture never happened consecutively. The standard and morph stimuli for a trial were randomly selected from within 10-s synthetic exemplars with constant statistics at the appropriate values.

The task was to select the interval most similar to the reference texture. Participants again had the option to listen to the reference or mean at any point during the block, to refresh their memory. Participants were informed that the probe stimulus would vary in duration from trial to trial and were instructed to use as much of the stimulus as possible when making their judgments, in order to maximize their performance.

Prior to beginning the experiment, participants completed a practice session with the same procedure described above for the step discrimination paradigm.

Data Exclusion

We again excluded the data from poorly performing participants with an inclusion criterion that was neutral with respect to the hypotheses: we analyzed only those participants that achieved at least 65% correct across all trials. On average, 72.9 of subjects met the inclusion criteria.

Experiment 1: Step size selection

This experiment was used to configure the step size in the subsequent experiments to a level that would be difficult to detect. It thus employed a different task than our other experiments: participants had to localize a step to the first or last half of a texture excerpt.

Stimuli

Each trial presented a single texture step that was 5-s in duration. The step in statistics occurred at either 1.25 or 3.75 s into the stimulus. The step could traverse one of four extents (100%, 50%, 25%, or 12.5% of the distance between the reference and mean), and could either step toward or away from the reference (as shown in Figure 2A). Three exemplars were created for each step position, magnitude, and reference texture (stimuli were randomly selected from these exemplars). The reference textures were the same six textures used in the step discrimination experiments (bees, sparrows, shaking coins, swamp insects, rain, and a campfire).

Procedure

Participants judged whether the step occurred in the first or second half of the interval. The experiment consisted of 192 trials in total, separated into 12 blocks (2 for each of the six reference textures). Each block contained 16 trials (2 step positions crossed with 2 step directions and 4 step magnitudes). Participants completed the experiment in sections of 6 blocks (96 trials). As in the texture discrimination experiments, participants had the option of listening to the reference or mean textures during the block, in order to refresh their memory as needed, and the order of the blocks was random subject to the constraint that two blocks with the same reference texture never occurred consecutively. Prior to beginning the experiment, participants completed a practice session consisting of 48 trials (6 blocks of 8 trials – 2 step positions at each of the 4 step magnitudes, with step direction randomly assigned) with feedback. Feedback was not provided in the main experiment.

Participants

Sixteen participants completed the experiment (10 female, mean age = 22.8, SD = 5.3).

Experiment 2: Step task validation

Stimuli

The step stimulus was 5s in duration, consisting of a texture step that either started at 25% or 75% of the distance between mean and reference, stepping to the midpoint (Same End, Figure 2D), or started at the midpoint, and stepped to either 25% or 75% of the distance between the mean and reference (Different End, Figure 2D). The step occurred either 2-s (Different End) or 3-s (Same End) from the endpoint. Five exemplars were synthesized for each step condition for each reference texture.

The morph stimulus was 2s in duration, randomly extracted from a 5-s exemplar with the desired statistics.

Procedure

The experiment consisted of 240 trials in total, separated into 24 blocks (4 for each of the six reference textures). Participants completed the experiment in sections of 12 blocks (120 trials). The step stimulus used on a trial was randomly chosen from the set of 5 exemplars.

Participants

Sixteen participants completed the experiment and 15 participants met the inclusion criterion (9 female, mean age = 25.3, SD = 5.8).

Experiment 3: Effect of stimulus history on texture judgments

Stimuli

The step stimulus was 5s in duration, with a step either 1 or 2.5s from the endpoint. There was also a condition without a step, in which the statistics of the first stimulus in the trial were set to the midpoint. There were thus a total of 5 conditions (constant statistics, step up at 2.5s, step down at 2.5s, step up at 1s, and step down at 1s). Five exemplars were synthesized for each step condition for each reference texture. The morph was two seconds in duration.

Procedure

The experiment consisted of 300 trials in total, separated into 30 blocks (5 for each of the six reference textures). Participants completed the experiment in sections of 6 blocks (60 trials).

Participants

Sixteen participants completed the experiment. Ten participants met the inclusion criterion (4 female, mean age = 26.7, SD = 5.7). The low inclusion rate appeared to be a fluke; inclusion rates in the other step discrimination experiments tended to be approximately 80%, and were similarly difficult.

Experiment 4: Shorter step durations

Stimuli

The step stimulus was 2s in duration, with a step either 0.4 or 1s from the endpoint (the results from the 0.4s step are not presented here for brevity, but produced a larger bias than the 1s step, as expected). Five exemplars were synthesized for each step condition for each reference texture. The morph was two seconds in duration.

Procedure

The experiment consisted of 240 trials in total, separated into 24 blocks (4 for each of the six reference textures). Participants completed the experiment in sections of 12 blocks (120 trials).

Participants

Sixteen participants completed the experiment. Sixteen participants met the inclusion criterion (12 female, mean age = 26.0, SD = 4.6).

Experiment 5: Shorter morph durations

Stimuli

The step stimulus was 5s in duration, with a step 1s from the endpoint. Five exemplars were synthesized for each step condition for each reference texture. The morph was one seconds in duration.

Procedure

The experiment consisted of 240 trials in total, separated into 24 blocks (4 for each of the six reference textures). All of the trials included a step 1s from the endpoint. Half the trials had an audible change inserted at the step (a silent gap or tone pulse), and are not analyzed here. Participants completed the experiment in sections of 6 blocks (60 trials).

Participants

Sixteen participants completed the experiment. Eleven participants met the inclusion criterion (4 female, mean age = 26.4, SD = 3.1).

Experiment 6: Constant statistics with varying stimulus duration

Stimuli

20 reference textures (Table S2) were selected from the larger set of 50 textures based on their statistical uniqueness and the realism of the resulting synthetic exemplars. The standard was either 1.5s or 3s in duration, counterbalanced across blocks. We used two different durations of the standard to test whether the standard duration would affect on the apparent integration window.

Procedure

The experiment consisted of 480 trials separated into 40 blocks of 12 trials, each based around a particular reference texture and standard duration. Participants completed the experiment in sections of 120 trials.

Participants

Twenty-five participants completed the experiment. Fifteen participants met the inclusion criterion (8 female, mean age = 25.3, SD = 4.8). The low inclusion rate appeared to be a fluke; inclusion rates in the other varying-duration experiments tended to be approximately 80%, and were similarly difficult.

Experiment 7: Effect of texture variability – step discrimination

Stimuli

12 reference textures were used: 6 less variable (birds, insects, beehive, shaking coins, ship anchor being raised, and crickets) and 6 more variable (frogs, motorbike, chewing carrots, galloping horses, shaking paper and ocean waves). These textures were selected by measuring the standard deviation of the texture statistics across 1-s windows in a large set of textures, and then choosing the textures that had highest and lowest variability.

The step stimulus contained a step either toward or away from the reference at 2.5s. The morph duration was extended to 5s to facilitate judgments of the more variable textures.

Procedure

The experiment contained 240 trials, completed in sections of 12 blocks (120 trials).

Participants

Sixteen participants completed the experiment. Thirteen participants met the inclusion criterion (6 female, mean age = 23.8, SD = 2.52).

Experiment 8: Effect of texture variability – varying duration

Stimuli

20 reference textures were used: 10 more variable textures and 10 less variable textures (Table S3). As in Experiment 7, the textures were selected by measuring the standard deviation of the texture statistics across 1s windows in a large set of texture and choosing the textures that had the highest and lowest variability. Different textures were used than in Experiment 7 in order to achieve a larger contrast in variability between the two groups to maximize the chances of seeing an effect. Because Experiment 6 found no effect of the standard duration, here it was set to 2s.

Procedure

The experiment consisted of 240 trials in total (20 blocks of 12 trials, grouped into two 120 trial sections).

Participants

Fourteen participants completed the experiment. Twelve participants met the inclusion criterion (9 female, mean age = 27.4, SD = 4.2).

Experiment 9: Effect of noise burst and silent gap

Stimuli

All conditions had a step 1s from the endpoint (towards or away from the reference). One third of the trials had a 200ms gap immediately after the step (replacing the texture waveform with silence), starting 1s from the endpoint of the step stimulus. Another third of the trials replaced 200ms of the texture with a spectrally matched noise burst, again starting 1s from the endpoint of the step. The rms level of the noise was set to the peak amplitude of the step texture for the trial (which we empirically found to produce a sense of continuity of the texture through the noise, akin to the classic continuity illusion with tones, and to phonemic restoration; the dB difference between the rms levels of the noise and the texture was between 10 and 20 dB, depending on the texture). The remaining third of the trials were identical to the 1s step conditions of Experiment 3. There were thus six conditions, each with a different type of step stimulus (steps up and down, step up and down with a gap, and steps up and down with a noise-filled gap).

Procedure

The experiment consisted of 360 trials (36 blocks), grouped into 3 sections of 120 trials (12 blocks). Participants were informed that the step stimulus would change over time and that some trials would contain a noise burst or a silent gap. However, because conditions were randomly ordered within blocks, participants did not know beforehand which trials would contain a noise burst or a gap, decreasing the likelihood of different listening strategies for the different conditions.

Participants

Sixteen participants completed the experiment. Twelve participants met the inclusion criterion (6 female, mean age = 25.0, SD = 1.8).

Experiment 10: Exclusion of foreground elements from texture integration

Stimuli

All conditions featured a step stimulus composed of three segments (3s, 1s, and 1s in duration, respectively) with different statistics, such that there were steps 2s and 1s from the endpoint (Figure 7A). The first segment (3 seconds) began at either the 25% or 75% point between the mean and reference. The second segment (1 second) stepped from 25% to 75% or 75% to 25%. The third segment (1 second) was generated from statistics at the midpoint of the mean-reference continuum. The segment durations and statistics were chosen such that judgments would be biased in opposite directions depending on whether the second segment was included in the statistic estimate.

In the level increment conditions, the level of the second segment was increased by 12dB (the level ramped up at the onset of segment 2 according to a 20ms raised cosine function and then ramped down at the offset of segment 2 via the same function), an amount empirically determined to be sufficient to cause the second segment to perceptually segregate from the other segments and for the first and third segments to be heard as continuing “behind” the second segment.

Five reference textures were used (sparrows, applause, swamp insects, rain, campfire). These were different from those in the other step experiments because the large change in statistics (from 25% to 75% or vice versa) necessitated less variable textures in order to avoid salient discontinuities at the location of the step (achieved with textures that were similar in variability to the mean texture, such that the variability did not change as much across the mean-reference continuum).

Procedure

The experiment consisted of 200 trials (20 blocks), grouped into 2 sections of 100 trials. Participants were informed that the step stimulus would change over time and that some trials would contain a level increment. Conditions were randomly ordered within blocks.

Participants

Fourteen participants completed the experiment. Thirteen participants met the inclusion criterion (8 female, mean age = 25.0, SD = 2.8).

Experiment 11: Step detection

This experiment tested the detectability of texture steps that were always at the same location in the stimulus. It thus employed a different task than our other experiments. Participants performed two tasks in separate sets of trials. In the first task, listeners judged whether a single stimulus contained a step. In the second task, listeners judged whether a step occurred between two stimuli separated by a silent interval (i.e., whether the two stimuli had the same or different statistics). The task order was counterbalanced across participants.

Stimuli

Depending on the task, each trial presented either a single 2s stimulus or two 1s stimuli separated by 400ms. The stimuli were identical apart from the 400ms interstimulus interval (ISI). On half of the trials, the statistics were constant within the 2s stimulus or across the two 1s stimuli. On the other half of trials the statistics underwent a step (1s into the 5s stimulus, or between the two 1s stimuli). The step could traverse one of three extents (100%, 50%, or 25% of the distance between the reference and mean), and could either step towards or away from the reference (as shown in Figure S7A). Five exemplars were created for each step magnitude and reference texture (stimuli were randomly selected from these exemplars). The reference textures were the same six textures used in the step discrimination experiments (bees, sparrows, shaking coins, swamp insects, rain, and a campfire).

Procedure

Participants either judged whether a statistics step occurred between the first and second halves of the stimulus (step detection), or whether the two stimuli on a trial had the same or different statistics (step detection with a gap). The experiment consisted of two sets of 144 trials, one for each task, with the order counterbalanced across participants. Each set of 144 trials contained 12 blocks (2 for each of the six reference textures). Each block contained 12 trials (2 stimulus configurations crossed with 2 step directions and 3 step magnitudes). Participants completed the experiment in sections of 6 blocks (72 trials). As in the texture discrimination experiments, participants had the option of listening to the reference or mean textures during the block, in order to refresh their memory as needed, and the order of the blocks was random subject to the constraint that two blocks with the same reference texture never occurred consecutively. Feedback was provided in the experiment.

Participants

Fourteen participants completed the experiment, with 13 meeting the acceptance criteria (4 female, mean age = 25.4, SD = 4.8).

QUANTIFICATION AND STATISTICAL ANALYSES

Power analysis to determine samples sizes

To estimate the number of participants necessary to yield stable results for our texture discrimination tasks we measured test-retest reliability of the results in pilot data. The pilot data (N = 23) was acquired for 1s step discrimination experiments that used the same six textures from Experiment 1 and others. We randomly divided the participants into two groups and measured the Pearson’s correlation coefficient between the vectors of performance vs. condition obtained for each group. We repeated the procedure 10,000 times for a range of sample sizes (N = 2 to 20). Test-retest reliability increased with sample size from 0.65 (N=2) to 0.96 (N=20). We selected a target sample size of N = 16 for all experiments, as this yielded an expected test-retest correlation value of 0.95. We then excluded participants from analysis who did not meet hypothesis-neutral performance criteria (resulting in sample sizes between 10 and 16, with expected test-retest reliability between .92 and .95). The exception to this was Experiment 6, where an atypically large number of poorly performing participants lead us to run an additional 9 participants.

Statistics

Error Bars

The error bars on measures of discrimination performance (e.g. that comprise the psychometric functions) plot SEM. The error bars on the bar graphs that quantify the bias induced by the steps plot 95% confidence intervals, to facilitate visual evaluation of significant differences.

Step Localization Experiment (1)

Statistical significance of differences between localization scores for different conditions, or between the scores for a particular condition and chance performance, were assessed with two-tailed t-tests.

Step Discrimination Experiments (2, 3, 4, 5, 7, 9, 10)

To estimate psychometric functions for each condition in the step experiments, we fit a logistic function to the mean data for each morph position. Confidence intervals on the data points and on the difference between the points of subjective equality for two step conditions were derived by bootstrap (10,000 samples). For every bootstrap iteration, a set of participants (equal in number to the total number of participants who met the performance-based inclusion criteria) was sampled with replacement. The points of subjective equality for each step condition were obtained from the psychometric functions fit to the data sample.

Significance values for comparisons of the bias (difference in points of subjective equality for the two step directions) in different conditions were estimated from the bootstrap distributions of the bias by fitting a Gaussian and then computing the p-value from the Gaussian (this allows estimation of the significance of values in the tail of the bootstrap distribution where there are not enough samples to reliably estimate the p-value from the histogram alone [64]). The statistical significance of the asymmetry in Experiment 3 was computed by performing the analogous procedure on the absolute values of the bias for the individual step directions (i.e., the difference between the point of subjective equality and the midpoint of the mean1507 reference continuum).

Duration Experiments (6 & 8)

We evaluated the reliability of the inflection point by bootstrap (10,000 samples). For every bootstrap iteration, a set of participants (equal in number to the total number of participants who met the performance-based inclusion criteria) was sampled with replacement. We fit a piecewise linear function (“elbow function” [26]) to the resulting data. Confidence intervals were estimated from the resulting distribution of the inflection point. P-values were estimated as described in the previous section.

Step Detection Experiment (11)

Statistical significance of differences between detection scores for a particular condition and chance performance was assessed with two-tailed t-tests.

DATA AND SOFTWARE AVAILABILITY

Code and data are available by request to the Lead Contact, Richard McWalter (mcwalter@mit.edu).

Highlights.

• Perceptual integration of sound texture statistics was probed with texture morphs

• Human listeners appear to average texture statistics over a multi-second window

• Averaging is extended for variable textures

• Averaging is selective, excluding foreground sounds that segregate from a texture