Markov models for the elucidation of allosteric regulation

Abstract

Allosteric regulation refers to the process where the effect of binding of a ligand at one site of a protein is transmitted to another, often distant, functional site. In recent years, it has been demonstrated that allosteric mechanisms can be understood by the conformational ensembles of a protein. Molecular dynamics (MD) simulations are often used for the study of protein allostery as they provide an atomistic view of the dynamics of a protein. However, given the wealth of detailed information hidden in MD data, one has to apply a method that allows extraction of the conformational ensembles underlying allosteric regulation from these data. Markov state models are one of the most promising methods for this purpose. We provide a short introduction to the theory of Markov state models and review their application to various examples of protein allostery studied by MD simulations. We also include a discussion of studies where Markov modelling has been employed to analyse experimental data on allosteric regulation. We conclude our review by advertising the wider application of Markov state models to elucidate allosteric mechanisms, especially since in recent years it has become straightforward to construct such models thanks to software programs like PyEMMA and MSMBuilder.

This article is part of a discussion meeting issue ‘Allostery and molecular machines’.

1. Introduction

The biochemical phenomenon of allostery involves the regulation of a protein's functional activity via ligand binding at a site that is typically distant from its active site. Allostery has been dubbed the ‘second secret of life’ after DNA [1], because it plays such a fundamental role in cellular signalling networks and disease. The pharmaceutical industry has also shown an interest in the development of allosteric drugs because targeting the allosteric sites of a protein offers certain advantages when compared with the orthosteric or primary binding site. For example, because allosteric sites are less conserved, allosteric ligands can be much more selective and safer with fewer side-effects [2]. Allostery is ubiquitous in biology and has been suggested as a universal property of all dynamic proteins [3], meaning that even those proteins that are not known to exhibit allosteric effects are likely to possess undiscovered allosteric sites.

It is unsurprising that the elusive mechanism behind this curious molecular ‘action at a distance’ has attracted intense scientific investigation for decades now. Early models of allostery were mostly two-state and focused on static, thermally averaged structures. Of particular importance are the KNF model (model of Koshland et al. [4]), also referred to as the ‘induced fit’ model, because it assumes that the binding of a ligand induces a change in the protein structure, and the MWC model (model of Monod et al. [5]), which supposes that the ligand preferentially stabilizes or destabilizes binding competent structures. These models explain some but not all of the observed experimental data on allostery. The crucial role of protein dynamics in allostery was first realized in a paper by Cooper & Drysden [6], where they suggested that allosteric communication can take place without any change in mean structural conformation. Since then, a diverse array of allosteric regulation mechanisms which involve varying contributions from the dynamics of the protein have been discovered; these have been summarized in figure 1. A unified theoretical framework for allosteric phenomena has emerged with the ensemble view of allostery, which focuses on the statistical nature of allostery [8]. The perturbation caused by allosteric ligands reshapes the original free-energy landscape of the protein, changing enthalpic and entropic factors that stabilize different protein conformations and redistributing the thermodynamic ensemble.

Figure 1.

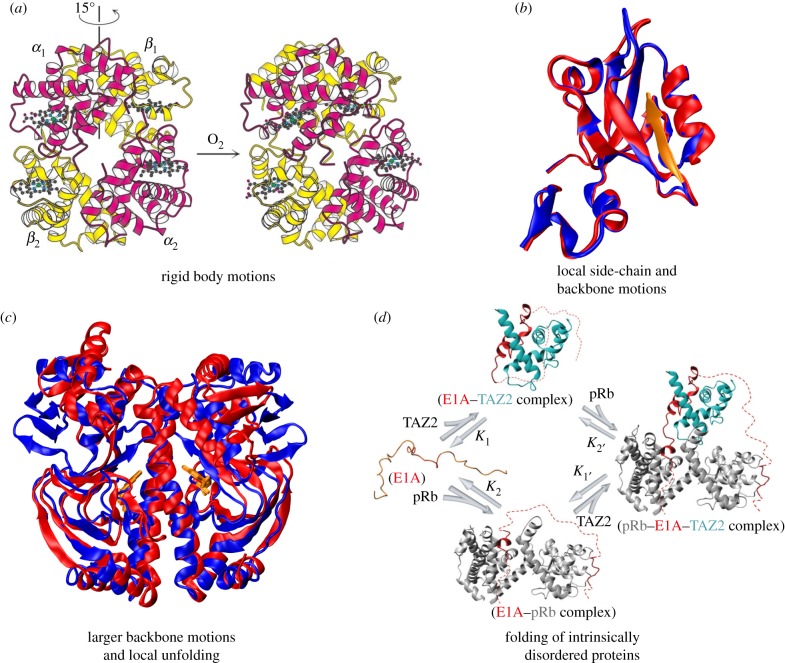
Allosteric systems representing conformational dynamics of folded structures and large-scale disorder. (a) Haemoglobin is an example of allosteric motion resulting from quaternary structure changes. The binding of oxygen to one haemoglobin subunit induces a 15° rotation of one α/β pair with respect to the other, which raises the affinity of haemoglobin for oxygen, causing the other subunits to also bind oxygen. (b) PDZ domain proteins are an example of allostery without significant structural changes, where ligand binding leads to modulation in distal side-chain motions. The superposition of the structures in the unbound (PDB 1BFE; blue) and bound (PDB 1BE9; red and peptide ligand in orange) states are shown. (c) The allosteric transition in the catabolite activator protein (CAP) upon binding of cyclic adenosine monophosphate (cAMP) is an example of allostery involving larger structural changes and local unfolding. The superposition of apo-CAP (PDB 2WC2; blue) and CAP-cAMP (PDB 1G6N; red) are shown. As CAP is a homodimer, it binds two cAMP molecules, which are highlighted in orange. (d) The binding of the intrinsically disordered protein E1A to the TAZ2 domain of CBP/p300 causes E1A to fold and subsequently bind pRb, yielding a ternary complex. Alternatively, E1A binds first to pRb and then the TAZ2 domain. TAZ2 and pRb do not associate directly, only within ternary complexes formed by binding of both proteins to E1A, which acts as molecular hub involving allosteric regulation. Reproduced with permission from Nature Publishing Group: Ferreon et al. [7]. (Online version in colour.)

In the light of this modern thermodynamic understanding of allostery, stochastic Markov models have become popular as a statistical tool that can provide insight into the mechanism behind allostery. Markov models are typically states-and-rates network models, which assume that a system exists in one of several discrete states and describe the probability of transitions between these states. The fundamental assumption of Markovian models is one of memorylessness, i.e. the probability of transition from one state to another depends only on the current state and not the history of the system.

In particular, Markov state models (MSMs) coupled with molecular dynamics (MD) simulations are being increasingly used to gain a detailed, atomistic and predictive understanding of biomolecular processes like allostery. MSMs are kinetic maps of a system's underlying free-energy landscape, which allow us to extract essential information on the perturbation caused by allosteric ligands in the protein's energy landscape. Allosteric modulations can often involve supra-millisecond timescales [9] and with current high-performance computing resources, simulation trajectories struggle to reach these. MSMs can, however, be built from multiple simulations much shorter than the timescale of interest and yet describe long timescale dynamics accurately. MSMs can be used for adaptive sampling [10] or be constructed from enhanced sampling simulations (e.g. replica exchange) [11], making them even more attractive for bridging the timescale gap. Once we have an MSM for a system, it can be used to calculate many quantities of interest and draw connections with experimental data. Finally, the resolution of an MSM can be smoothly tuned from granular and detailed to coarse and simple. They can therefore offer a reduced view of the ensemble of a protein's spontaneous fluctuations and generate human-comprehensible insights into an allosteric system.

It should be noted that, until now, the lion's share of the effort to provide a theoretical description of allostery has been dedicated to path and community analysis [12,13]. This approach models the protein as a network of its residues and tries to identify the clusters of atoms and the atomic interactions that connect the active site to its allosteric effector. This is markedly different from an MSM as the nodes of an MSM network do not represent fragments of the protein but rather different conformations of the full molecular system. However, a few papers have applied concepts from Markov modelling to traditional residue-based networks and these have also been discussed in this article.

2. Overview of Markov state modelling theory

MSMs normally consist of two components [14]:

• (a) a discretization of the system's state space into n disjoint sets S₁, … , S_n

• (b) a transition matrix of conditional transition probabilities P: P_ij(τ) = Prob(x_t+τ ∈ S_j|x_t ∈ S_i), where τ is the characteristic lag time for which the model is constructed.

Armed with this information, one can now correctly derive many thermodynamic and kinetic quantities of interest. These can be computed either by sampling an artificial trajectory from P or by performing algebraic computations on the transition matrix. For example, the transition matrix P gives rise to a stationary distribution π by virtue of the simple eigenvalue problem 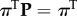. Moreover, the dominant contributions to the system dynamics can be obtained by solving 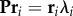for the eigenvectors r_i and eigenvalues λ_i of the system. The eigenvalues correspond to the relaxation timescales t_i =−τ/|ln(λ_i)|, while the eigenvectors represent the changes in the system that takes place within those timescales.

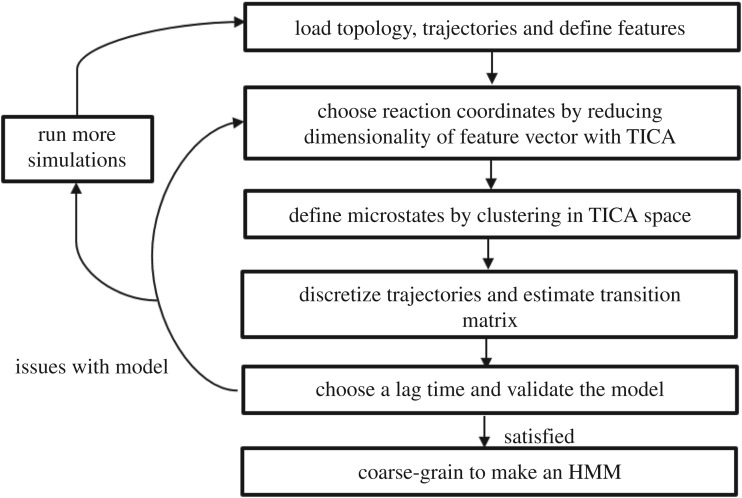
The technical complexities of constructing MSMs from MD trajectories can be circumvented with software libraries like PyEMMA [15] and MSMBuilder [16], which automate this procedure to a great extent. The most critical challenge for these software programs is finding a good discretization for the conformation space of the protein without relying on user intervention or specialized knowledge about the system. A typical analysis using PyEMMA or MSMBuilder is initiated by loading the molecular topology file and a list of the simulation trajectories one wants to analyse. Molecular descriptors or ‘features’ (e.g. distances between atoms, dihedral angles or contacts) are defined by the user, which are then computed for each frame in the simulation trajectories, thus transforming the Cartesian coordinate trajectories into feature vectors. The next step is to conduct a linear transformation on these feature vectors for dimension reduction using time-lagged independent component analysis (TICA) [17], which can identify a subspace in the feature space containing the slowest kinetic modes by maximizing the autocorrelation of the reduced collective coordinates. As TICA can capture the slow, chemically relevant transitions in a system, it is preferable to the more commonly used principal component analysis (PCA) for the construction of kinetic models because the latter only maximizes the variance in the reduced coordinates and pays no importance to kinetic information. The TICA reaction coordinates can be used to project the free-energy of the system along with them. Now that one has a convenient low-dimensional representation of the MD data, k-means clustering [18] is used to decompose the free-energy landscape into hundreds of discrete ‘microstates’ such that each frame of the trajectories can be assigned to one of these microstates using a Voronoi partitioning. The discretized trajectories are used to estimate an MSM of the microstates by counting the number of transitions between microstates, computing the transition count matrix (TCM), normalizing it with the total number of transitions emanating from each state and enforcing detailed balance on the obtained transition matrix using symmetrization. This model is useful in itself and can be used to calculate quantities of interest; however, it is too granular to provide a simple, intuitive picture of the dynamics of a protein. This can be achieved by coarse-graining the MSM into a hidden Markov model (HMM) with a few metastable states, using robust Perron cluster analysis (PCCA+) [19]. PCCA+ is a fuzzy version of the spectral algorithm for partitioning graphs that assigns each microstate a probability of belonging to a metastable macrostate. Whether the resulting HMM satisfies the Markovian assumptions can be verified with a Chapman–Kolmogorov test. The MSM procedure has been summarized as a flowchart in figure 2.

Figure 2.

The workflow for building MSMs from MD trajectories.

It must be stressed that while automated MSM construction software is very useful, these programmes are not yet at the stage where we can blindly use them as a black box tool. Users must exercise judgement when choosing input features that will be fed to the dimension reduction algorithm. Cartesian coordinates suffer from the defect of mixing local and global motions and therefore, interatomic distances should preferably be used in their place. The use of dihedral angles can also be problematic if the periodicity is not properly taken care of; the sines and cosines of these angles can be used instead. The choice of algorithm used for state space discretization is also critical for building a good MSM and must be made carefully. In the limit of infinite data, the final MSM should not really be affected by this choice; but in practice, we operate in the data poor regime. The recipe of TICA and k-means clustering used in PyEMMA has been subjected to some criticism in [20], because TICA is a non-unitary transformation which distorts the free-energy landscape and the geometrical nature of k-means clustering implies that borders between adjacent microstates do not respect free-energy barriers. The authors have proposed a combination of PCA and density-based clustering as an alternative method of defining the microstates [20]. Experimentation with different dimension reduction techniques, clustering algorithms and parameters therein is thus encouraged to ensure that the final MSM is robust to these choices, passes the tests for Markovianity, and has low statistical errors in the estimated kinetic quantities.

3. Applications of Markov modelling to study allostery

(a). Experimental studies

The earliest use of Markov modelling to study allostery was with the application of mechanistic Markov models to explain experimental data. Mechanistic models usually rely on a simple state-space discretization which does not consider atomistic detail, typically distinguishing only between bound/unbound or active/inactive states. Madsenb & Yeo in their 1998 study [21] used mechanistic Markov models to propose an allosteric mechanism for the concentration-dependent modulation of ion channel behaviour by drug molecules. The linear sequential mechanism which was then accepted for explaining the blockade of ion channel activity predicted that the channel activity will decrease monotonically with increasing concentration of a non-competitive inhibitor (NCI) molecule. However, experiments observed a more complex behaviour in some systems such as the skeletal muscle nicotinic acetylcholine receptor: increased activity at low concentrations of NCI in addition to the classic inhibition at high concentrations. To explain these results, the authors assumed a sterically limited drug binding model with two closely located but separate binding sites in the extracellular pore region of the ion channel, one inhibitory and one stimulatory. Their considerably more complex Markovian reaction network consisted of three connected, parallel activation pathways with the drug not bound at all, bound to the inhibitory site and bound to the stimulatory site. The stationary distribution of their Markov model was used to estimate quantities like mean open time per burst whose behaviour fell in line with experimental expectations. Boras et al. [22] used mechanistic Markov models to understand how the holoenzyme protein kinase A (PKA) is activated by the binding of cyclic adenosine monophosphates (cAMPs) to the protein's two cyclic nucleotide binding domains (CBDs) A and B on each regulatory (R) subunit. They examined five candidate reaction mechanisms whose parameters were fitted to the experimental data by minimizing the weighted sum of squares residual, and the goodness of fit for each was evaluated using an F-test. The resulting 20-state dually regulated model, which allowed both CBD-A and CBD-B binding to affect activation of the catalytic (C) subunits was found to be the best explanation for the experimental data. Their results show that CBD-B plays an important role in R‒C interaction and facilitates the release of the first C-subunit prior to the binding to CBD-A, highlighting the importance of heterodimer interactions and cooperativity in PKA activation.

(b). Simulation studies

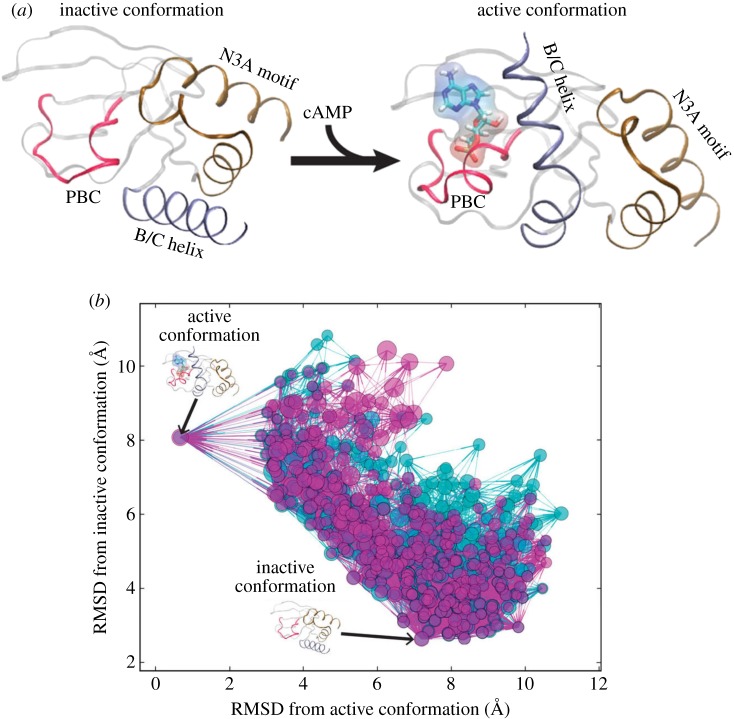
A majority of studies have focused on analysing MD simulations of allosteric proteins with Markov models. Malmstrom et al. studied conformational ensembles of CBD-A, one of the cyclic nucleotide binding domains of PKA in cAMP-free and cAMP-bound states (figure 3a) to understand the mechanism of allostery atomistically [23]. The MSMs built for both ensembles (figure 3b) show that the free-energy landscape is shallow with many inter-conversion pathways between the active and inactive states. The addition of cAMP slows down the transition rate from the active to the inactive state but not vice-versa, thereby increasing the population of the active state and indicating that conformational selection is the primary mechanism here. MSMs were also generated for each of the key structural motifs involved in the signal transduction process. These revealed that the change in dynamics of the B/C helix was the rate-limiting step and its motion was critical for signal propagation to the N3A motif (figure 3a).

Figure 3.

Ligand-induced protein allostery illustrated for the cyclic nucleotide-binding domain of the PKA regulatory subunit. (a) The experimentally determined conformational changes in the cyclic nucleotide-binding domain upon cAMP binding are shown. (b) From long-timescale, all-atom MD simulations, MSMs were calculated to elucidate the conformational ensembles of the cyclic nucleotide-binding domain for the cAMP-free (cyan) and cAMP-bound (magenta) states. The position of each conformational state node is the root mean square deviation (RMSD) of the corresponding representative conformation relative to the experimentally determined structures. The diameter of a node is proportional to the log of its equilibrium population, i.e. the larger the node the more probable the state at equilibrium. Reproduced with permission from Nature Publishing Group: Malmstrom et al. [23]. (Online version in colour.)

Thayer et al. [24] used the MD-MSM combination to study a small single-domain allosteric protein CRIB-PDZ, where the binding of an allosteric effector protein, Rho GTPase cdc42 resulted in a positive allosteric effect. They constructed a 5-state Markov model that showed allostery in CRIB-PDZ involves a sequence-induced fit for allosteric activation and conformational selection for ligand binding. A kinetic network analysis of the model also predicts that the PDZ protein binds to the protein ligand with a 12-fold greater probability in the allosteric route compared with the non-allosteric pathway, which is close to experimental observations. Buchenberg et al. [25] computationally investigated the photoswitchable PDZ domain (PDZ2S), for which time-resolved infrared spectroscopy had found that the allosteric transition occurs on multiple timescales. The cis-to-trans photoisomerization of the azobenzene residue was imitated using a potential-energy surface switching method. However, because their simulations were non-equilibrium (NEQ) in nature, Markovianity of conformational transitions could not be assumed. A related computational tool known as a dynamic network model is therefore used instead of a Markov model, which allows time-dependent transition probabilities to be determined. It was found that the photoinduced opening of the binding pocket was highly non-exponential in time. The results showed excellent agreement with experiment and identified three physically distinct phases of the time evolution: elastic response (approx. 0.1 ns), inelastic reorganization (approx. 100 ns) and structural relaxation (approx. 1 µs). The diversity of the NEQ trajectories also dispels the notion of a single directed allosteric pathway but rather points towards a multitude of possible paths, consistent with the ensemble view of allostery [8].

The Bowman group has pursued a line of investigation that is particularly relevant to the development of allosteric drugs. They are using MSMs and MD simulations to identify cryptic allosteric sites: transient pockets absent in crystalline structure that can nevertheless alter enzymatic activity. These sites can be potentially targeted by drugs. A 5000-state MSM of β-lactamase was built [26] and representative structures of each state were analysed for pockets with LIGSITE [27]. The pockets whose location coincided with the regions structurally coupled to the active site were identified as potential allosteric sites. The MSMs were very useful in quantifying observables like the probability of a pocket being open and the timescale for opening. A follow-up study from the same group combined this method with experiments [28], where the existence of the predicted pockets in β-lactamase from MD-MSM was confirmed with thiol labelling experiments. Pande and co-workers [29] ran large-scale MD simulations of the c-Src kinase protein with the Folding@home computing network. The resulting MSM identified key structural intermediates in the activation pathways of this protein and a novel allosteric site that could be used for drug design. Pontiggia et al. [30] studied the interconversion between the active and inactive states of nitrogen regulatory protein C (NtrC^R). In the apo form, NtrC^R exists in a conformational mixture of its active and inactive states. The active and inactive forms of the protein differ mainly in the helix α4 region, which is in allosteric communication with residue Asp54 whose phosphorylation preferentially stabilizes the active state. The landscape of the active–inactive interconversion was studied in great detail by conducting many short MD simulations with an aggregate simulation time of about a millisecond, using the Folding@home network. Important findings from the MSM constructed from these data included the discovery of multiple conversion pathways and the relative structural homogeneity of the active state compared with the inactive state, which was composed of several interconverting conformations. This was followed up with two long, unbiased MD runs of 21 µs and 71 µs, respectively, whose results agreed with those from the Folding@home simulations. This study is significant because the allosteric transition pathway was very well sampled, as opposed to most studies in this sub-discipline which suffer from chronic under-sampling.

Some studies using Markov modelling have focused more on pinpointing the actual intra-molecular pathway involved in allostery and identifying key players in the long-range signalling that takes place. A paper by Long & Brüschweiler [31] introduces the master equation-based approach for allostery by population shift (MAPS) which derives the timescales, amplitudes and pathways of signal transmission in peptides and proteins from dihedral angle dynamics. A master equation describes the evolution of a continuous-time Markov process and is usually of the form

where K is the transition rate constant matrix and c is a column vector containing the populations of each state of the model. The master equation can be subjected to constraints on populations and conformational transitions, which permits the systematic investigation of perturbations due to the allosteric ligand and their propagation within the molecule. They tested this approach with the alanine–pentapeptide by applying a harmonic potential to the dihedral angles of the terminal residue Ala5 and studying how this local conformational restraint is spread globally as monitored by the population shifts in the distribution of the other dihedral angles. The equilibrium distribution of the residues Ala1–Ala4 was found to be shifted towards the coil state. The timescales for re-equilibration in response to the perturbation were also calculated, and it was found that the timescales for the residues closer to the site of the perturbation were faster, meaning that it spread in a diffusive manner. Next, they applied this technique to millisecond simulations of the protein BPTI. A constraint was applied to the Cys14 residue and, surprisingly, it was found that communications between Cys14 and loop 2 could largely bypass the disulfide bond. In a study by Chennubhotla & Bahar [32], the Markov network formalism was used to find pathways of allosteric signal transduction in large molecules. They modelled the biomolecular structure as a network of residues through which information diffuses in a Markovian fashion. An affinity matrix that determines the probability of signal communication between residues was computed based on their interaction strength. The residue-level model can then be systematically reduced by a soft-partition of residues into coherent clusters, i.e. assigning each residue a probability of membership to clusters. The coarsening can be applied in stages and the resulting model is therefore inherently multi-resolution in nature. This technique allowed Chennubhotla and Bahar to automatically identify groups of residues acting as hubs and messengers for collecting and passing information across the network, respectively. They used it to study the bacterial chaperonin complex GroEL–GroES and identified two possible pathways for communication between the ATP binding and co-chaperonin binding sites. A more recent study by Amor et al. [33] takes a slightly different approach to identifying intra-molecular signalling pathways and allosteric sites. Here, a graph-theoretic approach was used and a Markov stability analysis on an atomistic graph representation of the protein performed to identify coherent communities of atoms in the signalling path. The adjacency graph for the molecule is built using bond energies from the DREIDING force-field [34]. Markov stability finds an optimized partition of this graph at every timescale and, as this Markov timescale is increased, the method virtually zooms out, scanning across increasingly larger scales looking for significant communities at different resolutions. The connectivity between two nodes is determined using a transient analysis of random walks that originate from the source node and is quantified by the ‘half-life’ of a propagating signal at the target node. This allows the determination of signalling pathways. Like the previous study, this technique is also inherently multiscale; however, unlike the previous study, this method only uses static crystal structures and not MD simulation data. A case study was performed using the active and inactive structures of the caspase-1 protein which is known to be allosteric. The analysis discovered that the active conformation possesses a more fluid and less compartmentalized structure which allows robust, long-distance signal propagation. Bonds and residues that were found to be critical in the active-to-allosteric pathway using transient random walk analysis tallied with previous mutagenesis experiments and new, alternative allosteric pathways were also identified. Finally, computational point mutagenesis studies on the caspase dimer revealed that pathways between the two active sites are distinct from allosteric-to-active pathways. This also agrees with experiments showing that mutating allosteric residues does not affect dimer cooperativity.

4. Conclusion

There is a quote which is often attributed to Einstein and is of particular relevance here: ‘Everything should be made as simple as possible, but not simpler’. Simpler two-state models of allostery are alluring but cannot capture the whole picture, because allosteric modulators do more than just act as an on–off switch. Markovian modelling can help us embrace the complexity and stochasticity that truly underlies allostery. In this brief review, we have seen how these models are compact enough to be predictive yet complex enough to be a sufficient description of the system. Markov models have been employed variously to gain an understanding of the reaction mechanism, the thermodynamics, the free-energy landscape perturbations, the population shifts, the hierarchy of timescales and the structural basis behind allostery.

Of course, because a model is only as good as the data one uses to estimate it, MSMs are subject to the same limitations that the MD simulations are. Insufficient sampling times and inaccurate force fields still plague MD simulations. Nevertheless, with the advent of exascale computing and continuing methodological improvements, Markov modelling and molecular simulation data are expected to greatly further our understanding of allostery.

Data accessibility

This article has no additional data.

Competing interests

We declare we have no competing interests.

Funding

We received no funding for this study.