Substrate protein dependence of GroEL–GroES interaction cycle revealed by high-speed atomic force microscopy imaging

Daisuke Noshiro; Toshio Ando

doi:10.1098/rstb.2017.0180

. 2018 May 7;373(1749):20170180. doi: 10.1098/rstb.2017.0180

Substrate protein dependence of GroEL–GroES interaction cycle revealed by high-speed atomic force microscopy imaging

Daisuke Noshiro ^1,², Toshio Ando ^1,^2,^✉

PMCID: PMC5941175 PMID: 29735734

Abstract

A double-ring-shaped tetradecameric GroEL complex assists proper protein folding in cooperation with the cochaperonin GroES. The dynamic GroEL–GroES interaction reflects the allosteric intra- and inter-ring communications and the chaperonin reaction. Therefore, revealing this dynamic interaction is essential to understanding the allosteric communications and the operation mechanism of GroEL. Nevertheless, how this interaction proceeds in the chaperonin cycle has long been controversial. Here, we directly image the dynamic GroEL–GroES interaction under conditions with and without foldable substrate protein using high-speed atomic force microscopy. Then, the imaging results obtained under these conditions and our previous results in the presence of unfoldable substrate are compared. The molecular movies reveal that the entire reaction pathway is highly complicated but basically identical irrespective of the substrate condition. A prominent (but moderate) difference is in the population distribution of intermediate species: symmetric GroEL : GroES₂ and asymmetric GroEL : GroES₁ complexes, and GroES–unbound GroEL. This difference is mainly attributed to the longer lifetime of GroEL : GroES₁ complexes in the presence of foldable substrate. Moreover, the inter-ring communication, which is the basis for the alternating action of the two rings, occurs at two distinct (GroES association and dissociation) steps in the main reaction pathway, irrespective of the substrate condition.

This article is part of a discussion meeting issue ‘Allostery and molecular machines’.

Keywords: chaperonin, GroEL, allostery, imaging, high-speed atomic force microscopy

1. Introduction

In bacteria, GroEL assists proper folding of many proteins in cooperation with its cochaperonin GroES [1,2]. GroEL is a cylindrical protein complex formed by two heptameric rings stacked back to back, each consisting of identical ATPase subunits [3]. GroES is a single homo-heptameric ring [4] and binds to the ends of the GroEL cylinder depending on the nucleotide state of GroEL. These multiple factors involved in the reaction cycle of this system make it difficult to analyse the reaction cycle with ensemble averaging methods. Nevertheless, several issues concerning this reaction cycle have been revealed by extensive biochemical and structural studies [5–7]. Unfolded substrate protein (SP) with exposed hydrophobic residues binds to GroEL at its apical domain [8]. Then, the SP is encapsulated into the hydrophilic cavity of GroEL after its binding to ATP and GroES [9,10]. The encapsulated SP can fold in this environment. Subsequently, GroES dissociates and then the SP is released into solution.

Because the two rings of GroEL are identical, these processes proceed at each ring. Then, an important question is raised: whether or not the molecular processes at one ring proceed independently of those at the opposite ring. Biochemical kinetic studies of ATP binding and hydrolysis put forward allosteric regulation with intra-ring positive cooperativity and inter-ring negative cooperativity as regard to ATP binding [11–13]. Based on this allosteric regulation, a model has been postulated in which only one ring binds GroES throughout the cycle, so that asymmetric GroEL : GroES₁ complexes (referred to as the bullet complexes) are exclusively formed [14]. The GroES-free ring (trans-ring) can bind ATP only after ATP is hydrolysed in the GroES-bound ring (cis-ring). Actual ATP binding to the trans-ring induces release of GroES, ADP and the encapsulated SP protein from the opposite ring, while the second GroES binds to the trans-ring to form a new cis-ring [15,16]. Thus, the two rings of GroEL alternately bind and release GroES and hence alternately function. Nonetheless, symmetric GroEL : (GroES)₂ complexes (referred to as the football complexes) have also been observed under electron microscopy [17–22]. Moreover, biochemical measurements in the presence of various concentrations of ATP and GroES have shown the folding activity to be nearly proportional to the population of football complexes as well as the abolishment of inter-ring negative cooperativity of ATP binding at [ATP] greater than approximately 50 µM [21,22]. The structural basis of this abolishment of inter-ring negative cooperativity has recently been revealed by the atomic structure of football complexes formed by a GroEL mutant with a very low ATPase activity [23]. In spite of these observations (for more details, see [24]), this model postulates that football complexes appear only as a transient intermediate in the reaction cycle, at the time when GroES binds to the trans-ring just before the completion of GroES release from the cis-ring.

To inspect this model more directly, solution kinetics studies with fluorescence energy transfer-based GroEL–GroES association detection [25–31] and single-molecule fluorescence microscopy observations [32–35] have been performed in the past two decades. Most of these studies revealed a part of the reaction pathway and detected football complexes not as a briefly subsisting intermediate but as a major one appearing during the reaction cycle in the presence of unfoldable or foldable SP. Very recently, dual-colour fluorescence cross-correlation spectroscopy analysis was performed using differently labelled GroES [36]. This study showed that football complexes were to an appreciable extent formed only in the presence of unfoldable SP, whereas both in the presence of foldable SP and in the absence of SP, football complexes were only transiently and hence rarely formed. Thus, even with single-molecule fluorescence approaches, inconsistent results have emerged. This may be partly due to different dyes [36] and dye-labelling sites being used. More seriously, the two rings of GroEL are too closely positioned to be resolved with fluorescence methods. Therefore, it is often very difficult to know from which ring a detected fluorescence signal comes. To solve this controversial issue definitely, we need a further direct method to monitor the dynamic binding and release of GroES occurring in nano-scale space.

Here we used high-speed atomic force microscopy (HS-AFM) [37,38] to directly visualize the dynamic GroEL–GroES interaction with time resolution of 0.23 s. HS-AFM has recently been used with great success to visualize protein molecules in dynamic action without disturbing their function [39,40]. In our previous HS-AFM study [41], we imaged the GroEL–GroES interaction in the presence of unfoldable SP, disulfide bond-reduced α-lactalbumin (α-LA), and revealed a nearly entire reaction scheme comprising a main circular pathway and a side pathway. In both pathways, football complexes appear as a major intermediate. In the main pathway, which occurs at approximately 67%, GroES alternately interacts with the two rings of GroEL. However, in the side pathway, which occurs at 33%, this alternate rhythm is disrupted; the second bound GroES dissociates before the first bound GroES dissociates. The pathway branching occurs at the bullet complexes, and the bullet complexes formed at the exit of the side pathway can enter either pathway at the respective constant probabilities. In the present HS-AFM study, we image the GroEL–GroES interaction in the absence and presence of foldable SP and compare the reaction schemes obtained under the three substrate conditions.

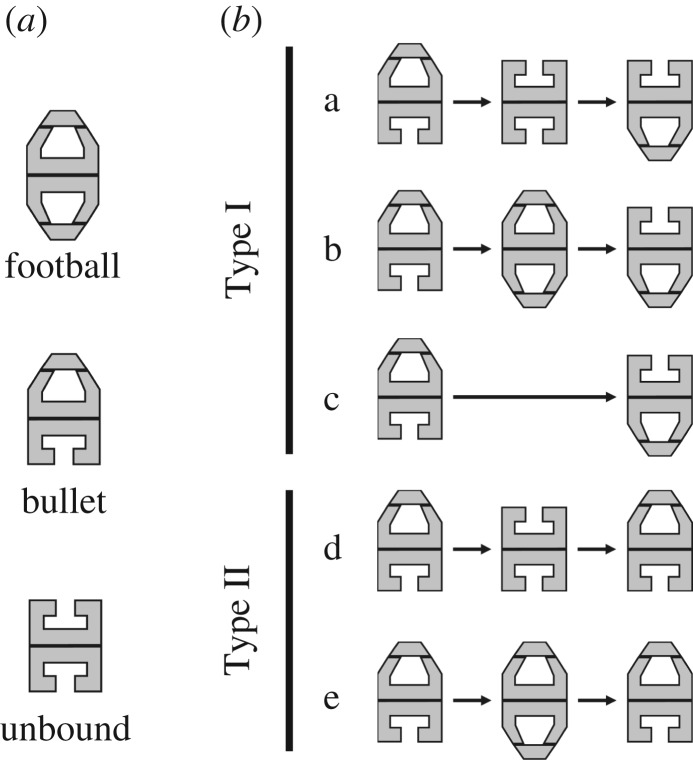
2. Intermediates and reaction patterns

To visualize the dynamic GroEL–GroES interaction by HS-AFM, the D490C GroEL mutant biotinylated at Cys490 with a bifunctional reagent (linker length, approx. 2.5 nm) was immobilized in a side-on orientation on the two-dimensional (2D) crystal surface of a tamavidin 2 mutein with a lowered isoelectric point (tamavidin 2-LPI) [42] formed directly on a bare mica surface (figure 1a). All imaging experiments were performed at 4.35 frames s⁻¹ (0.23 s per frame) under the conditions of 25°C, 100 mM KCl, 25 mM HEPES-KOH (pH 7.4), 5 mM MgCl₂, 2 mM ATP, 1 µM GroES, with or without 200 nM of a double mutant of maltose binding protein (DM-MBP) denatured with guanidine hydrochloride. Rhodanese was also used as a foldable SP. In the successive AFM images, three intermediates appeared (figure 1b; supplementary movies S1–S3): GroES–unbound, and bullet and football complexes (we express these intermediates as ‘U’, ‘B’ and ‘F’, respectively). The population ratios of these intermediates are summarized in table 1, including those obtained in the presence of α-LA [41] and rhodanese. The population ratio in the absence of SP was similar to that observed in the presence of α-LA (football complexes were a major intermediate: 53–67%), whereas bullet complexes most frequently appeared in the presence of DM-MBP or rhodanese (62–65%) and football complexes appeared at approximately 30%. A prominent feature observed in the presence of foldable SP was moderately frequent appearance of GroES–unbound GroEL (5–8%), which appeared only at 0.4% in the presence of α-LA and at 1.3% in the absence of SP.

Figure 1. — Assay system for HS-AFM imaging of dynamic GroEL–GroES interaction and captured images. (a) Schematic of assay system used for HS-AFM imaging. Tamavidin 2-LPI was two-dimensionally crystallized directly on a bare mica surface. GroEL D490C biotinylated at Cys490 located at its equatorial domain was tethered to the tamavidin 2-LPI 2D crystal surface through the biotin–tamavidin 2-LPI linkage with a linker length of approximately 2.5 nm. Because this crystal surface is resistant to non-specific protein binding, the tethered GroEL does not adsorb onto the surface. When the molecule is tapped briefly (approx. 100 ns) with the AFM-tip, the molecule makes contact with the surface. During imaging, the oscillation energy of the cantilever is partially transferred to the molecule by between 2 and 3 k_BT (k_B, Boltzmann constant; T, room temperature in kelvin) per tap, under the imaging conditions. This transferred energy is partitioned to many degrees of freedom of the molecule and quickly dissipates. Therefore, the tip- and surface-sample contacts do not affect the function of the molecule [40]. (b) HS-AFM images showing repeated GroES association and dissociation at the two rings of GroEL in the presence of denatured DM-MBP. The images are clipped from successive images captured at 4.35 frames s⁻¹. The dashed lines indicate the positions of toroid ends of the GroEL molecule. The arrowheads indicate GroES bound to GroEL. Besides football and bullet complexes, GroES–unbound GroEL also appeared at 2.53, 4.83 and 16.10 s. The bulk solution contains 1 µM GroES, 2 mM ATP and 0.2 µM denatured DM-MBP.

Table 1.

Frequency (%) of appearance of intermediate species under different substrate conditions. ‘n’ indicates the total number of captured frames.

		football	bullet	unbound	n
	no substrate	53.4	45.3	1.3	18 528
foldable substrate	DM-MBP	29.5	62.2	8.3	18 759
foldable substrate	rhodanese	30.4	64.9	4.7	5350
unfoldable substrate	α-LA^a	66.8	32.8	0.4	12 714

Open in a new tab

^aData from a previous study [41].

Next, we analysed the order of association and dissociation of GroES at the two rings of GroEL by choosing the bullet complexes as an initial state (figure 2). As observed previously in the presence of α-LA [41], these dynamic events are largely classified into Type I and Type II; in Type I, the cis/trans states interchange between the two rings after a round of dissociation and association of GroES, resulting in polarity change between the initial and second bullet complexes (i.e. B^↑ → X → B_↓; the vertical arrows indicate the polarity of bullet complexes and ‘X’ denotes F, U or none), whereas in Type II no cis/trans interchange occurs, resulting in no polarity change (i.e. B^↑ → X → B^↑; ‘X’ denotes F or U). Reaction patterns not belonging to either Type I or Type II (i.e. B → U → F and B → F → U) rarely appeared in the presence of DM-MBP (1.8% in total). We omit these cases from the analyses described below. The population ratios of all reaction patterns are summarized in table 2. As noted in table 2, the appearance frequency ratio between Type I and Type II processes is nearly independent of the substrate condition (Type I : Type II ≈ 3 : 1), although the Type II process appears more frequently in the presence of α-LA (Type I : Type II ≈ 2 : 1).

Figure 2. — Three intermediate species (a) and five sequential patterns of appearance and disappearance of these intermediate species (b) observed in the presence of foldable SP and in the absence of SP.

Table 2.

Frequency (%) of sequential patterns in which intermediate species appear in the GroES association and dissociation reaction under different substrate conditions. The second line from the top (first five headings) indicates sequential patterns (from left to right) of appearance and disappearance of intermediate species (F, football; B, bullet; U, GroES–unbound GroEL). ‘n’ indicates the total number of events used in this analysis.

	Type I			Type II
	B^↑UB^↓	B^↑FB^↓	B^↑B^↓	B^↑UB^↑	B^↑FB^↑	Type I	Type II	n
no substrate	6.9	52.5	13.6	1.7	25.3	73.0	27.0	1397
DM-MBP	23.7	38.0	13.1	8.6	16.6	74.8	25.2	1287
rhodanese	25.1	35.0	16.8	5.7	17.4	76.9	23.1	334
α-LA^a	2.4	55.7	10.7	0.4	30.8	68.8	31.2	1012

Open in a new tab

^aData from a previous study [41].

3. Decay kinetics of bullet and football complexes

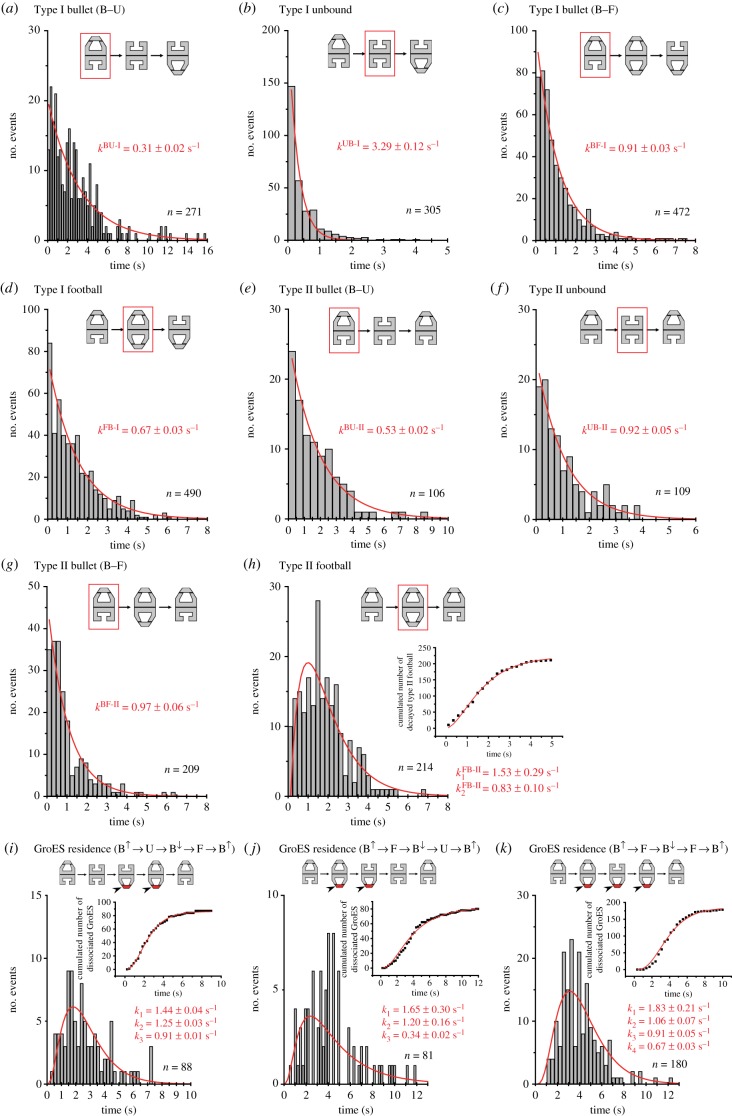
All histograms of lifetime for bullet complexes (figure 3a,c,e,g; electronic supplementary material, figures S1 and S2) were well fitted to single-exponential functions. All values of rate constants estimated by single-exponential fitting are given in table 3, together with those previously obtained in the presence of α-LA for comparison. The bullet complexes in both Type I and Type II processes (which we refer to as Type I bullet and Type II bullet, respectively) with or without DM-MBP decayed to either football complexes or GroES–unbound GroEL (figure 2), resulting in a pathway branching (i.e. B → F or B → U). In addition, direct decay into bullet complexes with altered polarity also occurred in the Type I process, irrespective of the substrate condition (i.e. B^↑ → B_↓). However, we think that this event is just apparent due to occasional miscapturing of GroES–unbound GroEL, because this GroES–unbound GroEL decays very fast into bullet complexes with opposite polarity: 3.29 ± 0.12 s⁻¹ (DM-MBP) and 8.16 ± 0.17 s⁻¹ (absence of SP). Because the rate constants of B → F and B → U transitions are approximately three-times different in the Type I process and approximately two-times different in the Type II process in the presence of DM-MBP (table 3), bullet complexes are further classified into two sub-types. We refer to as ‘B–F type’ and ‘B–U type’ the bullet complexes that undergo B → F and B → U transitions, respectively. It would be possible that the intermediates formed just prior to the bullet complexes might be responsible for the pathway branching and hence the sub-types. However, this is not the case, because the decay rates of these sub-types are nearly independent of the previous intermediate states, at least in the presence of DM-MBP (electronic supplementary material, figure S3); the bullet complexes appearing in the pathways F → B → F and U → B → F decay at 0.96 ± 0.03 and 1.00 ± 0.06 s⁻¹, respectively, while the bullet complexes appearing in the pathways F → B → U and U → B → U decay at 0.31 ± 0.04 and 0.24 ± 0.03 s⁻¹, respectively. Note that the small frequency of observing the pathway U → B → U hampered precise estimation of the rate constant. In the absence of SP, the bullet complexes appearing in the pathways F → B → F and U → B→ F decay at 1.26 ± 0.03 and 1.03 ± 0.06 s⁻¹, respectively (electronic supplementary material, figure S4). Considering the low appearance frequency of the pathway U → B → F, these values are nearly identical. For the case of Type II process, we could not perform this analysis as the appearance frequency of B → U is small. Nevertheless, in all cases, the probabilities in which bullet complexes decay to F or U are nearly independent of the intermediates formed just before the bullet complexes (electronic supplementary material, table S1). Thus, we conclude that the pathway branching occurring after bullet complexes originates from distinct B–F and B–U types of bullet complexes and that these sub-types are in rapid equilibrium.

Table 3.

Rate constants of various reaction steps in Type I and Type II processes. The second line from the top indicates sequential patterns (from left to right) of appearance and disappearance of intermediate species (F, football; B, bullet; U, GroES–unbound GroEL).

	Type I				Type II
	B^↑UB^↓		B^↑FB^↓		B^↑UB^↑		B^↑FB^↑
	k^BU-I (s⁻¹)	k^UB-I (s⁻¹)	k^BF-I (s⁻¹)	k^FB-I (s⁻¹)	k^BU-II (s⁻¹)	k^UB-II (s⁻¹)	k^BF-II (s⁻¹)	k^FB-II₁ (s⁻¹)	k^FB-II₂ (s⁻¹)
no substrate	0.40 ± 0.04	8.16 ± 0.17	1.21 ± 0.06	0.56 ± 0.01	—	—	1.31 ± 0.03	1.50 ± 0.12	0.61 ± 0.02
DM-MBP	0.31 ± 0.02	3.29 ± 0.12	0.91 ± 0.03	0.67 ± 0.03	0.53 ± 0.02	0.92 ± 0.05	0.97 ± 0.06	1.53 ± 0.29	0.83 ± 0.10
rhodanese	0.28 ± 0.03	4.50 ± 0.10	0.97 ± 0.04	0.51 ± 0.03	—	—	1.58 ± 0.08	1.97 ± 0.43	0.74 ± 0.07
α-LA^a	—	—	2.75 ± 0.06	0.49 ± 0.04	—	—	2.02 ± 0.06	1.14 ± 0.08	0.59 ± 0.03

Open in a new tab

^aData from a previous study [41].

When the histograms of lifetime for bullet complexes formed after F or U were combined, we obtained the following rate constants in the presence of DM-MBP: k^BU-I = 0.31 ± 0.02 s⁻¹, k^BF-I = 0.91 ± 0.03 s⁻¹, k^BU-II = 0.53 ± 0.02 s⁻¹ and k^BF-II = 0.97 ± 0.06 s⁻¹. These values as well as those obtained in the absence of SP (table 3) are significantly smaller than those in the presence of α-LA (k^BF-I = 2.75 ± 0.06 s⁻¹ and k^BF-II = 2.02 ± 0.06 s⁻¹). Besides this prominent feature, the appearance frequency of B–U type bullet in the presence of foldable SP is very high (Type I B–U : Type I B–F ≈ 2 : 3), compared with the case in the absence of SP (Type I B–U : Type I B–F ≈ 1 : 7).

All histograms of lifetime for football complexes in the Type I process (which we refer to as Type I football) were well fitted to single-exponential functions, under all substrate conditions (figure 3d; electronic supplementary material, figures S1 and S2). The estimated rate constants (k^FB-I) for the decay of F in the process B^↑ → F → B_↓, which are only moderately affected by the substrate condition (approx. 0.56 s⁻¹), are given in table 3. On the other hand, all histograms of lifetime for football complexes in the Type II process (which we refer to as Type II football) had a peak and were well fitted to a sequential two-step reaction model (figure 3h; electronic supplementary material, figures S1 and S2). The two rate constants for the decay of F in the process B^↑ → F → B^↑ (k^FB-II₁ and k^FB-II₂) estimated by the fitting are given in table 3.

All histograms of lifetime for GroES-unbound GroEL in the Type I process (for all substrate conditions) and Type II process (only for DM-MBP) were well fitted to single-exponential functions (figure 3b,f; electronic supplementary material, figures S1 and S2). The decay U → B in the Type I process occurs very fast (k^UB-I is greater than 3.0 s⁻¹), whereas the decay in the Type II process is much slower (k^UB-II = 0.92 s⁻¹ for DM-MBP).

4. Kinetics undergone by bound GroES

Here, we first describe the Type I process in the absence of SP. When GroES binds to the trans-ring of bullet complexes, this newly bound GroES undergoes the pathway of either (i) F → B^↑ → F → B^↓ or (ii) F → B → U. When GroES binds to GroES–unbound GroEL, this newly bound GroES undergoes the pathway of either (iii) B^↑ → F → B^↓ or (iv) B → U. Pathway (i) is the main pathway. Except for case (iv) where the dissociation of the bound GroEL follows a first-order reaction, the bound GroES undergoes multiple intermediates before its final dissociation. Here, we only analysed the histogram for the residence time of bound GroES undergoing pathway (i) (electronic supplementary material, figure S1g) as the probabilities of occurrence of the pathways (ii) and (iii) were low. The histogram for the residence time of bound GroES undergoing pathway (i) was well fitted to a sequential four-step reaction, as was previously observed in the Type I process in the presence of α-LA [41]. This fitting provided k₁ = 1.64 s⁻¹, k₂ = 0.85 s⁻¹, k₃ = 1.20 s⁻¹ and k₄ = 0.57 s⁻¹. The value of k₃ is close to that of k^BF-I (=1.21 s⁻¹), while the value of k₄ is close to that of k^FB-I (=0.56 s⁻¹). Moreover, the sum of 1/k₁ and 1/k₂ (1.79 s) is identical to the lifetime of Type I football (1/k^FB-I = 1.79 s). Therefore, we performed the data fitting again under the restrictions of k₃ = k^BF-I and k₄ = k^FB-I, which provided k₁ = 1.84 ± 0.21 s⁻¹ and k₂ = 0.81 ± 0.06 s⁻¹. The fact that 1/k₁ + 1/k₂ ≈ 1/k^FB-I holds, rather than 1/k₁ + 1/k₂ ≈ 1/k^BF-I, indicates that an additional, distinct Type I football (hereafter, we express this Type I football as F*) is formed en route to the decay of football complexes to bullet complexes.

Next, we analysed the residence time distribution of bound GroES undergoing the main pathway (i) F → B^↑ → F → B^↓ in the presence of DM-MBP (figure 3k). It was well fitted to a sequential four-step reaction with rate constants of k₁ = 1.83 ± 0.21 s⁻¹, k₂ = 1.06 ± 0.07 s⁻¹, k₃ (=k^BF-I) = 0.91 ± 0.05 s⁻¹ and k₄ (= k^FB-I) = 0.67 ± 0.03 s⁻¹. The sum of 1/k₁ and 1/k₂ again coincided with 1/k^FB-I. For the bound GroES undergoing pathway (ii) F → B → U, we obtained a moderately good fitting result, when a sequential three-step reaction was assumed: k₁ = 1.65 ± 0.30 s⁻¹, k₂ = 1.20 ± 0.16 s⁻¹ and k₃ = 0.34 ± 0.02 s⁻¹ (≈ k^BU-I = 0.31 s⁻¹) (figure 3j). For bound GroES undergoing pathway (iii) B^↑ → F → B^↓, an excellent fitting result was obtained, which provided k₁ = 1.44 ± 0.04 s⁻¹, k₂ = 1.25 ± 0.03 s⁻¹ and k₃ (=k^BF-I) = 0.91 ± 0.01 s⁻¹ (figure 3i).

5. Discussion

In this study, we could confirm that football complexes are not briefly subsisting but long-lived intermediates with lifetime of 1.5−2.0 s (Type I) or 1.9−2.6 s (Type II). Therefore, football complexes must be actively involved in the chaperonin function of GroEL. However, the frequency of appearance of football complexes moderately depends on the substrate condition, in the order of unfoldable SP (67%) > absence of SP (53%) > foldable SP (30%). This is partly due to the shorter lifetime of football complexes in the presence of foldable SP, but mainly due to the longer lifetime (and hence more frequent appearance) of bullet complexes in the presence of foldable SP.

The entire reaction pathway of the GroE system revealed by its direct observation with HS-AFM is much more complicated than previously realized, and also highly stochastic as with the previously suggested partial stochasticity of the ATPase reaction in the GroE system [28]. This complexity first results from the two distinct pathways, Type I and Type II. In the latter, the alternate rhythm of binding and release of GroES at the two rings is disrupted, which often occurs (25–33%), independently of the substrate condition. Second, GroES–unbound GroEL sometimes appears after bullet complexes, especially in the presence of foldable SP (5–8%). The resulting pathway branching (either B → F or B → U) occurs independently of the intermediates (F or U) formed just before the bullet complexes. Therefore, there must be two sub-types of bullet complexes (B–F type and B–U type) in rapid equilibrium, in both Type I and Type II processes.

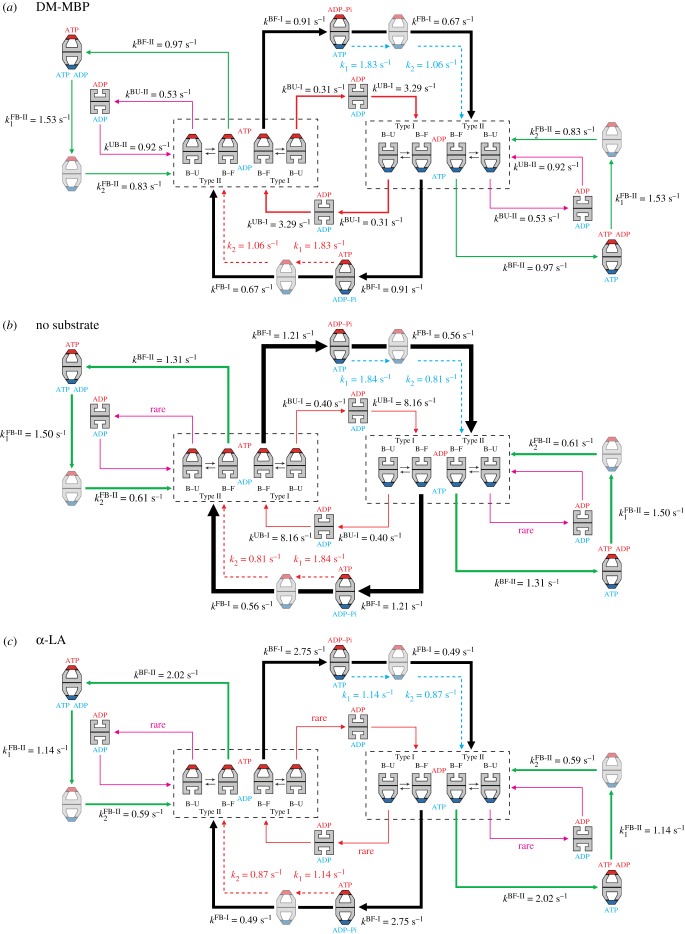
From the observed patterns of sequential GroES binding and release and the analysis of lifetime of all intermediates in each pathway and residence time of GroES, we constructed a model for the reaction scheme under each substrate condition, as shown in figure 4. The scheme in the presence of α-LA is the one modified from our previous study [41]. These schemes are partially tentative because several issues in this extremely complicated reaction are still open to clarification, as described below.

Figure 4. — Kinetic reaction schemes of GroEL–GroES interaction revealed by HS-AFM imaging under different substrate conditions. The football complexes (F*) shown in pale colours are apparently the same as but kinetically different from the football complexes formed immediately before. The thickness of arrows (shown with solid black, red, pink and green lines) along reaction pathways indicates the relative frequency of occurrence. The dashed red arrows indicate reaction processes occurring in the ring bound to GroES shown in red, while the dashed blue arrow indicates reaction processes occurring in the ring bound to GroES shown in blue. The order of k^FB-II₁ and k^FB-II₂ and the order of k₁ and k₂ are tentative. In the side pathway, the coexistence of ATP and ADP in one ring is shown but hypothetical. (a) Scheme of kinetic reaction in the presence of DM-MBP. (b) Scheme of kinetic reaction in the absence of SP. (c) Scheme of kinetic reaction in the presence of α-LA.

Although it is clear that F* occurs en route to the decay of F → B, this decay occurs twice in the main pathway of F → B^↑ → F → B^↓. Therefore, there are two possibilities: F → F* → B^↑ → F → B^↓ or F → B^↑ → F → F* → B^↓. If the former is the case, F* must originate in the newly formed (second) cis-ring of the first football complexes, rather than in the early formed (first) cis-ring of the first football complexes. One possibility is that F* is formed by an ATP-binding-induced conformational change in the second cis-ring (apical domain movement or a conformational change that can drive SP encapsulation). If F* is formed in the sequence F → B^↑ → F → F* → B^↓, one possibility is that ATP hydrolysis to ADP–Pi in the first cis-ring of the second football complexes induces the formation of F*. In this case, the rate of ATP hydrolysis into ADP–Pi in the presence of DM-MBP is 1/(1/k^FB-I + 1/k^BF-I + 1/k₁) = 0.32 s⁻¹ or 1/(1/k^FB-I + 1/k^BF-I + 1/k₂) = 0.28 s⁻¹. These values are close to the values estimated from biochemical studies in the presence of foldable SP, 0.31−0.36 s⁻¹ [35,43]. Note that the biochemically determined rate of ATP → ADP−Pi is an average over those in different pathways. Likewise, in the main pathway in the absence of SP, the rate of ATP hydrolysis into ADP−Pi can be estimated to be either 0.32 or 0.26 s⁻¹, again close to the reported values. In spite of these good agreements, we think that this is not the case because this model suggests a sequential two-step reaction for the final dissociation of bound GroES, contrary to the observed single-exponential distribution of Type I football. Therefore, it is very likely that F* originates from an ATP-binding-induced conformational change in the second cis-ring of football complexes.

Next, we discuss allosteric communications between the two rings of GroEL in the main circular pathway. The residence time analysis of bound GroES showed the coincidence of k₃ = k^BF-I, which indicates that the bound GroES on the cis-ring senses a certain change occurring in the trans-ring and vice versa. In the presence of SP, this B → F transition is accompanied by a series of events in the trans-ring: the ejection of SP, release of ADP, binding of new ATP and then GroES binding to the trans-ring. The concentration of ATP used here (2 mM) is nearly saturating, and the concentration of GroES (1 µM) is also nearly saturating, considering the second-order rate constant for GroES binding (1–3 × 10⁷ M⁻¹ s⁻¹) [44]. Therefore, this transition rate k^BF-I is identical to the rate of ADP release from the trans-ring, indicating that ADP remains bound for a while in the trans-ring, consistent with biochemical observations [45,46]. However, to alleviate the discrepancies regarding the presence of football complexes, an idea has been proposed that this ADP release retardation would occur only in the absence of SP and this negative cooperativity could be weakened in the presence of SP. Therefore, bullet complexes are accumulated in the absence of SP, whereas in the presence of SP the accelerated ADP dissociation and hence the accelerated ATP/GroES binding [27,45] leads to the formation of football complexes [26,28]. However, this idea is inconsistent with our observations. The value of k^BF-I in the absence of SP (1.21 s⁻¹) is instead somewhat larger than that in the presence of foldable SP (0.91–0.97 s⁻¹). Moreover, football complexes are formed in substantial amount (approx. 50%), even in the absence of SP. In our previous study [41], we proposed that the asymmetric bullet structure would cause a strain in the molecule and this strain would retard ADP release from the cis-ring, like the retardation of ADP release from the leading head of myosin V walking on actin filaments [39,47]. What is occurring in the cis-ring during this B → F transition? One possibility is ATP hydrolysis to ADP–Pi. The hydrolysis rate in the presence of DM-MBP calculated based on this assumption, 1/(1/k^FB-I + 1/k^BF-I) = 0.39 s⁻¹, is close to the biochemically estimated values, 0.31−0.36 s⁻¹. If this reaction does occur in the transition step, the two rings in the bullet complexes mutually communicate to suppress ATP hydrolysis in the cis-ring and ADP release from the trans-ring. Compared with the case of DM-MBP, the strength of this negative cooperativity is 30% weaker in the absence of SP and 200% weaker in the presence of α-LA, judging from the values of k^BF-I. This negative cooperativity ensures the release of SP from the trans-ring before this ring is capped with GroES. Another interpretation for k₃ = k^BF-I would be that the substrate-dependent ATP hydrolysis into ADP–Pi triggers ADP release from the opposite ring. The additional coincidence of 1/k₁ + 1/k₂ = k^FB-I also indicates an allosteric communication between the two rings. However, the ambiguity about physical or chemical events occurring in the transition steps corresponding to k₁ and k₂ prevents us from gaining insights into the nature of this communication. Nevertheless, we think that ATP-binding-induced conformational change occurring in the second cis-ring in football complexes triggers Pi release and hence GroES release from the opposite ring.

Finally, we discuss the Type II process. Type II bullet distinct from Type I bullet is responsible for the Type II process. The allosteric communication between the two rings in Type I bullet (corresponding to the coincidence of k₃ = k^BF-I) must be disrupted in the Type II process. In our previous HS-AFM study in the presence of α-LA, we proposed that the Type II process would occur due to incomplete nucleotide exchange (unlike the replacement of seven ADPs by seven ATPs) at the trans-ring of bullet complexes [41]. The disruption of the allosteric communication possibly causes partial ADP release from the trans-ring without ATP hydrolysis in the cis-ring. The reduced number of bound ATP in the new cis-ring must only induce a small conformational change in this ring, which would not be large enough to affect the opposite ring. This is consistent with the fact that the early bound GroES never dissociates in the Type II process. Nevertheless, several issues concerning the Type II process are still open to clarification. Since this process occurs to a non-negligible extent (25–33%), further studies are awaited on this process.

Supplementary Material

Supplementary Information

rstb20170180supp1.pdf^{(602.1KB, pdf)}

Data accessibility

This article has no additional data.

Authors' contributions

T.A. designed this study, developed the high-speed AFM instrument and mathematical methods to analyse the histograms of residence time of bound GroES and wrote the manuscript. D.N. prepared all samples used in this study, performed all high-speed AFM imaging experiments, and prepared all figures and tables. The final manuscript was prepared through discussions between T.A. and D.N.

Competing interests

We have no competing interests.

Funding

This work was supported by grants to T.A.: KAKENHI, Grants-in-Aid for Scientific Research (S) (no. 24227005 and no. 17H06121); KAKENHI, Grants-in-Aid for Research on Innovative Area (research in a proposed research area; no. 26119003) and CREST programme of the Japan Science and Technology Agency (no. JPMJCR13M1). This work was also supported in part by KAKENHI, Young Scientists (B) (no. 17K15433 to D.N.).

References

1.Hartl FU, Bracher A, Hayer-Hartl M. 2011. Molecular chaperones in protein folding and proteostasis. Nature 475, 324–332. ( 10.1038/nature10317) [DOI] [PubMed] [Google Scholar]
2.Hartl FU, Hayer-Hartl M. 2002. Molecular chaperones in the cytosol: from nascent chain to folded protein. Science 295, 1852–1858. ( 10.1126/science.1068408) [DOI] [PubMed] [Google Scholar]
3.Braig K, Otwinowski Z, Hegde R, Boisvert DC, Joachimiak A, Horwich AL, Sigler PB. 1994. The crystal structure of the bacterial chaperonin GroEL at 2.8 Å. Nature 371, 578–586. ( 10.1038/371578a0) [DOI] [PubMed] [Google Scholar]
4.Hunt JF, Weaver AJ, Landry S, Gierasch L, Deisenhofer J. 1996. The crystal structure of the GroES co-chaperonin at 2.8 Å resolution. Nature 379, 37–45. ( 10.1038/379037a0) [DOI] [PubMed] [Google Scholar]
5.A Horwich AL, Fenton WA. 2009. Chaperonin-mediated protein folding: using a central cavity to kinetically assist polypeptide chain folding. Q. Rev. Biophys. 42, 83–116. ( 10.1017/S0033583509004764) [DOI] [PubMed] [Google Scholar]
6.Chaudhuri TK, Verma VK, Maheshwari A. 2009. GroEL assisted folding of large polypeptide substrates in Escherichia coli: present scenario and assignments for the future. Prog. Biophys. Mol. Biol. 99, 42–50. ( 10.1016/j.pbiomolbio.2008.10.007) [DOI] [PubMed] [Google Scholar]
7.Jewett AI, Shea JE. 2010. Reconciling theories of chaperonin accelerated folding with experimental evidence. Cell. Mol. Life Sci. 67, 255–276. ( 10.1007/s00018-009-0164-6) [DOI] [PMC free article] [PubMed] [Google Scholar]
8.Clare DK, Bakkes PJ, van Heerikhuizen H, van der Vies SM, Saibil HR. 2009. Chaperonin complex with a newly folded protein encapsulated in the folding chamber. Nature 457, 107–110. ( 10.1038/nature07479) [DOI] [PMC free article] [PubMed] [Google Scholar]
9.Weissman JS, Hohl CM, Kovalenko O, Kashi Y, Chen S, Braig K, Saibil HR, Fenton WA, Norwich AL. 1995. Mechanism of GroEL action: productive release of polypeptide from a sequestered position under GroES. Cell 83, 577–587. ( 10.1016/0092-8674(95)90098-5) [DOI] [PubMed] [Google Scholar]
10.Mayhew M, da Silva AC, Martin J, Erdjument-Bromage H, Tempst P, Hartl FU. 1996. Protein folding in the central cavity of the GroEL-GroES chaperonin complex. Nature 379, 420–426. ( 10.1038/379420a0) [DOI] [PubMed] [Google Scholar]
11.Yifrach O, Horovitz A. 1995. Nested cooperativity in the ATPase activity of the oligomeric chaperonin GroEL. Biochemistry 34, 5303–5308. ( 10.1021/bi00016a001) [DOI] [PubMed] [Google Scholar]
12.Burston SG, Ranson NA, Clarke AR. 1995. The origins and consequences of asymmetry in the chaperonin reaction cycle. J. Mol. Biol. 249, 138–152. ( 10.1006/jmbi.1995.0285) [DOI] [PubMed] [Google Scholar]
13.Horovitz A, Willison KR. 2005. Allosteric regulation of chaperonins. Curr. Opin. Struct. Biol. 15, 646–651. ( 10.1016/j.sbi.2005.10.001) [DOI] [PubMed] [Google Scholar]
14.Xu Z, Horwich AL, Sigler PB. 1997. The crystal structure of the asymmetric GroEL-GroES-(ADP)₇ chaperonin complex. Nature 388, 741–750. ( 10.1038/41944) [DOI] [PubMed] [Google Scholar]
15.Rye HS, Burston SG, Fenton WA, Beechem JM, Xu Z, Sigler PB, Horwich AL. 1997. Distinct actions of cis and trans ATP within the double ring of the chaperonin GroEL. Nature 388, 792–798. ( 10.1038/42047) [DOI] [PubMed] [Google Scholar]
16.Rye HS, Roseman AM, Chen S, Furtak K, Fenton WA, Saibil HR, Horwich AL. 1999. GroEL-GroES cycling: ATP and nonnative polypeptide direct alternation of folding-active rings. Cell 97, 325–338. ( 10.1016/S0092-8674(00)80742-4) [DOI] [PubMed] [Google Scholar]
17.Schmidt M, Rutkat K, Rachel R, Pfeifer G, Jaenicke R, Viitanen P, Lorimer G, Buchner J. 1994. Symmetric complexes of GroE chaperonins as part of the functional cycle. Science 265, 656–659. ( 10.1126/science.7913554) [DOI] [PubMed] [Google Scholar]
18.Azem A, Kessel M, Goloubinoff P. 1994. Characterization of a functional GroEL₁₄(GroES₇)₂ chaperonin hetero-oligomer. Science 265, 653–656. ( 10.1126/science.7913553) [DOI] [PubMed] [Google Scholar]
19.Llorca O, Marco S, Carrascosa JL, Valpuesta JM. 1994. The formation of symmetrical GroEL-GroES complexes in the presence of ATP. FEBS Lett. 345, 181–186. ( 10.1016/0014-5793(94)00432-3) [DOI] [PubMed] [Google Scholar]
20.Beißinger M, Rutkat K, Buchner J. 1999. Catalysis, commitment and encapsulation during GroE-mediated folding. J. Mol. Biol. 289, 1075–1092. ( 10.1006/jmbi.1999.2780) [DOI] [PubMed] [Google Scholar]
21.Azem A, Diamant S, Kessel M, Weiss C, Goloubinoff P. 1995. The protein-folding activity of chaperonins correlates with the symmetric GroEL₁₄(GroES₇)₂ heterooligomer. Proc. Natl Acad. Sci. USA 92, 12 021–12 025. ( 10.1073/pnas.92.26.12021) [DOI] [PMC free article] [PubMed] [Google Scholar]
22.Sparrer H, Rutkat K, Buchner J. 1977. Catalysis of protein folding by symmetric chaperone complexes. Proc. Natl Acad. Sci. USA 94, 1096–1100. ( 10.1073/pnas.94.4.1096) [DOI] [PMC free article] [PubMed] [Google Scholar]
23.Koike-Takeshita A, Arakawa T, Taguchi H, Shimamura T. 2014. Crystal structure of a symmetric football-shaped GroEL:GroES2-ATP14 complex determined at 3.8 Å reveals rearrangement between two GroEL rings. J. Mol. Biol. 426, 3634–3641. ( 10.1016/j.jmb.2014.08.017) [DOI] [PubMed] [Google Scholar]
24.Taguchi H. 2015. Reaction cycle of chaperonin GroEL via symmetric ‘football’ intermediate. J. Mol. Biol. 427, 2912–2918. ( 10.1016/j.jmb.2015.04.007) [DOI] [PubMed] [Google Scholar]
25.Koike-Takeshita A, Yoshida M, Taguchi H. 2008. Revisiting the GroEL-GroES reaction cycle via the symmetric intermediate implied by novel aspects of the GroEL(D398A) mutant. J. Biol. Chem. 283, 23 774–23 781. ( 10.1074/jbc.M802542200) [DOI] [PMC free article] [PubMed] [Google Scholar]
26.Sameshima T, Iizuka R, Ueno T, Funatsu T. 2010. Denatured proteins facilitate the formation of the football-shaped GroEL-(GroES)₂ complex. Biochem. J. 427, 247–254. ( 10.1042/BJ20091845) [DOI] [PubMed] [Google Scholar]
27.Ye X, Lorimer GH. 2013. Substrate protein switches GroE chaperonins from asymmetric to symmetric cycling by catalyzing nucleotide exchange. Proc. Natl Acad. Sci. USA 110, E4289–E4297. ( 10.1073/pnas.1317702110) [DOI] [PMC free article] [PubMed] [Google Scholar]
28.Yang D, Ye X, Lorimer GH. 2013. Symmetric GroEL:GroES₂ complexes are the protein-folding functional form of the chaperonin nanomachine. Proc. Natl Acad. Sci. USA 110, E4298–E4305. ( 10.1073/pnas.1318862110) [DOI] [PMC free article] [PubMed] [Google Scholar]
29.Fei X, Ye X, LaRonde NA, Lorimer GH. 2014. Formation and structures of GroEL:GroES₂ chaperonin footballs, the protein-folding functional form. Proc. Natl Acad. Sci. USA 111, 12 775–12 780. ( 10.1073/pnas.1412922111) [DOI] [PMC free article] [PubMed] [Google Scholar]
30.Rye HS. 2001. Application of fluorescence resonance energy transfer to the GroEL-GroES chaperonin reaction. Methods 24, 278–288. ( 10.1006/meth.2001.1188) [DOI] [PMC free article] [PubMed] [Google Scholar]
31.Hosono K, Ueno T, Taguchu H, Motojima F, Zako T, Yoshida M, Funatsu T. 2008. Kinetic analysis of conformational changes of GroEL based on the fluorescence of tyrosine 506. Protein J. 27, 461–468. ( 10.1007/s10930-008-9157-9) [DOI] [PubMed] [Google Scholar]
32.Takei Y, Iizuka R, Ueno T, Funatsu T. 2012. Single-molecule observation of protein folding in symmetric GroEL-(GroES)₂ complexes. J. Biol. Chem. 287, 41 118–41 125. ( 10.1074/jbc.M112.398628) [DOI] [PMC free article] [PubMed] [Google Scholar]
33.Sameshima T, et al. 2010. Single-molecule study on the decay process of the football-shaped GroEL-GroES complex using zero-mode waveguides. J. Biol. Chem. 285, 23 159–23 164. ( 10.1074/jbc.M110.122101) [DOI] [PMC free article] [PubMed] [Google Scholar]
34.Taguchi H, Ueno T, Tadakuma H, Yoshida M, Funatsu T. 2001. Single-molecule observation of protein–protein interactions in the chaperonin system. Nat. Biotechnol. 19, 861–865. ( 10.1038/nbt0901-861) [DOI] [PubMed] [Google Scholar]
35.Ueno T, Taguchi H, Tadakuma H, Yoshida M, Funatsu T. 2004. GroEL mediates protein folding with a two successive timer mechanism. Mol. Cell 14, 423–434. ( 10.1016/S1097-2765(04)00261-8) [DOI] [PubMed] [Google Scholar]
36.Haldar S, Gupta AJ, Yan X, Miličić G, Hartl FU, Hayer-Hartl M. 2015. Chaperonin-assisted protein folding: relative population of asymmetric and symmetric GroEL:GroES complexes. J. Mol. Biol. 427, 2244–2255. ( 10.1016/j.jmb.2015.04.009) [DOI] [PubMed] [Google Scholar]
37.Ando T, Kodera N, Takai E, Maruyama D, Saito K, Toda A. 2001. A high-speed atomic force microscope for studying biological macromolecules. Proc. Natl Acad. Sci. USA 98, 12 468–12 472. ( 10.1073/pnas.211400898) [DOI] [PMC free article] [PubMed] [Google Scholar]
38.Ando T, Uchihashi T, Fukuma T. 2008. High-speed atomic force microscopy for nano-visualization of dynamic biomolecular processes. Prog. Surf. Sci. 83, 337–437. ( 10.1016/j.progsurf.2008.09.001) [DOI] [Google Scholar]
39.Kodera N, Yamamoto D, Ishikawa R, Ando T. 2010. Video imaging of walking myosin V by high-speed atomic force microscopy. Nature 468, 72–76. ( 10.1038/nature09450) [DOI] [PubMed] [Google Scholar]
40.Ando T, Uchihashi T, Scheuring S. 2014. Filming biomolecular processes by high-speed atomic force microscopy. Chem. Rev. 114, 3120–3188. ( 10.1021/cr4003837) [DOI] [PMC free article] [PubMed] [Google Scholar]
41.Yamamoto D, Ando T. 2016. Chaperonin GroEL-GroES functions as both alternating and non-alternating engines. J. Mol. Biol. 428, 3090–3101. ( 10.1016/j.jmb.2016.06.017) [DOI] [PubMed] [Google Scholar]
42.Takakura Y, Oka N, Kajiwara H, Tsunashima M. 2012. Engineering of novel tamavidin 2 muteins with lowered isoelectric points and lowered non-specific binding properties. J. Biosci. Bioeng. 114, 485–489. ( 10.1016/j.jbiosc.2012.06.009) [DOI] [PubMed] [Google Scholar]
43.Suzuki M, et al. 2008. Effect of the C-terminal truncation on the functional cycle of chaperonin GroEL: implication that the C-terminal region facilitates the transition from the folding-arrested to the folding-competent state. J. Biol. Chem. 283, 23 931–23 939. ( 10.1074/jbc.M804090200) [DOI] [PMC free article] [PubMed] [Google Scholar]
44.Motojima F, Chaudhry C, Fenton WA, Farr GW, Horwich AL. 2004. Substrate polypeptide presents a load on the apical domains of the chaperonin GroEL. Proc. Natl Acad. Sci. USA 101, 15 005–15 012. ( 10.1073/pnas.0406132101) [DOI] [PMC free article] [PubMed] [Google Scholar]
45.Grason JP, Gresham JS, Widjaja L, Wehri SC, Lorimer GH. 2008. Setting the chaperonin timer: the effects of K⁺ and substrate protein on ATP hydrolysis. Proc. Natl Acad. Sci. USA 105, 17 334–17 338. ( 10.1073/pnas.0807429105) [DOI] [PMC free article] [PubMed] [Google Scholar]
46.Madan D, Lin Z, Rye HS. 2008. Triggering protein folding within the GroEL-GroES complex, J. Biol. Chem. 283, 32 003–32 013. ( 10.1074/jbc.M802898200) [DOI] [PMC free article] [PubMed] [Google Scholar]
47.Purcell TJ, Sweeney HL, Spudich JA. 2005. A force-dependent state controls the coordination of processive myosin V. Proc. Natl Acad. Sci. USA 102, 13 873–13 878. ( 10.1073/pnas.0506441102) [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

rstb20170180supp1.pdf^{(602.1KB, pdf)}

Data Availability Statement

This article has no additional data.

[RSTB20170180C1] 1.Hartl FU, Bracher A, Hayer-Hartl M. 2011. Molecular chaperones in protein folding and proteostasis. Nature 475, 324–332. ( 10.1038/nature10317) [DOI] [PubMed] [Google Scholar]

[RSTB20170180C2] 2.Hartl FU, Hayer-Hartl M. 2002. Molecular chaperones in the cytosol: from nascent chain to folded protein. Science 295, 1852–1858. ( 10.1126/science.1068408) [DOI] [PubMed] [Google Scholar]

[RSTB20170180C3] 3.Braig K, Otwinowski Z, Hegde R, Boisvert DC, Joachimiak A, Horwich AL, Sigler PB. 1994. The crystal structure of the bacterial chaperonin GroEL at 2.8 Å. Nature 371, 578–586. ( 10.1038/371578a0) [DOI] [PubMed] [Google Scholar]

[RSTB20170180C4] 4.Hunt JF, Weaver AJ, Landry S, Gierasch L, Deisenhofer J. 1996. The crystal structure of the GroES co-chaperonin at 2.8 Å resolution. Nature 379, 37–45. ( 10.1038/379037a0) [DOI] [PubMed] [Google Scholar]

[RSTB20170180C5] 5.A Horwich AL, Fenton WA. 2009. Chaperonin-mediated protein folding: using a central cavity to kinetically assist polypeptide chain folding. Q. Rev. Biophys. 42, 83–116. ( 10.1017/S0033583509004764) [DOI] [PubMed] [Google Scholar]

[RSTB20170180C6] 6.Chaudhuri TK, Verma VK, Maheshwari A. 2009. GroEL assisted folding of large polypeptide substrates in Escherichia coli: present scenario and assignments for the future. Prog. Biophys. Mol. Biol. 99, 42–50. ( 10.1016/j.pbiomolbio.2008.10.007) [DOI] [PubMed] [Google Scholar]

[RSTB20170180C7] 7.Jewett AI, Shea JE. 2010. Reconciling theories of chaperonin accelerated folding with experimental evidence. Cell. Mol. Life Sci. 67, 255–276. ( 10.1007/s00018-009-0164-6) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSTB20170180C8] 8.Clare DK, Bakkes PJ, van Heerikhuizen H, van der Vies SM, Saibil HR. 2009. Chaperonin complex with a newly folded protein encapsulated in the folding chamber. Nature 457, 107–110. ( 10.1038/nature07479) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSTB20170180C9] 9.Weissman JS, Hohl CM, Kovalenko O, Kashi Y, Chen S, Braig K, Saibil HR, Fenton WA, Norwich AL. 1995. Mechanism of GroEL action: productive release of polypeptide from a sequestered position under GroES. Cell 83, 577–587. ( 10.1016/0092-8674(95)90098-5) [DOI] [PubMed] [Google Scholar]

[RSTB20170180C10] 10.Mayhew M, da Silva AC, Martin J, Erdjument-Bromage H, Tempst P, Hartl FU. 1996. Protein folding in the central cavity of the GroEL-GroES chaperonin complex. Nature 379, 420–426. ( 10.1038/379420a0) [DOI] [PubMed] [Google Scholar]

[RSTB20170180C11] 11.Yifrach O, Horovitz A. 1995. Nested cooperativity in the ATPase activity of the oligomeric chaperonin GroEL. Biochemistry 34, 5303–5308. ( 10.1021/bi00016a001) [DOI] [PubMed] [Google Scholar]

[RSTB20170180C12] 12.Burston SG, Ranson NA, Clarke AR. 1995. The origins and consequences of asymmetry in the chaperonin reaction cycle. J. Mol. Biol. 249, 138–152. ( 10.1006/jmbi.1995.0285) [DOI] [PubMed] [Google Scholar]

[RSTB20170180C13] 13.Horovitz A, Willison KR. 2005. Allosteric regulation of chaperonins. Curr. Opin. Struct. Biol. 15, 646–651. ( 10.1016/j.sbi.2005.10.001) [DOI] [PubMed] [Google Scholar]

[RSTB20170180C14] 14.Xu Z, Horwich AL, Sigler PB. 1997. The crystal structure of the asymmetric GroEL-GroES-(ADP)₇ chaperonin complex. Nature 388, 741–750. ( 10.1038/41944) [DOI] [PubMed] [Google Scholar]

[RSTB20170180C15] 15.Rye HS, Burston SG, Fenton WA, Beechem JM, Xu Z, Sigler PB, Horwich AL. 1997. Distinct actions of cis and trans ATP within the double ring of the chaperonin GroEL. Nature 388, 792–798. ( 10.1038/42047) [DOI] [PubMed] [Google Scholar]

[RSTB20170180C16] 16.Rye HS, Roseman AM, Chen S, Furtak K, Fenton WA, Saibil HR, Horwich AL. 1999. GroEL-GroES cycling: ATP and nonnative polypeptide direct alternation of folding-active rings. Cell 97, 325–338. ( 10.1016/S0092-8674(00)80742-4) [DOI] [PubMed] [Google Scholar]

[RSTB20170180C17] 17.Schmidt M, Rutkat K, Rachel R, Pfeifer G, Jaenicke R, Viitanen P, Lorimer G, Buchner J. 1994. Symmetric complexes of GroE chaperonins as part of the functional cycle. Science 265, 656–659. ( 10.1126/science.7913554) [DOI] [PubMed] [Google Scholar]

[RSTB20170180C18] 18.Azem A, Kessel M, Goloubinoff P. 1994. Characterization of a functional GroEL₁₄(GroES₇)₂ chaperonin hetero-oligomer. Science 265, 653–656. ( 10.1126/science.7913553) [DOI] [PubMed] [Google Scholar]

[RSTB20170180C19] 19.Llorca O, Marco S, Carrascosa JL, Valpuesta JM. 1994. The formation of symmetrical GroEL-GroES complexes in the presence of ATP. FEBS Lett. 345, 181–186. ( 10.1016/0014-5793(94)00432-3) [DOI] [PubMed] [Google Scholar]

[RSTB20170180C20] 20.Beißinger M, Rutkat K, Buchner J. 1999. Catalysis, commitment and encapsulation during GroE-mediated folding. J. Mol. Biol. 289, 1075–1092. ( 10.1006/jmbi.1999.2780) [DOI] [PubMed] [Google Scholar]

[RSTB20170180C21] 21.Azem A, Diamant S, Kessel M, Weiss C, Goloubinoff P. 1995. The protein-folding activity of chaperonins correlates with the symmetric GroEL₁₄(GroES₇)₂ heterooligomer. Proc. Natl Acad. Sci. USA 92, 12 021–12 025. ( 10.1073/pnas.92.26.12021) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSTB20170180C22] 22.Sparrer H, Rutkat K, Buchner J. 1977. Catalysis of protein folding by symmetric chaperone complexes. Proc. Natl Acad. Sci. USA 94, 1096–1100. ( 10.1073/pnas.94.4.1096) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSTB20170180C23] 23.Koike-Takeshita A, Arakawa T, Taguchi H, Shimamura T. 2014. Crystal structure of a symmetric football-shaped GroEL:GroES2-ATP14 complex determined at 3.8 Å reveals rearrangement between two GroEL rings. J. Mol. Biol. 426, 3634–3641. ( 10.1016/j.jmb.2014.08.017) [DOI] [PubMed] [Google Scholar]

[RSTB20170180C24] 24.Taguchi H. 2015. Reaction cycle of chaperonin GroEL via symmetric ‘football’ intermediate. J. Mol. Biol. 427, 2912–2918. ( 10.1016/j.jmb.2015.04.007) [DOI] [PubMed] [Google Scholar]

[RSTB20170180C25] 25.Koike-Takeshita A, Yoshida M, Taguchi H. 2008. Revisiting the GroEL-GroES reaction cycle via the symmetric intermediate implied by novel aspects of the GroEL(D398A) mutant. J. Biol. Chem. 283, 23 774–23 781. ( 10.1074/jbc.M802542200) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSTB20170180C26] 26.Sameshima T, Iizuka R, Ueno T, Funatsu T. 2010. Denatured proteins facilitate the formation of the football-shaped GroEL-(GroES)₂ complex. Biochem. J. 427, 247–254. ( 10.1042/BJ20091845) [DOI] [PubMed] [Google Scholar]

[RSTB20170180C27] 27.Ye X, Lorimer GH. 2013. Substrate protein switches GroE chaperonins from asymmetric to symmetric cycling by catalyzing nucleotide exchange. Proc. Natl Acad. Sci. USA 110, E4289–E4297. ( 10.1073/pnas.1317702110) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSTB20170180C28] 28.Yang D, Ye X, Lorimer GH. 2013. Symmetric GroEL:GroES₂ complexes are the protein-folding functional form of the chaperonin nanomachine. Proc. Natl Acad. Sci. USA 110, E4298–E4305. ( 10.1073/pnas.1318862110) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSTB20170180C29] 29.Fei X, Ye X, LaRonde NA, Lorimer GH. 2014. Formation and structures of GroEL:GroES₂ chaperonin footballs, the protein-folding functional form. Proc. Natl Acad. Sci. USA 111, 12 775–12 780. ( 10.1073/pnas.1412922111) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSTB20170180C30] 30.Rye HS. 2001. Application of fluorescence resonance energy transfer to the GroEL-GroES chaperonin reaction. Methods 24, 278–288. ( 10.1006/meth.2001.1188) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSTB20170180C31] 31.Hosono K, Ueno T, Taguchu H, Motojima F, Zako T, Yoshida M, Funatsu T. 2008. Kinetic analysis of conformational changes of GroEL based on the fluorescence of tyrosine 506. Protein J. 27, 461–468. ( 10.1007/s10930-008-9157-9) [DOI] [PubMed] [Google Scholar]

[RSTB20170180C32] 32.Takei Y, Iizuka R, Ueno T, Funatsu T. 2012. Single-molecule observation of protein folding in symmetric GroEL-(GroES)₂ complexes. J. Biol. Chem. 287, 41 118–41 125. ( 10.1074/jbc.M112.398628) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSTB20170180C33] 33.Sameshima T, et al. 2010. Single-molecule study on the decay process of the football-shaped GroEL-GroES complex using zero-mode waveguides. J. Biol. Chem. 285, 23 159–23 164. ( 10.1074/jbc.M110.122101) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSTB20170180C34] 34.Taguchi H, Ueno T, Tadakuma H, Yoshida M, Funatsu T. 2001. Single-molecule observation of protein–protein interactions in the chaperonin system. Nat. Biotechnol. 19, 861–865. ( 10.1038/nbt0901-861) [DOI] [PubMed] [Google Scholar]

[RSTB20170180C35] 35.Ueno T, Taguchi H, Tadakuma H, Yoshida M, Funatsu T. 2004. GroEL mediates protein folding with a two successive timer mechanism. Mol. Cell 14, 423–434. ( 10.1016/S1097-2765(04)00261-8) [DOI] [PubMed] [Google Scholar]

[RSTB20170180C36] 36.Haldar S, Gupta AJ, Yan X, Miličić G, Hartl FU, Hayer-Hartl M. 2015. Chaperonin-assisted protein folding: relative population of asymmetric and symmetric GroEL:GroES complexes. J. Mol. Biol. 427, 2244–2255. ( 10.1016/j.jmb.2015.04.009) [DOI] [PubMed] [Google Scholar]

[RSTB20170180C37] 37.Ando T, Kodera N, Takai E, Maruyama D, Saito K, Toda A. 2001. A high-speed atomic force microscope for studying biological macromolecules. Proc. Natl Acad. Sci. USA 98, 12 468–12 472. ( 10.1073/pnas.211400898) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSTB20170180C38] 38.Ando T, Uchihashi T, Fukuma T. 2008. High-speed atomic force microscopy for nano-visualization of dynamic biomolecular processes. Prog. Surf. Sci. 83, 337–437. ( 10.1016/j.progsurf.2008.09.001) [DOI] [Google Scholar]

[RSTB20170180C39] 39.Kodera N, Yamamoto D, Ishikawa R, Ando T. 2010. Video imaging of walking myosin V by high-speed atomic force microscopy. Nature 468, 72–76. ( 10.1038/nature09450) [DOI] [PubMed] [Google Scholar]

[RSTB20170180C40] 40.Ando T, Uchihashi T, Scheuring S. 2014. Filming biomolecular processes by high-speed atomic force microscopy. Chem. Rev. 114, 3120–3188. ( 10.1021/cr4003837) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSTB20170180C41] 41.Yamamoto D, Ando T. 2016. Chaperonin GroEL-GroES functions as both alternating and non-alternating engines. J. Mol. Biol. 428, 3090–3101. ( 10.1016/j.jmb.2016.06.017) [DOI] [PubMed] [Google Scholar]

[RSTB20170180C42] 42.Takakura Y, Oka N, Kajiwara H, Tsunashima M. 2012. Engineering of novel tamavidin 2 muteins with lowered isoelectric points and lowered non-specific binding properties. J. Biosci. Bioeng. 114, 485–489. ( 10.1016/j.jbiosc.2012.06.009) [DOI] [PubMed] [Google Scholar]

[RSTB20170180C43] 43.Suzuki M, et al. 2008. Effect of the C-terminal truncation on the functional cycle of chaperonin GroEL: implication that the C-terminal region facilitates the transition from the folding-arrested to the folding-competent state. J. Biol. Chem. 283, 23 931–23 939. ( 10.1074/jbc.M804090200) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSTB20170180C44] 44.Motojima F, Chaudhry C, Fenton WA, Farr GW, Horwich AL. 2004. Substrate polypeptide presents a load on the apical domains of the chaperonin GroEL. Proc. Natl Acad. Sci. USA 101, 15 005–15 012. ( 10.1073/pnas.0406132101) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSTB20170180C45] 45.Grason JP, Gresham JS, Widjaja L, Wehri SC, Lorimer GH. 2008. Setting the chaperonin timer: the effects of K⁺ and substrate protein on ATP hydrolysis. Proc. Natl Acad. Sci. USA 105, 17 334–17 338. ( 10.1073/pnas.0807429105) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSTB20170180C46] 46.Madan D, Lin Z, Rye HS. 2008. Triggering protein folding within the GroEL-GroES complex, J. Biol. Chem. 283, 32 003–32 013. ( 10.1074/jbc.M802898200) [DOI] [PMC free article] [PubMed] [Google Scholar]

[RSTB20170180C47] 47.Purcell TJ, Sweeney HL, Spudich JA. 2005. A force-dependent state controls the coordination of processive myosin V. Proc. Natl Acad. Sci. USA 102, 13 873–13 878. ( 10.1073/pnas.0506441102) [DOI] [PMC free article] [PubMed] [Google Scholar]

PERMALINK

Substrate protein dependence of GroEL–GroES interaction cycle revealed by high-speed atomic force microscopy imaging

Daisuke Noshiro

Toshio Ando

Abstract

1. Introduction

2. Intermediates and reaction patterns