A non-equilibrium approach to allosteric communication

Abstract

While the theory of protein folding is well developed, including concepts such as rugged energy landscape, folding funnel, etc., the same degree of understanding has not been reached for the description of the dynamics of allosteric transitions in proteins. This is not only due to the small size of the structural change upon ligand binding to an allosteric site, but also due to challenges in designing experiments that directly observe such an allosteric transition. On the basis of recent pump-probe-type experiments (Buchli et al. 2013 Proc. Natl Acad. Sci. USA 110, 11 725–11 730. (doi:10.1073/pnas.1306323110)) and non-equilibrium molecular dynamics simulations (Buchenberg et al. 2017 Proc. Natl Acad. Sci. USA 114, E6804–E6811. (doi:10.1073/pnas.1707694114)) studying an photoswitchable PDZ2 domain as model for an allosteric transition, we outline in this perspective how such a description of allosteric communication might look. That is, calculating the dynamical content of both experiment and simulation (which agree remarkably well with each other), we find that allosteric communication shares some properties with downhill folding, except that it is an ‘order–order’ transition. Discussing the multiscale and hierarchical features of the dynamics, the validity of linear response theory as well as the meaning of ‘allosteric pathways’, we conclude that non-equilibrium experiments and simulations are a promising way to study dynamical aspects of allostery.

This article is part of a discussion meeting issue ‘Allostery and molecular machines’.

1. Introduction

Describing the puzzling phenomenon of long-range communication between distant protein sites, allostery has been intensively studied in experiment and computation [1–9]. In spite of its importance as an elementary process of cell signalling as well as a target in pharmaceutical research, there is surprisingly little known about the underlying dynamical process of allosteric communication. Most commonly, allostery is related to the binding of a ligand to the allosteric site, which triggers the conformational change at a distant site of the protein. This so-called ‘allosteric transition’, however, has been rarely observed directly, in part because of the smallness of the structural changes, the experimental challenges to observe transition pathways and also because of the time-scale limitations of molecular dynamics (MD) simulations [10–14]. This situation is in striking variance to the protein folding problem, where several decades of theoretical and experimental work have resulted in a quite well-established picture of how folding and unfolding proceed [15]. This includes general scenarios such as two-state and downhill folding [16,17], dynamical mechanisms such as zipping or diffusion-limited processes [15], as well as a wealth of theoretical formulations, including the concepts of rugged energy landscapes and folding funnel [18,19] or Markov state models [20]. In comparison, a dynamical picture of the allosteric transition appears to be still in its infancy.

With ‘dynamics’, we here do not refer to the rates of ligand binding and unbinding, k_on and k_off, respectively. These rates represent very well-established concepts in biochemistry, as their ratio is related to the binding free energy via k_on/k_off = e^−ΔG/k_BT. With ‘dynamics’, we also do not mean equilibrium fluctuations, which are discussed as another possible mechanism of allostery with essentially no structural changes [21,22]. Rather, with ‘dynamics’ we refer to the non-equilibrium response that transfers a signal within an allosteric protein, triggered by ligand binding or unbinding. However, most experiments and theories of allostery have focused on equilibrium systems, i.e. the starting and end states of an allosteric transition, hence they cannot say much about possible intermediates.

The direct observation of non-equilibrium processes in an allosteric protein requires us to define a starting point (say, time t = 0) and a time-dependent observable describing the progress of the process. These requirements are naturally provided in a pump-probe-type experiment, in which an allosteric transition is triggered by light on a timescale that is fast compared with any biologically relevant timescale. In the realm of femtochemistry [23], that makes the difference between ‘kinetics’, which in essence is an equilibrium concept (as k_on/k_off = e^−ΔG/k_BT), and non-equilibrium ‘dynamics’. Designing photoswitchable proteins is one possible approach to achieve a phototriggerable system (besides temperature- [24,25] and pH-jumps [26,27]), which has already been applied to the protein folding problem [28–30]. In the context of allostery, this approach was recently demonstrated experimentally by Buchli et al. [31] and computationally by Buchenberg et al. [32] for a PDZ2 domain.

PDZ domains have been studied extensively as model systems for allosteric communication [33–36]. They represent an important class of protein interaction modules that are involved in the regulation of multiple receptor-coupled signal transduction processes. They share a common fold, which consists of two α-helices and six β-strands, with the second α-helix and the second β-strand forming the canonical binding groove (figure 1), and generally bind the C-terminus of their targets. One particularly illustrative example is the PDZ3 domain from PSD-95, which has a short additional third α-helix at the C-terminus. It has been shown that the removal of that helix, or its unfolding upon phosphorylation, significantly reduces the ligand binding affinity [34]. Here, we focus on the simpler PDZ2 domain from human tyrosine-phosphatase 1E (hPTP1E), which lacks that additional α-helix, but which has been demonstrated to possess allosteric properties as well [33], albeit not in the sense of functional allostery between two ligands. Both the PDZ2 and the PDZ3 domain have been studied, in particular, with regard to intramolecular signaling pathways [37–42], but the nature of the allosteric interaction remains a matter of debate. While they are discussed as examples for a modulated side-chain dynamics being responsible for the allosteric mechanism [33,34,43,44], ligand binding to the PFZ2 domain also results in a small but measurable structural change of about 0.5 Å RMSD [45].

Figure 1.

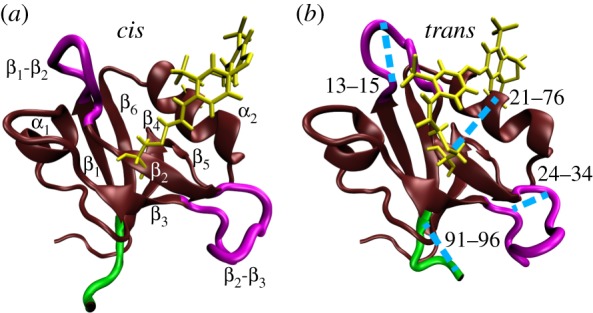
MD snapshots of PDZ2 in cis (a) and trans (b) equilibrium states, showing α-helices and β-sheets in brown, loop regions in purple, the C-terminal in green, and the azobenzene photoswitch including linker atoms in yellow. In a, labels indicate the regions β₁ (residues 6–12), β₂ (20–23), β₃ (35–40), α₁ (45–49), β₄ (57–61), β₅ (64–65), α₂ (73–80) and β₆ (84–90). Important loops connecting these regions include β₁-β₂ (13–19), β₂-β₃ (24–34), β₃-α₁ (41–44) and α₂-β₆ (81–83). In b, the blue lines indicate selected Cα-distances which characterize the conformational transition following cis–trans photoisomerization of PDZ2. Adapted with permission from Buchenberg et al. [32].

To explore in real time how such a structural change propagates through the protein, Buchli et al. [31] have covalently linked an azobenzene photoswitch across the binding groove of PDZ2 and used an ultrafast laser pulse that effects cis → trans photoisomerization of azobenzene. This results in a photoinduced opening of the binding pocket, which structurally mimics the apo-to-ligand-bound transition of native PDZ2 (figure 1). The latter has been verified with the help of NMR structure analysis of the starting and end points of the photoinduced transition [31], that is structurally very similar to the apo and ligand-bound structure of native PDZ2 [45]. Employing ultrafast time-resolved vibrational spectroscopy, they showed that the conformational rearrangement of the photoswitchable protein occurs on various timescales from pico- to microseconds in a highly non-exponential manner. The subsequent detailed MD study of the non-equilibrium dynamics by Buchenberg et al. [32] reproduced many of these findings and revealed a microscopic picture of the process.

Based on these experimental and computational works, in this perspective we want to outline a time-dependent non-equilibrium description of the dynamical process of allostery. Employing a time-scale analysis to reveal the ‘dynamical content’ [46–50] of the spectroscopic time traces as well as of the computed intramolecular Cα-distances of the protein, we investigate the origin of the non-exponential kinetics and overshootings exhibited by these observables. In particular, we identify three physically distinct phases of the time evolution, describing elastic response (≲0.1 ns), inelastic reorganization (approx. 100 ns) and structural relaxation (≳1 μs), and explain the dynamics in terms of the free-energy landscape of the allosteric transition. Issues such as the similarity to the ‘strange kinetics’ observed in downhill folding [51,52] as well as the interpretation of allosteric pathways [5,53] are discussed.

2. Real-time observation of the allosteric transition

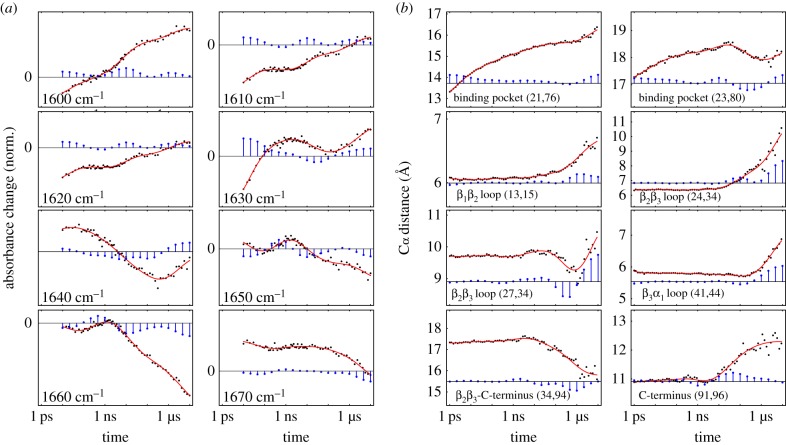
As a first impression of the time-resolved response of PDZ2 upon photoswitching, figure 2a displays results of the transient infrared (IR) experiment of Buchli et al. [31] at selected frequencies ω across the amide I band. As the corresponding C=O vibrators of the protein backbone are coupled among each other, the amide I band depends, in a rather indirect way, on the structure of the protein [54]. While it is usually not possible to infer detailed structural changes from the transient amide I spectrum, the various timescales of the process can still be determined. To that end, we show cuts of the transient IR difference spectrum and represent the resulting time traces s_ω(t) on a logarithmic time axis. The logarithmic scale represents an exponential decay with a single decay time τ by a sigmoidal-type shape, i.e. a smoothed step function around τ. Evidently, the time traces s_ω(t) in figure 2a do not exhibit one or a few well-defined decay times. Rather they show a whole spectrum of timescales, covering six decades in time from 10 ps to 10 μs.

Figure 2.

Time-dependent description of the structural response of a photoswitchable PDZ2 domain, using a logarithmic scale for the time axis. (a) Normalized transient IR time traces (black circles and red fits) across the amide I band in steps of 10 cm⁻¹, which are reproduced from Buchli et al. [31]. Owing to the limited time resolution, there are no experimental data for the first decade. (b) Time evolution (black circles and red fits) of selected Cα-distances of PDZ2, obtained from non-equilibrium MD simulations by Buchenberg et al. [32]. Blue bars indicate the associated dynamical content of experimental and MD data, i.e. the weight of timescale τ_i in a multiexponential response function. Adapted with permission from Buchli et al. [31] and Buchenberg et al. [32]. (Online version in colour.)

To facilitate a quantitative analysis, we define for each time trace a ‘dynamical content’ D_ω(τ_i), which is a probability distribution of the amount of dynamics occurring at timescale τ_i [46–49]. To this end, we perform a fit of s_ω(t) to a multiexponential response function (equation (6.1)), that assigns to each timescale τ_i a weight (or amplitude), the negative of which is the dynamical content (see Methods for details). Depending on the detection frequency, we can find in figure 2a virtually any decay time in the IR spectral response. Moreover, almost all time traces show one or even two ‘overshootings’ of the signal, which in some cases (e.g. for ω = 1630 and 1640 cm⁻¹) are quite prominent.

To comprise the above time-scale analysis in a single plot, figure 3a shows the ‘averaged dynamical content’ D(τ_i) (equation (6.2)) of the experimental data. Interestingly, the time-scale distribution reveals three well-defined maxima at 10 ps, 10 ns and 10 μs, with the first and last being at the boundaries of the distribution. It should be mentioned that the 10 ps process probably contains significant contributions from heating of the protein induced by the photoswitching, which is reflected in the IR spectra but does not necessarily affect the structure of the protein on that timescale [55,56]. The fact that D(τ_i) still rises at the maximum timescale considered indicates that the process is not quite completed within 10 μs. On the other hand, the similarity of the transient difference spectrum at 10 μs with the FTIR difference spectrum seems to suggest that the process is in fact almost completed [31].

Figure 3.

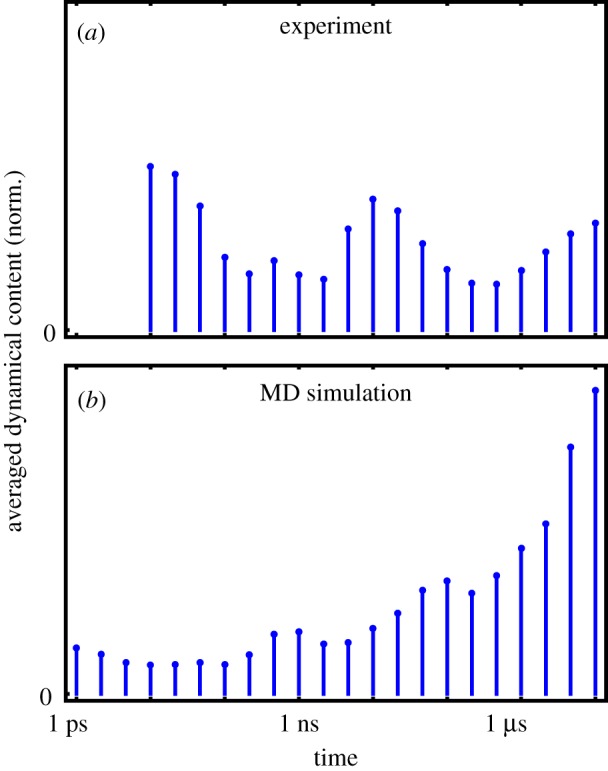
Averaged dynamical content D(τ_i) as a function of time constant τ_i, pertaining to (a) all available transient IR time traces from the experimental data [31] and (b) the time evolution of all Cα-distances from the MD data [32]. (Online version in colour.)

To facilitate a direct simulation of the above-described time-resolved experiments, Buchenberg et al. [32] performed non-equilibrium MD simulations of the allosteric transition in the PDZ2 domain. By mimicking the initial cis trans photoisomerization of the azobenzene photoswitch via a potential-energy surface switching method [57], 100 non-equilibrium trajectories of 1 μs length were generated, of which 20 randomly selected were extended to 10 μs. Performing an ensemble average to calculate time-dependent observables, photoinduced structural changes of PDZ2 were described in terms of the time evolution of backbone dihedral angles, residue–residue contacts and Cα-distances between residues. To conduct a time-scale analysis of the non-equilibrium MD data in a similar vein as done for the experimental results, here we focus on the time evolution of Cα-distances d_i,j(t) between residues i and j.

While a comprehensive collection of Cα-distances naturally yields a detailed description of the conformational dynamics, it is instructive to focus on a few representative coordinates that illustrate various important motions associated with the structural transition in PDZ2. Starting from the anchor residues of the photoswitch, the photoinduced structural perturbation is expected to propagate via various intermediate secondary structure segments to the C-terminus, chosen here as an example of a region that is quite remote from the perturbation. In this way, one finds that the relatively rigid α-helices and β-sheets of PDZ2 undergo only small modifications, while the flexible loops of the system, in particular β₁β₂ and β₂β₃, exhibit significant changes of numerous residue–residue contacts and backbone dihedral angles [58]. As representative examples, figure 2b shows Cα-distances d_i,j(t) that reflect the opening of the binding pocket (for (i, j) = (21, 76) and (23,80)) as well as conformational rearrangements of loops β₁β₂ (13,15), β₂β₃ (24,34), (27,34) and β₃α₁ (41,44). The response of the C-terminus is illustrated by its distance to β₂β₃ (34,94) and its end-to-end distance (91,96). A structural illustration of some of these distances is provided in figure 1.

Similar to the experimental results, we find that the MD time traces shown in figure 2b cover all timescales, from pico- to microseconds. As may be expected, we find picosecond dynamics mainly in the observables d_21,76 and d_23,80 describing the initial rearrangement around the binding pocket. That fast process, however, is somewhat artificial, as it is induced by the strong force applied by the photoswitch and therefore would not happen in the same way upon ligand binding/unbinding in the native system [59]. (For example, the sheer event of unbinding of a ligand takes on the order of 1 ns already [60].) On the other hand, structural dynamics on nano- and microsecond timescales is observed in all observables. Moreover, the MD time traces exhibit peculiar overshootings, e.g. (27,34), again quite similar to experiments.

Comparing the averaged dynamical content of the MD data (comprising 4650 Cα-distances, figure 3b) with experimental findings (figure 3a), we notice that the MD results also reveal maxima at the boundaries of the distribution. Because only relatively few Cα-distances report on the picosecond response of the binding pocket, the lower boundary maximum for MD is not very pronounced in the averaged dynamical content. Moreover, we find weak maxima around 1 and 100 ns, which are similar but not identical to the experimental results. Owing to the different nature of the observables, IR spectra and Cα-distances in fact are expected to represent different projections of the time-dependent structural evolution of the system. While the same timescales are present, the amplitudes of these timescales may, therefore, be different for experimental and MD data.

As indicated by the experimental averaged dynamical content shown in figure 3a, the photoinduced response of PDZ2 appears to occur in three phases which are characterized by timescales of 10 ps, 10 ns and 10 μs, respectively. Considering the overall similarity of IR and MD time traces with respect to timescales and general features (such as overshootings), in the following we assume that the non-equilibrium MD simulations provide at least a qualitative description of the allosteric transition in PDZ2. This allows us to exploit these simulations in order to develop a microscopic understanding of the underlying dynamical processes. Proceeding this way, Buchenberg et al. [32] identified the three phases of the structural transition as elastic response (≲0.1 ns), inelastic reorganization (approx. 100 ns) and structural relaxation (≳1 μs) of PDZ2, which are briefly described in the following.

Accounting for the initial process, the elastic phase describes the photoinduced opening of the binding pocket as described by the Cα-distance d_21,76. As shown in figure 2b, the time-dependent average value d_21,76(t) increases within 1 μs by approximately 0.3 nm, with the first half of the increase occurring within only 0.1 ns. Because this initial expansion of the binding pocket hardly involves conformational transitions including the crossing of free-energy barriers, the protein would elastically return to the initial state if the azobenzene switched back to its cis configuration. Hence, the first phase accounts for the elastic response of the protein. During the first tens of picoseconds, we also observe the dissipation of photoinduced excess kinetic energy, i.e. the cooling of PDZ2 to the solvent temperature [56,61].

The subsequent expansion of the binding pocket on a nanosecond timescale and the propagation of this conformational change via the adjacent β₁β₂ and β₂β₃ loops, however, require an inelastic rearrangement of the protein. As representative observables monitoring this second phase of the protein's response, figure 2b shows Cα-distances d_23,80, d_13,15, d_24,34 and d_27,34, which reflect these conformational rearrangements. The overshootings of d_23,80 and d_27,34 reflect complex reorganization of the binding pocket and the making and breaking of interresidue contacts, respectively [32]. Eventually, the structural changes of β₁β₂ and β₂β₃ extend via various ways to the distant C-terminal region, e.g. via contacts of β₂β₃ and the C-terminal loop (see the contact formation revealed by d_34,94(t)). Described by its end-to-end distance, d_91,96, the response of the C-terminus is seen to be delayed until approximately 10 ns, when d_91,96(t) starts to increase on a 100 ns timescale. Hence, we find that the inelastic phase begins on a timescale of a few nanoseconds and leads to a significant structural reorganization of PDZ2 on a 100 ns timescale.

The qualitative changes of the time evolution of most observables in figure 2b for t ≳ 1 μs indicate a new phase of structural dynamics. This third and final phase of the structural response of PDZ2 is found to describe the relaxation of the non-equilibrium conformational distribution towards the trans equilibrium state [32]. Employing density-based clustering [62] of the time-dependent structural distribution, this relaxation process has been shown to occur in a hierarchical way [63–65]. That is, we find that the relatively fast (100 ns) motion of the conformational reorganization in phase 2 represents a prerequisite of the slow (10 μs) structural relaxation in phase 3.

3. Free-energy landscape of the allosteric transition

While we have so far explained allosteric communication as a series of local structural changes, it is important to note that these changes do not necessarily occur in a directed sequence as in a falling row of dominoes, except for the fact that everything follows upon the initial 1 ps process around the binding pocket. Beyond that 1 ps process, similar timescales are found in figure 2b for all observables, regardless of whether they are close to or far away from the effector site. For example, the remote C-terminus settles already between approximately 100 ns and 1 μs (see d_91,96 and d_34,94 in figure 2b), significantly earlier than the binding pocket itself (d_21,76 and d_23,80 in figure 2b). Also the ensemble-averaged structural evolution seems to suggest that on all timescales numerous steps happen simultaneously.

To further investigate this notion, we change to a global view of the dynamics and perform a dihedral angle principal component analysis [66,67] of the cis and trans equilibrium trajectories. The well-established approach achieves an efficient dimensionality reduction of the high-dimensional atomic motion to a low-dimensional reaction coordinate that subsequently can be used for the interpretation of the considered process [68]. Employing the first two principal components PC1 and PC2 that reflect the largest variance of the protein motion, figure 4a shows the resulting cis and trans free-energy landscapes ΔG = − k_BT ln P(PC1, PC2), which can be directly obtained from the probability distribution P along these coordinates. We find that the cis and trans conformations are well separated along the first principal component, while the second principal component accounts for the conformational heterogeneity of the β₁β₂ and β₂β₃ loops. As a consequence, the latter is important for the description of the structural reorganization of these loops during the second phase of the allosteric transition.

Figure 4.

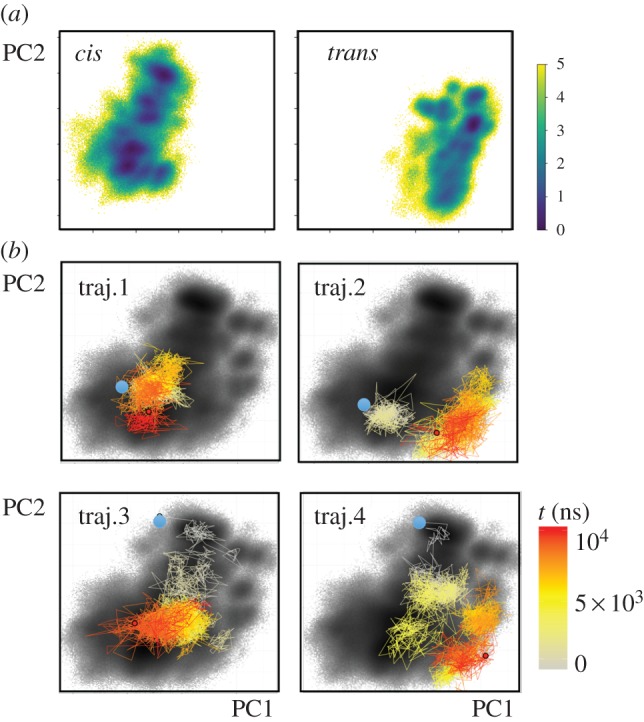
Two-dimensional representation of the free-energy landscape ΔG (in units of k_BT), plotted as a function of the first two principal components PC1 and PC2. (a) Energy landscapes associated with the cis and trans equilibrium states of PDZ2. (b) Free-energy landscape associated with the non-equilibrium allosteric transition, drawn as black background. The coloured lines indicate the time evolution of selected single non-equilibrium trajectories. Adapted with permission from Buchenberg et al. [32].

By calculating the probability distribution of all non-equilibrium trajectories, we may also define a free-energy landscape associated with the non-equilibrium evolution [32]. Figure 4b shows that this non-equilibrium energy surface overlaps well with the landscapes of the cis and trans equilibrium states, which suggests that our (up to 10 μs long) trajectories may be sufficient to cover a considerable part of the overall conformational transition. In the following, we adopt this representation to study the behaviour of single trajectories of the non-equilibrium simulation. Showing the colour-coded time evolution of four representative non-equilibrium trajectories in PC1–PC2 space, figure 4b reveals that all examples are vastly different, indicating a substantial structural diversity of the allosteric transition. Structural analyses show that these changes do not necessarily correspond to a directed sequence along certain residues, but may also occur non-locally. That is, if a protein contains rather rigid segments (such as the β barrel of PDZ domains), the initially applied conformational stress may directly propagate to distant sites and cause a structural change there. The feasibility of non-local and multiple simultaneous structural changes along a single trajectory together with the substantial heterogeneity found for different trajectories clearly suggest that the commonly used term ‘allosteric pathway’ should not be taken literally as in a falling row of dominoes [5,53].

Another interesting observation from figure 4 is the frequent changes and back-crossings of the trajectories between neighbouring conformations, which resemble a diffusive motion on the free-energy landscape, similar to that discussed for protein folding [18,19]. Rather than the conventional picture of two-state folding with a dominant free-energy barrier giving rise to single exponential kinetics, the structural rearrangements underlying allosteric communication resemble to a certain extent a ‘downhill folding’ scenario [16–18,51,52]. Proceeding from high-energy unfolded conformations to low-energy native states without passing major (say, ≳3 k_BT) free-energy barriers, downhill folders may exhibit numerous significantly populated conformational states that are connected by a large number of transition pathways. This structural and dynamical heterogeneity typically leads to highly non-exponential kinetics, which is what we see in figure 2. Just like for proteins that are characterized as downhill-folders [47], the dynamical content of figures 2 and 3 contains a continuum of timescales with some substructure, but without any clear gap that would indicate a separation of timescales between the crossing of a dominant barrier and the dynamics within free-energy basins. However, different from the protein folding problem, the system first evolves from an ordered initial state into a disordered ensemble, before it again relaxes into a relatively ordered final state, as evidenced by the relatively narrow cis and trans equilibrium free-energy surfaces (figure 4a) and the much wider non-equilibrium distribution (figure 4b). In this sense, allosteric communication may be considered as an ‘order–order’ transition.

4. Equilibrium versus non-equilibrium description

It is interesting to compare the above non-equilibrium approach with the more common equilibrium description of the structural dynamics associated with the allosteric transition. As prime examples of the latter, NMR experiments as well as MD simulations have observed significant changes of the equilibrium dynamics upon an allosteric transition [1,2,69,70]. These changes have been discussed as a possible driving force of allostery, in particular in the absence of essential structural changes [21,22]. The PDZ2 domain is considered as an example in this regard [33]. This raises the question to what extent equilibrium and non-equilibrium descriptions carry the same information on the allosteric transition.

If the protein responds linearly to the perturbation (e.g. caused by ligand binding), the dynamics observed in an equilibrium experiment (such as NMR spectroscopy) should contain the same dynamical content as the dynamics observed in a non-equilibrium experiment (such as pump-probe spectroscopy). This equivalence is a consequence of Onsager's regression hypothesis [71] which, however, holds only in the case of small non-equilibrium perturbations that explore regions on the free-energy surface that are not outside the energy landscape explored in the equilibrium case. In the case of the photoswitchable PDZ2 domain studied here, the linear response assumption may become questionable. First, it is clear from the discussion of figure 2 that the mechanical response of the protein (including overshootings, etc.) is inelastic, because, for example, contacts are broken and formed. These findings cannot be described by a harmonic force field (used, e.g. in the popular elastic network models [72,73]), in which all forces are linear. MD simulations using common biomolecular force fields as well as NMR experiments, on the other hand, certainly may account for these effects.

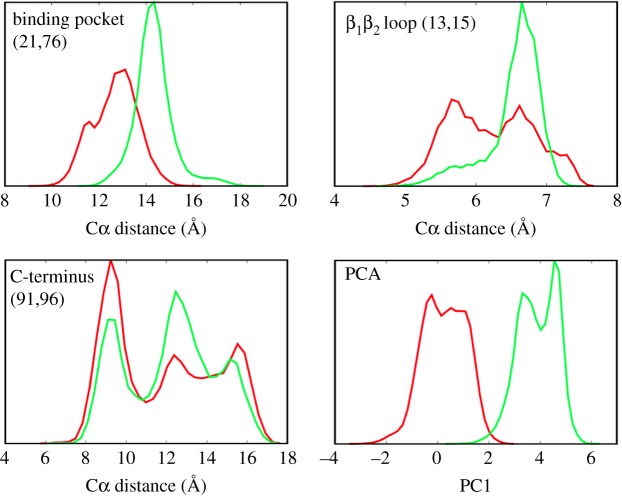
It is less clear, though, if the basic assumption of Onsager's regression hypothesis is appropriate; i.e. if the non-equilibrium perturbations explore the same free-energy surface than the equilibrium states. This hypothesis is also presumed by the ‘population shift’ model, which explains allostery in terms of a shift of the population probability of various equilibrium states [2]. Employing a principle component analysis, we have shown in figure 4a that the free-energy surfaces of the cis and trans equilibrium states hardly overlap, which challenges the idea of a population shift. Of course, the notion of overlapping free-energy surfaces depends to a large extend on the reaction coordinates used to represent the energy landscape [74]. This aspect is illustrated in figure 5, which compares the distribution of the first principle component (essentially the projection of figure 4a onto the PC1 axis) with distributions of selected Cα-distances. The distance distributions (which are similar to what an NMR experiment might measure) are seen to strongly overlap for the cis and trans equilibrium states, even in the case of the distance d_21,76, on which the photoswitch acts directly. For d_13,15, and even more so for d_91,96, the range of possible distances is essentially the same in both states of the protein; just various distances are weighted differently. The overlapping distributions of Cα-distances therefore seem to directly support the classic view of a population shift model [2].

Figure 5.

Different reaction coordinates may discriminate the cis (red) and trans (green) equilibrium states of PDZ2 differently. Shown are distributions of Cα distances (21,76), (13,15) and (91,96) as well as of the first principle component PC1. Adapted with permission from Buchenberg et al. [32]. (Online version in colour.)

The principal component analysis, on the the other hand, maximizes the separation between the two states by including all correlations between structural measures that go into the analysis. From the one-dimensional projection in figure 5, the overlap of both distributions is only 6%, which reduces further to 0.6% when the overlap is calculated using the first seven principal components which show structured distributions and slowly decaying autocorrelation functions [32]. As in fact the effective dimensionality of the dynamical system may be larger than seven [75–78], we expect the true overlap to be even smaller. That is, by employing a reaction coordinate that is able to account for the global conformational rearrangement of the allosteric transition, we find that free-energy surfaces of the cis and trans equilibrium states hardly overlap. Given the limited sampling of equilibrium MD trajectories, however, some asymptotically small overlap of the equilibrium energy landscapes with the full range of the non-equilibrium energy surface can never be ruled out. In that sense, the possible equivalence of visited equilibrium and non-equilibrium phase spaces becomes a somewhat academic and hardly verifiable question.

Looking at it from a different perspective, non-equilibrium experiments and simulations may be considered as an ‘importance sampling’ approach that facilitates an easy exploration of the parts of the energy landscape that account for the allosteric transition. That is, the non-equilibrium simulations cover the full energy landscape (figure 4b), while the equilibrium simulations separate the free-energy surfaces of the cis and trans states (figure 4a). In the same vein, various non-equilibrium enhanced sampling techniques exist that explore a rarely sampled transition state by mechanically pulling the system towards this direction [79–81]. In that sense, non-equilibrium experiments and simulations are an effective and direct way to study the real-time dynamics underlying the allosteric transition. Again, this is similar to the case of protein folding, where pump-probe-type (non-equilibrium) experiments have been designed to effectively study the folding dynamics [24–29].

5. Concluding remarks

Combining time-resolved IR spectroscopy and non-equilibrium MD simulations, this joint experimental/computational study has shown that the allosteric transition in PDZ2 amounts to a propagation of conformational change throughout the protein. The associated structural reorganization process is mediated by a change of atomic contacts and dihedral angles in the flexible loop regions of the system. This manifests itself in the transient overshooting of several observables (figure 2), which indicate that first some contacts need to be broken, before dihedral angles can change and new contacts are formed. In this sense, allosteric communication is a genuinely inelastic and nonlinear process. The non-equilibrium simulations have shown non-local and multiple simultaneous structural changes, even along single trajectories. Taken together with the exceeding structural heterogeneity found for different trajectories, we conclude that the notion of ‘allosteric pathways’ should not be taken literally as a directed sequence of structural changes along certain residues. The time evolution of the allosteric transition in PDZ2 rather resembles a downhill folding scenario, showing diffusive motion on a flat and rugged free-energy landscape, which gives rise to a large ensemble of different transition paths. Moreover, we have found that the common assumption of linear response becomes questionable in the case of the photoswitchable PDZ2 domain considered here, which also means that equilibrium and non-equilibrium methods may reveal different aspects of the allosteric system. In any case, we have demonstrated that non-equilibrium experiments and simulations are an effective and appealing way to study dynamical aspects of allostery.

Clearly, further studies are required to reveal if these findings are special for PDZ2 or may be found more generally in other allosteric systems. In particular, the photoswitch in the current model system is quite artificial, and it is, therefore, not clear a priori to what extent it affects the dynamics and the conclusions drawn here. To achieve a less artificial construct, a phototriggerable protein system enabling initiation of ligand-binding/unbinding would be desirable. To this end, a photoswitchable ligand may be designed such that its binding affinity to an allosteric protein changes in the two states of the photoswitch [82]. Ligand unbinding is a unimolecular reaction that does not include any diffusive (slow) step. Therefore, it may allow us to investigate the dynamic response of the protein in close analogy to the study of Buchli et al. [31]. Another very interesting construct, which would constitute a truly allosteric system, would be to attach the azobenzene-photoswitch to the C-terminal α-helix of PDZ3, and observe ligand unbinding upon photo-induced unfolding of the helix [30]. That helix has been shown to be allosterically coupled with peptide ligand binding [34]. In addition, site-specific vibrational labelling [83,84] would reveal site-specific information, similar to figure 2b from the MD simulation.

6. Methods

Following Shaw et al. [46], we define the ‘dynamical content’ D_j(τ) of a non-equilibrium time trace s_j(t) as the negative of its derivative with respect to the logarithm of time. To calculate D_j(τ) for the noisy experimental data [31] and MD data [32], we need to first smooth them by fitting to an appropriate function. To that end, we choose a multiexponential response function

6.1

where the time constants τ_i are kept fixed in the fit and distributed equally on a logarithmic scale with three terms per decade. The coefficients a_ij are the free fit parameters that result in a lifetime spectrum for each time trace s_j(t) as a function of time constant τ_i. As nicely discussed in Knyazev et al. [49], the time derivative of each exponential term in equation (6.1), when taken on a logarithmic time-axis, is reasonably well localized around the corresponding time constant τ_i. Hence, the definition of the dynamical content D_j(τ_i) given in Shaw [46] is equivalent to the negative of the lifetime spectra a_ij, i.e. D_j(τ_i) = − a_ij.

Fitting equation (6.1) corresponds to an inverse Laplace transformation, which is an ill-posed problem, because the exponential functions in equation (6.1) are not orthogonal to each other [50]. To render the fitting algorithm stable, we therefore introduce a penalty function 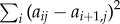that enforces a smooth spectrum of coefficients a_ij [48] and minimize a weighted sum of this penalty function together with the usual root mean square deviation of the fit function s_j(t) to the data. The weighting factor was determined empirically.

For the ‘averaged dynamical content’ D(τ_i), we calculate

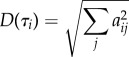6.2

and subsequently normalize it. In Shaw [46], the dynamical content was calculated from equilibrium correlation functions and hence is always positive (assuming the underlying dynamics is Markovian and diffusive [85]). In the non-equilibrium case considered here, positive and negative values a_ij can be obtained, which is why we average the squares of a_ij.

Data accessibility

This article has no additional data.

Authors' contributions

P.H. together with his research group carried out the experimental work, and G.S. together with his research group the computational work, on which this perspective is based. Both authors reanalysed the data and wrote the manuscript.

Competing interests

We declare we have no competing interests.

Funding

The work has been supported in part by a European Research Council (ERC)Advanced Investigator Grant (DYNALLO) and by the Swiss National Science Foundation (SNF) through the NCCR MUST and Grant 200021 165789/1 to P.H., as well as by Grant STO 247/10 to G.S. by the Deutsche Forschungsgemeinschaft.