Robust Proton Treatment Planning: Physical and Biological Optimization

Abstract

Accurately prediction of tumor control and toxicities in radiation therapy faces many uncertainties. Besides inter-patient variability in the response to radiation, there are also dosimetric uncertainties, i.e. differences between the dose displayed in a treatment planning system and the dose actually delivered to the patient. These uncertainties originate from several sources including imperfect knowledge of the patient geometry, approximation in the physics of radiation interaction with tissues, and uncertainties in the biological effectiveness of radiation. Generally, uncertainties are considered in the treatment planning process by applying margins. In intensity-modulated radiotherapy (IMRT), this leads to the planning target volume (PTV) concept. Intensity-modulated proton therapy (IMPT) is widely considered as the future of proton therapy. The treatment planning methods for IMPT and IMRT are similar and based on mathematical optimization techniques for both modalities. However, the PTV concept has fundamental limitations in IMPT. Therefore, researchers have developed robust optimization methods that directly incorporate uncertainties into the IMPT optimization problem. In recent years, vendors of commercial planning systems have started to implement these methods so that robust IMPT planning becomes available in clinical practice. This article summarizes uncertainties in proton therapy and the limitations of the PTV concept to deal with them. Subsequently, robust optimization techniques to overcome these limitations are reviewed.

1. Uncertainties in proton therapy planning

Treatment planning in proton therapy faces many uncertainties. The first uncertainty in the treatment planning chain is target delineation. Delineation of the gross tumor volume (GTV) based on CT, MR and PET imaging is challenging, in part because all current imaging modalities only visualize surrogates for the presence of tumor, but do not visualize the tumor per se. Delineation of the clinical target volume (CTV), which aims to include microscopic tumor infiltration into normal tissues faces even larger uncertainty [1] because microscopic tumor cannot be visualized with current imaging techniques. Following target delineation, there are also uncertainties in dose prescription. There is variability in tumor radiosensitivity between patients as well as heterogeneity within the individual patient’s tumor related to genomic and physiologic factors. Concepts of biological target volume have been proposed to quantitatively consider tumor heterogeneity based on imaging information but are not being used routinely in the clinic [2]. While these uncertainties may be the largest in the treatment planning chain, they are not specific to proton therapy and thus not the topic of this article. Instead this paper will focus on

• Uncertainties in predicting the physical dose distribution. Here we focus on the particle therapy specific problem of range uncertainty.

• Uncertainties in predicting the biological dose distribution, i.e. the uncertainty in predicting the distribution of RBE-weighted dose.

1.1 Physics uncertainties in proton therapy

Under the term physics uncertainties, we summarize all uncertainties in predicting the physical dose distribution delivered to the patient. Most physical uncertainties originate from an imperfect patient model. The most important input to treatment planning is the planning CT image, which has several limitations. First, the planning CT is only a snapshot of possible patient geometries which may not be reproducible in day-to-day treatment due to setup uncertainty, inter-fraction and intra-fraction organ motion. Second, the Hounsfield numbers obtained from the planning CT, which from a physics perspective display photon attenuation coefficients, are an imperfect input for dose calculation algorithms. Not only is there statistical noise in CT images, but there are systematic uncertainties because there is no well-defined relationship between Hounsfield numbers and tissue properties. Most prominently, uncertainty in the conversion of Hounsfield numbers to stopping power for proton beams represents a type of uncertainty that is unique for charged particle radiotherapy.

Besides uncertainties that arise from an imperfect patient model, additional approximations are being made. For example, pencil beam algorithms are being applied because of their computational efficiency at the cost of lower accuracy compared to Monte Carlo methods. Many of these uncertainties lead to errors in predicting the range of protons in a patient and thus the location of the distal dose fall-off. These can be on the order of several mm in water equivalent path length caused by the conversion from CT image to tissue properties, underestimation of scattering by analytical algorithms, and interfaces from low to high density tissues parallel to the beam affecting scattering [3, 4]. The impact of uncertainties related to imaging, setup, or dose calculation algorithms in proton therapy has been extensively studied [5–7]. Consequently, an additional range margin needs to be considered in proton therapy to ensure tumor coverage [8].

Treatment planners have long been aware of uncertainties in proton therapy planning and delivery, and consequently devised heuristics to ensure that tumor dose prescriptions and organ dose constraints are fulfilled despite errors in planning and delivery. Examples of such methods are:

• Choice of beam directions. Typically, it may be possible to minimize potential impact of range uncertainties by using a larger number of beam directions. In addition, carefully selecting beam angles not to go through regions of day-to-day anatomical variations or region with large anatomical density variations results in more robust plans.

• In treatment planning for passively scattered proton therapy, range and modulation of the spread-out Bragg peak is increased to account for range uncertainty. Widening of the aperture and compensator smearing is used to account for setup uncertainty. [9, 10]

Pencil beam scanning is gradually replacing passively scattered proton therapy [11, 12]. IMPT is seen as the future of proton therapy by many researchers and practitioners. IMPT uses treatment planning methods that are very similar to those used in IMRT planning [13]. For both modalities, clinical planning goals are formulated mathematically in terms of objective functions. Subsequently, mathematical optimization algorithms are used to determine pencil beam intensities that minimize the objective function value and, in that sense, best meet the planning goals.

At first glance it may appear logical to also use the same concept for handling uncertainty. Delivery uncertainties in IMRT are typically considered by a margin used to create a Planning Target Volume (PTV) or, in the case of moving targets, an Internal Target Volume (ITV). These margin assignments depend on the treatment site and tumor location although general recipes have been suggested [14]. However, the PTV concept has significant limitations and shortcomings in IMPT [7, 15]. The fundamental assumption behind the PTV concept is that the shape of the dose distribution is largely unaltered by the underlying changes of the patient geometry. Hence, it is assumed that, as long as the CTV moves within the boundaries of the PTV, and the PTV is irradiated to the prescribed dose, then the CTV is guaranteed to receive the prescribed dose. While this is an acceptable assumption in IMRT, it is no longer valid for protons.

This issue is illustrated in figures 1a and 2a for an ependymoma patient, in whom the target contains parts of the brainstem. The treatment plan consists of 3 coplanar beams and was created using conventional IMPT planning aiming at a prescription dose of 50 Gy physical dose (corresponding to 55 Gy(RBE) for a constant RBE of 1.1). 5% overdose was allowed in those parts of the CTV that do not overlay the brainstem. Additional planning objectives were conformity as well as minimizing dose to the brainstem and the surrounding healthy tissues. A 2 mm CTV to PTV margin was added for IMPT planning. Figure 1a shows the dose distribution (right panel) as well as the contributions of the 3 individual fields. Figure 2a shows the deviation from the prescription dose for the nominal scenario (no range error), a range overshoot scenario, and a range undershoot scenario. Range errors where modeled by upscaling and downscaling the Hounsfield numbers of the planning CT by 4.6%. Figure 2a illustrates that range errors do not simply lead to underdose at the edge of the CTV that could be compensated for by larger margins. Instead, range errors lead to hot spots and cold spots inside the target volume. The reason becomes apparent in figure 1a. A range error leads to a relative shift of the dose contributions, which consequently do not add up to the planned homogeneous target dose. For a range undershoot, an over-proportionate amount of dose is shifted back into the CTV. This leads to hot spots, which may be undesirable in those parts of the CTV that contain critical normal tissues such as the brainstem. For a range overshoot, an over-proportionate amount of dose is shifted out of the CTV, which causes cold spots in the CTV. The cause of such degradations of the dose distribution lies in the steep dose gradients in the dose contributions of individual fields. These are not influenced by adding larger margins, illustrating the need for new approaches to account for uncertainty.

Figure 1.

IMPT plans for an ependymoma patient in whom the target volume involves parts of the brainstem. The patient is treated with 3 posterior oblique beams. Pencil beams of approximately 3–5 mm sigma are assumed, corresponding to the latest generation of proton therapy machines. Shown is the dose distribution (right panel) and the dose contributions of the 3 beams. (a) conventional IMPT plan created based on a 2 mm CTV to PTV expansion. (b) robustly optimized plan accounting for range uncertainty. (c) LET re-optimized plan obtained after minimizing LET × dose in the brainstem while constraining the dose distribution to remain close to the conventional plan.

Figure 2.

Robustness analysis of the treatment plans in figure 1a and 1b. Shown is the overdose and underdose in percent of the prescription dose for the nominal scenario (no range error), range overshoot, and range undershoot.

In addition to this fundamental limitation, there are other shortcomings of the PTV concept in IMPT. For example, range uncertainties may vary across beam directions depending on depth of the target and the traversed tissue. However, IMPT optimizes all beam directions simultaneously based on their cumulative dose. Hence a joint target volume must be defined with limited possibilities to define beam specific margins.

The single field uniform dose (SFUD) technique is a widely-used heuristic to counteract the problem related to steep dose gradients in individual fields and dose degradation due to misalignment of beams [10]. SFUD treatments typically yield more robust plans than IMPT treatments with highly modulated fields. However, the use of a PTV together with SFUD still has several limitations. SFUD treatments sacrifice some of IMPT's potential to yield optimal plan quality in terms of OAR sparing, conformity, and minimization of integral normal tissue dose. Especially for complex shaped target volumes that wrap around OARs, SFUD treatments may lead to high doses delivered to OARs.

Numerous efforts are underway to reduce range uncertainties. For instance, image-guided radiation therapy, improved patient immobilization, adaptive planning techniques, and Monte Carlo based dose calculations are being developed. While these efforts may reduce required margins, there will always remain residual uncertainties.

1.2 Biological uncertainties

An additional uncertainty unique to heavy charged particle therapy stems from the assumption that the difference in biological effect between protons and photons is a constant, i.e. the Relative Biological Effectiveness (RBE) is defined as 1.1. The majority of measured RBE values use clonogenic cell survival in vitro as the endpoint. The relevance of these for clinical endpoints, particularly for normal tissue toxicities, is unclear. Nevertheless, cell survival experiments suggest that the RBE is not constant but increases towards the end of range [16]. It is generally assumed that the RBE increase with depth reflects an increase of RBE with linear energy transfer (LET). Therefore, most RBE models describe RBE as a function of dose, LET, and tissue specific parameters.

The distribution of LET in the target volume is typically not homogeneous even if the physical dose distribution is homogeneous, especially for highly modulated fields in IMPT. Therefore, LET dependence of RBE means that a homogeneous physical dose distribution corresponds to an inhomogeneous RBE-weighted dose distribution. Furthermore, large uncertainty in RBE models (i.e. how exactly RBE depends on dose, LET, and tissue parameters) causes substantial uncertainty in RBE-weighted dose.

Most proton RBE models are derived from the linear-quadratic cell survival model and use the α/β-ratio as tissue specific parameters [17–20]. It is assumed that tissues with low α/β show a larger increase of RBE with LET compared to tissues with high α/β. These models have in common that they effectively describe an approximately linear increase of RBE with LET. Hence, the biological dose b (i.e. RBE-weighted dose) can to first approximation be written as

$$b=\text{RBE}·d=(c_1+c_2\text{LET})·d$$

Here, c₁ and c₂ are parameters, which are uncertain, and which may depend on tissue type and prescription dose level. This equation contains the case of a constant RBE of 1.1, corresponding to the parameter values c₁ =1.1 and c₂ = 0.

The above equation suggests that the product of LET and dose (LET × dose), multiplied by a constant c₂, can be interpreted as the biological extra dose that can be attributed to high LET. In current practice, the physical dose distribution is the only physical quantity to characterize the quality of a treatment plan. In proton therapy, the product of LET and dose can be used as a second physical quantity to characterize a treatment plan. One advantage of using LET × dose as a surrogate for RBE is that it’s a pure physical quantity. It can be calculated quite accurately based on the treatment plan information [21] and does not depend on RBE model parameters. A quantitative interpretation of LET × dose requires scaling with the parameter c₂, which is highly uncertain. Nevertheless, it is an indicator for local increase or decrease of RBE-weighted dose.

Figure 3a shows the distribution of LET × dose, scaled by c₂ = 0.04 µm/keV, for the treatment plan in figure 1a. This parameter value yields an RBE of 1.1 in the center of 5 cm spread out Bragg beak for c₁ = 0. The figure illustrates that high LET × dose is predominantly observed at the edge of the target and that comparatively low values are observed in the center. In particular, high values of LET × dose are observed in the part of the brainstem that overlaps with the CTV. Hence, uncertainty in the knowledge on how much RBE increases with LET (parameter c₂) bears the risk that normal tissues within or near the target volume are overdosed biologically even though physical dose constraints are fulfilled. Likewise, regions of very low LET in the tumor may correspond to regions where RBE is lower than 1.1 so that these parts of the target receive a dose lower than intended.

Figure 3.

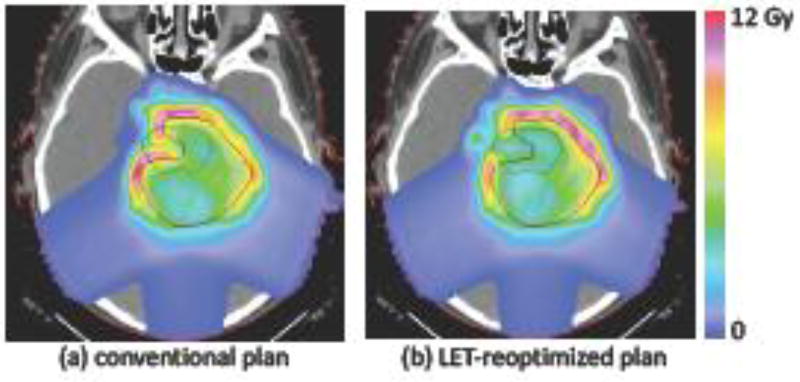
Distribution of the product of LET and dose (LET × dose) for (a) the conventional IMPT plan in figure 1a and (b) the LET re-optimized plan in figure 1c.

This result shown in figure 2a is again explained by considering the dose contributions of individual fields in figure 1a. The regions of high LET × dose correspond to regions where most of the dose is delivered using the Bragg peak rather than the entrance region of the beam. Similar to the case of range uncertainty, it is clear that this problem cannot be resolved by applying margins. Instead, LET or RBE effects must be included into IMPT treatment plan optimization directly.

Note that, because RBE increases with depth of a proton beam, RBE uncertainties are also a type of range uncertainties [19]. However, while local physical range errors as described in section 1.1 can be positive or negative, RBE related range errors are positive (i.e. increase the range relative to the planned range) if RBE values at the end of range are higher than 1.1 [16].

Potential variations in RBE are typically not considered in proton therapy planning although treatment planners may avoid certain beam angles due to concerns in RBE variations. This is particularly true if a normal tissue close to the distal dose fall-off has a maximum tolerance dose (such as the brainstem, spinal cord, or optic pathway).

2. Robust optimization for physical uncertainties

Instead of using margins and heuristics like SFUD, range or setup uncertainties can be accounted for in IMPT planning in a robust optimization framework [15, 22–29]. Robust optimization methods incorporate uncertainty directly into the treatment plan optimization problem for IMPT. Thereby, robust IMPT optimization methods can overcome shortcomings of the PTV concept and improve plan quality compared to margin based planning [30].

2.1 Conventional IMPT planning

To explain the idea of robust optimization, we first recall that IMPT planning is performed with the help of mathematical optimization algorithms. To that end, IMPT planning is formulated as a mathematical optimization problem, which means that clinical planning goals are translated into a mathematical description of what a good treatment plan is. This is done by defining an objective function f(d), a function of the dose distribution d which has a small value for good treatment plans and large values for bad treatment plans. IMPT planning is then performed by algorithms that find the pencil beam intensities that minimize the objective function f [10]. Formally, this is written as

$$\begin{array}{cc}{\text{minimize}}_x\hfill & f(d)\hfill \\ \text{subject to}\hfill & d_i={\sum }_j{D}_{\mathit{\text{ij}}}{x}_j\hfill \\ \hfill & x_j\ge 0\hfill \end{array}$$

where d_i is the dose in voxel i, x_j is the fluence of pencil beam j and D_ij denotes the dose contribution of pencil beam j to voxel i.

2.2 Robust IMPT planning

In this formulation of the IMPT planning problem, geometric uncertainty is modeled as uncertainty in the dose-influence matrix D_ij. Typically, it is assumed that the treatment machine can accurately deliver the treatment plan as specified by the pencil beam intensities x_j, ie. x_j is not uncertain. However, it is uncertain what dose distribution the treatment plan yields in the patient. The easiest approach to model uncertainty is to assume that different dose-influence matrices $D_{\mathit{\text{ij}}}^s$ may apply. Here, s is an index of possible error scenarios. For example, range uncertainty can be modeled via an overshoot and an undershoot scenario. The dose-influence matrix for an overshoot scenario can be calculated by downscaling of the Hounsfield numbers in the planning CT, such that all protons penetrate further into the patient compared to the original planning CT.

The next question is how a set of error scenarios can be incorporated into IMPT planning. In the robust IMPT planning literature, two approaches predominate: the probabilistic approach and the worst-case approach.

The probabilistic approach [15, 24], also referred to as stochastic programming in the optimization literature, minimizes a weighted sum of objective functions evaluated for all error scenarios. Formally this can be written as

$$\begin{array}{cc}{\text{minimize}}_x\hfill & {\sum }_s{p}_{s}f(d^s)\hfill \\ \text{subject to}\hfill & d_i^s={\sum }_j{D}_{\mathit{\text{ij}}}^s{x}_j\hfill \\ \hfill & x_j\ge 0\hfill \end{array}$$

Here, p_s represent importance weights for the error scenarios. Typically, a high weight is given to likely scenarios and a small weight to error scenarios that are considered possible but unlikely to occur. The probabilistic approach aims to find a treatment plan that yields a good treatment plan for all scenarios, ie. for all possible dose distributions d^s, the objective function value f (d^s) should be small. The relative importance of different scenarios can be controlled by p_s.

The worst-case approach [26], also referred to as minimax optimization, minimizes the maximum of objective functions, taken over all error scenarios. Formally this can be written as

$$\begin{array}{cc}{\text{minimize}}_x\hfill & {\text{max}}_{s}f(d^s)\hfill \\ \text{subject to}\hfill & d_i^s={\sum }_j{D}_{\mathit{\text{ij}}}^s{x}_j\hfill \\ \hfill & x_j\ge 0\hfill \end{array}$$

Hence, the worst-case approach determines the IMPT plan that is as good as possible for the worst error scenario.

There exist several variations of the worst-case approach to robust planning. In many cases, the objective function is a sum of contributions from individual voxels. Let us assume that the objective function is given by $f(d^s)={\sum }_i{f}_i(d_i^s)$. In the worst-case method originally suggested in [25], the worst case is determined on a voxel-by-voxel basis rather than for the composite objective function.

$$\begin{array}{cc}{\text{minimize}}_x\hfill & {\sum }_i\underset{s}{\text{max}}(f_i(d_i^s))\hfill \\ \text{subject to}\hfill & d_i^s={\sum }_j{D}_{\mathit{\text{ij}}}^s{x}_j\hfill \\ \hfill & x_j\ge 0\hfill \end{array}$$

A typical situation is that f_i is given by quadratic penalty functions for underdosing in the tumor and overdosing in OARs with maximum dose constraints. The method can then be interpreted as optimization of the worst-case dose distribution, where the worst case dose distribution contains, voxel-by-voxel, the worst dose than may occur for any error scenario (i.e. the lowest dose in the tumor and the highest dose in OARs).

2.3 Illustration of robust optimization for range uncertainty

Below we illustrate robust planning using the probabilistic approach for the ependymoma patient shown in figure 1. Robust IMPT planning is based on the CTV only and no PTV margin is used. For this example, only range uncertainty is considered and is modeled via three scenarios:

1. nominal scenario, i.e. no range error;

2. range overshoot, modeled by downscaling the Hounsfield numbers by 4.66%;

3. range undershoot, modeled by upscaling the Hounsfield numbers by 4.66%;

The weights p_s were chosen as 0.5 for the nominal scenario and 0.25 for the overshoot and undershoot scenario. This simple model is sufficient to demonstrate the main effects of robust optimization to make IMPT plans more resilient to range errors. It is most illustrative to analyze the dose distributions that the three fields contribute (Figure 1b), and compare these to the conventional IMPT plan (Figure 1a).

• Robust planning for range uncertainty avoids dose gradients in beam direction in the dose contributions of individual beams. As a consequence, shifting these dose distributions along the incident beam direction has only a moderate impact on the dose distribution in the patient.

• Robust planning for range uncertainty automatically extends the irradiated region distal to the target volume, i.e. it automatically generates the appropriate margin necessary to achieve target coverage for the assumed range error without the need to manually define PTV margins.

• Robust planning avoids placing the distal edge of a pencil beam in front of OARs. Instead, the lateral falloff is used to shape the dose distribution in the region where OAR and target abut.

Figure 2b demonstrates that the treatment plan obtained through robust planning is indeed more resilient to range errors compare to the conventional plan. Despite range undershoot or overshoot, a homogenous dose distribution is delivered to the CTV.

2.4 State of research

Robust IMPT optimization has been investigated almost exclusively for range and setup uncertainty. The published methods can be categorized into the probabilistic approach [15, 24] and different flavors of the worst-case approach: the composite worst case [26], the objective-wise worst case [23], and the voxel-wise worst case [22, 25]. Since robust planning techniques for IMPT were first investigated, the question whether one method is generally superior has been discussed. The probabilistic approach optimizes the average plan quality. It is possible that a plan does not achieve the desired dose quality for the worst scenario, for example in situations where a large number of scenarios are modeled. On the other hand, the minimax approach optimizes the plan for the worst case only and has no incentive to improve plan quality for more likely scenarios. It was shown that some methods do yield undesirable results in specific situations [31], but there is no comprehensive evidence that one method is generally superior. To first approximation, all methods achieve the features of robust plans described above if used adequately.

Most prior works have used a small set of discrete range and setup errors to model uncertainty [22, 25, 26] or sampled errors from a Gaussian distribution [24]. More recently, researchers developed improved methods to quantify dose uncertainty. Bangert et al [32] developed analytical methods to calculate expectation value and variance of the dose distribution for Gaussian range and setup errors without relying on sampling. Perko et al [33] used a technique called polynomial chaos expansion to develop a parameterized model of the dose distribution as a function of range and setup errors.

3. Robustness of IMPT plans against biological uncertainties

Robustness against geometric uncertainty is usually understood as ensuring that range or setup errors do not lead to overdosing of OARs or underdosing in the target. A similar notion of robustness can be applied to uncertainty in RBE. In that sense, a robust plan is one that does not cause overdosing of OARs if the RBE is higher than expected, or underdosing of the target if RBE is lower than expected. However, at this stage, there is no commonly agreed notion of robustness against RBE uncertainty.

High LET in critical structures within or near the target volume may potentially lead to higher RBE-weighted doses, and thereby increase the risk of side effects. However, it has been demonstrated that LET distributions can typically be modified while maintaining target prescriptions and normal tissue constraints [34–37] in terms of physical dose. An IMPT planning method to make IMPT plans more robust against this risk was recently suggested [37]. In this method, an IMPT plan is initially optimized based on physical dose (or equivalently, based on a constant RBE of 1.1). In a second step, the treatment plan is re-optimized regarding the LET distribution with the goal of avoiding high LET in critical structures within or near the target volume. During the second step, the physical dose distribution is constrained to remain close to the initial treatment plan obtained in the first step. It was shown that LET hotspots in OARs can typically be avoided by accepting very small degradations of the physical dose distribution. This method is illustrated in figure 1c and 3b. Here, the LET based re-optimization step is applied to the conventional IMPT plan shown in figure 1a. We enforced the constraint that target coverage and conformity do not worsen, while we allow a small increase of 3% in the brainstem gEUD and the mean dose in the normal tissue. The LET re-optimization step aims at minimizing the product of LET and dose (LET × dose) in the brainstem. The resulting LET × dose distribution is shown in figure 3b, which illustrates that high LET is now avoided inside the brainstem. Figure 1c shows how the treatment plan is modified. The LET re-optimized plan avoids pencil beams incident from the left (right side of the image) that stop in the brainstem. Instead, the fluence of pencil beams incident from the right (left side of the image) is increased, which deliver dose to the part of the target overlaying the brainstem via the entrance region of the beam.

Some authors have suggested performing IMPT treatment plan optimization based on RBE-weighted dose [38, 39]. In this case, IMPT planning is performed by evaluating the objective function f for biological dose rather than physical dose as in conventional IMPT planning. For the simplified linear RBE model considered above (and analogously for any other RBE model), this can formally be written as

$$\begin{array}{cc}{\text{minimize}}_x\hfill & f(b)\hfill \\ \text{subject to}\hfill & b_i=c_1{d}_i+c_2{L}_i{d}_i\hfill \\ \hfill & d_i={\sum }_j{D}_{\mathit{\text{ij}}}{x}_j\hfill \\ \hfill & L_i=\frac{1}{d_i}{\sum }_j{L}_{\mathit{\text{ij}}}{D}_{\mathit{\text{ij}}}{x}_j\hfill \\ \hfill & x_j\ge 0\hfill \end{array}$$

Here L_ij is the dose-averaged LET in voxel i for the dose contribution of pencil beam j, and L_i is the LET in voxel i averaged over all pencil beams. However, due to uncertainty in the RBE model (in this case mostly in the parameter c₂) this approach is typically considered insufficient and is not applied in practice. RBE-based IMPT planning in this pure form would yield treatment plans that are highly non-robust with respect to uncertainties in the RBE model parameters. This can best be illustrated for the case of target coverage. Suppose an objective function to minimize target underdose, such as the standard quadratic penalty function, is evaluated for RBE-weighted dose. This would yield treatment plans that lower the physical dose compared to conventional plans in those parts of the target where the LET is high - based on the assumption that RBE is higher than 1.1 in these regions. Consequently, these regions would be underdosed if the increase of RBE with LET was less than assumed in the RBE model.

This problem can potentially be addressed by applying robust optimization techniques to RBE-based IMPT planning. Whereas physical dose uncertainty corresponds to uncertainty in the dose-deposition matrix D_ij, uncertainty in the biological dose corresponds to uncertainty in the RBE model parameters. Assuming that different sets of RBE model parameters $(c_1^s,c_2^s)$ may apply, the stochastic programming approach applied to this situation would solve the IMPT planning problem

$$\begin{array}{cc}{\text{minimize}}_x\hfill & {\sum }_s{p}_{s}f(b^s)\hfill \\ \text{subject to}\hfill & b_i^s=c_1^s{d}_i+c_2^s{L}_i{d}_i\hfill \\ \hfill & d_i={\sum }_j{D}_{\mathit{\text{ij}}}{x}_j\hfill \\ \hfill & L_i=\frac{1}{d_i}{\sum }_j{L}_{\mathit{\text{ij}}}{D}_{\mathit{\text{ij}}}{x}_j\hfill \\ \hfill & x_j\ge 0\hfill \end{array}$$

To our knowledge, a formal application of robust optimization or stochastic programming to handle RBE uncertainties has not been demonstrated yet.

4. Discussion

Robust planning in commercial planning systems

Robust planning methods have initially been investigated as a method to incorporate organ motion and setup uncertainty in IMRT planning [40–45]. Only a few years later, similar concepts were applied to handling range und setup errors in IMPT. The fundamental limitations of the PTV concept in IMPT as described in section 1.1 led to the first implementations of robust planning methods in commercial TPS. Today, several vendors provide robust planning for proton therapy. Interestingly, these implementations cover all three methods described in section 2.2. Raystation provided the first commercial solution and has an implementation of the composite worst-case method; Pinnacle uses the probabilistic approach; and Eclipse follows the voxel-wise worst case method. Robust optimization methods for range and setup uncertainty should allow the transition from a research topic to a methodology that is available in clinical practice. This will give a broader group of practitioners the ability to evaluate these methods and develop practical guidelines on how to best use them.

Treatment plan evaluation for IMPT

The fundamental assumption behind the PTV concept is that, as long as the CTV moves within the boundaries of the PTV, and the PTV is irradiated to the prescribed dose, then the CTV is guaranteed to receive the prescribed dose. The assumption is not generally valid for IMPT because misalignment of the dose contributions for highly modulated fields may cause dose degradation anywhere inside the target volume. As a consequence, treatment plan evaluation for IMPT (especially for highly modulated fields) should explicitly consider the dose distributions evaluated for a set of range and setup errors. Most planning systems now have the capability to perform this in a convenient manner.

Robust planning for biological uncertainties

Robust planning methods to address RBE uncertainties are less developed than robust planning methods for physical uncertainty. A possible next step towards that goal may be to use the product of LET and dose as a second quantity (besides physical dose) to evaluate and create a treatment plan. LET × dose has several advantages in that regard:

• It is a well defined physical quantity that (unlike RBE) does not depend on any model parameters. Monte-Carlo dose calculation algorithms yield LET × dose at almost no additional computational cost, and also pencil beam algorithms can provide sufficient approximations.

• LET × dose can to first approximation be interpreted as a measure of the biological extra dose that comes for elevated LET, up to the scaling factor c₂. Hence, LET × dose is more accessible to a quantitative interpretation compared to LET itself.

• From a technical perspective, LET × dose has the advantage that it is a linear function of pencil beam fluence. Therefore, the same optimization algorithms that are well established for physical dose optimization can be applied.