Abstract
Positional fluctuations of an atom in a protein can be described as motion in an effective local energy minimum created by the surrounding protein atoms. The dependence of atomic fluctuations on both temperature (T) and pressure (P) has been used to probe the nature of these minima, which are generally described as harmonic in experiments such as x-ray crystallography and neutron scattering. Here, a quasiharmonic analysis method is presented in which the P-T dependence of atomic fluctuations is in terms of an intrinsic isobaric thermal expansivity αP and an intrinsic isothermal compressibility κT. The method is tested on previously reported mean-square displacements from P-T molecular dynamics simulations of lysozyme, which were interpreted to have a pressure-independent dynamical transition Tg near 200 K and a change in the pressure dependence near 480 MPa. Our quasiharmonic analysis of the same data shows that the P-T dependence can be described in terms of αP and κT where below Tg, the temperature dependence is frozen at the Tg value. In addition, the purported transition at 480 MPa is reinterpreted as a consequence of the pressure dependence of Tg and the quasiharmonic frequencies. The former also indicates that barrier heights between substates are pressure dependent in these data. Furthermore, the insights gained from this quasiharmonic analysis, which was of the energy landscape near the native state of a protein, suggest that similar analyses of other simulations may be useful in understanding such phenomena as pressure-induced protein unfolding.
I. INTRODUCTION
The concept of an energy landscape has been useful in describing a variety of phenomena in proteins, including protein function and folding.1,2 The structure of a folded protein from an X-ray crystallographic or nuclear magnetic resonance (NMR) solution structure determination can be considered to be a minimum in this rough landscape. Conformational transitions from this minimum to other local minima may occur: nearby conformations may correspond to states important for protein function, while farther ones may correspond to folding intermediates. The landscape has often been explored by using temperature variations of the system,3 which vary the thermal energy and the system volume via thermal expansivity. More recently, variations in pressure have also been used,4,5 which affects only the system volume via the compressibility. Pressure could change the shape or depth of minima or the distance or barriers between minima.
While the energy landscape is a multidimensional potential energy surface dependent on the coordinates of all atoms in the system, another useful concept is the local effective potential energy minimum in which a given atom fluctuates. In a given conformational state, the potential energy well is created by the neighboring atoms and can be characterized by the average position of the atom in that state and the mean-square fluctuations about that position. For instance, the temperature factors used in X-ray crystallographic refinement of structures arise in part from thermal fluctuations about an average position and thus can assess the width of the minimum. In addition, the mean-square displacements from neutron scattering studies can also be related to the mean-square fluctuations. In proteins, this local energy minimum is generally assumed to be an isotropic harmonic three-dimensional well although anisotropic and even anharmonic wells can be considered. In fact, an increasing number of protein structures in the Protein Data Bank6 (PDB) report anisotropic temperature factors.
The potential energy surface corresponding to a given conformational state of a protein is rough, with multiple local minima corresponding to many substates within the conformational state. Most atoms can be considered to fluctuate in a single energy minimum on a short enough time scale, although sometimes transitions to other local minima may occur via processes such as dihedral angle transitions.7,8 On longer time scales, the motions of a given atom couple to an increasing number of atoms, resulting in “collective motions”9 that can be considered as phonons in a normal mode approximation. Interestingly, the frequency distribution demonstrates a quadratic Debye behavior characteristic of acoustic phonons even at wavelengths significantly smaller than the size of the protein (i.e., time scales as low as ∼1 ps), apparently because the protein and solvent behave as a continuum due to the similarities in the weak interactions within the protein and between the protein and solvent.3 On longer time scales, these collective motions can also give rise to transitions to other substates. Interestingly, a dynamical transition has been observed in atomic fluctuations of protein atoms at a transition temperature Tg ∼ 200 K, which has been likened to the glass transition of the protein.10–12 Below Tg, the interpretation is that thermal energy is insufficient to make transitions so atoms get trapped in a single substate, which corresponds to an underlying potential energy minimum. On the other hand, above Tg, the interpretation is that thermal fluctuations cause transitions between different substates within the same conformational state. However, proteins are not typical glass-forming systems and thus do not necessarily follow typical glass behavior. In fact, a perhaps non-intuitive behavior of proteins is that they unfold at high pressure. This has been explained as the result of hydration of the interior of the protein, which results in a lower system volume since water molecules can fill voids in the folded protein.
To describe more complex motion, at least two types of deviation from strictly harmonic behavior can be considered.13,14 In a quasiharmonic approximation, individual atoms are considered to move in harmonic potentials but expansion or contraction of the system due to pressure or temperature changes are accounted for since they change the available space for a given atom created by its neighbors. Thus, the frequencies vary with volume, an approach used extensively for problems in condensed matter and materials physics.13,14 In a full anharmonic treatment, individual atoms are considered to move within energy basins that are anharmonic in shape, which leads to additional frequency changes with temperature than expected from volume changes alone. Thus, the frequencies are dependent on both volume and temperature. In the case of solids, the anharmonic contributions arise from complex phonon-phonon interactions.15 On the other hand, the total anharmonic contribution at a given pressure and temperature can be determined experimentally from appropriate measurements and thermodynamic relations.13
The approach of understanding how volume changes affect the frequencies apparently has not yet been applied to understanding the vibrational dynamics of biological molecules. Such a treatment may be useful because the complex dynamics of proteins described above even in one conformation state demonstrates the breakdown of a simple harmonic description of behavior of the component atoms. For instance, the nonlinear temperature dependence of the temperature factors above Tg12 and comparisons of quasiharmonic modes calculated from molecular dynamics simulations at room temperature with those from normal modes analysis9 suggest that the force constants are changing with temperature. In addition, the protein dynamical transition has been attributed to solvent-driven activation of anharmonic dynamics above Tg16,17 and the observation of transitional behavior of positional distributions from protein simulations at room temperature shows that the fluctuations can be considerably anharmonic.7 In particular, since transitions between substates appear to occur above Tg, which should increase the volume, a quasiharmonic approximation appears warranted for understanding the effects of temperature and pressure on fluctuations.
Examining atomic fluctuations in molecular dynamics simulations of biological macromolecules under pressure can provide information about their energy landscape. For example, Meinhold et al.5 used both pressure and temperature to explore the energy landscape of hen egg white lysozyme (HEWL) in water using molecular dynamics (MD) simulations at pressures between 0.1 and 1000 MPa and at temperatures from 20 to 320 K. Experimentally, HEWL reversibly denatures above 350 MPa or below 260 K on the hour time scale to an unfolded state that appears to be quite different from high temperature or chemical denaturant unfolded states.18 However, since the simulations were heated, pressurized, and equilibrated from the energy minimized NMR structure in less than 1 ns and the total length of each simulation was 1 ns, none of the simulations can be expected to be in the thermodynamically favored state. Instead, they probe the energy landscape near the native state. In these studies, the reported data are the time-dependent mean-square displacements d2(τ) of hydrogen atoms, which were chosen in part because they can be measured directly in neutron scattering experiments. Meinhold et al.5 have shown that the dynamics of protein hydrogen atoms are a good measure of the dynamics of all protein atoms. d2(τ = 1 ps)|P increased linearly with temperature below Tg ≈ 200 K and nonlinearly at a higher rate above Tg, which was ascribed to the protein dynamical transition. Since Tg appeared to be independent of pressure, they concluded that the barrier height between potential energy minima was independent of pressure. In addition, an effective environmental force constant, keff, for the underlying harmonic potential was obtained from d2(τ = 1 ps)|Tg from the linear regime below Tg. Interestingly, keff was found to increase linearly with pressure below 480 MPa and linearly but at a slower rate above 480 MPa, which was attributed to a qualitative change in the pressure response of the protein energy landscape.
Here, a method for analyzing atomic fluctuations in macromolecules is presented, which utilizes the quasiharmonic approximation in which the underlying modes are assumed to have frequencies that vary with volume. The approach is suited for macromolecules with rough potential energy landscapes with regions corresponding to defined conformational states, such as proteins. Assuming that each atom of the protein moves in a local effective potential created by its neighboring atoms, the protein is described as a classical Einstein-type model of a solid where the atoms are independent harmonic oscillators with identical quasiharmonic frequencies. The temperature and pressure dependence of the average atomic fluctuations of the protein are thus described in terms of an intrinsic isobaric thermal expansivity αP and an intrinsic isothermal compressibility κT, respectively. These are intrinsic properties of the protein, independent of direct solvent effects. To illustrate the applicability and utility of this approach, the HEWL simulation data from Meinhold et al.5 are reexamined using our quasiharmonic analysis. Although the analysis of mean-square fluctuations of protein heavy atoms would be ideal, Meinhold et al.5 report only mean-square displacements of hydrogen atoms, which are shown to be a good measure of the dynamics of all protein atoms. The approach leads to reassessment of the prior conclusions, namely, pressure independent barrier heights between local minima and a transition in the pressure response of the energy surface. Notably, we find the purported transition at 480 MPa can be interpreted as a consequence of the pressure dependences of Tg and of the quasiharmonic frequencies. The former also indicates that barrier heights between local minima are pressure dependent. More broadly, this type of quasiharmonic analysis of computer simulation of proteins may be useful in understanding phenomena such as pressure-induced protein unfolding. Although more proteins need to be examined, the results here suggest that while pressure might be expected to reduce fluctuations by compressive effects on a single substate, it may also favor transitions to other substates and thus enhance fluctuations. Since these other substates can include more solvated conformations, these transitions may ultimately lead to unfolding.
II. THEORETICAL METHODS
A. Quasiharmonicity and anharmonicity
Deviations from a purely harmonic system with a force constant k and volume and temperature independent frequencies can be described as quasiharmonic or anharmonic. Formally, a quasiharmonic system has vibrational frequencies that vary only because the effective available space changes as the material expands or contracts with pressure and/or temperature14 so that frequencies vary directly only with volume. In addition, an anharmonic system has vibrational frequencies that are dependent on both volume and temperature.14
Generally, a potential energy minimum can be described by a volume and temperature dependent effective force constant k(V,T) defined as
| (1) |
or, in terms of pressures and temperatures, as
| (2) |
where
| (3) |
| (4) |
In Eqs. (3) and (4), a harmonic system has (k/P)T = (k/T)P = 0, a quasiharmonic system has (k/T)V = 0 so that k(P, T) = k(V(P, T)), and an anharmonic system has all non-zero terms. Substituting Eqs. (3) and (4) into Eq. (2), the quasiharmonic approximation can be written as
| (5) |
The quantities in Eq. (5) can be identified with various thermodynamic parameters. For instance, the isothermal compressibility is
| (6) |
and the isobaric thermal expansivity is
| (7) |
The volume dependence of these quantities can be determined with respect to a reference pressure P0 and a reference temperature T0, and Δ denotes differences with respect to reference quantities. The dependence of κT on V can be described as
| (8) |
where κT,0 = κT(P0) and μ is a non-linearity index. Inserting this into Eq. (6) and integrating, one obtains the Moelwyn-Hughes isotherm19
| (9) |
Similarly, the dependence of αP on V can be described as
| (10) |
where αP,0 = αP(T0) and ν is another non-linearity index. Inserting this into Eq. (7) and integrating, one obtains
| (11) |
[Note that since the fits here are over a very small range of temperatures, the case of a volume independent αP such that ν = 0 is explicitly considered in Eq. (11).]
The volume dependence of the force constant can be determined assuming that the effective force constant gives rise to phonon modes with frequency ω. Recognizing that ω2 k,
| (12) |
where is the Grüneisen parameter.14 In addition, the Grüneisen parameter is related to the non-linearity index μ for a Debye solid (which also holds for an Einstein solid) by20
| (13) |
Next, substituting Eqs. (9)–(12) into Eq. (5) and integrating leads to
| (14) |
where k0 = k(P0, T0). Furthermore, if κT is assumed to be independent of T, κT,0 = κT(P0, T0) and if αP is assumed independent of P, αP,0 = αP(P0, T0).
B. Mean-square displacements
The most direct measure of the effective local potential from a simulation would be the mean-square atomic fluctuations averaged over all protein atoms. However, the quantity calculated from the simulations by Meinhold et al.5 is d2(τ) = , where ri(t) is the coordinate vector of atom i at time t, the angle brackets and over bar are the time and ensemble averages, respectively, of the hydrogen atoms, and τ = 1 ps.
Assuming that each hydrogen atom can be considered to be in an effective local harmonic potential subject to Brownian fluctuations, the mean-square displacement can be related to the mean-square fluctuations in the effective harmonic potential. In particular, assuming the energy minimum has a spring constant Mω02 and γ is the damping coefficient,
| (15) |
where ω12 = ω02 + γ2/4. For the case studied in Meinhold et al.,5 the factor in large parenthesis in the second equality averages to zero since the mean-square displacement is averaged over all hydrogen atoms in the protein, which each have a different phase shift, and the exponential factor is constant. Thus, the reported d2(τ) → 2σ2 = 6kBT/k, where k is the average local effective harmonic force constant for a hydrogen atom in the protein on a time scale τ so that only motions with time scales up to τ can contribute to the local effective harmonic potential. A slight increase in d2(τ) for the hydrogen atoms in a protein has been noted between τ = 1 ps and τ = 10 ps for hydrogens;4 however, it was concluded that the 1 ps time scale is sufficient for probing the energy landscape near the NMR structure.
C. Fitting procedures
The data used for testing this quasiharmonic analysis are taken from the MD simulations of HEWL found in the work of Meinhold et al.,5 which gives details of the simulation methods and are repeated in the supplementary material. Briefly, the simulations were performed using the Gromacs suite of programs21,22 with the all-atom OPLS-AA/L force field.23 The initial structure was 1GXV24 from the PDB,6 which was solved at 1 atm by NMR. The system was energy minimized, subsequently heated for 100 ps, and then pressurized and equilibrated for 600 ps using the extended-ensemble Nosé-Hoover/Parrinello-Rahman algorithms.25–28 The production phase of each temperature-pressure value was 1 ns and coordinates were saved at 0.1 ps for analysis. d2(1 ps) are reported for 0.1 MPa ≤ P ≤ 1000 MPa in 50 MPa intervals and 240 K ≤ T ≤ 320 K in 20 K intervals, which will be referred to as the “pressure” set, and for 0 K < T ≤ 320 K in 20 K intervals and P = 0.1, 300, 700, and 1000 MPa, which will be referred to as the “temperature” set. In addition, k was reported for 0.1 MPa ≤ P ≤ 1000 MPa in 50 MPa intervals. To account for differences in the definition of k as well as significant figures of constants, their data for k were scaled accordingly using slopes of d2 from the temperature set. The fits were performed using gnuplot. The goodness of fits for the parameters were examined via the reduced χ2, which is the mean-square residuals from the fit against the MD simulation data divided by the number of degrees of freedom, so that fits using different numbers of parameters can be compared.
III. RESULTS
The accuracy and utility of the quasiharmonic analysis are tested here by reexamining the MD simulation data for HEWL in the work of Meinhold et al.5 The reference state is chosen here as P0 = 0.1 MPa and T0 = 298 K, although results appear independent of the choice of reference state. Under the assumption that the “glass” transition involves a smooth (non-discontinuous) transition, the high temperature data (well above where the glass transition temperature for proteins is typically found, i.e., T >> 200 K) are first fit assuming a pressure and temperature dependent k and then the low temperature data (i.e., T << 200 K) are fit assuming that k is fixed to its value at (P, Tg) by varying Tg.
A. Above the “glass” transition
Above the “glass” transition temperature, the local atomic fluctuations of the protein are assumed to be close enough to harmonic so that any anharmonicity may be treated via a quasiharmonic approximation. In other words, the potential energy wells have force constants that are pressure and temperature dependent only via volumetric effects so are given by Eq. (14) in terms of a temperature-independent κT and a pressure-independent αP, respectively. Substituting Eq. (14) into Eq. (15), the mean-square displacement d2(P, T) is given by
| (16) |
where d02 = d2(P0, T0). The fits in this section utilize the pressure data set (i.e., 0.1 MPa ≤ P ≤ 1000 MPa at 240 K ≤ T ≤ 320 K) from the HEWL MD simulation.
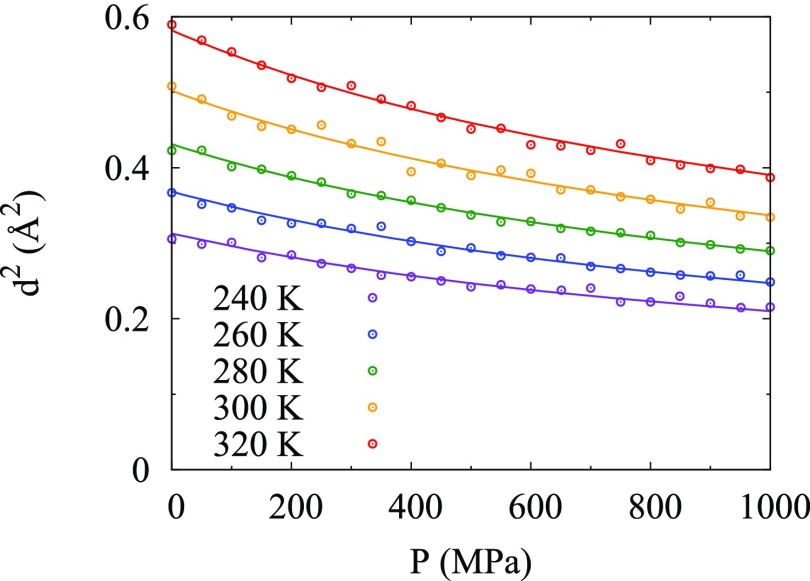
First, d2(P, T) calculated using Eq. (16) is fit to the MD pressure data to find d02, αP,0, κT,0, μ, and ν assuming ν 0 (Table S1 of the supplementary material). Since ν is very small with a very large uncertainty (ν = −0.004 ± 0.104), d2(P, T) is also fit to find d02, αP,0, κT,0, and μ assuming ν = 0 (Table I and Table S2 of the supplementary material). Next, since μ was found to be close to 1 (i.e., μ = 0.70 ± 0.10), the ideal gas value, d2(P, T), calculated using Eq. (18) with μ = 1 is fit to the MD pressure data to find d02, αP,0, κT,0, and ν assuming ν 0 (Table S3 of the supplementary material). Since ν is still small (ν = −0.01 ± 0.19), over the small temperature range examined here, αP appears independent of the volume [ν = 0 in Eq. (9)], although it is likely to depend on the volume over a larger temperature range. Thus, d2(P, T) is fit for d02, αP,0, and κT,0 assuming μ = 1 and ν = 0 (Table I and Table S4 of the supplementary material). The above-mentioned results all show good agreement with the simulation data and differences between fitting μ or ν and holding them fixed are barely visible to the eye so figures in the remainder of the main text are for the μ = 0.7 and ν = 0 case. In particular, d2(P, T) versus pressure P at various temperatures shows good agreement with the simulation data (Fig. 1).
TABLE I.
Fit of d2(P, T) to MD simulation data. In both cases, ν = 0.
| μ | Constant | Fit value | Uncertainty | χ2 × 105 |
|---|---|---|---|---|
| 0.70 ± 0.10 | d02 (Å2) | 0.494 6 | 0.002 0 |
|
| αP,0 (K−1) | 0.011 25 | 0.002 9 | ||
| κT,0 (MPa−1) | 0.001 62 | 0.000 5 | ||
| 1 | d02 (Å2) | 0.492 4 | 0.001 5 |
|
| αP,0 (K−1) | 0.006 24 | 0.000 09 | ||
| κT,0 (MPa−1) | 0.000 82 | 0.000 01 |
FIG. 1.
Fit of mean-square displacements d2(P, T) versus pressure P at various temperatures calculated with μ = 0.7 and ν = 0 using parameters in Table I compared to MD simulation data.
B. Below the glass transition
Although d2(P, T) calculated from Eq. (16) using parameters fit to the pressure data set, which contains data only at high temperatures, reproduce the high temperature region, they do not reproduce the low temperature region (i.e., Fig. S1 of the supplementary material). The most likely cause is the onset of glassy behavior. Here, the protein is assumed to exhibit glassy behavior in the low temperature region as in Meinhold et al.5 so that the thermal fluctuations are assumed to no longer cause transitions to other substates that lead to volume changes while pressure still causes volume changes. Thus, the volume below Tg at constant P is frozen at its Tg value but still is dependent on P with the same values of the parameters as above Tg and the magnitude of k at a given P becomes frozen at Tg. In other words, below the “glass” transition temperature, the local atomic fluctuations of the protein are assumed to be quasiharmonic with force constants that have a different value at each pressure but are independent of temperature but continuous at Tg with the high temperature values.
An important question in general is the possible pressure dependence of Tg, reminiscent of the question of the pressure dependence of Tg in glass forming materials.29 Meinhold et al.5 concluded from examining their data that Tg was independent of pressure. However, our approach identifies the pressure, temperature, and volumes dependences of Tg. For instance, if Tg is assumed to be independent of pressure, then
| (17) |
The pressure dependence of Tg can also be simply described by a linear equation
| (18) |
where Tg,0 is Tg at the reference pressure and c is a constant. Alternatively, if the volume at P relative to volume at the reference pressure is given by Eq. (9), Tg at P can be assumed to occur at the same volume change relative to Tg at the reference pressure, which is given by Eq. (11). Assuming ν = 0 as indicated by the results in Sec. III A, this implies that Tg is logarithmically dependent on pressure according to
| (19) |
where again Tg,0 is Tg at the reference pressure and c is a constant. Since the physical origin of αP,0 appears to be different from that of κT,0 as discussed in Sec. IV, the volume change associated with pressure that gives rise to changes in Tg with pressure is not assumed to have the same value of μ.
The mean-square displacements for the glass region (T < Tg) can then be related to values at Tg by
| (20) |
where
| (21) |
The values of d02, αP,0, and κT,0 take on the values from the high temperature region so that Tg and c are the only unknowns.
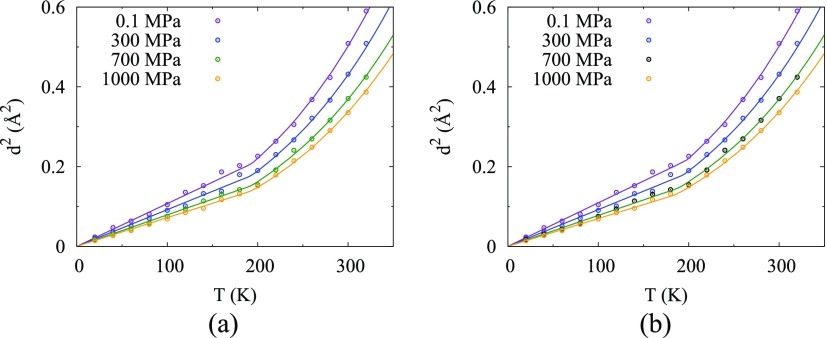
In this section, the parameters in Eq. (21) take on the values for d02, αP,0, and κT,0 in Table I. Equations (20) and (21) using different assumptions for the pressure dependence of Tg [Eqs. (17)–(19)] are fit to data for 0 K < T ≤ 160 K from the temperature data set (i.e., 0 K < T ≤ 320 K at P = 0.1, 300, 700, and 1000 MPa) of the MD simulation data for HEWL to find values for Tg,0 and c. Results for Tg,0 and c for with error analysis are reported in Table II (further details for μ = 1 and ν = 0 in Table S5 of the supplementary material and for fitted μ and ν = 0 in Table S6 of the supplementary material). First, d2(P, T) is fit assuming that Tg is invariant with respect to pressure [Eq. (17)]. When the calculated d2(P, T) is compared to the simulation data over the full range of temperatures [Fig. 2(a)], the temperature dependence over the entire temperature range is much improved and the predicted Tg,0 = 193 K is near other results for proteins.10–12 Next, assuming that Tg varies linearly with pressure [Eq. (18)] or logarithmically with pressure [Eq. (19)], the calculated d2(P, T) is compared to the simulation data, the temperature dependence is also good over the entire temperature range [shown for Eq. (19) in Fig. 2(b)]. Although difficult to see, logarithmic dependence of Tg gives the best fit since the reduced χ2 is ∼20% smaller than the constant Tg. Although the uncertainty in the value of c is large since data for only four values of pressure were used, the variation in Tg over the pressure range studied here is fairly large, from 201 K at 0.1 MPa to 191 K at 1000 MPa for μ = 1 and ν = 0.
TABLE II.
Fit of Tg to MD simulation data at low temperatures. In both cases, ν = 0.
| μ | Pressure dependence | Constant | Fit value | Uncertainty | χ2 × 105 |
|---|---|---|---|---|---|
| 0.70 ± 0.10 | Constant | Tg (K) | 192.8 | 2.2 |
|
| Linear | Tg,0 (K) | 197.2 | 3.0 |
|
|
| c (K/MPa) | 0.012 | 0.006 | |||
| Logarithmic | Tg,0 (K) | 199.9 | 3.1 |
|
|
| c | 24.8 | 12.5 | |||
| 1 | Constant | Tg (K) | 193.3 | 2.3 |
|
| Linear | Tg,0 (K) | 197.7 | 3.1 |
|
|
| c (K/MPa) | 0.012 | 0.006 | |||
| Logarithmic | Tg,0 (K) | 200.6 | 3.2 |
|
|
| c | 40.7 | 20.4 |
FIG. 2.
Mean-square displacement d2(P, T) versus temperature T at various pressures calculated with μ = 0.7 and ν = 0 using parameters in Table I, which follow Eq. (16) above Tg and (a) Eqs. (17), (20), and (21) below Tg, which is independent of pressure, or (b) Eqs. (19)–(21) below Tg, which varies with pressure, compared to MD simulation data.
C. The shape of the underlying potential
The effects of pressure on the shape of the underlying potential are also examined via an effective force constant k as a function of P. As in the work of Meinhold et al.,5 k are calculated from the displacements below Tg so that the underlying potential without the contributions of multiple conformational substates is being examined. Meinhold et al.5 calculated k using the following equation:
| (22) |
where the MD data were fitted for the slope in the denominator. In addition, by substituting Eqs. (17) and (18), or (19) into Eq. (21), k can be calculated by
| (23) |
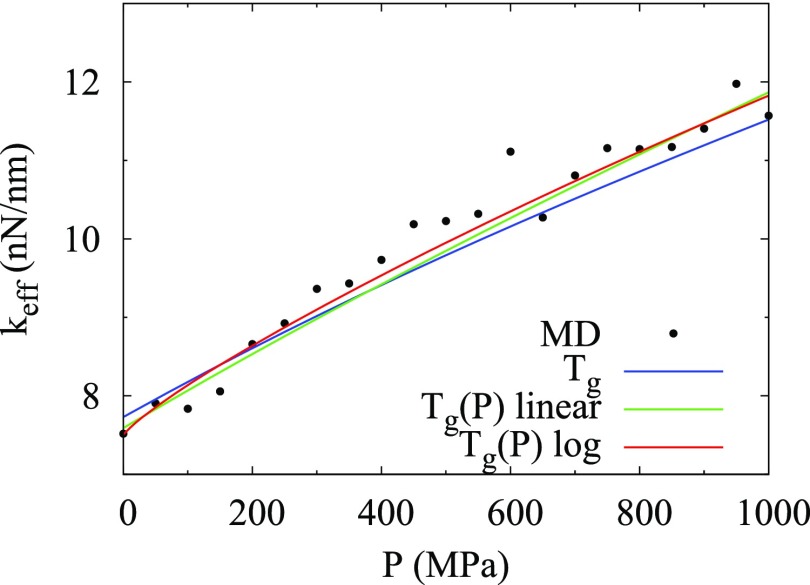
The effective force constant k calculated using Eq. (23) with parameters from Tables I and II can be compared to k from the MD simulation data. The calculated k assuming a pressure-dependent Tg(P) predict the curvature seen in the simulation k better than those calculated assuming a pressure-independent Tg (Fig. 3). Interestingly, when k in Eq. (23) is fit directly to the simulation data for k (i.e., the black dots in Fig. 3), the fitted parameters for a pressure-independent Tg or pressure-dependent Tg(P) (Tables S5 and S6 of the supplementary material) are similar to those determined by the fit to the temperature data set for d2 described above. In addition, although the reduced χ2 for fits to k are considerably higher than the fits to d2, the fits to k from simulation for a pressure-dependent Tg(P) are also better than a pressure-independent Tg, since the reduced χ2 is ∼20% smaller (Tables S5 and S6 of the supplementary material). Thus, a pressure-dependent Tg(P) is better than a pressure-independent Tg for fitting both the extensive simulation data for d2 as a function of temperature at only four pressures, and the extensive simulation data for k as a function of pressure.
FIG. 3.
Effective force constant k versus pressure calculated with μ = 0.7 and ν = 0 using parameters in Table I and either a pressure-independent Tg (blue line), the linearly pressure-dependent Tg(P) (green line), or the logarithmically pressure-dependent Tg(P) (red line), compared to MD simulation data for k (black dots).
IV. DISCUSSION
We begin with a discussion of how a quasiharmonic analysis can be used to interpret the physical origins of pressure and temperature effects on atomic fluctuations in proteins. The analysis is demonstrated on 1 ps mean-square displacements of protein hydrogen atoms only and not the surrounding solvent from 1 ns simulations of HEWL at different pressures and temperatures. Although the dynamics of heavy atoms are preferred, as pointed out in the Introduction, Meinhold et al.5 have shown that the dynamics of protein hydrogen atoms are a good measure of the dynamics of all protein atoms and thus the effective harmonic potential in which they move can be considered to be created by the protein environment. Thus, αP and κT found from these simulations are intrinsic to the protein. In particular, these intrinsic quantities differ from the partial quantities of proteins in aqueous solutions because the latter also contains contributions from surface hydration. In addition, they are limited to a single conformational state since more motion (i.e., transitions to other conformational states) will occur on the μs and ms time scales. However, even at the time scales of these simulations, an increase in the dependence of the fluctuations on temperature over what can be attributed to phonon modes of a single substate occurs above ∼200 K, which indicates that transitions to different substates occur. Thus, simulations on this time scale appear informative about dynamics of different substates within a conformational state, which are described in the quasiharmonic approximation via larger frequencies. Since the fluctuations are fit well assuming classical Einstein independent harmonic oscillators, these results indicate that the protein is not behaving like a true liquid above Tg but instead has a well-defined average structure reminiscent of a solid, consistent with the interpretation of the observed transition in proteins as a dynamical transition rather than a true glass-liquid transition.10–12 However, the oscillators are not truly non-interacting, which may be reflected in the best fit values of μ = 0.7 and ν = 0, while the ideal gas values are μ = 1 and ν = −1. In addition, since the assumptions that αP is independent of P and κT is independent of T (see Sec. II) give good agreement with the simulation data, temperature and pressure effects appear to arise from different physical processes.
The isobaric thermal expansion coefficient αP is a measure of the volume changes with temperature at constant pressure. Here, its physical origin is suggested by the dynamical transition temperature Tg found in the simulation data since Tg has been attributed in proteins to a minimum temperature where the thermal energy is sufficient to overcome activation energies to other substates. Thus, since the fitted value of αP describes the temperature dependence of the simulation data for the fluctuations above Tg, it can also be attributed to transitions to other substates. In particular, since αP is positive, the fluctuations increase not only directly due to temperature but also due to expansion caused by accessing other substates, in which an atom moves in a harmonic energy well similar to that in the underlying potential but with a shifted mean position. In addition, over the small temperature range examined here, αP appears independent of volume since ν = ∼0, and examination of a larger temperature range will be necessary to determine any volume dependence. However, the lack of dependence of αP on volume and thus the separation between neighboring atoms further supports that the physical origin of αP is mainly due to transitions between substates rather than in the effective energy wells of one substate.
The isothermal compressibility κT is a measure of the volume change with pressure at constant temperature. Here, κT was found to be almost directly proportional to the volume. More importantly, since the assumption that κT is the same above and below Tg (i.e., it is independent of the temperature) gives good agreement with the pressure dependence of the simulation data, pressure can be interpreted to have the same effect on the local minimum in the potential energy surface corresponding to a single substate below Tg as on the local minima associated with each substate above Tg, assuming the local minima of each substate are similar. In other words, κT describes the effects of pressure on the local minima in a given substate, regardless of which substate. In addition, since κT is positive, the effect of the increased pressure at this time scale is apparently to move the neighboring atoms closer, which narrows the effective energy well for a given atom and thus increases its k. However, at larger time scales, pressure has been noted to increase populations of other conformations in proteins.30
The dependence of Tg on pressure is also informative. A decreasing Tg with pressure appears to fit the simulation data for both d2 and k better than a constant Tg. This indicates that the barrier heights between substates are dependent on pressure in this simulation, in disagreement with Meinhold et al.,5 and in particular, pressure lowers the barriers. However, the scatter in values of d2 in the simulation data and large uncertainty in c (due in part to having d2 for only four pressures) make the pressure-dependence of Tg somewhat questionable. In addition, another subtle factor is that the heating and pressurizing in the HEWL data were for 100 ps and 600 ps, respectively, for each P-T value, and so slight relaxation due to pressure from the crystal structure may occur. In relation to this, simulations of dihydrofolate reductase (DHFR), which were heated and pressurized for 60 ps each using the Nosé-Hoover25,26 algorithm implemented in CHARMM,31 actually have the opposite sign for c (Huang, Rodgers, Hemley, and Ichiye, unpublished results). However, when the starting structure was equilibrated at a higher pressure (i.e., 220 atm), Tg was lower. Thus, both studies indicate that the barrier to collective motions may be decreased by high pressure, but whether it is apparent in the pressure dependence of Tg from P-T simulations starting from a single structure equilibrated at one pressure or if the pressure dependence of Tg,0 from P-T simulations starting from several structures equilibrated at different pressures may depend on the extent to which the simulation at a given P-T is allowed to relax to the pressure.
Regardless, the nonlinear increase with pressure of the force constant for the underlying potential energy minimum below Tg observed in the HEWL simulation data appears to be due to a combination of the pressure-dependent force constant of the underlying potential and the decrease in Tg with increasing pressure rather than a pressure-induced transition as suggested by Meinhold et al.5 While the pressure-dependence of Tg is described here by Eqs. (18) and (19), the exact dependency on pressure is not clear, and the fitted values of c should not be over-interpreted, given the large uncertainty due to being fit to data for only four pressures. In addition, the physical origins of the pressure dependence of Tg are likely not the same as those for κT and instead may be due to pressure affecting the separation of the substates from each other, whether mechanically or thermodynamically. If this also occurs for transitions between conformational states, the analysis presented here could help explain pressure-induced unfolding.
Finally, at longer time scales than examined here, motions occur that are better described as transitions to different conformational states. Since pressure, in addition to temperature, is known to affect populations of conformational states,30 αP and κT are likely to be affected. The dynamics of heavy atoms from simulations on longer timescales that explore the free energy surface or simulations that explore more of the potential energy surface by starting from proteins equilibrated at different pressures may be more informative about problems involving transitions to other conformational states, such as protein unfolding. In particular, results from simulations on a ∼50 ns time scale are intriguing since the fluctuations actually increase with pressure.32
V. CONCLUSIONS
Atomic fluctuations are important for the structure and function of proteins and can be determined experimentally from X-ray and neutron studies or calculated from molecular dynamics simulations. Here, a method for analyzing atomic fluctuations is developed in which the effective potential energy well for an atom is described as quasiharmonic so that volume changes due to temperature and pressure are separated in terms of an intrinsic αP and κT for the protein. The applicability of this quasiharmonic analysis is demonstrated on data from a previous molecular dynamics simulation of HEWL by Meinhold et al.5 In particular, the pressure and temperature dependence of the picosecond mean-square displacements of the HEWL simulations is shown here to be described by a quasiharmonic approximation with a constant αP and a volume dependent κT above Tg. Below Tg, the calculated displacements agree with the simulation data assuming that the temperature dependence is frozen at its Tg value but that the pressure dependence is the same as in the liquid region. Finally, the nonlinear pressure dependence of k appears to be due to the changes in Tg and frequencies with pressure rather than a transition in behavior. A quasiharmonic analysis can thus lead to a better understanding of the energy landscapes of complex biomolecules. Indeed, quasiharmonic analyses of atomic fluctuations from longer time scale simulations, especially if the solvent is also analyzed, could be useful in understanding problems such as protein folding.
SUPPLEMENTARY MATERIAL
See supplementary material for more information on the simulation methods of Meinhold et al.,5 for tables of fits of mean-square displacements with different assumptions for fitting μ and ν, and for figure of mean-square displacements versus temperature assuming no glass transition.
ACKNOWLEDGMENTS
T.I. is grateful for support from a grant from the National Institutes of Health No. R01 GM122441 and for support from the McGowan Foundation. J.M.R. and R.J.H. acknowledge support from the Department of Energy/National Nuclear Security Administration through Grant No. DE-NA-0002006 for the Carnegie/DOE Alliance Center (CDAC) and from the Alfred P. Sloan Foundation through the Deep Carbon Observatory. The views and conclusions contained in this document are those of the authors and should not be interpreted as necessarily representing the official policies or endorsements, either expressed or implied, of the U.S. Government. This work used computer time on the Extreme Science and Engineering Discovery Environment (XSEDE) granted via No. MCB990010, which is supported by the National Science Foundation Grant No. OCI-1053575 and the Medusa cluster, which is maintained by the University Information Services at Georgetown University.
REFERENCES
- 1.Frauenfelder H. and Leeson D. T., Nat. Struct. Biol. 5, 757 (1998). 10.1038/1784 [DOI] [PubMed] [Google Scholar]
- 2.Onuchic J. N. and Wolynes P. G., Curr. Opin. Struct. Biol. 14, 70 (2004). 10.1016/j.sbi.2004.01.009 [DOI] [PubMed] [Google Scholar]
- 3.Parak F. G., Rep. Prog. Phys. 66, 103 (2003). 10.1088/0034-4885/66/2/201 [DOI] [Google Scholar]
- 4.Meinhold L. and Smith J. C., Phys. Rev. E 72, 061908 (2005). 10.1103/physreve.72.061908 [DOI] [PubMed] [Google Scholar]
- 5.Meinhold L., Smith J. C., Kitao A., and Zewail A. H., Proc. Natl. Acad. Sci. U. S. A. 104, 17261 (2007). 10.1073/pnas.0708199104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Berman H. M., Westbrook J., Feng Z., Gilliland G., Bhat T. N., Weissig H., Shindyalov I. N., and Bourne P. E., Nucleic Acids Res. 28, 235 (2000). 10.1093/nar/28.1.235 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Ichiye T. and Karplus M., Proteins: Struct., Funct., Genet. 2, 236 (1987). 10.1002/prot.340020308 [DOI] [PubMed] [Google Scholar]
- 8.Ichiye T. and Karplus M., Biochemistry 27, 3487 (1988). 10.1021/bi00409a054 [DOI] [PubMed] [Google Scholar]
- 9.Ichiye T. and Karplus M., Proteins: Struct., Funct., Genet. 11, 205 (1991). 10.1002/prot.340110305 [DOI] [PubMed] [Google Scholar]
- 10.Vitkup D., Ringe D., Petsko G. A., and Karplus M., Nat. Struct. Biol. 7, 34 (2000). 10.1038/71231 [DOI] [PubMed] [Google Scholar]
- 11.Frauenfelder H., Phys. E 42, 662 (2010). 10.1016/j.physe.2009.08.005 [DOI] [Google Scholar]
- 12.Ringe D. and Petsko G. A., Biophys. Chem. 105, 667 (2003). 10.1016/s0301-4622(03)00096-6 [DOI] [PubMed] [Google Scholar]
- 13.Gillet P., Hemley R. J., and McMillan P. F., in Ultrahigh-Pressure Mineralogy: Physics and Chemistry of the Earth’s Deep Interior, edited by Hemley R. J. (Mineralogical Society of America, Washington, DC, 1998), Vol. 37, p. 525. [Google Scholar]
- 14.Fultz B., Prog. Mater. Sci. 55, 247 (2010). 10.1016/j.pmatsci.2009.05.002 [DOI] [Google Scholar]
- 15.Wallace D. C., Thermodynamics of Crystals, 1st ed. (John Wiley and Sons, New York, 1972). [Google Scholar]
- 16.Doster W., Cusack S., and Petry W., Nature 337, 754 (1989). 10.1038/337754a0 [DOI] [PubMed] [Google Scholar]
- 17.Fenimore P. W., Frauenfelder H., McMahon B. H., and Parak F. G., Proc. Natl. Acad. Sci. U. S. A. 99, 16047 (2002). 10.1073/pnas.212637899 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Nash D. P. and Jonas J., Biochemistry 36, 14375 (1997). 10.1021/bi970881v [DOI] [PubMed] [Google Scholar]
- 19.Harrison D. and Moelwyn-Hughes E. A., Proc. R. Soc. London, A 239, 230 (1957). 10.1098/rspa.1957.0035 [DOI] [Google Scholar]
- 20.Kharakoz D. P., Biophys. J. 79, 511 (2000). 10.1016/s0006-3495(00)76313-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Berendsen H. J. C., van der Spoel D., and van Drunen R., Comput. Phys. Commun. 91, 43 (1995). 10.1016/0010-4655(95)00042-e [DOI] [Google Scholar]
- 22.Lindahl E., Hess B., and van der Spoel D., J. Mol. Model. 7, 306 (2001). 10.1007/s008940100045 [DOI] [Google Scholar]
- 23.Kaminski G. A., Friesner R. A., Tirado-Rives J., and Jorgensen W. L., J. Phys. Chem. B 105, 6474 (2001). 10.1021/jp003919d [DOI] [Google Scholar]
- 24.Refaee M., Tezuka T., Akasaka K., and Williamson M. P., J. Mol. Biol. 327, 857 (2003). 10.1016/s0022-2836(03)00209-2 [DOI] [PubMed] [Google Scholar]
- 25.Nosé S., J. Chem. Phys. 81, 511 (1984). 10.1063/1.447334 [DOI] [Google Scholar]
- 26.Hoover W. G., Phys. Rev. A 31, 1695 (1985). 10.1103/physreva.31.1695 [DOI] [PubMed] [Google Scholar]
- 27.Parrinello M. and Rahman A., J. Appl. Phys. 52, 7182 (1981). 10.1063/1.328693 [DOI] [Google Scholar]
- 28.Nosé S. and Klein M. L., Mol. Phys. 50, 1055 (1983). 10.1080/00268978300102851 [DOI] [Google Scholar]
- 29.Hemley R. J., Jephcoat A. P., Mao H. K., Ming L. C., and Manghnani M. H., Nature 334, 52 (1988). 10.1038/334052a0 [DOI] [Google Scholar]
- 30.Akasaka K., Chem. Rev. 106, 1814 (2006). 10.1021/cr040440z [DOI] [PubMed] [Google Scholar]
- 31.Brooks B. R., Brooks C. L. III, A. D. MacKerell, Jr., Nilsson L., Petrella R. J., Roux B., Won Y., Archontis G., Bartels C., Boresch S., Caflisch A., Caves L., Cui Q., Dinner A. R., Feig M., Fischer S., Gao J., Hodoscek M., Im W., Kuczera K., Lazaridis T., Ma J., Ovchinnikov V., Paci E., Pastor R. W., Post C. B., Pu J. Z., Schaefer M., Tidor B., Venable R. M., Woodcock H. L., Wu X., Yang W., York D. M., and Karplus M., J. Comput. Chem. 30, 1545 (2009). 10.1002/jcc.21287 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Huang Q., Rodgers J. M., Hemley R. J., and Ichiye T., J. Comput. Chem. 38, 1174 (2017). 10.1002/jcc.24737 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
See supplementary material for more information on the simulation methods of Meinhold et al.,5 for tables of fits of mean-square displacements with different assumptions for fitting μ and ν, and for figure of mean-square displacements versus temperature assuming no glass transition.