Divalent Cation Removal by Donnan Dialysis for Improved Reverse Electrodialysis

Abstract

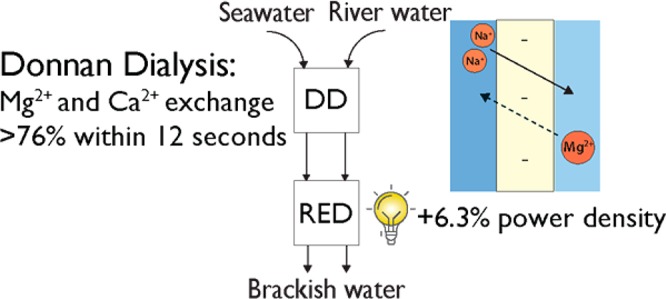
Divalent cations in feedwater can cause significant decreases in efficiencies for membrane processes, such as reverse electrodialysis (RED). In RED, power is harvested from the mixing of river and seawater, and the obtainable voltage is reduced and the resistance is increased if divalent cations are present. The power density of the RED process can be improved by removing divalent cations from the fresh water. Here, we study divalent cation removal from fresh water using seawater as draw solution in a Donnan dialysis (DD) process. In this way, a membrane system with neither chemicals nor electrodes but only natural salinity gradients can be used to exchange divalent cations. For DD, the permselectivity of the cation exchange membrane is found to be crucial as it determines the ability to block salt leakage (also referred to as co-ion transport). Operating DD using a membrane stack achieved a 76% reduction in the divalent cation content in natural fresh water with residence times of just a few seconds. DD pretreated fresh water was then used in a RED process, which showed improved gross and net power densities of 9.0 and 6.3%, respectively. This improvement is caused by a lower fresh water resistance (at similar open circuit voltages), due to exchange of divalent for monovalent cations.

Short abstract

This paper described a sustainable method of divalent cation exchange that avoids chemical and power usage to enhance renewable energy harvesting from natural salinity gradients.

Introduction

In the treatment of water there is an increasing interest in pretreatment technologies to enhance process efficiencies. For reverse electrodialysis (RED), where the controlled mixing of fresh water and seawater is used to harvest power, divalent cations in river water can significantly decrease RED performance.¹⁻³ In membrane-based processes that use natural waters, scaling can lead to lower efficiencies. Typical scaling consists of the divalent cations Ca²⁺ and Mg²⁺ with the anions SO₄^2– and CO₃^2–, which form salts with low solubilities leading to precipitation.⁴⁻⁷ These precipitates cause membrane fouling, which decreases water recoveries for filtration or current efficiencies for ED processes.

It is therefore of interest to remove divalent cations prior to these hardness-sensitive processes. Divalent cations can be precipitated by chemical precipitation or exchanged by processes such as ion exchange (IEX) or Donnan dialysis (DD).⁸ In a typical IEX process, a column loaded with ion-exchange resin is preconditioned with monovalent ions such as Na⁺ or H⁺, which can exchange for undesired divalent cations. The total charge of the ions in solution (concentration multiplied by valence of the ions) does not change; however, divalent cations are exchanged for monovalent cations in the resin. The driving force of this exchange is entropic gain: release of two monovalent cations by capturing a single divalent cation. After using IEX to exchange undesired divalent cations, the IEX resin has to be regenerated with a highly concentrated monovalent cation (or acid) containing stream. Typically, two IEX columns are required so one can exchange divalent cations while the other is regenerated. This doubles capital expenses and in addition requires chemicals (brine or acid) to regenerate the IEX resin.⁸

In contrast, DD is a technique that can exchange divalent cations continuously without the need for regeneration.⁹ The same mechanism is found in biological cell membranes, where Na⁺/Ca²⁺ exchangers use a gradient of Na⁺ to transport Ca²⁺ against its concentration gradient.¹⁰ This exchange process relies on ion exchange membranes, instead of ion exchange resins as used for IEX. The solution with undesired divalent cations is brought into contact with a cation exchange membrane (CEM), and on the other side of the CEM, there is a draw solution containing a high concentration of monovalent cations. This configuration allows for exchange of the divalent cations with monovalent cations in the draw solution. The driving force behind this process is a similar entropic gain as found in IEX, resulting in high Donnan potentials for monovalent species.¹¹⁻¹⁴

Recent studies on divalent cation exchange pretreatments have been performed by Vanoppen et al. for reverse-osmosis (RO), using IEX as well as DD.^8,15 In their work they found IEX to be substantially more cost-effective due to the high price of ion exchange membranes (300 €/m²) required for the DD process. However, they calculated that if the price of ion exchange membranes decreases to ∼10 €/m², the process becomes economically interesting, which is a price range comparable to RED.¹⁶

Previous work on RED has shown that divalent cations are a major challenge in this process and limit the obtainable power densities due to both membrane resistance increase and uphill transport.^1,2 The use of new membranes that do not suffer from significant membrane resistance increase overcomes the first limitation.¹⁷ However, uphill transport remains a problem due to the presence of divalent cations in the river water. Uphill transport is the exchange of divalent cations in the river water against their concentration gradient with monovalent cations in the seawater, which effectively lowers the obtainable voltage. Monovalent-selective CEMs could counter uphill transport; however, recent work showed that these monovalent selective CEMs have an increase in membrane resistance over time while multivalent permeable CEMs have stable resistances for longer times.¹⁸ Besides uphill transport, the low conductivity of the river water also limits power output. For a typical RED stack, the dominant resistance is that of the river water.¹⁹⁻²² There are two reasons for this low conductivity: First, the ionic conductivity of the river water is low, and therefore this compartment resistance in the RED stack is high. Recent studies have focused on decreasing this resistance either using decreased spacer thickness¹⁹ or by introducing dynamic spacer to lower the river water compartment thickness.²² As such, it was possible to reduce the resistance of this compartment, as its resistance scales linearly with compartment thickness. Second, the low river water concentration combined with a large concentration gradient between the seawater and the river water on either side of the membrane induces an increased membrane resistance in both AEMs and CEMs.^20,21 Both of these effects stress the importance of decreasing the river water resistance to decrease the overall stack resistance. DD can therefore be an attractive process to alleviate these resistances by exchanging divalent cations for monovalent cations with a higher activity (one divalent cation is exchanged for two monovalent cations), which decreases resistance.

In this work, we study the applicability of DD to exchange divalent cations from river water by using seawater as a draw solution, as shown in Figure 1. Studies using artificial natural waters are performed with different cation exchange membranes to show the proof-of-principle and to investigate the influence of membrane properties on DD performance. The effect of DD pretreatment on RED power harvesting is then assessed with natural river and seawater and compared to theoretical models to determine the maximum possible enhancement for RED with DD pretreatment.

Figure 1.

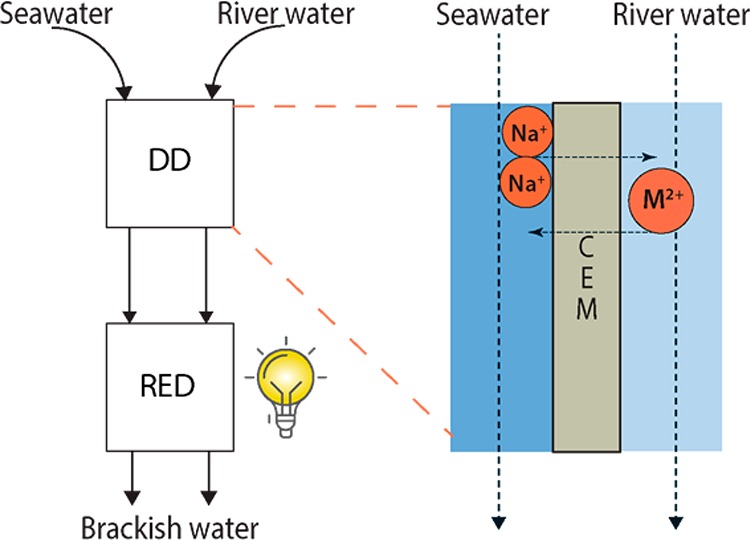
Schematic concept of DD as pretreatment, to exchange divalent cations from river water and subsequent use in combination with RED. In the DD pretreatment step, exchange of divalent cations for monovalent Na⁺ from seawater is achieved.

Theory

In this section, a detailed background of DD is given to understand the principles and to predict divalent cation exchange. The influence of river water ion concentration on RED performance is predicted to determine the theoretical benefits of using DD pretreatment as well.

DD

The driving force of DD is an entropic gain by exchanging a single divalent cation for two monovalent cations at the low concentration side. This entropic gain can be analyzed by Donnan potentials of the different ionic species. For each ionic species “i”, Donnan potentials can be calculated by their respective concentrations on each side of the membrane (eq 1).^8,9,13 Assumptions in this equation are that there is negligible convection through the membrane, that electroneutrality is conserved, and that the membrane is perfectly permselective (no co-ion transport through the membrane). The system will strive toward equilibrium, driven by entropy, and as such the Donnan potentials of each ionic species will equilibrate. This does not imply that their concentrations are equal; only the ratio of the ionic species to the power one over their respective valence will equilibrate. In the case of monovalent sodium (Na⁺, z = 1) and a divalent cation (M²⁺, z = 2) the following equilibrium will establish (eq 2):

1

2

where E_Don is the Donnan potential (V), R is the gas constant (8.314 J/(K·mol)), T is the temperature (K), F is the Faraday constant (96 485 C/mol), z is the valence of the ion (−), and a is the activity of ion i (M) in the concentrate (c) or diluate (d) compartment.

Donnan potentials depend on the respective activities of each ion across the membrane (eq 2). Therefore, when the ion activities in both streams are known, one can predict the direction of transport for each ion. For typical DD processes, the activity in the concentrate should be (at least) 10 times larger compared to that in the diluate to ensure sufficient driving force.¹³ For this application, when using (artificial) river and seawater, the activity ratio of ions in seawater and river water is ∼90. Donnan equilibria and concentrations over time are given in Figure 2 for Na⁺ and Mg²⁺. For each mole of divalent Mg²⁺ exchanged, double the quantity of moles of Na⁺ is exchanged until equilibrium is reached. This equilibrium can be determined from Donnan potentials for Na⁺ and Mg²⁺ (see Figure 2c) during the exchange. Initially, the Donnan potential of Mg²⁺ is lower than Na⁺. This means that Na⁺ will move with its concentration gradient (from seawater to river water), whereas Mg²⁺ will move against its concentration gradient (from river water to seawater), to maintain electroneutrality. This exchange will continue until the Donnan potentials of both ions are equal.

Figure 2.

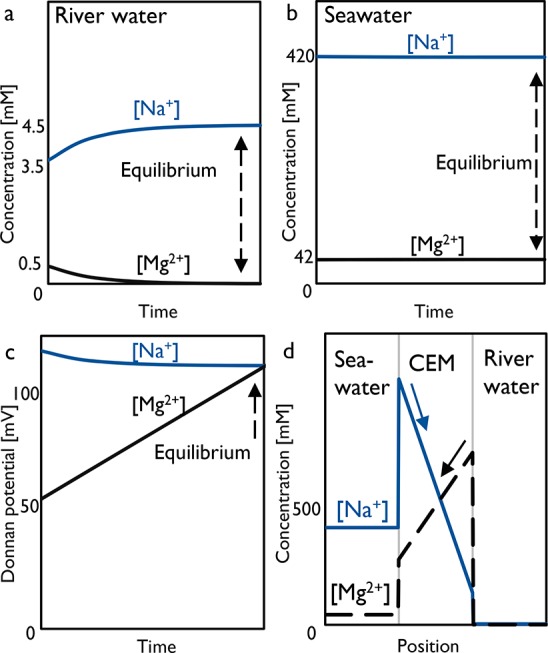
Theoretical batch DD process of river water with seawater as draw solution. Top figures show the concentrations over time in the river water (a) and seawater (b), respectively, where initial concentrations are for natural waters. Part c shows Donnan potentials of Na⁺ and Mg²⁺ over time. The large potential of Na⁺ (122 mV) compared to Mg²⁺ (57 mV) drives the exchange of Mg²⁺ uphill. Finally, at equilibrium, the Donnan potential of each cation is equal (in this case around 115 mV). Part d shows the initial cation concentration profiles in the seawater, CEM, and river water, respectively, calculated from the initial Donnan equilibrium. Straight arrows indicate transport direction for each cation and dashed arrows show equilibrium.

RED Model

DD treated water can subsequently be used as input for RED to harvest power from the salinity gradient. For RED, there is a trade-off between open circuit voltage (OCV), which increases at a lower river water salt concentration, and the resistance (R_stack), which decreases at a higher river water salt concentration. To predict the maximum obtainable power density in RED after complete exchange of divalent for monovalent cations in the river water using DD, a previously developed model by Veerman et al. is adapted.²³ The aim of this model is to understand the influence of the concentration of salt in the river water. Specific details on the model are given in the Supporting Information (SI 1).

The dependences of the open circuit voltage (OCV), stack resistance (R_stack), and power density (PD) are calculated as a function of the river water NaCl concentration. In the model, the effect of divalent cations is excluded, as the aim of the model is to establish the effect of complete divalent cation exchange by DD for RED. For natural river water, the NaCl concentration is 0.0035 M, which is well below the NaCl concentration with highest predicted power densities (between 0.01–0.02 M for this system). This trade-off between open circuit voltage and resistance in the stack is shown in Figure 3. The maximum power density at a concentration of 0.014 M NaCl enables a 13% increase in gross power density compared to natural river water (0.0035 M NaCl). In the Results and Discussion section, the experimental results obtained with DD pretreated water will be compared with this predictive model.

Figure 3.

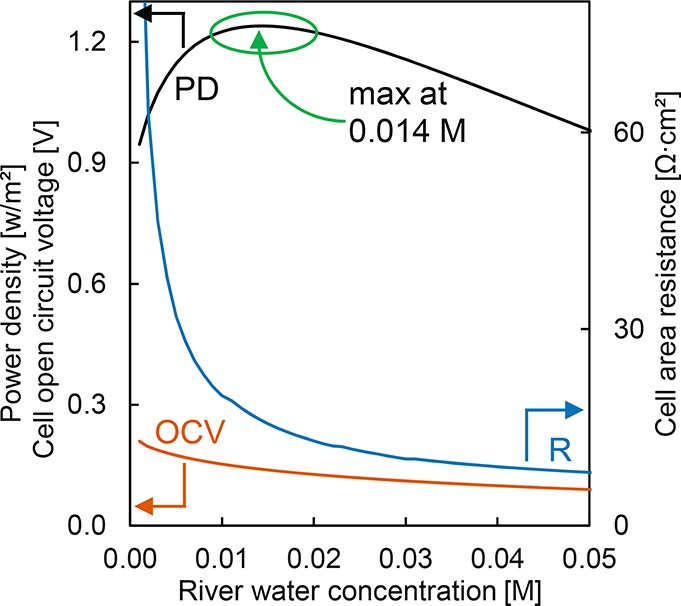
Modeled trade-off between RED stack performance and concentration of NaCl in river water in M. The graph shows the optimum between open circuit voltage (OCV) and cell area resistance (R). The optimum for gross power density (PD) is between 0.01 and 0.02 M with a maximum at 0.014 M. Seawater concentration (not shown) is at natural concentrations for the Waddensea (NL) (0.40 M).

Materials and Methods

Membranes and Chemicals

CEMs, Neosepta standard-grade CMX (Eurodia, France), multivalent-permeable T1, and standard-grade Type II CEMs (FUJIFILM, The Netherlands) were used for DD experiments; only T1 membranes are used for RED experiments. Anion exchange membranes (AEMs) Type I were used for the RED experiments (FUJFILM, The Netherlands). Potassium chloride, magnesium chloride hexahydrate, anhydrous calcium chloride, and potassium hexacyanoferrate (III) and potassium hexacyanoferrate (II) trihydrate, which act as a redox couple for RED, were purchased from Sigma-Aldrich. Sodium chloride (pharmaceutical grade) was kindly supplied by AkzoNobel (Hengelo, The Netherlands).

DD in Diffusion Cells and Stacks

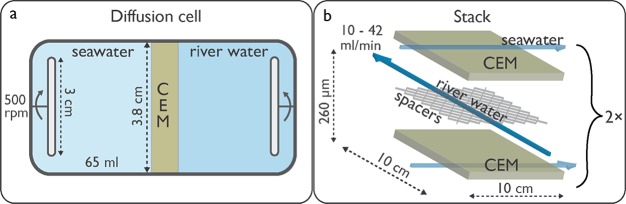
For lab-scale DD, diffusion cells with compartment volumes of 65 mL (with magnetic stirrers) and an active membrane area of 11.3 cm² were used. Three different CEMs were evaluated. These CEMs were soaked in the same draw solutions as used for DD for 24 h prior to use. Samples of river and seawater compartments were taken over time to monitor the cation concentrations. To scale-up and operate DD continuously, a crossflow RED stack (REDstack BV, The Netherlands) with a 10 × 10 cm² active area was used. Both setups are illustrated in Figure 4. Four CMX membranes were used to create two channels to feed fresh water and three channels to feed seawater. In this manner both CEMs in contact with the fresh water channel were used for ion exchange.

Figure 4.

Diffusion cell (a) and stack (b) configurations for DD used in this study. Cation exchange membranes are shown in dark green, river water is shown in dark blue, and seawater is shown in light blue; spacers and stir bars are shown in gray.

Polyamide woven spacers, to separate the membranes in DD and RED (Deukum GmbH, Germany), had a thickness of 260 μm and a free void fraction (volume) and free surface fraction (projected surface) of 0.726 and 0.476, respectively.

Ion chromatography (IC) was used to analyze the cation concentrations (Metrosep C6-150/4.0 column in a Metrohm 850 Professional IC with eluent of 1.7 mM HNO₃ and dipicolinic acid). Cation samples were diluted with 2 mM HNO₃ prior to analysis.

RED Stack Performance Evaluation

Reverse electrodialysis experiments were performed with 10 cell pairs of T1 CEM and Type I AEMs. These membranes were soaked for 24 h in 0.5 M NaCl prior to assembly in the stack. The T1 CEM was selected because of its superior RED performance in waters with divalent cations; however, it still suffers from uphill transport.¹⁷

A cross-flow RED stack (REDstack BV, The Netherlands) with an active area of 6.5 × 6.5 cm² was equipped with Pt-coated Ti mesh electrodes (Magneto Special Anodes BV, The Netherlands). The water composition obtained from DD was used as feed in the RED stack. The temperature was controlled (20 ± 1 °C) by a Julabo F12-ED thermostat, and pulsation dampeners (in-house built) were used to suppress pulsations caused by the peristaltic feedwater pumps (Cole Parmer). An in-house built flow meter (McMillan Co. 101 flo-sen) was used to measure the flow rate. For the electrode rinse, a solution of 0.25 M NaCl with 0.1 M K₄Fe(CN)₆ and 0.1 M K₃Fe(CN)₆ was used. An overpressure of 0.1 bar on the electrolyte was applied to ensure membrane and spacer packing.

Electrochemical analysis of the stack was performed as described in previous work.¹⁷ First, membranes were equilibrated with the feed solution for 20 min under current (20 A/m²). Next, the OCV and resistance by alternating current (AC) were measured. For the AC resistance, three measurements were performed at 10, 5, and 1 kHz in that order, at an amplitude of 0.01 A (2.4 A/m²) to measure the ohmic resistance of the stack. Finally, for the direct current (DC) resistance (including nonohmic resistance) and the power densities, 10 current steps from 0 to 50 A/m² and 10 current steps back to 0 A/m² were applied to measure the total resistance and calculate the stack power densities. Each current density was applied for 30 s before the voltage was measured to allow for buildup of boundary layers. Membranes were characterized on membrane resistance in 0.5 M NaCl using DC and permselectivity in 0.1/0.5 M NaCl.¹⁷

Results and Discussion

In this study, we investigate the exchange of divalent cations by DD, as a pretreatment for RED. First, results on DD are reported using lab-scale diffusion cells with three different CEMs. Based on the lab-scale study, the best membrane is selected for continuous operation in a membrane stack. The scale-up of DD in a membrane stack is performed, followed by using the pretreated water in a RED process to assess its effect.

DD in Lab-Scale Diffusion Cells

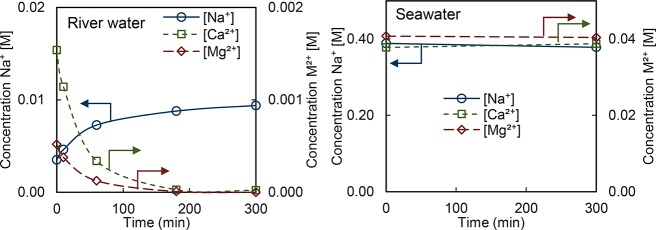
Figure 5 shows the cation concentrations in the river water during DD. The divalent cation concentrations decrease over time while the Na⁺ concentrations increase. After 180 min, the majority of divalent cations is removed (above the experimental detection limit of 0.1 mM). Correspondingly, in the seawater a small decrease in Na⁺ concentration and a small increase in divalent cation concentrations is observed. Since the absolute concentrations in the seawater are much higher than those in the river water, the relative change in these concentrations is small and therefore the composition of the seawater is hardly changed. These results demonstrate that the exchange of divalent for monovalent cations indeed occurs. Moreover, the reached equilibrium concentrations are equivalent to those predicted by the Donnan potential calculations, shown in the Supporting Information (SI 2).

Figure 5.

Concentrations of cations in the DD process with natural river (left) and seawater (right) across CMX in a small scale diffusion cell over time. Lines are shown to guide the eye. Measurements are triplicates and errors are typically below 1%.

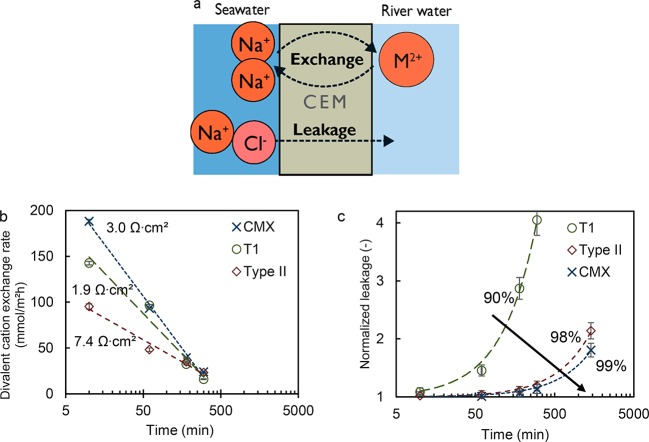
These measurements are performed for three different CEMs, and their performances are compared in Figure 6. The exchange rate should be as high as possible to allow for short residence times. It is expected that the membrane resistance is a suitable predictor for exchange rates, as it is a measure for ionic transport rate at a certain driving voltage. These driven voltages are defined by the concentrations in the solutions and are therefore equal for all CEMs. However, there is no clear correlation between the exchange rate and the electrical resistance. This difference, we believe, is caused by the significant leakage for the T1 membrane, which happens simultaneously with the exchange (see Figure 6a). The leakage is defined here as the total equivalent concentration (ion concentration times charge) in the river water at time t normalized to the starting concentration. Therefore, its effective exchange rates are lower than would be expected from its low resistance. For the best CEM, CMX, 98% divalent cation removal after 3 h with 40 mmol/(m²·h) is achieved.

Figure 6.

Schematic drawing of the exchange and leakage processes occurring in DD (a). Divalent cation exchange rates (b) and normalized leakage (c) of CMX, Type II, and T1 CEMs are shown as a function of log time. Resistances shown in the exchange rate graph are membrane area resistances (b) and percentages shown in the leakage graph are the permselectivities of each membrane (c). In the graph with exchange rates logarithmic trend lines and in the figure with leakage linear trend lines are plotted for visual aid.

Next to the exchange, there is the (unwanted) leakage of salts (due to co-ion (anion) diffusion) from the seawater through the CEM to the river water. The purpose of DD in this case is to exchange the divalent cations from the river water without a major increase of the total salt content in the river water, as this could lower the RED power density due to a lower driving force (salinity gradient). The model in the Theory section predicted an optimum NaCl concentration between 0.01–0.02 M, and in Figure 5, DD reaches the lower limit of this range (0.010 M). The normalized leakage depends on permselectivity; for 100% permselective membranes the normalized leakage should remain close to 1 (the initial concentration). In Figure 6, it is shown that the lowest permselective membrane T1, with a permselectivity of 90%, leaks more salt over time compared to Type II and CMX with permselectivities of 98% and 99%, respectively, as was expected. It appears that there is a trade-off for the divalent cation exchange rate between permselectivity and resistances, and a high (98%) permselectivity is desired to prevent significant leakage. For these reasons (high permselectivity and low leakage), the CMX membrane was selected for scale-up.

Scale-up of DD in Stacks

These lab-scale experiments show the potential of DD using cation exchange membranes with seawater as draw solution to exchange divalent cations from river water. Residence times or surface-to-volume ratios (∼17 m²/m³) are limiting factors in these cells, so to decrease residence times from hours to seconds, one must improve the membrane surface to treated volume ratio to obtain viable residence times. These high surface-to-volume ratios are required for a continuous and high-throughput process without the need for large vessels. For this reason, membrane stacks are investigated to improve surface-to-volume ratios compared with diffusion cells. Crossflow RED stacks have a very high surface-to-volume ratio (∼7700 m²/m³ in this study), as the active area is 10 × 10 cm² with a channel thickness of only 260 μm.

Scale-up of DD was performed using CMX membranes, as this membrane showed the lowest leakage and the highest exchange rate in diffusion cells. In Figure 7, the results for DD with CMX in a stack are shown. At residence times of only several seconds, there is already a clear decrease in Ca²⁺ in the river water through exchange for Na⁺, indicating the applicability of larger-scale operation of these systems. Similar divalent cation exchange rates are observed as in the diffusion cells (44 mmol/(m²·h) at 11.3 s). At residence times larger than 7 s, the exchange appears to level off. Initially, the diluate compartment consists of nearly 40 mol % of divalent cations; however, after DD the divalent cation content is reduced to between 13 to 4 mol % (divalent cation removal of 45 to 76%) at an exchange rate of 100–40 mmol/(m²·h) depending on residence time (from 2.7 to 11.3 s), shown in Supporting Information (SI 2). Similar removal results have been obtained in recent work on DD by Vanoppen et al., who achieved divalent cation removal of 70–80% at a rate of 20 mmol/(m²·h) using Fuji Type II CEMs in a stack.⁸

Figure 7.

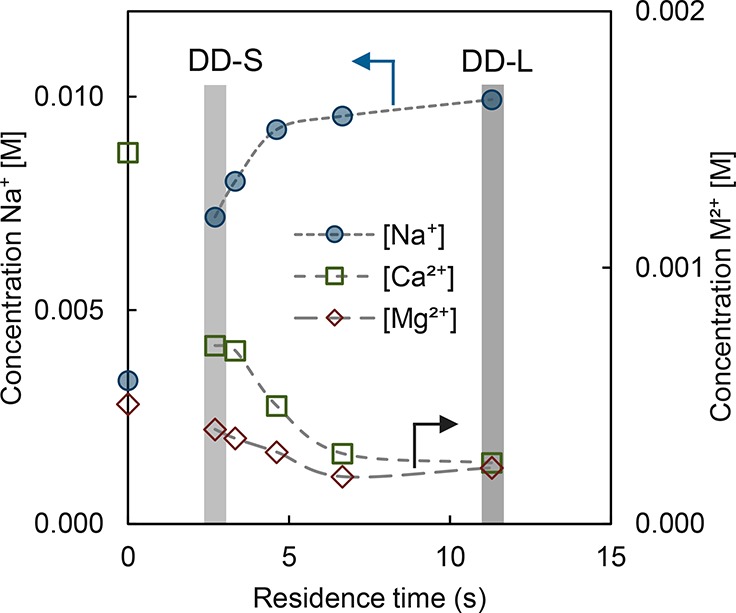
Concentrations as a function of residence time for the scale-up DD in the river water compartment. Short (DD-S) and long (DD-L) residence times for DD are indicated by gray bars; both are used for RED pretreatment. Relative errors of the cation concentrations are below 1%, and for clarity error bars are omitted.

The results shown here demonstrate that DD is scalable and that divalent cations can be removed with residence times of just a few seconds. Detailed comparison between DD in the cell and in the stack is given in the Supporting Information (SI 2).

RED Stack Performance

Finally, the effect of using DD pretreated river water for RED is investigated. Initially, RED experiments with benchmark concentrations (0.5 M vs 0.017 M) of NaCl are done for comparison with the model calculations and literature.^2,17 The model river and seawaters, as well as treated water by DD at a short (DD-S: 2.7 s) and long DD residence time (DD-L: 11.3 s), are used to evaluate the obtainable energy through RED. Water compositions for all streams are provided in the Supporting Information (SI 3).

In Figure 8, the measured OCV and cell area resistances are plotted together with the calculated values from the model. The two extremes of DD are shown in the graph. Longer DD residence times allow for longer exchange times for divalent cations with Na⁺, resulting in lower divalent cation concentrations. Effectively, the OCV in RED remains very similar before and after DD. This was unexpected as the DD pretreatment decreases divalent cation concentrations and thus should decrease the effect of uphill transport. This expected increase in OCV is shown in the model predictions (see Figure 8). However, we also exchange these divalent cations for Na⁺, and therefore the concentration gradient in RED decreases as well. In other words, the overall result is that the mitigation of divalent cation uphill transport and the decrease in Na⁺ gradient counterbalance each other and the OCV is minimally affected.

Figure 8.

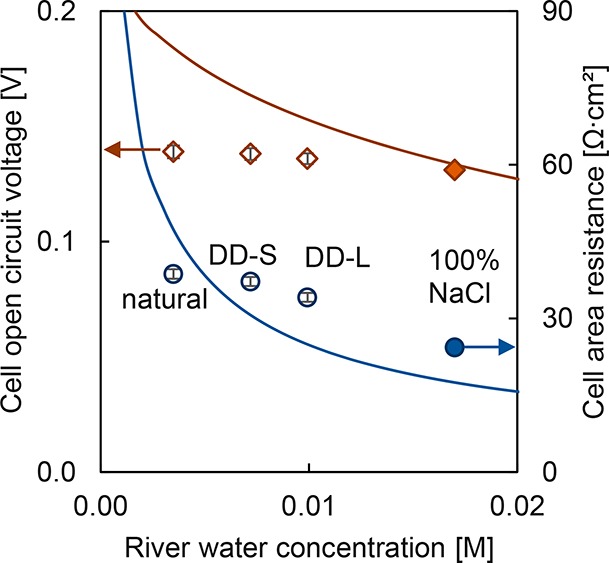
Cell OCV and cell area resistance versus river water NaCl concentration. Data (◆ = OCV, ● = area resistance) and model predictions (lines) are shown. Natural is untreated river water and DD-S and DD-L denote short and long DD pretreatment. Measurements are performed in triplicate, and error bars are standard deviations.

However, the cell resistance is just as important for determining the obtainable power density. In benchmark river water (0.017 M NaCl), this resistance is low due to the relatively high conductivity of the river water compartment. In contrast, natural river water contains divalent cations and a lower overall salt concentration, which result in a higher resistance. The river water treated by DD has a higher concentration of Na⁺, which has higher activity compared to divalent cations, and therefore the resistance of the river water compartment decreases. The predicted resistances are not in perfect agreement with the measured values, since divalent cations in water and membranes as well as gradient-induced resistances are not included in the predictions. These divalent cations decrease river water conductivity but increase membrane resistance, so the overall effect is not straightforward to predict. Qualitatively, the predictions do match the data showing that more exchanged Na⁺ for divalent cations decreases the cell resistance.

One could argue that simply increasing the river water conductivity has the same effect. To test this, seawater is mixed with river water to a conductivity equal to the one reached by DD-L, but with different composition (high divalent cation concentrations). RED stack resistances for this water are close to DD treated river water, but the OCV drops significantly due to both a high divalent cation concentration (uphill transport) and a lower overall gradient. This causes a decrease in power density of 21% compared to untreated water (Supporting Information (SI 4)).

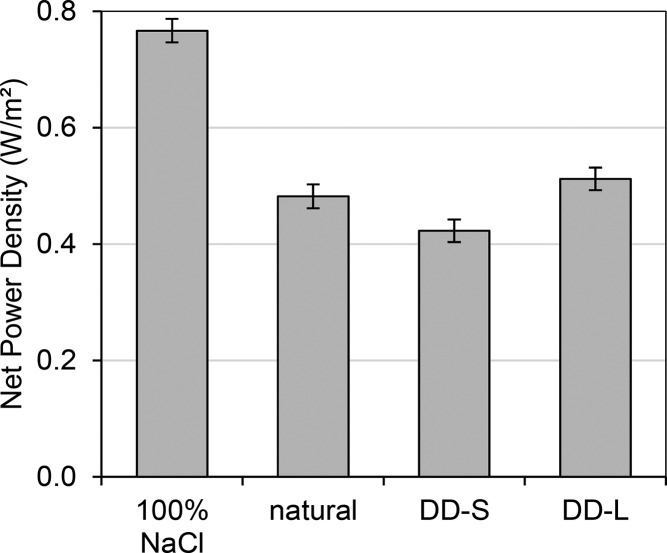
In the end, power density is the main performance parameter for RED as it takes both resistance and OCV effects into account. The OCV hardly changes while resistance decreases upon DD pretreatment. Gross power densities—the power output per m² of membrane cell pair area—with DD can be improved by 1.4 to 9.0% compared to the case without DD as determined by experiments. By using a model, a 13% improvement in gross power density is predicted for DD-L at 0.010 M NaCl. With the DD pretreatments in this study, not all divalent cations are exchanged; hence, in the RED experiments there are still ∼25% divalent cations present, which explains the lower improvements as compared to the predictions. These improvements in power density are achieved without any addition of chemicals (such as for IEX) or electrical energy (such as ED), by utilizing only a concentrated stream that is already present. The cost of DD, however, is an extra pretreatment step, which does require pumping energy. In Figure 9, the net power density after subtracting pumping losses for DD and RED is shown. At high flow velocities (DD-S) there is a large pressure drop and thus loss in net power density, whereas at low flow velocities (DD-L) this pressure drop is smaller. DD-L gives a net power density gain of 6.3% over the case without DD pretreatment.

Figure 9.

Net power densities with 100% NaCl, natural waters, and DD (short and long residence times) pretreated river water. Measurements are performed in triplicate, and error bars are standard deviations.

This work aimed to provide a proof of principle of using seawater to exchange divalent cations in the river water as pretreatment for RED. In this research, there is still room for optimization of the DD stack. Higher surface-to-volume ratios and enhanced mixing without drastic increases in pressure drops would allow further improvements in removal of divalent cations in DD. This could be achieved by using mixing promotors, such as profiled membranes.²⁴ In that way, more divalent cations can be exchanged, allowing the experimental power density improvements to approach the calculated 13% power density improvement. Furthermore, less scaling is another benefit of this pretreatment.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acssuschemeng.8b00879.

• Additional information on the RED model, Donnan potentials, and surface contact and residence times; scale up comparison between diffusion cells and stacks; and ionic compositions for all streams as well as RED results for premixing some seawater with river water (PDF)

The authors declare no competing financial interest.