Abstract
This study examines the Environmental Kuznets Curve hypothesis (EKC), considering the primary energy consumption among other country-specific variables, for a panel of the EU-28 countries during the period 1990–2014. By estimating pooled OLS regressions with Driscoll-Kraay standard errors in order to account for cross-sectional dependence, the results confirm the EKC hypothesis in the case of emissions of sulfur oxides and emissions of non-methane volatile organic compounds. In addition to pooled estimations, the output of fixed-effects regressions with Driscoll-Kraay standard errors support the EKC hypothesis for greenhouse gas emissions, greenhouse gas emissions intensity of energy consumption, emissions of nitrogen oxides, emissions of non-methane volatile organic compounds and emissions of ammonia. Additionally, the empirical findings from panel vector error correction model reveal a short-run unidirectional causality from GDP per capita growth to greenhouse gas emissions, as well as a bidirectional causal link between primary energy consumption and greenhouse gas emissions. Furthermore, since there occurred no causal link between economic growth and primary energy consumption, the neo-classical view was confirmed, namely the neutrality hypothesis.
Introduction
Energy is a crucial resource for any economy since all production and consumption undertakings are directly connected to energy consumption, hence ensuring the basis for economic activity and social welfare; however, the use of fossil fuels as primary source of energy caused a noteworthy upsurge in the global emissions of several potentially harmful gases [1]. Greenhouse gases (GHGs) absorb heat arriving from the Sun and retain it in the atmosphere which entails the increase of earth surface temperature [2]. Therefore, the matter of climate change driven by the increased quantity of GHGs polluting the atmosphere has depicted over the past two decades a major environmental concern caused by the phenomenon of global warming. However, the switch between renewable resources and fossil fuels is at the core of climate change mitigation strategy [3].
The CO2 emissions generated by the gaseous/liquid/solid fuel consumption are liable for more than 60% of the greenhouse effect [4] and represent the leading power source of the industry in general and of the automobile industry in particular, which are directly associated with economic growth and development [5]. While [6] forecasted a mean annual growth of emissions of approximately 1.8% until 2025, the most recent report of International Energy Outlook [7] estimated an increase of 34% of world energy-related CO2 emissions in 2040 relative to 2012, the developing non-OECD countries being held accountable for a considerable share, since they remain reliant on fossil fuels to fulfill the upsurge in energy demand. However, there is an anticipated depletion of oil resources, natural gas and uranium within a few decades and coal in almost two centuries [8]. Consequently, the United Nations Environment Programme via the International Resource Panel proposed a strategic approach towards a low carbon resource efficient Green Economy that pursues decoupling human wellbeing from resource consumption [9]. Thereby, relative decoupling supposes a slight rate of increase in resource employment compared to the growth rate of the economy, whilst absolute decoupling reveals a whole decline of resource use as an economy grows [10]. Alike, the European Union (EU) Sustainable Development Strategy [11] seeks to hinder and reduce environmental pollution, therefore supporting sustainable consumption and production in order to break the connection between economic growth and ecological deprivation. Consistent with the second commitment phase of the Kyoto Protocol 2013–2020 [12], EU set a 20% reduction target of GHG emissions to be achieved by 2020 compared to the 1990s level [13], and also a decrease by at least 40% below 1990 levels by 2030 [14].
Previous Environmental Kuznets Curve (EKC) studies on Europe explored various countries such as Austria [15], Croatia [16], France [17], Italy [18, 19], Portugal and Spain [20], Romania [21], Spain [22–25], United Kingdom [26]. However, to the best of our knowledge, there are not many studies that have explored the EKC hypothesis for pollutant emissions across EU-28. For instance, [27] tested the EKC hypothesis for municipal solid waste generation for a data panel consisting of 32 European states over 1997–2010. [28] explored the causal link between energy consumption, carbon dioxide emissions, economic growth, trade openness and urbanization, but for a panel of new EU member and candidate countries over the period 1992–2010. [29] studied the causal association between economic growth and CO2 emissions in a panel of 24 European nations from 1980 to 2010. Even if [30] selected EU-28 countries, the study analyzed the connections between residential energy consumption and income, within the timeframe between 1990–2013. Also, [31] investigated the transport energy by using Environmental Kuznets Curve hypothesis in the EU-27 countries over 1995-2009. The main features that distinguish the current paper from previous research on the topic are the research sample, as well as the employment of several types of emissions apart from carbon dioxide (CO2), namely sulfur oxides (SOx), nitrogen oxides (NOx), non-methane volatile organic compounds (NMVOCs), ammonia (NH3). The focus on EU-28 states is justified in the context of 2030 Framework for climate and energy [32] which put forward targets for greenhouse gas emissions decrease and renewable energy as part of the EU move to a competitive low carbon economy. Following a classical, logical structure, the next section highlights the literature review related to the EKC hypothesis, as well as to the relationship between CO2 emissions and economic growth. The data used for analysis, alongside the econometric framework are presented in Section 3. The empirical results and discussions are shown in Section 4, while the final section concludes the paper and provides policy implications.
Literature review
Previous evidence on Environmental Kuznets Curve
An extensive part of the specific literature explores the association between national income levels and the demand for greater environmental quality, namely the EKC hypothesis. According to [33], income inequity first rises with economic progress and then drops as economy advances to a certain level. Following the same reasoning, the EKC hypothesis points out that intensification in economic growth will primarily cause environmental pressure, but after a particular stage, increase in economic growth will lessen the environmental pressure. Specifically, EKC expects an inverted U-shaped association between environmental degradation and economic growth. Per se, initially economic growth will amplify CO2 emanations, but after a certain level (turning point) this connection will come to be the opposite. For that reason, after a certain period, upsurge in economic growth will lessen CO2 emissions, accordingly, economic growth itself being the way out for an uncontaminated setting. In Table 1 are summarized the turning points identified in earlier studies, by type of pollutant.
Table 1. Turning points reached in previous studies, by type of pollutant.
| Pollutant type | Study | Dataset | Period | Econometric technique | Turning point |
|---|---|---|---|---|---|
| Greenhouse gas emissions | [6] | 108 states | 1951–1986 | Fixed effects regressions | 35,428 (in 1986 U.S. $) |
| Greenhouse gas emissions | [34] | OECD and non-OECD states | 1960–1998 | Weibull specification | 15,599.90–21,185.83 (in 1990 U.S. $) |
| Greenhouse gas emissions | [35] | 16 metropolitan regions in Korea | 1990–2005 | Fixed effects and random effects regressions | 26,400–30,000 (in 2000 U.S. $) |
| Greenhouse gas emissions | [36] | 12 Middle East and North African states (MENA) | 1981–2005 | Panel Error-Correction | 37,263 (in 2005 international $) |
| Greenhouse gas emissions | [25] | Spain | 1874–2011 | Autoregressive distributed lag (ARDL) | 8,103 (in 1990 U.S. $) |
| Greenhouse gas emissions | [37] | 136 states | 1971–2010 | Ordinary least squares (OLS) with heteroskedasticity-robust standard errors | outside the sample and statistically insignificant |
| Greenhouse gas emissions | [38] | China | 1970–2015 | Auto regressive distributed lag (ARDL), fully modified ordinary least squares (FMOLS), dynamic ordinary least squares (DOLS) and impulse response and variance decomposition | 744,665 (in 2010 U.S. $) |
| Greenhouse gas emissions | [39] | Morocco | 1966–2014 | Ordinary least squares (OLS) | 7,800 (in 2010 U.S. $) |
| Emissions of sulfur oxides | [40] | Cross-section of urban areas located in 42 countries | 1977; 1982; 1988 | Random effects regressions | 4,000–5,000 (in 1985 U.S. $) |
| Emissions of sulfur oxides | [41] | 149 states | 1960–1990 | Ordinary least squares (OLS) | 3,670 (in 1985 U.S. $) |
| Emissions of sulfur oxides | [42] | 55 states | 1987–1988 | Ordinary least squares (OLS) | 2,900–3,800 (in 1985 U.S. $) |
| Emissions of sulfur oxides | [43] | 30 states | 1979–1987 | Fixed effects regressions | 8,700–10,700 (in 1990 U.S. $) |
| Emissions of sulfur oxides | [44] | 58 Turkish provinces | 1992–2001 | Pooled EGLS (cross-section weights) | 1,934 and 5,817 (in 2000 U.S. $) |
| Emissions of sulfur oxides | [45] | Tunisia | 1961–2004 | Johansen cointegration | 1,200 (in 2000 U.S. $) |
| Emissions of sulfur oxides | [35] | 16 metropolitan regions in Korea | 1990–2005 | Fixed Effects and Random Effects Regressions | 5,700 and 28,000 (in 2000 U.S. $) |
| Emissions of sulfur oxides | [37] | 136 states | 1971–2010 | Ordinary least squares (OLS) | 112,000 (in 2005 PPP adjusted U.S. $) |
| Emissions of nitrogen oxides | [42] | 55 states | 1987–1988 | Ordinary least squares | 5,500 (in 1985 U.S. $) |
| Emissions of nitrogen oxides | [35] | 16 metropolitan regions in Korea | 1990–2005 | Fixed Effects and Random Effects Regressions | 27,600 (in 2000 U.S. $) |
Source: Authors’ compilation based on literature review.
The starting point of the EKC pertains to [40] which showed that there is an inverted U-shaped relation between income level and environmental pressure; their findings were continued by [41–43]. Nevertheless, the EKC empirical evidence is still questioned and there is no consensus on the income level at which environmental degradation starts diminishing [46]. However, [47] noticed that the EKC is an important empirical factor, but most of the EKC studies are econometrically weak.
Likewise, [48] argued that the empirical outcomes highlight the omission of explanatory variables, while [49] noticed the use of dissimilar environmental quality indicators, estimation methods, economic features, and period covered. According to [50, 51], three approaches were observed at aiming to shed light on the inverted U-shaped link between pollutants and output.. The scale effect presumes that emissions are likely to increase as the number and variety of economic activity rise. The composition effect assumes that emissions would decrease as long as the goods produced in an economy become cleaner. The technique effect considers that emissions would decrease as the knowledge implied in manufacturing becomes less polluting. Besides, [52] explored the contribution of education by considering carbon dioxide emissions in Australia over 1950–2014 and find that increase in education rate has gradually counterbalanced the growth of per capita CO2 emissions ensuing from the economic growth.
The central assumption of EKC, respectively that global income is normally distributed and that all nations are supposed to follow a common development pattern is also suspicious [53]. Accordingly, inconsistent conclusions towards EKC come from cross-country examinations. In this regard, for two different datasets comprising OECD and non-OECD states, [34] provided evidence for EKC only for the OECD countries by estimating several linear or log-linear regression equations among variables, as well as quadratic or cubic. [54] supported the EKC for 43 developing countries over 1980–2004 via panel co-integration and panel long-run estimation techniques.
[55] employed the Johansen co-integration test and found evidence for the EKC in the case of low and lower middle income countries over 1975–2014, but failed to support the validity of EKC in the case of upper middle income and high income countries. [56] showed by using fully modified ordinary least squares (FMOLS) and dynamic ordinary least squares (DOLS) that the EKC is valid for a panel of 25 OECD states during 1980–2010. [57] supported the EKC in the energy-resource depletion model, for a panel of nine developed countries covering the period 2000–2013 through panel generalized method of moments (GMM). [36] applied panel unit root tests and co-integration techniques and did not confirm the EKC for 12 Middle East and North African Countries (MENA) over 1981–2005, except for Jordan. [58] used co-integration and Granger causality methods and revealed that EKC is not valid for ASEAN-5 economies, particularly for Indonesia, Malaysia, and Thailand. The results of the FMOLS panel estimator employed by [59] for 12 Middle East countries over 1990–2008 yielded evidence divergent to the EKC.
[60] estimated pooled, fixed effects, random effects, and generalized-least square regressions, but did not validate the EKC for 152 states over six years. Furthermore, contradictory evidence towards EKC hypothesis is also established in single country studies. [61] found that nuclear energy has a positive influence on environmental quality in Korea over 1971–2007 by employing the autoregressive distributed lag (ARDL) approach to co-integration. By using threshold co-integration tests, [62] revealed that EKC hypothesis is valid in India’s case during 1971–2008. [63] underlined the validity of EKC in Turkey over 1961–2010 using the ARDL method.
[64] used the Spatial Durbin Model and supported the presence of the EKC for per capita coal consumption in China between 1995 and 2012. [65] validated the EKC in Indonesia for the period 1971–2010 by utilizing ARDL method. In the case of Qatar, [66] employed the ARDL method over the timeframe 1980–2011 and rejected the EKC hypothesis when using carbon dioxide emissions, but confirmed the EKC when using ecological footprint. Otherwise, the pooled mean group estimates undertaken by [67] reject the EKC for the case of US over 1945–2004. As well, apart from the inverted U-shaped relationship between environmental degradation and economic growth, other findings pointed out diverse shapes. As such, monotonically decreasing curve denotes that environmental quality improves as income growths, whilst monotonically increasing curve involves the diminution of environmental quality as income rises. Moreover, the N-shaped curve unveils that environmental degradation appears again after a decline to a specific level.
Furthermore, by applying panel unit root and panel co-integration tests, [68] rejected the EKC for a sample of 21 Latin American and Caribbean nations during 1970–2007. By employing a multivariate vector error correction model (VECM), [69] did not confirm also the EKC hypothesis in Russia between 1990 and 2007 and neither did [70] for Cambodia over 1996–2012, by estimating GMM and two-stage least square regression models. [71] used the STIRPAT empirical model, as well as panel co-integration and FMOLS, but failed to support the EKC in five African states during 1980–2011.
A brief literature review that found different patterns on this topic is described in Table 2. However, even if [72] confirmed the EKC hypothesis, there was argued that the results cannot be generalized, being fragile without performing sensitivity analysis.
Table 2. Summary review of literature invalidating EKC hypothesis.
| Study | Dataset | Period | Econometric technique | Outcome |
|---|---|---|---|---|
| [73] | Chinese provincial level | 1985–2015 | VECM | EKC at aggregate-level for SO2 EKC may not exist at the provincial-level for SO2 |
| [74] | 100 states | 1960–1996 | Nonparametric panel model with individual effects | Upward sloping curve for CO2 |
| [44] | Turkey | 1968–2003 1992–2001 |
Johansen technique, Feasible Generalized Least Squares | Monotonically increasing curve for CO2 N-shaped for SO2 and PM10 |
| [45] | Tunisia | 1961–2004 | Johansen technique, Granger causality | Monotonically increasing curve for CO2 |
| [35] | Korea | 1990–2005 | Fixed-effects, Random-effects, Random coefficient regressions | Potential N-shaped curve for SO2 Dominant U-shaped curve for CO A region-specific U-shaped curve for NO2 |
| [75] | 8 states | 1970–2010 | ARDL | Inverted U-shaped curve for CO2 in Japan and South Korea N-shaped curve for Brazil, China, Egypt, Mexico, Nigeria, and South Africa |
| [76] | 25 Sub-Saharan Africa states | 1996–2010 | Ordinary Least Squares, Difference GMM, System GMM, Least Square Dummy Variable Corrector | Monotonically increasing curve for CO2 |
| [77] | 189 states | 1990–2012 | Fixed-effects and Random-effects panel regressions, Dynamic panel regressions, Heterogeneous panel regressions | Linearly increasing curve for CO2 |
| [78] | China | 1997–2012 | Non-spatial panel models and spatial Durbin model | Inverted N-shaped curve for CO2 |
| [51] | 17 OECD states | 1990–2012 | Fixed-effect panel regressions | N-shaped curve for per capita GHG emissions |
| [79] | India, China | 1971–2012 | ARDL | N-shaped curve for CO2 |
| [80] | Saudi Arabia | 1970–2014 | ARDL | GDP growth and CO2 emissions are positively and linearly associated |
Source: Authors’ compilation based on literature review.
Previous evidence on the causal link between CO2 emissions and growth
Other part of literature examines the causal relationship between energy consumption and economic growth. The pioneering examinations with regard to the economic growth—energy consumption connection belongs to [81] which found an unidirectional causality between the gross national product and energy consumption for the United States, whilst [82] did not provide any causal link.
There are two prevailing divergent hypothetical points of view on the connection between energy consumption and economic growth [83, 84]. The neo-classical view, known as the neutrality hypothesis [85, 86], claims that there are other significant factor inputs in the production process than energy and no causal link occurs between energy consumption and economic growth. Thus, a nation may follow a protectionist energy strategy for lowering CO2 emanations deprived of compromising growth. The antagonist view, referred as the non-neutrality hypothesis of energy, suggests that energy is a fundamental factor input in the production process and energy conservation policies may obstruct the economic growth. Subsequently, three theoretical models derive from the latter approach [87]. The growth hypothesis [88–92] advocates a uni-directional causality from energy consumption to economic growth and pretends that energy conservation policies will have negative effects on economic growth. The conservation hypothesis [93, 94] supports a uni-directional causality from economic growth to energy consumption and motivates that energy conservation policies will not impair economic growth.
The feedback hypothesis [104–107] postulates a bidirectional causality between energy consumption and economic growth and asserts that energy conservation policies may weaken economic growth performance, so growth variations are reflected back to energy consumption. Overview of the studies that investigated the causal link between CO2 emissions and economic growth is showed in Table 3.
Table 3. Brief literature review on the causal relation between CO2 emissions and economic growth.
| Study | Dataset | Period | Econometric technique | Outcome |
|---|---|---|---|---|
| [95] | 88 states | 1960–1990 | Co-integration analysis, Error Correction Model | Bidirectional causality between per capita CO2 emissions and per capita GDP for country-group of Africa Unidirectional causality running from per capita GDP to per capita CO2 emissions for country-group of Central America Unidirectional causality running from per capita CO2 emissions to per capita GDP for country-group of Europe |
| [4] | Turkey | 1968–2005 | ARDL | Lack of causality between per capita CO2 emissions and real GDP per capita |
| [96] | China, India | 1965–2009 | Co-integration analysis, Granger causality analysis | Unidirectional causality running from economic growth to CO2 emissions |
| [97] | Malaysia | 1980–2009 | Johansen-Julius co-integration, ARDL, VECM | Bidirectional causality between economic growth and CO2 emissions |
| [98] | Indonesia | 1975–2011 | ARDL, VECM | Bidirectional causality between economic growth and CO2 emissions |
| [99] | BRICS states | 1990–2010 | Panel causality analysis | CO2–GDP feedback for Russia Unidirectional causality running from GDP to CO2 in South Africa Unidirectional causality running from CO2 to GDP in Brazil |
| [100] | 54 states | 1990–2011 | Dynamic simultaneous-equation panel data models | Unidirectional causality running from CO2 emissions to economic growth for Europe and Central Asia, Latin America and the Caribbean Bidirectional causality between CO2 emissions and economic growth for Middle Eastern, North African, and sub-Saharan panel |
| [101] | 51 states | 1995–2013 | Simultaneous-equation models estimated by the GMM. | Bidirectional causal relationships between CO2 emissions and economic growth |
| [102] | 17 MENA states | 1990–2012 | Simultaneous-equation panel data VAR model | Unidirectional causality running from economic growth to CO2 emissions |
| [84] | Pakistan | 1971–2009 | Johansen-Julius co-integration, ARDL, VECM | Bidirectional causalities between energy consumption, economic growth and the CO2 emissions |
| [103] | G7 states | 1820–2015 | Nonparametric co-integration, Causality tests, Cross-validated local linear regression | Nonlinear causal relationship between CO2 and economic growth |
Source: Authors’ compilation based on literature review.
Data and methodology
Sample and variables
Our data sample covers the period 1990–2014 for a panel consisting of the EU-28 countries. The variables used for analysis, as well as their definition and data sources are presented in Table 4. All variables, except GDPCG, ENVTR, GFCF, RD, FFEC, EMPL, INDVA, and CPI are expressed in natural logs.
Table 4. Description of the variables used for analysis.
| Variables | Definition | Unit of measurement | Time frame availability | Data source |
|---|---|---|---|---|
| GDPC | GDP per capita | Constant 2010 US dollars | 1990–2015 | World Bank (NY.GDP.PCAP.KD) |
| GDPCG | GDP per capita growth | Annual % | 1990–2015 | World Bank (NY.GDP.PCAP.KD.ZG) |
| GGE | Greenhouse gas emissions | Tons per capita | 1990–2014 | Eurostat (sdg_13_10) |
| GGEI | Greenhouse gas emissions intensity of energy consumption | Index (2000 = 100) | 1990–2014 | Eurostat (tsdcc220) |
| ESOX | Emissions of sulfur oxides | Tons | 1990–2014 | Eurostat (tsdpc260) |
| ENOX | Emissions of nitrogen oxides | Tons | 1990–2014 | Eurostat (tsdpc270) |
| ENMVOC | Emissions of non-methane volatile organic compounds | Tons | 1990–2014 | Eurostat (tsdpc280) |
| ENH3 | Emissions of ammonia | Tons | 1990–2014 | Eurostat (tsdpc290) |
| GGET | Greenhouse gas emissions from transport | Million tons of CO2 equivalent | 1990–2014 | Eurostat (tsdtr410) |
| ENVTR | Environmental tax revenues | % of total revenues from taxes and social contributions | 1995–2015 | Eurostat (t2020_rt320) |
| PEC | Primary energy consumption | Million tons of oil equivalent (TOE) | 1990–2015 | Eurostat (tsdcc120) |
| GIECRE | Gross inland consumption of renewable energies | 1,000 tons of oil equivalent | 1990–2015 | Eurostat (tsdcc320) |
| GFCF | Gross fixed capital formation | % of GDP | 1995–2016 | Eurostat (tipsna20) |
| RD | Research and development expenditure | % of GDP | 1996–2014 | World Bank (GB.XPD.RSDV.GD.ZS) |
| FFEC | Fossil fuel energy consumption | % of total | 1990–2015 | World Bank (EG.USE.COMM.FO.ZS) |
| EMPL | Employment in high- and medium-high-technology manufacturing sectors | % of total employment | 1995–2014 | Database for Institutional Comparisons in Europe (DICE) |
| INDVA | Industry, value added | % of GDP | 1990–2016 | World Bank (NV.IND.TOTL.ZS) |
| CPI | Corruption Perceptions Index | Score | 1995–2016 | Database for Institutional Comparisons in Europe (DICE) |
Source: Authors’ own selection based on databases’ availability.
A part of preceding studies that tested the EKC hypothesis used only pollutant emissions, economic growth, and energy consumption [2, 21, 24, 28, 36, 59, 60, 104], while other examinations furthermore considered new variables such as electricity consumption, trade openness, corruption, and government effectiveness index [70], electricity production [61], oil prices [25], population and urbanization [44, 55, 71, 78], trade [1, 56, 58, 62, 66, 75, 79, 80]. In line with [108–110] we control for the technology level via FFEC and EMPL. We employ the fossil fuel energy consumption to account for the level of use of dirty energy, which causes air pollution in the combustion process. As well, the employment in high- and medium-high-technology manufacturing sectors is included in as much as highly skilled labor contributes to the development of an efficient fabrication process that can stimulate energy savings and pollution deterrence. According to [52], an advanced level of comprehension to integrate cleaner technologies and collective responsiveness among people will drive higher ecological standards. INDVA is applied to control for the scale, whilst CPI aims to control for the selected states political state. Corrupted or unstable political regimes damage industrial progress and destroy the application of environmental policy in pollution abatement undertakings [110]. In the same vein, [111] concluded that prior communist nations had trouble introducing modern productive equipment conceived in capitalistic countries and depended on old and inefficient tools. On the contrary, [112] revealed that regulatory stringency positively influence efficiency, arguing that more rigorous emission standards lead firms to search for more efficient methods of fuel use and emissions decrease. However, further country-specific variables employed within current research are environmental tax revenues, gross inland consumption of renewable energies [51, 56], as well as gross fixed capital formation and research and development expenditure [51, 65, 85]. According to [113] amongst nations variation systematically differs conditional on its richness, on institutional features, and on its whole commitment to the diffusion of renewable energy.
Econometric methods
In order to examine the EKC hypothesis we followed the approach of [35, 44, 51, 76, 77, 104]. The long-run relationship between pollutant emissions, GDP per capita, environmental tax revenues, primary energy consumption, gross inland consumption of renewable energies, gross fixed capital formation, research and development expenditure, and other cross-country control variables, is given as follows:
| (1) |
where i = 1, …, 28 and t = 1990, …, 2014 reveal the country and time, respectively, whereas PE denotes the pollutant emissions which take form of greenhouse gas emissions, greenhouse gas emissions intensity of energy consumption, emissions of Sulphur oxides, emissions of nitrogen oxides, emissions of non-methane volatile organic compounds, emissions of ammonia, and greenhouse gas emissions from transport. αit indicates the country specific fixed effect.
The parameters δ1i–δ11i are the long-run elasticities related to each explanatory variable of the panel. εit describes the estimated residuals which characterize deviations from the long-run equilibrium.
Considering the inverted U-shaped EKC hypothesis, the sign of δ1i is expected to be positive and the sign of δ2i is expected to be negative, whilst the monetary value representing the turning point is computed by τ = exp[-β1/(2β2)] [23, 49, 60, 76].
Furthermore, our aim was to establish the causal links between greenhouse gas emissions, economic growth, primary energy consumption, and environmental tax revenues.
Therefore, according to [59, 84, 88, 89, 104], we assessed the stationarity of data using a battery of first generation tests, such as Levin, Lin and Chu (LLC), Im, Pesaran and Shin (IPS), Augmented Dickey-Fuller (ADF), and Phillips-Perron (PP), as well as second generation checks, namely the cross-sectionally augmented Dickey-Fuller (CADF). However, the IPS unit root test [114] allows for heterogeneous autoregressive coefficients.
Subsequently, we performed the heterogeneous panel co-integration test proposed by Pedroni [115, 116] since it allows cross-section interdependence with different individual effects, alongside Kao [117] and Johansen approaches [118], as well as Westerlund [119]:
| (2) |
where i = 1, …, 28 for each country in the panel and t = 1990, …, 2014 denotes each year of the period. Besides, the parameters αi and δi allow country-specific fixed effects and deterministic trends. By pursuing the two-step procedure of Engle-Granger, the long-run model specified in Eq (2) is estimated in which the one period lagged residuals serve as the error correction term.
The dynamic error correction model is presented below:
| (3a) |
| (3b) |
| (3c) |
| (3d) |
where Δ signifies the first-difference operator, q represents the lag length set at one according to likelihood ratio tests, and u exposes the serially uncorrelated error term.
Empirical results
Summary statistics, correlations and unit root examination
Table 5 shows the descriptive statistics of the selected variables over the period 1990–2014. By type of pollutant emissions, Cyprus (GGE), Bulgaria (GGEI), Poland (ESOX), and Germany (ENOX, ENMVOC, ENH3, GGET) show the highest mean value, whereas Lithuania (GGE), Czech Republic (GGEI), Luxembourg (ESOX), and Malta (ENOX, ENMVOC, ENH3, GGET) register the lowest mean value. In terms of correlations (Table 6), strong uphill linear relationships between primary energy consumption and selected emissions such as ESOX, ENOX, ENMVOC, ENH3 and GGET were noticed.
Table 5. Descriptive statistics of the selected variables (raw data).
| Variables | Mean | Median | Max | Min | Std. Dev. | Skewness | Kurtosis | Jarque-Bera | Prob | Obs |
|---|---|---|---|---|---|---|---|---|---|---|
| GDPC | 28,975.18 | 26,046.77 | 111,069.20 | 3,582.86 | 19,231.61 | 1.33 | 5.89 | 449.0606 | 0.00 | 700 |
| GDPCG | 2.19 | 2.24 | 25.56 | -14.56 | 3.71 | -0.24 | 7.26 | 527.7636 | 0.00 | 690 |
| GGE | 11.04 | 10.10 | 35.60 | 4.40 | 4.59 | 1.94 | 9.01 | 1550.705 | 0.00 | 727 |
| GGEI | 100.28 | 100.00 | 138.00 | 77.00 | 8.93 | 0.63 | 4.52 | 113.6375 | 0.00 | 700 |
| ESOX | 396,956.60 | 130,796.50 | 5,311,611.00 | 16.00 | 625,070.50 | 2.93 | 14.48 | 4846.56 | 0.00 | 700 |
| ENOX | 449,170.30 | 205,027.50 | 2,949,082.00 | 3,834.00 | 588,987.30 | 1.87 | 5.81 | 636.4299 | 0.00 | 700 |
| ENMVOC | 387,457.70 | 166,212.50 | 3,389,448.00 | 1,838.00 | 558,010.20 | 2.33 | 8.22 | 1426.401 | 0.00 | 700 |
| ENH3 | 150,963.10 | 67,826.00 | 792,928.00 | 1,498.00 | 190,731.40 | 1.78 | 5.26 | 519.789 | 0.00 | 700 |
| GGET | 32.18 | 12.46 | 186.78 | 0.34 | 45.90 | 1.80 | 4.89 | 483.6149 | 0.00 | 700 |
| ENVTR | 7.59 | 7.36 | 15.39 | 2.45 | 1.88 | 0.53 | 3.23 | 28.01873 | 0.00 | 581 |
| PEC | 57.68 | 24.55 | 333.30 | 0.60 | 78.62 | 1.96 | 5.94 | 727.6009 | 0.00 | 728 |
| GIECRE | 4,398.73 | 1,680.70 | 38,354.20 | 0.00 | 5,901.79 | 2.20 | 8.51 | 1508.345 | 0.00 | 728 |
| GFCF | 22.29 | 21.90 | 38.40 | 5.40 | 4.12 | 0.55 | 4.83 | 117.3547 | 0.00 | 616 |
| RD | 1.39 | 1.19 | 3.91 | 0.20 | 0.86 | 0.84 | 2.87 | 59.8458 | 0.00 | 504 |
| FFEC | 76.39 | 79.85 | 100.00 | 12.29 | 17.92 | -1.20 | 4.06 | 205.9476 | 0.00 | 717 |
| EMPL | 5.45 | 5.30 | 11.37 | 0.60 | 2.59 | 0.10 | 2.32 | 10.67386 | 0.00 | 513 |
| INDVA | 28.26 | 28.58 | 55.85 | 10.69 | 6.45 | 0.27 | 4.32 | 57.45635 | 0.00 | 682 |
| CPI | 20.60 | 7.50 | 92.00 | 2.60 | 26.08 | 1.44 | 3.48 | 200.6982 | 0.00 | 567 |
Source: Authors’ computations. Notes: For the definition of variables, please see Table 4.
Table 6. Correlation matrix.
| Variables | GDPC | GDPCG | GGE | GGEI | ESOX | ENOX | ENMVOC | ENH3 | GGET | ENVTR | PEC | GIECRE | GFCF | RD | FFEC | EMPL | INDVA | CPI |
| GDPC | 1.00 | |||||||||||||||||
| GDPCG | -0.18*** | 1.00 | ||||||||||||||||
| GGE | 0.56*** | -0.03 | 1.00 | |||||||||||||||
| GGEI | -0.08** | 0.07* | 0.32*** | 1.00 | ||||||||||||||
| ESOX | -0.23*** | -0.05 | 0.00 | 0.17*** | 1.00 | |||||||||||||
| ENOX | 0.16*** | -0.15*** | 0.08** | 0.01 | 0.79*** | 1.00 | ||||||||||||
| ENMVOC | 0.08** | -0.11*** | -0.06 | -0.01 | 0.80*** | 0.97*** | 1.00 | |||||||||||
| ENH3 | 0.09** | -0.12*** | -0.04 | -0.07* | 0.75*** | 0.95*** | 0.96*** | 1.00 | ||||||||||
| GGET | 0.37*** | -0.19*** | 0.09** | -0.14*** | 0.63*** | 0.94*** | 0.91*** | 0.91*** | 1.00 | |||||||||
| ENVTR | -0.15*** | 0.05 | -0.06 | 0.11*** | -0.28*** | -0.40*** | -0.41*** | -0.37*** | -0.43*** | 1.00 | ||||||||
| PEC | 0.21*** | -0.17*** | 0.05 | -0.10*** | 0.72*** | 0.97*** | 0.95*** | 0.94*** | 0.96*** | -0.46*** | 1.00 | |||||||
| GIECRE | 0.13*** | -0.14*** | -0.21*** | -0.25*** | 0.54*** | 0.75*** | 0.81*** | 0.78*** | 0.78*** | -0.47*** | 0.81*** | 1.00 | ||||||
| GFCF | -0.18*** | 0.31*** | 0.03 | 0.01 | 0.01 | -0.11*** | -0.08* | -0.10** | -0.17*** | -0.08** | -0.12*** | -0.02 | 1.00 | |||||
| RD | 0.69*** | -0.23*** | 0.31*** | -0.20*** | -0.16*** | 0.27*** | 0.24*** | 0.24*** | 0.39*** | -0.31*** | 0.39*** | 0.46*** | -0.14*** | 1.00 | ||||
| FFEC | 0.00 | -0.05 | 0.19*** | 0.15*** | 0.10*** | 0.11*** | 0.01 | 0.09** | 0.07* | 0.38*** | 0.00 | -0.33*** | -0.21*** | -0.40*** | 1.00 | |||
| EMPL | 0.02 | 0.05 | 0.04 | -0.06 | 0.36*** | 0.37*** | 0.40*** | 0.40*** | 0.33*** | -0.20*** | 0.42*** | 0.26*** | 0.12*** | 0.33*** | -0.07 | 1.00 | ||
| INDVA | -0.45*** | 0.22*** | -0.15*** | 0.14*** | 0.14*** | 0.07* | 0.12*** | 0.14*** | -0.08** | -0.08* | 0.07* | 0.07* | 0.48*** | -0.02 | -0.08** | 0.64*** | 1.00 | |
| CPI | 0.20*** | -0.15*** | -0.09** | -0.44*** | -0.26*** | -0.12*** | -0.12*** | -0.06 | -0.00 | -0.09** | -0.03 | 0.12*** | -0.31*** | 0.25*** | -0.17*** | -0.12*** | -0.24*** | 1.00 |
Source: Authors’ computations.
*** indicates the statistical significance at 1% levels. For the definition of variables, please see Table 4.
** indicates the statistical significance at 5% levels. For the definition of variables, please see Table 4
* indicates the statistical significance at 10% levels. For the definition of variables, please see Table 4
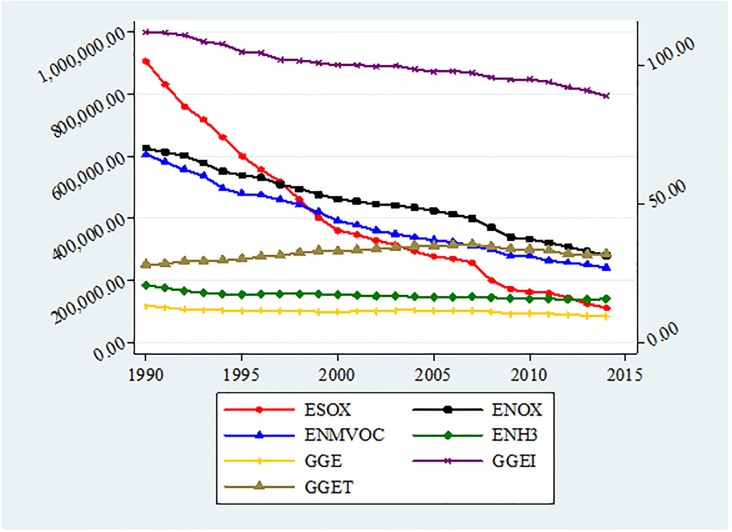
Fig 1 shows the mean value of pollutant emissions in EU-28 countries. We acknowledge a downward trend of emissions, proving that the European Union is making a considerable effort in order to fulfill the targets related to the second pledge period of the Kyoto Protocol. However, a noteworthy decrease was registered in the case of sulfur oxides determined by shifting from high-sulfur solid and liquid fuels to low sulfur fuels for power and heat fabrication aims within the energy, industry and domestic areas, developments in energy efficiency, and the establishment of flue gas desulfurization equipment in new and current industrial equipment.
Fig 1. Mean value of pollutant emissions in EU-28.
Source: Authors’ own elaboration. Notes: For the definition of variables, please see Table 4.
The results comprised in Table 7 show the presence of cross-section dependence, similar to the previous findings of [99]. Hence, in order to remove this inconvenience, we considered Driscoll-Kraay standard errors in the fixed-effects models, comparable to [2]. Such standard errors are heteroskedasticity consistent, also being robust to very general forms of cross-sectional and temporal dependence [120].
Table 7. Cross-section dependence test results.
| Variables | Breusch-Pagan LM | Pesaran scaled LM | Bias-corrected scaled LM | Pesaran CD |
|---|---|---|---|---|
| GDPC | 7607.5*** | 262.93*** | 262.37*** | 86.52*** |
| GDPCG | 3024.42*** | 96.25*** | 95.69*** | 50.84*** |
| GGE | 3216.89*** | 103.25*** | 102.69*** | 39.3*** |
| GGEI | 4899.07*** | 164.43*** | 163.85*** | 55.7*** |
| ESOX | 7154.35*** | 246.45*** | 245.87*** | 73.83*** |
| ENOX | 4991.48*** | 167.79*** | 167.21*** | 64.54*** |
| ENMVOC | 6293.44*** | 215.14*** | 214.56*** | 52.68*** |
| ENH3 | 3137.43*** | 100.36*** | 99.78*** | 38.47*** |
| GGET | 4346.25*** | 144.32*** | 143.74*** | 51.59*** |
| ENVTR | 1853.75*** | 53.67*** | 52.97*** | 9.91*** |
| PEC | 3271.74*** | 105.24*** | 104.68*** | 16.88*** |
| GIECRE | 7254.74*** | 250.1*** | 249.54*** | 84.26*** |
| GFCF | 2095.22*** | 62.45*** | 61.79*** | 26.8*** |
| RD | 2694.94*** | 84.27*** | 83.49*** | 27.52*** |
| FFEC | 4852.64*** | 162.74*** | 162.18*** | 60.86*** |
| EMPL | 3208.35*** | 102.94*** | 102.2*** | 35.24*** |
| INDVA | 3386.24*** | 109.41*** | 108.87*** | 47.31*** |
| CPI | 7165.61*** | 246.86*** | 246.2*** | 84.42*** |
Source: Authors’ computations.
*** indicates the statistical significance at 1% level. For the definition of variables, please see Table 4.
Further, in line with [121] we perform two categories of stationarity tests, according to their cross-section dependence assumption, respectively the so called first generation that assume cross-section independence (Table 8), as well as the second generation that allow for cross-section dependence between the cross-section units (Table 9). As we can notice, the variables are non-stationary in their levels, but become stationary after taking the first difference. Hence, we conclude that all series are I(1).
Table 8. First generation panel unit root test results.
| Variables | LLC | IPS | ADF | PP | LLC | Breitung | IPS | ADF | PP | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Levels | First differences | ||||||||||
| Intercept | GDPC | -4.62*** | 0.72 | 48.89 | 44.92 | Intercept | 1.17 | -0.42 | 3.54 | 37.48 | 36.02 |
| GDPCG | -12.89*** | -11.77*** | 239.29*** | 235.58*** | -10.7*** | -3.98*** | -9.01*** | 186.48*** | 198.18*** | ||
| GGE | -0.1 | 0.42 | 83.89*** | 83.72*** | -1.38* | 4.71 | 0.68 | 69.23 | 94.24*** | ||
| GGEI | 0.38 | 3.81 | 55.52 | 56.8 | -3.54*** | 1.68 | -2.54*** | 91.36*** | 89.3*** | ||
| ESOX | -0.19 | 6.51 | 38.27 | 41.21 | -0.74 | 4.14 | 1.51 | 46.33 | 43.85 | ||
| ENOX | 2.65 | 4.81 | 63.8 | 69.29 | -2.04** | 2.5 | -0.71 | 75.94** | 79.12** | ||
| ENMVOC | -1.56* | 3.93 | 82.01** | 78.04** | -1.31* | 3.19 | -1.23 | 85.66*** | 79.12** | ||
| ENH3 | -9.45*** | -6.72*** | 182.32*** | 166.92*** | -6.92*** | 1.09 | -5.85*** | 146.18*** | 143.35*** | ||
| GGET | -4.17*** | -1.17 | 59.17 | 62.35 | 2.34 | 8.01 | 3.22 | 73.94* | 56.93 | ||
| ENVTR | -1.92** | -1.43* | 65.15 | 68.17 | 1.08 | 1.74 | 0.85 | 59.89 | 56.19 | ||
| PEC | -5.36*** | -3.91*** | 108.63*** | 111.86*** | -0.08 | 3.9 | 1.81 | 53.28 | 94.74*** | ||
| GIECRE | 1.58 | 5.91 | 26.76 | 28.96 | -4.13*** | -0.79 | -2.97*** | 98.43*** | 79.76** | ||
| GFCF | -1.59* | -1.91** | 80.03** | 50.67 | -2.9*** | -0.76 | -3.21*** | 93.79*** | 49.73 | ||
| RD | -0.43 | 3.33 | 38.58 | 35.42 | -0.94 | 2.4 | -0.38 | 73.19* | 74.84** | ||
| FFEC | 5.77 | 8.38 | 18.82 | 21.17 | 1.52 | 5.46 | 2.7 | 57.42 | 36.09 | ||
| EMPL | -1.28 | -0.06 | 68.16 | 74.63** | -4.78*** | -1.55* | -4.02*** | 105.37*** | 102.62*** | ||
| INDVA | -3.78*** | -1.49* | 73.02* | 82.23** | -11.68*** | -0.52 | -5.53*** | 318.2*** | 48.99 | ||
| CPI | 4.48 | 6.1 | 7.39 | 7.38 | 0.28 | 0.57 | 3.89 | 18.46 | 18.95 | ||
| Intercept and trend | GDPC | -12.9*** | -11.69*** | 239.01*** | 242.05*** | Intercept and trend | -10.8*** | -3.87*** | -9.33*** | 192.57*** | 228.36*** |
| GDPCG | -20.83*** | -21.1*** | 445.1*** | 806.35*** | -17.33*** | -10.9*** | -17.73*** | 343.66*** | 1912.96*** | ||
| GGE | -15.93*** | -15.98*** | 339.79*** | 409.63*** | -15.49*** | -5.97*** | -17.5*** | 342.98*** | 756.72*** | ||
| GGEI | -25.49*** | -25.27*** | 535.4*** | 740.92*** | -22.12*** | -10.32*** | -23.58*** | 489.05*** | 1659.86*** | ||
| ESOX | -17.27*** | -16.33*** | 343.84*** | 359.57*** | -17.27*** | -10.68*** | -16.46*** | 312.72*** | 367.78*** | ||
| ENOX | -17.37*** | -18.04*** | 373.57*** | 446.99*** | -14.41*** | -7.26*** | -16.44*** | 313.00*** | 1340.09*** | ||
| ENMVOC | -16.14*** | -15.94*** | 334.8*** | 374.03*** | -13.28*** | -7.35*** | -16.05*** | 306.78*** | 372.32*** | ||
| ENH3 | -16.61*** | -15.65*** | 324.43*** | 421.16*** | -15.46*** | -6.96*** | -13.97*** | 272.45*** | 374.08*** | ||
| GGET | -12.88*** | -12.71*** | 304.18*** | 300.72*** | -16.07*** | -3.43*** | -15.56*** | 353.61*** | 360.65*** | ||
| ENVTR | -12.65*** | -12.94*** | 258.19*** | 283.55*** | -8.7*** | -9.47*** | -10.63*** | 204.28*** | 266.51*** | ||
| PEC | -18.65*** | -18.21*** | 385.09*** | 490.16*** | -19.08*** | -8.36*** | -20.91*** | 480.65*** | 857.53*** | ||
| GIECRE | -21.39*** | -21.43*** | 441.63*** | 492.82*** | -18.23*** | -13.24*** | -18.5*** | 371.38*** | 1087.21*** | ||
| GFCF | -11.81*** | -11.8*** | 239.18*** | 260.53*** | -9.94*** | -5.82*** | -8.9*** | 177.47*** | 218.2*** | ||
| RD | -8.38*** | -9.37*** | 195.89*** | 508.07*** | -8.82*** | -5.01*** | -8.45*** | 174.26*** | 233.05*** | ||
| FFEC | -16.95*** | -17.32*** | 371.29*** | 412.5*** | -14.88*** | -6.72*** | -16.24*** | 319.42*** | 677.16*** | ||
| EMPL | -17.66*** | -15.56*** | 310.33*** | 427.82*** | -14.99*** | -7.68*** | -10.78*** | 221.95*** | 300.8*** | ||
| INDVA | -19.7*** | -17.65*** | 362.45*** | 360.33*** | -15.69*** | -9.42*** | -14.15*** | 270.04*** | 349.4*** | ||
| CPI | -20.25*** | -15.07*** | 299.1*** | 304.61*** | -18.74*** | -6.08*** | -12.36*** | 230.66*** | 243.6*** | ||
Source: Authors’ computations. Notes: lag lengths are determined via Schwarz Info Criterion. LLC reveals Levin, Lin and Chu t* stat. IPS reveals Im, Pesaran and Shin W-stat. ADF reveals Augmented Dickey-Fuller Fisher Chi-square. PP reveals Phillips–Perron Fisher Chi-square. LLC assumes common unit root process. IPS, ADF, and PP assumes individual unit root process. Probabilities for ADF and PP are computed using an asymptotic Chi-square distribution. Probabilities for the LLC, Breitung, and IPS tests are computed assuming asymptotic normality. For the definition of variables, please see Table 4.
*** indicates the statistical significance at 1% levels.
** indicates the statistical significance at 5% levels.
* indicates the statistical significance at 10% levels.
Table 9. Second generation panel unit root investigation—Pesaran’s CADF test.
| Deterministics chosen | Variables | Levels | First differences | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| t-bar | cv10 | cv5 | cv1 | Z[t-bar] | P-value | t-bar | cv10 | cv5 | cv1 | Z[t-bar] | P-value | |||
| Constant | GDPC | -1.39 | -2.07 | -2.15 | -2.30 | 1.95 | 0.97 | Constant | -2.65 | -2.07 | -2.15 | -2.30 | -4.82 | 0.00 |
| GDPCG | -5.78 | 0.00 | -9.50 | 0.00 | ||||||||||
| GGE | -0.12 | 0.45 | -7.68 | 0.00 | ||||||||||
| GGEI | -2.03 | -2.07 | -2.15 | -2.30 | -1.51 | 0.07 | -3.90 | -2.07 | -2.15 | -2.30 | -11.60 | 0.00 | ||
| ESOX | -1.66 | -2.07 | -2.15 | -2.30 | 0.47 | 0.68 | -2.95 | -2.07 | -2.15 | -2.30 | -6.48 | 0.00 | ||
| ENOX | -2.29 | -2.07 | -2.15 | -2.30 | -2.90 | 0.00 | -3.71 | -2.07 | -2.15 | -2.30 | -10.60 | 0.00 | ||
| ENMVOC | -1.98 | -2.07 | -2.15 | -2.30 | -1.23 | 0.11 | -2.86 | -2.07 | -2.15 | -2.30 | -6.01 | 0.00 | ||
| ENH3 | -2.33 | -2.07 | -2.15 | -2.30 | -3.15 | 0.00 | -3.56 | -2.07 | -2.15 | -2.30 | -9.75 | 0.00 | ||
| GGET | -2.15 | -2.07 | -2.15 | -2.30 | -2.15 | 0.02 | -3.24 | -2.07 | -2.15 | -2.30 | -8.06 | 0.00 | ||
| ENVTR | -1.10 | 0.14 | -4.59 | 0.00 | ||||||||||
| PEC | -2.08 | -2.07 | -2.15 | -2.30 | -1.81 | 0.04 | -3.66 | -2.07 | -2.15 | -2.30 | -10.30 | 0.00 | ||
| GIECRE | -2.24 | -2.07 | -2.15 | -2.30 | -2.62 | 0.00 | -3.79 | -2.07 | -2.15 | -2.30 | -11.03 | 0.00 | ||
| GFCF | -1.80 | -2.07 | -2.15 | -2.30 | -0.25 | 0.40 | -2.89 | -2.07 | -2.15 | -2.30 | -6.14 | 0.00 | ||
| RD | -1.92 | -2.07 | -2.15 | -2.32 | -0.94 | 0.17 | -2.91 | 0.00 | ||||||
| FFEC | 0.40 | 0.65 | -8.91 | 0.00 | ||||||||||
| EMPL | -2.69 | 0.00 | -5.50 | 0.00 | ||||||||||
| INDVA | -0.34 | 0.37 | -6.85 | 0.00 | ||||||||||
| CPI | -6.46 | 0.00 | -9.44 | 0.00 | ||||||||||
| Constant & Trend | GDPC | -2.24 | -2.58 | -2.66 | -2.81 | 0.41 | 0.66 | Constant & Trend | -2.69 | -2.58 | -2.66 | -2.81 | -2.16 | 0.02 |
| GDPCG | -2.69 | 0.004 | -6.41 | 0.00 | ||||||||||
| GGE | 2.29 | 0.989 | -9.14 | 0.00 | ||||||||||
| GGEI | -2.37 | -2.58 | -2.66 | -2.81 | -0.33 | 0.37 | -4.22 | -2.58 | -2.66 | -2.81 | -10.87 | 0.00 | ||
| ESOX | -1.96 | -2.58 | -2.66 | -2.81 | 2.00 | 0.977 | -3.19 | -2.58 | -2.66 | -2.81 | -5.01 | 0.00 | ||
| ENOX | -2.71 | -2.58 | -2.66 | -2.81 | -2.29 | 0.01 | -3.91 | -2.58 | -2.66 | -2.81 | -9.09 | 0.00 | ||
| ENMVOC | -2.02 | -2.58 | -2.66 | -2.81 | 1.64 | 0.949 | -3.23 | -2.58 | -2.66 | -2.81 | -5.24 | 0.00 | ||
| ENH3 | -2.35 | -2.58 | -2.66 | -2.81 | -0.24 | 0.404 | -3.75 | -2.58 | -2.66 | -2.81 | -8.17 | 0.00 | ||
| GGET | -2.53 | -2.58 | -2.66 | -2.81 | -1.25 | 0.105 | -3.34 | -2.58 | -2.66 | -2.81 | -5.85 | 0.00 | ||
| ENVTR | 2.50 | 0.99 | -3.41 | 0.00 | ||||||||||
| PEC | -2.18 | -2.58 | -2.66 | -2.81 | 0.76 | 0.78 | -4.33 | -2.58 | -2.66 | -2.81 | -11.50 | 0.00 | ||
| GIECRE | -2.61 | -2.58 | -2.66 | -2.81 | -1.69 | 0.05 | -4.06 | -2.58 | -2.66 | -2.81 | -9.95 | 0.00 | ||
| GFCF | -2.50 | -2.58 | -2.66 | -2.81 | -1.05 | 0.15 | -3.02 | -2.58 | -2.66 | -2.81 | -4.01 | 0.00 | ||
| RD | -2.17 | -2.58 | -2.67 | -2.83 | 0.61 | 0.73 | -0.37 | 0.36 | ||||||
| FFEC | 1.62 | 0.947 | -7.89 | 0.00 | ||||||||||
| EMPL | -0.75 | 0.23 | -3.51 | 0.00 | ||||||||||
| INDVA | 1.35 | 0.911 | -5.16 | 0.00 | ||||||||||
| CPI | -4.75 | 0.00 | -6.31 | 0.00 | ||||||||||
Source: Authors’ computations. Notes: For the definition of variables, please see Table 4.
Panel regression analysis
Table 10 provides the results of pooled OLS regressions with Driscoll-Kraay standard errors. According to F statistic, all the estimated models are statistically highly significant, and the values related to R-squared reveal that it could explain between 32% and 98% of the variability in pollutant emissions. The coefficients related to GDP per capita and squared GDP per capita are statistically significant in all the estimated models, except the models 4, 6 and 7. Nevertheless, the EKC hypothesis is confirmed in case of ESOX and ENMVOC. Furthermore, the output of fixed-effects regressions with Driscoll-Kraay standard errors is showed in Table 11. The estimated regressions appear to fit the data rather well since they can explain almost 42% and 87% of the pollutant emissions variation. An inverted U-shaped curve emerges in case of all selected harming emanations, except ESOX and GGET. With regard to the environmental tax revenues, we acknowledge that the expectation concerning ecological damage reduction is not supported since almost all the estimated models show a positive influence of such taxes on pollutant emissions. While primary energy consumption drives pollution, we notice, with some exceptions, that renewable energies consumption reduces pollutant emissions, as previously found by [56]. In terms of research and development expenditure, like [51], our results reinforce the beneficial effect of innovation on environmental pollution. As regards the variables employed to control for the scale effect, technique effect and political condition, we ascertain mixed evidence.
Table 10. Pooled OLS regressions with Driscoll-Kraay standard errors.
| Independent variables | Dependent variables | ||||||
|---|---|---|---|---|---|---|---|
| GGE (1) |
GGEI (2) |
ESOX (3) |
ENOX (4) |
ENMVOC (5) |
ENH3 (6) |
GGET (7) |
|
| GDPC | -2.05*** | -0.53*** | 4.66*** | -0.43 | 1.67*** | -1.05 | 0.58* |
| (-4.95) | (-4.67) | (6.03) | (-1.02) | (3.13) | (-1.74) | (1.84) | |
| GDPCSQ | 0.13*** | 0.03*** | -0.27*** | 0.03 | -0.08*** | 0.06* | -0.01 |
| (5.67) | (4.77) | (-6.56) | (1.28) | (-3.04) | (1.93) | (-0.45) | |
| ENVTR | 0.02** | 0.00 | 0.10*** | 0.03** | 0.03** | 0.05*** | -0.01** |
| (2.99) | (1.06) | (4.23) | (2.21) | (2.33) | (3.77) | (-2.55) | |
| PEC | 0.13*** | 0.01 | 1.48*** | 0.94*** | 0.83*** | 0.89*** | 0.80*** |
| (10.17) | (1.35) | (23.32) | (47.65) | (21.28) | (33.03) | (41.61) | |
| GIECRE | -0.14*** | -0.01* | -0.35*** | 0.04*** | 0.19*** | 0.12*** | 0.13*** |
| (-6.14) | (-1.81) | (-6.50) | (3.58) | (9.02) | (5.74) | (15.59) | |
| GFCF | 0.01** | -0.00 | 0.02 | 0.00 | -0.02*** | -0.01* | -0.01* |
| (2.93) | (-0.09) | (1.27) | (0.42) | (-3.17) | (-1.82) | (-1.98) | |
| RD | -0.06 | 0.01 | -0.34* | -0.17*** | -0.37*** | -0.35*** | -0.27*** |
| (-1.63) | (1.08) | (-2.05) | (-3.67) | (-7.99) | (-5.73) | (-6.30) | |
| FFEC | -0.00*** | 0.00 | -0.01* | 0.00** | -0.00 | 0.00 | 0.00*** |
| (-5.05) | (0.88) | (-1.86) | (2.75) | (-1.06) | (1.14) | (3.00) | |
| EMPL | -0.01** | -0.00 | -0.06* | -0.02** | 0.01 | -0.01 | 0.01*** |
| (-2.53) | (-1.14) | (-1.92) | (-2.99) | (0.62) | (-0.99) | (3.22) | |
| INDVA | 0.02*** | 0.00 | 0.03*** | 0.00 | 0.02*** | 0.04*** | -0.01*** |
| (8.98) | (0.64) | (6.54) | (0.83) | (3.07) | (9.92) | (-4.10) | |
| CPI | -0.00 | -0.00*** | -0.00** | -0.00*** | -0.00*** | 0.00 | -0.00*** |
| (-1.42) | (-4.34) | (-2.71) | (-3.89) | (-3.76) | (1.56) | (-6.48) | |
| _cons | 10.16*** | 7.26*** | -10.98** | 10.28*** | -0.79 | 10.77*** | -5.47*** |
| (5.57) | (12.58) | (-2.89) | (4.67) | (-0.31) | (3.75) | (-3.45) | |
| F statistic | 4274.60*** | 71.77*** | 173364.36*** | 154719.35*** | 67864.83*** | 117622.81*** | 219042.44*** |
| R-sq | 0.63 | 0.32 | 0.83 | 0.97 | 0.96 | 0.92 | 0.98 |
| Obs | 470 | 470 | 470 | 470 | 470 | 470 | 470 |
| N Countries | 28 | 28 | 28 | 28 | 28 | 28 | 28 |
Source: Authors’ computations. Numbers in the parentheses represent t-stat values. For the definition of variables, please see Table 4.
*** indicates the statistical significance at 1% levels.
** indicates the statistical significance at 5% levels.
* indicates the statistical significance at 10% levels.
Table 11. Fixed-effects regressions with Driscoll-Kraay standard errors.
| Independent variables | Dependent variables | ||||||
|---|---|---|---|---|---|---|---|
| GGE (1) |
GGEI (2) |
ESOX (3) |
ENOX (4) |
ENMVOC (5) |
ENH3 (6) |
GGET (7) |
|
| GDPC | 2.68*** | 0.84** | -0.99 | 1.62*** | 5.15*** | 1.42** | 0.84*** |
| (6.70) | (2.76) | (-0.74) | (3.49) | (8.78) | (2.57) | (5.33) | |
| GDPCSQ | -0.14*** | -0.05*** | -0.03 | -0.10*** | -0.29*** | -0.08** | -0.01 |
| (-6.43) | (-3.01) | (-0.44) | (-4.12) | (-8.54) | (-2.63) | (-1.53) | |
| ENVTR | 0.00 | 0.00 | 0.01 | 0.01 | -0.01 | 0.02*** | 0.00 |
| (0.67) | (0.46) | (0.42) | (1.59) | (-1.35) | (4.32) | (0.01) | |
| PEC | 0.69*** | 0.02 | 0.85*** | 0.64*** | 0.14 | 0.31*** | 0.39*** |
| (19.67) | (0.53) | (7.10) | (7.11) | (1.54) | (5.41) | (5.64) | |
| GIECRE | -0.02*** | 0.02*** | -0.13* | -0.04 | 0.04** | -0.02 | 0.02*** |
| (-3.02) | (3.00) | (-1.99) | (-1.76) | (2.42) | (-1.48) | (4.56) | |
| GFCF | -0.00** | -0.00** | 0.02*** | 0.00 | 0.00 | 0.00* | 0.00** |
| (-2.27) | (-2.79) | (3.42) | (1.66) | (1.20) | (2.08) | (2.62) | |
| RD | 0.04** | 0.02** | -0.23*** | 0.01 | -0.13*** | 0.03 | 0.03 |
| (2.98) | (2.20) | (-3.73) | (0.53) | (-3.92) | (1.27) | (1.61) | |
| FFEC | 0.01*** | 0.01*** | 0.04*** | 0.02*** | 0.01*** | 0.01*** | 0.00* |
| (17.95) | (18.02) | (8.90) | (19.87) | (4.58) | (8.02) | (1.96) | |
| EMPL | 0.01*** | -0.00 | 0.05 | 0.05*** | 0.07*** | 0.02*** | 0.02*** |
| (3.86) | (-0.91) | (1.15) | (5.51) | (4.63) | (3.74) | (4.24) | |
| INDVA | 0.01*** | 0.01*** | 0.08*** | 0.01*** | 0.03*** | 0.01* | -0.01*** |
| (7.54) | (6.39) | (6.28) | (5.88) | (4.06) | (1.85) | (-3.74) | |
| CPI | -0.00 | -0.00* | 0.00** | -0.00* | -0.00** | 0.00*** | -0.00*** |
| (-0.72) | (-1.99) | (2.23) | (-1.87) | (-2.47) | (3.03) | (-6.87) | |
| _cons | -14.22*** | -0.29 | 17.49*** | 2.06 | -13.04*** | 3.09 | -6.11*** |
| (-7.63) | (-0.19) | (3.40) | (0.95) | (-4.94) | (1.21) | (-7.29) | |
| F statistic | 7045.93*** | 1520.21*** | 1487.69*** | 4101.01*** | 325.65*** | 386.02*** | 1287.52*** |
| within R-sq | 0.87 | 0.81 | 0.76 | 0.82 | 0.72 | 0.42 | 0.71 |
| Obs | 470 | 470 | 470 | 470 | 470 | 470 | 470 |
| N Countries | 28 | 28 | 28 | 28 | 28 | 28 | 28 |
Source: Authors’ computations. Numbers in the parentheses represent t-stat values. For the definition of variables, please see Table 4.
*** indicates the statistical significance at 1% levels.
** indicates the statistical significance at 5% levels.
* indicates the statistical significance at 10% levels.
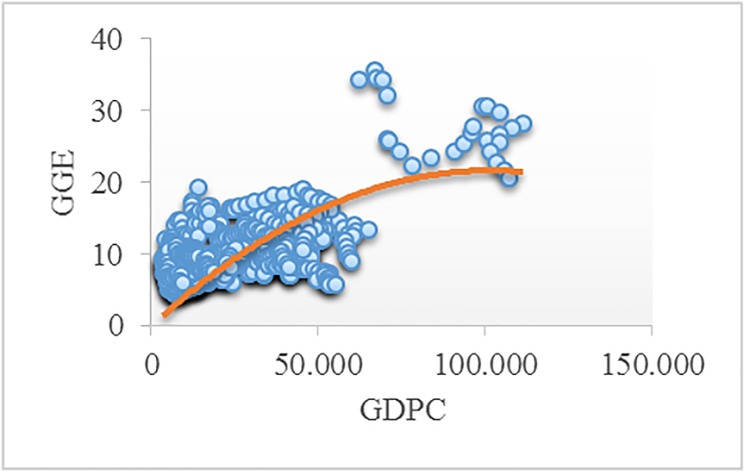
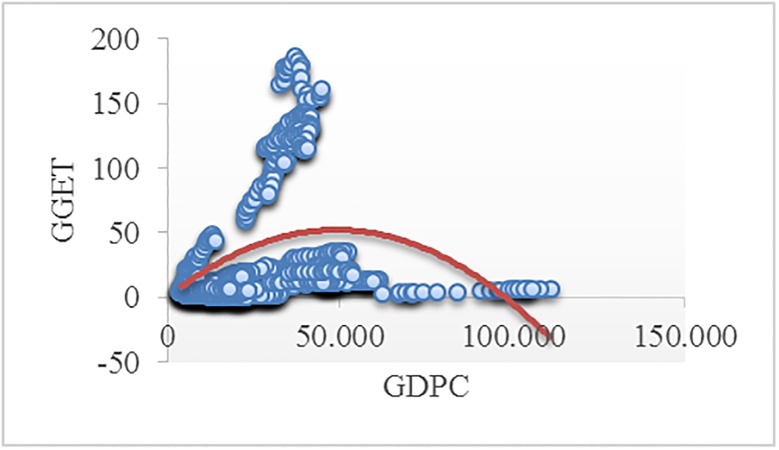
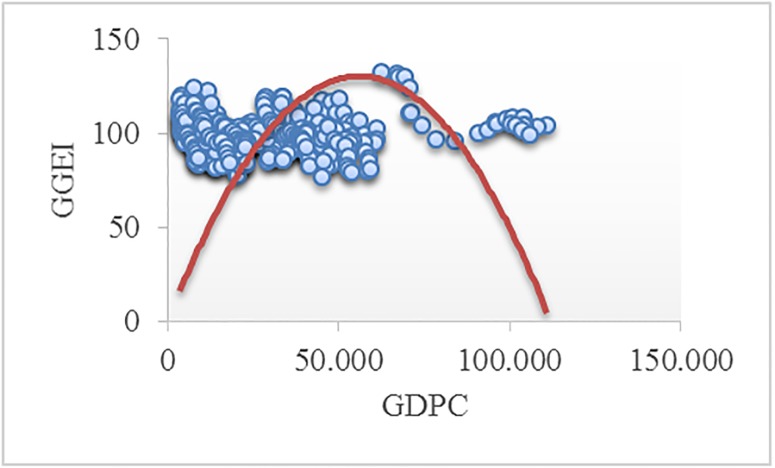
Figs 2–8 reveals the plotted graphs between GDP per capita and pollutant emissions.
Fig 2. Plotted graphs between GDP per capita and greenhouse gas emissions in EU-28.
Source: Authors’ own elaboration.
Fig 8. Plotted graphs between GDP per capita and greenhouse gas emissions from transport in EU-28.
Source: Authors’ own elaboration.
Fig 3. Plotted graphs between GDP per capita and greenhouse gas emissions intensity of energy consumption in EU-28.
Source: Authors’ own elaboration.
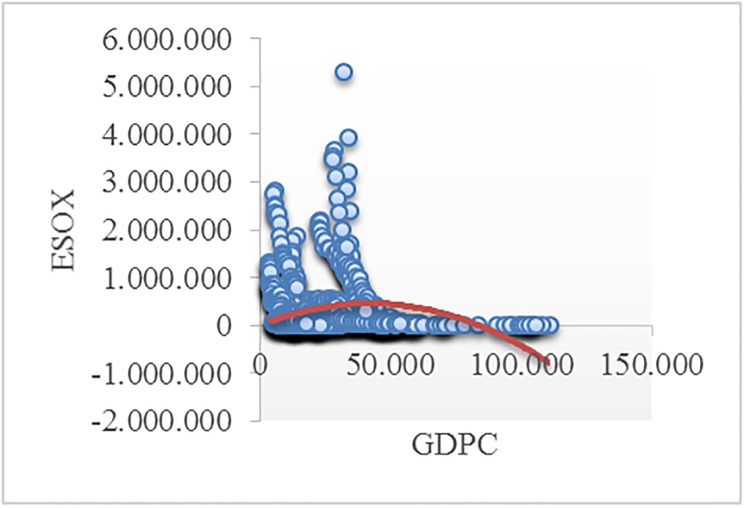
Fig 4. Plotted graphs between GDP per capita and emissions of sulfur oxides in EU-28.
Source: Authors’ own elaboration.
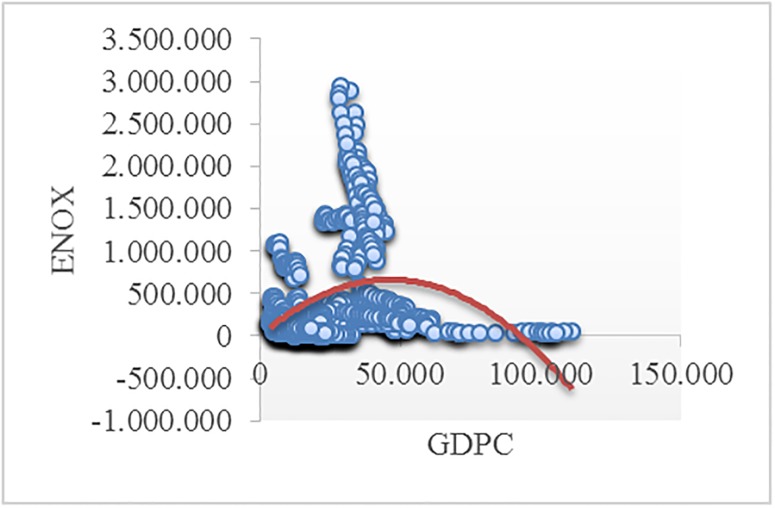
Fig 5. Plotted graphs between GDP per capita and emissions of nitrogen oxides in EU-28.
Source: Authors’ own elaboration.
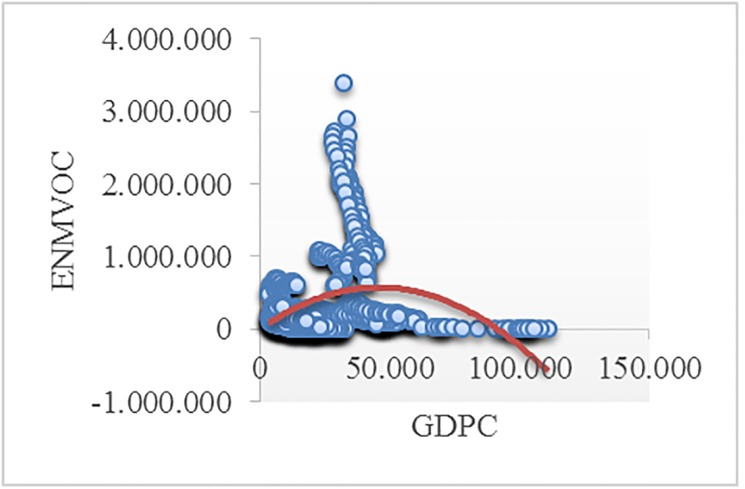
Fig 6. Plotted graphs between GDP per capita and emissions of non-methane volatile organic compounds in EU-28.
Source: Authors’ own elaboration.
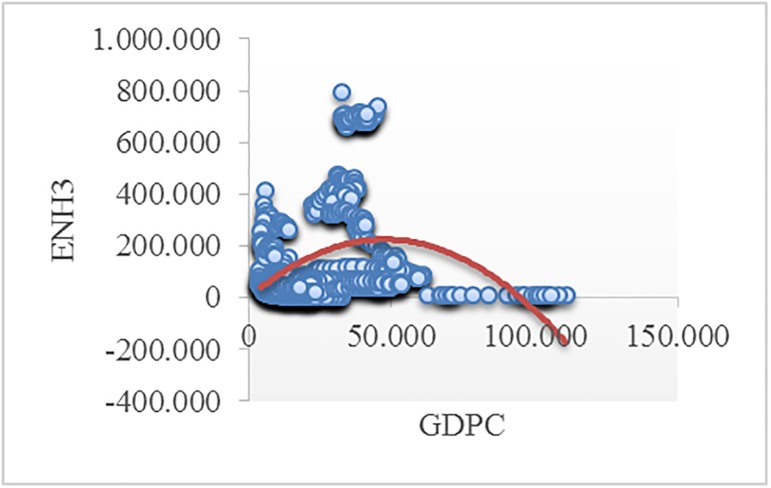
Fig 7. Plotted graphs between GDP per capita and emissions of ammonia in EU-28.
Source: Authors’ own elaboration.
The EKC hypothesis appears to be sustained since the inversed U-shaped curve tends to fit properly at least for greenhouse gas emissions. In addition, Table 12 exhibits the estimated turning points. We notice that the values of the established turning points are not in line with previous studies [38, 39] that employed GDP per capita (in 2010 U.S. $). However, alike [37, 63, 65, 97, 122], we notice values which lie outside the sample, namely for GGE (pooled OLS estimations) and ENOX (fixed-effects estimations). Moreover, [17] underlined a higher likelihood of identifying turning points outside the sample in case of developing countries than developed countries.
Table 12. Estimated turning points from current study (in 2010 U.S. $).
| Panel regression analysis | GGE | GGEI | ESOX | ENOX | ENMVOC | ENH3 | GGET |
|---|---|---|---|---|---|---|---|
| Pooled OLS regressions | 3,570 (outside the sample) | 20,895 | 6,097 | - | 43,393 | - | - |
| Fixed-effects regressions | 18,041.52 | 5,691.36 | - | 2,885.07 (outside the sample) | 8,115.80 | 7,835.30 | - |
Source: Authors’ own elaboration. Notes: For the definition of variables, please see Table 4.
Co-integration and causality investigation
The outcome of Pedroni panel co-integration test [115, 116] is presented in Table 13. According to [88, 89, 104], the statistics based on the dimension approach pools the autoregressive coefficients across different states for the unit root tests on the estimated residuals considering common time factors and heterogeneity across countries. To examine the null hypothesis of no co-integration, ρi = 1, the following unit root test towards the residuals [88, 89, 104] is performed:
| (4) |
Table 13. Pedroni (Engle Granger based) test results.
| Panel A: Within-dimension | ||||
| Panel co-integration test | Individual intercept | Individual intercept and individual trend | ||
| Statistic | Weighted Statistic | Statistic | Weighted Statistic | |
| Panel v-Statistic | 1.87** | -1.25 | -0.90 | -4.31 |
| Panel rho-Statistic | 0.71 | -0.01 | 3.02 | 2.07 |
| Panel PP-Statistic | -3.22*** | -8.16*** | -4.52*** | -9.12*** |
| Panel ADF-Statistic | -7.45*** | -9.91*** | -7.87*** | -9.62*** |
| Panel B: Between-dimension | ||||
| Panel co-integration test | Statistic | Statistic | ||
| Group rho-Statistic | 2.51 | 4.37 | ||
| Group PP-Statistic | -10.74*** | -11.59*** | ||
| Group ADF-Statistic | -10.34*** | -9.46*** | ||
Source: Authors’ computations. Schwarz Info Criterion was selected for lag length.
*** indicates the statistical significance at 1% levels
** indicates the statistical significance at 5% levels
* indicates the statistical significance at 10% levels
As shown in panel A, panel PP and panel ADF statistics strongly reject the null hypothesis of no co-integration. Additionally, the statistics based on the between-dimension are based on the mean values of the individual autoregressive coefficients related to the unit root tests of the residuals for each member state. The results from panel B reinforce that panel PP and panel ADF statistics reject the null hypothesis of no co-integration at the significance level of 1%.
The second test of panel co-integration employed within current examination is the Kao test (the outcome is reported in Table 14). [117] suggests an ADF panel co-integration test where the vectors of co-integration are homogeneous. However, according to [123], this test is based on a panel version of the ADF test on the residual (εit):
| (5) |
Table 14. Kao (Engle Granger based) test results.
| ADF (t-Statistic) | Residual variance | HAC variance |
|---|---|---|
| -2.94*** | 11.52 | 3.76 |
Source: Authors’ computations. Schwarz Info Criterion was selected for lag length.
*** indicates the statistical significance at 1% levels.
** indicates the statistical significance at 5% levels.
* indicates the statistical significance at 10% levels.
Further, the following ADF statistic is produced:
| (6) |
where depicts the estimated variance, describes the estimated long-run variance of the error term which follows the standard normal distribution, and τADF reveals the ADF statistic for Eq (5). Thus, since the probability of ADF is 0.0274, the results provide support for the hypothesis of co-integration among all variables.
The third co-integration approach used is depicted by Fisher-type panel co-integration test [118] showed in Table 15. The Johansen Fisher panel co-integration test aggregates the p-values of individual Johansen maximum eigen-value and trace statistics [124]; this test also rejects the null hypothesis of no co-integration.
Table 15. Fisher (combined Johansen) test results.
| Hypothesized No. of CE(s) | Fisher Stat. (from trace test) | Fisher Stat. (from max-eigen test) |
|---|---|---|
| None | 380.2*** | 299.7*** |
| At most 1 | 160.3*** | 111.5*** |
| At most 2 | 95.9*** | 76.11** |
| At most 3 | 96.44*** | 96.44*** |
Source: Authors’ computations. Schwarz Info Criterion was selected for lag length. Probabilities are computed using asymptotic Chi-square distribution.
*** indicates the statistical significance at 1% levels.
** indicates the statistical significance at 5% levels.
* indicates the statistical significance at 10% levels.
Further, the Westerlund test [119] is employed (the outcome is showed in Table 16). Contrary to [121], the null hypothesis of no cointegration between greenhouse gas emissions, economic growth, primary energy consumption, and environmental tax revenues is rejected. Therefore, when the cross-dependence is considered in the panel, there exists a long-run equilibrium relationship between the variables.
Table 16. The output of Westerlund panel cointegration test.
| Statistic | Value | Z-value | P-value |
|---|---|---|---|
| Gt | -2.80 | -5.64 | 0.00 |
| Ga | -5.44 | 2.01 | 0.98 |
| Pt | -11.14 | -3.18 | 0.00 |
| Pa | -5.49 | -1.02 | 0.15 |
Source: Authors’ computations. Note: Gt and Ga reveal the group mean statistics that examine the null of no cointegration for the whole panel against the alternative of cointegration. Pt and Pa are the panel statistics that test the null of no cointegration against the alternative of cointegration for the panel as a whole. Bartlett-Kernel window width set according to 4(T/100)2/9 ≈ 3.
Onward, since the variables are co-integrated, a panel vector error correction model is estimated in order to perform Granger-causality tests presented in Table 17. The panel error correction model, Eqs (3a)–(3d), allows two sources of causality, namely short-run causality via the lagged difference terms, as well as long-run causality by mean values of the error correction terms. With respect to Eq (3a), environmental tax revenues show a statistically significant influence on the short-run on GDP per capita growth. Concerning Eq (3b), there ensues a unidirectional causality running from economic growth to greenhouse gas emissions as in [96, 102]. In addition, primary energy consumption has a statistically significant effect on GHG emissions. In Eq (3c), we noticed the statistically significant influence of GHG emissions and primary energy consumption on environmental tax revenues. Eq (3d) shows that GHG emissions and environmental tax revenues have a statistically significant impact on primary energy consumption. However, in as much as there is no causal link between GDPCG and PEC, the neo-classical view is confirmed, respectively the neutrality assumption. Moreover, the error correction term is statistically significant, but reveals a relatively slow speed of adjustment towards equilibrium.
Table 17. Granger causality based on panel vector error correction model.
| Excluded | Short-run causality | Long-run causality | |||
|---|---|---|---|---|---|
| Dependent variable | |||||
| ΔGDPCG | ΔGGE | ΔENVTR | ΔPEC | ECT | |
| ΔGDPCG | - | 10.94*** | 2.17 | 3.04 | -0.40*** |
| ΔGGE | 1.87 | - | 7.59** | 13.18*** | 0.003*** |
| ΔENVTR | 6.74** | 4.41 | - | 17.11*** | -0.02** |
| ΔPEC | 2.35 | 8.97** | 8.12** | - | 0.002** |
Source: Authors’ computations. For the definition of variables, please see Table 4.
*** indicates the statistical significance at 1% levels.
** indicates the statistical significance at 5% levels.
* indicates the statistical significance at 10% levels.
Conclusions
The objective of the present study was to firstly examine the EKC hypothesis and subsequently the causal relationships between greenhouse gas emissions, economic growth, primary energy consumption, and environmental tax revenues, for a panel consisting of the EU-28 countries over the period 1990–2014. Since we noticed cross-sectional dependence in each of the variables in the panel, we employed Driscoll-Kraay standard errors. The results of pooled OLS regressions confirmed the EKC hypothesis for emissions of sulfur oxides and emissions of non-methane volatile organic compounds, whereas the outcome of fixed-effects estimations validated furthermore the EKC approach for greenhouse gas emissions, greenhouse gas emissions intensity of energy consumption, emissions of nitrogen oxides, emissions of non-methane volatile organic compounds and emissions of ammonia. Additionally, the estimation of a panel vector error correction model shows the presence of a short-run unidirectional causality from GDP per capita growth to greenhouse gas emissions, as well as a bidirectional causal link between primary energy consumption and greenhouse gas emissions. Besides, the neo-classical view was endorsed, respectively the neutrality hypothesis.
The main policy implication deriving from our research can be formulated as follows: EU-28 states should promote the use of renewable energies that are constantly replenished and which will never end. Accordingly, the use of renewable energy will contribute to the decrease of GHGs emissions, while also reducing the reliance on fossil fuel markets. Besides, EU-28 may benefit from enhanced employment opportunities due to jobs occurrence in new cleaner technologies. Finally, as future research endeavors, our aim is to extend the empirical analysis in order to test the EKC hypothesis utilizing a composite index of environmental performance.
Data Availability
All relevant data are within the paper.
Funding Statement
The authors received no specific funding for this work.
References
- 1.Javid M, Sharif F. Environmental Kuznets curve and financial development in Pakistan. Renew Sust Energ Rev. 2016;54:406–14. doi: 10.1016/j.rser.2015.10.019 [Google Scholar]
- 2.Ozokcu S, Ozdemir O. Economic growth, energy, and environmental Kuznets curve. Renew Sust Energ Rev. 2017;72:639–47. doi: 10.1016/j.rser.2017.01.059 [Google Scholar]
- 3.Kumar S, Fujii H, Managi S. Substitute or complement? Assessing renewable and nonrenewable energy in OECD countries. Appl Econ. 2015;47(14):1438–59. doi: 10.1080/00036846.2014.997922 [Google Scholar]
- 4.Ozturk I, Acaravci A. CO2 emissions, energy consumption and economic growth in Turkey. Renew Sust Energ Rev. 2010;14(9):3220–5. [Google Scholar]
- 5.Marjanovic V, Milovancevic M, Mladenovic I. Prediction of GDP growth rate based on carbon dioxide (CO2) emissions. J Co2 Util. 2016;16:212–7. [Google Scholar]
- 6.Holtz-Eakin D, Selden TM. Stoking the Fires—Co2 Emissions and Economic-Growth. J Public Econ. 1995;57(1):85–101. doi: 10.1016/0047-2727(94)01449-X [Google Scholar]
- 7.EIA. International Energy Outlook 2016. Washington, DC 20585: 2016 DOE/EIA-0484(2016).
- 8.Omer AM. Energy, environment and sustainable development. Renew Sust Energ Rev. 2008;12(9):2265–300. doi: 10.1016/j.rser.2007.05.001 [Google Scholar]
- 9.UNEP. Decoupling natural resource use and environmental impacts from economic growth. 2011 DTI/1388/PA.
- 10.UNEP. Decoupling 2: Technologies, opportunities and policy options. 2014 DTI/1795/PA.
- 11.Review of the EU Sustainable Development Strategy (EU SDS)—Renewed Strategy, 10917/06 (2006).
- 12.Conference of the Parties serving as the meeting of the Parties to the Kyoto Protocol, FCCC/KP/CMP/2012/13/Add. 1 (2013).
- 13.Europe 2020—A strategy for smart, sustainable and inclusive growth, COM(2010) 2020 final (2010).
- 14.Council Conclusions, EUCO 169/14 (2014).
- 15.Friedl B, Getzner M. Determinants of CO2 emissions in a small open economy. Ecol Econ. 2003;45(1):133–48. doi: 10.1016/S0921-8009(03)00008-9 [Google Scholar]
- 16.Ahmad N, Du LS, Lu JY, Wang JL, Li HZ, Hashmi MZ. Modelling the CO2 emissions and economic growth in Croatia: Is there any environmental Kuznets curve? Energy. 2017;123:164–72. doi: 10.1016/j.energy.2016.12.106 [Google Scholar]
- 17.Iwata H, Okada K, Samreth S. Empirical study on the environmental Kuznets curve for CO2 in France: The role of nuclear energy. Energ Policy. 2010;38(8):4057–63. doi: 10.1016/j.enpol.2010.03.031 [Google Scholar]
- 18.Benti JPC, Moutinho V. CO2 emissions, non-renewable and renewable electricity production, economic growth, and international trade in Italy. Renew Sust Energ Rev. 2016;55:142–55. doi: 10.1016/j.rser.2015.10.151 [Google Scholar]
- 19.Cialani C. Economic growth and environmental quality: An econometric and a decomposition analysis. Management of Environmental Quality: An International Journal. 2007;18(5):568–77. [Google Scholar]
- 20.Moutinho V, Varum C, Madaleno M. How economic growth affects emissions? An investigation of the environmental Kuznets curve in Portuguese and Spanish economic activity sectors. Energ Policy. 2017;106:326–44. [Google Scholar]
- 21.Shahbaz M, Mutascu M, Azim P. Environmental Kuznets curve in Romania and the role of energy consumption. Renew Sust Energ Rev. 2013;18:165–73. [Google Scholar]
- 22.Esteve V, Tamarit C. Is there an environmental Kuznets curve for Spain? Fresh evidence from old data. Econ Model. 2012;29(6):2696–703. [Google Scholar]
- 23.Esteve V, Tamarit C. Threshold cointegration and nonlinear adjustment between CO2 and income: The Environmental Kuznets Curve in Spain, 1857–2007. Energ Econ. 2012;34(6):2148–56. doi: 10.1016/j.eneco.2012.03.001 [Google Scholar]
- 24.Sephton P, Mann J. Further evidence of an Environmental Kuznets Curve in Spain. Energ Econ. 2013;36:177–81. [Google Scholar]
- 25.Balaguer J, Cantavella M. Estimating the environmental Kuznets curve for Spain by considering fuel oil prices (1874–2011). Ecological Indicators. 2016;60:853–9. doi: 10.1016/j.ecolind.2015.08.006 [Google Scholar]
- 26.Fosten J, Morley B, Taylor T. Dynamic misspecification in the environmental Kuznets curve: Evidence from CO2 and SO2 emissions in the United Kingdom. Ecol Econ. 2012;76:25–33. doi: 10.1016/j.ecolecon.2012.01.023 [Google Scholar]
- 27.Arbulu I, Lozano J, Rey-Maquieira J. Tourism and solid waste generation in Europe: A panel data assessment of the Environmental Kuznets Curve. Waste Manage. 2015;46:628–36. doi: 10.1016/j.wasman.2015.04.014 [DOI] [PubMed] [Google Scholar]
- 28.Kasman A, Duman YS. CO2 emissions, economic growth, energy consumption, trade and urbanization in new EU member and candidate countries: A panel data analysis. Econ Model. 2015;44:97–103. doi: 10.1016/j.econmod.2014.10.022 [Google Scholar]
- 29.Ahmed A, Uddin GS, Sohag K. Biomass energy, technological progress and the environmental Kuznets curve: Evidence from selected European countries. Biomass Bioenerg. 2016;90:202–8. doi: 10.1016/j.biombioe.2016.04.004 [Google Scholar]
- 30.Pablo-Romero MD, Sanchez-Braza A. Residential energy environmental Kuznets curve in the EU-28. Energy. 2017;125:44–54. doi: 10.1016/j.energy.2017.02.091 [Google Scholar]
- 31.Pablo-Romero MP, Cruz L, Barata E. Testing the transport energy-environmental Kuznets curve hypothesis in the EU27 countries. Energ Econ. 2017;62:257–69. doi: 10.1016/j.eneco.2017.01.003 [Google Scholar]
- 32.Energy Efficiency and its contribution to energy security and the 2030 Framework for climate and energy policy, COM(2014) 520 final (2014).
- 33.Kuznets S. Economic growth and income inequality. The American Economic Review. 1955;45(1):1–28. [Google Scholar]
- 34.Galeotti M, Lanza A, Pauli F. Reassessing the environmental Kuznets curve for CO2 emissions: A robustness exercise. Ecol Econ. 2006;57(1):152–63. doi: 10.1016/j.ecolecon.2005.03.031 [Google Scholar]
- 35.Park S, Lee Y. Regional model of EKC for air pollution: Evidence from the Republic of Korea. Energ Policy. 2011;39(10):5840–9. doi: 10.1016/j.enpol.2011.06.028 [Google Scholar]
- 36.Arouri ME, Ben Youssef A, M’henni H, Rault C. Energy consumption, economic growth and CO2 emissions in Middle East and North African countries. Energ Policy. 2012;45:342–9. doi: 10.1016/j.enpol.2012.02.042 [Google Scholar]
- 37.Anjum Z, Burke PJ, Gerlagh R, Stern DI. Modeling the Emissions-Income Relationship Using Long-Run Growth Rates. In: Crawford School of Public Policy CfCEP, editor. CCEP Working Paper 2014.
- 38.Riti JS, Song DY, Shu Y, Kamah M. Decoupling CO2 emission and economic growth in China: Is there consistency in estimation results in analyzing environmental Kuznets curve? J Clean Prod. 2017;166:1448–61. [Google Scholar]
- 39.Anas M. Environmental Kuznets curve for the Moroccan economy. Archives of Business Research. 2017;2(12):148–55. [Google Scholar]
- 40.Grossman GM, Krueger AB. Environmental Impacts of a North American Free Trade Agreement. 1991.
- 41.Shafik N, Bandyopadhyay S. Economic growth and environmental quality: Time series and cross-country evidence. 1992.
- 42.Panayotou T. Empirical Tests and Policy Analysis of Environmental Degradation at Different Stages of Economic Development. 1993. [Google Scholar]
- 43.Selden TM, Song DQ. Environmental-Quality and Development—Is There a Kuznets Curve for Air-Pollution Emissions. J Environ Econ Manag. 1994;27(2):147–62. doi: 10.1006/jeem.1994.1031 [Google Scholar]
- 44.Akbostanci E, Turut-Asik S, Tunc GI. The relationship between income and environment in Turkey: Is there an environmental Kuznets curve? Energ Policy. 2009;37(3):861–7. doi: 10.1016/j.enpol.2008.09.088 [Google Scholar]
- 45.Fodha M, Zaghdoud O. Economic growth and pollutant emissions in Tunisia: An empirical analysis of the environmental Kuznets curve. Energ Policy. 2010;38(2):1150–6. doi: 10.1016/j.enpol.2009.11.002 [Google Scholar]
- 46.Dinda S. Environmental Kuznets Curve hypothesis: A survey. Ecol Econ. 2004;49(4):431–55. [Google Scholar]
- 47.Stern DI. The rise and fall of the environmental Kuznets curve. World Dev. 2004;32(8):1419–39. doi: 10.1016/j.worlddev.2004.03.004 [Google Scholar]
- 48.Magnani E. The Environmental Kuznets Curve: development path or policy result? Environ Modell Softw. 2001;16(2):157–65. doi: 10.1016/S1364-8152(00)00079-7 [Google Scholar]
- 49.Kaika D, Zervas E. The Environmental Kuznets Curve (EKC) theory-Part A: Concept, causes and the CO2 emissions case. Energ Policy. 2013;62:1392–402. doi: 10.1016/j.enpol.2013.07.131 [Google Scholar]
- 50.Apergis N, Christou C, Gupta R. Are there Environmental Kuznets Curves for US state-level CO2 emissions? Renew Sust Energ Rev. 2017;69:551–8. doi: 10.1016/j.rser.2016.11.219 [Google Scholar]
- 51.Alvarez-Herranz A, Balsalobre-Lorente D, Shahbaz M, Cantos JM. Energy innovation and renewable energy consumption in the correction of air pollution levels. Energ Policy. 2017;105:386–97. doi: 10.1016/j.enpol.2017.03.009 [Google Scholar]
- 52.Balaguer J, Cantavella M. The role of education in the Environmental Kuznets Curve. Evidence from Australian data. Energ Econ. 2018;70:289–96. [Google Scholar]
- 53.Kaika D, Zervas E. The environmental Kuznets curve (EKC) theory. Part B: Critical issues. Energ Policy. 2013;62:1403–11. doi: 10.1016/j.enpol.2013.07.130 [Google Scholar]
- 54.Narayan PK, Narayan S. Carbon dioxide emissions and economic growth: Panel data evidence from developing countries. Energ Policy. 2010;38(1):661–6. doi: 10.1016/j.enpol.2009.09.005 [Google Scholar]
- 55.Azam M, Khan AQ. Testing the Environmental Kuznets Curve hypothesis: A comparative empirical study for low, lower middle, upper middle and high income countries. Renew Sust Energ Rev. 2016;63:556–67. doi: 10.1016/j.rser.2016.05.052 [Google Scholar]
- 56.Ben Jebli M, Ben Youssef S, Ozturk I. Testing environmental Kuznets curve hypothesis: The role of renewable and non-renewable energy consumption and trade in OECD countries. Ecological Indicators. 2016;60:824–31. doi: 10.1016/j.ecolind.2015.08.031 [Google Scholar]
- 57.Khan SAR, Zaman K, Zhang Y. The relationship between energy-resource depletion, climate change, health resources and the environmental Kuznets curve: Evidence from the panel of selected developed countries. Renew Sust Energ Rev. 2016;62:468–77. doi: 10.1016/j.rser.2016.04.061 [Google Scholar]
- 58.Chandran VGR, Tang CF. The impacts of transport energy consumption, foreign direct investment and income on CO2 emissions in ASEAN-5 economies. Renew Sust Energ Rev. 2013;24:445–53. [Google Scholar]
- 59.Ozcan B. The nexus between carbon emissions, energy consumption and economic growth in Middle East countries: A panel data analysis. Energ Policy. 2013;62:1138–47. doi: 10.1016/j.enpol.2013.07.016 [Google Scholar]
- 60.Almeida TAN, Cruz L, Barata E, Garcia-Sanchez I-M. Economic growth and environmental impacts: An analysis based on a composite index of environmental damage. Ecological Indicators. 2017;76:119–30. [Google Scholar]
- 61.Baek J, Kim HS. Is economic growth good or bad for the environment? Empirical evidence from Korea. Energ Econ. 2013;36:744–9. doi: 10.1016/j.eneco.2012.11.020 [Google Scholar]
- 62.Kanjilal K, Ghosh S. Environmental Kuznet’s curve for India: Evidence from tests for cointegration with unknown structural breaks. Energ Policy. 2013;56:509–15. doi: 10.1016/j.enpol.2013.01.015 [Google Scholar]
- 63.Boluk G, Mert M. The renewable energy, growth and environmental Kuznets curve in Turkey: An ARDL approach. Renew Sust Energ Rev. 2015;52:587–95. doi: 10.1016/j.rser.2015.07.138 [Google Scholar]
- 64.Hao Y, Liu YM, Weng JH, Gao YX. Does the Environmental Kuznets Curve for coal consumption in China exist? New evidence from spatial econometric analysis. Energy. 2016;114:1214–23. doi: 10.1016/j.energy.2016.08.075 [Google Scholar]
- 65.Sugiawan Y, Managi S. The environmental Kuznets curve in Indonesia: Exploring the potential of renewable energy. Energ Policy. 2016;98:187–98. doi: 10.1016/j.enpol.2016.08.029 [Google Scholar]
- 66.Mrabet Z, Alsamara M. Testing the Kuznets Curve hypothesis for Qatar: A comparison between carbon dioxide and ecological footprint. Renew Sust Energ Rev. 2017;70:1366–75. [Google Scholar]
- 67.Kim DH, Huang HC, Lin SC. Kuznets Hypothesis in a Panel of States. Contemp Econ Policy. 2011;29(2):250–60. doi: 10.1111/j.1465-7287.2010.00218.x [Google Scholar]
- 68.Zilio M, Recalde M. GDP and environment pressure: The role of energy in Latin America and the Caribbean. Energ Policy. 2011;39(12):7941–9. [Google Scholar]
- 69.Pao HT, Yu HC, Yang YH. Modeling the CO2 emissions, energy use, and economic growth in Russia. Energy. 2011;36(8):5094–100. doi: 10.1016/j.energy.2011.06.004 [Google Scholar]
- 70.Ozturk I, Al-Mulali U. Investigating the validity of the environmental Kuznets curve hypothesis in Cambodia. Ecological Indicators. 2015;57:324–30. doi: 10.1016/j.ecolind.2015.05.018 [Google Scholar]
- 71.Lin BQ, Omoju OE, Nwakeze NM, Okonkwo JU, Megbowon ET. Is the environmental Kuznets curve hypothesis a sound basis for environmental policy in Africa? J Clean Prod. 2016;133:712–24. [Google Scholar]
- 72.Moosa IA. The econometrics of the environmental Kuznets curve: an illustration using Australian CO2 emissions. Appl Econ. 2017;49(49):4927–45. doi: 10.1080/00036846.2017.1296552 [Google Scholar]
- 73.Xu T. Investigating Environmental Kuznets Curve in China-Aggregation bias and policy implications. Energ Policy. 2018;114:315–22. doi: 10.1016/j.enpol.2017.12.027 [Google Scholar]
- 74.Azomahou T, Laisney F, Van PN. Economic development and CO2 emissions: A nonparametric panel approach. J Public Econ. 2006;90(6–7):1347–63. doi: 10.1016/j.jpubeco.2005.09.005 [Google Scholar]
- 75.Onafowora OA, Owoye O. Bounds testing approach to analysis of the environment Kuznets curve hypothesis. Energ Econ. 2014;44:47–62. doi: 10.1016/j.eneco.2014.03.025 [Google Scholar]
- 76.Abid M. Impact of economic, financial, and institutional factors on CO2 emissions: Evidence from Sub-Saharan Africa economies. Util Policy. 2016;41:85–94. doi: 10.1016/j.jup.2016.06.009 [Google Scholar]
- 77.Dong BM, Wang F, Guo YB. The global EKCs. Int Rev Econ Financ. 2016;43:210–21. doi: 10.1016/j.iref.2016.02.010 [Google Scholar]
- 78.Kang YQ, Zhao T, Yang YY. Environmental Kuznets curve for CO2 emissions in China: A spatial panel data approach. Ecological Indicators. 2016;63:231–9. [Google Scholar]
- 79.Pal D, Mitra SK. The environmental Kuznets curve for carbon dioxide in India and China: Growth and pollution at crossroad. J Policy Model. 2017;39(2):371–85. doi: 10.1016/j.jpolmod.2017.03.005 [Google Scholar]
- 80.Samargandi N. Sector value addition, technology and CO2 emissions in Saudi Arabia. Renewable and Sustainable Energy Reviews. 2017;78:868–77. [Google Scholar]
- 81.Kraft J, Kraft A. On the Relationship Between Energy and GNP The Journal of Energy and Development 1978;3(2):401–3. [Google Scholar]
- 82.Akarca AT, Long TV. On the Relationship between Energy and Gnp—a Reexamination. J Energy Dev. 1980;5(2):326–31. [Google Scholar]
- 83.Alam MJ, Begum IA, Buysse J, Van Huylenbroeck G. Energy consumption, carbon emissions and economic growth nexus in Bangladesh: Cointegration and dynamic causality analysis. Energ Policy. 2012;45:217–25. doi: 10.1016/j.enpol.2012.02.022 [Google Scholar]
- 84.Mirza FM, Kanwal A. Energy consumption, carbon emissions and economic growth in Pakistan: Dynamic causality analysis. Renew Sust Energ Rev. 2017;72:1233–40. doi: 10.1016/j.rser.2016.10.081 [Google Scholar]
- 85.Soytas U, Sari R, Ewing BT. Energy consumption, income, and carbon emissions in the United States. Ecol Econ. 2007;62(3–4):482–9. doi: 10.1016/j.ecolecon.2006.07.009 [Google Scholar]
- 86.Menegaki AN. Growth and renewable energy in Europe: A random effect model with evidence for neutrality hypothesis. Energ Econ. 2011;33(2):257–63. doi: 10.1016/j.eneco.2010.10.004 [Google Scholar]
- 87.Tugcu CT, Ozturk I, Aslan A. Renewable and non-renewable energy consumption and economic growth relationship revisited: Evidence from G7 countries. Energ Econ. 2012;34(6):1942–50. doi: 10.1016/j.eneco.2012.08.021 [Google Scholar]
- 88.Apergis N, Payne JE. Energy consumption and economic growth in Central America: Evidence from a panel cointegration and error correction model. Energ Econ. 2009;31(2):211–6. doi: 10.1016/j.eneco.2008.09.002 [Google Scholar]
- 89.Apergis N, Payne JE. Energy consumption and growth in South America: Evidence from a panel error correction model. Energ Econ. 2010;32(6):1421–6. doi: 10.1016/j.eneco.2010.04.006 [Google Scholar]
- 90.Bowden N, Payne JE. The causal relationship between US energy consumption and real output: A disaggregated analysis. J Policy Model. 2009;31(2):180–8. doi: 10.1016/j.jpolmod.2008.09.001 [Google Scholar]
- 91.Narayan PK, Smyth R. Energy consumption and real GDP in G7 countries: New evidence from panel cointegration with structural breaks. Energ Econ. 2008;30(5):2331–41. [Google Scholar]
- 92.Chontanawat J, Hunt LC, Pierse R. Does energy consumption cause economic growth?: Evidence from a systematic study of over 100 countries. J Policy Model. 2008;30(2):209–20. doi: 10.1016/j.jpolmod.2006.10.003 [Google Scholar]
- 93.Lise W, Van Montfort K. Energy consumption and GDP in Turkey: Is there a co-integration relationship? Energ Econ. 2007;29(6):1166–78. doi: 10.1016/j.eneco.2006.08.010 [Google Scholar]
- 94.Huang BN, Hwang MJ, Yang CW. Causal relationship between energy consumption and GDP growth revisited: A dynamic panel data approach. Ecol Econ. 2008;67(1):41–54. doi: 10.1016/j.ecolecon.2007.11.006 [Google Scholar]
- 95.Dinda S, Coondoo D. Income and emission: A panel data-based cointegration analysis. Ecol Econ. 2006;57(2):167–81. [Google Scholar]
- 96.Govindaraju VGRC Tang CF. The dynamic links between CO2 emissions, economic growth and coal consumption in China and India. Appl Energ. 2013;104:310–8. doi: 10.1016/j.apenergy.2012.10.042 [Google Scholar]
- 97.Saboori B, Sulaiman J. Environmental degradation, economic growth and energy consumption: Evidence of the environmental Kuznets curve in Malaysia. Energ Policy. 2013;60:892–905. doi: 10.1016/j.enpol.2013.05.099 [Google Scholar]
- 98.Shahbaz M, Hye QMA, Tiwari AK, Leitao NC. Economic growth, energy consumption, financial development, international trade and CO2 emissions in Indonesia. Renew Sust Energ Rev. 2013;25:109–21. doi: 10.1016/j.rser.2013.04.009 [Google Scholar]
- 99.Cowan WN, Chang TY, Inglesi-Lotz R, Gupta R. The nexus of electricity consumption, economic growth and CO2 emissions in the BRICS countries. Energ Policy. 2014;66:359–68. doi: 10.1016/j.enpol.2013.10.081 [Google Scholar]
- 100.Omri A, Nguyen DK, Rault C. Causal interactions between CO2 emissions, FDI, and economic growth: Evidence from dynamic simultaneous-equation models. Econ Model. 2014;42:382–9. doi: 10.1016/j.econmod.2014.07.026 [Google Scholar]
- 101.Chaabouni S, Zghidi N, Ben Mbarek M. On the causal dynamics between CO2 emissions, health expenditures and economic growth. Sustain Cities Soc. 2016;22:184–91. [Google Scholar]
- 102.Abdouli M, Hammami S. Investigating the causality links between environmental quality, foreign direct investment and economic growth in MENA countries. Int Bus Rev. 2017;26(2):264–78. doi: 10.1016/j.ibusrev.2016.07.004 [Google Scholar]
- 103.Shahbaz M, Shafiullah M, Papavassiliou VG, Hammoudeh S. The CO2–growth nexus revisited: A nonparametric analysis for the G7 economies over nearly two centuries. Energ Econ. 2017;65:183–93. [Google Scholar]
- 104.Apergis N, Payne JE. The emissions, energy consumption, and growth nexus: Evidence from the commonwealth of independent states. Energ Policy. 2010;38(1):650–5. doi: 10.1016/j.enpol.2009.08.029 [Google Scholar]
- 105.Belke A, Dobnik F, Dreger C. Energy consumption and economic growth: New insights into the cointegration relationship. Energ Econ. 2011;33(5):782–9. doi: 10.1016/j.eneco.2011.02.005 [Google Scholar]
- 106.Eggoh JC, Bangake C, Rault C. Energy consumption and economic growth revisited in African countries. Energ Policy. 2011;39(11):7408–21. doi: 10.1016/j.enpol.2011.09.007 [Google Scholar]
- 107.Fuinhas JA, Marques AC. Energy consumption and economic growth nexus in Portugal, Italy, Greece, Spain and Turkey: An ARDL bounds test approach (1965–2009). Energ Econ. 2012;34(2):511–7. doi: 10.1016/j.eneco.2011.10.003 [Google Scholar]
- 108.Managi S, Hibiki A, Tsurumi T. Does trade openness improve environmental quality? J Environ Econ Manag. 2009;58(3):346–63. doi: 10.1016/j.jeem.2009.04.008 [Google Scholar]
- 109.Fujii H, Managi S. Which industry is greener? An empirical study of nine industries in OECD countries. Energ Policy. 2013;57:381–8. doi: 10.1016/j.enpol.2013.02.011 [Google Scholar]
- 110.Fujii H, Managi S. Economic development and multiple air pollutant emissions from the industrial sector. Environ Sci Pollut R. 2016;23(3):2802–12. doi: 10.1007/s11356-015-5523-2 [DOI] [PubMed] [Google Scholar]
- 111.Fujii H, Managi S. Optimal production resource reallocation for CO2 emissions reduction in manufacturing sectors. Global Environ Chang. 2015;35:505–13. doi: 10.1016/j.gloenvcha.2015.06.005 [Google Scholar]
- 112.Johnstone N, Managi S, Rodriguez MC, Hascic I, Fujii H, Souchier M. Environmental policy design, innovation and efficiency gains in electricity generation. Energ Econ. 2017;63:106–15. doi: 10.1016/j.eneco.2017.01.014 [Google Scholar]
- 113.Galeotti M, Rubashkina Y, Salini S, Verdolini E. Environmental policy performance and its determinants: Application of a three-level random intercept model. Energ Policy. 2018;114:134–44. doi: 10.1016/j.enpol.2017.11.053 [Google Scholar]
- 114.Im KS, Pesaran MH, Shin Y. Testing for unit roots in heterogeneous panels. J Econometrics. 2003;115(1):53–74. doi: 10.1016/S0304-4076(03)00092-7 [Google Scholar]
- 115.Pedroni P. Critical values for cointegration tests in heterogeneous panels with multiple regressors. Oxford B Econ Stat. 1999;61:653–70. [Google Scholar]
- 116.Pedroni P. Panel cointegration: asymptotic and finite sample properties of pooled time series tests with an application to the PPP hypothesis: new results. Econometric Theory 2004;20:597–627. [Google Scholar]
- 117.Kao C. Spurious regression and residual-based tests for cointegration in panel data. J Econometrics. 1999;90(1):1–44. doi: 10.1016/S0304-4076(98)00023-2 [Google Scholar]
- 118.Johansen S. Estimation and Hypothesis-Testing of Cointegration Vectors in Gaussian Vector Autoregressive Models. Econometrica. 1991;59(6):1551–80. doi: 10.2307/2938278 [Google Scholar]
- 119.Westerlund J. Testing for error correction in panel data. Oxford B Econ Stat. 2007;69(6):709–48. doi: 10.1111/j.1468-0084.2007.00477.x [Google Scholar]
- 120.Hoechle D. Robust standard errors for panel regressions with cross–sectional dependence. The Stata Journal. 2007;7(3):281–312. [Google Scholar]
- 121.Jardón A, Kuik O, Tol RSJ. Economic growth and carbon dioxide emissions: An analysis of Latin America and the Caribbean. Atmósfera. 2017;30(2):87–100. [Google Scholar]
- 122.Iwata H, Okada K, Samreth S. A note on the environmental Kuznets curve for CO2: A pooled mean group approach. Appl Energ. 2011;88(5):1986–96. doi: 10.1016/j.apenergy.2010.11.005 [Google Scholar]
- 123.Abdullah S, Morley B. Environmental taxes and economic growth: Evidence from panel causality tests. Energ Econ. 2014;42:27–33. [Google Scholar]
- 124.Lean HH, Smyth R. CO2 emissions, electricity consumption and output in ASEAN. Appl Energ. 2010;87(6):1858–64. doi: 10.1016/j.apenergy.2010.02.003 [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
All relevant data are within the paper.