Skeletal Shape Correspondence through Entropy

Abstract

We present a novel approach for improving the shape statistics of medical image objects by generating correspondence of skeletal points. Each object’s interior is modeled by an s-rep, i.e., by a sampled, folded, 2-sided skeletal sheet with spoke vectors proceeding from the skeletal sheet to the boundary. The skeleton is divided into three parts: the up side, the down side and the fold curve. The spokes on each part are treated separately and, using spoke interpolation, are shifted along that skeleton in each training sample so as to tighten the probability distribution on those spokes’ geometric properties while sampling the object interior regularly. As with the surface/boundary-based correspondence method of Cates et al., entropy is used to measure both the probability distribution tightness and sampling regularity, here of the spokes’ geometric properties. Evaluation on synthetic and real world lateral ventricle and hippocampus datasets demonstrate improvement in the performance of statistics using the resulting probability distributions. This improvement is greater than that achieved by an entropy-based correspondence method on the boundary points.

I. Introduction

Establishing correspondence among similar shapes is essential for accurate statistical shape analysis [1, 2] in many biomedical applications such as understanding the anatomic structural differences in various stages of growth or disease [3–6]. This is often achieved by identifying a set of sparsely sampled and well-corresponding landmarks on organs or regions of interest across the shape instances.

Several representations of geometric models [3, 7–11] have been proposed to describe anatomical structures. The most popular one is the surface/boundary-based point distribution model (PDM) (e.g., [1, 12, 13]). Another well studied representation describes a shape using a set of parameterized basis functions such as spherical harmonics (SPHARM) [3, 8, 14], which defines an ambiguous correspondence and has been shown to be inadequate for some biomedical shapes that have non-uniform spherical parameterizations [15]. Deriving from the m-reps [16, 17], skeletal representations have proven powerful for shape analysis [11, 18–20] and biomedical applications [21–24] that need the rich features (e.g., local thickness and orientation) provided by the skeleton for quantifying the symmetric properties of organ shapes.

A key direction in the correspondence optimization research has been the computation of an objective function based on the determinant of the covariance matrix [25] and later on the minimum description length (MDL) [26, 27] to tighten the probability distribution of anatomically homologous points across a dataset (see Section II-B). In general, the MDL is approximately equivalent to minimum entropy [21, 28]. According to this, an energy function that encodes the entropy of the geometric properties of the points in the ensemble of shapes (the geometry entropy) summed with the entropies of the point distribution on each shape’s boundary (the regularity entropy) was proposed in [1] to solve the point correspondence problem. This combined entropy allows them to optimize the geometric accuracy and the statistical simplicity of the shape model. However, in their method the shapes were described as boundary-based PDMs, which ignore many of the higher order geometric features (e.g., local orientation) [18, 29].

In this paper, we adopt the skeletal model – termed as the s-rep [30] – which samples not just the object boundary but also its interior. The s-rep (Fig. 1) is formed by an approximately medial folded 2-sided skeletal sheet with a vector called a spoke proceeding from every skeletal point on the sheet to and approximately normal to the object’s boundary.

Fig. 1.

Left: an example of s-rep for lateral ventricle that is sampled as a folded 3 ×13 skeletal sheet; right: object boundary (yellow) implied by that s-rep.

Our purpose is to build a novel correspondence method based on the aforementioned combined entropy to optimize the spoke geometry while keeping the spoke distribution in each object interior regular. Once correspondence is established, the s-rep provides an intrinsic coordinate system for the points in the object interior and near exterior that supports statistics on object geometry and object appearance.

The first contribution of this paper is a novel spoke sliding mechanism that shifts the discrete spokes to an interpolated spoke along the part of the skeletal sheet from which it proceeds. Spoke interpolation [24, 31, 32] is used to produce the new spoke at the shifted position.

The second contribution is a novel form of s-rep in which the skeletal positions of the up spokes, down spokes, and fold spokes are not necessarily shared (see Fig. 4b). This new s-rep form is produced iteratively with the spoke shifting.

Fig. 4.

(a) A skeletal sheet has its 3 × 13 skeletal points projected as a unit grid. The diamonds and balls respectively denote the interior and the exterior grid positions. Each interpolated spoke has coordinate (u + Δu, v + Δv) (e.g., the spoke at the red dot is (1.5, 1.2), and at the cyan dot (0.5, 6.6)). (b) Part of the s-rep before and after shifting. The shared skeletal points (white balls in original s-rep) split and shift to a new place with its spoke. The cyan ball is the skeletal pt. of the up spoke, magenta (down) and yellow (fold).

The third contribution is the spoke regularity properties that can effectively measure the regularity of the subregions bounded by the spokes representing an object.

The final contribution is to improve spoke correspondence by minimizing a weighted sum of the entropy of the spokes’ geometric properties over the shape training population (the geometry entropy) and the within-object spokes’ distributional entropy for each shape’s interior (the regularity entropy).

Evaluated on synthetic and real word datasets consisting of lateral ventricles and hippocampi, the proposed method effectively improved the tightness and regularity of the spoke distribution and reduced shape variances. Also, when compared to entropy-based optimization of a boundary PDM, our method yields PDMs that are superior in specificity and compactness while maintaining generalization in the first few eigenmodes.

The remainder of this paper is organized as follows. Section II presents the shape representation schemes and overviews the previous related work along with common correspondence validation metrics which are adopted in this paper. Section III describes our correspondence method. Section IV details the experiments and presents measurements of the statistical performance of spoke optimization and boundary PDM optimization. Section V discusses this new correspondence method, including its possible improvements and applications.

II. Background

A. Shape Representation Schemes

We utilized three shape representations: SPHARM, PDM, and s-rep. We used finite-dimensional PDMs derived from each representation for the comparisons as discussed in Section IV. SPHARM and PDM are described in Supplementary Section 2.

A continuous s-rep describes an object interior by two functions: a 2D folded skeletal surface p(u, v) and a spoke function S(u, v), a vector field pointing from p(u, v) to the boundary (see Fig. 1). At each non-fold position on p(u, v) there are both an “up” spoke and a “down” spoke. The vector S can be decomposed into

$$S(u,v)=\mathrm{U}(u,v)·r(u,v)$$ (1)

where u, v parameterize the s-rep skeletal surface’s long and short axes respectively, U(u, v) is a unit vector field pointing in the direction of S(u, v), and r(u, v) is a scalar distance function from the skeletal surface to the object boundary.

In the computer an s-rep is discretely sampled from the continuous skeletal model at m × n skeletal points. In this discrete s-rep, each up spoke shares a skeletal point with a down spoke, and fold spokes share a skeletal point with both an up and a down spoke. The grid structure on the skeletal sheet forms a collection of quadrilaterals with a skeletal point at each corner. The object interior can be completely represented by interpolating the discrete s-rep into a continuous skeleton with a continuous field of spokes forming a continuous s-rep whose spokes fill the interior of the object. This representation does not rely on any inherent parameterization. Statistical analysis is applied to these sparse spokes [19, 24, 33].

For a new object, previous methods [5, 30, 34] obtained s-reps by an optimization that fits the interpolated form of a previously defined s-rep template to the object. An improved fitting process, both automatic and stable, was developed by Tu et al. [35]. It produces s-reps via thin plate spline warping of a reference s-rep. Both forms of fit yield reasonable initial correspondence.

Free software named “Pablo” developed by the UNC MIDAG (Medical Image Display and Analysis Group) team supports s-rep production and visualization; it can be downloaded from http://www.nitrc.org/projects/sreps/. In this paper, we divide the skeleton into its three parts: up spokes proceeding from the skeletal sheet top, down spokes proceeding from the skeletal sheet bottom, and fold spokes. For the k spokes on each part, the set of spoke tails on the skeletal sheet forms a PDM to which Kendall’s PDM scaling strategy [36] can be applied to yield a point on ℝ¹ × 𝕊^3k−4; the directional component of each spoke abstractly lives on the unit 2-sphere 𝕊². Therefore, the geometric properties of this s-rep abstractly live on ℝ^k+1 × 𝕊^3k−4 × (𝕊²)^k. More information on this is provided in Supplementary Sections 1–2.

B. Previous Work on Correspondence

Cootes and Taylor [7] first posed the correspondence problem combined with principal component analysis (PCA) on manually defined significance points in a 2D boundary PDM. Manually placing landmarks is error-prone, subjective and time-consuming, which makes this approach impractical for defining correspondence, the more so in 3D than 2D.

Various attempts have been made to solve the correspondence problem automatically [3, 12, 27, 37, 38]. They can be categorized according to which of three alternative ways for building correspondence they follow. The first way is to manipulate surface correspondence simultaneously while computing geodesic deformation that is optimal according to an elastic Riemannian metric [13, 39–41]. The second way is to use a consistent, shape-sensitive method for fitting the object representation to the object, for each object in the training set [5, 30, 42–44]. The third way is to tighten the resulting probability distribution on the representation properties [1, 25, 26, 28, 45].

Srivastava et al. [13] and Jermyn et al. [39] introduced an elastic correspondence method that treats shape comparisons and surface correspondence in a joint manner. Kurtek et al. [10, 40] proposed a mechanism for computing geodesic paths between surfaces that are invariant to the parameterizations of surfaces and other shape-preserving transformations of surfaces, which was re-formulated and extended in [41] as a landmark-constrained correspondence method.

There are two extensively used methods based on fitting consistency. The first is applied to boundary PDMs based on SPHARM. The second is applied to s-reps and consequently to s-rep implied boundary PDMs.

The SPHARM-based method uses a PDM made from the vertices of a triangular tiling of the object boundary. It produces consistency in the areas of the tiles and in the orientations of the tiles relative to the parameterizing sphere. Kelemen et al. [42] used this method to describe a population of 3D hippocampal shapes. Inspired by their experiments, Gerig et al. [3] applied the same method to study the similarity of lateral ventricles. Styner et al. [43, 44] addressed the correspondence problem for anatomical objects through SPHARM-implied PDMs.

The s-rep-based method [5, 30] achieves correspondence by fitting a predefined template to each object instance. It achieves consistency either by deformation according to a common set of landmarks or by fitting each object over the coefficients of common eigenmodes produced by the PCA-like method called CPNS (Composite Principal Nested Spheres) [46, 47].

Correspondence based on tightening the probability distribution began with the work of Kotcheff and Taylor [25]. They posed the problem as one of finding the circle-based parameterization for each object in the training set that yields the tightest distribution. They measured tightness from the covariance matrix ⅀ on derived PDMs. Their measure was F_D = ln det (⅀ + αI), where I is the identity matrix and α is a parameter that prevents the modes with smallest eigenvalues from disturbing the optimization process. F_D = Σ_k ln(λ_k + α), where {λ_k} are all the eigenvalues of ⅀ (principal variances) and α is a user-chosen parameter.

Davies et al. [26] proposed a different objective function based on ⅀: MDL of the geometric representation. In [27] they developed a 3D statistical shape model (SSM) based on a PDM description with an infinite number of points derived from a continuous parameterization. Later, they extended the MDL approach to this PDM/SSM representation in [12]. Their method manipulated correspondence by reparameterizing each training shape. The regularity of the points on each object in this method was achieved via the deformation of the common parameterization.

Thodberg [28] suggested a rough approximation to the MDL objective function for computational simplicity, which is a slightly modified version of the actual MDL approach by Davies et al. [26]. Styner et al. [48] described an empirical study that extended Thodberg’s simplified approximate MDL objective function by incorporating various local curvatures (geometric information) to improve correspondence.

The entropy H(Z)of a multi-dimensional Gaussian distribution on the multivariate Z is linear in F with α = 0 if all the principal variances are used. Thus for a fixed dimension, minimizing F is equivalent to minimize the geometric entropy H(Z) if all the principal variances are used and are offset by α. Realizing this, Cates et al. [1] recast the boundary PDMs correspondence problem in terms of entropy. This allowed them to express not only the geometric properties but also the regularity properties by entropy on each object. Their objective function was $Q=H_{\mathit{Geometry}}(Z)-{\sum }_{i=1}^N{H}_{\mathit{Regularity}}({\mathit{Object}}_i)$. In both entropies, offsetting the principal variances by α was used. Q was minimized by shifting the points along each object boundary.

Other methods try to obtain correspondence through various geometric features. Brett et al. [49], Hill et al. [50] and Wang et al. [51, 52] proposed various shape properties (e.g., regions of high curvature) to establish point correspondences. Shi et al. [53] represented sulcal shapes as square-root velocity functions of continuous open curves and computed geodesics in the quotient space, trying to preserve important local geometry. Oguz [45] presented an extension of [1] by combining the features of point location with curvature and image based features. Her work illustrates how multiple modalities can be included in an entropy-based approach.

In this paper we present a correspondence method adopting the aforementioned combined entropy for our s-rep to improve correspondence of the sparse spokes. That is, we describe the object as an s-rep and shift the spokes on the skeletal sheet to tighten the probability distribution of spoke geometry while keeping the spoke distribution in each object interior regular.

III. Methods

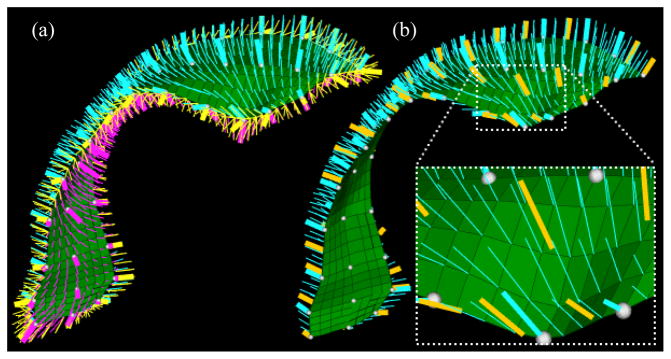
Recall that our method optimizes the combined entropy in a training set of s-reps by sliding each of the sparse spokes (the thickened spokes of the same color in Fig. 2) on each object onto an interpolated spoke on the part of the skeletal sheet from which it proceeds. In this section, we elaborate on each of the method’s components: a) spoke shifting through interpolation, b) regularity properties calculation contributing to regularity entropy, c) geometric properties calculation contributing to geometry entropy, d) objective function and optimization.

Fig. 2.

Discrete s-reps of two lateral cerebral ventricles, each represented as a 3 ×13 sparse grid of spokes (the colored thickened lines). The thin gray spokes are the interpolated spokes describing the object interior. The color indicates the initial correspondence before any shifting using entropies.

A. Spoke Shifting through Interpolation

As previously discussed and as illustrated in Fig. 3a, an s-rep is made up of three regions of spokes: up, down and fold. The spoke shifting within each region is done independently. For an m × n s-rep, there are (m − 2) × (n − 2) up (or down) spokes emanating from an interior grid position; the remainder emanate from an exterior grid position (the fold). The interior up and down spokes should be allowed to shift on the interior of the respective region via a skeletal-based interpolation method proposed in [32]. The spokes emanating from the fold should be allowed to shift only on the fold via the spoke interpolation method in [24]. The spokes emanating from the corner of the grid are not allowed to shift. Fig. 3b visualizes the shifting of the up region.

Fig. 3.

(a) Each object is modeled with three regions: an up (cyan), a down (magenta) and a fold region (yellow). The green grids represent the skeletal sheet. (b) The up skeletal sheet with the original sparse spokes shown as thickened cyan lines; the interpolated spokes shown as thin cyan lines; the shifted spokes shown in thickened yellow. The thickened cyan spokes S(u, v) are shifted to the thickened yellow position S(u + Δu, v + Δv) by a small step (Δu, Δv), and interpolating to that position.

To optimize the aforementioned combined regularity and geometry statistics, each sparse spoke S(u, v) is slid to the shifted spoke at the interpolated position (u + Δu, v + Δv), where Δu, Δv ∈ (−1,1). Neighboring spokes are constrained so that their tails cannot cross on the skeletal sheet.

In general, each movable spoke has restrictions on where it can shift to, according to the following criteria:

1. For the interior up and down spokes (diamonds in Fig. 4a), Δu ∈ (−1, 1) and Δv ∈ (−1, 1).

2. The spokes on the exterior of the grid (green balls in Fig. 4a), be they up, down or fold spokes, shift to the same types of spokes in an adjacent quad edge by changing only Δu or Δv. That is, for these spokes, the shifting is Δu = 0, Δv ∈ (−1, 1) or Δu ∈ (−1, 1), Δv = 0.

3. For the corner spokes (blue balls in Fig. 4a), the shifting is Δu = 0 and Δv = 0.

After applying the above shifting independently to each region, the resulting s-rep may well not have any two spokes which share a skeletal position (see Fig. 4b).

To produce correspondence, the spoke shifting is optimized iteratively until convergence is achieved. Whereas the interpolation used in the shifting is always based on the original s-rep; the regularity and geometric properties to be discussed in Sections III-B, C are always based on the shifted s-rep.

B. Regularity Properties

Regularity is measured for each s-rep separately. The grid of its sparse spokes is formed into curvilinear quads on both the skeletal sheet (connecting four neighbor spoke tails, shown as green balls and black grids in Fig. 5a–c) and the object boundary (connecting four neighbor spoke tips, shown as green or red sheets in Fig. 5a). At the fold there are curvilinear segments on the skeleton rather than quads. Both sets of quads are used to measure regularity. For each set, three properties contribute to our regularity measure. We wanted these properties to be close to probabilistically independent, thus allowing entropies of each to be summed to form the overall regularity entropy. We took these three properties to be the horizontal lengths of the quad sides, the vertical lengths of the quad sides, and the geometric similarity of the quads. The latter has to do with angles of the quad corners and the relative orientations of the surface normals there. For each of the three properties their values for a particular quad on the skeletal surface and that for the corresponding quad on the object boundary are correlated, so the entropy term for each property must involve a feature (or, for the 3^rd property, features) measuring the property on skeletal surface together with one measuring that property on the boundary surface. Therefore, the features tuples used to compute the three respective regularity entropy terms are as follows:

Fig. 5.

Visualization of an 3 × 8 s-rep. (a) This s-rep has 24 up/down spokes (blue/magenta lines), 18 fold spokes (red lines). These spokes form 14 skeletal quads for the up/down region, each with a corresponding boundary quad (e.g., B₅ denotes a boundary quad). (b–c) Each quad is divided into (2³)² sub-quads. (d) Each sub-quad in B₅ is further subdivided into two triangles. (e) An example of the curvilinear segments on the skeleton and its corresponding fold region on the boundary. H and V denote the horizontal and vertical directions respectively. More subdivision is visualized in Supplementary Fig. 1 for up/down region and Supplementary Fig. 2 for fold region.

1. (vertical quad edge length on skeletal surface, vertical quad edge length on the boundary surface); this pair is taken over all quad edges and yields an entropy E_vel.

2. (horizontal quad edge length on skeletal surface, horizontal quad edge length on the boundary surface); this pair is taken over all quad edges and yields an entropy E_hei.

3. (for the skeletal quad: angle cosine between edges at the lower right corner of a quad, angle cosine between edges at the upper left corner of that quad, angle cosine between the normals at each of these quad corners, for the boundary quad: the same three features); this tuple is taken over all quads and yields an entropy E_cos.

All of these were computed by decimating the quads into 16 subquads, interpolating the s-rep spokes at the subquad vertices, each producing skeletal and boundary positions, and then computing the properties by combining the information from the relevant subquads.

Similar properties are computed for the region bounded by the fold curve on the skeleton and the corresponding fold region on the boundary (Fig. 5e).

All the quad edges are curved. As visualized in Fig. 5, we measure the lengths and angles by subdividing the quads and summing the lengths and averaging the angles measured from each subdivision. Moreover, quad subdivision into triangles handles the fact that the subdivision is curved. The normal swing is an approximation counting from the upper-left corner sub-triangle (e.g., the orange triangle in Fig. 5d) to the bottom-right corner sub-triangle (e.g., the yellow triangle).

C. Geometric Properties

Tightening the probability distribution on the geometric properties of the s-reps in the training set is the basic means of producing correspondence. These properties include the positions of the skeletal points p_i = p(u_i, v_i), the spoke radii r_i = r(u_i, v_i), and the spoke directions U_i = U(u_i, v_i), where i is the index of each spoke. As with the regularity properties calculation, the geometric properties for the up, down and fold regions are also calculated separately and then combined across all regions. The geometric properties of the spokes in each region are computed in the same way.

A complication is that the entropy formulas used to measure tightness assume the properties are Euclidean, i.e., the Pythagorean theorem applies, but unfortunately this does not hold for many of the aforementioned geometric properties. We deal with this by Euclideanizing the relevant properties via Principal Nested Spheres (PNS) analysis [46] and making them commensurate before applying PCA and thence the entropy formulas. The commensurated form of each scale factor of the k^th s-rep, denoted by γ^k, is γ̄ × log(γ^k/γ̄), where γ̄ is the geometric mean of γ^k and k = 1,2,…, N. Each Euclideanized feature resulting from the PNS on the scaled skeletal points ${\mathrm{p}}_i^k$ is commensurated by multiplying it by γ̄. The commensurated, Euclideanized form of the spoke radii $r_i^k$, are similarly ${\overline{r}}_i\times log(r_i^k/{\overline{r}}_i)$, with γ̄_i = the geometric mean of the radii of the i^th spoke, i = 1,2,…, n. The Euclideanized features produced by PNS applied to each spoke direction U_i, which abstractly lives on 𝕊², are commensurated by multiplying by γ̄_i.

The result of this process is a collection of commensurate zero-mean features that can be concatenated to form a Euclidean feature tuple describing each s-rep. The sample covariance matrix derived from these tuples is used to form the geometry entropy E_geo, as will be described in Section III-D.

D. Energy Function and Optimization

Euclideanization and commensuration of the geometric features of the i^th s-rep, i = 1,2, …, n, yields a k-dimensional feature tuple X_i that approximately follows a multivariate Gaussian distribution, X ~ N(μ, Σ), where μ is the mean tuple, Σ is a k × k covariance matrix, k is the feature dimension of each s-rep, and n is the number of s-reps in the training set [46]. This formulation can also be applied to the regularity properties after they have been made zero-mean and commensurate. The entropy of such an X is

$$H(x)=\frac{d}{2}+\frac{d}{2}ln2\pi +\frac{1}{2}\sum _{i=1}^{d}ln{\lambda }_i$$ (2)

where d is the number of non-zero eigenvalues of Σ and λ₁, λ₂, …, λ_d are the non-zero eigenvalues of Σ.

In our application d < k, with the effect that computed eigenvalues beyond the d^th are small and contain almost pure noise. Including these in the sum contributes dominating negative terms of large magnitude to H(x). Recall that Cates et al. method used a constant factor to prevent the smallest modes (those with smallest eigenvalues), which mainly constitute effects of noise, from disturbing the optimization process. In our method, we handle this problem by removing those eigenvalues with contribution (λ_iΣ λ_i) smaller than a prior threshold ϑ and correspondingly lowering d. This approach is applied separately to compute the geometric entropy E_geo and each of the three regularity entropies (E_cos, E_hel and E_vel) for each object. For all entropies ϑ = 0.01 is used (see Supplementary Section 5.3 and Supplementary Table II).

The regularity entropy $E_{\mathit{reg}}^i$ of the i^th s-rep is computed as

$$E_{\mathit{reg}}^i=E_{\mathit{cos}}^i+E_{\mathit{hel}}^i+E_{\mathit{vel}}^i$$ (3)

where E_cos indicates the angle cosine entropy, E_hel and E_vel indicate the horizontal and the vertical edge lengths entropies separately as discussed in Section III-B. The overall regularity entropy of the N training s-reps is $E_{\mathit{reg}}={\sum }_{i=1}^N{E}_{\mathit{reg}}^i$.

The correspondence is established by solving the optimization problem given by

$$\underset{x}{\text{argmin}}f(x)=\left\{x\mid f(x)=\mathrm{\omega }{E}_{\mathit{geo}}-E_{\mathit{reg}}\right\}$$ (4)

where ω is the weight used to balance the tightness and regularization and x is the collection of (Δu, Δv) that shift the spokes. For the results reported later, we use the NEWUOA optimizer [54] to minimize (4) and use the one-plus-one evolutionary optimizer [55] to avoid local optima. However, other optimizers are possible.

IV. EVALUATION AND RESULTS

A series of experiments were performed to evaluate the proposed correspondence method. We first introduced the data sets in use. Second, we set the parameters involved in our objective function. Then we applied the proposed method to different data sets to investigate the tightness and regularity of the spoke distribution and the statistical parameters that were extensively used previously [12, 43, 45, 56, 57] to measure the correspondence quality. Finally, we compared our method with two of the state-of-the-art PDM-based methods, namely, SPHARM-PDM (spherical harmonics point distribution model) [15] and ShapeWorks [58] which is an up-to-date, enhanced open-source distribution of Cates et al. method [1]. Our program was implemented in C++ and Matlab. All experiments presented here were done on 64-bit 8GB 4-core PC.

The correspondence quality measurements used in this paper: specificity, generalization, and compactness, are detailed in Supplementary Section 3. Briefly, specificity measures the degree to which the model generates objects that are similar to those in the training set, which is also understood as a nearest-neighbor graph distance whose meaning is elucidated in [59]; generalization measures the average reconstruction error for all training objects; compactness of a model evaluates the total variance of the model. For all three metrics, lower values are desirable.

A. Data Sets

Three types of data sets were employed for the results reported in this paper: synthetic objects and real world lateral ventricles and hippocampi.

1) Synthetic Objects

A set of 80 synthetic lateral ventricles s-reps with all spokes identical except one that was shifted by a small random distance were produced to evaluate how the correspondence optimization affects the spoke variance.

2) Lateral Ventricles

We were provided set of lateral ventricles that were semi-automatically segmented from magnetic resonance imaging (MRI) images in neonates [60]. Each ventricle was preprocessed using SPHARM-PDM and deformed to an initial skeletal model (manually defined by an expert) using thin plate spline registration. We selected 31 resulting ventricle s-reps for our tests presented here.

3) Hippocampi

We were provided s-reps fitted to a set of binary images of the hippocampi that were segmented from the MRI scans from normal control datasets in a schizophrenia study [5]. We randomly selected 40 of them for our tests.

For the latter two data sets, a Procrustes alignment based on the boundary points and their corresponding skeletal points implied by s-rep spokes was performed before applying the proposed correspondence method.

B. Parameter Selection

We first determined the best interpolation level (∂) for computing the regularity and geometric properties. Then we studied how to determine the weight to best balances the tightness and regularization entropies.

1) Interpolation Level

The regularity properties described in Section III-B were computed based on subdivision of the curved quad edges into 2^∂ linear pieces. We sought the ∂ that balances the accuracy and efficiency by investigating the changes of the skeletal and boundary quad areas and of the 3D region volume bounded by the corresponding quad-quad (or line-quad for fold region) pair and the average time used for interpolating to each region of 10 different s-reps with ∂ = 0,1,…,8 on the real lateral ventricles.

As shown in Supplementary Fig. 3, both areas and the volume change significantly as we increase ∂ up to 2, but there is little change when we increase ∂ from 2 to any high level. That is, ∂ = 0 or ∂ = 1 is inappropriate for the regularity properties computation; while ∂ = 2 or 3 can achieve adequate accuracy. Since ∂ = 3 takes three times the time of ∂ = 2 (Supplementary Table I), we use ∂ = 2: each edge is divided into 4 sub-edges, each quad is divided into 16 sub-quads.

2) The Weight for the Tightness and Regularization

Consider the weight ω on E_geo in (4). For different datasets, different values of ω yield best correspondence quality, as measured through s-rep implied boundary points. As an example, Supplementary Fig. 4 compares the statistical performance via specificity, generalization, and compactness measures (Supplementary Section 3) for the real lateral ventricles using different ω. S-rep spoke tips (∂ = 0) were collected and used as boundary PDMs for these measurements. The results show that ω = 4 obtains the best performance.

We suggest that ω = E_reg/E_geo is a reasonable initial value to try for any particular dataset, where E_reg and E_geo are calculated from the input, aligned s-reps; then one would switch ω up and down to investigate if better results can be obtained. This approach yielded weights ω = 30, ω = 4 and ω = 13, respectively used for our synthetic objects, real lateral ventricles and hippocampi.

C. Comparisons between Aligned and Optimized S-reps

We applied the proposed method to the three aforementioned datasets and compared the entropies, shape variances and correspondence quality measurements between the aligned, non-optimized s-reps (referred to as aligned s-reps) and the correspondence-optimized s-reps from our method (referred to as optimized s-reps). S-rep spoke tips at subdivision level 0 (∂ = 0) were used as the implied boundary points (PDMs) for the statistical measurements in this subsection.

1) Synthetic Objects

We began with a predefined template s-rep from a lateral ventricle (Fig. 6a). Each synthetic s-rep was formed from the template by moving only one particular fold spoke. The spoke was moved to an interpolated fold position by a small distance according to a Gaussian distribution (Fig. 6b–c). As depicted in Fig. 6c–d, after our program is applied the spokes agreement improved in location as well as lengths. Similar results were observed in Supplementary Fig. 6.

Fig. 6.

(a) The template s-rep; (b) the fold curve (green curve) and fold spoke (red line) of the template and the 80 synthetic s-reps on top of each other, with the corresponding fold spoke dispersed from the original place (the red line pointing out from the green ball in oval) by a step with σ = 0.4; (c–d) the corresponding spaced spokes distribution before and after correspondence optimization, respectively. The color denotes each case in the training s-reps.

The evolution of entropy values during the optimization are illustrated in Fig. 7 (left panel). During the iterations E_geo decreases from −10.47 to −38.64. E_reg changes little (from the beginning of 531.76 to the end of 533.95); nevertheless, the 3D region volumes bounded by the fold curve on skeleton and the corresponding quad on boundary associated with this fold spoke have their variances in the ratio $\frac{{\sigma }_{\mathit{optimized}}}{{\sigma }_{\mathit{original}}}=0.16$; and as shown in Table I, the standard deviation of each regularity property decreases. All three metrics of the shape model performance improved (Supplementary Fig. 7) in a similar way as that graphed in Fig. 8.

Fig. 7.

Left: entropies and the objective function (f(x)in (4)) during the iterations for the 80 synthetic objects; right: the changing of E_geo of the up region for the real hippocampi.

Table I.

Standard deviation of the quad regularity properties associate with that fold spoke across the training set before and after optimization. Vertical edge length on skeleton (σ_{vel_s}), vertical edge length on boundary (σ_{vel_b}), angle cosine of the upper-left corner (σ_{cos_ul}), angle cosine of the bottom-right corner (σ_{cos_br}) and angle cosine of the normal swing (σ_{cos_ns}).

	σvel_s	σvel_b	σcos_ul	σcos_br	σcos_ns
Original	0.0059	0.0059	0.0417	0.0469	0.1414
Optimized	0.0007	0.0008	0.0208	0.0323	0.0262

Fig. 8.

Comparisons between optimized and aligned s-reps for the hippocampi. (a) specificity; (b) generalization; (c-d) compactness with s-reps geometric properties and with s-rep implied PDMs, respectively. For all three metrics, lower values are desirable.

2) Hippocampi

For the hippocampi dataset the entropies of up, down and fold regions were minimized separately. In each region, E_reg increased and E_geo decreased (e.g., Fig. 7, right panel for up region) in a similar pattern (Supplementary Table III).

The correspondence quality between the optimized s-reps and the aligned s-reps are compared in Fig. 8. The error bars graphed on each line show the significance differences in each metric. The specificity (Fig. 8a) and generalization (Fig. 8b) measures for the s-rep-implied PDMs are based on the s-rep shape space. The compactness measures were computed both from the s-reps native geometric properties (Fig. 8c) and then from the s-rep-implied PDMs (Fig. 8d), whether on geometric properties or PDMs, were all computed via CPNS. For all three measures lower values mean better performance.

The optimized s-reps are superior in compactness and specificity. In generalization, the aligned s-reps are superior for a number of eigenmodes (M > 10). However, the compactness graphs suggest that fewer than 10 eigenmodes would be enough for statistical applications, and in this range the generalization of the optimized s-reps are slightly superior.

3) Lateral Ventricles

For the lateral ventricle dataset the entropies of all three regions are shown in Table II. In all regions, E_reg increases (reflecting improved regularity) while E_geo decreases (reflecting a tightened probability distribution). The entropies of the up and the down regions have similar values because of the symmetry of the brain lateral ventricle, but E_geo of the up region decreases more than that of the down region, possibly because the surface of the up region has lower curvature and its spoke geometries are less tight at the beginning.

Table II.

Regularity entropy (E_reg in (4)) and geometry entropy (E_geo in (4)) of each region before (R1) and after (R2) optimization.

	Up region		Down region		Fold region
	Ereg	Egeo	Ereg	Egeo	Ereg	Egeo
R1	290.0	−35.7	305.4	−36.6	214.4	−35.4
R2	334.8	−41.2	348.2	−38.0	226.3	−50.2

As shown in Table III, optimization yields smaller geometric eigenvalues in all regions. The dominant portion of this decrease is in the first six eigenvalues (Supplementary Fig. 8). The portion of total variance captured by the two dominant eigenvalues increased (Table IV), suggesting that the optimized s-reps capture more variance in fewer principal directions.

Table III.

Total variances (Σλ_i) of the lateral ventricle s-reps.

	Up region	Down region	Fold region
Aligned	0.0034	0.0031	0.0019
Optimized	0.0029	0.0028	0.0015

Table IV.

Contribution of the first two dominant s-rep eigenvalues before and after optimization.

	Up region (%)		Down region (%)		Fold region (%)
	Before	After	Before	After	Before	After
λ1	36.73	39.10	38.04	42.04	31.32	37.17
λ2	22.67	25.08	21.39	23.00	23.65	27.06

The statistical shape model performance of optimized s-reps compared with aligned s-reps is laid out in Fig. 9. As with Fig. 8 in Section IV-C2, S(M) (Fig. 9a) and G(M) (Fig. 9b) measures for the s-reps are based on s-rep shape spaces. C(M) was computed via CPNS from both s-reps features (Fig. 9c) and then from s-rep-implied PDM features (Fig. 9d).

Fig. 9.

Comparisons between optimized and aligned s-reps for the real lateral ventricles. (a) specificity; (b) generalization; (c–d) compactness with s-reps geometric features and with s-rep-implied PDMs (∂ = 0), respectively.

As with the previous hippocampi dataset, the optimized s-reps are also superior to the aligned s-reps in compactness and specificity. In generalization, the optimized s-reps are superior in the first 9 eigenmodes, which would be enough for statistical applications according to the compactness graph.

D. Comparisons between S-reps and PDM-based Methods

As a further validation of the proposed method, this experiment compares the statistical performance among the optimized s-rep implied PDMs, the SPHARM-PDM and the ShapeWorks on real lateral ventricles and hippocampi datasets.

On inspection, all the resulting s-reps appear to be of good quality and imply high quality boundary PDMs. As an example, Fig. 10 shows the surface mesh of the mean PDM implied by the optimized s-reps as well as its deformations along the first two dominant s-rep implied PDM eigenmodes. Each main eigenmode describes some plausible pattern of shape changes observed in the population.

Fig. 10.

The hippocampi (first row) and lateral ventricles (second row) model mean and ±3 standard deviations in two eigenmodes. The shapes are generated from boundary PDMs implied by the optimized s-reps level 2 (∂ = 2) spoke tips.

The PDM-based evaluations for the s-reps involved in our comparison were based on spoke boundary points only (named B_PDM) and on boundary and skeletal points (named BS_PDM), for each optimized s-rep at interpolation level 2. This yields a B_PDM of 1218 points and a BS_PDM of 2212 points for a 3 × 13 lateral ventricle s-rep; and of 738 and 1332 points, respectively for a 3 × 8 hippocampus s-rep. The SPHARM-PDMs used subdivision level 10 and SPHARM degree 11, which yields a PDM with 1002 points. The ShapeWorks used these SPHRM-PDMs as the input and optimized them with scaling off. All PDMs were scaled to lie in a same space.

The comparisons of statistical measurements among these PDMs are laid out in Fig. 11 (top row for lateral ventricles and bottom row for hippocampi).

Fig. 11.

Comparisons among the optimized s-rep implied PDMs, the SPHARM-PDM and the ShapeWorks on lateral ventricles (top row) and hippocampi (bottom row). The compactness for all models were computed via CPNS. All figures share the same legend as located in the middle column.

For both data sets, the specificity and compactness measures on our optimized s-rep implied PDMs are noticeably superior to both the SPHARM-PDM and the ShapeWorks methods. The generalization measure on s-reps is better than both methods for low numbers of eigenmodes (M), e.g., M < 15 for lateral ventricles and M < 5 for hippocampi, but worse than the optimized PDMs at higher numbers especially for hippocampi. This is probably because the hippocampi have small curvature and most of the shape variance in the training population located on the boundary so that pure boundary PDM optimization performs better.

The BS_PDM gains in all measures over the B_PDM for both objects, suggesting that the skeletal points capture some interior correspondence. This observation is consistent with [4, 22, 61] that the use of point information alone ignores many of the higher order geometric features that s-reps provide, such as orientation and width.

As shown in Supplementary Fig. 9, PCA-based compactness measures on the PDMs, albeit not properly applicable to the aforementioned non-Euclidean shape representations (see Section II-A and Supplementary Section 1), led to the same conclusion as those based on CPNS.

V. CONCLUSION AND FUTURE WORK

In this work we proposed a novel group-wise optimization of skeletal properties to establish an enhanced s-rep correspondence. The proposed method represents each object in the training set as an s-rep, whose spokes are shifted along its skeletal part using spoke interpolation in each sample so as to tighten the probability distribution on those spokes’ geometric properties while sampling the object interior regularly. The correspondence is established by minimizing an objective function that balances entropy derived from geometric properties and entropy derived from regularity properties. All these properties are computed from s-rep spokes.

This method effectively lowers the entropies and improves the correspondence of the spokes. It noticeably tightens the distribution of the corresponding spokes over the training set and disperses the spokes of each s-rep regularly. And it noticeably reduces the total variance of the spoke geometries. Moreover, the proposed method yields models with improved model properties as measured via generalization, specificity and compactness. Surprisingly, on our two objects sets, the --result of our entropy-based correspondence optimization on the skeleton showed superior boundary point statistics even when compared to an entropy-based boundary correspondence methodology.

In this work, we evaluated the established s-rep correspondence with respect to model shape probability distributions. Main applications of shape models though include classification, hypothesis testing, segmentation via shape statistics, and registration in statistically generated shape spaces. These applications were not evaluated here and future research is needed to show the improvement of our s-rep correspondence method for these purposes.