RF Pulse Methods for Use with Surface Coils: Frequency-modulated Pulses and Parallel Transmission

Abstract

The first use of a surface coil to obtain a ³¹P NMR spectrum from an intact rat by Ackerman and colleagues initiated a revolution in magnetic resonance imaging (MRI) and spectroscopy (MRS). Today, we take it for granted that one can detect signals in regions external to an RF coil; at the time, however, this concept was most unusual. In the approximately four decade long period since its introduction, this simple idea gave birth to an increasing number of innovations that has led to transformative changes in the way we collect data in an in vivo magnetic resonance experiment, particularly with MRI of humans. These innovations include spatial localization and/or encoding based on the non-uniform B₁ field generated by the surface coil, leading to new spectroscopic localization methods, image acceleration, and unique RF pulses that deal with B₁ inhomogeneities and even reduce power deposition. Without the surface coil, many of the major technological advances that define the extraordinary success of MRI in clinical diagnosis and in biomedical research, as exemplified by projects like the Human Connectome Project, would not have been possible.

Graphical Abstract

Introduction

The first in vivo surface coil ³¹P NMR spectra published by Ackerman et al [1] initiated a revolution in magnetic resonance imaging (MRI) and spectroscopy (MRS). Today, we take it for granted that one can detect signals in regions external to an RF coil, but at the time this concept was most unusual since in every application ranging from chemistry in small samples to imaging humans, the conventional thinking required circumscribing volume coils where the sample was inserted into and contained within the coil. This unusual strategy of detecting signals adjacent to a simple loop of wire certainly ignited the field of in vivo MRS immediately. Magnetic resonance (MR) in general, but particularly MRS, suffers from limited sensitivity, a problem that is exceptionally pronounced when the volume of interest is actually much smaller than the coil and sample dimensions, as encountered when working with large samples contained within circumscribing RF coils. With its simple planar loop geometry, the surface coil provided for the first time a convenient new probe for in vivo MRS that yields high sensitivity for the tissue region immediately adjacent to it [2, 3]. In addition, because its RF field (B₁) drops off in both radial and axial directions, early in vivo MRS studies exploited this spatial dependence of B₁ for achieving spatial localization without using pulsed B₀-gradient coils, which in those days were unshielded and produced large eddy currents that degraded spectral quality.

In the early days of surface coil MRS, much effort was devoted to developing B₁-localization techniques that could provide control in positioning the volume of interest precisely. NMR journals were soon publishing many articles introducing new localization techniques that exploited the spatially dependent B₁ of one or more surface coils. The main techniques of that period were called depth pulse [4, 5], rotating frame zeugmatography (RFZ) [6–8], and Fourier series windows [9–11]. Still today, there are significant advantages to using B₁-versus B₀-gradient techniques. Unlike B₀-gradient fields, B₁ fields can be switched on and off rapidly (in 1–2 microseconds), and negligible eddy currents and acoustic noise are produced when pulsing B₁ coils. Furthermore, B₁-localization techniques can be performed without using a spin- or stimulated-echo acquisition, which inevitably forfeits signal from many low-gyromagnetic ratio (γ• nuclei that have spin-spin relaxation time (T₂) values comparable to or less than the minimum achievable echo time, TE.

Following the development of actively-shielded B₀-gradient coils, B₁-localization techniques were largely superseded by B₀-gradient methods due mainly to their greater flexibility in controlling the dimensions and placement of the MRS voxel. In response to these technological developments, our research focus turned to creating methods to produce uniform flip angles with RF coils that have highly inhomogeneous B₁, like a surface coil, using so-called adiabatic pulses [12–16]. Developments in adiabatic pulses, as well as in frequency-modulated pulse techniques in general, continue to take place at a rapid pace, and the number of applications where they play key roles is ever expanding for both MRS and MRI research.

In the past decade, interesting new approaches for performing MRI with B₁ gradients have been introduced based on the localized and spatially varying fields generated by arrays of surface coils. These techniques are based on parallel imaging (PI) strategies that are now commonly used to accelerate image acquisition in MRI (e.g., SENSE [17] and GRAPPA [18]). Due to recent developments in parallel transmit (pTx) capabilities (e.g., [19, 20], and reviewed in [21]) with multi-coil arrays that can apply independent RF waveforms to each channel simultaneously, the prospects for achieving much greater localization precision and the potential for new effective B₁-gradient techniques has led to exciting possibilities in this area.

Herein we provide our perspectives on two important areas in biomedical MRI and MRS that can be linked directly to the introduction of surface coils by Ackerman and colleagues. Specifically, these are 1) frequency-modulated (FM) pulses, and 2) parallel transmission (pTx).

Overview of frequency-modulated pulses

Nowadays the types FM pulses and their applications are quite diverse. Some FM pulses, such as the popular chirp [22] and hyperbolic secant (HS) pulses [23], can function in an adiabatic manner, whereby the flip angle remains close to π above a user-defined threshold RF amplitude. Other FM pulses, like the 2D versions of chirp and HS pulses [24–26], function adiabatically only when taking certain trajectories in k-space. Of note, the first volume-selective (3D) adiabatic pulse, which was introduced only recently, can be implemented with pTx to enable undersampling of its 3D k-space trajectory and this can be used to shortened its overall duration [27].

Adiabatic π-pulses are commonly implemented in localized MRS sequences due to their ability to produce a uniform π flip angle over a broad bandwidth, without using a high level of peak RF power. One such sequence is known as LASER (localization by adiabatic selective refocusing) [16]. LASER and versions thereof (e.g., semi-LASER [28, 29]) are commonly used nowadays to perform single-voxel MRS and spectroscopic imaging.

In MRI, FM pulses are playing key roles in novel spatiotemporal-encoding (SPEN) techniques [26, 30, 31] that offer the possibility to overcome many of the problems plaguing the widely used single-shot imaging method, EPI (echo planar imaging). The SPEN techniques exploit the fact that the phase of the transverse magnetization (M_xy) following a frequency-swept pulse is a quadratic function of the resonant frequency. By applying a B₀ gradient that imparts a spatially dependent resonant frequency, the vertex of this quadratic phase function can be controlled and moved at will through space as a function of time. SPEN techniques have been developed utilizing one or more adiabatic π-pulses, a non-adiabatic π/2-FM-pulse, or 2D versions of these. In 2D SPEN, the magnetization phase is a parabolic function in position. Spin-echo SPEN techniques offer high tolerance to B₀ inhomogeneity and are having utility for studying tissues in which variations in magnetic susceptibility are large, like the prefrontal orbital cortex of the human brain [32].

Basics of FM pulses

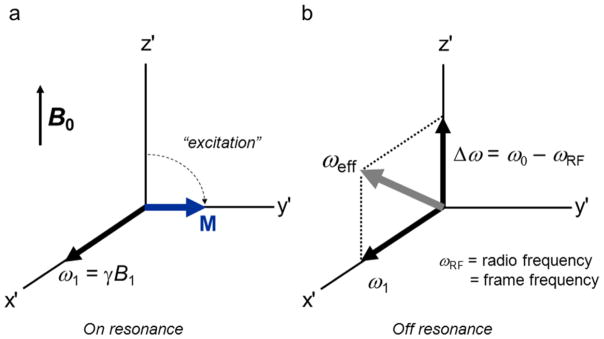
A rotating reference frame (x′y′z′) provides the best platform from which to visualize the motion of a magnetization vector M experiencing the torque from a magnetic field vector B. In a frame rotating about B₀ at the angular velocity ω_RF of B₁, the on-resonance condition occurs when the RF frequency is equal to the spin’s resonant frequency; i.e., when ω_RF = ω₀ (Fig. 1a). An important feature of any RF pulse is how uniformly it rotates M when a frequency offset Δω occurs, as for example in the presence of a field gradient used for slice selection. In the off-resonance case, the axis of rotation is tilted out of the transverse plane (Fig. 1b).

Figure 1.

A rotating frame of reference showing the magnetic field components as angular velocity vectors, ω₁ î and Δω k̂, for the case in which the RF pulse is applied (a) on resonance and (b) off resonance.

Usually, the pulse shapes used in MRI and MRS are amplitude-modulated (AM). The most common examples include shapes defined by sinc and gauss functions. These originated in the early days of MRI and were derived from a Fourier transform (linear) approximation to the Bloch equations. The frequency offset (Δω) range over which a pulse rotates the magnetization is known as the pulse bandwidth, b_w. The bandwidth is inversely proportional to the pulse duration T_p and depends on the specific pulse pattern (e.g., sinc versus gauss) and the flip angle that is used. The latter is a consequence of the non-linearity of the Bloch equations.

With AM pulses, the carrier frequency (ω_RF) remains constant during RF irradiation. With FM pulses, the pulse can be both amplitude and frequency modulated. This difference is illustrated in Fig 2. Implementation of FM pulses on MR scanners usually requires modulating the pulse phase, instead of modulating the pulse frequency. Comparisons of the amplitude and phase functions (B₁(t) and ϕ(t)) and slice profiles of two AM pulses and an FM pulse are shown in Fig. 3. The slice profiles produced by these pulses were obtained from Bloch simulations using the pulse parameters listed in Table 1. Slice profiles as a function of the peak of the B₁(t) function (B₁^max) are shown in Fig. 4. It can be seen that the FM pulse produces the same π rotation when the RF amplitude (ω₁^max =γB₁^max/2π) meets or exceeds the threshold value that satisfies the adiabatic condition.

Figure 2.

The difference between an AM only pulse (left) and a pulse that is both amplitude and frequency-modulated (right). Note that the frequency of the carrier under the sinc-shaped AM envelope varies in time in the FM case.

Figure 3.

Modulation functions and slice profiles of two commonly used AM pulses, sinc and sinc·gauss, and the FM pulse known as the hyperbolic secant (HS) pulse. Bloch equations were used to calculate the magnetization profiles, M_xy/M₀ and M_z/M₀, as a function of offset frequency, for flip angles of π/2 and π, respectively. (a,b) AM functions, B₁(t), (c,d) phase-modulation functions, ϕ(t), and (e,f) slice profiles of the pulses. In the plot of the π/2 slice profiles (e), the phase profiles of the transverse magnetization existing at the end of the pulses are also shown (dashed lines). The sinc pulse had two side-lobes. The sinc·gauss pulse was synthesized by taking the product of the B₁(t) function of a sinc pulse having single side-lobes and the B₁(t) function of a gauss pulse truncated at 10% of maximum. The HS pulse was synthesized using a time-bandwidth product, Δω_maxT_p/π, of 12. Other pulse parameters were chosen to achieve 2000 Hz bandwidth (FWHM) and are listed in Table 1.

TABLE 1.

Properties of different RF pulses

	flip angle = π/2			flip angle = π†
	sinc	sinc·gauss	HS*	sinc	sinc·gauss	HS*
R ( = bwTp)	5.94	4.32	14.06	4.52	2.71	11.94
Pulse parameters for producing bandwidth (FWHM) = 2000 Hz:
Tp (s)	0.00297	0.00216	0.007	0.00226	0.00135	0.00597
γB1max/2π (Hz)	474	466	300	1188	1426	874
Erel§	1.13	1.0	1.25	5.4	5.8	6.8

^†To facilitate comparisons between AM and FM pulses, flip angle = π corresponds to M_z=−0.99M₀

^*HS pulse synthesized using Δω_maxT_p/π = 12

^§ $E_{\text{rel}}\propto \underset{0}{\overset{T_{\mathrm{p}}}{\int }}{B}_1^2\left(t\right)dt$

Figure 4.

Slice profiles (M_z/M₀) produced by (a) sinc, (b) sinc·gauss, and (c) HS pulses as a function of RF amplitude (B₁ ^max). It can be seen that the slice profiles of the sinc and sinc·gauss pulses vary as a function of B₁ ^max and exhibit undesirable side-lobes at the higher RF amplitudes. On the other hand, the slice profile produced by the HS pulse remains highly invariant as the RF amplitude changes and the pulse continues to produce inversion (M_z ≤ − 0.99M₀) above a threshold B₁ ^max where it functions in an adiabatic manner. Bloch equations were used to generate these simulations. The sinc pulse had two side-lobes. The sinc·gauss pulse was synthesized by taking the product of the B₁(t) function of a sinc pulse (number of side-lobes = 1) and the B₁(t) function of a gauss pulse (truncated at 10% of maximum). The HS pulse was synthesized using a time-bandwidth product, Δω_maxT_p/π, of 12. The durations of the pulses were T_p = 2.97 ms, 2.16 ms, and 6 ms, for the sinc, sinc·gauss, and HS pulse, respectively, as needed to excite ~2000 Hz bandwidth (FWHM).

With an FM pulse, ω_RF is time dependent, and therefore, the amplitude of Δωk̂ and the amplitude and orientation of the effective field ω⃗_eff change during the pulse. Here we briefly describe the motions of the time-dependent magnetization and the field components in a rotating frame, in response to an FM pulse. At any moment during the pulse, the rate at which ω⃗_eff (t) changes its orientation is given by the instantaneous angular velocity, dα(t)/dt, where α is the angle between ω⃗_eff and the z′-axis. At the beginning of the pulse (t = 0), if Δω ≫ 0, then the magnitude of Δωk̂ is very large relative to that of ω₁ î, and thus, the initial orientation of ω⃗_eff will be approximately collinear with z′. As ω_RF(t) increases during the pulse, Δω decreases and ω⃗_eff (t) rotates toward the transverse plane. When ω_RF(t) = ω₀, the orientation of ω⃗_eff is parallel to ω₁ î, regardless of the magnitude of the ω₁ î . In a classical adiabatic half-passage (AHP), the orientation of ω⃗_eff is swept in this manner from z′ to an axis in the transverse plane. In an adiabatic full-passage (AFP), the sweep of ω_RF(t) continues past resonance so that the final orientation of ω⃗_eff is parallel with −z′ (i.e., at the end of the AFP, Δω ≪0). During an adiabatic pulse, a magnetization vector (M) which is parallel to ω⃗_eff will tend to follow ω⃗_eff, provided that |ω⃗_eff (t)| ≫ |dα(t)/dt|, for all t. This inequality is known as the “adiabatic condition”. In simple terms, the adiabatic condition states that, at all times during the pulse, the rate at which ω⃗_eff changes its orientation must be small relative to the rate at which a magnetization vector rotates about ω⃗_eff. Adiabatic pulses can be designed to tolerate extreme B₁-inhomogeneity. As can be seen from Fig. 4, above a threshold RF amplitude the HS pulse operates adiabatically and thus continues to invert magnetization despite further increases of RF amplitude, whereas the profiles of the AM pulses degrade in this non-linear regime.

A desirable feature of certain FM pulses is their ability to perform a given rotation of M using lower B₁^max than that required by an equivalent (bandwidth-matched) AM pulse (see Table 1). On the other hand, for given settings of flip angle and bandwidth b_w, the RF energy deposited (SAR) by different RF pulses (both AM and FM pulses) are not so different. On the surface, this may not seem to be true, and thus, a more careful inspection is required to understand why. Table 1 lists pulse duration (T_p), RF amplitude (B₁^max), and relative SAR (E_rel) of the different pulses analyzed by Bloch simulations. These pulses are compared for two flip angles (= π/2 or π) keeping the bandwidth fixed at 2 kHz (b_w ≡ FWHM). It can be seen that the relative SAR of the HS π pulse appears to be 26% larger than that of the sinc pulse, and this therefore appears to contradict the statement above. However, after viewing the slice profiles in Figs. 3 and 4, it can be appreciated why the HS appears to deposit more RF energy. That is, the sinc pulse rotates to a flip angle much smaller than the desired value over much of the bandwidth (i.e., away from the slice center, M_z > −0.99M₀), and only in this undesirable way is the sinc able to achieve lower SAR than the HS pulse. Of note, the duration of the HS pulse is ~2.6-fold longer than the sinc pulse. FM pulses generally require a longer T_p than the equivalent AM pulse, which in some cases can be a disadvantage of these pulses.

Design and optimization methods for FM pulses

So far, the only AM pulses discussed were those obtained from a linear approximation (i.e., FT) to the Bloch equations. However, several methods have been developed to obtain solutions to the Bloch equations and these have shown great utility for generating both AM and FM pulses with improved performance specifications (e.g., see Refs [23, 33–42]). The Shinnar-Le Roux (SLR) algorithm is probably the most popular method to generate pulses for slice selection (e.g., for excitation pulses that produce a flat baseband with sharp boundaries). A key to the SLR algorithm is the so-called hard-pulse approximation allowing the RF pulse to be mapped into two complex polynomials (called the forward SLR transform). During a pulse, M rotates about the vector sum of ω₁ î and Δω k̂, where the latter is due to the gradient field. The basic idea of the hard-pulse approximation is that, if the angle is small, the rotation can be modeled by two sequential rotations. Given the two related polynomials, the inverse SLR transform is used to calculate the RF pulse that produces these polynomials. This inverse transform reduces RF pulse design to polynomial design. The Shinnar-Le Roux algorithm is fast and slice profiles can be calculated analytically.

Another major advance in RF pulse design came with the development of the k-space description of RF pulses that assumes a low flip angle approximation [43]. This formalism led to not only new types of one-dimensional slice-selective pulses, but also multi-dimensional RF pulses.

Finally, valuable methods have been developed to reduce the RF energy deposited during slice selection using gradient modulation. Two such methods are VERSE [44] and GOIA [45].

Surface Coils in Correcting B₁ Inhomogeneities

Potential advantages of using an array of surface coils instead of a circumscribing volume coil was first introduced for the purpose of achieving signal-to-noise ratio (SNR) gains [46]. As in phased array radar, the idea was to simultaneously but independently acquire signals from an array of closely positioned receiver coils whose mutual inductance had been minimized. The signal from each of the array elements would be processed through its own receiver chain, ultimately getting digitized and stored individually, and combined subsequently. The authors of that work [46] suggested that such an “array offers the SNR and resolution of a small surface coil over fields-of-view (FOV) normally associated with body imaging with no increase in imaging time. However, the concept did not gain popularity immediately, likely because the SNR as well as signal intensity was not spatially uniform due to the B₁ gradients associated with the surface coils in such an array. This went contrary to common practice at the time of generating as uniform a B₁-field as possible over the region being imaged, for example the human head or a subsection of the torso. Spatial variations in signal intensity is clearly deleterious for visualizing images since they can dominate the contrast in the image, overpowering the tissue contrast one needs to see for applications like clinical diagnosis.

The use of surface coil arrays gained popularity, however, with methods that embraced the spatial variations of the B₁ and used it for spatial encoding [17, 18, 47] to supplement the encoding achieved by the B₀ gradients, thus accelerating image acquisition. Consequently, the surface coil had found another use that transformed the landscape of how we spatially encode magnetic resonance images. Today, most advanced imaging approaches employ highly accelerated acquisitions enabled by the spatial encoding inherent in an array of surface coils, including for example in major initiatives like the Human Connectome Project [48–51].

The sensitivity profiles of surface coils are not the only source of B₁ inhomogeneities in an image. This became obvious with the increasing push to high magnetic fields, motivated primarily by harvesting potential gains for MRS and functional brain imaging (fMRI) [52, 53]. An example of this is illustrated in Fig. 5, which shows electromagnetic simulation of the transmit B₁ field (usually designated as B₁⁺) for a circumscribing body volume coil at 7T (300 MHz). When unloaded, this coil generates a highly uniform B₁ (Fig. 5, upper panel) within its boundaries; however, when the human body is inserted into the coil, the B₁ field becomes highly inhomogeneous, even showing up strongest in the human head despite the fact that the head is very much outside the RF coil (Fig. 5, lower panel) [54].

Figure 5.

Electromagnetic simulations of the transmit B₁ field in a body RF coil at 7 T. The coil produces a homogenous B₁ when empty (top figure) but not when loaded with the human body (lower figure). Adapted from [54].

Figure 6 displays experimentally obtained images of transmit B₁ magnitude at 7T in the entire human head for the same type of volume coil employed for the simulation of the previous image, but scaled to dimensions compatible with the human head. This coil also generated a highly uniform B₁ field when unloaded. Yet within the human head, the transmit B₁ magnitude, which was mapped directly experimentally in this case, shows extreme non-uniformity within each of the transverse slices shown and in the head-foot direction (i.e., z-direction). Of particular note is the low B₁ magnitude over the temporal lobes (bottom images, Fig. 6) and the cerebellum (not shown). The prominence of such B₁ inhomogeneities at high magnetic fields gained widespread recognition with the initial work on human imaging conducted at 4T [55, 56], at a time when the highest magnetic fields employed for human clinical imaging was 1.5T; later, the degree of this inhomogeneity was shown experimentally to increase in going to even a higher field [57].

Figure 6.

Transmit B₁ magnitude in the human head at 7 T, generated by a volume TEM coil. The color code is proportional to μTesla/V. From [48].

The spatial non-uniformities in B₁⁺ observed at very high fields were ascribed to “the result of spatial phase distribution and amplitude modulation by the interference of the RF traveling waves determined by a given sample-coil configuration” based on experiments conducted at 7T [58]. Similar conclusions were reached using simulations [59] and analytical calculations performed for a sphere [60]. Essentially, the conclusion is that one is no longer operating in the near-field regime where the wavelengths are large compared to object size. Instead we are moving towards the far-field regime where wavelengths are small compared to object size, leading to a traveling wave behavior. When the wavelength of the RF employed is small compared to object dimensions (which is the case in the human head and particularly the human torso relative to 300 MHz (7T proton resonance frequency) wavelength of ~12 cm), the B₁ and accompanying electric fields propagate from the source creating them (the current carrying elements in the RF coil) to and through the object being imaged, getting attenuated and reflected from boundaries during this process, ultimately leading to a complex destructive and constructive interference pattern.

The implications of these conclusions were examined by breaking a circumscribing head “volume” coil in effect into decoupled independent local coil elements and controlling each element individually, i.e. a multichannel transmit implementation [19]. After the amplification stage, the output of the single RF channel was split into different channels using a power splitter and the phase of each channel was adjusted [19]. An eight channel transmit and receive (Tx/Rx) array coil was employed with the same elements being used both for transmission and reception (Fig. 7A). With such a coil connected to an 8-channel receiver, it was possible to transmit with one element and receive with all the elements in the array simultaneously but separately.

Figure 7.

Eight channel transmit/receive RF coil (A) and experimental relative phases measured in the human head from two different individual elements of this coil (B). Lower row shows experimentally measured transmit B₁ magnitude in a cylindrical “phantom” when the individual transmit B₁ vectors from each channel are first experimentally determined, transmitting one channel at a time and receiving with all channels, and subsequently are added according to the constructs shown below each figure (the color code is in arbitrary units). The white ellipse in C, D, and E depicts approximate boundaries of a human head. Adapted from [61].

The afore-described multichannel transmit and receive hardware enabled experimental mapping of B₁⁺ phase and amplitude of each individual element and reconstruction of B₁⁺ either for the circularly polarized (CP) “volume” coil mode¹ or using other constructs [61]. For the coil shown in Fig. 7A, the B₁⁺ phase pattern in the human head obtained by pulsing only one element and receiving from all elements simultaneously is illustrated for two different individual channels in Fig. 7B; this phase pattern is highly non-uniform spatially [61] as would be expected from the traveling wave nature of the RF at this magnetic field strength. The experimentally measured phase variation is complex and easily covers the range 2π over the human head. When the transmission is in the CP volume coil mode, and the RF power is delivered to all 8 channels simultaneously with the appropriate channel-dependent phases, the vector (i.e., complex) addition of B₁⁺ produced by each element is constructive in some places (e.g., the center of the head) or leads to partial cancellation in others, resulting in a “volume coil” transmit B₁ amplitude pattern shown in Fig. 7C [61]. If we approximate where the human head boundaries would be and superimpose it on this pattern (white line in Fig. 7C), one would see in the human head the well-known pattern, bright center transmit B₁ profile, as documented at 4 and 7 T in [62]. If, on the other hand, one transmits with each element individually and forms a construct based on B₁⁺ magnitudes alone, analogous to what can be done for multichannel receive operation, then the pattern is no longer center bright (Fig. 7D); on the contrary, it is weak in the center and strong in the periphery [61].

Thus, the transmit B₁ inhomogeneities exist at high magnetic fields not because of some fundamental physical principles like a “dielectric resonance”, but arise from a particular set of coil configuration and sample geometry. Therefore, inhomogeneity can be rectified by manipulating the configuration of the current carrying elements and/or their phases and amplitudes, so as to control the interference of RF waves emanating from them; in its most generalized form, this is the concept of multichannel transmit coils with each coil element driven separately, what is now known as parallel transmit or pTx (e.g., [19, 20, 61, 63–65]). For these coil elements, today we are back to the original surface coil loop that Ackerman used on a rat, albeit with larger dimensions. The loops work well for 7T or lower fields especially for the human head. With larger objects and higher fields, such at he human torso at 7T or human head or torso at higher magnetic fields, increasingly dipole antennas come into play but in combination with the surface coil loop in their most advanced form (e.g. [66–68] and references therein).

Using various strategies such as B₁-shimming (e.g., [19, 69–73]), transmit sense (e.g., [65, 74, 75]), spoke pulses (e.g., [76–82]), and k-T pulses [83]), the pTx technique aims to generate uniform flip angles over a targeted region such as the brain (also see reviews [84, 85] and references therein). An example of this is shown in Fig. 8, where the flip angle is mapped in two slices in the human head. When the coil is operated in the volume coil mode, the flip-angle shows extensive spatial non-uniformity because of the inhomogeneous B₁⁺ as shown previously in Fig. 6. However, using pTx and, in this case, specifically multiband (MB) pTx pulses, the flip angle uniformity is improved dramatically [81].

Figure 8.

Multiband 2 slice RF excitation in the human brain at 7T for volume coil mode (circularly polarized) and with pTx MB pulse using the same resulting total RF power. Sixteen-channel RF pulses were designed with a single spoke with the base pulse being a sinc·gauss pulse having a duration of 1 ms and time-bandwidth product (b_wT_p) = 10. Adapted from [48, 81].

One of the most significant challenges facing ultrahigh fields is SAR (the power deposited into the subject). Often it is stated that power requirements (hence also SAR assuming most of the power was deposited in the sample) increases quadratically with the magnetic field [86, 87]; however, increasingly, evidence is accumulating demonstrating that power requirements and deposition at ultrahigh fields can be considerably less than the quadratic field dependence of the near-field formulation, including when going from 7 T to 10.5 T, as demonstrated experimentally [88], or even up to 23.5 T as demonstrated using electromagnetic simulations (1 GHz proton resonance frequency) as shown with simulations [89].

Nevertheless, remaining under the SAR limits considered safe for humans remains a challenge for very high fields. The solution to this challenge turns out to be provided by pTx using an array of many local coils (e.g., [81, 88, 90–95] and references therein). In one of the first attempts to perform imaging of the human torso at 7T, a relatively uniform transmit B₁ was achieved over the targeted anatomy (prostate) while improving ~4-fold the transmit efficiency and hence power requirements for a given flip angle in the targeted anatomy; this was done with an 8 channel pTx using B₁ shimming (i.e., so called 1-spoke pulses) [70]. Simulations also indicated that local SAR was reduced as well. Thus, pTx in fact provides the means simultaneously to homogenize the flip angle over the targeted organ of interest as well as increase transmit power efficiency (i.e., flip angle achieved at a given power).

Today, more advanced pulse design strategies than that employed by [70] aim for a desired spatial pattern of B₁⁺ (e.g., uniform flip angle over a predetermined target) and search for a solution in the presence of a power related penalty term, such as local and/or global SAR and/or total RF energy contained in the pulse. This procedure typically generates an “L-curve” that describes the performance of the pulse with respect to the targeted performance (e.g., B₁⁺ uniformity) versus the regularized power parameter. Such an L curve is illustrated in Fig. 9 for a multiband RF pulse design for 7 T brain imaging using a 16 channel parallel transmit coil [81]. The crossing between the horizontal and vertical dashed lines, labeled “Same fidelity” and “Same energy”, identify the performance of the same coil operated in a circularly polarized (CP) “volume coil” mode. At the same RMSE as the CP mode, the RF energy of the pulse is reduced significantly (~60% for the same flip angle). The best compromise is where the L shaped curve has an elbow, indicated by the arrow (Fig. 9).

Figure 9.

Sixteen channel pTx pulse design for a multiband RF pulse that excites two slices simultaneously in the human brain at 7T. The L shaped curve quantifies tradeoffs, in this specific case, between total RF energy of the RF pulse and excitation errors (i.e., root mean square error (RMSE)). The crossing between the horizontal and vertical dashed lines, labeled “Same fidelity” and “Same energy”, identify the performance of the same coil operated in a circularly polarized mode. Adapted from [48, 81].

RF coil design has a significant impact on the gains that can be achieved in reducing local and/or global SAR. For example, a design with coil elements distributed not only azimuthally but also along the z-direction (often referred as a z-coil), first introduced by Adriany et al. [96–98], and subsequently pursued in other high field efforts (e.g., [99, 100]), significantly improves local and/or global SAR reduction with pTx pulses [94, 101, 102]. Many of these transmit arrays use the surface coil of the original Ackerman design but with different dimensions of course, dictated by the sample size.

Using these approaches coupled with appropriate coil layouts, we have demonstrated that it will be possible to perform imaging even in the human torso at 10.5T without violating local and global SAR guidelines; in fact, whatever one can do at 7T with single spoke RF pulses, one can do at 10.5T with two-spoke pulses with the same or even lower local SAR using pTx [68]. This is extremely encouraging since there are a lot of useful imaging studies in the torso one can execute with single spoke pulses at 7T (e.g., [82, 103]), including with single-spoke simultaneous multislice multiband excitation [104].

All experiments described herein were performed following an informed, written consent according to protocols reviewed and approved by our institution’s internal review board.

Conclusion

Introduction of the surface coil for detecting signals from intact systems was a revolution in MRS and MRI. Without it, many of the major technological advances we see today would not have been possible. Certainly, this is true in the studies pursued by the authors of this article over long careers that have taken them from a point where in vivo spectroscopy and imaging was just starting, to today’s very advanced studies of the human body, particularly the human brain at very high magnetic fields.

Highlights.

• The invention of the surface coil by Ackerman and colleagues initiated a revolution in MRS and MRI

• The surface coil motivated developments in new ways to produce uniform flip angle despite extreme B₁ inhomogeneity using FM pulses

• FM pulses allow unique types of MRI and MRS sequences that tolerate extreme B₁ and B₀ inhomogeneity, such as SPEN and LASER

• Spatial encoding available through an array of surface coils enable highly accelerated imaging

• Parallel transmit pulses using an array of surface coils is critical for achieving uniform flipangles and reducing power deposition in ultrahigh field MRI and MRS