Abstract
Based on the FitzHugh–Nagumo (FHN) neuron model subjected to sine-Wiener (SW) noise, impacts of SW noise on weak periodic signal detection are investigated by calculating response measure Q for characterizing synchronization between the input signal and the output temporal activities of the neuron. It is numerically demonstrated that the response measure Q can achieve the optimal value under appropriate and moderate intensity or correlation time of SW noise, suggesting the occurrence of SW-noise-induced stochastic resonance. Furthermore, the optimal value of Q is sensitive to correlation time. Consequently, the correlation time of SW noise has a great influence on the performance of signal detection in the FHN neuron.
Keywords: Sine-Wiener noise, FitzHugh–Nagumo neuron, Signal detection
Introduction
Noise is ubiquitous in real systems and noise has very constructive effect on the dynamics of nonlinear systems (Faisal et al. 2008; Gammaitoni et al. 1998; Hänggi 2002). The remarkable examples about the constructive role of noise are stochastic resonance (SR) (Benzi et al. 2004; Gammaitoni et al. 1998) and coherent resonance (CR) (Gang et al. 1993; Pikovskyj and Kurths 1997). The SR phenomenon is first discovered by Benzi and collaborators when investigating the periodical occurrence of ice ages (Wiesenfeld and Moss 1995). Now SR is widely used to name phenomenon that response of nonlinear system to external signal reach maximum at the moderate noise intensity. With the deepening of related researches, it is found that the spike activities in nonlinear systems can also reach the state with high regularity in an internal noise-driven excitable system even without external driving signal (Pikovskyj and Kurths 1997). This phenomenon is known as CR by Pikovskyj and Kurths (1997) to differ it from the familiar SR phenomenon.
There are many noise sources in nervous system, such as the opening and closing of ion channels, the diffusion and binding of signal molecules to receptors (Faisal et al. 2008). As the basic information processing devices, neurons exert its functionality in a very noisy environment (Ermentrout et al. 2008). However, neurons can detect feeble target signal from complex background signals (Ermentrout et al. 2008; Faisal et al. 2008). The natural question emerges what is the mechanism of distinguishing weak target signal from complex background signals? The importance of noise in nervous system has been repeatedly confirmed by numerous studies (Faisal et al. 2008; Kish et al. 2015; Wang et al. 2014). It is the widely accepted that SR and CR are considered to be two good potential mechanisms for understanding weak signal detection of neuron in the noisy environment (Liang et al. 2011; Stacey and Durand 2000; Volkov et al. 2003). A typical example is that the crayfish mechanoreceptor is more easily to detect distant fin movements of predatory fish in turbulent water rather than still water (Bezrukov and Vodyanoy 1995; Wiesenfeld and Moss 1995).
Relatively earlier studies mainly focus on the effects of Gaussian noise on signal detection due to its conveniences and universality. However, Gaussian noise is not always suitable for modeling the random effect in an arbitrary dynamical process. For example, Gaussian noise is not suitable for modeling the random phase variation derived from a periodic signal traversing a random medium or interface (Liang et al. 2011). Moreover, Gaussian noise is unbound. In other words, it has a chance to take very large value. But all physical parameters are always bounded (Cai and Wu 2004). Consequently, the range of application of Gaussian noise is limited. More and more attention is paid to bounded non-Gaussian noises recently. For example, signal transmission can be enhanced by phase noise (Kang et al. 2013; Volkov et al. 2003); phase noise derived from time-varying initial signal phase can induce resonance (Liang et al. 2010); phase noise can effectively improve the capacity of detecting weak signal (Liang et al. 2011).
Besides noise, many other factors have great influences on signal detection in nervous system. Like noise, initial phase diversity in external signal can be regard as another feasible mechanism for weak signal detection (Liang and Liu 2016). Feedback and time delay also play a significant role in resonance and signal detection (Wang et al. 2017a, b; Yao et al. 2016). Autpase feedback and channel noise can enhance the performance of weak periodic signal detection in Hodgkin–Huxley (HH) neuron if appropriate parameters are used (Ma and Tang 2017; Yilmaz and Ozer 2015). Moreover, electromagnetic radiation can induce model selection and transition of electrical activities in neuron, thereby contributing to transmission of complex signals (Ge et al. 2017; Lu et al. 2017; Wang et al. 2017c; Wu et al. 2017; Xu et al. 2017). The high-frequency (HF) or spatially periodic force with appropriate strength and frequency may augment signal detection and transmission (Yao et al. 2015; Yao and Zhan 2010).
As another type of bounded non-Gaussian noises, sine-Wiener (SW) noise also attracts much attention recently. SW-noise-induced spike death can be observed in an excitable system where delayed feedback exists (Guo et al. 2012a). SW noise can induce phase transitions in a time-delayed genotype selection model (Ning and Liu 2016; Yang and Ning 2017). The interplay between time delays and cross-correlation SW (CCSW) noises in tumor–immune system was surveyed by analyzing stationary probability distribution (Guo et al. 2012b; Guo and Mei 2014). In our previous studies, we studied in detail the effects of bounded noise on the formation and instability of spiral wave in square lattice (Yao et al. 2017b) and small-world networks (Yao et al. 2017a), respectively. In addition, we also found that CCSW noises can induce CR in FHN neuron model (Yao et al. 2017c). Although many efforts have been contributed in this area, there is no report about the role of SW noise in weak signal detection in the FHN neuron model.
Model and simulation
FHN neuron model is a simplified variant of the famous HH model and widely used to describe the electrical activities of neuron. The time evolution equations for FHN model yield (Yang et al. 2012)
| 1 |
| 2 |
here a small parameter ε results in that x(t) and y(t) have the different time scales. As a consequence, dynamics can be separated into fast and slow ones. The fast variable x(t) describe the membrane voltage, while slow variable y(t) represents the effective membrane conductivity of the neuron. Icos(ωt) is an external sub-threshold (i.e. weak) periodic driving signal with an amplitude of 0.32 and an angular frequency of 0.3 (Yang et al. 2012) and the external driving signal itself cannot evoke a spike under the given parameters of I = 0.32 and ω = 0.3 (Yang et al. 2012).
The explicit definition of SW noise η(t) yields (Ning and Liu 2016; Yang and Ning 2017)
| 3 |
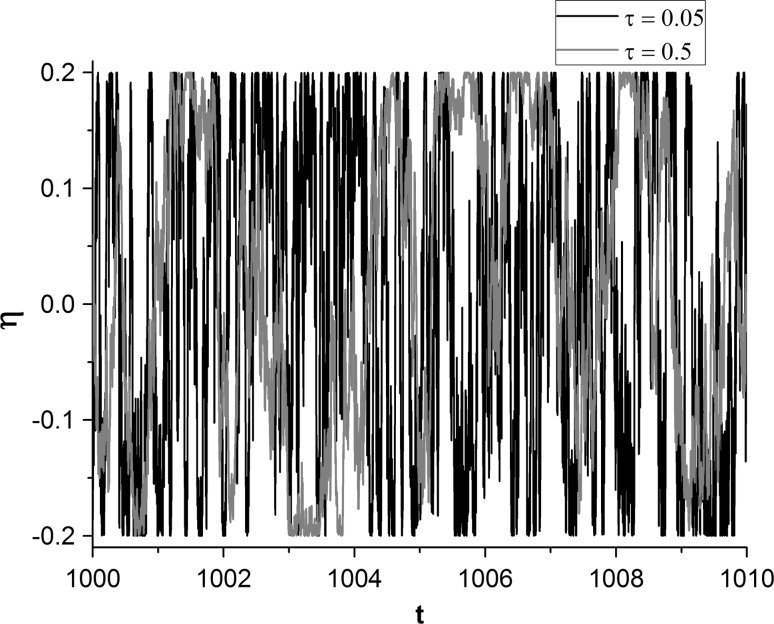
here A and τ are the amplitude and self-correlation time of SW noise, respectively. As shown in the time series of the SW noise, a larger τ means faster fluctuation (Fig. 1). B(t) is a standard Wiener processes. The mean and auto-correlation function of SW noise η(t) are respectively obtained as follows (Ning and Liu 2016; Yang and Ning 2017):
| 4 |
| 5 |
Fig. 1.
Time series of the SW noise for different correlation time
According to Euler’ algorithm with a time step Δt = 0.001 time units, Eqs. (1) and (2) are discretized in our numerical simulations as follows:
| 6 |
| 7 |
In the numerical simulation, the time evolution of standard Wiener processes B(t) is controlled by the following formula (Fox et al. 1988; Ning and Liu 2016; Yang and Ning 2017):
| 8 |
here χ1 and χ2 are two independent uniformly distributed random numbers on the unit interval.
The response of system on the external periodic signal are measured by Fourier coefficient Q giving by (Yang et al. 2012)
| 9 |
Fourier coefficient Q (also called response measure in the remainder of this article) quantifies synchronization between the input frequency ω and the output temporal activities of neuron. Larger Q indicates better synchronization between input signal the response of system. Synchronization of neuronal signal is regarded as one of mechanisms to code and transmit information (Qu et al. 2012; Shi et al. 2017; Zhao et al. 2017). Therefore, larger Q also represents more information transported through particular forcing frequency ω (Yang et al. 2012). In reality, sub-threshold oscillations cannot encode information and information is encoded through large spikes of electrical activities in neuron. Consequently, a threshold of xs is set to distinguish spikes from sub-threshold oscillations. If x(t) > xs, its value is kept unchanged; otherwise, its value is equal to − 1 (Yang et al. 2012). The transient processes are discarded by setting a sufficiently large T0 = 1000 time units. Moreover, a sufficiently large time interval is chosen by setting m = 500 periods of weak periodic signal in the calculation of Q.
Results
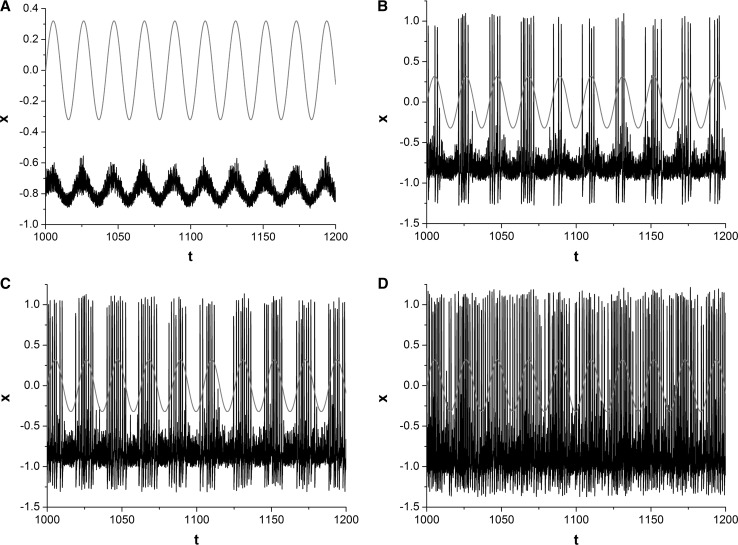
The effect of amplitude A of SW noise on the electrical activities of FHN neuron is investigated firstly. Without loss of generality, correlation time τ is set as 0.05. For different amplitude A, the time series of x(t) (dark curves) and weak periodic signal (red curves) are shown in Fig. 2. SW noise cannot evoke spikes when amplitude is small (such as A = 0.05) (Fig. 2a). There are some SW-noise-evoked spikes appearing in the positive half period of input periodic signal when A is strong enough (such as A = 0.15) (Fig. 2b). Therefore, synchronization between input periodic signal and the output temporal activities of FHN neuron can be observed (Fig. 2b). Further increasing amplitude (such as A = 0.2) results in more SW-noise-evoked spikes emerging in the positive half period of input periodic signal (Fig. 2c). The synchronization between input signal and the output of system is obviously enhanced (Fig. 2c). Therefore, information carried by input period signal can be effectively detected and transmitted. But SW noise with too much amplitude makes the spikes of neuron appearing in the whole period of input period signal (Fig. 2d), and decrease the synchronization between input signal and the response of system (Fig. 2d), which suggests the capacity of signal processing of neuron is degraded again. In reality, there is no component of input periodic signal in the output temporal activities of the neuron (Fig. 2d). The above-mentioned results reveal that there are the optimal amplitudes of SW noise to obtain better synchronization between input signal and the output of system. In other words, SW-noise-induced SR phenomenon can be observed and information carried by weak period signal can be effectively recognized and transmitted by neuron through SW-noise-induced SR.
Fig. 2.
Sampled time series of variable x for different amplitudes. a A = 0.05; b A = 0.15; c A = 0.2; d A = 0.35. Correlation time τ is set as 0.05. The moderate amplitude A of SW noise makes synchronization between weak periodic signal (red line) and the output of system better. (Color figure online)
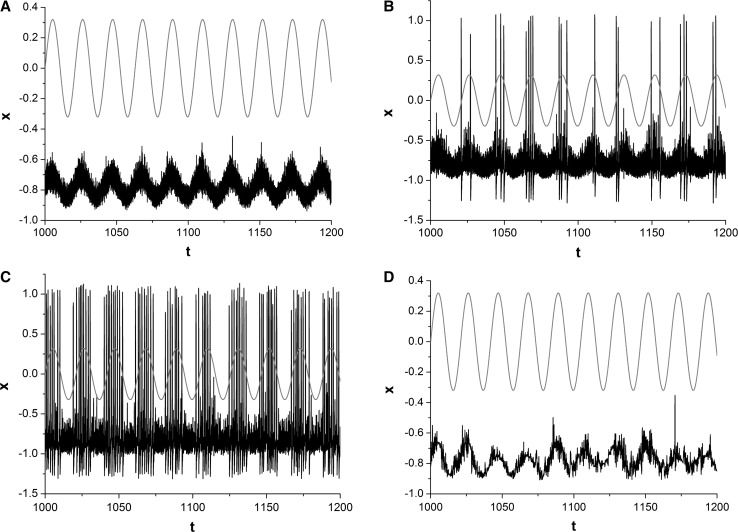
We then investigate how correlation time of SW noise influences the dynamics of neuron. The time series of x(t) (dark curves) and weak periodic signal (red curves) are represented in Fig. 3, for different correlation time τ of SW noise. The amplitude of SW noise is fixed to 0.2 without generality. For small correlation time (such as τ = 0.001), there is no spikes evoked by SW noise (Fig. 3c). SW-noise-evoked spikes begin sparsely to appear in the positive half period of input period signal (Fig. 3b). The synchronization between input periodic signal and the output of system starts to emerge (Fig. 3b). There are more SW-noise-evoked spikes emerging in the positive half period of input period signal with the further increase of correlation time τ of SW noise (Fig. 3c). SW noise can significantly reinforce synchronization, thus makes the capability of signal detection and signal processing of neuron stronger. However, when correlation time is too long, SW noise cannot evoke any spikes, and there are only sub-threshold oscillations around resting state (Fig. 3d). Information carried by period signal is completely disappeared in the output of system (Fig. 3d).
Fig. 3.
Sampled time series of variable x for different correlation times. a τ = 0.001; b τ = 0.01; c τ = 0.05; d τ = 5. Amplitude A is set as 0.2. The moderate correlation time τ of SW noise makes synchronization between weak periodic signal (red line) and the output of system better. (Color figure online)
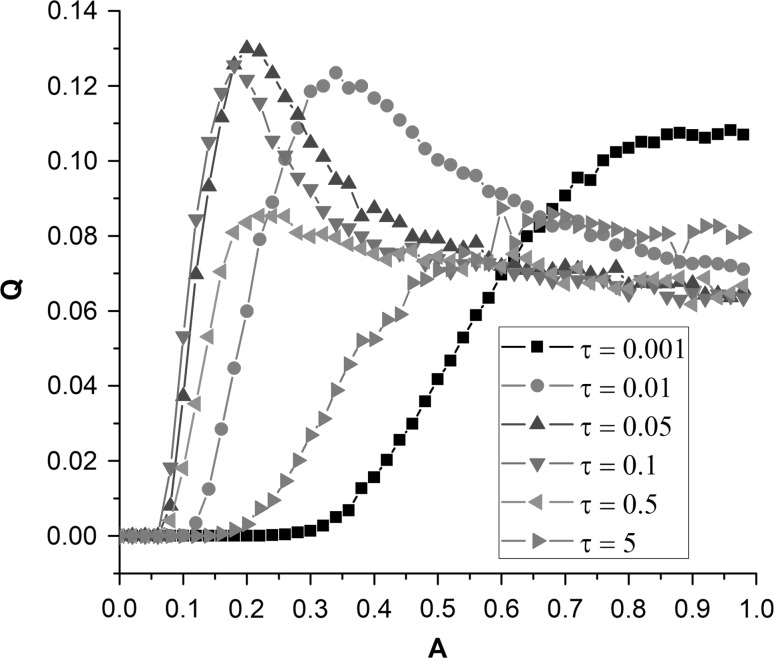
From a point of quantitative view, we calculate Fourier coefficient Q to investigate the effect of amplitude on signal detection in the FHN neuron model. The dependences of Q on amplitude A for different correlation time τ are shown in Fig. 4. When amplitude is small, SW noise cannot evoke any spikes; there are only sub-threshold oscillations around resting state. Therefore, the value of Q is equal to 0. As the increase of amplitude A, spikes gradually appear in, thus the value of Q increase. But for different correlation time τ, there are obvious difference in the changing trend of Q with increasing A. For small or large τ (such as τ = 0.001 or τ = 5), the value of Q monotonically increase with the increase of amplitude A. For moderate correlation time (such as τ = 0.01 or τ = 0.05, etc.), the value of Q first quickly increases, reaches the maximum at moderate amplitude, and then decrease as the increasing amplitude A (Fig. 4). There are obvious peaks in the curves of Q versus A, which quantitatively confirms the occurrence of SW-noise-induced SR phenomenon.
Fig. 4.
Dependencies of response measure Q on increasing amplitude A. The peaks indicate the occurrence of SW-noise-induced stochastic resonance phenomenon
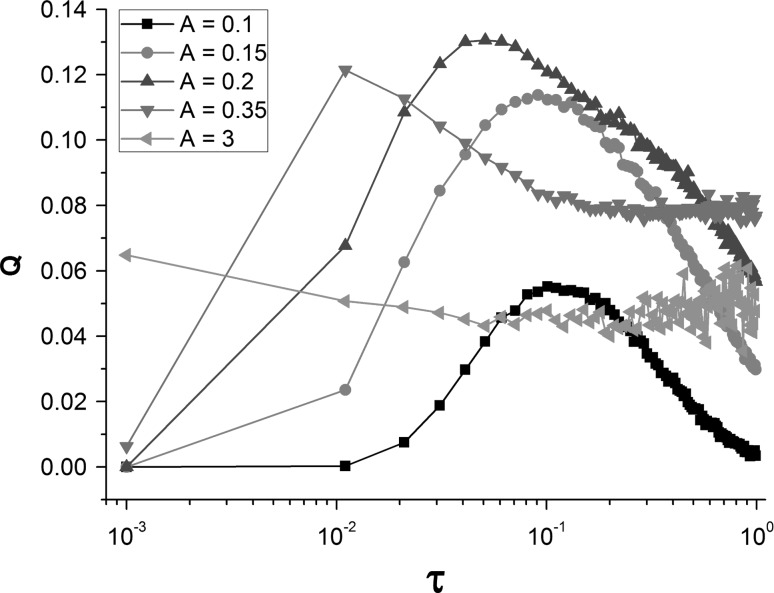
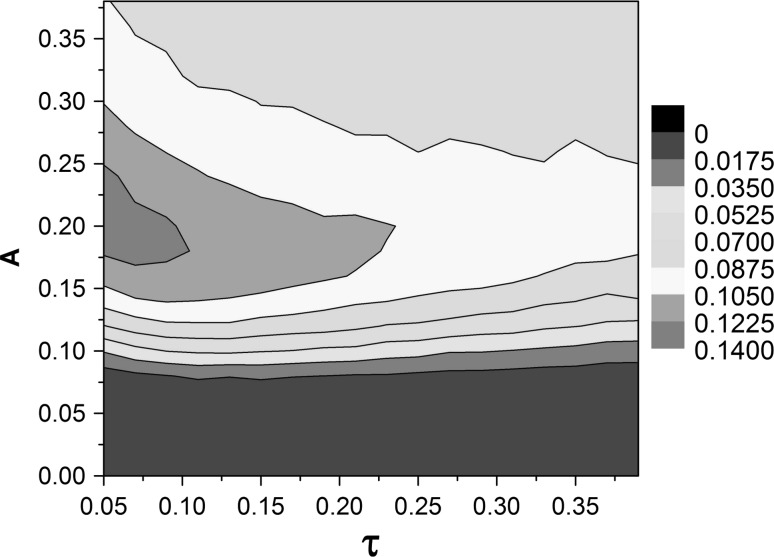
Next, the effect of correlation time τ on signal detection is explored by drawing the curves of Q versus τ for different amplitude A. The resonance peaks can be observed when amplitude A is ranging from 0.1 to 0.35 (Fig. 5). Therefore, SR can be induced by correlation time of SW noise. But it may disappear for large amplitude, such as A = 3 (Fig. 5). Furthermore, the value of Q is more sensitive to correlation time τ than amplitude A (Fig. 5). To get a global view and get the optimal parameter combinations of amplitude A and correlation time τ, the contour plot of Fourier coefficient Q in the A–τ plane is depicted in Fig. 6. The red area indicates the existence of SW-noise-induced SR phenomenon. The maximum of Q = 0.13 is achieved at A = 0.2 and τ = 0.05. Moreover, when amplitude A is fixed, the tiny change of correlation time τ may give rise to an obvious decrease of Q, thus, the correlation time of SW noise has a great influence on the performance of signal detection.
Fig. 5.
Dependencies of response measure Q on increasing correlation time τ. The peaks indicate the occurrence of SW-noise-induced stochastic resonance phenomenon
Fig. 6.
Contour plot of Q in the A–τ plane. The area with larger Q value indicates the occurrence of SW-noise-induced stochastic resonance, i.e. the best performance of weak periodic signal detection in the FHN neuron
Conclusion
In this study, we investigate the effect of SW noise on weak periodic signal detection in the FHN neuron. It is numerically demonstrated that amplitude and correlation time of SW noise can significantly influence electrical activities of FHN neuron. Fourier coefficient Q is used to quantify synchronization between the input frequency ω and the output temporal activities of FHN neuron. Larger Q represents more synchronization and better performance of signal detection. The value of Q increases with increasing amplitude or correlation time of SW noise, reaches the maximum at moderate amplitude or correlation time, and then finally decreases with the further increase of amplitude or correlation time, which is typical signature of noise-induced stochastic resonance. In other words, the best performance of signal detection is achieved at moderate amplitude or correlation time. Furthermore, the value of Q is more sensitive to correlation time than amplitude. The results reported here provide a possible mechanism for weak signal detection and signal transmit in nervous system.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No. 31601071).
References
- Benzi R, Sutera A, Vulpiani A. The mechanism of stochastic resonance. J Phys A: Gen Phys. 2004;14:L453–L457. doi: 10.1088/0305-4470/14/11/006. [DOI] [Google Scholar]
- Bezrukov SM, Vodyanoy I. Noise-induced enhancement of signal transduction across voltage-dependent ion channels. Nature. 1995;378:362–364. doi: 10.1038/378362a0. [DOI] [PubMed] [Google Scholar]
- Cai GQ, Wu C. Modeling of bounded stochastic processes. Probab Eng Mech. 2004;19:197–203. doi: 10.1016/j.probengmech.2004.02.002. [DOI] [Google Scholar]
- Ermentrout GB, Galán RF, Urban NN. Reliability, synchrony and noise. Trends Neurosci. 2008;31:428–434. doi: 10.1016/j.tins.2008.06.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Faisal AA, Selen LPJ, Wolpert DM. Noise in the nervous system. Nat Rev Neurosci. 2008;9:292–303. doi: 10.1038/nrn2258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fox RF, Gatland IR, Roy R, Vemuri G. Fast, accurate algorithm for numerical simulation of exponentially correlated colored noise. Phys Rev A. 1988;38:5938–5940. doi: 10.1103/PhysRevA.38.5938. [DOI] [PubMed] [Google Scholar]
- Gammaitoni L, Hänggi P, Jung P, Marchesoni F. Stochastic resonance. Rev Mod Phys. 1998;70:45–105. doi: 10.1103/RevModPhys.70.223. [DOI] [Google Scholar]
- Gang H, Ditzinger T, Ning CZ, Haken H. Stochastic resonance without external periodic force. Phys Rev Lett. 1993;71:807–810. doi: 10.1103/PhysRevLett.71.807. [DOI] [PubMed] [Google Scholar]
- Ge M, Jia Y, Xu Y, Yang L. Mode transition in electrical activities of neuron driven by high and low frequency stimulus in the presence of electromagnetic induction and radiation. Nonlinear Dyn. 2017;91:515–523. doi: 10.1007/s11071-017-3886-2. [DOI] [Google Scholar]
- Guo W, Mei DC. Stochastic resonance in a tumor–immune system subject to bounded noises and time delay. Phys A. 2014;416:90–98. doi: 10.1016/j.physa.2014.08.003. [DOI] [Google Scholar]
- Guo W, Du LC, Mei DC. Coherence and spike death induced by bounded noise and delayed feedback in an excitable system. Eur Phys J B. 2012;85:1–7. doi: 10.1140/epjb/e2011-20818-1. [DOI] [Google Scholar]
- Guo W, Du LC, Mei DC. Transitions induced by time delays and cross-correlated sine-Wiener noises in a tumor–immune system interplay. Phys A. 2012;391:1270–1280. doi: 10.1016/j.physa.2011.11.007. [DOI] [Google Scholar]
- Hänggi P. Stochastic resonance in biology. How noise can enhance detection of weak signals and help improve biological information processing. Chemphyschem A Eur J Chem Phys Phys Chem. 2002;3:285–290. doi: 10.1002/1439-7641(20020315)3:3<285::AID-CPHC285>3.0.CO;2-A. [DOI] [PubMed] [Google Scholar]
- Kang XS, Liang XM, Lü HP. Enhanced response to subthreshold signals by phase noise in a Hodgkin–Huxley Neuron. Chinphyslett. 2013;30:018701–018704. [Google Scholar]
- Kish EA, Granqvist CG, Der A, Kish LB. Lognormal distribution of firing time and rate from a single neuron? Cogn Neurodyn. 2015;9:459–462. doi: 10.1007/s11571-015-9332-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liang XM, Liu ZH. Effect of initial phase diversity on signal detection in excitable systems. Sci China Technol Sci. 2016;59:376–386. doi: 10.1007/s11431-015-5983-0. [DOI] [Google Scholar]
- Liang X, Dhamala M, Zhao L, Liu Z. Phase-disorder-induced double resonance of neuronal activity. Phys Rev E. 2010;82:010902–010905. doi: 10.1103/PhysRevE.82.010902. [DOI] [PubMed] [Google Scholar]
- Liang X, Zhao L, Liu Z. Phase-noise-induced resonance in a single neuronal system. Phys Rev E. 2011;84:031916–031920. doi: 10.1103/PhysRevE.84.031916. [DOI] [PubMed] [Google Scholar]
- Lu L, Jia Y, Liu W, Yang LJ. Mixed stimulus-induced mode selection in neural activity driven by high and low frequency current under electromagnetic radiation. Complexity. 2017;2017:7628537. [Google Scholar]
- Ma J, Tang J. A review for dynamics in neuron and neuronal network. Nonlinear Dyn. 2017;89:1569–1578. doi: 10.1007/s11071-017-3565-3. [DOI] [Google Scholar]
- Ning LJ, Liu P. The effect of sine-Wiener noises on transition in a genotype selection model with time delays. Eur Phys J B. 2016;89:201. doi: 10.1140/epjb/e2016-70138-y. [DOI] [Google Scholar]
- Pikovsky AS, Kurths J. Coherence resonance in a noise-driven excitable system. Phys Rev Lett. 1997;78:775–778. doi: 10.1103/PhysRevLett.78.775. [DOI] [Google Scholar]
- Qu J, Wang R, Du Y, Cao J. Synchronization study in ring-like and grid-like neuronal networks. Cogn Neurodyn. 2012;6:21–31. doi: 10.1007/s11571-011-9174-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shi JC, Luo M, Huang CS. Cooperative effect of random and time-periodic coupling strength on synchronization transitions in one-way coupled neural system: mean field approach. Cogn Neurodyn. 2017;11:383–390. doi: 10.1007/s11571-017-9437-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stacey WC, Durand DM. Stochastic resonance improves signal detection in hippocampal CA1 neurons. J Neurophysiol. 2000;83:1394–1402. doi: 10.1152/jn.2000.83.3.1394. [DOI] [PubMed] [Google Scholar]
- Volkov EI, Ullner E, Zaikin AA, Kurths J. Oscillatory amplification of stochastic resonance in excitable systems. Phys Rev E. 2003;68:026214–026220. doi: 10.1103/PhysRevE.68.026214. [DOI] [PubMed] [Google Scholar]
- Wang RB, Wang GZ, Zheng JC. An exploration of the range of noise intensity that affects the membrane potential of neurons. Abstr Appl Anal. 2014;2014:801642–801652. [Google Scholar]
- Wang C, Guo S, Xu Y, Tang J, Alzahrani F, Hobiny A. Formation of autapse connected to neuron and its biological function. Complexity. 2017;2017:5436737. [Google Scholar]
- Wang LF, Qiu K, Jia Y. Effects of time delays in a mathematical bone model. Chin Phys B. 2017;26:030503–030509. doi: 10.1088/1674-1056/26/3/030503. [DOI] [Google Scholar]
- Wang Y, Ma J, Xu Y, Wu F, Zhou P. The electrical activity of neurons subject to electromagnetic induction and gaussian white noise. Int J Bifurc Chaos. 2017;27:1750030–1750041. doi: 10.1142/S0218127417500304. [DOI] [Google Scholar]
- Wiesenfeld K, Moss F. Stochastic resonance and the benefits of noise: from ice ages to crayfish and SQUIDs. Nature. 1995;373:33–36. doi: 10.1038/373033a0. [DOI] [PubMed] [Google Scholar]
- Wu F, Wang C, Jin W, Ma J. Dynamical responses in a new neuron model subjected to electromagnetic induction and phase noise. Phys A. 2017;469:81–88. doi: 10.1016/j.physa.2016.11.056. [DOI] [Google Scholar]
- Xu Y, Jia Y, Ge M, Lu L, Yang LJ, Zhan X. Effects of ion channel blocks on electrical activity of stochastic Hodgkin-Huxley neural network under electromagnetic induction. Neurocomputing. 2017 [Google Scholar]
- Yang H, Ning LJ. Phase transitions induced by time-delay and different noises. Nonlinear Dyn. 2017;88:2427–2433. doi: 10.1007/s11071-017-3387-3. [DOI] [Google Scholar]
- Yang LJ, Liu WH, Yi M, Wang CJ, Zhu QM, Zhan X, Jia Y. Vibrational resonance induced by transition of phase-locking modes in excitable systems. Phys Rev E. 2012;86:016209–016215. doi: 10.1103/PhysRevE.86.016209. [DOI] [PubMed] [Google Scholar]
- Yao C, Zhan M. Signal transmission by vibrational resonance in one-way coupled bistable systems. Phys Rev E. 2010;81:061129–061136. doi: 10.1103/PhysRevE.81.061129. [DOI] [PubMed] [Google Scholar]
- Yao C, He Z, Luo J, Shuai J. Resonance induced by a spatially periodic force in the reaction-diffusion system. Phys Rev E. 2015;91:052901–052906. doi: 10.1103/PhysRevE.91.052901. [DOI] [PubMed] [Google Scholar]
- Yao C, Ma J, Li C, He Z. The effect of process delay on dynamical behaviors in a self-feedback nonlinear oscillator. Commun Nonlinear Sci Numer Simul. 2016;39:99–107. doi: 10.1016/j.cnsns.2016.02.025. [DOI] [Google Scholar]
- Yao Y, Deng H, Ma C, Yi M, Ma J. Impact of bounded noise and rewiring on the formation and instability of spiral waves in a small-world network of Hodgkin–Huxley neurons. PLoS ONE. 2017;12:e0171273. doi: 10.1371/journal.pone.0171273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yao Y, Deng H, Yi M, Ma J. Impact of bounded noise on the formation and instability of spiral wave in a 2D Lattice of neurons. Sci Rep. 2017;7:43151. doi: 10.1038/srep43151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yao Y, Yi M, Hou D. Coherence resonance induced by cross-correlated sine-Wiener noises in the FitzHugh–Nagumo neurons. Int J Mod Phys. 2017;31:1750204. doi: 10.1142/S0217979217502046. [DOI] [Google Scholar]
- Yilmaz E, Ozer M. Delayed feedback and detection of weak periodic signals in a stochastic Hodgkin–Huxley neuron. Phys A. 2015;421:455–462. doi: 10.1016/j.physa.2014.10.096. [DOI] [Google Scholar]
- Zhao J, Deng B, Qin Y, Men C, Wang J, Wei X, Sun J. Weak electric fields detectability in a noisy neural network. Cogn Neurodyn. 2017;11:81–90. doi: 10.1007/s11571-016-9409-x. [DOI] [PMC free article] [PubMed] [Google Scholar]