Abstract
Population genetic methods are widely used to retrace the introduction routes of invasive species. The unsupervised Bayesian clustering algorithm implemented in STRUCTURE is amongst the most frequently used of these methods, but its ability to provide reliable information about introduction routes has never been assessed. We simulated microsatellite datasets to evaluate the extent to which the results provided by STRUCTURE were misleading for the inference of introduction routes. We focused on an invasion scenario involving one native and two independently introduced populations, because it is the sole scenario that can be rejected when obtaining a particular clustering with a STRUCTURE analysis at K = 2 (two clusters). Results were classified as “misleading” or “non-misleading”. We investigated the influence of effective size, bottleneck severity and number of loci on the type and frequency of misleading results. We showed that misleading STRUCTURE results were obtained for 10% of all simulated datasets. Our results highlighted two categories of misleading output. The first occurs when the native population has a low level of diversity. In this case, the two introduced populations may be very similar, despite their independent introduction histories. The second category results from convergence issues in STRUCTURE for K = 2, with strong bottleneck severity and/or large numbers of loci resulting in high levels of differentiation between the three populations. Overall, the risk of being misled by STRUCTURE in the context of introduction routes inferences is moderate, but it is important to remain cautious when low genetic diversity or genuine multimodality between runs are involved.
Introduction
The reconstruction of introduction routes is important for the management of biological invasions because it facilitates (i) the design of strategies to prevent future invasions by targeting the source area (Mack et al. 2000) and (ii) the development of measures to control invasive populations which effectiveness depends on the genetic composition and geographical origin of introduced individuals (Roderick and Navajas 2003). From an academic point of view, retracing the introduction routes of invasive alien species is a prerequisite to accurately compare ancestral and derived populations to infer ecological and evolutionary processes which determine the invasion success (Keller and Taylor 2008). When there are at least two invasive populations, crucial historical and demographical characteristics of their introductions typically include the number of independent introductions from the native area and the number of serial introductions involving intermediate invasive populations. However, identification of the source of an introduced population is a complex task, because of the highly stochastic nature of the introduction process (Estoup and Guillemaud 2010). Many population genetics methods and tools are now widely used to retrace the introduction routes of invasive species. This approach is somewhat risky, because the methods involved are often dependent on demographic and genetic equilibria, but invasions often involve demographic disequilibrium, through strong bottlenecks followed by rapid population growth, for example. Despite this limitation and the risks of using population genetics methods inappropriately in the specific context of biological invasions, only a few of these methods have been formally evaluated (e.g., Estoup and Guillemaud 2010; Guillemaud et al. 2010).
Among population genetics methods, unsupervised individual Bayesian clustering methods are widely used. The popularity of these methods is due to their ability to infer genetic structure correctly in many situations and their apparent simplicity (several “click-and-play” software suites are available). STRUCTURE (Pritchard et al. 2000; Falush et al. 2003; Hubisz et al. 2009) is the most frequently used software for clustering, with more than 28,000 citations for the three references indicated above in Google Scholar in September 2017. STRUCTURE aims to sort individuals in an unsupervised way into K clusters (K being defined by the user), assuming Hardy–Weinberg/linkage equilibrium within clusters (Porras-Hurtado et al. 2013). In theory, if K is set to the true number of population, samples belonging to the same population will be classified into the same cluster. More broadly, because knowing or inferring the true number of population is not always possible, samples belonging to the same cluster are at least considered as sharing a close evolutionary history. STRUCTURE is known to perform well in most cases, but it can be misleading in some situations, particularly in the presence of isolation by distance (Frantz et al. 2009; Schwartz and McKelvey 2009), clusters of very different sizes (Kalinowski 2011; Puechmaille 2016), family groups (Anderson and Dunham 2008; Rodríguez-Ramilo and Wang 2012; Rodríguez-Ramilo et al. 2014), or high proportions of missing data (Smith and Wang 2014).
STRUCTURE and other software suites based on similar methods are frequently used in the context of introduction routes inferences (Estoup and Guillemaud 2010; Lawson Handley et al. 2011; Cristescu 2015). In some cases, STRUCTURE is used directly to contrast models of invasion history, mainly for comparisons of scenarios involving either multiple independent introductions from a native population, or a single introduction from the native area followed by serial introduction(s) from this primary introduced area. Being able to differentiate between the two scenarios is of great importance especially because serial introductions may be associated with a major eco-evolutionary change in a particular invasive population that can then act as a bridgehead for a larger scale invasion (Lombaert et al. 2010; Guillemaud et al. 2011). In this context, exploring clustering patterns with only two genetic clusters (K = 2) is considered as informative. Indeed, one of the clustering patterns that can be obtained makes it possible to reject the hypothesis of independent introductions: if all samples from the invaded areas group together in one cluster, and all samples from the native area group in the other cluster, this allows rejecting the hypothesis of independent introductions and is considered to provide fairly conclusive evidence about a single introduction from the native area (Fig. 1). For example, Ascunce et al. (2011) explored the worldwide invasion history of the fire ant Solenopsis invicta with a total of 2144 colonies sampled from 75 geographic locations, including 39 native (South America) and 36 invaded (USA, China, Australia) areas. They found that all samples from invasive populations clustered together when analyzing the data with STRUCTURE at K = 2 and concluded that only one introduction from the native area occurred. They then used approximate Bayesian computation to test whether the oldest invasive population in the USA was the source of all other invasive populations in distant areas. Similarly, Cordero et al. (2017) analyzed 378 individuals of the Manila clam Ruditapes philippinarum from 9 geographic locations, including 3 native (Asia) and 6 invaded (North America and Europe) areas. They found that STRUCTURE analyses at K = 2 grouped all samples of invasive populations into the same cluster. They concluded that a single native Asian introduction of the species into North America was very likely, and that North America then became the source of the European outbreak. Such use of STRUCTURE in the context of invasion biology is very common (e.g., Lachmuth et al. 2010; Papura et al. 2012; Robert et al. 2012; Bolte et al. 2013; Fontaine et al. 2013; Sanz et al. 2013; Zhang et al. 2014; Yu et al. 2014; Zhou et al. 2015; Guillemaud et al. 2015; Rewicz et al. 2015; Dieni et al. 2016; Zhu et al. 2017). However, invasions frequently involve major demographic events, such as strong bottlenecks followed by genetic drift, which may significantly impair our ability to determine introduction routes correctly from a given STRUCTURE result. This may account for the contradictory outcomes sometimes obtained with different population genetics methods. For example, Mallez et al. (2015) found conflicting results when trying to infer the origin of the invasive Portuguese outbreak of the pinewood nematode Bursaphelenchus xylophilus: while FST values suggested a native North American origin, STRUCTURE suggested an origin from an oldest invasive population in Japan for these samples, because all invasive samples from Portugal and Japan belonged to one cluster and all native samples belonged to another cluster while analyzing K = 2 patterns.
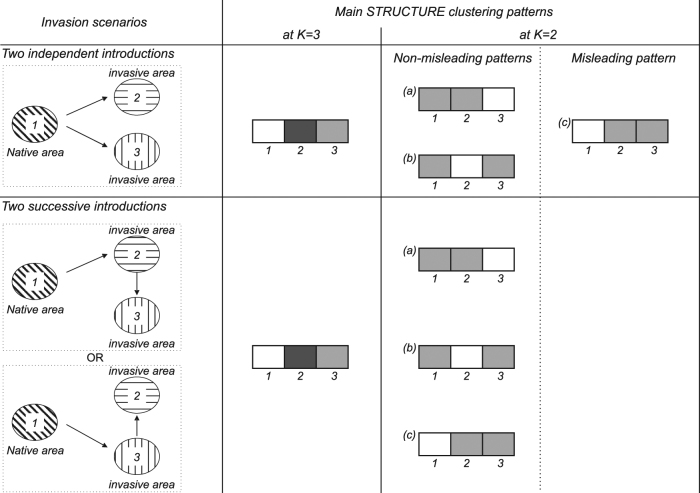
Fig. 1.
Schematic representations of the main STRUCTURE clustering patterns that can be obtained at K = 3 and K = 2 according to different invasion scenarios (either independent or serial) involving one native and two invasive populations. Other patterns with admixture are also possible but are not shown here because they are less informative in the context of invasion routes. At K = 3, with 3 samples, the same pattern (i.e., each sample constitutes a cluster) is likely to be found whatever the scenario, and thus no valuable information about the origin of introduced populations can be deduced. On the contrary, patterns obtained at K = 2 can be informative: whereas clustering patterns a and b can be obtained in both independent and serial scenario, pattern c should only be found if introductions are serial. If obtained, this pattern c would lead a STRUCTURE user to eliminate the independent scenario as a likely one
In this study, we evaluated the risk of incorrect introduction route inferences based on STRUCTURE analyses, for the simple case of an invasion scenario involving one native population and two independently introduced populations. We chose to simulate this scenario because it is the sole one that can be rejected when obtaining a particular clustering with a STRUCTURE analysis at K = 2 (Fig. 1). We simulated a large number of microsatellite datasets drawn from populations of various effective sizes and bottleneck severities. STRUCTURE analyses were performed on these simulated datasets and the resulting clustering patterns at K = 2 were classified as “misleading” or “non-misleading”. We then explored the effect of demographic parameters on the likelihood of misleading patterns being obtained, to identify and predict the situations in which the use of STRUCTURE in a context of introduction routes inference may be risky.
Methods
Scenario description and data simulation
We chose to simulate a scenario with two independent introductions because it is the only one that can be rejected from a STRUCTURE analysis when considering two introduced populations and a native one (Fig. 1). We thus defined a simple historical scenario in which two invasive populations (populations 2 and 3) were independently founded 50 generations ago from the same native population (population 1). Both invasive populations were subjected to a demographic bottleneck lasting 20 generations (Fig. 2a). The effective sizes of all three populations at equilibrium (N) and the effective number of founders of the two invasive populations during the bottlenecks (NF) could take different values: 10000, 1000, 100, 10, and 2 individuals, with N ≥ NF. Log10(N/NF) was considered to quantify bottleneck severity.
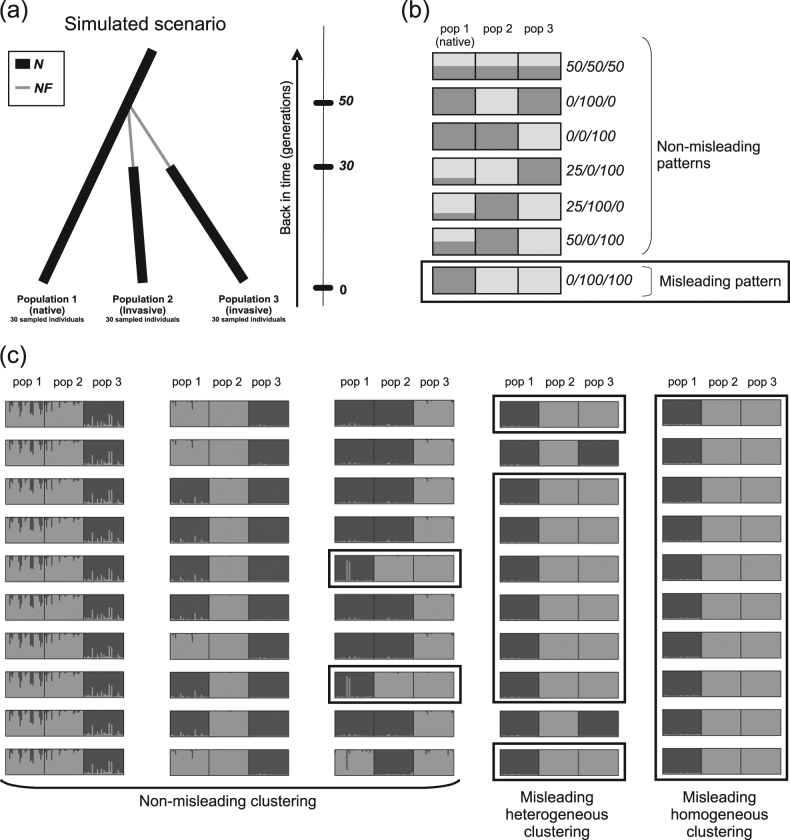
Fig. 2.
Simulated scenario and main observed STRUCTURE patterns at K = 2. a Graphical representation of the simulated scenario in which two invasive populations (populations 2 and 3) are independently derived from the native population (population 1). N is the effective size at equilibrium and NF is the effective number of founders during the bottlenecks. b Schematic representations of the main patterns obtained in the STRUCTURE runs for K = 2 and their associated summarized codes. The misleading pattern, inconsistent with the simulated scenario, is boxed. c Five examples of clusterings obtained over ten STRUCTURE runs for K = 2, and their associated classification. In this study, we focused on “misleading homogeneous clusterings” and “misleading heterogeneous clusterings”, in which “misleading patterns” were found in all ten runs or predominated, respectively, for a given dataset. Runs displaying the misleading pattern are boxed
We used DIYABC version 2.0.4 software (Cornuet et al. 2014) to generate microsatellite multilocus genotype datasets through a coalescent process. We evaluated the effect of the number of loci on the analyses, by performing simulations with 10, 20, or 100 unlinked microsatellite markers. For each combination of N, NF, and number of loci, a total of 500 replicate datasets were generated. For all datasets, a sample of 30 diploid individuals per population was simulated. We used a generalized stepwise mutation model, with realistic values for all three parameters (Jarne and Lagoda 1996; Estoup et al. 2002): the mean mutation rate (set to 5 × 10−4), the mean parameter of the geometric distribution defining the number of microsatellite repeats gained or lost during mutation events (set to 0.22) and the mean mutation rate for single-nucleotide insertion/deletion (set to 10−8). In total, we simulated 22,500 datasets (15 sets of parameters × 3 numbers of loci × 500 replicate datasets). We developed a pipeline with PERL scripts, available at https://doi.org/10.5281/zenodo.1002658, to automate the processing of the datasets (simulations and subsequent STRUCTURE and post-STRUCTURE analyses).
STRUCTURE analyses and misleading clustering
For each of the 22,500 simulated datasets, a Bayesian clustering analysis was performed in parallel, on a 120-cores computer cluster, with STRUCTURE software version 2.3.4 (Pritchard et al. 2000). We chose the admixture model with correlated allele frequencies and no linkage between loci. We used default values for all the other parameters. Each run consisted of a burn-in period of 105 Markov chain Monte Carlo (MCMC) iterations, followed by 5 × 105 MCMC iterations. This run length is considered to be long enough to obtain precise estimates of parameters (Pritchard et al. 2010), but we also tried runs of double this length for some combinations of parameters with 100 loci. The results obtained were the same (data not shown). We carried out ten replicate runs for each dataset and each value of K, the number of genetic clusters, with K taking values of 1, 2, 3 and 4. Although K = 2 constituted the focal analysis of our study, we tested multiple values of K in order to infer its most likely value as follow: for each dataset, if the mean natural logarithm of the likelihood of the data ln(P(X|K)) was maximal for K = 1, then the inferred number of clusters was 1; otherwise, we determined the best value of K (either K = 2 or K = 3) by the ΔK method (Evanno et al. 2005).
We investigated the ability of STRUCTURE to clarify introduction routes by focusing on K = 2 analyses. With K = 2, the two samples from an introduced population may or may not cluster together. With the scenario simulated here, in which the two invasive populations result from two independent introductions, the two samples of the introduced populations would not be expected to cluster together (Fig. 1). Indeed, the two independent drift pulses at work during these two introductions (i.e., the bottleneck events) should make the introduced populations more genetically different from each other than from the native population, from which they are separated by a single drift pulse. Consequently, STRUCTURE would yield a misleading pattern if the native population sample belonged to one cluster and the two invasive population samples both belonged to the other at K = 2. Indeed, this could be considered evidence for a lack of independence of the two populations, with one invasive population being the source of the other (Figs. 1 and 2b). Such a clustering pattern, hereafter referred to as “misleading clustering”, would lead most STRUCTURE users to an incorrect interpretation, according to which a “serial introductions” scenario would be more likely than the “independent introductions” scenario. Note that STRUCTURE analyses carried out on three population samples with K = 3 are, theoretically, unsuitable for comparisons of independent and serial introductions scenarios, because each population sample would probably form its own cluster (Fig. 1).
For analysis of the 225,000 STRUCTURE runs with K = 2 and estimation of the frequency of misleading clusterings, the STRUCTURE output was characterized as follows. From the output file of each run, we extracted the proportion of membership QiA and QiB of population sample i for clusters A and B, respectively (with QiB = 1–QiA). The QiA and QiB values were coded as 0, 25, 50, 75, or 100 when belonging to the [0;0.2],]0.2;0.4[, [0.4;0.6],]0.6;0.8 [or [0.8;1] intervals, respectively. For each STRUCTURE run, we summarized the clustering pattern by a code C1A/C2A/C3A, where CiA is the membership code of population sample i for cluster A. For example, the clustering code would be 0/0/100 for a STRUCTURE run output in which Q1A = 0.12, Q2A = 0.05, and Q3A = 0.96. Note that belonging to cluster A or B has no specific meaning, and the subscripts A and B can thus be permuted. For example, clustering codes 0/0/100 and 100/100/0 summarize the same pattern and are pooled together as 0/0/100. Given the simulated scenario of independent introductions of the two invasive populations, 0/100/100 was the code considered to correspond to misleading clustering (Fig. 2b). All other clustering codes were considered non-misleading in the context of introduction routes inference. Focusing on the codes instead of the proportions of membership made it possible to pool together slightly different clustering patterns in the same category.
Given the stochastic processes involved in the MCMC analysis, the ten replicated STRUCTURE runs performed on a single dataset could conceivably generate different results, a phenomenon called genuine multimodality (Jakobsson and Rosenberg 2007; Porras-Hurtado et al. 2013). Clustering results for a given dataset were considered to be homogeneous if the same clustering code (as defined above) was obtained in all ten runs. They were otherwise considered to be heterogeneous. We evaluated the global occurrence of misleading clustering in the analyses of the simulated datasets, and focused on two critical categories of misleading clusterings (Fig. 2c):
-
(i)
“Misleading homogeneous clusterings”: for one dataset, all ten runs homogeneously provide the misleading clustering pattern 0/100/100.
-
(ii)
“Misleading heterogeneous clusterings”: for one dataset, the ten runs are not homogeneous (i.e., genuine multimodality is observed) and the misleading clustering pattern 0/100/100 predominates.
In addition, we quantified the proportion of datasets for which the most frequent clustering pattern was also represented by the run with the highest log-likelihood of the data.
Effect of demographic parameter values on misleading clustering
For each number of simulated microsatellite loci (10, 20, or 100), the variables “proportion of analyses yielding misleading homogeneous clusterings” and “proportion of analyses yielding misleading heterogeneous clusterings” were analyzed independently with a generalized linear model, using a binomial probability distribution of the residual error and a logit link function. The following factors were included as fixed effects: effective population size N and bottleneck severity log10(N/NF). We used the Akaike information criterion (AIC) to select the best model from the various models of different complexity. Analyses were performed with R software V3.2.2 (R Development Core Team 2015).
Link between summary statistics of genetic diversity and STRUCTURE patterns
We summarized each simulated dataset, by using ARLSUMSTAT version 3.5 software (Excoffier and Lischer 2010) to compute the mean number of alleles and the mean expected heterozygosity in each population sample, and the pairwise FST values between each pair of populations. We also used in-house PERL scripts to compute (i) the mean individual assignment likelihood (Rannala and Mountain 1997) (Li→j) of each invading population (samples 2 and 3) to each possible source population (i.e., either the native population or the other invasive population), and (ii) the number of alleles shared by the invasive population samples.
For the comparison of datasets leading to “misleading homogeneous clusterings”, “misleading heterogeneous clusterings” and “non-misleading clusterings”, we specifically explored a few genetic diversity summary statistics: (i) expected heterozygosity of the native population sample, (ii) mean expected heterozygosity of both invasive population samples and (iii) the ratio of alleles shared by the two invasive population samples to the total number of alleles in the two samples. For each summary statistic and each number of loci, pairwise Mann–Whitney tests with Holmes correction for multiple comparisons were performed.
We also compared STRUCTURE results with those obtained by two other methods traditionally used to identify source populations: (i) the “FST-based method” and (ii) the “assignment likelihood-based method” (Genton et al. 2005; Pascual et al. 2007; Ciosi et al. 2008; Tepolt et al. 2009; Thibault et al. 2009; Papura et al. 2012; Mallez et al. 2015; Dieni et al. 2016). For an “independent introductions” scenario, we would expect the FST between the two invasive population samples to be larger than the FST values between the native population and each of the invasive population samples (i.e., FST 2–3 > FST 1–2 and FST 2–3 > FST 1–3). We would also expect both invasive population samples to be best assigned to the native population sample (i.e., L2→1 > L2→3 and L3→1 > L3→2).
For each dataset, a global exact test for population genotypic differentiation (Raymond and Rousset 1995a) was carried out with GENEPOP software version 4.3 (Raymond and Rousset 1995b). If a dataset displayed no population differentiation, we made the prudent and standard decision of not trying to infer any evolutionary relationship between the population samples. Consequently, such datasets were considered to generate non-misleading results for all methods.
Results
Effect of demographic parameter values on simulated datasets
The 500 simulated datasets for each parameter set are summarized with some common statistics in Table S1. Decreasing effective population sizes (N) generate lower intra-population and higher inter-population genetic diversities. Increasing bottleneck severity (log10(N/NF)) generates lower intra-population genetic diversities for both invasive samples, and overall higher inter-population genetic diversity. The main impact of a larger number of loci is a decrease in the variance of all summary statistics. Overall, the chosen parameter values (for N and NF) yield a large number of different combinations of genetic diversity for evaluation of the ability of STRUCTURE software to explore introduction routes in different situations.
Overall STRUCTURE results
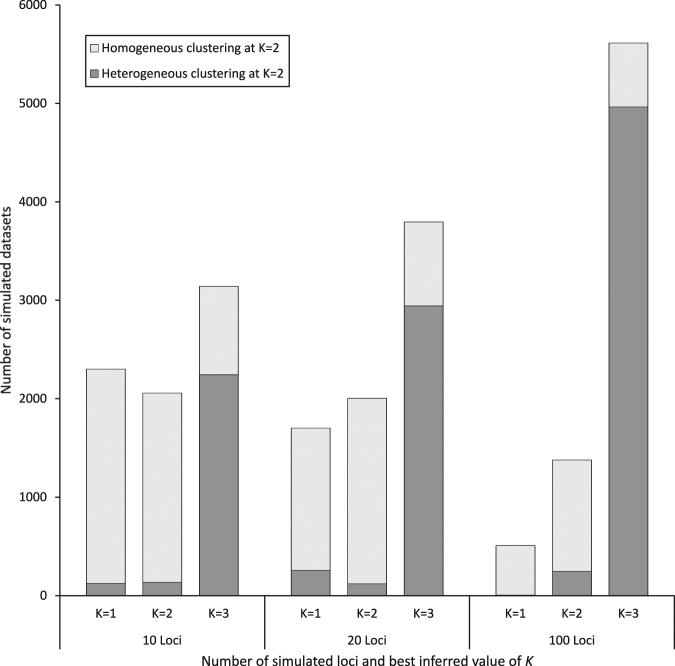
The best value of K inferred was most frequently three (Fig. 3 and Fig. S1). The proportion of datasets for which the best number of clusters was K = 3 increased strongly with increasing numbers of loci (41.9, 50.6, and 74.9% for 10, 20, and 100 loci, respectively). More than 80% of the simulated datasets for which K = 3 was inferred by the ΔK method had heterogeneous clustering codes (i.e., genuine multimodality) at K = 2 (Fig. 3). By contrast, when the number of inferred clusters was one or two, multimodality at K = 2 was found in less than 10% of all datasets.
Fig. 3.
Distribution of the best number of clusters K inferred by Evanno’s method for each number of loci, and the proportion for which there was an absence (homogeneous clustering) or presence (heterogeneous clustering) of genuine multimodality in the ten STRUCTURE runs carried out at K = 2
Occurrence of misleading STRUCTURE patterns
Three categories of clustering codes at K = 2 accounted for more than 95% of all runs (see Table S2 for details): (i) clusterings in which all populations were fully admixed and undistinguishable with STRUCTURE (i.e., the 50/50/50 code), (ii) clusterings in which the two invasive samples belonged to different clusters (i.e., the C1A/100/0 and C1A/0/100 codes) and (iii) the misleading clusterings defined earlier (see Methods), in which the two invasive samples belonged to the same cluster, whereas the native sample belonged to the other cluster (i.e., the 0/100/100 code, Fig. 2b).
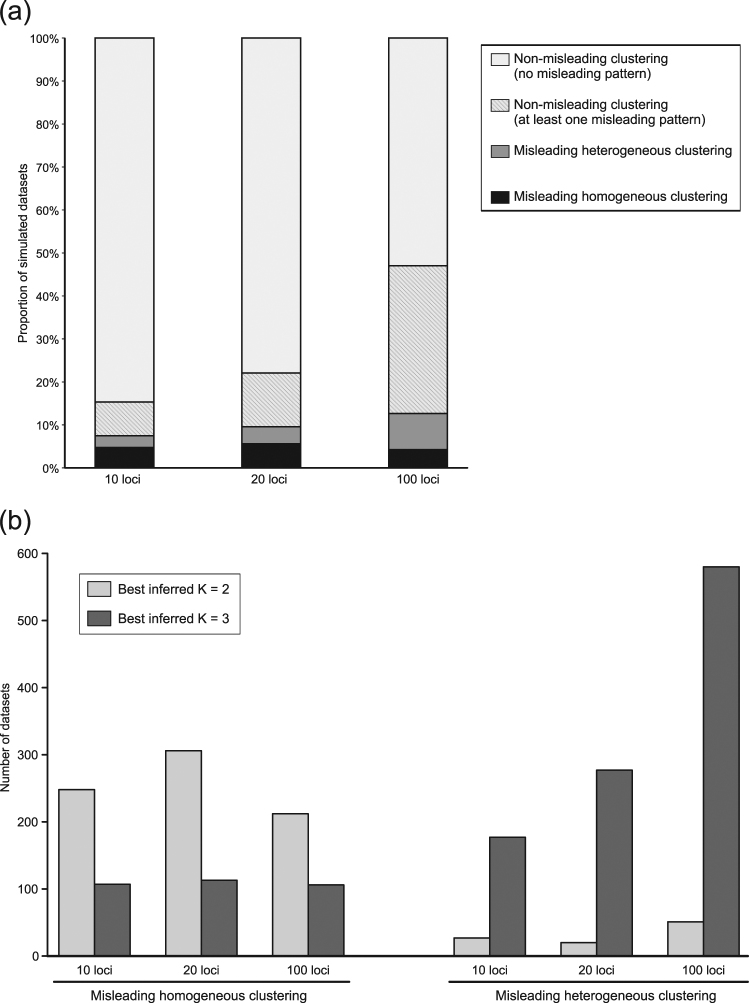
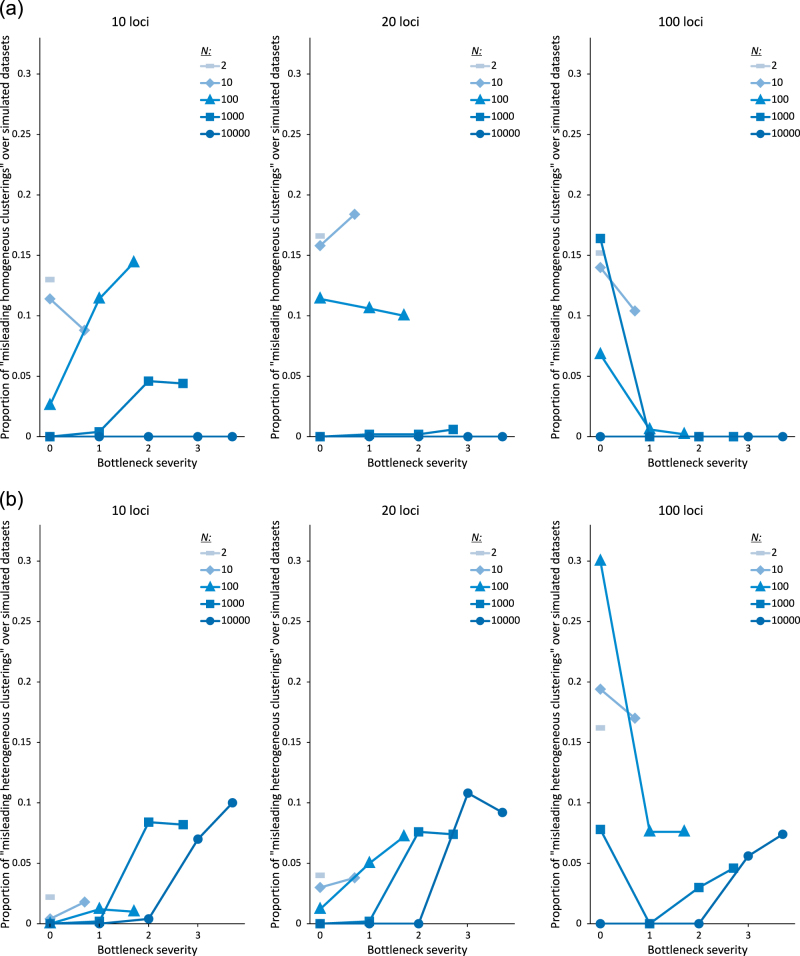
Overall, the proportion of datasets with at least one misleading clustering pattern over the ten STRUCTURE runs (“misleading homogeneous clusterings”, “misleading heterogeneous clusterings” and non-misleading clusterings with at least one run yielding a misleading pattern) was 15.31, 22.07, and 47.01% for 10, 20, and 100 simulated loci, respectively (Fig. 4a and Fig. S2), and very similar proportions were obtained with more (0.1 and 0.9) and less (0.3 and 0.7) stringent QiA cutoff values (instead of 0.2 and 0.8 for QiA) for the encoding of pattern results (Table S3).
Fig. 4.
a Proportion of datasets with and without misleading patterns (Fig. 2b) for the ten STRUCTURE runs at K = 2. b Best inferred number of clusters K obtained by Evanno’s method for each number of loci within the datasets displaying misleading homogeneous (left) and misleading heterogeneous clusterings (right)
The frequency of “misleading homogeneous clusterings” was similar for different numbers of loci, and was rather low overall (between 4.24 and 5.59% of the datasets, Fig. 4a). “Misleading heterogeneous clusterings” were also infrequent, but their frequency increased with the number of loci: 2.71, 3.96, and 8.41% for 10, 20, and 100 loci, respectively (Fig. 4a). Overall, 7.45, 9.55, and 12.65% of datasets for 10, 20, and 100 loci, respectively, yielded misleading results. For some combinations of parameters, this proportion reached 36.8% of datasets (Fig. S2). K = 2 was most often (70%) inferred for datasets yielding “misleading homogeneous clusterings”, and K = 3 was most often (91%) inferred for datasets leading to “misleading heterogeneous clusterings” (Fig. 4b).
For 85.8% of all datasets, the code of the run with the highest log-likelihood of the data was the code that predominates over the 10 runs. However, this proportion dropped to only 40.5% when considering specifically the datasets displaying “Misleading heterogeneous clusterings”.
Effect of demographic parameter values on STRUCTURE results
For the response variable “proportion of analyses yielding misleading homogeneous clusterings”, the best model according to the AIC always included the effective population size at equilibrium N, which was highly significant whatever the number of simulated loci (Table 1). Lower N values resulted in a higher proportion of misleading homogeneous clusterings (Fig. 5a). The best model also included bottleneck severity, log10(N/NF), and the interaction between the two main factors for 10 and 100 loci. Bottleneck severity was significant only for 10 loci, and had a positive effect: the stronger the bottleneck, the higher the proportion of misleading homogeneous clusterings. The interaction between the two factors was significant in both models (Table 1 and Fig. 5a).
Table 1.
Results obtained with the best model selected from the various statistical models run for the response variables “proportion of analyses yielding homogeneous misleading clusterings” and “proportion of analyses yielding heterogeneous misleading clusterings”
| Response variable | Number of loci | Factors of selected model | Estimate | Std error | z-value (df = 7499) | P |
|---|---|---|---|---|---|---|
| Proportion of analyses yielding homogeneous misleading clusterings | ||||||
| 10 | N | −0.004 | 0.0005 | −7.931 | <0.0001 | |
| log10(N/NF) | 0.399 | 0.084 | 4.746 | <0.0001 | ||
| N x log10(N/NF) | 0.001 | 0.0002 | 5.185 | <0.0001 | ||
| 20 | N | −0.005 | 0.0005 | −9.658 | <0.0001 | |
| 100 | N | −0.0003 | 0.00006 | −5.757 | <0.0001 | |
| log10(N/NF) | −0.194 | 0.259 | −0.749 | 0.4540 | ||
| N × log10(N/NF) | −0.028 | 0.005 | −5.190 | <0.0001 | ||
| Proportion of analyses yielding heterogeneous misleading clusterings | ||||||
| 10 | N | −0.0002 | 0.00007 | −3.496 | 0.0005 | |
| log10(N/NF) | 1.107 | 0.114 | 9.672 | <0.0001 | ||
| N × log10(N/NF) | 0.00004 | 0.00002 | 1.827 | 0.0677 | ||
| 20 | N | −0.0004 | 0.00006 | −5.977 | <0.0001 | |
| log10(N/NF) | 0.574 | 0.079 | 7.178 | <0.0001 | ||
| N × log10(N/NF) | 0.00009 | 0.00002 | 4.854 | <0.0001 | ||
| 100 | N | −0.0009 | 0.0001 | −9.666 | <0.0001 | |
| log10(N/NF) | −0.801 | 0.068 | −11.715 | <0.0001 | ||
| N × log10(N/NF) | 0.0003 | 0.00003 | 11.245 | <0.0001 | ||
Note: Significant P-values, for a 5% threshold of significance, are shown in bold
Fig. 5.
Proportion of simulated datasets yielding (a) misleading homogeneous clusterings and (b) misleading heterogeneous clusterings as a function of the parameters “effective population size at equilibrium” (N) and “bottleneck severity” (log10(N/NF)). Each proportion was calculated for 500 datasets
For the response variable “proportion of analyses yielding misleading heterogeneous clusterings”, the full model was selected for all numbers of simulated loci (Table 1). The effective population size at equilibrium N was significant in all cases, and had a negative effect (Fig. 5b). Bottleneck severity log10(N/NF) was also strongly significant for all numbers of loci, but its effect was positive for 10 and 20 loci and negative for 100 loci. The interaction between the two factors was significant for 20 and 100 loci, with a positive effect (Table 1).
Links between summary statistics for genetic diversity and STRUCTURE patterns
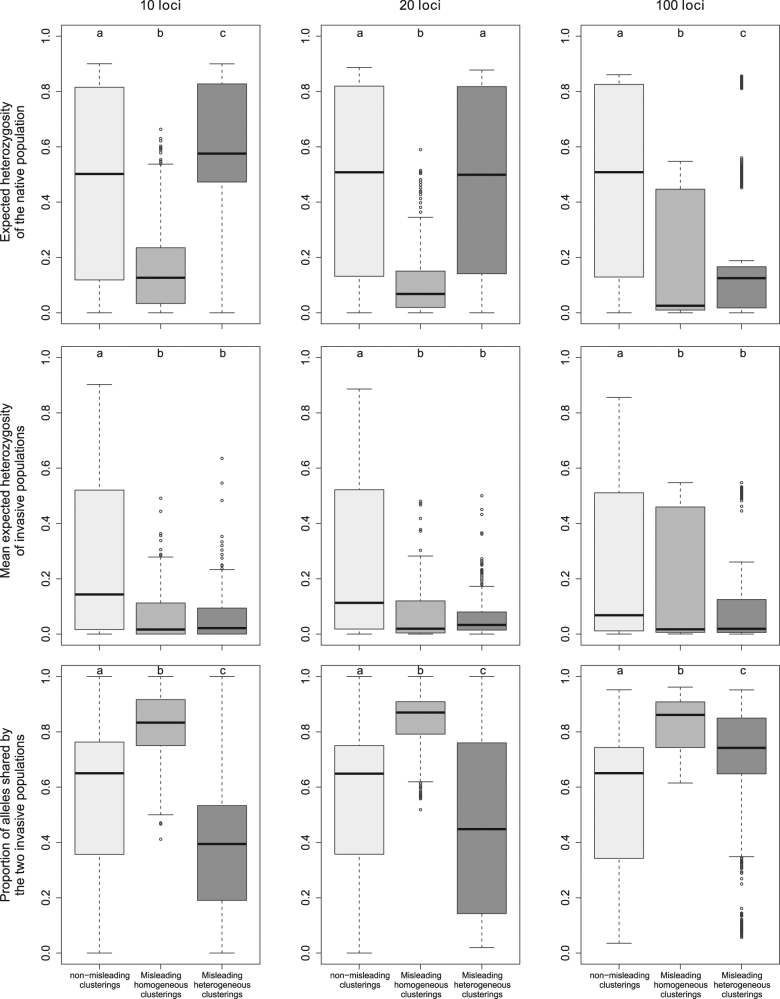
The diversity of the native population, as assessed by its expected heterozygosity in the datasets with “misleading homogeneous clusterings”, was significantly lower than that for “non-misleading” datasets, with median values ranging from 0.025 to 0.126 depending on the number of loci considered (Fig. 6). On the contrary, no clear trend could be observed for datasets with “misleading heterogeneous clusterings”. For these datasets, the mean expected heterozygosity was relatively high with 10 loci, intermediate with 20 loci and low with 100 loci, but, in each case, extreme low and high values were observed. The diversity of invasive populations, which was affected by both the diversity of the native population and bottleneck severity, was low for both kinds of misleading clusterings (Fig. 6). In comparisons with the “non-misleading” datasets, the proportion of alleles shared by the two invasive populations was higher for the datasets with “misleading homogeneous clusterings” regardless of the number of loci, and lower for “misleading heterogeneous clusterings”, except for 100 loci for which it was higher (Fig. 6).
Fig. 6.
Tukey boxplots representing population genetics summary statistics for simulated datasets yielding non-misleading clusterings, misleading homogeneous clusterings or misleading heterogeneous clusterings. Within each frame, plots labeled with different letters are significantly different at the 5% level of significance (Mann–Whitney tests)
Outcomes for comparisons of STRUCTURE clusterings with results from FST-based and assignment likelihood-based methods were very mixed, depending on the type of “misleading clusterings” considered. 86.5, 93.6, and 99.1% of datasets with “misleading homogeneous clusterings” in STRUCTURE provided misleading results with at least one of the methods based on FST or assignment likelihood, when considering 10, 20, and 100 loci, respectively (Fig. 7). By contrast, datasets with “misleading heterogeneous clusterings” in STRUCTURE analysis were rarely (for 10 and 20 loci), or at least not as strongly (for 100 loci), associated with misleading results with the other methods: this was the case for 15.2, 24.9, and 67.5% of these datasets for 10, 20, and 100 loci, respectively (Fig. 7). Note that, overall, STRUCTURE generates less misleading results than the other two methods, while the assignment likelihood-based method generates the worse results.
Fig. 7.
Venn diagrams illustrating the distribution of misleading results for three methods: the FST-based method, the assignment likelihood-based method, and STRUCTURE. Each diagram was produced with 7,500 datasets. The Venn diagrams on the left correspond to homogeneous misleading clustering with STRUCTURE, whereas those on the right correspond to heterogeneous misleading clustering with STRUCTURE
Discussion
We used simulated microsatellite datasets for a particular invasion scenario to determine whether the method implemented in the widely used STRUCTURE software (Pritchard et al. 2000) could mislead users trying to infer introduction routes. We focused on a scenario with two independent introductions from a native population because this scenario can be rejected when obtaining some particular clustering results, which is not true for serial introductions scenarios when the chronology of introductions is not known. We found that, for a true scenario of two independent invasions from a single source, STRUCTURE runs could give misleading clustering patterns (i.e., the two invasive populations clustered together at K = 2). In about 10% of all simulated datasets, the results led to incorrect interpretation, with all (“homogeneous misleading clusterings”) or most (“heterogeneous misleading clusterings”) of the runs for a given dataset yielding the misleading pattern. Some combinations of demographic parameters resulted in higher frequencies of misleading results with STRUCTURE, and increasing the number of loci also led to an overall increase in the frequency of misleading results. Our results suggested that the two types of misleading clustering hazard, homogeneous and heterogeneous misleading clusterings, were very different. We suggest that (i) “homogeneous misleading clusterings” probably arise from a large probability of independently drawing the same alleles twice from a native population with low genetic diversity and that (ii) “heterogeneous misleading clusterings” probably randomly arise from convergence problems in STRUCTURE.
For “homogeneous misleading clustering”, the effective size of the native population has the strongest effect: the smaller this effective population size, the higher the risk of obtaining misleading clustering patterns over all STRUCTURE runs. Such “homogeneous misleading clusterings” occurred principally when the two invasive populations were very alike: they shared a large proportion of alleles, and the FST-based and likelihood assignment-based methods frequently yielded the same clustering pattern. Accordingly, the number of clusters inferred by the Evanno’s method was most frequently K = 2, which was not expected given the three-population simulated scenario. Invasive populations encounter founder effects and genetic drift (Simberloff 2009; Lawson Handley et al. 2011), which are random processes. In this context, the probability of independently drawing the same allele twice from a given native population is directly dependent on its frequency. This probability is equal to the expected homozygosity of the considered allele, and is therefore rather low when the number of allele is high, but can actually get large when the diversity is limited. As a matter of fact, “homogeneous misleading clusterings” were observed with datasets in which the native population displayed a very low expected heterozygosity, implying that there were only one or a few highly frequent alleles at each locus (Allendorf 1986).
The interpretation of “heterogeneous misleading clusterings” is less clear-cut, but several lines of evidence suggest the involvement of convergence issues in STRUCTURE runs. Indeed, “heterogeneous misleading clusterings” at K = 2 most often occurred when the best K value was undoubtedly 3, which corresponds to the true number of population. More generally, this category of misleading clusterings was associated with a better ability to differentiate the three populations. This may explain why the proportion of “heterogeneous misleading clusterings” was higher for a larger number of loci, for which more information is available to properly differentiate populations (Evanno et al. 2005; Waples and Gaggiotti 2006; Hubisz et al. 2009). This is indeed entirely consistent with what is observed in the context of genome-scale phylogenies in which a larger amount of data is known to exacerbate the potential for bias to be misleading when the model used to describe the data is not properly chosen (Phillips et al. 2004; Rodríguez-Ezpeleta et al. 2007; Kumar et al. 2012). Besides, for 10 and 20 simulated loci, the proportion of “heterogeneous misleading clusterings” was positively related to bottleneck severity, which accentuates differences between populations. Overall, we suggest that “heterogeneous misleading clustering” probably results from a convergence problem in the MCMC procedure of STRUCTURE: when an inappropriate number of clusters is imposed—here K = 2 whereas the data are more consistent with K = 3—multimodalities are often observed (Pritchard et al. 2000; Jakobsson and Rosenberg 2007), and sometimes, by chance, a large proportion of misleading clustering events occur in the various runs, resulting in “heterogeneous misleading clusterings”. The important role of randomness is further supported by the weak association between such clusterings and the log-likelihood of the data.
Conclusion and general recommendations
This study was based on a single simple invasion scenario with only three populations. More complex scenarios should be studied in the future, for example by increasing the number of native populations, including admixture or isolation by distance, or manipulating divergence times, but this study constitutes a crucial first step, providing important information about the use of clustering methods in the context of biological invasions.
We found that STRUCTURE yielded misleading results, but at a low frequency. However, our results suggest that some situations should be analyzed with care. First, invasion biologists should be very cautious if the diversity of the native population is low: independent introductions from a single source population with low genetic diversity are likely to produce genetic signals similar to that expected for serial introductions. Such misleading results are difficult to spot, as they are consistent with the results of other methods, such as FST- or assignment likelihood-based methods. In this context, quantitative methods may be very useful. Approximate Bayesian calculation, for example, has proven to be very powerful in a very similar context (Guillemaud et al. 2010). Second, multimodal STRUCTURE results should be interpreted very cautiously, particularly if large numbers of loci are used. This is sobering news, because many published studies interpret STRUCTURE results at different K values, including those displaying genuine multimodality. This problem is not specific to the exploration of introduction routes and has much wider implications (Meirmans 2015). Multimodality is often a sign of poor convergence of STRUCTURE runs, and is therefore likely to lead to results of limited biological meaning. In such situations, other methods (e.g., FST-based, assignment likelihood-based or principal component analysis) may make it possible to determine whether the STRUCTURE results are misleading or not. Also, the log-likelihood of the data estimated by the software may help to reject a meaningless clustering, but this statistic should be interpreted with great care (Jakobsson and Rosenberg 2007). More generally, it is important to keep in mind that STRUCTURE results have to be interpreted cautiously (Pritchard et al. 2010) and, in the context of invasion routes inferences, it should rather be used as a tool to clarify the scenery and decrease the number of genetic units from a large number of population samples to a few main clusters before quantitative analyses, such as approximate Bayesian computation, are performed (Lombaert et al. 2014).
Data accessibility
Simulated datasets, STRUCTURE outputs and the home-made PERL pipeline used to simulate, analyze, and post-process the data were deposited at Zenodo: https://doi.org/10.5281/zenodo.1002658.
Electronic supplementary material
Acknowledgements
We thank Margarita Correa, Arnaud Estoup, Thibaut Malausa, and Ferran Palero for fruitful comments and discussions. We also thank Alexandre Dehne-Garcia for assistance with the computer cluster.
Author contributions
E.L., T.G., and E.D. conceived and designed the study. E.D. wrote the scripts and ran the simulations and analyses. E.L. and E.D. analyzed the data. E.L., T.G., and E.D. wrote the paper.
Compliance with ethical standards
Conflict of interest
The author declares that they have no competing interests.
Footnotes
Electronic supplementary material
The online version of this article (10.1038/s41437-017-0042-1) contains supplementary material, which is available to authorized users.
References
- Allendorf FW. Genetic drift and the loss of alleles versus heterozygosity. Zoo Biol. 1986;5:181–190. doi: 10.1002/zoo.1430050212. [DOI] [Google Scholar]
- Anderson EC, Dunham KK. The influence of family groups on inferences made with the program Structure. Mol Ecol Resour. 2008;8:1219–1229. doi: 10.1111/j.1755-0998.2008.02355.x. [DOI] [PubMed] [Google Scholar]
- Ascunce MS, Yang CC, Oakey J, Calcaterra L, Wu WJ, Shih CJ, et al. Global invasion history of the fire ant Solenopsis invicta. Science. 2011;331:1066–1068. doi: 10.1126/science.1198734. [DOI] [PubMed] [Google Scholar]
- Bolte S, Fuentes V, Haslob H, Huwer B, Thibault-Botha D, Angel D, et al. Population genetics of the invasive ctenophore Mnemiopsis leidyi in Europe reveal source–sink dynamics and secondary dispersal to the Mediterranean Sea. Mar Ecol Prog Ser. 2013;485:25–36. doi: 10.3354/meps10321. [DOI] [Google Scholar]
- Ciosi M, Miller NJ, Kim KS, Giordano R, Estoup A, Guillemaud T. Invasion of Europe by the western corn rootworm, Diabrotica virgifera virgifera: multiple transatlantic introductions with various reductions of genetic diversity. Mol Ecol. 2008;17:3614–3627. doi: 10.1111/j.1365-294X.2008.03866.x. [DOI] [PubMed] [Google Scholar]
- Cordero D, Delgado M, Liu B, Ruesink J, Saavedra C. Population genetics of the Manila clam (Ruditapes philippinarum) introduced in North America and Europe. Sci Rep. 2017;7:39745. doi: 10.1038/srep39745. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cornuet JM, Pudlo P, Veyssier J, Dehne-Garcia A, Gautier M, Leblois R, et al. DIYABCv2.0: a software to make approximate Bayesian computation inferences about population history using single nucleotide polymorphism, DNA sequence and microsatellite data. Bioinformatics. 2014;30:1187–1189. doi: 10.1093/bioinformatics/btt763. [DOI] [PubMed] [Google Scholar]
- Cristescu ME. Genetic reconstructions of invasion history. Mol Ecol. 2015;24:2212–2225. doi: 10.1111/mec.13117. [DOI] [PubMed] [Google Scholar]
- Dieni A, Brodeur J, Turgeon J. Reconstructing the invasion history of the lily leaf beetle, Lilioceris lilii, in North America. Biol Invasions. 2016;18:31–44. doi: 10.1007/s10530-015-0987-z. [DOI] [Google Scholar]
- Estoup A, Guillemaud T. Reconstructing routes of invasion using genetic data: why, how and so what? Mol Ecol. 2010;19:4113–4130. doi: 10.1111/j.1365-294X.2010.04773.x. [DOI] [PubMed] [Google Scholar]
- Estoup A, Jarne P, Cornuet JM. Homoplasy and mutation model at microsatellite loci and their consequences for population genetics analysis. Mol Ecol. 2002;11:1591–1604. doi: 10.1046/j.1365-294X.2002.01576.x. [DOI] [PubMed] [Google Scholar]
- Evanno G, Regnaut S, Goudet J. Detecting the number of clusters of individuals using the software STRUCTURE: a simulation study. Mol Ecol. 2005;14:2611–2620. doi: 10.1111/j.1365-294X.2005.02553.x. [DOI] [PubMed] [Google Scholar]
- Excoffier L, Lischer HEL. Arlequin suite ver 3.5: a new series of programs to perform population genetics analyses under Linux and Windows. Mol Ecol Resour. 2010;10:564–567. doi: 10.1111/j.1755-0998.2010.02847.x. [DOI] [PubMed] [Google Scholar]
- Falush D, Stephens M, Pritchard JK. Inference of population structure using multilocus genotype data: Linked loci and correlated allele frequencies. Genetics. 2003;164:1567–1587. doi: 10.1093/genetics/164.4.1567. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fontaine MC, Gladieux P, Hood ME, Giraud T. History of the invasion of the anther smut pathogen on Silene latifolia in North America. New Phytol. 2013;198:946–956. doi: 10.1111/nph.12177. [DOI] [PubMed] [Google Scholar]
- Frantz AC, Cellina S, Krier A, Schley L, Burke T. Using spatial Bayesian methods to determine the genetic structure of a continuously distributed population: clusters or isolation by distance? J Appl Ecol. 2009;46:493–505. doi: 10.1111/j.1365-2664.2008.01606.x. [DOI] [Google Scholar]
- Genton BJ, Shykoff JA, Giraud T. High genetic diversity in French invasive populations of common ragweed, Ambrosia artemisiifolia, as a result of multiple sources of introduction. Mol Ecol. 2005;14:4275–4285. doi: 10.1111/j.1365-294X.2005.02750.x. [DOI] [PubMed] [Google Scholar]
- Guillemaud T, Beaumont MA, Ciosi M, Cornuet JM, Estoup A. Inferring introduction routes of invasive species using approximate Bayesian computation on microsatellite data. Heredity. 2010;104:88–99. doi: 10.1038/hdy.2009.92. [DOI] [PubMed] [Google Scholar]
- Guillemaud T, Blin A, Le Goff I, Desneux N, Reyes M, Tabone E, et al. The tomato borer, Tuta absoluta, invading the Mediterranean Basin, originates from a single introduction from Central Chile. Sci Rep. 2015;5:8371. doi: 10.1038/srep08371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guillemaud T, Ciosi M, Lombaert E, Estoup A. Biological invasions in agricultural settings: Insights from evolutionary biology and population genetics. C R Biol. 2011;334:237–246. doi: 10.1016/j.crvi.2010.12.008. [DOI] [PubMed] [Google Scholar]
- Hubisz MJ, Falush D, Stephens M, Pritchard JK. Inferring weak population structure with the assistance of sample group information. Mol Ecol Resour. 2009;9:1322–1332. doi: 10.1111/j.1755-0998.2009.02591.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jakobsson M, Rosenberg NA. CLUMPP: a cluster matching and permutation program for dealing with label switching and multimodality in analysis of population structure. Bioinformatics. 2007;23:1801–1806. doi: 10.1093/bioinformatics/btm233. [DOI] [PubMed] [Google Scholar]
- Jarne P, Lagoda PJL. Microsatellites, from molecules to populations and back. Trends Ecol Evol. 1996;11:424–429. doi: 10.1016/0169-5347(96)10049-5. [DOI] [PubMed] [Google Scholar]
- Kalinowski ST. The computer program STRUCTURE does not reliably identify the main genetic clusters within species: simulations and implications for human population structure. Heredity. 2011;106:625–632. doi: 10.1038/hdy.2010.95. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keller SR, Taylor DR. History, chance and adaptation during biological invasion: separating stochastic phenotypic evolution from response to selection. Ecol Lett. 2008;11:852–866. doi: 10.1111/j.1461-0248.2008.01188.x. [DOI] [PubMed] [Google Scholar]
- Kumar S, Filipski AJ, Battistuzzi FU, Kosakovsky Pond SL, Tamura K. Statistics and truth in phylogenomics. Mol Biol Evol. 2012;29:457–472. doi: 10.1093/molbev/msr202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lachmuth S, Durka W, Schurr FM. The making of a rapid plant invader: genetic diversity and differentiation in the native and invaded range of Senecio inaequidens. Mol Ecol. 2010;19:3952–3967. doi: 10.1111/j.1365-294X.2010.04797.x. [DOI] [PubMed] [Google Scholar]
- Lawson Handley LJ, Estoup A, Evans DM, Thomas CE, Lombaert E, Facon B, et al. Ecological genetics of invasive alien species. Biocontrol. 2011;56:409–428. doi: 10.1007/s10526-011-9386-2. [DOI] [Google Scholar]
- Lombaert E, Guillemaud T, Cornuet JM, Malausa T, Facon B, Estoup A. Bridgehead effect in the worldwide invasion of the biocontrol harlequin ladybird. PLoS One. 2010;5:e9743. doi: 10.1371/journal.pone.0009743. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lombaert E, Guillemaud T, Lundgren J, Koch R, Facon B, Grez A, et al. Complementarity of statistical treatments to reconstruct worldwide routes of invasion: the case of the Asian ladybird Harmonia axyridis. Mol Ecol. 2014;23:5979–5997. doi: 10.1111/mec.12989. [DOI] [PubMed] [Google Scholar]
- Mack RN, Simberloff D, Lonsdale WM, Evans H, Clout M, Bazzaz FA. Biotic invasions: causes, epidemiology, global consequences, and control. Ecol Appl. 2000;10:689–710. doi: 10.1890/1051-0761(2000)010[0689:BICEGC]2.0.CO;2. [DOI] [Google Scholar]
- Mallez S, Castagnone C, Espada M, Vieira P, Eisenback JD, Harrell M, et al. Worldwide invasion routes of the pinewood nematode: What can we infer from population genetics analyses? Biol Invasions. 2015;17:1199–1213. doi: 10.1007/s10530-014-0788-9. [DOI] [Google Scholar]
- Meirmans PG. Seven common mistakes in population genetics and how to avoid them. Mol Ecol. 2015;24:3223–3231. doi: 10.1111/mec.13243. [DOI] [PubMed] [Google Scholar]
- Papura D, Burban C, van Helden M, Giresse X, Nusillard B, Guillemaud T, et al. Microsatellite and mitochondrial data provide evidence for a single major introduction for the neartic leafhopper Scaphoideus titanus in Europe. PLoS One. 2012;7:e36882. doi: 10.1371/journal.pone.0036882. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pascual M, Chapuis MP, Mestres F, Balanya J, Huey RB, Gilchrist GW, et al. Introduction history of Drosophila subobscura in the New World: a microsatellite-based survey using ABC methods. Mol Ecol. 2007;16:3069–3083. doi: 10.1111/j.1365-294X.2007.03336.x. [DOI] [PubMed] [Google Scholar]
- Phillips MJ, Delsuc F, Penny D. Genome-scale phylogeny and the detection of systematic biases. Mol Biol Evol. 2004;21:1455–1458. doi: 10.1093/molbev/msh137. [DOI] [PubMed] [Google Scholar]
- Porras-Hurtado L, Ruiz Y, Santos C, Phillips C, Carracedo A, Lareu MV. An overview of STRUCTURE: applications, parameter settings, and supporting software. Front Genet. 2013;4:98. doi: 10.3389/fgene.2013.00098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pritchard JK, Stephens M, Donnelly P. Inference of population structure using multilocus genotype data. Genetics. 2000;155:945–959. doi: 10.1093/genetics/155.2.945. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pritchard JK, Wen W, Falush D (2010) Documentation for structure software: Version 2. http://pritch.bsd.uchicago.edu.
- Puechmaille SJ. The program STRUCTURE does not reliably recover the correct population structure when sampling is uneven: subsampling and new estimators alleviate the problem. Mol Ecol Resour. 2016;16:608–627. doi: 10.1111/1755-0998.12512. [DOI] [PubMed] [Google Scholar]
- R Development Core Team (2015) R: a language and environment for statistical computing. R Foundation for Statistical Computing,Vienna, Austria. https://www.R-project.org/.
- Rannala B, Mountain JL. Detecting immigration by using multilocus genotypes. Proc Natl Acad Sci USA. 1997;94:9197–9201. doi: 10.1073/pnas.94.17.9197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raymond M, Rousset F (1995a) An exact test for population differentiation. Evolution 49:1280–1283 [DOI] [PubMed]
- Raymond M, Rousset F (1995b) Genepop (version. 1.2), a population genetics software for exact tests and ecumenicism. J Hered 86:248–249
- Rewicz T, Wattier R, Grabowski M, Rigaud T, Bącela-Spychalska K. Out of the black sea: phylogeography of the invasive killer shrimp Dikerogammarus villosus across Europe. PLoS One. 2015;10:e0118121. doi: 10.1371/journal.pone.0118121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robert S, Ravigne V, Zapater MF, Abadie C, Carlier J. Contrasting introduction scenarios among continents in the worldwide invasion of the banana fungal pathogen Mycosphaerella fijiensis. Mol Ecol. 2012;21:1098–1114. doi: 10.1111/j.1365-294X.2011.05432.x. [DOI] [PubMed] [Google Scholar]
- Roderick GK, Navajas M. Genes in new environments: genetics and evolution in biological control. Nat Rev Genet. 2003;4:889–899. doi: 10.1038/nrg1201. [DOI] [PubMed] [Google Scholar]
- Rodríguez-Ezpeleta N, Brinkmann H, Roure B, Lartillot N, Lang BF, Philippe H. Detecting and overcoming systematic errors in genome-scale phylogenies. Syst Biol. 2007;56:389–399. doi: 10.1080/10635150701397643. [DOI] [PubMed] [Google Scholar]
- Rodríguez-Ramilo ST, Toro MA, Wang J, Fernández J. Improving the inference of population genetic structure in the presence of related individuals. Genet Res (Camb) 2014;96:e003. doi: 10.1017/S0016672314000068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rodríguez-Ramilo ST, Wang J. The effect of close relatives on unsupervised Bayesian clustering algorithms in population genetic structure analysis. Mol Ecol Resour. 2012;12:873–84. doi: 10.1111/j.1755-0998.2012.03156.x. [DOI] [PubMed] [Google Scholar]
- Sanz N, Araguas RM, Vidal O, Diez-del-Molino D, Fernández-Cebrián R, García-Marín JL. Genetic characterization of the invasive mosquitofish (Gambusia spp.) introduced to Europe: population structure and colonization routes. Biol Invasions. 2013;15:2333–2346. doi: 10.1007/s10530-013-0456-5. [DOI] [Google Scholar]
- Schwartz MK, McKelvey KS. Why sampling scheme matters: the effect of sampling scheme on landscape genetic results. Conserv Genet. 2009;10:441–452. doi: 10.1007/s10592-008-9622-1. [DOI] [Google Scholar]
- Simberloff D. The role of propagule pressure in biological invasions. Annu Rev Ecol Evol Syst. 2009;40:81–102. doi: 10.1146/annurev.ecolsys.110308.120304. [DOI] [Google Scholar]
- Smith O, Wang J. When can noninvasive samples provide sufficient information in conservation genetics studies? Mol Ecol Resour. 2014;14:1011–1023. doi: 10.1111/1755-0998.12250. [DOI] [PubMed] [Google Scholar]
- Tepolt CK, Darling JA, Bagley MJ, Geller JB, Blum MJ, Grosholz ED. European green crabs (Carcinus maenas) in the northeastern Pacific: genetic evidence for high population connectivity and current-mediated expansion from a single introduced source population. Divers Distrib. 2009;15:997–1009. doi: 10.1111/j.1472-4642.2009.00605.x. [DOI] [Google Scholar]
- Thibault I, Bernatchez L, Dodson JJ. The contribution of newly established populations to the dynamics of range expansion in a one-dimensional fluvial-estuarine system: rainbow trout (Oncorhynchus mykiss) in Eastern Quebec. Divers Distrib. 2009;15:1060–1072. doi: 10.1111/j.1472-4642.2009.00606.x. [DOI] [Google Scholar]
- Waples RS, Gaggiotti O. What is a population? An empirical evaluation of some genetic methods for identifying the number of gene pools and their degree of connectivity. Mol Ecol. 2006;15:1419–1439. doi: 10.1111/j.1365-294X.2006.02890.x. [DOI] [PubMed] [Google Scholar]
- Yu X, He T, Zhao J, Li Q. Invasion genetics of Chromolaena odorata (Asteraceae): extremely low diversity across Asia. Biol Invasions. 2014;16:2351–2366. doi: 10.1007/s10530-014-0669-2. [DOI] [Google Scholar]
- Zhang B, Edwards O, Kang L, Fuller S. A multi-genome analysis approach enables tracking of the invasion of a single Russian wheat aphid (Diuraphis noxia) clone throughout the New World. Mol Ecol. 2014;23:1940–51. doi: 10.1111/mec.12714. [DOI] [PubMed] [Google Scholar]
- Zhou HX, Zhang RM, Tan XM, Tao YL, Wan FH, Wu Q, et al. Invasion genetics of woolly apple aphid (Hemiptera: Aphididae) in China. J Econ Entomol. 2015;108:1040–1046. doi: 10.1093/jee/tov074. [DOI] [PubMed] [Google Scholar]
- Zhu BR, Barrett SCH, Zhang DY, Liao WJ. Invasion genetics of senecio vulgaris: loss of genetic diversity characterizes the invasion of a selfing annual, despite multiple introductions. Biol Invasions. 2017;19:1–13. doi: 10.1007/s10530-016-1266-3. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Simulated datasets, STRUCTURE outputs and the home-made PERL pipeline used to simulate, analyze, and post-process the data were deposited at Zenodo: https://doi.org/10.5281/zenodo.1002658.