History of the fragmentation of the African rain forest in the Dahomey Gap: insight from the demographic history of Terminalia superba

Abstract

Paleo-environmental reconstructions show that the distribution of tropical African rain forests was affected by Quaternary climate changes. They suggest that the Dahomey Gap (DG)—the savanna corridor that currently separates Upper Guinean (UG, West Africa) and Lower Guinean (LG, western Central Africa) rain forest blocks—was forested during the African Humid Holocene period (from at least 9 ka till 4.5 ka), and possibly during other interglacial periods, while an open vegetation developed in the DG under drier conditions, notably during glacial maxima. Nowadays, relics of semi-deciduous forests containing UG and LG forest species are still present within the DG. We used one of these species, the pioneer tree Terminalia superba (Combretaceae), to study past forest fragmentation in the DG and its impact on infraspecific biodiversity. A Bayesian clustering analysis of 299 individuals genotyped at 14 nuclear microsatellites revealed five parapatric genetic clusters (UG, DG, and three in LG) with low to moderate genetic differentiation (Fst from 0.02 to 0.24). Approximate Bayesian Computation analyses inferred a demographic bottleneck around the penultimate glacial period in all populations. They also supported an origin of the DG population by admixture of UG and LG populations around 54,000 (27,600–161,000) years bp, thus before the Last Glacial Maximum. These results contrast with those obtained on Distemonanthus benthamianus where the DG population seems to originate from the Humid Holocene period. We discuss these differences in light of the ecology of each species. Our results challenge the simplistic view linking population fragmentation/expansion with glacial/interglacial periods in African forest species.

Introduction

Past climate changes have presumably played a major role on the diversity and distribution of African tropical forest species. The important climatic oscillations of the Pleistocene, in particular from 1.05 Ma, have caused major fragmentation-expansion cycles of tropical forests around the Gulf of Guinea (Dupont et al. 2001; Miller and Gossling 2014). Their consequences on biodiversity patterns remain, however, little documented (Demenou et al. 2016). One way to better understand the history of past forest fragmentation and their impact on plant diversity is to confront genetic data of forest species from fragmented forest areas to hypotheses deduced from palaeocological data (Demenou et al. 2016).

The dense tropical humid forests from West and Central Africa, which constitutes the Guineo-Congolian phytochorion, is fragmented in two blocks by the Dahomey Gap (DG), a ca. 200 km wide corridor dominated by open vegetation in Benin, Togo and eastern Ghana. Westwards, the Upper Guinean (hereafter UG) rain forest extends from Sierra Leone to Ghana. Eastwards, the Lower Guinean (LG) rain forest extends from southern Nigeria to the Republic of Congo and is followed by the Congolian rain forest (Co) extending through the Democratic Republic of Congo until the Albertine rift in East Africa.

Pollen analyses from marine and lake sediment cores located in and around the DG allow to document vegetation changes during the Holocene and late Pleistocene (Dupont and Weinelt 1996; Tossou 2002; Salzmann and Hoelzmann 2005; Miller and Gossling 2014). In the DG, a core in Lac Sélé reveals that the region was occupied by a closed forest during the mid Holocene (from c. 8400 to 4500 yr bp) but savannas expanded rapidly from 4500 to 3400 cal. yr bp following the Climatic Pejoration of the Holocene (HCP), a dry period characterised by less rainfall and more seasonality (Marchant and Hooghiemstra 2004), and although a return to wetter conditions lead to a forest-savanna mosaic from 3300 to 1100 yr bp, savannas re-expanded and have dominated the DG over the last 1100 yr (Salzmann and Hoelzmann 2005).

The sediment cores collected in the DG do not reach the Last Glacial Maximum (LGM) but Pleistocene paleoenvironments were reconstructed in adjacent forested areas. Lake Bosumtwi in Ghana is particularly interesting because it lies close to the western margin of the DG and is now in a moist semi-deciduous forest area, while it was surrounded by a grassy formation with the presence of mountain forest between 22–9 ka (Giresse et al. 1994). A recent core in this lake encompassing half-million years reveals six main periods of forest vegetation, congruent with those reported in marine core of the Niger delta (Dupont 2011), and which are interpreted as synchronous to the last interglacials, while open vegetation dominated during the glacial periods (Miller and Gossling 2014). A marine core facing the coast of DG also recorded evidence of extended rain forests during the early and mid Holocene and the previous interglacial (130–115 ka), and extended savannas and open woodlands during the last glacial period, particularly between 70 and 15 ka (Dupont and Weinelt 1996). Hence, the DG must have been dominated by an open vegetation during most of the late Quaternary but it became forested during a part of the current interglacial (mid Holocene), when the African rain forest reached its maximal extension to form a single block, and it may have been forested during the peaks of other interglacial periods. We therefore expect that populations of forest species underwent recurrent range shifts, demographic changes, fragmentation or population admixture events during the Quaternary, as forests expanded during interglacials and retreated during glacials, leaving signatures in their genetic structures.

Currently, the DG is constituted mainly of savanna, with fragments of gallery forest, swamp forest and dense semi-deciduous forest that contain typical Guineo-Congolian forest species. The origin of this relict forest flora is unclear but we can propose two hypotheses. (i) Ancestral (before LGM) origin: current DG populations survived the LGM in micro-refugia so that they diverged from UG and/or LG populations before the LGM. (ii) Recent (humid Holocene) origin: current DG populations originate from UG and/or LG when these forest blocks expanded during the Humid Holocene period to cover the DG. These hypotheses can potentially be disentangled by the patterns of genetic variation within and between populations, although UG, LG and DG populations may also have been affected by more recent gene flow, depending on the efficiency of seed and pollen dispersal and their genetic structure might have built up over multiple glacial cycles. Information on dispersal distances, and more generally on the ecological niche of species, is therefore also needed to interpret patterns of genetic variation.

Recent genetic studies performed on African rain forest tree species revealed phylogeographical breaks separating differentiated genetic clusters in most species, suggesting past forest fragmentation (reviewed in Hardy et al. 2013) that occurred in the last 200,000 years according to the few molecular dating studies available (e.g., Demenou et al. 2016; Duminil et al. 2015; Piñeiro et al. 2017). These studies focused on forests from LG and sometimes UG but few of them inferred the origin of forest species in the DG (Ewédjè 2012; Demenou et al. 2016). A study on Distemonanthus benthamianus (Dialioideae, Leguminosae) provided good support for the hypothesis that its DG population derived from a recent admixture of UG and LG populations during the Humid Holocene (13–7 ka) and that it experienced substantial genetic drift due to founder event and/or a population decline during the Holocene climatic pejoration (HCP, around 3 ka; Demenou et al. 2016). Although these results are consistent with paleovegetation data regarding the history of forest cover in the DG, the history of a species is not necessarily that of the forest it inhabits, so that data from several species are needed.

The present study focuses on a pioneer tree species, Terminalia superba Englers et Diels (Combretaceae), which is characteristic of UG and LG semi-deciduous forests. It also occurs in the DG, in isolated forest fragments, gallery forests and in secondary semi-deciduous forests. It is a pioneer light-demanding, upper canopy deciduous tree, wind dispersed, probably pollinated by insects (Raju et al. 2012; Meunier et al. 2015). Our main objective is to determine the origin of DG populations of T. superba in order to better understand the history of the DG. We therefore conducted large-scale genetic analyses of this species and coalescent simulations for demographic inference, using nuclear SSR markers to: (1) determine if the DG, UG and LG populations of T. superba belong to distinct genetic clusters; (2) infer and date signatures of past demographic changes (decline, expansion or bottleneck) in each considered genetic cluster; (3) infer the origin of the DG population (ancestral or recent, UG and/or LG or admixture) and when it separated from its ancestral population(s); (4) determine the gene dispersal distance to assess the colonisation and gene flow potential of this species. All these different objectives, and a comparison between species with different ecological characteristics, could help better understand the history of the forest.

Material and methods

Study species and sampling

Terminalia superba (Combretaceae) is a Guineo-Congolian African pioneer tree naturally distributed from Sierra Leone to the Democratic Republic of Congo. It is representative of tropical secondary semi-deciduous forests (Burkill 1985) with an average annual rainfall exceeding 1500 mm and a dry season of less than 4 months (Orwa et al. 2009). It is also found in recent agricultural fields when it is spared during deforestation. T. superba has been planted in several other countries in Africa, America and Asia, for economical purposes because it shows high growth rates in plantations (Doucet et al. 2016).

It is a big tree up to 50 m in height and 150 cm in stem diameter, which grows 0.7 cm per years and reaches sexual maturity at 40 cm diameter. The inflorescences (7–18 cm) are axillary spikes wearing greenish white flowers. Fruits are small samaras with two rigid lateral wings (1.5–2.5 × 4–7 cm, including the wing) and are mainly dispersed by wind (Orwa et al. 2009; Meunier et al. 2015). They develop during the rainy season and mature at the onset of the dry season, coinciding with the leafless period; the duration of fruiting varies from 6 to 9 months. If two dry seasons occur, the maximum seed production occurs in the longer one (Orwa et al. 2009). T. superba has an effective system of self-incompatibility (Orwa et al. 2009). Pollination and gene dispersal patterns are little documented. However, various insects (Coleoptera, Diptera, Hemiptera, Hymenoptera and Lepidoptera) are known to pollinate flowers (Orwa et al. 2009).

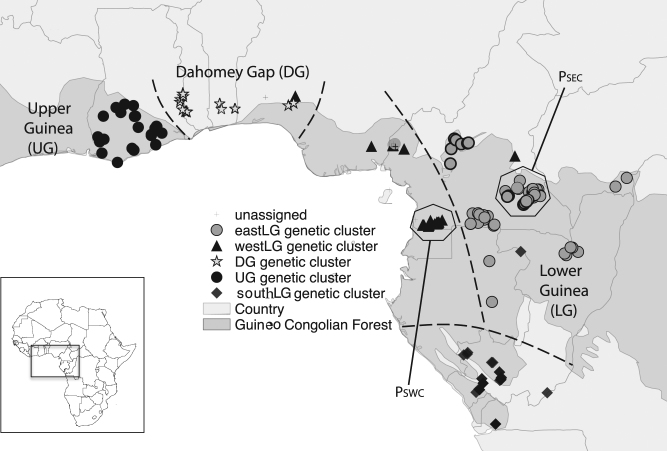
Leaf or cambium samples were collected in the field by the authors and by collaborators to cover, as far as possible, the whole natural distribution area of T. superba. Samples were directly dried in silica-gel, ensuring efficient DNA preservation. We genotyped 299 georeferenced (GPS) individuals originating from 10 different countries from Ghana to the Republic of the Congo, specifically, 220 samples from LG, 37 from UG and 42 from DG (Fig. 1). Only a few samples were obtained from Nigeria. Two areas from Cameroon were more intensively sampled along the trails of natural forest concessions (P_SWC in south-west with N = 70 individuals and P_SEC in south east with N = 57) to assess the Spatial Genetic Structure (SGS) and estimate indirectly gene dispersal distances in these local populations.

Fig. 1. Sampling and genetic structure of Terminalia superba according to Bayesian clustering (STRUCTURE) of 271 individuals genotyped at 14 nuclear microsatellites.

The inset delimits the part of Africa covered. Each symbol represents an individual assigned to a particular genetic cluster because its admixture coefficient is >50%, or unassigned (+symbol) when the largest coefficient is 50%. Each of the five areas delimited by stippled lines is dominated by a single genetic cluster, and considered as a “Population” for further analyses. P_SWC and P_SEC indicate two more densely sampled local populations used to assess the fine-scale genetic structure and estimate gene dispersal distances

Microsatellites genotyping and Bayesian clustering analyses

Total DNA for each sample was extracted using the NucleoSpin plant kit (Macherey-Nagel) following the manufacturer’s instructions. We genotyped 14 nuclear microsatellites (nSSRs) following the protocol described in Demenou et al. (2015) (Table S1 in Appendix S1). For each PCR product, 1.5 µL were directly added to 12 µL of Hi-Di Formamide (Life Technologies, Carlsbad, California, USA) and 0.3 µL of MapMarker® 500 labelled with DY-632 (Eurogentec, Seraing, Belgium) and genotyped on an ABI3730 sequencer (Applied Biosystems, Lennik, The Netherlands). Genotypes were analysed with GeneMapper version 3.7 (Applied Biosystems).

We used the individual-based Bayesian genetic clustering method implemented in STRUCTURE 2.3.4 (Falush et al. 2003) to infer genetic clusters, with the admixture and independent allele frequencies models. We also used TESS (Chen et al. 2007) to assess genetic clusters, but the results did not bring additional insights compared to the STRUCTURE results (not presented). To avoid artefacts due to highly related individuals in a densely sampled area from southwestern Cameroon, the latter was subsampled randomly (keeping 42 of the 70 individuals), keeping 271 of the 299 genotyped individuals. Furthermore, to avoid artefacts due to null alleles, null alleles were declared for each locus by (i) setting the option RECESSIVEALLELES = 1, (ii) declaring that each locus has a recessive allele called “0”, and (iii) attributing the genotype “00” to individuals that did not show any visible allele at a locus while most other loci from the same PCR mix amplified a visible allele (we allowed at most one exception). K = 1 to 10 genetic clusters were tested with runs of 10⁶ generations (burnin period of 10⁵ generations) and 10 runs at each K. The online application STRUCTURE HARVESTER (Earl and vonHoldt 2012) was used to visualise likelihood values across K, and detect the K that best fit the data, using both the mean posterior probability (PP) of the data L(K) and the approach of Evanno et al. (2005) (ΔK). For each individual, the proportion of genome attributed to a given genetic cluster is the Q value. To define the geographic boundaries of each genetic cluster we performed a spatial interpolation of Q-values in QGIS (QGIS Development Team 2009), using an inverse distance weighting of 2°, and we overlapped the resulting coloured maps to identify their boundaries visually (see Fig. S1 in Appendix S2). The geographic groups of individuals separated by these boundaries are hereafter called “Populations” and are mostly composed of individuals with high Q-values for the same genetic cluster, with a few exceptions (i.e. when an individual assigned to a cluster is surrounded by individuals assigned to another cluster, Appendix S2).

Genetic diversity analyses and differentiation parameters

The five populations obtained (see Results) were used as basis to compute genetic diversity and differentiation parameters (Table 1). For each population, total number of alleles (A ₀), allelic richness (R _S), expected heterozygosity (H _e), deviation from Hardy–Weinberg equilibrium (HWE) were computed for each locus with SPAGeDi 1.5 (Hardy and Vekemans 2002). Null allele frequencies were estimated with INEst 1.0 (Chybicki and Burczyk 2009), which also provided corrected estimates of the inbreeding coefficient (Fi). The private allelic richness (R _priv) was computed with the rarefaction procedure implemented in hp-rare 1.1 (Kalinowski 2005), considering random resampling of 46 gene copies per population and locus to compute a mean number of private alleles per population (Table 1). Differentiation between pairs of populations was computed using F _ST and R _ST, the latter being based on allele sizes. We expect R _ST > F _ST if stepwise mutations have contributed to differentiation, leading to a phylogeographic signal whereby populations show different mean allele sizes, and we used an allele size permutation test described in Hardy et al. (2003) to assess its statistical significance. Corrected values of F _ST were also computed between populations using FreeNA (Chapius and Estoup 2007), following the so-called ENA method which efficiently corrects for the positive bias induced by the presence of null alleles on F _ST.

Table 1.

Genetic diversity and differentiation parameters of the five populations recognised in T. superba using 14 nuclear SSR loci

Population	Differentiation parameters: F ST/R ST					Diversity parameters
	SouthLG	EastLG	WestLG	DG	UG	N	A 0	R S	He	F i	R priv
SouthLG		0.118	0.110	0.211	0.105	31	78	5.22	0.514	0.000	0.55
EastLG	0.153 (0.147)		0.004	0.057	0.044	90	246	11.50	0.734	0.061	2.03
WestLG	0.165 (0.156)	0.020 (0.020)		0.069	0.039	61	212	11.04	0.735	0.003	1.49
DG	0.241 (0.219)	0.068 (0.058)	0.057 (0.045)		0.020	52	201	11.37	0.752	0.066	1.85
UG	0.239 (0.219)	0.072 (0.067)	0.059 (0.052)	0.022 (0.019)		37	212	13.13	0.810	0.002	2.64
All samples	F ST = 0.089 (0.081)			R ST = 0.064		271	381	13.42	0.778

Diversity: N: sample size, A ₀: Total number of alleles, R _s: rarefied allele richness (among k = 46 gene copies per locus), He: expected heterozygosity corrected for sample size, F _i: inbreeding coefficient estimated by INEst, R _priv: private alleles richness (k = 46), Differentiation: F _ST below and R _ST above the diagonal; tests of phylogeographical signal (i.e. R _ST > F _ST) were non-significant, Under parentheses: corrected F _ST using the ENA correction method for null alleles described in Chapuis and Estoup (2007)

SouthLG southern Lower Guinea, EastLG Eastern Lower Guinea, WestLG western Lower Guinea, DG Dahomey Gap, UG Upper Guinea

Characterisation of Spatial Genetic Structure and estimation of gene dispersal distances in two local populations

SGS allows the estimation of historical gene dispersal distances (Vekemans and Hardy 2004), which is important to infer the migration potential of the species during range shift or the potential for genetic admixture between populations. To this end, SGS must be assessed at a scale one to two orders of magnitude larger than the scale of gene dispersal. SGS was assessed in two local populations within forest concessions: P_SWC in south-west Cameroon (Forest Management Unit FMU 09.024) and P_SEC in south-east Cameroon (FMU 10.038, 10.030-031), where respectively 70 and 57 individuals separated by <150 km were sampled (Fig. 1). We followed the approach of Vekemans and Hardy (2004) to quantify the strength of SGS using the statistic S _p = −b/(1–F(1)), where F(1) is the average kinship coefficient (F _ij, computed using J. Nason’s estimator in SPAGeDi, Hardy and Vekemans 2002) between nearby individuals (here < 1 km apart) and b is the slope of the regression of F _ij on the natural logarithm of d _ij, the spatial distance between individuals.

We then estimated gene dispersal distances following the method described in Hardy et al. (2006) based on the kinship–distance curve. We estimated Wright’s neighbourhood size, defined as N _b = 4πD _e.σ _g ² where D _e is an effective population density and σ _g ² half the mean squared parent–offspring distance, using the relationship N _b = (F ₁−1)/b _LD where the regression slope, b _LD, is computed within a restricted distance range σ _g > d _ij > 20σ _g (between σ _g and 100 σ _g for P_SEC because we had too few pairs of individuals in some distance intervals) (Hardy et al. 2006). Gene dispersal distance (σ _g) was then deduced after estimating the effective population density D _e. Mean population densities (D) of trees that flower and bear fruits regularly (dbh > 40 cm for T. superba) were obtained from forest management plans and reached D = 88.5 trees/km² in FMU 09.024 and D = 311 trees/km² in FMU 10.038 and 10.030–31. Assuming that the ratio of effective to census population sizes, Ne/N, typically ranges from 0.1 to 0.5 in plant populations (Frankham 1995), we used three estimates of effective population densities (D _e): D _e = D/2, D/4 or D/10. Thus we used D _e = 44.25, 22.12 or 8.85 trees/km² and D _e = 155.5, 77.8 or 31.1 trees/km² for P_SWC and P_SEC, respectively.

Inference of the demographic history and the origin of the Dahomey Gap population

The demographic history of each population (see Results) was inferred using an Approximate Bayesian Computation (ABC) approach implemented in the software DIYABC v2.0 (Cornuet et al. 2014). The principle is to simulate data sets, with a structure matching the real data set, under various evolutionary scenarios defined by demographic (change in population size, split or fusion of populations) and genetic (mutation rate and mode) parameters extracted from user-defined prior distributions. Summary statistics describing genetic diversity and differentiation (Appendix S3) are then used to assess which simulated data sets are most similar to the observed data set, allowing to obtain posterior distributions of the parameters of interest. The most likely evolutionary scenario is identified as the one with the highest PP (Beaumont et al. 2002; Marjoram et al. 2003; Beaumont 2010).

Nature and dating of demographic changes

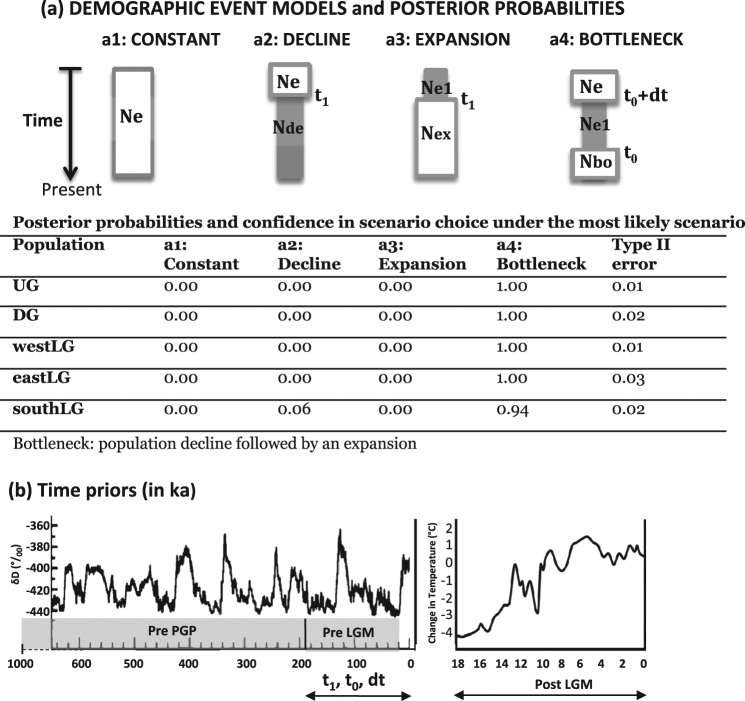
The demographic history of each population was investigated for the last 200 ka, including the last two climatic cycles of the late Pleistocene and the Holocene according to Dupont et al. (2001) and Dupont and Weinelt (1996). We first tested for each of the five populations detected (UG, DG, westLG, eastLG and southLG; see Results) four models of demographic changes with broad time priors (200 ka to present; A. DEMOGRAPHIC EVENT MODELS, Fig. 2): (a1) constant population size, (a2) population decline, (a3) population expansion, (a4) population bottleneck followed by expansion (hereafter “population bottleneck” for short). In doing so, we implicitly assumed that genetic signatures within populations reflect demographic changes and are not biased by population (sub)structure or past admixture, a potential problem that will be investigated later. The timing of inferred demographic events was then estimated by computing posterior distribution of time parameters from the 1% best simulated data sets (mode value and 95% confidence interval).

Fig. 2. Design of demographic ABC tests applied on each population using DIYABC and posterior probabilities.

a DEMOGRAPHIC EVENT MODELS: compare four scenarios to identify the nature and the timing of population size changes using broad time priors t ₀ and t ₁ = t ₀ + dt (effective size priors on Ne: 1000–100,000; Ne1: 10–2000). b Time priors: illustration of the late Quaternary climate changes used to select time priors (t ₀, dt and t ₁) for testing the impact of particular climatic periods: PrePGP (pre-Penultimate Glacial Period), PreLGM (pre-Last Glacial Maximum), PostLGM (post Last Glacial Maximum). Demographic changes were investigated in the last two periods, using a uniform prior distribution for t ₀, dt and t ₁: U(0,200 ka). Left graph: variations of deuterium (δD) in Antarctic ice core as a proxy for global temperature since 600 ka (IPCC 2007, http://www.ipcc.ch/publications_and_data/ar4/wg1/en/figure-6-3.html). Right graph: temperature change during the last cycle (since 18 ka) (http://www.lakepowell.net/sciencecenter/paleoclimate.htm)

Origin of the Dahomey Gap population

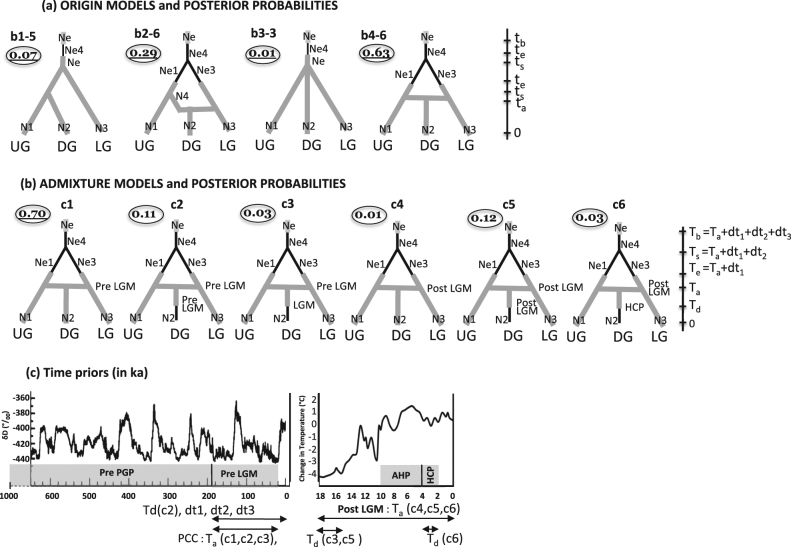
We then used DIYABC to determine the origin of the DG population, considering its relationship with the two adjacent forest populations, UG and westLG. Four sets of scenarios were considered (B: ORIGIN MODELS; Fig. 3a, Fig. S2 in Appendix S4): (b1) DG population originates only from UG; (b2) DG population originates from a split event from UG followed by an admixture with westLG population; (b3) DG, UG and westLG populations diverged simultaneously from an ancestral population and (b4) DG population results from the admixture of the UG and westLG populations. We discarded the hypothesis that DG population could originate only from LG because it is inconsistent with the F _ST values (see Results). As past demographic bottlenecks were detected for the three populations in model A (see Results), for each of the four origin scenarios (b1–b4) we tested several sub-scenarios, differing by the relative timing of demographic changes and population split or admixture events, to assess if the population bottleneck occurred either after the split between UG and westLG in each daughter population (b1-1 to b1-4; b2-1 to b2-4, b3-1 and b3-2 and b4-1 to b4-4; see Fig. S2 in Appendix S4), or in the ancestral population before the split between UG and LG (b1-5 and b1-6; b2-5 and b2-6, b3-3 and b3-4 and b4-5 to b4-6; see Fig. S2 in Appendix S4). We first identified within each of the four origin models the sub-scenario best supported by the data, and then we compared these four scenarios (highest PP in scenarios b1-5, b2-6, b3-3 and b4-6; see results and Fig. 3a) to identify the most likely one.

Fig. 3. Design of ABC test models to assess the origin and timing of the DG population and the posterior probabilities (encircled values).

a ORIGIN MODELS compare four sets of scenarios to assess the relationships between the DG population and its adjacent UG and LG populations (b1–b4) and within each set the relative timing of the bottleneck and population split or admixture events. All 22 scenarios tested are depicted in Fig.S2 (Appendix S4) while here are represented only the scenarios for which the timing of the bottleneck had highest support within each set. Effective size priors on Ne: 1000–100,000, N1: 1000–80,000, N2: 1000–30,000, N3: 1000–50,000 and Ne1, Ne2, Ne3 and Ne4 between 10–2000, and time priors on t _b (time of bottleneck) between 140–190 ka, t _e (time of expansion), t _s (time of split), t _a (time of admixture) and t _div (time of divergence) between 0–190 ka. b ADMIXTURE MODELS: compare six admixture scenarios derived from scenario b4-6, the most supported origin model, and assuming that the DG population derived from an admixture event occurring before (c1 to c3) or after (c4 to c6) the LGM, and that it remained of constant size (c1, c4) or was followed by a population size reduction before the LGM (c2), during the LGM (c3), just after the LGM (c5) or during the HCP (c6). c Time priors used to test the impact of particular climatic periods: PreLGM (pre-LGM period: 20–190 ka), PostLGM(post LGM period: 0–20 ka), LGM (Last Glacial Maximum: 15.5–20 ka), HCP (Holocene Climatic Pejoration: 2–4 ka)

As the origin test supported an admixture event (scenario b4-6; see Results), the last test performed aimed to infer when the admixture occurred (before or after the LGM) and whether the DG effective population size underwent a population decline during the HCP or the LGM, or a founder effect during its initial formation (C: ADMIXTURE MODELS; Fig. 3b). To this end six scenarios were tested: (c1) formation of DG population by admixture with small effective population size before the LGM (Pre_LGM, 190–20 ka); (c2) formation of DG population by admixture with subsequent decline of the population size, both events occurring before the LGM (Pre_LGM, 190–20 ka); (c3) formation of DG population by admixture before the LGM (Pre_LGM, 190–20 ka) with a decline of the population size during the LGM (LGM, 20–15.5 ka); (c4) formation of DG population by admixture with small effective population size after the LGM (Post_LGM, 20–0 ka); (c5) formation of DG population by admixture with subsequent decline of the population size, both events occurring after the LGM (Post_LGM, 20–0 ka); (c6) formation of DG population by admixture after the LGM (Post_LGM, 20–0 ka) followed by a decline of the population size during the HCP (4–2 ka).

Prior distributions and summary statistics for ABC analysis

The specification of prior distribution is a general problem in Bayesian model choice (Souza et al. 2012; Oaks et al. 2013; Hickerson et al. 2014) and is essential for credible results (Demenou et al. 2016). We tested a set of effective size (Ne) priors in preliminary simulations to assess a range of Ne giving simulated genetic structures compatible with the observed data set (pre-evaluation option of DIYABC). For all models, we used effective size distributed uniformly as follow: Ne: 1000–100,000, N1: 1000–80,000 and N3: 1000–50,000, respectively for phases of large size of ancestral population, for UG and LG current populations; N2 between 1000 and 30,000 for current DG population size (because preliminary analyses consistently showed lower DG population size); Ne₁, Ne2, Ne3 and Ne4 between 10 and 2000 for case of bottleneck.

All summary statistics available in DIYABC 2.0.4 were used (Appendix S3). A million simulations were performed for each scenario. We assumed a mean generation time of 100 years, consistent with data on the mean annual diameter growth and the average diameter of fruiting trees. For eastern LG, Morin-Rivat et al. (2017) reported a mean increment in diameter at breast height (bdh) of 0.53 ± 0.11 cm/year and a mean age of trees of 142 years, which should approach the mean generation time (mean age of reproducing trees) given the bell-shaped dbh distribution. The mean annual diameter growth varies according to location, ranging from 4.7 to 11.2 mm in T. superba (Detienne et al. 1998; De Ridder et al. 2013), so that a mean generation time of 100 years is a reasonable estimate for this species, and well within the range generation time estimates of tropical dense forest trees according to Baker et al. (2014).

Validation of the within population demographic changes analyses

False signatures of demographic changes can result from population structuring and/or contemporary gene flow (Mazet et al. 2016). To validate our approach and assess whether our inferences of demographic changes within population (detection of bottlenecks, see Results) could have been biased substantially by the population structure, we simulated data sets corresponding to our origin models but with constant population sizes, or a bottleneck, and checked for signatures of demographic changes in the resulting populations (Appendix S5).

Results

Population genetic structure

Bayesian clustering analyses show that the mean likelihood (L(K)) of the data increased from K = 1 to K = 5, reached a plateau at K = 5 and decreased for higher K (Fig. 4). Low variance among replicates were obtained at K = 2, K = 3 and K = 5. At K = 2, the two genetic clusters correspond to samples from West Africa (UG and DG) on one side and from Central Africa (LG) on the other side. When K = 3, the previous LG genetic cluster splits into a northern cluster and a southern cluster. When K = 5, the northern LG genetic cluster splits in two parapatric genetic clusters named eastLG and westLG, and samples from DG and UG also separate in two clusters (Fig. 1; Fig. S1 of Appendix S2 from Supporting material). Hereafter we retain K = 5 genetic clusters to delimit geographically five populations as it is best suited to address questions on the origin of the DG population, but solutions at lower K already indicate that the DG samples are more closely related to the UG ones.

Fig. 4.

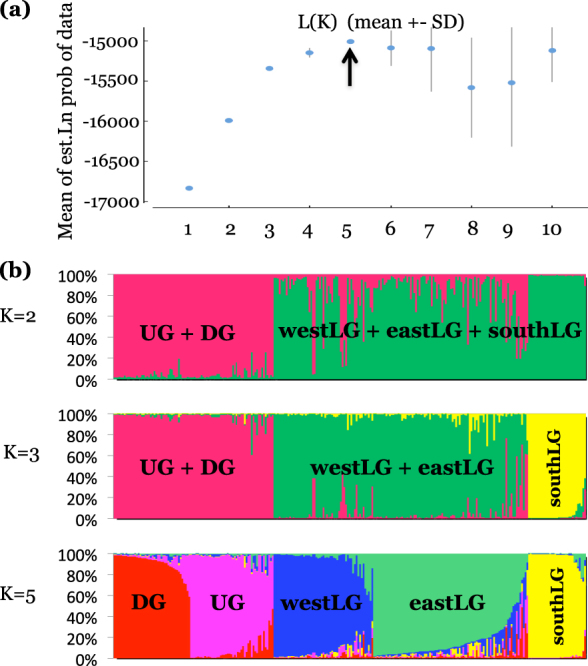
Results of the Bayesian clustering analysis performed with STRUCTURE (Falush et al. 2003) on 271 Terminalia superba samples genotyped at 14 microsatellite loci. a Posterior log-likelihood of the data according to the number K of genetic clusters (10 repetitions for each K). b Histograms of the individual admixture proportions to genetic clusters for K = 2, 3 or 5 with indication of their geographic origin: Upper Guinea (UG), Dahomey Gap (DG) or Lower Guinea (LG)(see Fig. 1)

The pairwise F _ST values revealed relatively high genetic differentiation (F _ST between 0.153 and 0.241; Table 1) between the southLG population and the four other ones. Among the latter, DG was more differentiated from westLG and eastLG populations (F _ST: 0.057 and 0.068, respectively) than from the UG population (F _ST = 0.022). The eastern and western LG populations were little differentiated (F _ST = 0.020). The corrected F _ST values were slightly smaller than the uncorrected F _ST but the bias due to null alleles was small in general (Table 1). All F _ST values were significantly larger than zero and no phylogeographical signal was inferred (R _ST not significantly different from F _ST for all pairs of populations).

Genetic diversity patterns

Genetic diversity indices were globally high in this species (Table 1). The UG population was the most diversified (R _s = 13.13 and H _e = 0.810) and southLG by far the less diversified population (R _s = 5.22 and H _e = 0.514). The DG population exhibited relatively high genetic diversity (R _s = 11.37 and H _e = 0.752), lower than the UG population but very similar to the two northern LG populations (11.04 and 11.50 for R _s, and 0.735 and 0.734 for H _e, respectively for westLG and eastLG). Inbreeding coefficients (F _i) were close to zero for UG, westLG and southLG populations and reached 0.06–0.07 for eastLG and DG populations after correcting for null alleles. In general, most of the loci were in HWE in all populations; except for loci P5, P42 and P44 in eastLG population; P5 and P42 in westLG population; P5 and P8 in southLG population; P5, P42 and P44 in DG population and P32 in UG population. This HW disequilibrium is mostly related to the presence of null alleles (frequency between 0 and 0.593, Table S2 in Appendix S1) but also to a substructuring of the genetic diversity within populations (in eastLG and DG).

Fine-scale spatial genetic structure and gene dispersal distance estimation

In two local populations of Cameroon, the regression slope b _LD of the pairwise kinship coefficient on the logarithm of spatial distance (Fig. S3 in Appendix S6) was highly significant (P < 0.001) with b _LD = −0.009 and −0.004 for P_SWC and P_SEC respectively, leading to Sp statistic values of 0.009 and 0.004 (Table 2).

Table 2.

Estimates of spatial genetic structure (SGS) and gene dispersal parameters for two local populations from Cameroon

Local populations	N	F (1)	b LD (s.e.)	Sp	D (ind / km2)	Nb	σ g (m) (De = D/2)	σ g (m) (De = D/4)	σ g (m) (De = D/10)
PSWC	70	0.047 *	−0.009* (0.002)	0.009	88.5	80 (13–136)	400 (326–474)	517 (467–567)	817 (488–1150)
PSEC	57	0.018 *	−0.004* (0.001)	0.004	311	197 (67–367)	–	470 (320–620)	670 (549–791)

SGS parameters: N: Number of individuals genotyped, F ₍₁₎: Pairwise kinship coefficient between individuals separated by the first distance class F(d < 1 km), b _LD: regression slope of kinship coefficient values on the logarithm of the spatial distance between individuals, Sp: Intensity of SGS. P-value of Mantel tests between the matrices of genetic and geographic distances: * for p < 0.05

Gene dispersal parameters: D: Density of mature trees t (dbh > 40 cm); Nb: Wright’s neighbourhood size (95% confidence interval); σ _g: characteristic gene dispersal distance (square root of half the mean squared parent–offspring distance) (95% confidence interval)

We estimated dispersal distance (σ _g) in local population P_SWC for all the three effective densities (D _e) when regressing kinship on ln(d) within a σ _g−20σ _g distance range. For local population P_SEC, the algorithm did not converge for this distance range but it succeeded when regression was performed within a σ _g−100σ _g range for the densities D _e = D/4 and D/10. The neighbourhood size estimated ranged from Nb = 80 to 197 individuals (Table 2). The gene dispersal distances estimates were similar in both local populations and ranged from σ _g = 400 to 817 m over the three effective densities (Table 2).

Demographic events occurring within each population

For all five populations, the ABC analysis (models a1 to a4) strongly supported scenarios involving a population bottleneck occurring in the last 200 ka, with a PP of 94 to 100%, and rejected scenarios involving population constancy, decline or expansion (Fig. 2). The confidence in scenario choice was high (Type error II rate < 0.04). This analysis suggested a pre-LGM bottleneck for all populations occurring between 153.300 and 62.100 yr bp with 95% credibility interval between 25.900 and 189.000 yr bp The modes of the posterior distributions of effective sizes indicated that DG population current effective size (N _x = 25,000, Table S4 in Appendix S7) is up to three times lower than those of UG and westLG populations (77,600 and 38,600, respectively; Table S4 in Appendix S7). The detailed results of posterior distributions are presented in Appendix S8.

When this approach was applied on simulated data sets with diverging or admixed populations under constant sizes, the method inferred population constancy or decline, but never a bottleneck (Table S3 in Appendix S5). Simulated bottlenecks in such models were correctly detected when applying the method on each population. As bottlenecks were detected in all real populations, the present simulations tend to validate our two-step approach in the conditions explored. Hence, in the population parameters space investigated, genetic substructuring or admixture does not seem to cause a substantial bias in demographic inference within population.

Origin of the Dahomey Gap population

The ABC analysis (Model B) indicated for each of the four origin possibilities of the DG population, that the most supported scenario implied a bottleneck occurring in the ancestral population before the divergence between UG and westLG, with subsequent population expansion either in the ancestral population (scenarios b1-5: 72% and b3-3: 74%) or in each daughter population (UG and westLG) (b2-6: 78% and b4-6: 74%; Fig. 3a).

Among those four origin scenarios, the admixture origin of DG population (scenario b4-6: 63%) stood out for its best fit to the observed data, and the second best fitting scenario implied one split event from UG followed by one admixture event with westLG (scenario b2-6: 29%). Low PPs were obtained for the two other scenarios, assuming a UG only origin (scenario b1-5: 7%) or a simultaneous split of the three populations from a common ancestor (scenario b3-3: 1%). The type II error for the choice of scenario b4-6 is 0.13. Additional tests of origin failed to separate scenarios involving multiple admixture events or multiple splits followed by admixture events, as could be expected from repeated range fragmentation/expansion cycles driven by glacial/interglacial conditions (results not shown).

The model C (ADMIXTURE MODELS) analysis with specific time scales provided highest support for the scenario c1 (PP = 70%, Fig. 3b) suggesting the formation of the DG population before the LGM by admixture, with a higher contribution of UG (80%), with a simultaneous decline of population effective size by founder effect, but without subsequent population decline. The posterior distribution of the timing of the admixture event suggests that it occurred around 54,400 (95% credibility interval 27,600–161,000) years bp It also suggests that bottleneck in the ancestral population seem to have started during or just after the penultimate interglacial around 92,520 (95% credibility interval 39,990–173,138) years bp and ended before the LGM around 68,020 (95% credibility interval 31,880–165,028) years bp, with the split of ancestral population occurring around 72,620 (95% credibility interval 33,040–166,188) years bp (Table S4 in Appendix S7).

However, this test does not reject clearly all alternative scenarios. In particular, scenario c2 and c5, which assume a possible decline of population size during the LGM and HCP, presented PPs reaching 11 and 12%, respectively. The type II error for the choice of scenario c1 is 0.16. The detailed results of posterior distributions are presented in Appendix S8.

Discussion

The present study is the second of its kind focussing on the history of the DG using phylogeographic data and ABC inferences. Its originality lies in the use of a pioneer tree species of semi-deciduous forests, Terminalia superba, to compare the differences of responses to climate change with Distemonanthus benthamianus, a pioneer species found in more evergreen forests and which was studied using the same approach (Demenou et al. 2016). Our phylogeographic results can also be compared to some extent with those reported for other wide-ranging Guineo-Congolian tree species presenting populations in the DG, such as Pentadesma butyracea (Ewédjè 2012), Symphonia globulifera (Budde et al. 2013), Erythrophleum suaveolens (Duminil et al. 2013) and Milicia excelsa (Daïnou et al. 2014).

Detection of genetic discontinuities with low differentiation among T. superba populations

Genetic subdivisions at the continental scale are generally observed in African forest trees (e.g. Budde et al. 2013; Hardy et al. 2013; Daïnou et al. 2014; Duminil et al. 2015; Demenou et al. 2016), probably due to the presence of (past) barriers to gene flow. Our phylogeographical study of T. superba also detected genetic discontinuities separating five parapatric genetic clusters. The southern Lower Guinean population is the most differentiated and displays the lowest diversity. It is probably little connected to northern LG populations because the species occurs at very low density in the evergreen forests of Gabon. In UG, only one genetic cluster was observed, a situation also documented in other species (Daïnou et al. 2014; Duminil et al. 2015; Demenou et al. 2016). However, as only individuals from Ghana were available to represent UG in the present study, it is difficult to rule out further genetic structuring West of UG. The high diversity level of the UG population suggests however that it has maintained a large effective population size. In northern Lower Guinea, two weakly differentiated populations were obtained: a western population gathers individuals from coastal regions of Cameroon, while an eastern population groups all the individuals of central and eastern Cameroon, Central African Republic, Gabon and the north of the Republic of Congo. This kind of east-west differentiation pattern in Lower Guinean forest was also observed in other species (Hardy et al. 2013; Demenou et al. 2016).

The genetic differentiation between the T. superba populations (F _ST = 0.088), especially between UG, DG and northern LG populations (F _ST between 0.022 and 0.068), was relatively low compared to other studied species which typically showed F _ST > 0.1 and often F _ST > 0.2 between the three considered areas (Table 3). This low differentiation could be explained by recent differentiation between DG and adjacent populations, by ancient differentiation with continuous gene flow, or by the maintenance of high effective population sizes (Ne). High Ne is supported by our demographic analyses (Table S4 in Appendix S7), and by limiting genetic drift it would explain both low population differentiation and the high genetic diversity found in each T. superba population compared to other species (mean He > 0.7 in T. superba while He < 0.7 in most other species for microsatellite markers except for Symphonia globulifera; Table 3). Our analysis of the SGS pattern allowed us to infer information on gene flow and compare it to other species. We found that our indirect estimates of gene dispersal distances in T. superba, ranging from 400 m to 800 m, are comparable to the values found in D. benthamianus (400 m to 1200 m; Debout et al. 2011) and cannot explain the low level of population differentiation in T. superba compared to D. benthamianus (F _ST ranging from 0.20 to 0.35). The positive inbreeding coefficient (F _i) in DG population may result from its fragmented state and the substructuring of the genetic diversity (Wahlund effect). Nevertheless, this inbreeding value remains low so that using all local populations of the DG as a single large DG population, as done in this study, should not cause substantial bias in our analyses. In conclusion, our comparative analysis suggests that T. superba has maintained relatively high effective population sizes since the divergence between UG, DG and northern LG populations, while the southern LG population has undergone much higher genetic drift.

Table 3.

Comparison of genetic diversity and population differentiation between Upper Guinea, Dahomey Gap and Lower Guinea for several forest tree species

	Nb. nSSR	Population genetic diversity (H e)				Pairwise genetic differentiation (F ST)
Species		UG	DG	LG	GCR	UG/DG	UG/LG	DG/LG
Terminalia superba (1)	14	0.810	0.752	0.749	0.778	0.022	0.072	0.069
Distemonanthus benthamianus (2)	11	0.522	0.553	0.633	0.689	0.20	0.35	0.22
Symphonia globulifera (3)	5	–	0.770	0.786	0.860	–	–	0.266
Milicia excelsa + Milicia regia (4)	7	0.683	0.600	0.478	0.643	0.15	0.20–0.25	0.12–0.16
Pentadesma butyracea (5)	7	0.57	0.45	0.59	0.69	0.32	0.26	0.42
Erythrophleum suaveolens (6)	9	–	0.651	0.658	–	–	–	0.21
Erytrophleum ivorense (6)	9	0.745	–	0.677	–	–	∼0.09	–

UG Upper Guinea, DG Dahomey Gap, LG Lower Guinea, GCR Guineo-Congolian region

H _e: Expected heterozygosity

(1) This study: for LG we have grouped the three LG genetic clusters (wLG, eLG and sLG)

(2) Demenou et al. (2016): the underlined value is an average over three genetic clusters

(3) Budde et al. (2013): underlined values are average over two genetic clusters; GCR: He value was computed without UG

(4) Daïnou et al. (2014): M. regia occurs solely in UG (He value for UG is here for this species only); the DG population (M. excelsa) here includes a few individuals from the semi-deciduous forests of the UG; the underlined value is an average over two genetic clusters

(5) Ewédjè (2012)

(6) Duminil et al. (2013): Cluster SW (in Duminil et al. 2013) associated with DG here is centred on the DG but extends well beyond into the UG and LG. Underlined values are averages over two genetic clusters

Demographic history and ancestral origin (before LGM) of the DG T. superba population

ABC model-based tests (Model A) indicated that all T. superba populations display a genetic signature of a demographic bottleneck that occurred before the LGM (Pre_LGM). A signal of demographic bottleneck before the LGM was not expected for the DG population under the hypothesis, based on palaeocological data (Dupont and Weinelt 1996; Tossou 2002; Salzmann and Hoelzmann 2005), that the current DG population would originate from the recent Holocene Humid period, as found in D. benthamianus (Demenou et al. 2016). During the last 3000 years, human activities also have had a role at the level of the DG, not necessarily for the initial fragmentation of its forests (Maley 1999; Sowunmi 1999, Tossou 2002; Assi-Kaudjhis et al. 2010) but most likely for maintaining its fragmented state. However, the time-scale is probably too short to have led to a visible genetic signature in the T. superba DG population.

It must be recalled that the demographic tests used can potentially be biased because they assume that the populations were isolated and without substructure (e.g. Peter et al. 2010; Mazet et al. 2015, 2016). In the present work, we delimited our populations as geographic areas largely dominated by one genetic cluster (Appendix S2), although it is clear that each population is substructured to some extent, as isolation by distance was detected. However, when we applied our procedure on simulated genetic data where populations of constant size derived from an ancestral population or from admixture between populations to assess the potential bias in demographic inferences, we found that population structure could lead to a signal of population decline but not a signature of bottleneck (decline + expansion) as detected in this study (Appendix S5). Moreover, in preliminary ABC analyses where we defined each population as the set of individuals with admixture proportion Q > 0.7 towards a given genetic cluster, rather than as a delimited geographic area, we obtained very similar demographic inferences (results not shown). Although this is reassuring for interpreting our findings, we must keep in mind that ABC model-based inferences rely on a set of model assumptions that cannot be easily controlled in natural populations. Hence, we should view our findings as probable hypotheses rather than as clear demonstrations of past demographic events, and wait for further theoretical work assessing the real bias made in demographic inferences due to substructuring or gene flow to confirm our results (but see Peter et al. 2010; Mazet et al. 2015 2016; Chikhi et al. 2017).

The demographic model most consistent with the observed data (model c1, Fig. 3) suggests that the bottleneck detected is contemporary to the divergence between West African forest (UG) and central African forest (LG), and would have started at a period corresponding to the last interglacial (LIG, 130–115 ka) or the beginning of the last glacial period (t1 in Table S4 in Appendix S7). The post-bottleneck demographic expansion would have started around 68,000 years bp (31,880–165,028 95% HPD; Table S4 in Appendix S7). These inferences must be taken with caution because their precision is very limited but the 95% HPD supported that the expansion started at the latest around 32,000 years bp and thus suggest that a bottleneck event associated with a fragmentation of an ancestral population was not concomitant with a phase of glacial maximum in T. superba. Always according to the most supported model, after the re-expansion of LG and UG populations they started to admix, leading to the current DG population which would have formed before the LGM, around 54,400 (27,600–161,000) years bp So, the current DG population of T. superba would result from the admixture of UG and westLG populations, with a higher contribution of UG (80%), and would have survived the LGM. There is no evidence of a substantial impact of the LGM (scenarios c3) or of the more recent HCP (scenarios c6) on population size. The DG population formation occurred with a simultaneous decline of population effective size, probably due to a founder effect.

Past demographic changes have also been detected in other Guineo-Congolian tree species. For Symphonia globulifera, Budde et al. (2013) reported historical demographic bottlenecks occurring during LGM for Benin and West Cameroon populations and during the penultimate glacial period for south Cameroon and Gabon population. In Erythrophleum suaveolens and E. ivorense genetic clusters, Duminil et al. (2013, 2015) reported also historical demographic bottlenecks but that started between 125,000 and 50,000 years ago and interpreted them as signatures of forest decline and fragmentation following a new glacial cycle. Attempts to identify demographic changes in Pentadesma butyraceae (Ewédjè 2012) and Milicia excelsa (Daïnou et al. 2010) were less conclusive, possibly due to the limited number of markers available and their limited polymorphism in these species (Table 3). Demographic changes detected in D. benthamianus (Demenou et al. 2016) are particularly interesting to compare with those in T. superba because the sampling and methods used were very similar, as detailed below.

Difference in response of T. superba and D. benthamianus to past climate change

The patterns of genetic clustering in T. superba and D. benthamianus (Demenou et al. 2016) are very similar, and the DG populations would have resulted from the admixture of UG and western LG populations in both species, but the inferred demographic histories of the two species differ on two main points: (i) the origin of the DG population would be pre-LGM for T. superba and post-LGM for D. benthamianus, and (ii) the divergence between UG and western LG populations seems much older in D. benthamianus (c. 500 kyr bp, 95% credibility interval from 200 to 960 kyr), where divergence would have accumulated over multiple glacial-interglacial cycles, than in T. superba (c. 73 kyr bp, 95% credibility interval from 33 to 166 kyr) where it would date from the last glacial cycle. Although these results should be confirmed using other approaches (e.g. molecular dating based on DNA sequences), these differences might be related to the ecology of each species. Terminalia superba is a pioneer, light-demanding, upper canopy deciduous tree, wind dispersed, probably pollinated by insects (Raju et al. 2012; Meunier et al. 2015). It has similar characteristics as D. benthamianus but prefers semi-deciduous forests whereas D. benthamianus also occur in secondary evergreen forests. As explained above, we found no evidence indicating that gene flow could be stronger in T. superba to explain its much lower level of population differentiation.

To check further whether the respective climatic niches could explain the difference of response between the two species, we selected 102 to 103 occurrence points from respectively 187 and 1513 occurrence points of T. superba and D. benthamianus taken from the RAINBIO database (Dauby et al. 2016; Table S12 in Appendix S9), keeping per species no more than one occurrence point per square grid cell of 10 km side situated in the northern hemisphere. Student’s t tests on each of 19 bioclimatic variables (Hijmans et al. 2005) showed that eight of them differed significantly between the two species (Table S13 in Appendix S9). Among them, Precipitation of warmest quarter (Bio18) and Annual mean temperature (Bio1) discriminated most the two species: T. superba occurs in areas on average warmer by about 0.5° C annual temperature and with on average 84 mm of precipitation less during the warmest quarter than D. benthamianus. This test confirms field observation that T. superba tends to occur in drier habitat. During the dry conditions of the LGM, T. superba may therefore have persisted better and over a larger area than D. benthamianus. This might explain why our demographic inferences suggest that T. superba survived in the DG during the LGM while D. benthamianus recolonised the DG after the LGM. If our demographic inferences were confirmed by further work, they would even show that T. superba expanded not during an interglacial period but at the beginning of a glacial period, an unexpected behaviour for a Guineo-Congolian forest tree.

Conclusion

This genetic work confirms that African rain forest tree populations experienced fragmentation and demographic changes probably in response to cyclical climate change as suggested by palaeovegetation studies, but the timing of these changes seem to be non-synchronous between species. For T. superba, our results support an unexpected pre-LGM admixture origin of the DG population (around 54 ka bp). For D. benthamianus, by contrast, our previous work showed a post-LGM admixture origin of the DG population, which is congruent with paleovegetation reconstructions indicating that the tropical African rain forest formed a single block during the Holocene Humid Period (c. 9000–4500 yr bp). These contrasted results demonstrated that the demographic history and the response to climate change of plant species might be different even for species displaying similar phylogeographic patterns, depending probably on various intrinsic factors, like differences in the ecology of tropical tree species. This study also suggests that the transition periods between the peaks of glacial and interglacial periods are probably also important to consider when studying the impact of climate change on species distribution and abundance because these transitions are not smooth. The commonly held view that rain forest species expanded maximally during interglacials and reached their lowest population size and highest fragmentation during the peaks of glacial periods is probably far too simplistic. Finally, this work highlights the relevance of combining Bayesian demographic analyses, SGS-based estimation of dispersal and climatic niche analysis to compare species histories.

Data archiving

Data available from the Dryad Digital Repository: 10.5061/dryad.4m83g

Compliance with ethical standards

Conflict of interest

The authors declare that they have no competing interests.