Finite-Size Effects of Binary Mutual Diffusion Coefficients from Molecular Dynamics

Abstract

Molecular dynamics simulations were performed for the prediction of the finite-size effects of Maxwell-Stefan diffusion coefficients of molecular mixtures and a wide variety of binary Lennard–Jones systems. A strong dependency of computed diffusivities on the system size was observed. Computed diffusivities were found to increase with the number of molecules. We propose a correction for the extrapolation of Maxwell–Stefan diffusion coefficients to the thermodynamic limit, based on the study by Yeh and Hummer (J. Phys. Chem. B, 2004, 108, 15873−15879). The proposed correction is a function of the viscosity of the system, the size of the simulation box, and the thermodynamic factor, which is a measure for the nonideality of the mixture. Verification is carried out for more than 200 distinct binary Lennard–Jones systems, as well as 9 binary systems of methanol, water, ethanol, acetone, methylamine, and carbon tetrachloride. Significant deviations between finite-size Maxwell–Stefan diffusivities and the corresponding diffusivities at the thermodynamic limit were found for mixtures close to demixing. In these cases, the finite-size correction can be even larger than the simulated (finite-size) Maxwell–Stefan diffusivity. Our results show that considering these finite-size effects is crucial and that the suggested correction allows for reliable computations.

1. Introduction

The knowledge of diffusion in liquid mixtures is essential for the design and optimization of various industrial processes.¹⁻⁹ Although experimental methods are constantly improving,¹⁰⁻¹⁶ measurements of diffusion coefficients for multicomponent systems are not always feasible or straightforward to perform. Diffusion experiments may require specialized equipment and materials and they can be very time-consuming and expensive.^11,17 For these reasons, semiempirical models such as the Stokes–Einstein,¹⁸ Chapman–Enskog,¹⁹ and Wilke–Chang²⁰ models have been developed for predicting diffusion coefficients.²¹⁻²⁷ However, the applicability of these models is usually limited to gases or infinitely dilute mixtures.

In this context, molecular dynamics (MD) simulations are a powerful tool to complement or even, in some cases, substitute experiments for computing diffusion coefficients.²⁸⁻⁴¹ In MD simulations, the trajectories of molecules in a simulation box are obtained by integrating Newton’s second law. Conventional MD simulations yield Maxwell–Stefan (MS) diffusion coefficients, from which Fick diffusivities can be calculated using the so-called thermodynamic factor.^{6−8,42−44}

One of the advantages of MD is that these simulations are not limited to diffusion in bulk fluids but can also be employed for more complex systems like the diffusion of gases/liquids in porous membranes.⁴⁵⁻⁵⁰ Due to the intrinsic inclusion of the nonideal behavior of mixtures, MD simulations have the potential to foster the deep understanding of diffusion phenomena⁵¹⁻⁵³ and verify empirical correlations for predicting diffusivities.⁵⁴⁻⁵⁸ It is important to note that, even with modern computers, the number of molecules considered in a typical MD simulation is orders of magnitude lower than the thermodynamic limit. Thus, it is important to take into account finite-size effects when calculating diffusion coefficients. Previously, simulations of thermodynamic and transport properties for systems close to critical points⁵⁹⁻⁶¹ and phase transitions⁶²⁻⁶⁴ have also shown that corrections for the finite size effects should be applied.

It has been shown that self-diffusivities computed from MD simulations scale linearly with N^–1/3, where N is the number of molecules in the simulation box.⁶⁵ Yeh and Hummer⁶⁶ performed a detailed investigation of this behavior for Lennard–Jones (LJ) particles and water molecules. The authors found that the finite-size effects originate from hydrodynamics and derived a correction term. By adding this term to the computed self-diffusivity by MD simulation, the self-diffusivity in the thermodynamic limit can be accurately determined. Several studies verified the applicability of the YH correction for systems of nonspherical molecules.⁶⁷⁻⁶⁹ According to Yeh and Hummer,⁶⁶ the system size effects of the diffusivity of charged molecules in a polar or ionic medium cannot be accurately corrected with the proposed term. These deviations are due to the strong electrostatic interactions, and thus, the correction term needs rescaling.

To the best of our knowledge, no study has focused on the finite-size effects of MS or Fick diffusivities and noninfinitely diluted mixtures, obtained from MD simulations. In this study, we show that, depending on the size of the system, there can be significant differences between the simulated (finite size) and real (thermodynamic limit) MS diffusion coefficients in binary mixtures. For systems close to demixing, the finite-size correction can be even larger than the simulated diffusivity. For self-diffusion, the finite-size effects depend only on the box size, temperature, and viscosity, but for MS diffusivity, there is also a strong dependence on the nonideality of the mixture (represented by the thermodynamic factor). We propose a finite-size correction for MS diffusion and verify its accuracy for a large number of LJ and molecular mixtures.

This paper is organized in five sections. In Section 2, theoretical aspects of self and MS diffusion are briefly discussed. In Section 3, details of the MD simulations and the studied mixtures are explained. A detailed analysis of the results of the MD simulations and the proposed correction term to finite-size mutual diffusivities is provided in Section 4. Finally, the conclusions of this study are summarized.

2. Theory

There are two approaches for obtaining transport properties from MD simulations: (a) nonequilibrium molecular dynamics (NEMD), which employ an external driving force generating a net flux in the system,^28,70−77 and (b) equilibrium molecular dynamics (EMD), where transport coefficients are computed from time-correlation functions in a system at equilibrium, without the presence of external forces.^9,75,77,78 In this work, we perform only EMD simulations. Sampling time correlations can be achieved via two formulations, which are intrinsically identical: Einstein and Green–Kubo.^75,77,78 The Einstein formulation is used in this work. For an overview of EMD and NEMD methods, the reader is referred to the reviews by Liu et al.⁹ and Peters et al.¹¹

The following three types of diffusion coefficients are discussed in this manuscript: (1) the self-diffusion coefficient (D_self), which is the diffusivity of a tagged particle in a medium due to its Brownian motion; (2) the Fick diffusivity (D_Fick), which is the coefficient of the linear relation between the mass flux and the concentration gradient in the system; (3) the MS diffusivity (Đ_MS), which describes mass transport due to the gradient in chemical potential of a species in a mixture. D_self has to do with the motion of individual molecules, while D_Fick and Đ_MS are due to the collective motion of all molecules in the system. Hence, for D_Fick and Đ_MS, the term “collective” or “mutual” diffusion is used. Although the MS diffusivity provides a more general description of transport diffusion in multicomponent mixtures,⁴² the Fick diffusivity is widely used in industry due to its simplicity. For homogeneous mixtures, the Fick and MS diffusion coefficients are related by the so-called thermodynamic factor (Γ), which is related to the nonideality of the system.^79,80 An extensive analysis and comparison of Fick and MS diffusion coefficients can be found in literature.⁴²⁻⁴⁴ A more detailed description of these three types of diffusion coefficients is provided in the following two subsections.

2.1. Self-Diffusion Coefficients

The self-diffusion coefficient of species i (D_i,self) can be expressed as the mean-square displacement of each molecule of species i:

1

where t is the correlation time, N_i is the number of molecules of species i, and r_j,i is the position of j-th molecule of species i. The angle brackets denote an ensemble average. Self-diffusion coefficients computed from MD simulations depend strongly on the number of molecules, N, in the simulation box. More specifically, it was shown that self-diffusivity scales linearly with 1/N^1/3, which is equivalent to 1/L, where L is the side length of the simulation box.⁶⁵ Yeh and Hummer⁶⁶ studied the size dependency of computed self-diffusion coefficients and derived an analytic correction term to compensate for the observed system-size effects. The correction term was developed on the basis of the hydrodynamic theory for a spherical particle in a Stokes flow with imposed periodic boundary conditions. These authors showed that the difference between the self-diffusivity in an infinite (nonperiodic) and a finite (periodic) system is due to the difference in hydrodynamic self-interactions.^65,81 For the rest of this manuscript, we will refer to their correction term as the “YH correction”. Accordingly, the self-diffusion coefficient of species i in the thermodynamic limit (D_i,self^∞) can be estimated from the finite-size self-diffusion coefficient obtained from MD simulations (D_i,self) by adding the YH correction (D^YH):⁶⁶

2

where k_B is the Boltzmann constant, L is the side length of the simulation box, and η is the shear viscosity of the system at temperature T. ξ is a dimensionless constant equal to 2.837297 for cubic simulation boxes with periodic boundary conditions.⁶⁶ Similar to the YH correction, equations have been derived for simulations in noncubic boxes⁸²⁻⁸⁴ and for confined fluids.⁸⁵ It is important to note that the YH correction does not explicitly depend on the size of molecules in a fluid or intermolecular interactions. This means that all species of a multicomponent mixture experience identical finite-size effects.

In EMD simulations, the required shear viscosity can be computed from the autocorrelation of the off-diagonal components of the stress tensor (P_αβ):^77,78,86,87

3

where V is the volume of the system. The components of the stress tensor are composed of two parts: an ideal and a virial term. The first part is due to the total kinetic energy of particles, and the second is constructed from intra- and intermolecular interactions.^77,88,89 The three off-diagonal components of the stress tensor (P_xy, P_xz, and P_yz) yield three values for the shear viscosity, which are equal for isotropic fluids. As shown in the work of Yeh and Hummer⁶⁶ and Moultos et al.⁶⁹ as well as in the current study (Supporting Information), the shear viscosity is independent of the system size. Therefore, the viscosity is a constant in eq 2.

2.2. Maxwell–Stefan and Fick Diffusion Coefficients

MS diffusion coefficients can be obtained from the Onsager coefficients (Λ_ij), computed from the crosscorrelation of the displacement of the molecules of species i and j:^{5−7,9,32,54}

4

where N_i and N_j are the number of molecules of species i and j, respectively, and N is the total number of molecules in the mixture. r_l,j is the position of the l-th molecule of species j. The Onsager coefficients (Λ_ij) in eq 4 are defined in a reference frame in which the velocity of the center of mass is zero.³² Hence, the Onsager coefficients of a binary mixture are correlated by means of the molar masses of the two constituent species (M₁ and M₂):³²

5

The Onsager coefficient of species i (Λ_ii) can be split into an autocorrelation term, which is the self-diffusivity of species i (D_i,self), and a crosscorrelation term (CC_ii):^6,51

6

The Onsager coefficient of two different species (Λ_ij, where i ≠ j) is a displacement crosscorrelation of the constituent two species:

7

The MS diffusion coefficient of a binary system is a linear combination of the Onsager coefficients. These relations for binary, ternary, and quaternary mixtures are listed in the articles by Krishna and van Baten³² and Liu et al.⁵⁴ For a binary mixture with mole fractions of x₁ and x₂, a single MS diffusion coefficient is defined (Đ_12,MS = Đ_21,MS = Đ_MS):³²

8

Using the constraint of eq 5, eq 8 can be rewritten as separate functions of the Onsager coefficients:

9

Equations 8 and 9 are valid for both ideal and nonideal diffusing binary mixtures. For ideal diffusing mixtures, the crosscorrelation between the particles is rather small compared to the self-diffusivities, which means that in eqs 6–8 (x₂/x₁)CC₁₁ + (x₁/x₂)CC₂₂ – 2CC₁₂ ≪ x₂D_1,self + x₁D_2,self, and therefore, the MS diffusivity (eq 8) can be simplified to the Darken equation (Đ_Darken):^6,51,54

10

Converting MS to Fick diffusivities requires the so-called thermodynamic factor Γ:^7,42,79

11

where Γ is the thermodynamic factor of a binary mixture and γ₁ is the activity coefficient of species 1. For an n-component mixture, the thermodynamic factor is defined as a matrix whose elements are⁴³

12

where δ_ij is the Kronecker delta. Σ indicates that the derivative is taken at constant mole fractions of all species, except for the n^th species.⁴³

A stable single-phase binary mixture requires that Γ > 0.^79,80 For systems approaching phase separation, Γ approaches zero. For ideal mixtures, Γ = 1 by definition. Binary mixtures with a thermodynamic factor between 0 and 1 favor interactions between the same species over interactions between different species. Systems with a thermodynamic factor larger than one exhibit associating behavior.^28,43 Thermodynamic factors can be calculated with equations of state,^32,42 Kirkwood–Buff integrals,^9,90−92 or the permuted Widom test particle insertion method.^93,94 In this study, the thermodynamic factors for binary systems are obtained from finite-size Kirkwood–Buff coefficients. The finite-size Kirkwood–Buff integral equals:⁹

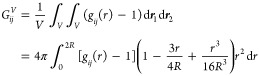13

where g_ij(r) is the radial distribution function, r = |r₁ – r₂|, and the integration is over a finite spherical subvolume V with radius R. As G_ij^V scales linearly with 1/R, the Kirkwood–Buff coefficient in the thermodynamic limit can be obtained by extrapolating the linear regime to 1/R → 0.⁹⁵ It is important to note that one needs to correct for finite-size effects of the radial distribution function. This correction is performed using the procedure outlined by Ganguly and van der Vegt⁹⁶ and Milzetti et al.,⁹⁷ For a binary system, the thermodynamic factor follows from

14

Similar expressions exist for ternary and muticomponent systems.^91,92

3. Simulation Details

All simulations in this study were performed in cubic simulation boxes. Periodic boundary conditions were imposed in all directions. All MD simulations were conducted with LAMMPS⁹⁸ (version 16 Feb. 2016). The initial configurations and LAMMPS input files were constructed with PACKMOL⁹⁹ and VMD.¹⁰⁰

To study the finite-size effects of MS diffusion coefficients in binary mixtures, two sets of MD simulations were carried out. The first set consists of binary LJ systems. All parameters and properties of these simulations are reported in dimensionless units with the ϵ and σ parameters of the first species as the base units: σ₁ = σ = 1, ϵ₁ = ϵ = 1, and mass = m₁ = m = 1. The characteristics of the second species (ϵ₂, σ₂, and m₂ = σ₂³), mole fractions (x), and adjustable parameters (k_ij) of all studied LJ systems are listed in Table 1. The applied temperature T and pressure p in the simulations are 0.65 and 0.05, respectively. The number density of the studied systems is between 0.14 and 0.89. A time step of 0.001 is used for the integration of equations of motion. Displacement and stress correlation functions are computed for a total length of 200 million time steps. In total, 320 distinct LJ systems with four system sizes (500, 1000, 2000, and 4000 particles) are simulated. To create a sound data set, systems in which phase separation occurs or a considerable deviation of the pressure or temperature from the specified conditions is observed are excluded from the data analysis. These systems correspond to a small fraction of the total data set. The second set of MD simulations includes 9 binary mixtures consisting of molecular systems. An overview of these mixtures, consisting of methanol as the first component and water, ethanol, acetone, methylamine, or carbon tetrachloride as the second component, is listed in Table 2. For each mixture, four system sizes (250, 500, 1000, and 2000 molecules) are considered. The temperature and pressure are specified to be 298 K and 1.0 atm. The total length of each simulation is 200 ns with an integration time step of 1 fs.

Table 1. Specifications of the Studied LJ Systems^a.

specification	values
total number of particles	500, 1000, 2000, 4000
independent simulations	10, 10, 5, 5
x1	0.1, 0.3, 0.5, 0.7, 0.9
ϵ2/ϵ1	1.0, 0.8, 0.6, 0.5
σ2/σ1	1.0, 1.2, 1.4, 1.6
m2/m1	(σ2/σ1)3
kij	0.05, 0.0, −0.3, −0.6

^aLJ particle type 1 has σ₁ = σ = 1.0, ϵ₁ = ϵ = 1.0, and mass = m₁ = 1.0 in dimensionless units.⁷⁷ As explained in the Supporting Information (eq. S3), k_ij is an adjustable parameter to the Lorentz–Berthelot mixing rules, controlling the nonideality in the mixtures.

Table 2. Specifications of All Studied Binary Molecular Systems^a.

specification	values
total number of molecules	250, 500, 1000, 2000
independent simulations	10, 10, 10, 10
second component (mole fraction)	water (0.1, 0.3, 0.5, 0.7, 0.9)
	ethanol (0.5)
	acetone (0.5)
	methylamine (0.5)
	carbon tetrachloride (0.1)

^aThe first component for all mixtures is methanol. The mole fraction of the second component is specified in parentheses. The force field parameters are available in the Supporting Information.

The force fields used in this work for both LJ and molecular systems are explained in detail in the Supporting Information. For the LJ systems, interactions are truncated and shifted to zero at a cutoff radius of 4σ.⁷⁷ The Lorentz–Berthelot mixing rules with an adjustment parameter (k_ij), controlling the nonideality of mixtures, are applied to the LJ parameters of dissimilar particles.⁷⁷ For the molecular systems, the SPC/E model¹⁰¹ and the model proposed by Tummala and Striolo¹⁰² are used for water and carbon tetrachloride molecules, respectively. The force field parameters for methanol,¹⁰³ ethanol,¹⁰³ acetone,¹⁰⁴ and methylamine^105,106 are obtained from the Transferable Potential for Phase Equilibria (TraPPE) force field.¹⁰⁶ The LJ interactions are truncated at 10.0 Å, and analytic tail corrections for energy and pressure are included.⁷⁷ The Lorentz–Berthelot mixing rules for dissimilar interaction sites are applied.⁷⁷ Long-range electrostatic interactions are taken into account by means of the particle–particle particle–mesh (PPPM) method with a relative precision of 10^–6.⁷⁷ It is important to note that the aim of this study is not to compare computed transport properties with experiments but to study finite-size effects observed in mutual diffusion coefficients. We adopt these well-known force fields, which have already been used by many researchers for computing transport properties.^{6−8,55,69,107−109}

For both data sets and each data point, at least five independent simulations were carried out to obtain the average properties and their 95% confidence intervals. For better sampling of displacement and stress correlation functions, the order-n algorithm was used.^75,110 As explained in the previous section, the thermodynamic factors were calculated from the RDFs of the constituent species using finite-size Kirkwood–Buff integrals.⁹² The RDFs were computed from MD simulations of large systems in the canonical ensemble. These systems contain 25 000 LJ particles (first set of simulations) and 13 500 molecules (second set of simulations). The total length of simulations for computing the Kirkwood–Buff integrals is 10 million time steps for the LJ systems and 10 ns for the molecular mixtures.

4. Results and Discussions

We performed two sets of simulations. The first set consists of 250 distinct binary LJ systems, and the second set includes 9 binary mixtures consisting of methanol, water, ethanol, acetone, methylamine, and carbon tetrachloride. For each set, four system sizes were considered (Tables 1 and 2). All raw data for diffusion coefficients, shear viscosities, and thermodynamic factors is provided in the Supporting Information.

Previous studies on the system-size dependencies of self-diffusion coefficients are limited to pure fluids and infinitely diluted mixtures. Figure 1 shows an example of the self-diffusivities of the two components of a binary LJ systems as a function of the length of the simulation box (L). Like in pure fluids, the computed self-diffusion coefficients vary linearly with the inverse of the simulation box length. The linear regression at 1/L = 0 yields the self-diffusivity for an infinite system size (D_i,self^∞), which is shown in the same figure as a horizontal line. The finite-size self-diffusivities corrected with D^YH (Equation 2) are plotted as red squares. As expected, the corrected self-diffusivities collapse on the horizontal line, indicating the validity of YH correction.

Figure 1.

Self-diffusion coefficients of a binary LJ mixture (x₁ = 0.9) as a function of the simulation box length (L). Blue circles are the computed self-diffusion coefficients in the finite systems, and red squares are the corrected values using the YH correction term (eq 2). The dashed lines indicate extrapolation to the thermodynamic limit, and the solid lines show the extrapolated self-diffusivities. The second component has ϵ₂ = 0.5 × ϵ₁ and σ₂ = 1.2 × σ₁, and the adjustable parameter (k_ij) to the Lorentz–Berthelot mixing rules is 0. The error bars are smaller than the symbols.

In Figure 2, the differences between the infinite and finite-size self-diffusivities (D_i,self^∞ – D_i,self) are plotted as a function of the YH correction (D^YH), for all entries in the data set examined. For the majority of the cases, the YH correction term is able to predict the finite-size discrepancies very accurately. However, while the correction is almost perfect for molecular mixtures, a systematic overprediction of self-diffusivities can be observed for LJ systems. This overprediction becomes more pronounced as the difference between the size and the interaction energies of the species in the system increases. Out of the 250 LJ systems considered, 13 correspond to systems containing particles with large dissimilarities in size (σ₂/σ₁ equal to 1.6 and 1.4) and interaction energy (ϵ₂/ϵ₁ equal to 0.5 and 0.6). This finding indicates that, although the YH correction can be safely applied to binary systems with a wide variety of composition, nonideality, and relative size of particles, limitations exist for mixtures with significant differences between the size of the molecules and interaction energies.

Figure 2.

Finite-size corrections required for self-diffusion coefficients as a function of the YH correction (D^YH, Equation 2) for (a) LJ and (b) molecular mixtures computed with 500 LJ particles/250 molecules (blue circles), 1000 LJ particles/500 molecules (red squares), 2000 LJ particles/1000 molecules (green diamonds), and 4000 LJ particles/2000 molecules (magenta pentagons). Closed and open symbols represent the corrections to the self-diffusivity of species 1 and species 2, respectively. The dashed lines indicate perfect agreement. Statistical uncertainties are listed in the Supporting Information.

Figure 3 illustrates the finite-size effects of the Darken equation (Đ_Darken, eq 10) and MS diffusivities (Đ_MS, eq 8) for the same binary LJ mixture of Figure 1. In the top figure, it is shown that the application of the YH correction, D^YH, to the self-diffusivities of species 1 and 2 to the Darken equation (Equation 10) accurately accounts for the finite-size effects of Đ_Darken. In the bottom figure, the application of the same corrections to MS diffusion coefficients is shown. The corrected Đ_MS (red squares) are systematically lower than the extrapolated MS diffusivity, indicating that D^YH is not a valid correction for the finite effects of Đ_MS. To further investigate this, the finite-size effect of the MS diffusivity can be obtained from eq 6 and 9 as follows:

15

where α′ is a constant, which is unknown at this point. Đ_MS^∞ and Đ_MS are the MS diffusivities in the thermodynamic limit and finite-size systems, respectively. CC_ii^∞ and CC_ii are the infinite and finite-size displacement crosscorrelation functions of species i. As shown in Figure 3, in nonideal mixtures, the total displacement crosscorrelation function of all particles has a considerable contribution to the finite-size effect. At this point, we hypothesize that a modified YH correction term can be applied directly to the MS diffusion coefficients. Thus, the crosscorrelation terms of eq 15, CC_ii^∞–CC_ii, can be a function or simply a modification factor of the YH correction. Since the crosscorrelation terms are directly related to the nonideality of a mixture, it is expected that this modification factor is a function of the thermodynamic factor (Γ):

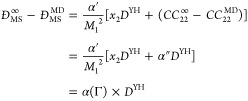16

where α(Γ) is the modification factor to the YH correction, accounting for the finite-size effects of the MS diffusion coefficient. In the example shown in Figure 3, the thermodynamic factor of the mixture, Γ, is 0.35 and the modification factor required to scale the YH correction from the red squares to the green squares is roughly 3, which is approximately equal to 1/Γ. To examine if 1/Γ is a suitable modification of the YH correction for correcting the finite-size effect of MS diffusion coefficients, a phenomenological approach is followed: In Figure 4, 1/Γ is compared to the required modification factor to D^YH for all LJ (blue circles) and molecular (green diamonds) systems. The good agreement observed suggests that 1/Γ is a suitable modification factor to the YH correction for MS diffusion coefficients. Hence, eq 16 can be rewritten as

17

Figure 3.

Diffusion coefficients of a binary LJ mixture (x₁ = 0.9) as a function of the simulation box length (L). Blue circles are the computed Darken (eq 10) and MS (eq 8) diffusivities. Red and green squares are the corrected values according to the YH (eq 2) and the MSYH (eq 17), respectively. The dashed lines show extrapolation to the thermodynamic limit, and the solid lines show the extrapolated values. The second component has ϵ₂ = 0.5 × ϵ₁ and σ₂ = 1.2 × σ₁, and the adjustment parameter (k_ij) to the Lorentz–Berthelot mixing rules is 0. The error bars are smaller than the symbols.

Figure 4.

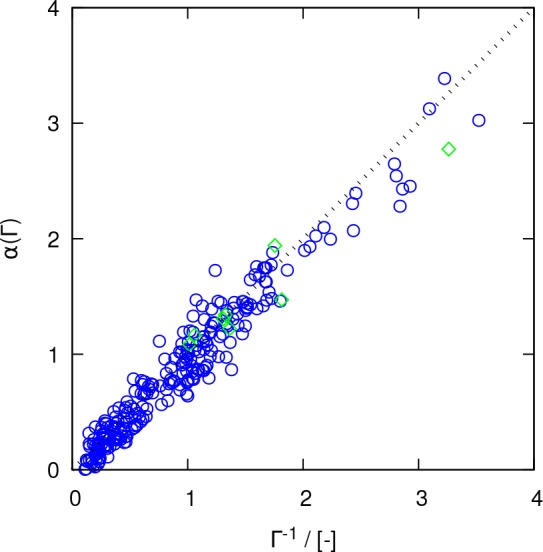
Modification factor to the YH correction (α) as a function of the thermodynamic factor (Γ) for nonideal mixtures according to eq 16. Blue circles and green diamonds show the modification factors for the LJ and molecular systems, respectively. The thermodynamic factor for ideal mixtures equals 1. The dashed line indicates perfect agreement. Statistical uncertainties are listed in the Supporting Information.

In the rest of the manuscript, the last term (D^YH/Γ) will be called the “Maxwell–Stefan Yeh−Hummer (MSYH)” correction (Đ^MSYH = D^YH/Γ). The results shown in Figure 4 suggest that describing the correction for MS as a function of only Γ seems to be sufficient; however, the possibility that other (still unknown) factors contribute to the correction cannot be ruled out. The applicability of Đ^MSYH in multicomponent mixtures is not examined in this work.

By combining eqs 11 and 17, the finite-size correction to the Fick diffusion coefficient for a binary mixture can be calculated from

18

where D_Fick^∞ and D_Fick are Fick diffusivities in infinite and finite-size systems, respectively. Interestingly, the same YH correction that is applied to self-diffusivities can mitigate the finite-size effects of Fick diffusion coefficients, regardless of the ideality or nonideality of the mixture.

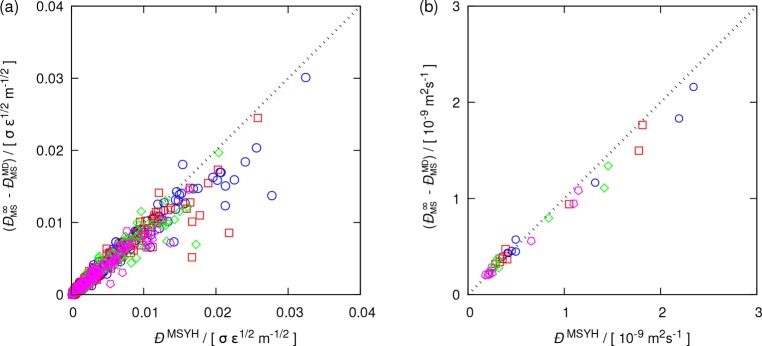
In Figure 5, the correction for the finite-size effects of MS diffusion coefficients (Đ_MS^∞ – Đ_MS) are compared to the predicted MSYH correction (Đ^MSYH) for the studied LJ (Figure 5a) and molecular systems (Figure 5b). As expected from Figure 4, a rather good agreement can be seen for both sets. These results suggest that Đ^MSYH works equally good for simple systems such as LJ systems and for nonspherical molecular systems with long-range electrostatic interactions. As proposed by Moultos et al.,⁶⁹ a minimum number of 250 molecules was used for all molecular systems. For a smaller number of particles, the shape and anisotropic structure of constituent molecules may play a role and affect the accuracy of the YH correction. Since no outlier is observed for the molecular systems in Figure 5b, the same criterion for the minimum number of molecules seems to be applicable to the MSYH correction.

Figure 5.

Correction needed for the MS diffusion coefficients versus the MSYH correction term (Đ^MSYH, eq 17) for (a) LJ and (b) molecular systems computed with 500 LJ particles/250 molecules (blue circles), 1000 LJ particles/500 molecules (red squares), 2000 LJ particles/1000 molecules (green diamonds), and 4000 LJ particles/2000 molecules (magenta pentagons). The dashed lines show perfect agreement. The statistical uncertainties are listed in the Supporting Information.

While the proposed MSYH correction (see Figure 5) seems to perform fairly accurately, two important points should be noted. (1) The MSYH correction overpredicts the finite-size effects of MS diffusivities for LJ systems. This is consistent with the earlier observations for self-diffusivities (Figure 2a). The MSYH correction is based on the YH correction (Equation 17), so any overprediction of D^YH will affect Đ^MSYH. To show the cause of this overprediction, the same comparison as in Figure 5, between the required corrections, is considered. However, instead of the analytic YH correction, the differences between the computed infinite and finite-size Darken diffusivities are used (see Figure 6). For molecular mixtures, no difference is noticed. This is expected since the YH correction performs well according to Figure 2b. Note that the overprediction observed in Figures 2a and 5a is not present in Figure 6a and the data points are symmetrically distributed on both sides of the diagonal line. This indicates that the less accurate predictions by the YH correction resulted in the overpredictions shown in Figure 5 and that the proposed modification of eq 17 does not introduce any systematic deviations. (2) The data points shown in Figures 4–6 for MS diffusivities are more scattered compared to those of self-diffusion coefficients illustrated in Figure 2. The cause can be the large statistical uncertainties of thermodynamic factors and finite-size MS diffusivities as well as the extrapolation of MS diffusion coefficients (Đ_MS) to the thermodynamic limit (reported in the Supporting Information). These influences are expected to contribute to the scattering of the data in Figures 4 and 5.

Figure 6.

Correction needed for the MS diffusion coefficients versus the extrapolated Darken equation with the modification factor included (Γ^–1(Đ_Darken^∞ – Đ_Darken)) for (a) LJ and (b) molecular systems computed with 500 LJ particles/250 molecules (blue circles), 1000 LJ particles/500 molecules (red squares), 2000 LJ particles/1000 molecules (green diamonds), and 4000 LJ particles/2000 molecules (magenta pentagons). The dashed lines show perfect agreement. The statistical uncertainties are listed in the Supporting Information.

As the MSYH correction is related to the YH correction via the thermodynamic factor, three possible scenarios for studying the significance of the MSYH correction can be conceived: (1) In the case of Γ = 1, the behavior of the mixture is ideal. The YH correction can directly be applied to self, MS, and Fick diffusivities. (2) For 0 < Γ < 1, the constituent species of the mixture tend to self-associate and the cross-interactions are less pronounced. Since Γ is smaller than 1, the modification factor makes the MSYH correction larger than the YH correction. (3) For associating mixtures with thermodynamic factors larger than 1, the correction decreases to smaller values than the YH correction. For mixtures with very large thermodynamic factors, the finite-size correction becomes negligible and overlaps with the statistical uncertainty of the computed MS diffusion coefficient.

To show the importance of the MSYH correction for systems with 0 < Γ < 1, we consider a mixture of methanol–carbon tetrachloride (x_methanol = 0.90). This mixture has a small thermodynamic factor approximately equal to 0.18. Accordingly, the modification factor to the YH correction for MS diffusivities would be approximately 6 (≈1/0.18). To investigate the magnitude of the finite-size effect, in Figure 7, the Darken and MS diffusion coefficients of this mixture are shown for four system sizes. As expected, both the YH and MSYH corrections can accurately predict the finite-size diffusivities. Whereas the finite-size effect for the self-diffusivites is at most 20% of the uncorrected value, the finite-size effect for MS diffusivites can be as large as 60% of the computed values in the current MD simulations. The contribution of the finite-size effect becomes even more pronounced for Γ → 0, i.e., close to demixing. Therefore, considering the MSYH correction is particularly important for such systems.

Figure 7.

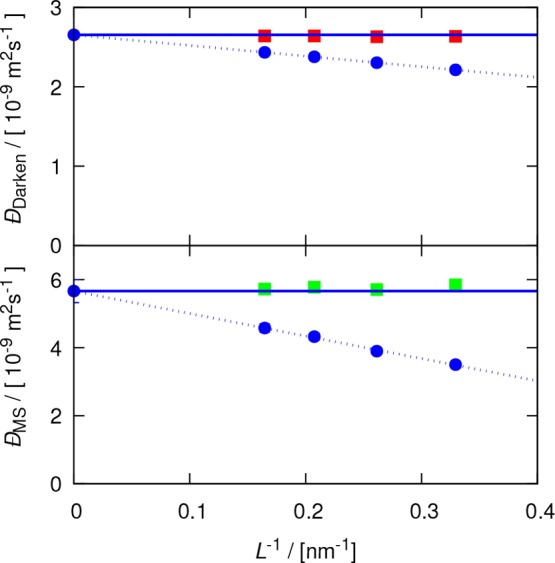
Binary Darken (Equation 10) and MS (Equation 8) diffusivities for a mixture of methanol–carbon tetrachloride (x_methanol = 0.9) as a function of the simulation box (L). Blue circles are the computed diffusion coefficients in MD simulations. Red and green squares are the corrected diffusivities according to the YH (Equation 2) and MSYH (eq 17) corrections, respectively. Dashed lines show extrapolation to the thermodynamic limit, and solid lines are the extrapolated values.

5. Conclusion

Molecular dynamics is a powerful tool to predict binary diffusion coefficients of nonideal mixtures. Even with modern computers, the number of molecules used in a typical simulation is orders of magnitude lower than the thermodynamic limit; therefore, it is important to take into account finite-size effects when calculating diffusion coefficients. Yeh and Hummer have developed a correction term (D^YH) to compensate for the finite-size effects of self-diffusion coefficients of pure fluids. This correction is a function of only the shear viscosity and the length of the simulation box. In this work, we verified the applicability of this correction to a wide range of nonideal binary mixtures. On the basis of the work of Yeh and Hummer, we present a Maxwell–Stefan YH correction, Đ^MSYH, for finite-size effects of computed Maxwell–Stefan diffusion coefficients, Đ^MSYH = D^YH/Γ, in which Γ is the thermodynamic factor. This correction is verified for a large set of Lennard–Jones systems as well as several molecular mixtures, and excellent predictions are obtained. For mixtures with a thermodynamic factor close to zero (i.e., close to demixing), this correction may become even larger than the computed finite-size Maxwell–Stefan diffusion coefficient. This highlights the importance of the finite-size corrections. In future work, a similar correction may be derived for multicomponent mixtures, in which the formulation of Maxwell–Stefan diffusivities is much more complex than those for binary mixtures.^42,80

Glossary

Nomenclature

α

constant coefficient (−)

r_j,i

position of molecule j of species i (m)

Đ^MSYH

Maxwell–Stefan Yeh−Hummer (MSYH) correction to finite-size MS diffusivity (m²·s^–1)

Đ_Darken

Maxwell–Stefan (MS) diffusivity in ideal mixtures computed from Darken equation (eq 10) (m²·s^–1)

Đ_MS

Maxwell–Stefan (MS) diffusivity (m²·s^–1)

Đ_MS^MD

Maxwell–Stefan (MS) diffusivity computed from MD simulations (m²·s^–1)

Đ_MS^∞

Maxwell–Stefan (MS) diffusivity in the thermodynamic limit (m²·s^–1)

δ_ij

Kronecker delta (−)

ϵ_i

Lennard–Jones (LJ) energy parameter for species i (ϵ)

η

shear viscosity (Pa· s)

Γ

thermodynamic factor (−)

γ_i

activity coefficient of species i (−)

Λ_ij

Onsager coefficient (m²·s^–1)

σ_i

Lennard–Jones (LJ) size parameter for species i (σ)

ξ

Constant value for the YH correction, 2.837297 for cubic simulation boxes (−)

c_t

total number density (m^–3)

CC_ij

displacement crosscorrelation function of species i and j (m²·s^–1)

CC_ij^MD

finite-size displacement crosscorrelation function of species i and j computed from MD simulations (m²·s^–1)

CC_ij^∞

displacement crosscorrelation function of species i and j in the thermodynamic limit (m²·s^–1)

D^YH

Yeh−Hummer (YH) correction to finite-size self-diffusivity (m²·s^–1)

D_Fick

Fick diffusivity (m²·s^–1)

D_Fick^MD

Fick diffusivity resulted from MD simulations (m²·s^–1)

D_Fick^∞

Fick diffusivity in the thermodynamic limit (m²·s^–1)

D_i,self

self-diffusivity of species i (m²·s^–1)

D_i,self^MD

self-diffusivity of species i computed from MD simulations (m²·s^–1)

D_i,self^∞

self-diffusivity of species i in the thermodynamic limit (m²·s^–1)

G_ij

Kirkwood–Buff coefficient between species i and j (m³)

g_ij

radial distribution function (RDF) between species i and j (−)

k_B

Boltzmann constant (= 1.38065 × 10²³ J·K^–1)

k_ij

an adjustable parameter for the Lorentz–Berthelot mixing rules (−)

L

side length of the cubic simulation box (m)

M_i

molar mass of species i (kg·mol^–1)

m_i

mass of a Lennard–Jones (LJ) particle (m)

N

total number of molecules (−)

N_i

number of molecules of species i (−)

p

hydrostatic pressure (Pa)

P_αβ

off-diagonal stress tensor components (Pa)

T

temperature (K)

t

time (s)

V

volume of the simulation box (m³)

x_i

mole fraction of species i (−)

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jctc.8b00170.

• The force field parameters, for both Lennard–Jones (LJ) and molecular mixtures; a detailed description of all MD simulation results for different system sizes (PDF)

• Simulation results (diffusivities and viscosities) for all studied LJ and molecular systems (ZIP)

• LAMMPS code (ZIP)

This work was sponsored by NWO Exacte Wetenschappen (Physical Sciences) for the use of supercomputer facilities, with financial support from the Nederlandse Organisatie voor Wetenschappelijk Onderzoek (Netherlands Organisation for Scientific Research, NWO). T.J.H.V. acknowledges NWO-CW (Chemical Sciences) for a VICI grant.

The authors declare no competing financial interest.