Signal Space Separation Method for a Biomagnetic Sensor Array Arranged on a Flat Plane for Magnetocardiographic Applications: A Computer Simulation Study

Abstract

Although the signal space separation (SSS) method can successfully suppress interference/artifacts overlapped onto magnetoencephalography (MEG) signals, the method is considered inapplicable to data from nonhelmet-type sensor arrays, such as the flat sensor arrays typically used in magnetocardiographic (MCG) applications. This paper shows that the SSS method is still effective for data measured from a (nonhelmet-type) array of sensors arranged on a flat plane. By using computer simulations, it is shown that the optimum location of the origin can be determined by assessing the dependence of signal and noise gains of the SSS extractor on the origin location. The optimum values of the parameters L_C and L_D, which, respectively, indicate the truncation values of the multipole-order ℓ of the internal and external subspaces, are also determined by evaluating dependences of the signal, noise, and interference gains (i.e., the shield factor) on these parameters. The shield factor exceeds 10⁴ for interferences originating from fairly distant sources. However, the shield factor drops to approximately 100 when calibration errors of 0.1% exist and to 30 when calibration errors of 1% exist. The shielding capability can be significantly improved using vector sensors, which measure the x, y, and z components of the magnetic field. With 1% calibration errors, a vector sensor array still maintains a shield factor of approximately 500. It is found that the SSS application to data from flat sensor arrays causes a distortion in the signal magnetic field, but it is shown that the distortion can be corrected by using an SSS-modified sensor lead field in the voxel space analysis.

1. Introduction

Development of a sensor system that can measure biomagnetic signals in room-temperature environments has gained great interest. One promising candidate among room-temperature sensors for biomagnetic systems is magnetoresistive (MR) sensors [1–4], which can lead to the development of novel low-initial-cost and maintenance-free biomagnetic systems. A potential near-future application of such systems is a low-cost magnetocardiography (MCG) system using MR sensors [5]. Such low-cost and maintenance-free MCG systems could replace the 12-lead electrocardiogram (ECG) now routinely used in daily clinical examinations.

However, to develop such low-cost systems, one major problem is the removal of ambient noise magnetic fields that exist in urban hospital environments. Biomagnetic signals are many orders of magnitude weaker than these ambient interference magnetic fields, called environmental noise. To reduce the influence of such environmental noise, biomagnetic measurements have traditionally relied on two kinds of hardware-based solutions: one is magnetically shielded rooms (MSRs) and the other is gradiometer sensors [6].

According to a purely technical point of view, use of an MSR would be advantageous even for MR sensor systems. However, the use of a high- or a medium-quality MSR may invalidate our goal, which is developing low-initial-cost biomagnetic systems, because MSRs are, in general, very costly and the use of even a medium-quality MSR causes a considerable increase of the total initial cost of the system. Gradiometers can significantly reduce the environmental noise, and the reduction ratio of a typical first-order gradiometer is believed to reach almost two orders of magnitude [6], although the noise reduction capability strongly depends on the precision in sensor manufacturing. However, for MR sensor systems, it is currently unknown whether gradiometers can be incorporated into the MR sensor hardware design. No gradiometer-type MR sensors have been developed so far.

Therefore, to attain the goal of developing low-cost biomagnetic systems, it may not be possible to rely on traditional hardware-based methods. This paper addresses a third option, developing software shielding methods, namely, efficient signal processing methods for environmental noise cancellation. A number of signal processing methods have been developed for this purpose, and arguments for and against those methods can be found in [7]. This paper focuses on a method called signal space separation (SSS), which was originally proposed for environmental noise cancellation for magnetoencephalography (MEG) SQUID sensor arrays [8–10].

The SSS method has an excellent characteristic that it imposes almost no prerequisites on the data or sources (i.e., it does not use any restrictive data or source models). One mild prerequisite of the SSS method, which can naturally be fulfilled, is that the region in which sensors are installed should be source-free (i.e., no current sources in that region). Under this assumption, the method decomposes the measured data into two components originated from the so-called “internal” and “external” regions. The internal region refers to a region that is closer to the origin than the sensors are, and the external region refers to the one that is farther from the origin than the sensors are.

The method can efficiently suppress interferences overlapped onto biomagnetic signals if clever choices of the origin location can make the internal and external regions match the signal and interference regions, respectively. It is not difficult to find such origin locations for helmet-type sensor arrays used in MEG. However, the SSS method has not been considered applicable to data from nonhelmet-type sensor arrays, such as sensor arrays arranged on a flat plane, which are usually used for MCG systems, because it does not seem possible to find an appropriate origin location for those nonhelmet-type arrays.

This paper presents a computer simulation-based investigation that explores the possibility of applying the SSS method to data measured from an array of sensors arranged on a flat plane. The goal of the investigation is to show that the SSS method is still effective for data from such flat sensor arrays. A series of computer simulations are performed assuming flat sensor arrays whose sensor arrangement is typical in MCG applications [11–15]. Using the results of these computer simulations, this paper seeks optimal values for numerical parameters used in the SSS method, showing that their choices are crucial for the effective use of the SSS method when applied to flat sensor arrays. It is found that the application of the SSS method to flat sensor data causes a distortion of signals but that this distortion can be corrected by using the SSS-modified lead field in the voxel space analysis.

This paper is organized as follows. In Section 2, the SSS method is described in detail, including the analysis of the problems caused when the SSS method is applied to flat sensor data. Section 3 presents computer simulation-based investigation, which shows the effectiveness of the SSS method for data from flat sensor arrays. This section includes empirical determinations of SSS parameters crucial to attain optimal performance of the SSS method. Section 4 summarizes the findings of the investigation.

2. Signal Space Separation Method

2.1. Data Model

Biomagnetic measurement is conducted using a sensor array, which simultaneously measures the signal with multiple sensors. Let us define the measurement of the mth sensor as y_m. The measurement from the whole sensor array is expressed as a column vector y : y = [y₁, y₂,…,y_M]^T. Here, M is the number of sensors, and the superscript T indicates the matrix transpose. Throughout this paper, plain italics indicates scalars, lowercase boldface indicates vectors, and uppercase boldface indicates matrices.

The location in the three-dimensional space is represented by r : r = (x, y, z). The source magnitude at r is denoted by a scalar s(r). The source vector is denoted by s(r), and the source orientation is denoted by η = [η_x, η_y, η_z]^T. We thus have the relationship: s(r) = s(r)η. Let us assume that a unit-magnitude source exists at r. When this unit-magnitude source is directed in the x, y, and z directions, the outputs of the mth sensor are, respectively, denoted by l_m^x(r), l_m^y(r) and l_m^z(r). Let us define an M × 3 matrix L(r) whose mth row is equal to [l_m^x(r), l_m^y(r), l_m^z(r)]. This matrix L(r), referred to as the lead field matrix, represents the sensitivity of the sensor array at r. When the unit-magnitude source at r is oriented in the η direction, the outputs of the sensor array are expressed as l(r) = L(r)η. This column vector l(r), referred to as the lead field vector, represents the sensitivity of the sensor array in the direction of η at the location r.

The outputs of the sensor array y are expressed as the sum of a magnetic signal b and additive sensor noise, represented by a random vector ε

$$\begin{array}{c}\mathbf{y}=\mathbf{b}+\mathbf{\epsilon }.\end{array}$$ (1)

Here, the magnetic signal b is expressed as

$$\begin{array}{c}\mathbf{b}={\mathbf{b}}_S+{\mathbf{b}}_I.\end{array}$$ (2)

Here, b_S, called the signal vector, represents the biomagnetic signal that is the target of the measurements, and b_I, called the interference vector, represents the interference overlapped onto the signal b_S. In this paper, the interference b_I represents so-called environmental noise, and sources of environmental noise are assumed to be located much farther from the sensors than the sources of interest are. Sources of environmental noise are, in general, located from several meters (in cases of the noise sources such as electronic appliances in a laboratory) to several kilometers (in cases of urban environmental noise sources such as the subway noise) distant from the magnetically shielded room.

The sources that generate b_S are confined to a region called the source space (e.g., the source space is the cardiac region for MCG and the brain region for MEG measurements). Let us assume that a total of Q discrete sources exist in the source space. Their locations are denoted by r₁,…, r_Q, their orientations by η₁,…, η_Q, and their magnitudes by s₁,…, s_Q. Then, the source distribution is expressed as

$$\begin{array}{c}s\left(\mathbf{r},t\right)=\sum _{q=1}^Q{s}_q{\mathbf{\eta }}_q\delta \left(\mathbf{r}-{\mathbf{r}}_q\right),\end{array}$$ (3)

where δ(r) indicates the Dirac delta function. The signal vector b_S is expressed as

$$\begin{array}{c}{\mathbf{b}}_S={\int }_{\mathrm{\Omega }}\mathbf{L}\left(\mathbf{r}\right)\sum _{q=1}^Q{s}_q{\mathbf{\eta }}_q\delta \left(\mathbf{r}-{\mathbf{r}}_q\right)d\mathbf{r}=\sum _{q=1}^Q{s}_q{\mathbf{l}}_q,\end{array}$$ (4)

where l_q represents the lead field vector of the qth source obtained such that l_q = L(r_q)η_q.

2.2. Derivation of SSS Basis Vectors

One fundamental assumption of the SSS method is that the sensors are installed in a source-free region, which is referred to as the sensor region. Then, the magnetic field at r, B(r), is expressed using the spherical polar coordinate r = (r, θ, ϕ) by

$$\begin{array}{c}\mathbf{B}\left(r\right)=-{\mu }_0\sum _{\mathrm{\ell }=1}^{\infty }\sum _{m=-\mathrm{\ell }}^{\mathrm{\ell }}{\alpha }_{\mathrm{\ell },m}\frac{{\mathbf{\nu }}_{\mathrm{\ell },m}\left(\theta ,\varphi \right)}{r^{\mathrm{\ell }+2}}-{\mu }_0\sum _{\mathrm{\ell }=1}^{\infty }\sum _{m=-\mathrm{\ell }}^{\mathrm{\ell }}{\beta }_{\mathrm{\ell },m}{r}^{\mathrm{\ell }-1}{\mathbf{\omega }}_{\mathrm{\ell },m}\left(\theta ,\varphi \right),\end{array}$$ (5)

where μ₀ indicates the magnetic permeability of free space. In (5), ν_ℓ,m(θ, ϕ) and ω_ℓ,m(θ, ϕ) are the modified vector spherical harmonics [8, 16]. The index parameter ℓ is called the multipole-order or multipole parameter. In the right-hand side of (5), the first term represents the magnetic field generated from sources located closer to the origin than the sensors are.

The second term represents the magnetic field from sources located farther from the origin than the sensors are. The region closer to the origin than the sensors is referred to as the internal region, and the region farther from the origin than the sensors is referred to as the external region. Let us define the polar radial coordinate of the sensor nearest to the origin as r_D^min and the radial coordinates of the sensor farthest from the origin as r_D^max. The internal region is formally defined as the region with r < r_D^min and the external region as the region with r > r_D^max. The region with r_D^min < r < r_D^max is called the intermediate region.

Let us derive the SSS basis vectors. To do so, the magnetic signal detected by the jth sensor is denoted by b_j and the location and the normal vector of the jth sensor by r_j and ζ_j. Then, we have

$$\begin{array}{c}{b}_j=\mathbf{B}\left({\mathbf{r}}_j\right)·{\mathbf{\zeta }}_j=b_{\mathrm{int}}^j+b_{\text{ext}}^j,\end{array}$$ (6)

where the notation “·” indicates taking the inner product between two vectors (note that when the area of the pickup coils is taken into consideration, the sensor signal b_j is obtained as a surface integral of B(r_j) · ζ_j over the area of the jth pick-up coil). Here, b_int^j and b_ext^j, respectively, represent magnetic components originating from the internal and external regions. These components are expressed as

$$\begin{array}{c}{b}_{\mathrm{int}}^j=-\sum _{\mathrm{\ell }=1}^{\infty }\sum _{m=-\mathrm{\ell }}^{\mathrm{\ell }}{\alpha }_{\mathrm{\ell },m}\frac{\left[{\mathbf{\nu }}_{\mathrm{\ell },m}\left({\theta }_j,{\varphi }_j\right)·{\zeta }_j\right]}{r_j^{\mathrm{\ell }+2}},\\ b_{\text{ext}}^j=-\sum _{\mathrm{\ell }=1}^{\infty }\sum _{m=-\mathrm{\ell }}^{\mathrm{\ell }}{\beta }_{\mathrm{\ell },m}{r}_j^{\mathrm{\ell }-1}\left[{\mathbf{\omega }}_{\mathrm{\ell },m}\left({\theta }_j,{\varphi }_j\right)·{\zeta }_j\right],\end{array}$$ (7)

where we set μ₀ = 1 for simplicity. Let us define the internal and external components of the vector b as b_int = [b_int¹,…,b_int^M]^T and b_ext = [b_ext¹,…,b_ext^M]^T, which are expressed such that

$$\begin{array}{c}{\mathbf{b}}_{\mathrm{int}}=\sum _{\mathrm{\ell }=1}^{\infty }\sum _{m=-\mathrm{\ell }}^{\mathrm{\ell }}{\alpha }_{\mathrm{\ell },m}{\mathbf{c}}_{\mathrm{\ell },m},\\ {\mathbf{b}}_{\text{ext}}=\sum _{\mathrm{\ell }=1}^{\infty }\sum _{m=-\mathrm{\ell }}^{\mathrm{\ell }}{\beta }_{\mathrm{\ell },m}{\mathbf{d}}_{\mathrm{\ell },m},\end{array}$$ (8)

where column vectors c_ℓ,m and d_ℓ,m are given by

$$\begin{array}{c}{\mathbf{c}}_{\mathrm{\ell },m}=\left[\begin{array}{c}\frac{1}{r_1^{\mathrm{\ell }+2}}\left[{\mathbf{\nu }}_{\mathrm{\ell },m}\left({\theta }_1,{\varphi }_1\right)·{\mathbf{\zeta }}_1\right]\\ ⋮\\ \frac{1}{r_M^{\mathrm{\ell }+2}}\left[{\mathbf{\nu }}_{\mathrm{\ell },m}\left({\theta }_M,{\varphi }_M\right)·{\mathbf{\zeta }}_M\right]\end{array}\right],{\mathbf{d}}_{\mathrm{\ell },m}=\left[\begin{array}{c}{r}_1^{\mathrm{\ell }-1}\left[{\mathbf{\omega }}_{\mathrm{\ell },m}\left({\theta }_1,{\varphi }_1\right)·{\mathbf{\zeta }}_1\right]\\ ⋮\\ r_M^{\mathrm{\ell }-1}\left[{\mathbf{\omega }}_{\mathrm{\ell },m}\left({\theta }_M,{\varphi }_M\right)·{\mathbf{\zeta }}_M\right]\end{array}\right].\end{array}$$ (9)

Truncating the summation with respect to the multiple order ℓ to L_C for b_int and L_D for b_ext, we finally obtain

$$\begin{array}{c}\mathbf{b}={\mathbf{b}}_{\mathrm{int}}+{\mathbf{b}}_{\text{ext}}=\sum _{\mathrm{\ell }=1}^{L_C}\sum _{m=-\mathrm{\ell }}^{\mathrm{\ell }}{\alpha }_{\mathrm{\ell },m}{\mathbf{c}}_{\mathrm{\ell },m}+\sum _{\mathrm{\ell }=1}^{L_D}\sum _{m=-\mathrm{\ell }}^{\mathrm{\ell }}{\beta }_{\mathrm{\ell },m}{\mathbf{d}}_{\mathrm{\ell },m}.\end{array}$$ (10)

Thus, defining

$$\begin{array}{c}\mathbf{C}=\left[{\mathbf{c}}_{1,-1},{\mathbf{c}}_{1,0},{\mathbf{c}}_{1,1},\dots ,{{{\mathbf{c}}_{L_C}}_{,}}_{L_C}\right],\\ \mathbf{D}=\left[{\mathbf{d}}_{1,-1},{\mathbf{d}}_{1,0},{\mathbf{d}}_{1,1},\dots ,{{{\mathbf{d}}_{L_D}}_{,}}_{L_D}\right],\\ \alpha ={\left[{\alpha }_{1,-1},{\alpha }_{1,0},{\alpha }_{1,1},\dots ,{{{\alpha }_{L_C}}_{,}}_{L_C}\right]}^T,\\ \beta ={\left[{\beta }_{1,-1},{\beta }_{1,0},{\beta }_{1,1},\dots ,{{{\beta }_{L_D}}_{,}}_{L_D}\right]}^T,\end{array}$$ (11)

we obtain

$$\begin{array}{c}\mathbf{b}={\mathbf{b}}_{\mathrm{int}}+{\mathbf{b}}_{\text{ext}}=\mathbf{C}\mathit{\alpha }+\mathbf{D}\mathit{\beta }=\left[\mathbf{C},\mathbf{D}\right]\left[\begin{array}{l}\mathit{\alpha }\\ \mathit{\beta }\end{array}\right]=\mathbf{S}\mathbf{x},\end{array}$$ (12)

where S = [C, D] and x = [α^T, β^T]^T. Here, C is an M × N_C matrix, and D is an M × N_D matrix, where

$$\begin{array}{c}{N}_C=L_C^2+2L_C,\\ N_D=L_D^2+2L_D.\end{array}$$ (13)

Note that the truncation values L_C and L_D correspond to the highest spatial frequencies possibly contained in b_int and b_ext [9, 17], respectively. Therefore, setting these parameters at too low values may result in an insufficient representation of the signal vectors b_int and b_ext. The effects of L_C and L_D for data from the 306-channel Elekta Neuromag have been investigated and values of L_C = 8 and L_D = 3 were found to be sufficient for such data sets in [8, 9].

2.3. SSS Signal Extractors

Equation (12) is the basis for estimating the internal and external components b_int and b_ext from given magnetic signal data b. That is, the least squares estimate $\widehat{\mathbf{x}}={\left[{\widehat{\mathbf{\alpha }}}^T,{\widehat{\mathbf{\beta }}}^T\right]}^T$ is obtained as

$$\begin{array}{c}\widehat{\mathbf{x}}={\left({\mathbf{S}}^T\mathbf{S}\right)}^{-1}{\mathbf{S}}^T\mathbf{b}.\end{array}$$ (14)

Then, b_int and b_ext are estimated as

$$\begin{array}{c}{\widehat{\mathbf{b}}}_{\mathrm{int}}=\mathbf{C}\widehat{\mathit{\alpha }},\end{array}$$ (15)

$$\begin{array}{c}{\widehat{\mathbf{b}}}_{\text{ext}}=\mathbf{D}\widehat{\mathit{\beta }}.\end{array}$$ (16)

We now derive SSS signal extractors and rewrite (15) and (16) using these extractors. To do so, let us define an operation to make a new column vector [a_i,…,a_j]^T by using the ith to jth components of a = [a₁,…,a_M]^T as [a]_{[i : j]} (namely, [a]_{[i : j]} = [a_i,…,a_j]^T). From (14), we have

$$\begin{array}{c}\widehat{\alpha }={\left[{\left({\mathbf{S}}^T\mathbf{S}\right)}^{-1}{\mathbf{S}}^T\mathbf{b}\right]}_{\left[1:N_C\right]}.\end{array}$$ (17)

With a small positive constant κ, the relationship

$$\begin{array}{c}\widehat{\mathit{\alpha }}={\left[{\left({\mathbf{S}}^T\mathbf{S}\right)}^{-1}{\mathbf{S}}^T\mathbf{b}\right]}_{\left[1:N_C\right]}\approx {\left[{\left({\mathbf{S}}^T\mathbf{S}+\kappa \mathbf{I}\right)}^{-1}{\mathbf{S}}^T\mathbf{b}\right]}_{\left[1:N_C\right]},\end{array}$$ (18)

holds. Then, using the matrix inversion formula

$$\begin{array}{c}{\left({\mathbf{S}}^T\mathbf{S}+\kappa \mathbf{I}\right)}^{-1}{\mathbf{S}}^T\mathbf{b}={\mathbf{S}}^T{\left({\mathbf{S}\mathbf{S}}^T+\kappa \mathbf{I}\right)}^{-1}\mathbf{b},\end{array}$$ (19)

we get

$$\begin{array}{c}\widehat{\mathit{\alpha }}\approx {\left[{\left({\mathbf{S}}^T\mathbf{S}+\kappa \mathbf{I}\right)}^{-1}{\mathbf{S}}^T\mathbf{b}\right]}_{\left[1:N_C\right]}={\left[{\mathbf{S}}^T{\left({\mathbf{S}\mathbf{S}}^T+\kappa \mathbf{I}\right)}^{-1}\mathbf{b}\right]}_{\left[1:N_C\right]}={\mathbf{C}}^T{\left({\mathbf{S}\mathbf{S}}^T+\kappa \mathbf{I}\right)}^{-1}\mathbf{b}\approx {\mathbf{C}}^T{\left({\mathbf{S}\mathbf{S}}^T\right)}^{-1}\mathbf{b}={\mathbf{C}}^T{\left({\mathbf{C}\mathbf{C}}^T+{\mathbf{D}\mathbf{D}}^T\right)}^{-1}\mathbf{b}.\end{array}$$ (20)

Using (15) and (20), we obtain

$$\begin{array}{c}{\widehat{\mathbf{b}}}_{\mathrm{int}}\approx {\mathbf{C}\mathbf{C}}^T{\left({\mathbf{C}\mathbf{C}}^T+{\mathbf{D}\mathbf{D}}^T\right)}^{-1}\mathbf{b}.\end{array}$$ (21)

Thus, the internal component b_int can be extracted by multiplying

$$\begin{array}{c}{\mathbf{P}}_{\mathrm{int}}={\mathbf{C}\mathbf{C}}^T{\left({\mathbf{C}\mathbf{C}}^T+{\mathbf{D}\mathbf{D}}^T\right)}^{-1},\end{array}$$ (22)

with the magnetic-field data b. That is, the matrix P_int acts as a projector that passes the internal components and blocks the external ones (note that since (P_int)² = P_int and (P_int)^T = P_int do not hold, P_int is not actually a projector). Therefore, we call P_int the SSS signal extractor in this paper.

In exactly the same manner, we can derive

$$\begin{array}{c}{\widehat{\mathbf{b}}}_{\text{ext}}=\mathbf{D}\widehat{\mathit{\beta }}\approx {\mathbf{D}\mathbf{D}}^T{\left({\mathbf{C}\mathbf{C}}^T+{\mathbf{D}\mathbf{D}}^T\right)}^{-1}\mathbf{b},\end{array}$$ (23)

and the SSS external-signal extractor P_ext is derived as

$$\begin{array}{c}{\mathbf{P}}_{\text{ext}}={\mathbf{D}\mathbf{D}}^T{\left({\mathbf{C}\mathbf{C}}^T+{\mathbf{D}\mathbf{D}}^T\right)}^{-1}.\end{array}$$ (24)

This P_ext passes the external components but blocks the internal ones.

2.4. Interference Suppression

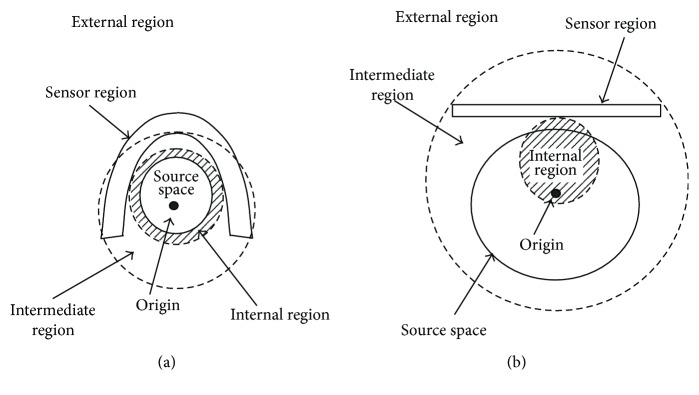
A key condition for the success of the SSS interference suppression is that the origin is properly set such that the source space Ω is included within the internal region and the interference sources are located within the external region. A typical configuration between the helmet-type sensor array and the source space is depicted in Figure 1(a). As can be seen in this figure, an appropriate location of the origin can be found so that the internal region covers the whole source space and the external region covers all locations of interference sources. (Note that, in this paper, interference indicates only environmental noise, and its sources are assumed to be located much farther from the sensors than the signal sources.)

Figure 1.

(a) A typical configuration of the internal region relative to the source space for a helmet-type sensor array. As can be seen, an appropriate location of the origin can be found such that the internal region covers the whole source space. (b) A possible configuration of the internal region relative to the source space in case of a flat sensor array. The internal region cannot entirely cover the source space, which extends into an intermediate region. In these figures, the inner circle with a broken line indicates the boundary between the internal and intermediate regions. The outer circle with a broken line indicates the boundary between the intermediate and external regions.

When this key condition is met, (10) provides a natural separation between the signal and interference. That is, when the source space is included within the internal region, the relationship

$$\begin{array}{c}{\mathbf{b}}_S\in \mathrm{s}\mathrm{p}\mathrm{a}\mathrm{n}\left(\mathbf{C}\right),\end{array}$$ (25)

holds, where the notation span (C) indicates the span of the column vectors of C. This span (C) is referred to as the internal subspace in this paper. That is, since the signal vector b_s belongs to the internal subspace, b_s is expressed as a linear combination of the column vectors of C

$$\begin{array}{c}{\mathbf{b}}_S=\sum _{j=1}^{N_C}{\alpha }_j{\mathbf{c}}_j=\mathbf{C}\mathit{\alpha },\end{array}$$ (26)

where c_j is the jth column of C, α_j is the jth expansion coefficient, and α is a column vector containing the coefficients (i.e., α = [α₁,…,α_NC]^T). Thus, denoting an N_D × 1 column vector whose elements are all zero by 0, we can derive the relationship

$$\begin{array}{c}{\mathbf{P}}_{\mathrm{int}}{\mathbf{b}}_S={\mathbf{P}}_{\mathrm{int}}\mathbf{C}\mathit{\alpha }={\mathbf{P}}_{\mathrm{int}}\mathbf{S}\left[\begin{array}{l}\mathit{\alpha }\\ \mathbf{0}\end{array}\right]=\mathbf{C}\left[{\mathbf{C}}^T{\left({\mathbf{S}\mathbf{S}}^T\right)}^{-1}\mathbf{S}\left[\begin{array}{l}\mathit{\alpha }\\ \mathbf{0}\end{array}\right]\right]=\mathbf{C}{\left[{\mathbf{S}}^T{\left({\mathbf{S}\mathbf{S}}^T\right)}^{-1}\mathbf{S}\left[\begin{array}{l}\mathit{\alpha }\\ \mathbf{0}\end{array}\right]\right]}_{\left[1:N_C\right]}=\mathbf{C}\left[{\left({\mathbf{S}}^T\mathbf{S}\right)}^{-1}{\mathbf{S}}^T\mathbf{S}\left[\begin{array}{l}\mathit{\alpha }\\ \mathbf{0}\end{array}\right]\right]=\mathbf{C}\mathit{\alpha }={\mathbf{b}}_S.\end{array}$$ (27)

The equation above indicates that the SSS signal extractor P_int passes the signal vector b_S with no distortion.

The assumption that the interference sources are located within the external region leads to

$$\begin{array}{c}{\mathbf{b}}_I\in \mathrm{s}\mathrm{p}\mathrm{a}\mathrm{n}\left(\mathbf{D}\right),\end{array}$$ (28)

where span(D) is referred to as the external subspace. Since the interference vector b_I belongs to the external subspace, the interference vector b_I is expressed as

$$\begin{array}{c}{\mathbf{b}}_I=\sum _{j=1}^{N_D}{\beta }_j{\mathbf{d}}_j=\mathbf{D}\mathit{\beta },\end{array}$$ (29)

where d_j is the jth column of D, β_j is the jth expansion coefficient, and β is a column vector containing coefficients β = [β₁,…,β_ND]^T . Again denoting the N_C × 1 column vector whose elements are all zero by 0, we have the relationship

$$\begin{array}{c}{\mathbf{P}}_{\mathrm{int}}{\mathbf{b}}_I={\mathbf{P}}_{\mathrm{int}}\mathbf{D}\mathit{\beta }={\mathbf{P}}_{\mathrm{int}}\mathbf{S}\left[\begin{array}{l}\mathbf{0}\\ \mathit{\beta }\end{array}\right]=\mathbf{C}{\left[{\left({\mathbf{S}}^T\mathbf{S}\right)}^{-1}{\mathbf{S}}^T\mathbf{S}\left[\begin{array}{l}\mathbf{0}\\ \mathit{\beta }\end{array}\right]\right]}_{\left[1:N_C\right]}=\mathbf{C}\mathbf{0}=\mathbf{0}.\end{array}$$ (30)

The equation above indicates that the extractor P_int completely blocks the interference vector b_I.

Consequently, using (1) and (2), we show

$$\begin{array}{c}{\mathbf{P}}_{\mathrm{int}}\mathbf{y}={\mathbf{P}}_{\mathrm{int}}{\mathbf{b}}_S+{\mathbf{P}}_{\mathrm{int}}+{\mathbf{b}}_I+{\mathbf{P}}_{\mathrm{int}}\epsilon ={\mathbf{b}}_S+{\epsilon }^{\prime }.\end{array}$$ (31)

The equation above indicates that, by multiplying the extractor P_int with the data vector y, the signal vector b_S is selectively extracted with no distortion.

In (31), ε′ : (ε′ = P_intε) indicates the noise in the SSS-cleaned data. Assuming that the sensor noise ε is Gaussian with the covariance matrix σ²I, the covariance matrix of ε′, Σ_ε′ is derived such that

$$\begin{array}{c}\underset{{\epsilon }^{\prime }}{\Sigma }=〈{\epsilon }^{\prime }{\left({\epsilon }^{\prime }\right)}^T〉={\mathbf{P}}_{\mathrm{int}}〈{\epsilon \epsilon }^T〉{\mathbf{P}}_{\mathrm{int}}^T={\sigma }^2{\mathbf{P}}_{\mathrm{int}}{\mathbf{P}}_{\mathrm{int}}^T,\end{array}$$ (32)

where we have 〈εε^T〉 = σ²I and the notation 〈·〉 indicates averaging. The equation above shows that P_intP_int^T can be considered as the noise gain of the SSS interference suppression process. Particularly, since the diagonal elements of Σ_ε′ expresses the gain relationship between the variances of the input and output noises, we define the noise gain G_ε such that

$$\begin{array}{c}{G}_{\epsilon }=\frac{1}{M}\underset{j=1}{\overset{M}{\Sigma }}{\left[\underset{{\epsilon }^{\prime }}{\Sigma }\right]}_{j,j},\end{array}$$ (33)

where [Σ_ε′]_j,j indicates the jth diagonal element of the matrix Σ_ε′.

2.5. SSS Method for Flat Sensor Arrays

In Figure 1(b), a possible configuration of the internal region relative to the source space and sensors is depicted for the case of a flat sensor array. As shown here, the internal region may not cover the entire source space, and the source space is extended into the intermediate region. As a result, the lead field vector of a signal source, l_q, may have components expanded by the columns of D, as well as components expanded by the columns of C, resulting in

$$\begin{array}{c}{\mathbf{l}}_q=\mathbf{C}{\mathit{\alpha }}^{\prime }+\mathbf{D}{\mathit{\beta }}^{\prime },\end{array}$$ (34)

where α′ and β′ are column vectors containing the expansion coefficients.

Therefore, by applying the SSS extractor P_int to l_q, we have

$$\begin{array}{c}{\mathbf{P}}_{\mathrm{int}}{\mathbf{l}}_q={\mathbf{P}}_{\mathrm{int}}\left[\mathbf{C}{\mathit{\alpha }}^{\prime }+\mathbf{D}{\mathit{\beta }}^{\prime }\right]=\mathbf{C}{\mathit{\alpha }}^{\prime }={\tilde{\mathbf{l}}}_q.\end{array}$$ (35)

That is, the extractor P_int changes the lead field of this signal source from l_q to ${\tilde{\mathbf{l}}}_q$. Assuming that Q signal sources exist, the signal vector b_S(t) is expressed as

$$\begin{array}{c}{\mathbf{b}}_S\left(t\right)=\sum _{q=1}^Q{s}_q\left(t\right){\mathbf{l}}_q.\end{array}$$ (36)

This signal vector changes to ${\tilde{\mathbf{b}}}_S\left(t\right)$, which is given by

$$\begin{array}{c}{\tilde{\mathbf{b}}}_S\left(t\right)={\mathbf{P}}_{\mathrm{int}}{\mathbf{b}}_S\left(t\right)={\mathbf{P}}_{\mathrm{int}}\sum _{q=1}^Q{s}_q\left(t\right){\mathbf{l}}_q=\sum _{q=1}^Q{s}_q\left(t\right){\mathbf{P}}_{\mathrm{int}}{\mathbf{l}}_q=\sum _{q=1}^Q{s}_q\left(t\right){\tilde{\mathbf{l}}}_q.\end{array}$$ (37)

It is clear here that applying the SSS extractor P_int distorts the signal vector b_S(t). This is a problem that occurs when the SSS method is applied to data measured with a flat sensor array. Computer simulation-based investigation of the signal distortion and its correction are given in Section 3.6.

As can be seen in Figures 1(a) and 1(b), the external region does not differ between helmet and flat sensor arrays. In this paper, we assume that all interference is environmental noise and no interference sources exist in the vicinity of sensors. Since, under this assumption, we assume that all interference sources are located in the external region, the interference vector b_I(t) does not have components belonging to span (C), and applying P_int to the data vector removes the interference vector.

2.6. Evaluation of the SSS Method's Performance

As discussed in the preceding sections, a flat sensor array imposes nonideal conditions on the SSS interference suppression, and (25) is never fulfilled. In addition, the existence of sensor calibration errors (which will be considered in Section 3.4) could, to some extent, invalidate the assumption in (28). Therefore, for data from flat sensor arrays, the relationships

$$\begin{array}{c}{\mathbf{P}}_{\mathrm{int}}{\mathbf{b}}_S={\mathbf{b}}_S,\\ {\mathbf{P}}_{\mathrm{int}}{\mathbf{b}}_I=0,\end{array}$$ (38)

will never be attained.

We can evaluate the performance of the SSS method for data from flat sensor arrays by checking how close the SSS-processed results come to (38). Namely, we define the performance measures such that

$$\begin{array}{c}{G}_S=\frac{‖{\mathbf{P}}_{\mathrm{int}}{\mathbf{b}}_S‖}{‖{\mathbf{b}}_S‖},\end{array}$$ (39)

$$\begin{array}{c}{G}_I=\frac{‖{\mathbf{P}}_{\mathrm{int}}{\mathbf{b}}_I‖}{‖{\mathbf{b}}_I‖}.\end{array}$$ (40)

In the equations above, G_S is called the signal gain. Ideally, G_S is equal to 1, and deviation of G_S from 1 is a measure of performance degradation of the SSS method. G_I is called the interference gain. Ideally, G_I is equal to zero, indicating that the method completely blocks the interference. Thus, a deviation of G_I from 0 is a measure of the performance degradation. Note that 1/G_I has been often called the shield factor in the previous literature [9, 18]. We use G_S and G_I (or 1/G_I, the shield factor), as well as the noise gain G_ε in (33) to evaluate the performance of the SSS method when it is applied to data from flat sensor arrays in Section 3.

3. Computer Simulation

3.1. Problems with Flat Sensor Data for SSS Applications

In order to show that the SSS method is still effective for data from sensors arranged on a flat plane, a series of computer simulation has been performed. First, we clarify the problems caused when the SSS method is applied to flat sensor data by comparing two cases of SSS application: one in which a helmet-type sensor array is used and the other in which a flat sensor array is used. For helmet-type sensor arrays, the key condition for the SSS method can be fulfilled, that is, one can find a proper location of the origin so that the internal region includes the source space and the external region includes the locations of interference sources, as depicted in Figure 1(a). Therefore, the SSS method can effectively suppress the interference with no signal distortion. For flat sensor arrays, however, the internal region covers only a part of the source space, which extends into the intermediate region, as depicted in Figure 1(b). Therefore, the signal vector has both external and internal components, and, as a result, the signal vector is distorted through the SSS application.

Let us first check this fact. An array of sensors and the coordinate system used in our computer simulation are shown in Figure 2(a). The sensor array consists of 64 sensors arranged in an 8 × 8 configuration on the plane z = 10 cm; the plane on which sensors are arranged is called the sensor plane. The sensor array covers an area of 20 cm × 20 cm, and the sensors measure only the z component of the magnetic field, which is the component normal to the sensor plane. This sensor arrangement is almost the same as the one in the MC-6400MCG system (Hitachi High-Technologies Corporation, Tokyo, Japan), which is used in a number of investigations [11–13]. A similar sensor arrangement is used in the KRISS 64-channel biomagnetometer (Bio-Signal Research Center, KRISS, Daejeon, Korea). Therefore, the arrangement of the sensor array assumed in this computer simulation can be considered as a typical one used in current clinical MCG studies.

Figure 2.

(a) An array of sensors and the coordinate system used in our computer simulation. The sensor array consists of 64 sensors arranged in an 8 × 8 configuration on the plane z = 10 cm, called the sensor plane. The sensor array covers an area of 20 cm × 20 cm, and the sensors measure the z component of the magnetic field, which is the component normal to the sensor plane. The source space (−10 ≤ x ≤ 10 cm, −10 ≤ y ≤ 10 cm, −7 ≤ z ≤ 7 cm) is shown. (b) The source time course assumed for a source located at (−3 cm, 0 cm, and 2 cm). (c) The signal sensor data b_S(t) are shown in the upper panel, and the signal plus sensor-noise data b_S(t) + ε are shown in the lower panel. Here, sensor noise was added to the signal data with the signal-to-noise ratio (SNR) of 10. The sensor time courses are normalized to the maximum value in each panel, and the ordinate indicates the normalized values.

A single source was assumed to exist at (−3 cm, 0 cm, and 2 cm), and the source time course assigned to this source is shown in Figure 2(b). The signal sensor data b_S(t) were computed by projecting the source time course through the sensor lead field obtained using the Biot-Savart law. The signal data b_S(t) are shown in the upper panel of Figure 2(c). Sensor noise was then added to the signal data with a signal-to-noise ratio (SNR) of 10 to generate the signal plus sensor-noise data, b_S(t) + ε, which are shown in the lower panel of Figure 2(c). Here, the sensor noise was assumed to be the white Gaussian noise uncorrelated between different sensor channels, that is, the noise vector had a statistical property of ε ~ N(ε | 0, σ²I), where σ² is the variance of the noise in all sensor channels.

In order to generate environmental noise, four interference sources were assumed to exist; their coordinates and distances from the center of the sensor array are shown in Table 1. The locations of these interference sources with respect to the sensor array are shown in Figure 3(a). Four random time courses shown in Figure 3(b) were assigned to these four interference sources, and the interference data b_I(t) were computed. The generated interference data are shown in Figure 3(c).

Table 1.

Locations of interference sources assumed in a computer simulation.

Source number	Location (cm)	Distance from the sensor array (cm)
1	(−60, 130, 200)	238
2	(300, −150, 360)	485
3	(−72, −80, −200)	236
4	(−105, −150, −100)	214

Figure 3.

(a) Locations of four interference sources shown with respect to the sensors. (b) Random (normalized) time courses assigned to the four interference sources. (c) Generated interference sensor data b_I(t). These interference sensor data are computed by projecting the interference-source time courses in (b) through the sensor lead field obtained using the Biot-Savart law. The sensor time courses are normalized, and the ordinate indicates the normalized values.

We applied the SSS extractors to b_S(t) and b_I(t) in order to check how large the internal and external components are in each of b_S(t) and b_I(t). The upper and lower panels, respectively, of Figure 4(a) show P_intb_S(t) and P_extb_S(t). Here, P_intb_S(t) and P_extb_S(t) indicate the internal and external components contained in b_S(t). These results show that the signal vector b_S(t) contains a considerable amount of external components, confirming the validity of our analysis in Section 2.5. The upper and lower panels, respectively, of Figure 4(b) show P_intb_I(t) and P_extb_I(t). Here, P_intb_I(t) is nearly equal to zero, and P_extb_I(t) is almost the same as b_I(t). These results verify our arguments in Section 2.5 that b_I(t) contains almost no internal components.

Figure 4.

Results of experiments that apply the SSS extractors to b_S(t) and b_I(t) computed assuming the flat sensor array in Figure 2(a). (a) The upper and lower panels, respectively, show P_intb_S(t) and P_extb_S(t), which indicate the internal and external components in b_S(t). (b) The upper and lower panels, respectively, show P_intb_I(t) and P_extb_I(t), which indicate the internal and external components in b_I(t). In the sensor time courses in (a), they are normalized to the maximum value from the upper panel, and the sensor time courses in (b), they are normalized to the maximum value from the lower panel.

We performed the same experiments using an MEG helmet-type sensor array for comparison; the arrangement of the helmet sensors used in this computer simulation is shown in Figure 5(a). The upper and lower panels, respectively, of Figure 5(b) show P_intb_S(t) and P_extb_S(t), and the upper and lower panels, respectively, of Figure 5(c) show P_intb_I(t) and P_extb_I(t). These results clearly confirm that the amount of the external components in b_S(t), as well as the amount of the internal components in b_I(t), is very small, explaining why the SSS method works well for data from helmet-type sensor arrays used in MEG.

Figure 5.

Results of the same experiments in which the SSS extractors are applied to b_S(t) and b_I(t), assuming a helmet-type sensor array used in MEG. (a) Locations of sensors in the helmet-type array assumed in this computer simulation. The sensor arrangement is from the 275-channel whole head sensor array of the Omega™ (VMS Medtech, Coquitlam, Canada). (b) The upper and lower panels, respectively, show P_intb_S(t) and P_extb_S(t). (c) The upper and lower panels, respectively, show P_intb_I(t) and P_extb_I(t). In the sensor time courses in (b), they are normalized to the maximum value from the upper panel, and the sensor time courses in (c), they are normalized to the maximum value from the lower panel.

3.2. Optimal Location of the Origin

We next explored the optimal location of the origin for SSS application to flat sensor data. The origin location significantly affects the final results of the SSS interference suppression, and, thus it is one of the most important parameters in the SSS implementation. In order to see how the origin location affects the SSS results, the internal component P_intb_S(t) and the external component P_extb_S(t) were computed with the origin set at four different locations of (0, 0, and z_ori) where z_ori was equal to 9 cm, 6 cm, 3 cm, and 0 cm. (Note that the center of the sensor array is located at (0 cm, 0 cm, and 10 cm)). Here, the signal sensor data (plus sensor noise) b_S(t) + ε shown in Figure 2(c) were used. The truncation values L_C and L_D were, respectively, set at 7 and 3, which are the values found to be optimal in previous investigations [8, 9]. Results of this experiment are shown in Figure 6, exhibiting a general tendency that the signal leakage becomes larger when the origin becomes closer to the sensor plane (z = 10 cm). However, the results also show that when the origin becomes farther from the sensor plane, the SSS results become significantly noisy. In summary, the location of the origin affects both the amount of signal leakage and the noise in the SSS results.

Figure 6.

The internal component P_int(b_S(t) + ε) and the external component P_ext(b_S(t) + ε) of the signal vector (plus sensor noise) with four different locations of the origin (0, 0, and z_ori): (a) z_ori = 0 cm, (b) z_ori = 3 cm, (c) z_ori = 6 cm, and (d) z_ori = 9 cm. The upper panel indicates the internal components, and the lower indicates the external components P_extb_S(t). The filled circle shows the location of the origin, and the square indicates the location of the source. In each pair of the sensor time courses, they are normalized to the maximum value from the upper panel, and the ordinate indicates the normalized values.

The amount of signal leakage can be assessed by the signal gain G_S defined in (39). Let us derive a quantitative relationship of the signal gain G_S versus z_ori. To do this, voxels with 0.5 cm intervals were assumed in a 3-dimensional source space (−10 ≤ x ≤ 10 cm, −10 ≤ y ≤ 10 cm, and −7 ≤ z ≤ 7 cm), which is shown in Figure 2(a). The signal sensor data b_S(t) were computed by setting the signal source at one of the voxel locations, and the signal gain G_S was computed using b_S(t). The mean signal gain was computed by averaging the signal gains obtained from all voxel locations. Here, the SSS extractor was derived with z_ori varied from 0 cm to 10 cm. The mean signal gain versus z_ori is plotted with a broken line in Figure 7(a). It can be seen in these plots that G_S gradually decreases as the origin becomes closer to the sensor plane.

Figure 7.

(a) Plots of the mean signal gain G_S, the noise gain G_ε, and their ratio G_S/G_ε versus the z coordinate of the origin z_ori. The signal sensor data b_S(t) were computed by setting the signal source at one of the voxel locations, and the signal gain G_S was obtained. The mean signal gain was computed by averaging G_S obtained from all voxel locations. (b) The mean interference gain G_I versus z_ori. The plot with the broken line shows the case r_I = 20 m, and the plot with the solid line shows the case r_I = 5 m. The interference data b_I were computed by setting a source at 100 equally spaced locations on the surface of a sphere with a radius of r_I, and the interference gain G_I was obtained. The mean interference gain was computed by averaging G_I obtained from all 100 source locations. The sphere with a radius r_I is shown in the upper part.

The noise gain G_ε is also plotted in Figure 7(a), and we can see that the noise gain becomes significantly larger as the origin becomes farther from the sensor plane, confirming the general tendency observed in Figure 6. The ratio G_S/G_ε is also plotted in Figure 7(a), and it can be seen that the ratio gradually increases as the origin becomes closer to the sensor plane. It reaches maximum at z_ori approximately equal to 9 cm.

We next performed computer simulation to derive the relationship between the interference gain G_I and the origin location z_ori. To do this, we assumed a sphere with its radius equal to r_I and its center at the center of the sensor array; such a sphere is shown in the upper part of Figure 7(b). The surface of the sphere was defined as a region where interference sources exist, and the interference data b_I(t) were computed by assuming that a single interference source exists on the surface. The interference gain G_I was computed with 100 different locations of the interference source, and the mean interference gain is computed and plotted with respect to the origin parameter z_ori. Here, denoting the polar coordinate of the interference source by (r_I, θ, ϕ), 100 locations of the interference source were determined as locations with 10 equal-interval θ and 10 equal-interval φ.

The plots of G_I with respect to z_ori are shown in Figure 7(b). Here, two cases, r_I = 5 m and r_I = 20 m, are shown. The case r_I = 5 m represents cases in which an interference source is located relatively near to the sensors, and the case r_I = 20 m represents cases in which an interference source is located relatively far from the sensors. These plots indicate that the interference gain generally decreases as the origin becomes closer to the sensors, and it reaches a minimum at z_ori ≈ 9 cm for both cases.

3.3. Choices of L_C and L_D, Truncated Values of Multipole-Order ℓ

We explore the optimal values of the parameters L_C and L_D, which are the truncation values of the multipole-order ℓ introduced in (10). So far, these parameters have been set at the values found to be optimal in previous investigations [8, 9], and so, L_C and L_D were, respectively, set at 7 and 3 in the preceding subsections. In Figure 8, the signal gain G_S, noise gain G_ε, and their ratio G_S/G_ε are plotted with respect to z_ori for three different values of L_C (L_C = 5, 6, and 7) and two different values of L_D (L_D = 2 and 3). The noise gain is plotted in Figure 8(a), the signal gain in Figure 8(b), and the gain ratio in Figure 8(c). In these figures, the broken lines indicate the results with L_D = 2, and the solid lines indicate those with L_D = 3.

Figure 8.

(a) The signal gain G_S, (b) noise gain G_ε, and (c) their ratio G_S/G_ε plotted with respect to the origin's z coordinate, z_ori, for three values of L_C (L_C = 5, 6, and 7) and two values of L_D (L_D = 2 and 3). The broken lines indicate the results with L_D = 2, and the solid lines indicate those with L_D = 3.

It can be seen that the noise gain is considerably smaller when L_D = 2 than when L_D = 3. The signal gain when L_D = 2 is greater than when L_D = 3. The differences in the signal and noise gains among different values of L_C are generally small. These results suggest that L_D should be set at 2, rather than 3. In Figure 8(c), the plots of the gain ratio G_S/G_ε for L_D = 2 are shown to have peak maxima when z_ori > 8, regardless of the value of L_C. The results in Figure 8 suggest that, as far as the signal and noise gains concerned, L_D = 2 should be the best choice, and any value of L_C = 5, 6, and 7 may be chosen if we set z_ori such that z_ori > 8.

The interference gain is plotted with respect to z_ori for the three values of L_C and the two values of L_D in Figure 9. Here, the cases r_I = 5 m and r_I = 20 m are, respectively, shown in Figures 9(a) and 9(b), where the broken lines indicate the results of L_D = 2 and the solid lines indicate those of L_D = 3. These plots show that regardless of the values of L_C and L_D, there is a general tendency that the gain decreases as the origin becomes closer to the sensors, and it reaches a minimum near z_ori equal to 9 cm. Namely, the value of z_ori ≈ 9 cm gives the minimum interference gain (the maximum shield factor) for all values of L_C and L_D. On the basis of the results in Figures 8 and 9, we can conclude that the origin parameter z_ori should be set at 9, that is, the best origin location is determined as (0, 0, and 9), which is 1 cm below the center of the sensor array. We use this value throughout the experiments described below.

Figure 9.

The interference gain plotted with respect to the origin's z coordinate, z_ori, for three values of L_C (L_C = 5, 6, and 7) and two values of L_D (L_D = 2 and 3). (a) The distance to the interference source r_I is set at 5 m. (b) The distance to the interference source r_I is set at 20 m. The broken lines indicate the results with L_D = 2, and the solid lines indicate those with L_D = 3.

3.4. Influence of Sensor Calibration Errors

The SSS method is known to be very sensitive to sensor calibration errors, and an accurately calibrated sensor array is needed for effective suppression of interference [18]. Sensor calibration errors are known to severely affect the shielding capability, so the influence of sensor calibration errors on the interference gain G_I is investigated by using erroneous sensor locations and orientations when computing the SSS basis vectors. Here, the sensor location error E_loc is assessed using

$$\begin{array}{c}{E}_{\mathrm{l}\mathrm{o}\mathrm{c}}=\left(\frac{1}{M}\right)\sum _{j=1}^M\frac{‖{\mathbf{r}}_j^d-{\widehat{\mathbf{r}}}_j^d‖}{‖{\widehat{\mathbf{r}}}_j^d‖},\end{array}$$ (41)

where r_j^d is the true location of the jth sensor, and ${\widehat{\mathbf{r}}}_j^d$ is the calibrated location of this sensor. Note that ${\widehat{\mathbf{r}}}_j^d$ is assumed to contain an error. Here, r_j^d is obtained by adding (small) random displacements to ${\widehat{\mathbf{r}}}_j^d$. The signal vector b_S(t) and the interference vector b_I(t) were computed using the true location r_j^d, while the SSS basis vectors were computed using the calibrated location ${\widehat{\mathbf{r}}}_j^d$. In exactly the same manner, the error in the sensor orientation, E_ori, is assessed using

$$\begin{array}{c}{E}_{\mathrm{o}\mathrm{r}\mathrm{i}}=\left(\frac{1}{M}\right)\sum _{j=1}^M\frac{‖{\mathbf{\zeta }}_j-{\widehat{\mathbf{\zeta }}}_j‖}{‖{\widehat{\mathbf{\zeta }}}_j‖},\end{array}$$ (42)

where ζ_j is the true normal vector of the jth sensor, and ζ_bj is the calibrated normal vector, which is ${\widehat{\mathbf{\zeta }}}_j=\left(0,0,1\right)$. Here, ζ_j is obtained by adding random vectors to ${\widehat{\mathbf{\zeta }}}_j$. The signal vector b_S(t) and the interference vector b_I(t) were computed using ζ_j, while the SSS basis vectors were computed using the erroneous orientation ${\widehat{\mathbf{\zeta }}}_j$.

In Figure 10, the interference gain is plotted with respect to r_I, the distance to the interference source, for the three values of L_C and the two values of L_D. Again, the broken lines indicate the results with L_D = 2, and the solid lines indicate those with L_D = 3. Here, the plots in Figure 10(a) indicate the case of no calibration error (E_loc = E_ori = 0). The plots in Figures 10(b)–10(d), respectively, indicate the cases E_loc = E_ori = 0.03%, E_loc = E_ori = 0.1%, and E_loc = E_ori = 1%. In Figures 10(b)–10(d), the mean values obtained over 100 Monte Carlo trials are plotted. That is, a set of random values were assigned as the errors of sensor locations and orientations in each trial, and the mean results from 100 such trials are plotted.

Figure 10.

The plots of the interference gain G_I with respect to the distance to the interference source, r_I, for the three values of L_C and the two values of L_D. (a) No calibration errors (E_Loc = E_Ori = 0). (b) Calibration errors of E_Loc = E_Ori = 0.03%. (c) Calibration errors of E_Loc = E_Ori = 0.1%. (d) Calibration errors of E_Loc = E_Ori = 1%. The broken lines indicate the results with L_D = 2 and the solid lines indicate those with L_D = 3. The origin was set at (0 cm, 0 cm, and 9 cm) (z_ori = 9 cm).

First, we can observe that the interference gain (i.e., the shield factor) is seriously affected by the calibration errors. When there are no calibration errors, the shield factor 1/G_I for r_I > 15 m is greater than 10⁴ with L_D = 2 but it drops to less than 30 when E_loc = E_ori = 1%. Regarding the optimal choices of the parameters L_C and L_D, the choice of L_D = 2 mostly gives greater shield factor than L_D = 3. There are no significant differences among the choices of L_C, but the choice of L_C = 6 gives slightly better results when E_loc = E_ori > 0.1%. Since such errors as E_loc = E_ori > 0.1% may be considered the practical values of sensor calibration errors, the choices of L_C = 6 and L_D = 2 are determined as the best choices for the truncation of the multipole parameter ℓ. Note that, according to the arguments for signal and noise gains in Section 3.3, the choices of L_C = 6 and L_D = 2 also give the best results.

With the choices of L_C = 6, L_D = 2, and z_ori=9 cm, the interference gain G_I is replotted with respect to r_I, the distance to the interference source. The results are shown in Figure 11(a). It can be seen that the shield factor (1/G_I) exceeds 10⁴ for r_I > 15 m when no calibration errors exist but that the shield factor drops to 100 when calibration errors of 0.1% exist, and to 30 when calibration errors of 1% exist. With the parameter settings, L_C = 6, L_D = 2, and 1% sensor calibration errors, signal and noise gains versus z_ori are plotted in Figure 11(b). Here, the plot with the solid line indicates the case of no calibration errors, and the plot with the broken line indicates the case of 1% calibration errors. The two plots nearly overlap, and this fact confirms that the influence of calibration errors on the signal and noise gains is small.

Figure 11.

(a) The interference gain G_I replotted with respect to r_I, the distance to interference sources. The choices of L_C = 6, L_D = 2, and z_ori = 9 cm were used. (b) The signal and noise gains versus the origin's z coordinate (z_ori). The plots with the solid line indicate the case of no calibration errors, and the plots with the broken line indicate the case of 1% calibration errors. The multiple-order truncation was set such that L_C = 6 and L_D = 2.

3.5. The Performance of the SSS Method for Different Sensor Arrays

Here, the SSS performance with two different types of flat sensor arrays is tested: one is a sensor array with a larger sensor coverage and the other is a sensor array consisting of vector sensors. In the sensor array with a larger coverage, the sensors are arranged on a 24 cm × 24 cm coverage area and consist of 10 × 10 sensors that measure the magnetic field normal to the sensor plane. This sensor array is a larger-scale version of the sensor array used in the preceding subsections. The vector sensor array consists of 6 × 6 vector sensors arranged on a 20 cm × 20 cm coverage area. Here, a vector sensor indicates a set of three sensors; each measures one of the x, y, and z components of the magnetic field, and therefore this sensor array actually has a total of 108 sensors.

Assuming the sensor array with a larger sensor coverage, the interference gain G_I versus r_I (the distance to the interference sources) was plotted in Figure 12(a). It can be seen that the plots in this figure are almost the same as the plots in Figure 11(a), suggesting that the influence of the number of sensors and sensor coverage on the shielding capability is rather small. The signal and noise gains with respect to the origin's z coordinate (z_ori) were plotted in Figure 12(b), where the plot with the solid line indicates the case of no calibration errors and the plot with the broken line indicates the case of 1% calibration errors. Again, we can observe that the plots here are very similar to the plots in Figure 11(b).

Figure 12.

The SSS performance computed by assuming a larger sensor array in which the sensors are arranged on a 24 cm × 24 cm coverage area and consist of 10 × 10 sensors that measures the magnetic field normal to the sensor plane. (a) The interference gain G_I plotted with respect to r_I for six different calibration errors. The choices of L_C = 6, L_D = 2, and z_ori = 9 cm were used. (b) The signal and noise gains versus the origin's z coordinate (z_ori). The plots with the solid line indicate the case of no calibration errors, and the plots with the broken line indicate the case of 1% calibration errors. The multiple-order truncation was set such that L_C = 6 and L_D = 2.

The SSS performance for the vector sensor array was investigated. The interference gain G_I versus r_I was plotted in Figure 13(a). We can observe significant improvements in the shielding capability.

Figure 13.

The SSS performance computed by assuming a vector sensor array in which the array consists of 6 × 6 vector sensors arranged on a 20 cm × 20 cm coverage area. (a) The interference gain G_I plotted with respect to r_I for six different calibration errors. The choices of L_C = 6, L_D = 2, and z_ori = 9 cm were used. (b) The signal and noise gains versus the origin's z coordinate (z_ori). The plots with the solid line indicates the case of no calibration errors, and the plots with the broken line indicates the case of 1% calibration errors. The multiple-order truncation was set such that L_C = 6 and L_D = 2.

That is, with 1% calibration errors, the vector sensor array has a shield factor of approximately 500 (G_I = 2 × 10⁻³). The two sensor arrays with normal-component-only sensors have shield factors of nearly 30 with 1% calibration errors, according to Figures 11(a) and 12(a). These results are consistent with the previous investigation [19], which have reported SSS performance improvements due to the use of tangential sensors. The signal and noise gains with respect to the origin's z coordinate (z_ori) are plotted for the vector sensor array in Figure 13(b). It can be seen that the plots here are very similar to the plots in Figure 11(b)or 12(b), indicating that these gains are not affected by the use of vector sensors.

3.6. Correction of Signal Distortion in Source Space Analysis

3.6.1. Two-Dimensional Current-Density Reconstruction Experiments

As discussed in Section 2.5, the SSS-processed signal vector ${\tilde{\mathbf{b}}}_S\left(t\right)$$\left({\tilde{\mathbf{b}}}_S\left(t\right)={\mathbf{P}}_{\mathrm{int}}{\mathbf{b}}_S\left(t\right)\right)$ becomes distorted because the SSS application causes the removal of the external components from the signal vector b_S(t). This distortion, however, can be corrected by using the SSS-modified lead field because the distorted signal vector is expressed as a sum of distorted lead field vectors, as shown in (37). A series of computer simulations were performed to verify this idea. The results for 2-dimensional current-density mapping are presented in Figure 14.

Figure 14.

(a) Upper panel: the signal plus sensor-noise time courses b_S(t) + ε. Lower panel: the interference time courses b_I(t). (b) Upper panel: the interference-overlapped sensor time courses y(t). Lower panel: the SSS interference removal results P_inty(t). These time courses are normalized to the maximum value in each panel. (c) The current-density map obtained from b_S(t) + ε. (d) The current-density map obtained from interference-overlapped sensor time courses y(t). (e) The current-density map obtained from the SSS interference-removal results P_inty(t) with the original lead field L(r). (f) The current-density map obtained using P_inty(t) with the SSS-modified lead field $\tilde{\mathbf{L}}\left(\mathbf{r}\right)={\mathbf{P}}_{\mathrm{int}}\mathbf{L}\left(\mathbf{r}\right)$. Here, two-dimensional current-density maps on the plane z = 2 cm, which is the plane 8 cm below the sensor plane, are reconstructed using the field map at t = 1200. The signal data b_S(t) were computed assuming two sources, located at (−5 cm, 4 cm, and 3 cm) and (4 cm, −3 cm, and 3 cm).

The signal data b_S(t) were computed assuming the two sources located at (−5 cm, 4 cm, 3 cm) and (4 cm, −3 cm, and 3 cm). The signal plus sensor-noise data b_S(t) + ε are shown in the upper panel of Figure 14(a). The interference b_I(t) is generated by assuming the same four sources as in Figure 3(a); the generated interference is shown in the lower panel of Figure 14(a). The upper panel of Figure 14(b) shows the sensor time courses y(t); y(t) = b_S(t) + ε + ξ b_I(t), where a positive constant ξ controls the signal-to-interference ratio (SIR) (The SIR is defined as the ratio 〈‖b_S(t)‖〉/〈‖ξ b_I(t)‖〉 in this computer simulation), which was set equal to 0.25 in this computer simulation. The SSS interference suppression results P_inty(t) are shown in the lower panel of Figure 14(b).

The current-density reconstruction was performed using RENS beamformer, proposed in [20, 21]. The current-density map obtained from the signal plus sensor-noise data, b_S(t) + ε, is shown in Figure 14(c). This map works as the ground truth for the following experiments. The current-density map obtained from the interference-overlapped data y(t) is shown in Figure 14(d). The results far from the ground truth are obtained due to the overlap of the large interference.

The current-density reconstruction was performed twice, using the SSS results P_inty(t) with the original lead field L(r) and with the SSS-modified lead field $\tilde{\mathbf{L}}\left(\mathbf{r}\right)$: $\tilde{\mathbf{L}}\left(\mathbf{r}\right)={\mathbf{P}}_{\mathrm{int}}\mathbf{L}\left(\mathbf{r}\right)$. The current-density map obtained with the original lead field L(r) is shown in Figure 14(e). A considerable amount of distortion can be seen in this current-density map, although the SSS method seems to have nearly perfectly removed the interference according to the SSS-processed time courses (the lower panel of Figure 14(b)). The current-density map obtained with the SSS-modified lead field is shown in Figure 14(f). Here, results very close to the ground truth can be obtained; these results verify the idea that the signal distortion can be compensated for by using the SSS-modified lead field in the voxel space analysis.

3.6.2. Three-Dimensional Source Localization Experiments

Next, three-dimensional source localization experiments were performed. Reconstruction results obtained using the signal plus sensor-noise data shown in Figure 2(c) are shown in Figure 15(a). A single source is reconstructed near (−3, 0, and 2), which is the location assumed for the data generation. These results work as the ground truth when evaluating the following results. The interference-overlapped sensor data y(t) were computed using the interference data shown in Figure 3(c) overlapped onto these signal plus sensor-noise data with the SIR equal to 0.25. The source reconstruction was performed using the interference-overlapped sensor data y(t), and the results are shown in Figure 15(b). A large influence from the interference can be seen here.

Figure 15.

(a) Source reconstruction results obtained using the signal plus sensor-noise time courses in Figure 2(c). (b) Source reconstruction results obtained using the sensor time courses y(t) created by adding the interference data shown in Figure 3(c) onto the signal plus sensor-noise time courses in Figure 2(c). (c) Source reconstruction results obtained using the SSS interference removal results P_inty(t) with the original lead field L(r). (d) Source reconstruction results obtained using the SSS interference removal results P_inty(t) with the SSS-modified lead field $\tilde{\mathbf{L}}\left(\mathbf{r}\right)$. The RENS beamformer [20, 21] was applied to the field data at t = 1260 for three-dimensional source reconstruction.

The source reconstruction was carried out using the SSS interference suppression results P_inty(t) with the original lead field L(r). The results are shown in Figure 15(c), in which a single source is reconstructed but the location of the source differs considerably from the assumed location. The source reconstruction was then carried out using the SSS-modified lead field $\tilde{\mathbf{L}}\left(\mathbf{r}\right)$, and the results are shown in Figure 15(d). These results are almost the same as the ground truth, verifying the effectiveness of the use of the SSS-modified lead field in the voxel space analysis.

4. Discussion and Summary

This paper presented computer simulation-based investigation to explore the possibility of applying the SSS method to data measured from an array of sensors arranged on a flat plane, which is commonly used in magnetocardiographic applications. The findings from the investigation are summarized as follows:

1. When applying the SSS method to data from a flat sensor array, a signal vector has components of the external subspace as well as those of the internal subspace. As a result, the signal is distorted through the SSS interference suppression process.

2. The signal distortion can be compensated for by using the SSS-modified lead field in voxel space analysis. The computer simulations using two-dimensional current-density mapping and three-dimensional source localization confirmed that the distortion can be corrected in the voxel space.

3. The origin location can significantly affect the results of the SSS method. It is shown that the optimal location of the origin can be determined by assessing the dependence of signal and noise gains of the SSS extractor on the origin location. The optimal location is empirically found to be approximately 1 cm below the sensor plane for typical flat sensor arrays used in MCG applications.

4. The optimal values of the parameters L_C and L_D, the truncation values of the multipole-order ℓ, can also be determined by evaluating dependences of the signal, noise, and interference gains (shield factor) on these parameters. Results of computer simulation suggest L_D = 6 and L_D = 2 to be the optimal choices for typical flat sensor arrays currently used in clinical magnetocardiography.

5. The sensor calibration errors affect the shielding capability. The shield factor exceeds 10⁴ for interference originating from fairly distant sources (r_I > 15 m) when no calibration errors exist. However, the shield factor drops to approximately 100 when the calibration errors become 0.1% and to 30 when the calibration errors become 1%.

6. The shielding capability can significantly be improved by using vector sensors, which measure the x, y, and z components of the magnetic field. With 1% calibration errors, a vector sensor array still maintains a shield factor of approximately 500, while the arrays with sensors measuring only the normal direction have a shield factor of about 30 with the same 1% calibration errors.

Finally, it should be emphasized that the SSS interference suppression method is effective even for arrays of sensors arranged on a flat plane. This is the main finding in this paper. The use of such signal processing methods with low-cost sensors, such as magnetoresistive sensors, can lead to the development of low-initial-cost and maintenance-free magnetocardiography systems, which in the near future may replace the electrocardiogram now routinely used in hospitals.

Conflicts of Interest

The authors declare that they have no conflicts of interest.