Big Data Toolsets to Pharmacometrics: Application of Machine Learning for Time‐to‐Event Analysis

Abstract

Additional value can be potentially created by applying big data tools to address pharmacometric problems. The performances of machine learning (ML) methods and the Cox regression model were evaluated based on simulated time‐to‐event data synthesized under various preset scenarios, i.e., with linear vs. nonlinear and dependent vs. independent predictors in the proportional hazard function, or with high‐dimensional data featured by a large number of predictor variables. Our results showed that ML‐based methods outperformed the Cox model in prediction performance as assessed by concordance index and in identifying the preset influential variables for high‐dimensional data. The prediction performances of ML‐based methods are also less sensitive to data size and censoring rates than the Cox regression model. In conclusion, ML‐based methods provide a powerful tool for time‐to‐event analysis, with a built‐in capacity for high‐dimensional data and better performance when the predictor variables assume nonlinear relationships in the hazard function.

Study Highlights

WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC?

✓ Tools used for big data analysis have not been introduced to the community of pharmacometrics or quantitative clinical pharmacology. There is no report to introduce machine‐learning techniques to analyze time‐to‐event data that have been conventionally analyzed using the Cox regression model from the ASCPT community.

WHAT QUESTION DID THIS STUDY ADDRESS?

✓ Cox model, as the de facto standard, has long been used for survival analysis, although it is known that it operates under potentially oversimplified assumptions. Given that, what benefits can the ML‐based methods bring to survival analysis?

WHAT THIS STUDY ADDS TO OUR KNOWLEDGE

✓ ML‐based methods outperformed the Cox model in predictive performance when covariates manifest the nonlinear relationships in the hazard function, and in identifying influential variables of high‐dimensional data, with less sensitivity to data sizes and censoring rates.

HOW THIS MIGHT CHANGE CLINICAL PHARMACOLOGY OR TRANSLATIONAL SCIENCE

✓ Big data tools such as ML‐based methodologies can potentially serve as more powerful and flexible pharmacometrics tools to provide accurate and robust survival analysis in clinical studies over conventional approaches.

Time‐to‐event analysis, also referred to as survival analysis in this study, is performed to analyze the expected time‐to‐event occurrence. This technique was originally developed for clinical studies, and now has been applied to many other areas, e.g., engineering, economics, finance, healthcare, marketing, business process optimization, and even public policy. The survival data (or time‐to‐event data) are often featured by censoring in the data when there is no event during the study period. For survival analysis, the Cox proportional hazard (PH) regression model1, 2 is one of the most commonly used analysis methods, which links predictors of interest, also referred to as covariates in this study, to relevant hazard function, without predefining a particular distribution for the baseline hazard. Similar regression‐based methods also include the accelerated failure time (AFT) model3, 4, 5 and parametric PH model.6 Although these methods have been conventionally used for survival analysis, they are essentially an endeavor to explicitly model the underlying relationships among the variables under certain assumptions that the hazard function of the predictor variables are constant over time and their effects are additive in one scale. Of note, these assumptions may be oversimplified when modeling real‐world data. In addition, owing to rapid advances in information technologies, data have become overwhelmingly large, raising significant computational challenges for conventional regression‐based survival analysis methods. For example, high‐dimensional data become common when more covariates than observations are collected. Although the constrained version of regression‐based method can mitigate the issue of high‐dimensional data, the linear additive assumption for covariates still lacks a validity check before modeling application.7 Therefore, developments of advanced data analytic techniques for survival analysis are still of high importance.

In the past decades, the development of machine learning (ML) methods has impacted a broad spectrum of research areas,8, 9 including handling survival data. ML methods are data‐driven by nature, with minimal model assumptions and feature the capacity to deal with high‐dimensional data. In the 1990s, the artificial neural networks (ANN) were applied for more flexible modeling of covariate effects in the survival function, offering new insight for clinical and physiological hypothesis generation.10, 11 Subsequently, the decision tree‐based ML algorithm, the random survival forest (RSF) approach, was developed in the 2000s for survival analysis,12, 13, 14 showing advanced performances in the identification of important covariates and predictive capability. Recently, the support vector machine (SVM) was proposed to process survival data.15 The concept of deep learning,16 as deployed in the AlphaGo program,17 representing the latest development in artificial intelligence, has also been adapted for survival analysis.18 Despite these applications of ML algorithms, the ML‐based survival analysis has not been well recognized and there is currently no systematic evaluation for ML algorithms with regard to their performance advantages over the conventionally used regression‐based methods (e.g., Cox model). In this study, we performed extensive simulations to evaluate: i) whether performances of conventional regression‐based methods can be significantly compromised if the survival data defy their specific model assumptions; ii) whether the ML‐based methods outperform the conventional methods in scenarios when the true underlying hazard function assumes more complex relationships with the corresponding covariates; and iii) whether the ML‐based methods are capable of accommodating high‐dimensional survival data and are superior to conventional methods in both identifying the significant covariates and making reliable predictions. Furthermore, based on a set of covariate effects derived from a real exposure–response (E‐R) analysis of an anticancer therapy study, we simulated real‐world survival data sets to assess the effectiveness and flexibility of ML‐based methods. For the ML‐based methods, we adopted the well‐developed ANN and RSF as proxies for the ML approach, whereas the ordinary Cox model was used as a representative proxy for the regression‐based survival analysis method. In the remainder of this article, without loss of generality, right‐censored data were generated in the simulations.

METHODS

Descriptions of established methodologies are provided in the Supplementary Information, with only critical aspects of the procedures highlighted here.

Simulations of time‐to‐event data

Simulations of survival data hold unique strength in investigating the specific properties, performance, and adequacy of survival analysis methods. Survival data in this study were simulated based on preset Cox models,19 yet with specific changes. Without loss of generality, the Weibull distribution was used for survival time generation. By changing the relations of predictor variables in the hazard function, more nonlinear cases can be created. Detailed mathematical formulation and the procedure of simulating survival data with preset censoring rate is described in the Supplementary Information.

We simulated the survival data via two approaches: i) by hypothetical mathematical models (Table 1), and ii) by clinically relevant models (Table 2). With approach i, six groups of survival data sets were generated with different relationships between the predictor variables in the hazard function: (1) linear, (2) nonlinear, (3) interaction, (4) nonlinear + interaction, (5) nonlinear + interaction + correlation, and (6) high‐dimension. With approach ii, three groups of survival data sets were simulated based on a real‐world E‐R relationship for an anticancer drug with different relationships for the predictor variables, including (A) linear + interaction, (B) nonlinear, and (C) nonlinear + interaction. In each group, multiple data sets (e.g., 500) were generated to conduct predictive performance evaluations. Each data set consisted of training data and testing data that were independently generated from the same given model.

Table 1.

Summary of simulated bivariate models ( ${\beta }_1=-0.6$, ${\beta }_2=0.3$)

Model	Description	Relationship for covariates in hazard function
I	Linear	${\beta }_1{x}_1+{\beta }_2{x}_2$
II	Nonlinear	${\beta }_1{e}^{{x_1}^2}+{\beta }_{2}cos{x}_2$
III	Interaction	$2x_1{x}_2$
IV	Nonlinear + Interaction	${\beta }_1{e}^{{x_1}^2}+{\beta }_{2}cos{x}_2+2x_1{x}_2$
V	Nonlinear + Interaction + Correlation	${\beta }_1{e}^{x_1^2}+{\beta }_{2}cos{x}_2+2x_1{x}_2,cor(x_1,x_2)=0.7$

Table 2.

Summary of clinically relevant models for data generation

Model	Description	Relationship for covariates in hazard function
A	Interaction between ECOG and Ctrough	${\beta }_1\times ECOG+{\beta }_2\times Tumorsize+{\beta }_3\times C_{trough}+{\beta }_{13}\times ECOG\times C_{trough}$
B	Nonlinear drug exposure effects	${\beta }_1\times ECOG+{\beta }_2\times Tumorsize+{\beta }_{13}\times \frac{60\times C_{trough}}{30+C_{trough}}$
C	Interaction between nonlinear drug exposure effect and ECOG	${\beta }_1\times ECOG+{\beta }_2\times Tumorsize+{\beta }_{13}\times \frac{60\times C_{trough}}{30+C_{trough}}\times (1-ECOG)$

Machine‐learning based survival analysis

In recent years, ML algorithms have been extensively disposed in various domains; in this study, two well‐established ML‐based methods, RSF and ANN, were applied on simulation data for survival analysis. The methodologies are provided in the Supplementary Information. For RSF, 200 trees were built and a log‐rank splitting rule for survival curves20 was applied to establish the model. For ANN, we adopted the partial logistic regression approach (PLANN)10 based on a three‐layer, feed‐forward neural network among several previously proposed ANN strategies for survival analysis.10, 21, 22, 34 A grid search strategy was incorporated for finding the optimal setting of ANN by fivefold validation.23

Performance evaluation for survival model

It is desirable that a survival model could correctly distinguish between high‐risk and low‐risk individuals, and predict a probability of the event of interest prior to a specified time. Prediction accuracy is therefore an important metric for performance evaluation of a survival model. One popular evaluation metric for prediction accuracy, concordance index (C‐index)24 (see Supplementary Information for the estimation procedure), was used to compare model performance between the conventional Cox model and ML‐based approaches (i.e., RSF and ANN). The C‐index is related to the area under the receiving operating characteristic (ROC) curve, and is regularly used as prediction error estimation. In addition, the C‐index does not depend on a single fixed time for evaluation, and specifically accounts for the presence of the censoring. Over multiple simulation data sets, mean C‐index was obtained for the same given model to mitigate the stochastic effect from randomly generated data sets.

RESULTS

Simulations based on mathematical models

To demonstrate the appealing properties of ML‐based approaches in survival analysis, e.g., minimal assumption for data and capacity to deal with high‐dimensional data, we simulated six groups of survival data from hypothetical mathematical models (1–6) (see METHODS section). As shown in Table 1, five bivariate models (I–V) were designed to represent various relationships among predictor variables $\mathbf{x}=(x_1,x_2)$ with progressively increasing complexity. In Model I, two covariates have an effect on the hazard with linear relationships. Model II assumes a case where covariate affects the risk function nonlinearly. Interaction between covariates is manifested in Model III. Model IV consists of both a nonlinear and interaction term of covariates. In Model V, the relationship among covariates remains the same as Model IV, while covariates are correlated. We designed Model VI to represent the high‐dimensional scenario, in which 250 covariates were sampled from multivariate normal distribution with 200 observations. In the model, 250 covariates follow linear additive relationship, and the covariate coefficients are set to zero except for the first 25 covariates (covariate coefficients as 0.2; mutually correlated with each other with correlation coefficient of 0.7), so that we can examine if a survival model can correctly describe such high‐dimensional data, and offer insights into the preset important covariates even when they are sparse (i.e., 25/250). Both ML‐based methodologies (RSF and ANN) and the Cox model are applied to the simulated data for performance evaluations.

Visual inspection of simulated data

Survival data were generated from Models I‐V with sample size n = 500 and censoring rate of 0.25. Figure 1 displays the Kaplan–Meier25 curves of the generated data from the five models. The curve for Model I (linear additive relationship between covariates; lower green curve) is significantly different from the other Models, despite the covariates being drawn from the same distribution, suggesting that relationship assumption among covariates may have significant impact on survival assessment. If the real survival data defy the linear additive assumption (say “nonlinear relationship” as Model II), application of the Cox model to the data is equivalent to using the model suitable for Model I curve to analyze Model II curve (Figure 1), where suboptimal estimation due to model misspecification could be expected.

Figure 1.

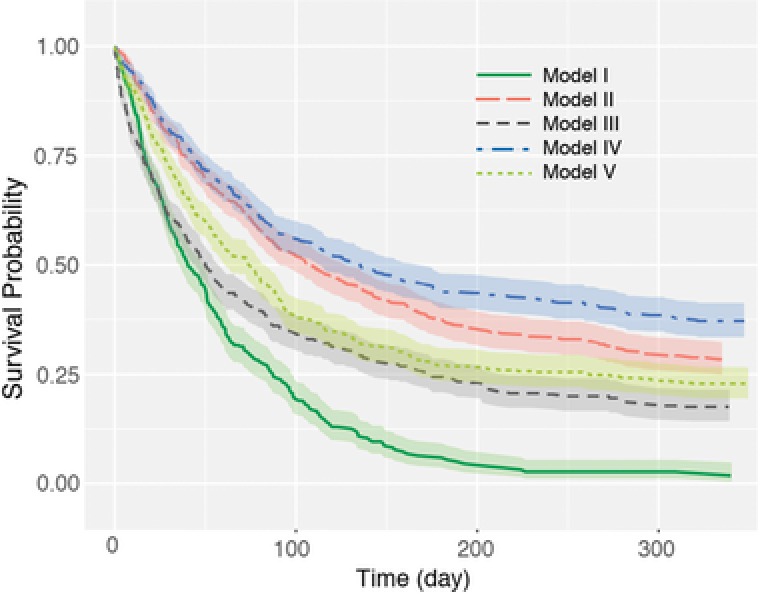
Kaplan–Meier survival curves for the simulation data sets from bivariate models I–V. Shaded areas denote the confidence intervals ($\alpha =0.05$).

Predictive performance of different survival analysis models

For each of Models from I to V, 500 data sets were independently generated, in which each data set consists of one training and one testing data independently generated from the given model with the sample size of 500 and censoring rate of 0.25. For each data set, the training data were used to fit the Cox model or train the ML‐based method (i.e., RSF and ANN, respectively), whereas the testing data were used to examine the prediction ability reflected by the C‐index (briefly, a value of 1 representing perfect prediction, while a value of 0.5 refers to a random guess; see METHODS for the details). For the 500 data sets, the mean prediction assessment (average C‐index value) was obtained for the given Model. Figure 2 shows an example of survival predictions of two virtual subjects from a data set generated by Model II. In this case, the “red” subject had an event at the 19^th day, while the “green” subject had an event at the 85^th day. The true underlying survival functions (dotted curves) reflect that the “red” subject has lower survival probability than the “green” subject. Predictions from the Cox model (dashed curves) yielded the reversed survival curves (i.e., the “red” subject has a greater survival probability than the “green” subject, which is opposite to the true setting), while RSF (solid curves) provided correct predictions for these two subjects and steep decreases of survival probability can be seen around the 19^th and 85^th day for them, respectively. This example shows the insufficiency of the Cox model in analyzing survival data with a nonlinear relationship among predictor variables. In a similar manner, performance comparisons were conducted for all models and for all survival analysis methods. The results of the prediction ability by C‐index are shown in Figure 3. From the figure, there is no significant difference in prediction performance for Model I (Linear) between Cox model and ML approaches. For Models II–V that are not linear or additive for covariates in the hazard function, the Cox model generally provided a C‐index score of around 0.5 (meaning random guessing for prediction), while the ML‐based approach provided a C‐index of around 0.75, in which RSF demonstrated slightly better prediction ability than ANN.

Figure 2.

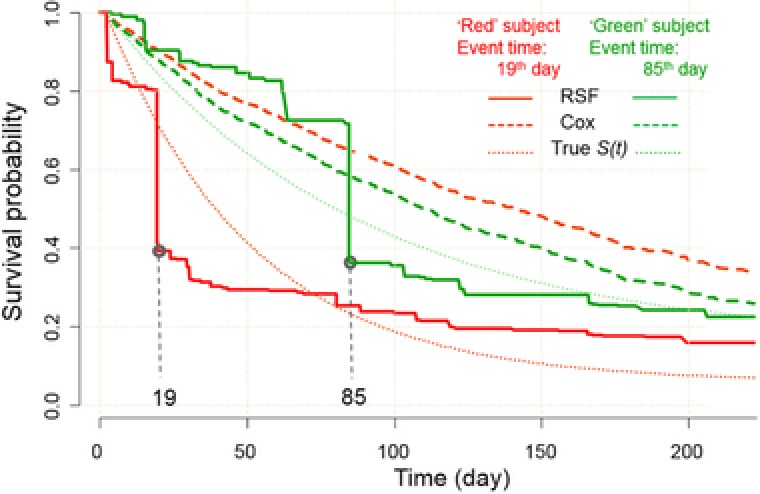
An example of survival prediction performance for two hypothetical subjects. In simulation, the “red” subject experienced an event at 19th day, and the “green” sample experienced an event at 85th day. $S(t)$ indicates survival function; RSF, random survival forest; ANN, artificial neural network.

Figure 3.

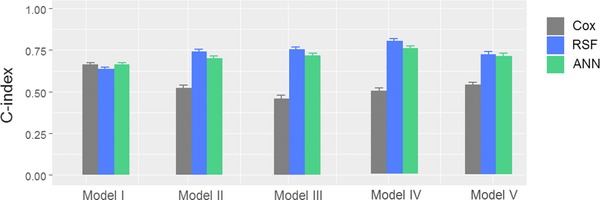
Prediction errors in terms of C‐index (concordance index) by Cox model, ANN, and RSF. Results are based on 500 repeated simulations. Mean and standard deviation of C‐index are displayed.

For simulated data based on Model VI (high‐dimensionality), the Cox model failed to yield reasonable estimation due to the parameter identifiability issue (i.e., number of observations (200) less than number (250) of predictor variables). In contrast, the ML‐based approaches RSF and ANN produced C‐index values around 0.71 for predictive performance assessment. Importantly, ML‐based approaches were also able to capture influential predictors based on their relative importance for ANN,26 and variable importance (VIMP) for RSF.12, 27 Relative importance is estimated directly from neural network weight connections, while VIMP is calculated by prediction error change after noising up a variable. For both metrics, positive values indicate the corresponding variables have high predictive power, while zero or negative values indicate nonpredictive variables with low predictive power. When applied to simulated data by Model VI, both ANN and RSF identified the first 25 important covariates set by the true model, as illustrated in Figure 4. These results, taken together, demonstrate that ML‐based approaches can outperform the Cox model for the survival data with nonlinear and additive relationships in the hazard function and high dimensionality.

Figure 4.

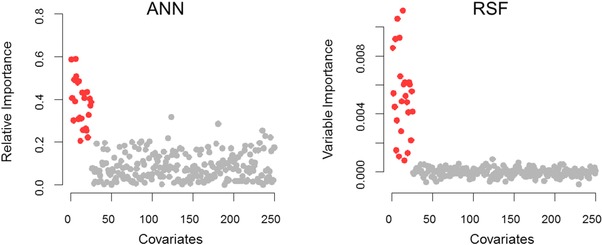
The predictor importance of ANN and RSF for high‐dimensional simulated data based on Model VI, evaluated by relative importance and VIMP, respectively. The preset significant covariates are indicated in red. The results showed that the first preset 25 important covariates were identified with relatively larger importance values than the nonsignificant covariates by both RSF and ANN.

Data sensitivity testing

The above simulations were performed with predefined sample size (n = 500 for Models I–V, and n = 200 for Model VI) and censoring rate (0.25). In this section, the effects of sample size and censoring rate on model performances were examined to test the robustness of ML‐based survival methods.

First, the impact of censoring rate was investigated, where the censoring rate from 0 through 0.25 and 0.5 to 0.75 was used to generate survival data for each simulation model. Following the same procedure as the previous section, the ML‐based methods and Cox model were applied to the generated survival data to conduct predictions. The C‐index was then calculated to measure the predictive performance of different survival analysis methods (Supplementary Figure S1). In general, predictions based on low‐level censoring data provided greater C‐index values, suggesting that data censoring negatively affected the survival prediction for all approaches. Given a fixed censoring rate, ML approaches outperformed the Cox regression model in predictive performance for Models II–V that represent nonlinear relationships for predictor variables in the hazard function. For high‐dimensional data generated from Model VI, the Cox model could not work properly due to over‐parameterization. For Model II–VI, the RSF and ANN rendered similar C‐index values. For Model I, all approaches provided comparable C‐index values when the censoring rate was low (e.g., 0); however, when the censoring rates were high (e.g., 0.75), the Cox model offered slightly better prediction accuracy than the ML‐based approaches. This is partly because the simulation data were generated by the same Cox model used for regression. The study results also indicate that, in the presence of model misspecification for scenarios of Model II–IV, the performance of the Cox model can be significantly compromised, and the performance of the RSF and ANN methods, as fully data‐driven methods, can be negatively impacted when the data censoring rate is high but at a lesser extent than the Cox model.

Subsequently, to investigate the effect of sample size on predictive performance, survival data were generated at varying sample sizes, n = 200, 400, 600, 800, 1,000 with a fixed censoring rate of 0.25. The study results show that both ML‐based approaches consistently gave greater C‐index values than the Cox model regardless of sample size for data sets generated from Models II–V. For Model VI, RSF and ANN yielded similar C‐index values across all sample sizes, except for a slight decrease for ANN when sample size was 200. In contrast, the Cox model failed to converge at sample size n = 200, and generated increasing C‐index values that reached its maximum at n = 400. The C‐index values for Cox model were consistently lower than those for ML‐based approaches (Supplementary Figure S2). For data generated from Model I, the Cox model performs slightly better than ML‐based approaches, as the Cox model is the true model used for data generation.

Model evaluation using clinically relevant simulated data

To further verify the usefulness of ML‐based survival methods, a well‐established clinical model was used to simulate the survival data for performance check. Specifically, survival data were generated based on a real‐case drug E‐R analysis model. E‐R analysis examines the relationship between drug exposure and clinical outcomes that are often binary outcomes (e.g., progression‐free survival or overall survival of cancer patients). It has been reported that, in an E‐R analysis, the effect of drug exposure on clinical outcomes is often confounded with other patient‐specific risk factors.28 For example, for anticancer treatment, clinical response is not only dictated by drug exposure but also by baseline disease severity and other factors.

The simulations were based on an E‐R relationship for an anticancer drug, derived from an attempt to investigate the association between overall survival and predictors of interest including drug exposure in terms of drug trough concentrations (C_trough), the Eastern Cooperative Oncology Group (ECOG) performance score (a metric for quality‐of‐life (QOL) with “0” indicating optimal QOL of being fully active and “1” indicating restrictedness in physically strenuous activity), and the baseline tumor size. In our simulations, three models with nonlinear hazard functions (Models A–C in Table 2) were used to stand for the following scenarios: i) interaction between ECOG and C_trough (Model A), ii) nonlinear drug exposure effects (Model B), and iii) interaction between the nonlinear drug exposure effect and ECOG (Model C). In Models B and C, the nonlinear drug exposure effect was modeled as an E_max‐type function, $\frac{E_{max}\times C_{trough}}{E{C}_{50}+C_{trough}}$ , where the relevant parameters were derived from registrational clinical trial data.

Survival data were simulated following the same process as outlined in the previous section. C_trough and baseline tumor size were drawn from normal distributions with clinically observed mean and variances, and ECOG was drawn from a binomial distribution (Supplementary Table S1). The corresponding coefficients for covariates (i.e., ${\beta }_1,{\beta }_2,{\beta }_3$ and β₁₃ in Model A) were derived by fitting clinically observed data with the predefined model (e.g., Model A). For each model, 500 data sets were generated, where each data set consists of one training data set and one testing data set, with a sample size of 500 and a censoring rate of 0.25. The Cox model, ANN, and RSF were applied to the same simulated data for performance comparison. The C‐index was used to assess the prediction accuracy for the different survival methods. Summary statistics (mean ± standard deviation) of the C‐index are listed in Table 3. As shown, the Cox model only produced C‐index values round 0.5 for data sets generated from all three Models A‐C. This is expected, as all the simulation models deviate from the linear and additive assumption underlying the Cox model. In contrast, both ML approaches gave comparably higher C‐index values (∼0.7 for Models A and C, ∼0.6 for Model B) than the Cox model, suggesting better predictive performance of ML‐based approaches for survival analysis, especially when the hazard function manifests a more than linear relation to the predictor variables.

Table 3.

Mean and standard deviation of prediction accuracy (C‐index) of Cox, RSF, and ANN for E‐R relationship simulations, respectively

	Model A	Model B	Model C
Cox	0.50 ± 0.01	0.49 ± 0.02	0.49 ± 0.02
RSF	0.70 ± 0.01	0.59 ± 0.02	0.70 ± 0.01
ANN	0.68 ± 0.03	0.61 ± 0.02	0.69 ± 0.03

DISCUSSION

Cox model is subject to certain modeling assumptions that are challenging to be fully verified before its use and to substandard performance for high‐dimensional data. In this study, we evaluated the utilization and performance of ML‐based approaches (RSF and ANN as proxies) for survival analysis as an alternative to the conventional Cox regression model. Model performances were assessed by applying the Cox model and ML approaches to the simulated survival data sets assuming different types of hazard functions for predictor variables with/without high dimensionality. The C‐index metric was employed to evaluate and compare their predictive accuracy. Our simulation results, taken together, suggest that the ML‐based approach outperforms the Cox model either when the hazard function deviates from linear and additive relationships, or when handling high‐dimensional data, by virtue of its data‐adaptive property.

There have been the extensive studies reporting ML applications in disease diagnosis and prognosis. Based on the reports, RSF showed superior or noninferior performance to the Cox model for predicting the survival of patients with breast cancer,29 prostate cancer,30 and systolic heart failure based on baseline characteristics.31 ANN was reported to outperform the Cox model in survival prediction of kidney failure32 and breast cancer occurrence.33, 34 ANN and RSF were also evaluated to have comparable prediction performance in a head‐to‐head evaluation of breast cancer survival in microarray studies.33, 35 Our study offers a systematic performance evaluation of ML approaches and the Cox model through simulations with known true models and demonstrated good prediction performances associated with ML‐based methods.

One appealing feature of ML methods is that it can cope with data of high‐dimensionality, even in situations where there are more variables than observations. This is consistent with our finding that both ANN and RSF can successfully capture the preset significant predictor variables out of high‐dimensional survival data by Garson's algorithm and VIMP, respectively. While our main purpose is to demonstrate how to effectively use ML methods in high‐dimensional survival problems, it is worth noting that other methods for covariate importance evaluation are also available, including the connection weights approach, the partial derivatives for ANN (reviewed previously36), and the minimal depth for RSF.13 To accommodate the Cox model in large feature settings, variable selection and dimension reduction techniques have been developed, e.g., the univariate shrinkage37 and penalized partial likelihood approach.38 Nonetheless, these improved versions should be used with caution, as the linear additive relationship between covariates in hazard function is still assumed.

A virtual case was created based on an E‐R relationship that involves both patient‐level drug exposure and disease characteristics as confounding covariates. For all the scenarios with different degrees of nonlinearities in the tested hazard functions, ANN and RSF demonstrate reasonable predictive performance, while the Cox regression model can produce random predictions. Given all the flexible features inherent to the ML techniques, higher regard is warranted to utilize these approaches in both the regulatory setting and industrial drug development.

Besides the aforementioned ANN and RSF methods, several alternative ML approaches for survival analysis will be further assessed in our future research. SVM highlights a more recent ML method that has been adapted to handle right‐censored data in many circumstances. The modified support vector regression (SVR) algorithm for survival analysis was proposed in 2007.39 Van Belle et al.15 later developed an SVR‐based method making use of ranking and regression constraints for right‐censored data. The results of their study indicated that the SVR method outperforms the Cox model for high‐dimensional data, while for clinical data the models have similar performance. Recently, deep learning was applied to Faraggi‐Simon ANN to analyze survival data and showed better predictive ability when compared with the Cox model.18 Given the availability of multiple ML approaches, the choice of method may depend on the totality of a situation, including the types of data collected, the size of data set, and the computational efficiency. To qualify the best model, a significant number of possible model configurations need to be assessed. For instance, the architecture of an ML model can be complex, with many potential permutations on fitting weights, number of hidden nodes, and hyperparameters for ANN, and number of trees and splitting rules for RSF. At the same time, caveats should be given to the limitations of ML approaches, one of which is characterized as a “black box.” Whereas the regression coefficients in the Cox model can be interpreted as the likelihood of an outcome given values of the covariates, neither RSF nor ANN seems suitable for providing such interpretation. RSF becomes even more of a black box due to potential model uncertainty induced by the trees that differ across bootstrap samples. Overall, the success of implementing ML‐based methods is dictated by both model selection and model fine‐tuning.

In summary, our study demonstrates high flexibility and reliability of ML‐based approaches for survival analysis, even in situations when the Cox model fails to produce results with the desired accuracy. The study results support the application of ML methods for time‐to‐event analysis.

Supporting information

SUPPLEMENTARY TEXT

Big Data Toolsets to Pharmacometrics: Application of Machine Learning for Time‐to‐Event Analysis

Figure S1. The effect of survival data censorship on the prediction performance. Each panel (a–f) corresponds to one of the models (I–VI). For each group of bars, colors (from light to dark) indicate different censoring rates (from high to low). C‐index was estimated with 500 replications for each level of censorship, with sample size = 500. Mean and standard deviation are displayed.

Figure S2. The effect of sample size on the model prediction performance. Each panel (a–f) corresponds to one of the models (I–VI). C‐index was estimated with 500 replications for each sample size n = 200, 400, 600, 800, 1,000 under a censoring rate of 0.25. Mean and standard deviation are displayed.

Table S1. Descriptive statistics of covariates derived from a New Drug Application (NDA) submission for anticancer therapy