Recidivism in a Sample of Serious Adolescent Offenders

Abstract

Objectives

A broad research literature in criminology documents key aspects of how criminal offending develops and changes over the life span. We contribute to this literature by showcasing methods that are useful for studying medium-term patterns of subsequent criminal justice system involvement among a sample of serious adolescent offenders making the transition to early adulthood.

Methods

Our approach relies on 7 years of post-enrollment follow-up from the Pathways to Desistance Study. Each person in the study was adjudicated delinquent for or convicted of one or more relatively serious offenses during adolescence. Their local jurisdiction juvenile court petition records and their adult FBI arrest records were systematically searched.

Results

We estimate in-sample 7-year recidivism rates in the 75% to 80% range. Our analysis also provides recidivism rate estimates among different demographic groups within the sample. Extrapolated long-term recidivism rates are estimated to be on the order of 79% to 89%.

Conclusions

The Pathways data suggest that recidivism rates of serious adolescent offenders are high and quite comparable to the rates estimated on other samples of serious offenders in the extant literature. Our analysis also reveals a pattern of heightened recidivism risk during the earliest months and years of the follow-up period followed by a steep decline.

1. Introduction

It is common criminological knowledge that young persons who experience formal contact with the criminal justice system also exhibit high rates of reoffending. Whether the outcome is self-reported offending (Piquero et al., 2013; Nagin and Paternoster, 1991; 2000) or some official measure of recidivism such as rearrest (Visher et al., 1991; Dean et al., 1996; Blumstein et al, 1985; Piquero et al., 2002; Kurlychek et al., 2012), new appearances in juvenile court (Manski and Nagin, 1998), police contacts (Greenberg, 1991; Kurlychek et al., 2006), or criminal convictions (Blumstein et al., 1985; Piquero et al., 2003; 2007), the story is the same: recidivism rates are high and failure is a common experience. In saying this, we do not mean to suggest that our field has arrived at a consensus regarding why recidivism rates are high; it most certainly has not. And it is also true that little is known about the medium-term recidivism behaviors among serious juvenile offenders who are navigating the transition from adolescence to adulthood, a decidedly under-researched transition period (Loeber and Farrington, 2012). Using officially recorded data on post-enrollment court referrals and arrests from the Pathways to Desistance Study (Mulvey et al., 2004), this paper reports recidivism rates and waiting time distributions to advance criminological knowledge about this difficult population at a pivotal point in the lifespan.

Most studies of offending trajectories using the Pathways dataset to this point have relied on the self-report survey measures of offending in the sample (Monahan et al., 2009; Mulvey et al., 2010). In relying exclusively on the official record measures of recidivism in the Pathways data, our analysis complements earlier studies based on these same study participants (see, for example, Piquero et al., 2013). In so doing, we make a concerted effort to illustrate some of the key analytical and methodological issues that arise in such analyses and ways of usefully and rigorously addressing them. Our use of the comparatively recently collected Pathways data also allows us to consider and comment on the generality of earlier modeling efforts (i.e., Schmidt and Witte, 1988; Kurlychek, Bushway, and Brame, 2012) based on older data sets, different groups of offenders, in different locations, and using different criminal history record search protocols. Importantly, our analysis also confronts the limitations of missing data that typically arise in criminological recidivism and panel studies, which has not been typical of prior research.

2. Measuring Criminal Desistance and Recidivism

The rigorous measurement of recidivism is one of the central research tasks in criminology (Maltz, 1984; Schmidt and Witte, 1988; Blumstein and Nakamura, 2009; Kurlychek et al., 2012). It has been long recognized that the processes which drive recidivism may differ quite markedly from the processes which influence individuals to initiate their offending (Blumstein and Graddy, 1983; Blumstein et al., 1986). A pre-requisite to documenting these differences involves the careful measurement of both recidivism and longer-term patterns of reoffending (Schmidt and Witte, 1988; Smith and Brame, 1994; Blumstein, 2010; Kurlychek, Bushway, and Brame, 2012; Brame et al., 2012; Brame et al., 2014a; Brame et al., 2014b).

Previous research on offending during the transition from adolescence to adulthood leads to three broad conclusions: (1) most but not all juvenile offenders eventually cease their offending either during or soon after the transition to adulthood; (2) short- and medium-term recidivism rates of juvenile offenders notably serious juvenile offenders are quite high; and (3) most adults who engage in criminal activity (as measured by official records such as arrest and conviction) also have significant histories of juvenile criminal involvement (see e.g., Blumstein et al., 1986; Gottfredson and Hirschi, 1990; Sampson and Laub, 1993; Piquero et al., 2003; 2007; Loeber and Farrington, 2012). Research examining developmental trajectories of offending behavior reveals considerable heterogeneity and variability in the extent to which people establish an enduring pattern of contact with and involvement in the criminal justice system (Nagin and Land, 1993; Land, McCall, and Nagin, 1996; Laub, Sampson, and Nagin, 1998; Piquero et al., 2002; Lattimore et al., 2004; Piquero, Brame, and Lynam, 2004; Broidy et al., 2003; Piquero, Farrington, and Blumstein, 2007; Piquero et al., 2013). This literature, however, has only a limited number of studies that have examined juvenile offenders who have official criminal histories indicating a record of involvement in serious and/or violent forms of criminal behavior (see Blumstein et al., 1986; Visher et al., 1991; Dean et al., 1996; Piquero et al., 2002; Brame et al., 2003; Laub, Nagin, and Sampson, 1998; Lattimore et al., 2004; Mulvey et al., 2010), even though there would seem to be special concerns about the transition to adulthood among these adolescents.

The studies that do exist provide evidence of high levels of continued offending. Blumstein et al. (1985) provided a comprehensive overview of recidivism patterns in several birth cohort studies, including Cambridge (London), Racine (Wisconsin), Philadelphia (1945 cohort), and Marion County (Oregon). These studies consistently reveal high recidivism rates (on the order of 60% to over 80%); the highest recidivism rates were observed for youth with multiple prior offenses. Subsequent research also suggests that so-called “deep-end” offenders experience great difficulty transitioning away from offending as they move into adulthood. For example, Visher et al. (1991) examined a random sample from a parole cohort of the California Youth Authority from the time of their release in FY1982 until the end of September 1985. Considering the 1,949 persons followed up, a total of 1,710 were rearrested within the study period a failure rate of nearly 90%. Dean et al. (1996) studied a cohort of 16- and 17-year-old offenders released from North Carolina training schools in 1988 and 1989 who were followed between 5 and 7 years. Approximately 70% of these youth were rearrested during the follow-up period. Their analysis used a split-population survival time model which allowed for the estimation of a long-term failure rate of nearly 78%. Brame et al. (2003) studied a subsample of adolescent offenders within the 1958 Philadelphia Birth Cohort who had experienced a police contact for an index offense as a juvenile and estimated that nearly 40% of these offenders went on to experience at least 1 police contact in adulthood (by age 27) for another index offense. Kalist and colleagues (2015) studied a large sample of Pennsylvania juveniles (N = 74,684) over the 1997–2005 period and used court referrals as a measure of recidivism. Their analysis reports an overall recidivism rate of 45.6% (49.8% for males and 31.7% for females). Taken together, these studies suggest that recidivism rates among serious juvenile offenders are troublingly high as they stand at the threshold of adulthood.

2.1 Limitations of Prior Research

There are some key sources of uncertainty in this literature. First, most of these studies are based on older datasets. In fact, there has been little medium- to long-term recidivism research conducted among contemporary samples of serious adolescent offenders as they make the transition to adulthood. Our study fills this gap. Another issue is that the record searches on which the recidivism measures were based were typically conducted exclusively within the city or state where the study originated. For example, the study by Dean et al. (1996) which focused on North Carolina training school releasees was based on state arrest record searches. Since the Charlotte metropolitan area (and several other sizable urban areas) straddle the state line between North and South Carolina, it is reasonable to question whether the recidivism rates observed in that study would have been higher if South Carolina arrest records had been searched as well. Another, somewhat related concern is that most recidivism studies focus on a sample that is drawn entirely from a single geographic unit (i.e., a single city or a single state). Finally, some studies confine themselves to reporting a terminal recidivism rate (i.e., a binary fail/no fail outcome) without attending to the additional information that is available from a careful study of the waiting time to a recidivism event (Maltz, 1984).

As we will describe below, the research presented in this paper provides a powerful framework for addressing each of these issues. As such, this investigation provides useful information about the recidivism patterns in the Pathways data and serves as a methodological approach that can influence recidivism research more generally. In addition, our research formally attends to the fact that not everyone who was targeted to participate in the study actually did so. We propose methods that should prove useful for addressing the ambiguity created by excluding cases with missing data from recidivism studies where active consent and participation of the persons being studied is required. At the same time, our methods rely on formal parametric survival time models that emanate from a well-developed empirical literature on criminal recidivism. We demonstrate that many of the patterns seen in historical criminal recidivism studies are also evident in our contemporary sample of serious adolescent offenders in Phoenix and Philadelphia and we argue that they are significant for both theory and policy.

3. Study Overview

Our study examines a large sample of serious adolescent offenders from the Pathways to Desistance Study followed up for 7 years using subsequent criminal history information drawn from local juvenile court petition records and FBI arrest records. This study represents a significant advance over previous efforts in several key respects: (1) most previous studies have been based exclusively on local or state record searches while ours is based on a national record search (during the adult years), which is exceptionally rare in the extant literature (see Piquero et al., 2014); (2) most studies are focused on offenders in a single local or state jurisdiction while ours spans two jurisdictions in different parts of the country with a large sample in each jurisdiction (Philadelphia and Phoenix); (3) most studies are based on relatively broad cohorts of offenders while ours is targeted at measuring the experiences of adolescents who have been adjudicated for serious criminal offenses as juveniles and who were then followed into early adulthood, a group that is of great interest for criminological theory and criminal justice policy (Laub and Sampson, 2003); and (4) our deployment of both non-parametric and parametric methods of investigating recidivism behavior (both its occurrence and timing) over a 7-year follow-up period. In Section 4, we describe the Pathways study methodology in more detail and provide an overview of the data. Section 5 presents our recidivism rate estimates for the Pathways sample as a whole and for major subgroups in the study. Finally, Section 6 presents our conclusions and suggestions for future research.

4. Study Overview

The context for this research is the Pathways to Desistance study, a large longitudinal study of serious adolescent offenders from Maricopa County, Arizona, and Philadelphia County, Pennsylvania. Our analysis is based on a detailed review of local juvenile court petition records and FBI arrest histories compiled on each of the study participants over an 84-month follow-up period. With these data, we are able to develop a rigorous recidivism analysis -- based on formal parametric survival time models -- where we measure the waiting time to the first rearrest or new petition at the local juvenile court after the incident that triggers enrollment in the study.

4.1 Sampling

The Pathways study was designed to examine the mechanisms that influence the cessation of antisocial activity within a group of serious adolescent offenders who are making the transition from adolescence to early adulthood (see Mulvey et al., 2004). Across both sites, 1,668 youth were invited to participate; 314 of these youth declined while the remaining 1,354 youth were enrolled (81.2% enrollment rate). The enrollment effort spanned the period from November 2000 to January 2003. Table 1 summarizes these results.

Table 1.

Pathways Participation by Site and Gender

Group	Total Eligible	Number of Participants	Participation Rate (%)
All Cases Combined	1668	1354	81.2
Males	1434	1170	81.6
Females	234	184	78.6
Philadelphia	882	700	79.4
Phoenix	786	654	83.2
Philadelphia Males	756	605	80.0
Philadelphia Females	126	95	75.4
Phoenix Males	678	565	83.3
Phoenix Females	108	89	82.4

To be eligible for inclusion in the study, potential participants had to have been: (1) less than 18 years old at the time of the offense that triggered study eligibility; and (2) found guilty of a serious offense (overwhelmingly felony offenses, with a few exceptions for some property offenses, misdemeanor sexual assault, or misdemeanor weapons offenses). Enrollment of males was limited to 15% drug offenders (a drug cap) to maintain a heterogeneous sample of serious offenders. All females and all youth whose cases were being considered for trial in the adult system were approached if they met the age and adjudicated crime requirements.

The enrolled sample represented approximately one in three adolescents adjudicated on the enumerated charges in these two locales during the recruitment period. With the exception of 16 persons who had turned 18 by the time the formal petition was filed, all study participants were under age 18 at the time of the petition that triggered their enrollment in the study. The average age of the participants at the gateway petition was 16.2 with a standard deviation of 1.1. The sample is ethnically diverse (20% white, 41% black, 33.5% Hispanic, and 5% “other”; Table 2) with disproportionately more black persons in Philadelphia and disproportionately more white and Hispanic persons in Phoenix. Enrolled cases had, on average, 2.92 petitions (with standard deviation 2.14, range 1–15) including the study gateway petition. For 437 individuals (32.2% of the participants), the gateway petition was their initial petition to the court. The most serious charge at the gateway petition was a person crime in 547 cases (40.4%), a property crime in 341 cases (25.2%), a weapons-related violation in 135 cases (10.0%), a drug violation in 210 cases (15.5%), a sex offense in 52 cases (3.8%), and a residual category of “other” offenses in 53 cases (3.9%). In 4 cases, all charges were ultimately dismissed and in another 12 cases, the charge at the gateway petition could not be determined. Additional details regarding the recruitment procedures and sample characteristics can be found in Schubert et al. (2004).

Table 2.

Participation by Race/Ethnicity and Age

Group	Total Eligible	Number of Participants	Participation Rate (%)
All Cases Combined	1668	1354	81.2
White	370	274	74.1
Black	708	561	79.0
Hispanic	522	454	87.0
Other	68	65	95.6
Age 13	11	8	72.7
Age 14	278	226	81.3
Age 15	373	292	78.3
Age 16	514	420	81.7
Age 17	476	392	82.4
Age 18	16	16	100.0

4.2 Official Criminal Record Searches

In an effort to understand how officially recorded criminal behavior changes and evolves over time, Pathways study investigators gathered subsequent juvenile court petition records from the local jurisdictions in the study and national arrest history records from the Federal Bureau of Investigation for each of the 1,354 persons who were initially enrolled in the Pathways study. The procedures used produced records of juvenile court petitions prior to age 18 for the study participants and arrest records (nationwide) for the entire sample. These two sources were reconciled to eliminate possible duplicate recording of incidents. With these criminal history searches in hand, we are able to conduct a 7-year recidivism study that allows us to measure both the prevalence and over-time variation in the risk of recidivism as the study participants move from their adolescent years into early adulthood.

5. Results

We begin by examining the overall patterns of recidivism found in the Pathways juvenile court petition and adult arrest record searches. For each person in the Pathways sample, these recidivism records cover the period to the 84-month post-baseline interview (note that, for operational reasons of scheduling and conducting interviews, this period extends as far as 87 months for a small number of cases). Next, we document both the prevalence of and waiting-times to recidivism for the sample as a whole and major subgroups within the sample. Finally, we consider a series of parametric statistical models that have proven useful for the study of criminal recidivism in previous research and we examine the fit of these models to the Pathways recidivism data. These models allow us to comment on key features of the time-to-recidivism distribution (e.g., whether there is a turning point in the over-time risk of recidivism), how much change might actually be occurring in the risk of recidivism over time, and the likely long-term recidivism rate extending beyond the follow-up period in the data.

5.1 Estimating the Recidivism Rate for the Entire Pathways Sample

In this section, we use the Pathways data to estimate the 7-year recidivism rate for the population of serious adolescent offenders from which the Pathways sample (N = 1,354) was drawn. We also consider the waiting time between the gateway petition and the first subsequent arrest or juvenile court petition after that point. Like other recidivism studies in criminology, this analysis allows us to see how the risk of the first recidivism event varies over the course of the 7-year follow-up period.

As in many studies where participation is based on active and voluntary consent (e.g., the National Youth Survey, the National Longitudinal Survey of Youth), the 1,354 Pathways study participants were a subset of the 1,668 persons who were targeted for study enrollment (a difference of 314 cases). In order to develop valid estimates of the recidivism rate for the entire population of interest not just those who are willing and able to participate in a study it is useful to consider the uncertainty created by the absence of these cases. This type of ancillary but important analysis is uncommon in the extant literature. As such, we include these missing cases in our analysis in an effort to bound the recidivism rate estimates for the entire target population (Manski, 2003:18–21). Not surprisingly, we do not have much information about these missing persons but we do know their age, sex, race, and city (Philadelphia or Phoenix).

Our record check procedures revealed that the number of persons in our sample with a subsequent juvenile court petition or adult arrest is 1,045 (which means that 309 persons did not have a subsequent recorded contact). A special case of estimating the recidivism rate for the Pathways sample occurs when we are willing to assume that the recidivism rate for the participants is exactly equal to the recidivism rate for the nonparticipants. This is called the missing-completely-at-random (MCAR) estimate of the recidivism rate (Manski, 2003:18–21). We obtain the MCAR estimate by dividing 1,045 by 1,354 to obtain 0.772 or 77.2%. Using the Bonferroni-corrected bootstrap methods discussed by Manski (2003:18–21; see also Manski and Nagin, 1998), we find that [0.749, 0.794] forms a 95% confidence interval for the 7-year recidivism rate.

We are not able to measure the recidivism rates of the 314 missing cases. We can, however, form bounds on the recidivism rate which formally consider the possibility that the 314 missing cases differ in important ways from the 1,354 observed cases. The lower bound is attained by assuming that none of the missing persons recidivated. This calculation is 1,045 divided by 1,668 = 0.626 or 62.6%. We reach the upper bound when we assume that all of the missing persons recidivated, which would be (1,045+314)/1,668 = 0.815 or 81.5%. We can also estimate Bonferroni-corrected 95% confidence limits for the bounds using the bootstrap (Manski, 2003:18–21). Our analysis reveals that this confidence interval is [0.600, 0.836]. Table 3 summarizes the results of our assessment of recidivism prevalence in the Pathways data.

Table 3.

Pathways Recidivism Rate Estimates

Calculation	Estimate	95% CI
Missing Completely at Random	0.772	0.749,0.794
MA Bounds	0.626,0.815	0.600,0.836

These bounds invoke minimal assumptions such as the following: (1) the police departments and juvenile court records on which we relied, reported the recidivism events in a way that our procedures would identify them; (2) our efforts to match these individuals to the searched databases resulted in a correct linkage with our records; (3) the arrests and petitions were recorded in a manner that correctly locates them within the time frame of our follow-up period; and (4) independence of observations. So these bounds do require some assumptions, but these assumptions are minimal; they would be required in any reasonable recidivism study. What the analysis makes no assumptions about is the recidivism rate of the missing cases. In that sense, our analysis makes fewer assumptions than conventional studies that disregard the missing cases.

A couple of comments about these estimates are in order. First, the MCAR estimate is well within the range of what has been revealed by previous studies. Indeed, even the wider terrain covered by the minimal assumptions bounds are in the range of the recidivism rates we would expect to see given the nature of the Pathways sample. Second, as Manski (1995, 2003) has noted in similar analyses of this sort (see also Brame et al., 2012), sampling error is a much smaller source of uncertainty than missing data. In fact, the missing data poses an identification problem. That is, the data by themselves are insufficient to generate a valid point-estimate of the recidivism rate. The data must be combined with strong and untestable assumptions in order to make progress (Manski, 2011). Considering the minimal assumptions bounds, the uncertainty in the recidivism rate created by the missing cases means that the actual rate could be as low as 62.6% or as high as 81.5%. If we graft uncertainty due to sampling error again using the 95% Bonferroni-corrected bootstrap-based confidence interval onto this problem, the width of the interval expands only slightly to [60%, 83.6%].

This is a wide interval; much wider than we typically see for sampling-error based confidence intervals. But, in some ways, it is quite compelling because it tells us what the data combined with the most minimal assumptions are capable of telling us about the recidivism rate. When faced with interval estimates like these, Manski (1995:28–29) argues that social scientists and policy analysts should acknowledge the fact that before we examine a data set like the Pathways data, the interval of uncertainty for the recidivism rate is [0,1]. The examination of our data has allowed us to substantially reduce the width of this interval. With this in mind, it is reasonable to wonder whether there is a useful middle ground analysis that makes weaker assumptions than those on which the MCAR estimate is based but stronger than those underlying the interval estimate. We now turn to one potentially useful middle ground approach.

5.2 A Missing-at-Random Estimate for the Entire Sample

One way we can plausibly reduce the uncertainty in this estimate is to ask the following question: what would the recidivism rate have been if the missing cases were randomly missing after conditioning on the site (Philadelphia or Phoenix), age at study entry, sex, and race? This is quite a different matter than the MCAR scenario, which assumes that missingness is independent of all factors, measured and unmeasured. In contrast to the fairly restrictive MCAR analysis, the key assumption of this analysis is that the data are missing at random (MAR) after conditioning on the information provided by the above mentioned factors, known both for study participants and nonparticipants (Little and Rubin, 1987). This, of course, is a much weaker assumption than MCAR and one that, in our view, has substantially greater credibility. To the extent that an MAR analysis yields a different point estimate than a MCAR analysis, one must conclude that: (1) there are clear patterns of missingness in the context of factors that can be measured for everyone; and (2) those same factors are correlated with the recidivism outcome among the set of fully observed cases. At a minimum, such an analysis provides an important sensitivity check on the MCAR point estimate.

To conduct the MAR analysis, we divided the original sample of 1,668 persons into s = 1,2, · · · S = 71 strata based on the study site (Philadelphia or Phoenix), race/ethnicity (black, Hispanic, white, and other), sex (male, female), and age at time of study gateway petition (13–18). After identifying these strata, we discovered that there was 1 black male in Phoenix who was 13 years old and 1 black female in Phoenix who was 14 years old who did not participate in the study. These two persons were unusual because they occupied strata where there were no participants. Since we have no participants to whom they can be compared we dropped them from the analysis, leaving an effective sample size of 1,666 persons dispersed across s = 1,2, · · · S = 69 strata.

Within each stratum, s, there are nr_s people who are observed to recidivate, there are ns_s people who were not observed to recidivate (i.e., successes), and there are nm_s people whose recidivism status is unknown (i.e., missing due to nonparticipation). We can obtain the totals of each of these numbers by summing across the strata. For example, NR_s is the sum of nr_s across each of the s = 1:69 strata. Then, we get the MCAR estimate of the recidivism rate by: (1) multiplying the recidivism rate in each stratum by the proportion of the total number of participants in each stratum; and (2) summing this product across each of the strata. By comparison, the MAR estimate of the recidivism rate is obtained by: (1) multiplying the recidivism rate in each stratum by the proportion of the total number of people (both the participants and the non-participants); and (2) summing this product across each of the strata. So, the key difference between the two approaches is whether we weight each stratum’s recidivism rate by the fraction of participants in that stratum or the fraction of cases in that stratum (Fleiss et al., 2013).

This pair of calculations yields a MAR-weighted 7-year recidivism rate estimate of 76.9% which is within a single percentage point of the MCAR estimate of 77.2%. Thus, the within-sample variability in participation rates is not strongly correlated with the observed 7-year recidivism rates. This builds confidence but does not prove that the MCAR assumption is plausible. A threat to the validity of both analyses is that other factors besides city, age, sex, and race/ethnicity influence whether people are missing. It would be most troubling, for example, if missingness is influenced by someone’s tendency to recidivate. But there is no way to conduct any further tests for these possibilities with the observed data alone. The only other option would be to rely on the minimal assumption bounds presented earlier. We think it is reassuring that our estimate of the recidivism rate barely changes after conditioning on the basic set of demographic characteristics described in Tables 1 and 2.

So, the foregoing analysis suggests some reason for confidence that the results are not highly sensitive to the missing cases (and by extension to the study recruitment processes). It is our observation that all modern observational studies of delinquency and criminal behavior (especially those with both a survey and official record component) have a sizable group of “initial missing cases” like those described here. Our effort in this study is simply to document the bounds of uncertainty created by these missing cases, an approach that is the exception and not the rule in the extant literature.

5.3 Recidivism Rates for Demographic Subgroups

We now turn to an analysis of the recidivism rates for different subgroups within the Pathways sample (see Figure 1). Each of the vertical lines within this chart shows the minimal assumptions bounds for that group. The black dots inside each of these intervals reveals the MAR estimate of the recidivism rate for that subgroup. Because most of the uncertainty in these analyses is due to the missing cases rather than sampling error, Figure 1 is simplified to only depict the uncertainty due to nonresponse.

Figure 1.

MCAR and Minimal Assumptions Recidivism Rates for Different Subgroups in the Pathways Dataset

The leftmost vertical line in Figure 1 simply depicts the interval estimate from Table 1. The next two vertical lines provide a statistical comparison of the male and female recidivism rates. While the 95% confidence intervals overlap for the males and females, it seems most likely that the males have a higher recidivism rate than the females. The MAR rate for the males is on the order of 80% while the female rate is less than 60%. Although there is some uncertainty about the difference between the sexes due to missing data, the only scenario where male and female recidivism rates could be similar would be one where nearly all of the missing females recidivated while nearly none of the missing males recidivated. There is no reason to suspect that this is a likely set of circumstances (although our data cannot formally rule it out; for a similar situation in estimating the cumulative prevalence of arrest, see Brame et al., 2014a).

Figure 1 also suggests that both the MAR estimates and the range of uncertainty given minimal assumptions are similar for both the Philadelphia and Phoenix sites. The remaining subgroup analyses all focus on the males as the females provide insufficient numbers of cases to support detailed subgroup analysis. The results of these analyses show that all of the intervals overlap and that most of the MAR recidivism rate estimates lie in the high-70% to low-80% range.

5.4 Recidivism Waiting Time Distribution

We now turn our attention to the question of how much time typically lapses between the onset of the follow-up period and the first recidivism event. As Maltz (1984) has noted there is a good deal of useful information embedded within the waiting time distribution; when we reduce recidivism to a binary (yes/no) outcome measure, we run the risk of ignoring this useful information. Therefore, an important feature of our approach is that we bring the waiting-time patterns to center stage. Given the 7-year follow-up period in the Pathways study, we express the waiting times in terms of months ranging from 1 to 84. Our analyses are parameterized so that an individual who recidivates within the first month after the gateway petition is defined as having a failure time of 1. We focus on three issues in particular: (1) a nonparametric overview of the waiting time distribution; (2) the estimation of parametric models of the waiting time distribution; and (3) analysis of the median waiting time to the first post-gateway recidivism event. The first two issues are addressed exclusively in terms of the observed cases and ignore the missing cases. Recognizing that it is possible to bound the quantiles of a waiting time distribution when some of the data are missing (Manski, 2003), we return to a formal consideration of how the missing cases might affect our conclusions about the median waiting time to the first recidivism event.

Our main analytical task in studying the waiting time distribution is to specify the parametric waiting time models. We consider two parametric waiting time distributions that have been extensively used in criminal recidivism studies: (1) a model based on the split-population exponential (S_E) distribution (a 2 parameter specification); and (2) a model based on the split-population lognormal (S_L) distribution (a 3 parameter specification) (Maltz, 1984; Schmidt and Witte, 1988; Dean et al., 1996; Kurlychek et al., 2012). These distributions have both been repeatedly shown to closely approximate empirical waiting times to recidivism among populations of serious offenders such as those included in the Pathways study. The term “split-population” refers to the possibility that an observed population is actually a mixture of two underlying subpopulations. In the case of a split-population waiting-time model, the two populations are: (1) a group of persons who will never recidivate no matter how long they are followed; and (2) a population of persons who will be observed to recidivate provided we follow them long enough to measure that event. Criminologists typically refer to the first group as “desisters” and the second group as “persisters” (Blumstein et al., 1985). In our view, the extant literature clearly indicates that split-population specifications -- which assume that some fraction of the population permanently desists -- are a necessary feature of an adequate survival time model for criminal recidivism.

In any finite sample with a limited follow-up period, we are only able to identify the following two groups: (1) those who are observed to recidivate within the follow-up period (definite persisters); and (2) those who are not observed to recidivate within the follow-up period (a mixture of desisters and persisters who have not yet recidivated but eventually will). A split- population model uses the observed failure time distribution as a basis for extrapolating to an estimate of the long-term limiting recidivism rate (and, its complement, the desistance rate). As noted by Rhodes (1989), Lattimore and Linster (1993), and Kurlychek et al. (2012), the use of a parametric waiting time model to prospectively estimate the desistance rate is an inherently ambiguous enterprise. Still, with longer follow-up periods such as the 7-year period in this study, the identification of the long-term recidivism or desistance rate rests on a more solid footing (compared to say, a 3-year or 5-year study). Our study thus addresses the field’s need for recidivism rate estimates that are based on contemporary data sets with at least a 5-to-7 year follow-up threshold (see, for example, Kurlychek et al., 2006, 2007).

A central concept in criminal recidivism models is the hazard rate. In discrete time, the hazard rate measures the risk of failure in any given time period as a fraction of the people who have not failed before that time period begins (see, for example, Kurlychek et al., 2006). The question in any given population of people who have offended in the past is how the hazard rate changes over time. Declining hazard rates are typically a dominant feature of recidivism studies in the criminological literature. Consistent with that literature, both the split-population exponential and split-population lognormal models predict a declining hazard but they take on different parametric forms. The split-population exponential model assumes a constant hazard rate, but only for the people who are in the persister group. The split-population mixture guarantees that when the persisters are combined with the desisters, the hazard rate will fall monotonically throughout the follow-up period.

The simpler of our two parametric models is the 2-parameter S_E model. Theoretically, this model assumes that there is a population of desisters and a population of persisters who fail at a constant hazard rate throughout the follow-up period. Our more complicated 3-parameter S_L model assumes there is a population of desisters and a population of persisters who fail with a hazard that rises to a peak and then declines into a sustained period of a relatively low hazard rate. In other words, the hazard rate mostly declines but it is not, strictly speaking, a monotonic pattern. Such a pattern might indicate comparatively short periods of time early in the follow-up period when people are off the street or are on the street but are behaving in ways that allow them to avoid criminality or the official detection of criminality. This notwithstanding, both models accommodate the dominant theme of a declining hazard rate.

Previous research with these models generally indicates that the S_E model fits criminal recidivism data quite well although there may be some incremental benefits of moving to the more complicated S_L model (Maltz, 1984; Schmidt and Witte, 1988). For example, Kurlychek et al. (2012) discovered that the S_L model technically outperformed the S_E model. However, their study also revealed that all of the benefit occurred in estimates during the first 3–5 years of their 18-year follow-up; beyond that beginning window, the S_E model performed just as well.

To estimate these statistical models, we need to define the cumulative distribution function (CDF) and probability density function (PDF) of the failure time distribution. The CDF, F(t), is an estimate of the proportion of persons who have failed by time t. The PDF, f(t) gives us the estimated proportion of the entire sample failing in the time interval [t,t + dt). The splitting parameter, δ estimates the proportion of persons that would fail as t → ∞. Each person who is observed to recidivate contributes log(δ) + log[f(t)] to the log-likelihood function while the contribution of each person who has not recidivated by the end of the follow-up period is log[1 - δ + δ(1 - F(t)]. Table 4 presents the estimators for the CDF, F(t), and the PDF, f(t), for the S_E and S_L models. In addition to these terms, we also need to estimate the long-term limiting recidivism rate, δ (conditional, of course, on the correctness of the model specification). Theoretically, δ measures the proportion of the population that will ultimately fail if the within-follow-up recidivism process is extrapolated forward. Its complement, 1 δ, can be viewed as the long-term desistance rate. Variation in δ between the two models can be viewed as a measure of the sensitivity of the inference about δ to a precise model specification. For example, if we obtain wildly different estimates of δ between the two models, it can be viewed as one indicator of fragility in our conclusions about long-term behavior patterns.

Table 4.

CDF and PDF for S_E and S_L Models

Quantity	SE	SL
F(t)	1 − exp(−θt)	$\mathrm{\Phi }\left[\frac{log(t)-\mu }{\sigma }\right]$
f(t)	θ exp(−θt)	$\frac{1}{t\sqrt{2\pi {\sigma }^2}}exp\left(-\frac{{[log(t)-\mu ]}^2}{2{\sigma }^2}\right)$

We programmed the likelihood functions and then used the maxLik( ) function in R to estimate these models. In both the S_E and S_L estimators, the likelihood rapidly converged from our starting values using Newton-Raphson optimization. The parameter estimates from the two models are presented in Table 5.

Table 5.

Parameter Estimates

SE		SL
Parameter	Estimate	Parameter	Estimate
θ	0.043	μ	2.848
δ	0.788	σ	1.464
		δ	0.887
loge(ℒ)	-4945.223	loge(ℒ)	-4925.550
AIC	-4947.223	AIC	-4928.550
BIC	-4952.434	BIC	-4936.366

The log-likelihood function is somewhat higher for the S_L model but at the cost of a third parameter. Since the models being compared are not nested, a conventional likelihood ratio test is inapplicable. Instead, Table 5 presents the Akaike Information Criterion (AIC) and the Bayesian Information Criterion (BIC) based on formulas described in Wasserman (2000). The AIC for a specific model is given by the difference between the log-likelihood for a specific model and the number of parameters, p, to be estimated for that model: log(L) - p. The BIC is on a similar footing but exacts an additional penalty for the sample size: log(L) - p/2 x log(N).

As Table 5 shows, in the case of both AIC and BIC, the split-population lognormal model (S_L) is the preferred specification. This result provides support for the idea that there is a turning point in the risk of recidivism after a short period of time in the follow-up period (just 2 months in our study). The δ parameter estimates suggest some variability in our inference about long-term desistance and recidivism patterns depending on which model we use. But this variability is within the range of about 79% to 89%. Either of these estimates implies a long-term failure rate that is quite high. Because of the various nonlinearities in these likelihood functions, the other parameter estimates are not easy to interpret. Still, they can be used as tools for drawing curves to represent the hazard and cumulative distribution functions implied by these statistical models which can, in turn, be compared to what we see in the observed data.¹

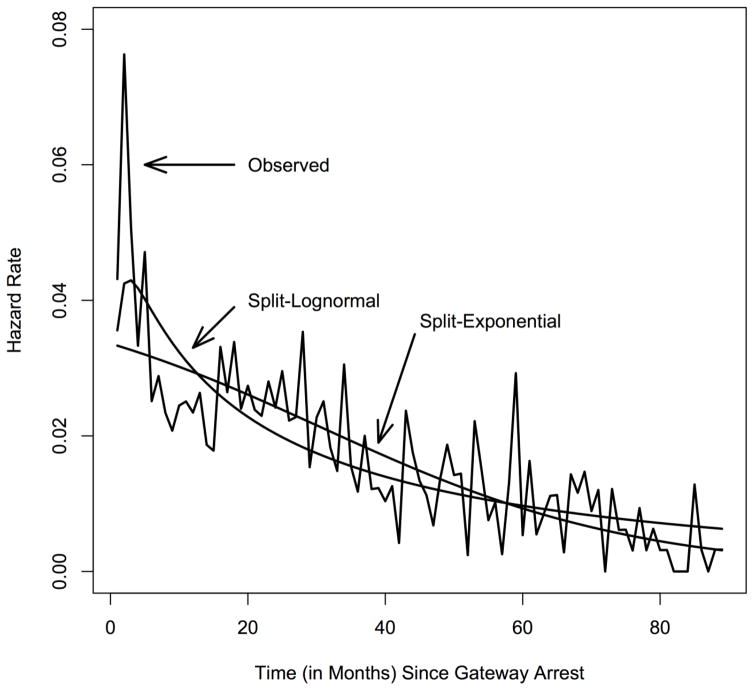
The hazard rate is useful for seeing how the risk of recidivism varies over the course of the follow-up period. The cumulative distribution function is useful for understanding how the final recidivism rate accumulates over the follow-up period. It is also helpful for estimating quantiles of the waiting time distribution. For example, we can use the cumulative distribution function estimates from these models to derive MCAR estimates of the median waiting time to the first recidivism event. Figure 2 presents the hazard rate while Figure 3 reveals the cumulative distribution function for the 7-year follow-up period in the Pathways data.

Figure 2.

Pathways Hazard Rate Estimates Through the 84-Month Follow-Up Period

Figure 3.

Pathways Cumulative Recidivism (CDF) Rate Estimates Through the 84-Month Follow-Up Period

Figures 2 and 3 reveal a few important features of how the risk of recidivism varies over the follow-up period. First, the risk of failure mostly declines over the follow-up period. This is evidenced by the prevailing decline in the hazard rate of Figure 2 and the steeper increase in the cumulative recidivism rate in the earlier months followed by a less steep increase in the later months that is shown in Figure 3. Our two models make very different theoretical claims about the reason for this decline. The S_E model suggests that the decline is an artifact of the way the population mixes the desisters and the persisters while the S_L model suggests that there is real decline in the risk of recidivism over time -- even for the persisters.²

Figure 4 plots the differences between the observed and predicted cumulative distribution functions for our two models. This plot suggests that for about the first 1.5 years of the follow-up period the lognormal model fits the data best. After that time, however, there is very little to distinguish between the two models. This provides support for the idea that a simple process like the one postulated by the S_E model can be a powerful lens through which to view recidivism data (for additional discussion of this point, see Kurlychek et al., 2012). A further feature of all three plots is the convergence of the predictions and the observed data as the follow-up period progresses and the failure rate begins to approach zero. It is worth pointing out that most of what we see in this analysis is reasonably consistent with findings from the adult felon population studied by Kurlychek et al. (2012) and older studies of prison releasees discussed in Maltz (1984) and Schmidt and Witte (1988).

Figure 4.

Differences Between Fitted and Actual Values of the Cumulative Failure Distribution

5.5 Recidivism Waiting Times With Missing Cases Included

We now consider the sensitivity of our estimates of the median time to recidivism depending on different assumptions we might make about the failure times of the 314 initially missing cases. Again, we reiterate that this is a universal problem in crime and delinquency research. Our goal here is simply to document the bounds of uncertainty. The logic behind this analysis rests on Manski’s (1995:24–26) observation that quantiles can be set-identified with censored samples while the mean or expectation can neither be set- nor point-identified. Essentially, what this means is that we examine the 50th percentile of the failure distribution’s waiting time under two extreme assumptions: (1) the failure time of the missing cases is 1; and (2) the failure time of the missing cases is at or above the sample maximum. Provided the proportion of the cases that are missing is less than 50% and the failure rate in the observed sample exceeds 50%, the median will be interval-identified. By contrast, the mean would not be identifiable (from the data alone) with any censored data.

To investigate these patterns in the Pathways data, we recall that the median waiting time assuming the missing cases are MAR is 24 months (with bootstrap-based 2.5th and 97.5th percentiles of [22,26]). If we assume that the missing cases all have a low waiting time to recidivism, the median drops to 16 months; at the other extreme, the median rises to 35 months. Figure 5 reveals the bounds and the bootstrap-based 2.5th and 97.5th percentiles of the sampling distribution for these waiting time estimates. The leftmost box in this plot reveals the sampling distribution of the median waiting time (the point estimate is 24 months) to rearrest assuming the missing cases are missing at random. Since the lower (16 months) and upper (35 months) bounds of the median waiting time are also point estimates, the boxplots also reveal the sampling distribution for each of these estimates. The “minimal assumptions” estimate of the 95% confidence interval enclosing these bounds, then, is [13,42.5] because 13 months is the 2.5th percentile of the lower bound's sampling distribution and 42.5 months is the 97.5th percentile of the upper bound's sampling distribution.

Figure 5.

Bounds on the Waiting Time to Recidivism (Entire Pathways Sample Including Both Participants and Nonparticipants)

Consistent with our bounds on the fraction of the sample that recidivates, these results indicate that uncertainty due to the missing cases dominates uncertainty due to sampling error; specifically, the bounds without sampling error are [16,35] and with sampling error they expand to [13,42.5]. Of course, these results may mask important variation that exists at the subgroup level. To address this potential concern, we consider variation in the waiting time distribution for the same subgroups we examined earlier. The results of this analysis are presented in Figure 6. For most of the subgroups, the MAR estimates lie between 20 and 30 months. Also, for most groups, the identification intervals are at least 10 months wide. It was not possible to estimate the identification intervals for the median waiting time among the Philadelphia females since their observed failure rate was less than 50% and the median cannot be estimated when more than 50% of the cases have not yet been observed to fail. Overall, this figure suggests that our greatest uncertainty in estimating the median waiting time to recidivism lies with the females in the Pathways data.

Figure 6.

Bounds on Median Waiting Time to Recidivism by Different Subgroups of the Pathways Sample (Both Participants and Nonparticipants)

6. Discussion and Conclusions

This paper documents basic recidivism and long-term criminal justice contact patterns in a prominent criminological data set the Pathways to Desistance Study. The Pathways data provides rich, detailed longitudinal information about criminal offending in a sample of serious adolescent offenders. The work presented in this paper reveals what is known about the recidivism rates and failure time distributions of these offenders based on 7-year criminal history searches of the local juvenile court records and the FBI criminal history database.

As is commonly the case in studies of criminal behavior, we encountered the ambiguity that some of the persons who were selected to be in the study did not participate. For the Pathways study, this meant that the criminal history records of these missing individuals were not searched. An important feature of our analysis is that we highlight the uncertainty created by these cases something that most other longitudinal studies do not explicitly consider. As it turns out, these cases do create some uncertainty about the real recidivism rate in the Pathways sample (and the population that the Pathways sample represents). But our analysis also reveals that our estimate of the Pathways recidivism rate barely changes when we adopt a substantially less restrictive model of recidivism rates that makes much weaker assumptions about the missing cases. This, of course, will not always be the case. So, we think the methods used here have practical value beyond this particular study and will be of significant value to criminologists who are working with criminal recidivism data.

Several substantive features of the analysis are worth careful consideration as criminologists continue to study recidivism patterns. First, recent work by Kurlychek et al. (2012) has highlighted the theoretical content of parametric failure time models. For example, the Kurlychek et al. study found that a split-population lognormal failure time model provided the best fit to 18-year recidivism data within a sample of 1970’s era New Jersey convicted felons. However, Kurlychek and her colleagues also noted that the split-population exponential model fit almost as well, particularly in the later years of the study. With that in mind, it is useful to note that the split-population exponential model makes two key assumptions: (1) there are two groups of people, desisters and persisters; and (2) the persisters fail at a constant hazard rate. The declining hazard rate in a split-population exponential world is entirely an artifact of the mixing of these two groups of people not a within-person phenomenon (Kurlychek et al., 2012). The fact that this simple models fits the contemporary Pathways data set as well as it does should be an important point of departure for future recidivism research. Going forward, it will be important to continue monitoring the Pathways recidivism patterns to see how the criminal careers of these persons progress as they move into their middle adulthood years. The field does not have enough 10+ year recidivism studies, so the Pathways study provides us with an important opportunity for the long-term study of recidivism and desistance.

Second, our study adds to a deep literature on juvenile offenders which shows that youngsters who are at the “deep end” of the juvenile justice system frequently encounter significant additional difficulties with the criminal justice system as they move into adulthood. While many of the Pathways offenders appear to ultimately desist (Mulvey et al., 2014), it appears that many of them do not do so quickly or suddenly. Instead there appears to be a continued period of activity for many of the Pathways men that eventually declines to a low level, by the mid-20’s. Importantly, this same pattern appears in both the self-report of offending trajectories reported by Piquero et al. (2013) and official record trajectories estimated on the Pathways sample (Mulvey et al., 2014). This particular set of findings also closely align with research reported by Paternoster et al. (2014) looking at prison releasees in Delaware. That is, they find a high recidivism rate coinciding with generally declining trajectories of offending frequency.

Both studies report small fractions of people who are persisting in offending at a high rate by the mid-20’s while the majority of the sample is declining or exhibiting offending rates that are very close to zero by the mid-20’s. Overall, this is a strong pattern of concordance between the self-report and official record windows on the Pathways participants (see also, Piquero et al., 2014). A key direction for future research both with the Pathways data and other data sources is to identify triggers of change that will help us predict the onset and timing of these longer-term patterns of desistance and cessation from involvement in the criminal justice system, an especially important topic for theoretical and policy matters.

In this regard, it is also worth underscoring the finding that the split-population log-normal model fits better for the first part of the time series but no better for the rest of the series. Recall that the split-population lognormal model (a 3-parameter model) assumes that there are two groups of people: one who will never fail and another group who fail according to a lognormal hazard (a rising risk of recidivism followed by a much longer period of declining risk). The split-population exponential model is simpler (a 2-parameter model); it also assumes two groups but the second group has a constant risk of recidivism. So, the debate between these two perspectives is whether the observed declining risk of recidivism is relatively time stable. If the risk truly declines, there are two reasons that could be true: (1) the high risk people fail first, leaving a residual group of lower risk people; or (2) there is something about getting up each day and making it through that day without getting into trouble that causally reduces the risk of recidivism on the next day. In one sense, these results imply that there is a strong(er) argument for a group differentiation, with two groups having different rearrest rates, in the early part of the series and a reasonable assumption of equal rates of rearrest across the sample as a whole in the later part of the series.³

Such a result could have implications for how we think of involvement with rehabilitation/treatment services. If there is a group of juveniles with markedly higher rates of rearrest within a short time frame after their disposition, it would make sense to identify these adolescents and focus services on them. Although we are not in a position to develop this idea further in these analyses, this differentiation in early patterns may not just be interesting, but might also have broader policy and practice implications. In short, these results highlight the possibility that there may be a group of serious offenders who are qualitatively different from those who eventually reoffend over the entire follow up period. Attention to both short- and long-term patterns and intervention effects are necessary in develop a more nuanced, and possibly more effective policy response to serious adolescent offenders.