MOMD Analysis of NMR Line Shapes from Aβ-Amyloid Fibrils: A New Tool for Characterizing Molecular Environments in Protein Aggregates

Abstract

The microscopic-order–macroscopic-disorder (MOMD) approach for ²H NMR line shape analysis is applied to dry and hydrated 3-fold- and 2-fold-symmetric amyloid-Aβ₄₀ fibrils and protofibrils of the D23N mutant. The methyl moieties of L17, L34, V36 (C–CD₃), and M35 (S–CD₃) serve as probes. Experimental ²H spectra acquired previously in the 147–310 K range are used. MOMD describes local probe motion as axial diffusion (R tensor) in the presence of a potential, u, which represents the spatial restrictions exerted by the molecular surroundings. We find that R_|| = (0.2–3.3) × 10⁴ s⁻¹, R_⊥ = (2.2–2.5) × 10² s⁻¹, and R is tilted from the ²H quadrupolar tensor at 60–75°. The strength of u is in the (2.0–2.4)kT range; its rhombicity is substantial. The only methyl moieties affected by fibril hydration are those of M35, located at fibril interfaces. The associated local potentials change form abruptly around 260 K, where massive water freezing occurs. An independent study revealed unfrozen “tightly-peptide-bound” water residing at the interfaces of the 3-fold-symmetric Aβ₄₀ fibrils and at the interfaces of the E22G and E22Δ Aβ₄₀-mutant fibrils. Considering this to be the case in general for Aβ₄₀-related fibrils, the following emerges. The impact of water freezing is transmitted selectively to the fibril structure through interactions with tightly-peptide-bound water, in this case of M35 methyl moieties. The proof that such waters reside at the interfaces of the 2-fold-symmetric fibril, and the protofibril of the D23N mutant, is new. MOMD provides information on the surroundings of the NMR probe directly via the potential, u, which is inherent to the model; a prior interpretation of the same experimental data does so partially and indirectly (see below). Thus, MOMD analysis of NMR line shapes as applied to amyloid fibrils/protein aggregates emerges as a consistent new tool for elucidating the properties of, and processes associated with, molecular environments in the fibril.

Graphical Abstract

1. INTRODUCTION

β-Amyloids are relatively small peptides (36–45 residues) produced by endoproteolitic cleavage of the amyloid precursor protein, which form fibrils. Aβ₄₀- and Aβ₄₂-amyloid fibrils and associated aggregates are the main molecular manifestations of Alzheimer’s disease.^1–4 Effective preventive and therapeutic agents for this devastating and fatal illness do not exist yet. To aid in developing such agents, it is important to acquire better information on the structural and dynamic properties of these systems; the purpose of this study is to do so.

We focus on dry and hydrated fibrils built of the wild-type (WT) Aβ₄₀ peptide^5–7 and protofibrils of its D23N mutant.⁸ The Aβ₄₀ monomer comprises a longer β₁-strand, a shorter β₂-strand, a connecting loop, and an unstructured N-terminal segment. Amyloid fibrils exhibit extensive polymorphism.^5–9 The polymorphs differ primarily in the manner in which the monomers assemble to yield basic structural units that underlie the protofilament, which in turn underlies the fibril (see below). The basic structural units associated with the WT Aβ₄₀ peptide are layers comprising three monomers (Figure 1a)⁵ or two monomers (Figure 1b).^6,7 They expand into β-sheets within the scope of a parallel in-register cross-β structure. These β-sheets, which run parallel to the fibril axis, form protofilaments with inner interfaces made of β₂-strands and outer interfaces made of β₁-strands.^5–7 The protofilaments intertwine to yield 2-fold-symmetric striated ribbon fibrils and 3-fold-symmetric twisted fibrils.^5–11

Figure 1.

Atomic representations of the 3-fold-symmetric Aβ₄₀ fibril (a) and the 2-fold-symmetric fibril (b), viewed down the fibril axis. Hydrophobic, polar, negatively charged, and positively charged amino acid side chains are green, magenta, red, and blue, respectively. Backbone nitrogen and carbonyl oxygen atoms are cyan and pink, respectively. The unstructured N-terminal residues 1–8 are omitted.⁷ Atomic representations of the protofibril of the D23N mutant viewed down the fibril axis. All of the nonhydrogen atoms of residues 15–40 are depicted. The central pair of a four-pair-containing structure (c).⁸ Atomic representation of the fibril of the E22Δ mutant viewed down the fibril axis. Hydrophobic, polar (and glycine), negatively charged, and positively charged amino acid side chains are white, green, red, and blue, respectively (d).⁹

The monomers of the D23N mutant form double-layered units (Figure 1c), which yield protofibrils (short curly fibrils) that exhibit an antiparallel cross-β setup.⁸

Water is an important component of the hydrated fibrils. A detailed solid-state NMR-based study, focusing largely on the water distribution in the 3-fold-symmetric WT fibril, has been published recently.¹² Five water pools were detected. Pool 1 contains tightly-peptide-bound water at the inner protofilament interface, which in this case forms a central pore; pool 2 contains such water at the outer protofilament interface. These waters contribute 2 and 5%, respectively, to the total fibril-associated water. Pools 3, 4, and 5 are loosely-peptide-bound water associated with the unstructured N-terminal segment, interfibrillar water, and matrix water; they contribute ~43, ~20, and ~30% to the total water, respectively. Figure 2 shows water pools 1–3.¹² Water pools 3–5 freeze at ~260 K; water pools 1 and 2 do not do so.

Figure 2.

Schematic of the 3-fold-symmetric Aβ₄₀ fibril with the M35 side chain depicted in yellow viewed down the fibril axis. The dashed curves show the unstructured N-terminal segment;¹² the residues specified are irrelevant in the present context.

In general, this picture also applies to the fibrils of the E22Δ and E22G mutants of Aβ₄₀.¹² The basic structural unit of the fibril of the E22Δ mutant is shown in Figure 1d.

It is of interest to correlate the results of ref 12 on the water setup/distribution in the fibril to the results obtained with NMR line shape analysis, which is a powerful method for elucidating local structural dynamics.^13–22 In principle, this method provides information on the rates of internal μs–ms motions, the spatial restrictions exerted at the site of their occurrence by the molecular surroundings, and related features of local geometry. A publication that precedes by several months that of ref 12 reports on the analysis of ²H line shapes from the 2-fold- and 3-fold-symmetric WT Aβ₄₀ fibrils and the D23N protofibrils.²² The methyl moieties (C–CD₃) of L17, L34, and V36, as well as those (S–CD₃) of M35, serve as probes. ²Hspectra were acquired from (dry) lyophilized powders and fully hydrated samples in the 147–300 K temperature range. It was found that hydration affects exclusively the M35 methyl moieties, with the respective ²H line shapes exhibiting an abrupt change around 260 K.

The authors of ref 22 analyzed their experimental ²H line shapes with the traditional composite-of-multi-simple-mode (MSM) perspective, where the overall model comprises several independent simple motional modes.^13–17 For valine, one has rotameric jumps around χ₁ among three sites with population distribution (w:1:1). For leucine, one has rotameric jumps around the corners of a tetrahedron housing the four magnetically inequivalent conformers (out of the nine conformers associated with χ₁ and χ₂); the population distribution is (w:1:1:1). The methionine line shapes are analyzed with the valine model below ~260 and the leucine model above ~260 K; jumps along an arc of length l centered at the C^γ–S bond are also included. Linear dependence on inverse temperature is imposed on ln(k) (k, exchange rate) and ln(w). The latter dependence has nonzero intercept; the authors of ref 22 interpret this as violation of the Boltzmann law, implying additional active degrees of freedom. The abrupt change around ~260 K is interpreted in terms of different side-chain conformations contributing to the restricted motion of the M35 methyl moiety above and below this temperature. The surroundings of the probe are represented implicitly by the activation energies for the rotameric jumps and the energy differences between the major and minor conformers.

Recently, we have developed the microscopic-order–macroscopic-disorder (MOMD) approach for NMR line shape analysis from polycrystalline samples, which explicitly incorporates the effect of the surroundings.^18–21 MOMD (developed originally for electron spin resonance applications)¹⁸ is based on the stochastic Liouville equation (SLE) developed by Freed and co-workers for treating rotational reorientation in anisotropic media.^23–25 The key elements, including type of motion, spatial restrictions, and local geometry, are treated generally within their rigorous three-dimensional (3D) tensorial requirements. The local motion is described by a diffusion tensor, R, and the local restrictions on the part of the environment by an anisotropic potential, u (in units of kT), in terms of which an ordering tensor, S, may be defined. Parameter combinations can be devised by monitoring the tensor magnitude, symmetry, and orientation. This enables a continuous range of scenarios and thus comparison among different cases within the scope of the same general model. The benefits of the MOMD/NMR approach compared to the MSM method have been demonstrated in refs 19–21.

Here, we apply MOMD to the experimental ²H line shapes of ref 22. The diffusion tensor is found to be adequately represented as axially symmetric with rate constants R_|| and R_⊥. In general, the potential, u, is expanded in the full basis set of the Wigner rotation matrix elements. From the present experimental data, we found that preserving the (lowest-order) L = 2, M = 0, and K = 0 or 2 terms is sufficient. The expression for u thus features two terms with respective coefficients $c_0^2$ and $c_2^2$ in the expansion. The ordering tensor, S, is allowed to be tilted with respect to the effective (i.e., reduced from its static value by the very fast methyl rotation) quadrupolar tensor, 〈Q〉. All of the methyl-moiety motions investigated below are consistently described by this model.

The effect of the surroundings manifests itself in terms of the form and symmetry of the anisotropic local potential and the tilt angle between the principal axis of the R/S tensor (see below) and the principal axis of the 〈Q〉 tensor. The MOMD-based picture differs qualitatively from the MSM-based picture. New insights into the properties of fibril environments emerge from the application of MOMD.

A theoretical summary is provided in Section 2; results and discussion are given in Section 3; and conclusions appear in Section 4.

2. THEORETICAL SUMMARY

The MOMD theory as applied to NMR data has been delineated previously.^19,20 For convenience, its basics are given below. Figure 3 shows the MOMD frame scheme for a deuterium nucleus: L is the space-fixed laboratory frame; C is the local director frame fixed in the molecule; M denotes the principal axis system (PAS) of the local ordering tensor, S, taken the same (for simplicity) as the PAS of the local diffusion tensor, R; and Q denotes the PAS of the partially averaged quadrupolar tensor. The M and Q frames are fixed in the probe.

Figure 3.

MOMD frames: L, lab frame; C, local director; M, local ordering/local diffusion frame: Q, effective quadrupolar tensor frame.

The Euler angles Ω_CM (associated with the orientation and diffusion of the probe relative to the local director) are time-dependent. The Euler angles Ω_MQ = (α_MQ, β_MQ, γ_MQ) are time-independent. Given that the Q frame is axially symmetric, one has γ_MQ = 0. For simplicity, the angle α_MQ is set equal to 0. Thus, the orientation of Z_M (main ordering/diffusion axis) relative to Z_Q (the principal axis of the effective quadrupolar tensor) is given by the polar angle, β_MQ. Since there is no “macroscopic order”, one has to calculate ²H spectra for a large enough number of Ω_LC values and sum the emerging line shapes according to a random distribution.^18–20

The stochastic Liouville equation (SLE) for a rigid particle diffusing in anisotropic medium with director parallel to the external magnetic field is given by^23–25

$$\begin{gathered} (\frac{\partial }{\partial t})\rho (\mathrm{\Omega },t)=[-\mathrm{i}\mathcal{H}{(\mathrm{\Omega })}^{\mathrm{X}}-{\mathrm{\Gamma }}_{\mathrm{\Omega }}]\rho (\mathrm{\Omega },t),\text{with}{\mathrm{\Gamma }}_{\mathrm{\Omega }}{P}_0(\mathrm{\Omega }) \\ =0 \end{gathered}$$ (1)

where ℋ(Ω)^X is the superoperator for the orientation-dependent spin Hamiltonian; Γ_Ω is a Markovian operator for the rotational reorientation of the spin-bearing moiety (probe), with the Euler angles Ω→(α, β, γ) (Ω_CM in the notation above) representing the orientational angles; and P₀(Ω) represents the unique equilibrium probability distribution.

A simple form of the diffusion operator, Γ_Ω, is²³

$$-{\mathrm{\Gamma }}_{\mathrm{\Omega }}=R{\nabla }_{\mathrm{\Omega }}^{2}P(\mathrm{\Omega },t)-(R/k_{\mathrm{B}}T){(sin\beta )}^{-1}\partial /\partial \beta [sin\beta TP(\mathrm{\Omega },t]$$ (2)

where R is the isotropic rotational diffusion rate, ${\nabla }_{\mathrm{\Omega }}^2$ is the rotational diffusion operator in the Euler angles Ω, and T is the restoring torque. The latter is equal to ∂u/∂β for an axial restoring potential, e.g., $u\cong -3/2(c_0^2{(cos\beta )}^2)$ (the coefficient $c_0^2$ is expressed in kT). The expression of Γ_Ω for rhombic diffusion tensor and rhombic potential is given in ref 24.

In this study, we are using an axial diffusion tensor, R, yielding in the absence of any restricting potential three decay rates, ${\tau }_K^{-1}=6R_{\perp }+K^2(R_{\Vert }-R_{\perp })$, where K = 0, 1, and 2 (K is the order of the rank 2 diffusion tensor). R_|| and R_⊥ are the principal values of R; one may also define τ_|| = 1/(6R_||) and τ_⊥ = 1/(6R_⊥).

For a uniaxial local director, one may expand the potential in the complete basis set of the Wigner rotation matrix elements, $D_{0,K}^L({\mathrm{\Omega }}_{\text{CM}})$, which are proportional to the spherical harmonics. One has²⁴

$$u({\mathrm{\Omega }}_{\text{CM}})=\sum _{L=1}^{\infty }\sum _{K=-L}^{+L}{c}_K^L{D}_{0,K}^L({\mathrm{\Omega }}_{\text{CM}})$$ (3)

with u(Ω_CM) and $c_K^L$ being dimensionless. If only the lowest, L = 2, terms are preserved, one obtains the real potential^24,25

$$u({\mathrm{\Omega }}_{\text{CM}})\approx -c_0^2{D}_{0,0}^2({\mathrm{\Omega }}_{\text{CM}})-c_2^2[D_{0,2}^2({\mathrm{\Omega }}_{\text{CM}})+D_{0,-2}^2({\mathrm{\Omega }}_{\text{CM}})]$$ (4)

with $c_0^2$ evaluating the strength of the potential, and $c_2^2$ its rhombicity.²⁴ This form of u(Ω_CM) is used herein.

Local order parameters are defined as^24,25

$$\begin{gathered} \langle D_{0,K}^2({\mathrm{\Omega }}_{\text{CM}})\rangle =\int \mathrm{d}{\mathrm{\Omega }}_{\text{CM}}{D}_{0,K}^2({\mathrm{\Omega }}_{\text{CM}})exp[-u({\mathrm{\Omega }}_{\text{CM}})]/\int \mathrm{d}{\mathrm{\Omega }}_{\text{CM}}exp[-u({\mathrm{\Omega }}_{\text{CM}})],K \\ =0,2 \end{gathered}$$ (5)

For at least 3-fold symmetry around the local director, C, and at least 2-fold symmetry around the principal axis of the local ordering tensor, Z_M, only $S_0^2\equiv \langle D_{0,0}^2({\mathrm{\Omega }}_{\text{CM}})\rangle$ and $S_2^2\equiv \langle D_{0,2}^2({\mathrm{\Omega }}_{\text{CM}})+D_{0,-2}^2({\mathrm{\Omega }}_{\text{CM}})\rangle$ survive.²⁴ The Saupe order parameters relate to irreducible tensor components, $S_0^2$ and $S_2^2$, as $S_{xx}=(\sqrt{3/2}{S}_2^2-S_0^2)/2,S_{yy}=(\sqrt{3/2}{S}_2^2+S_0^2)/2$, and $S_{zz}=S_0^2$.

3. RESULTS AND DISCUSSION

The issues of interest include the effect of hydration and temperature on restricted methyl-moiety motion. Differences among the three fibril variants studied are also of interest.

3.1. Qualitative Analysis

Figure S1 of the Supporting Information shows the ²H spectra from dry and hydrated 3-fold- and 2-fold-symmetric Aβ₄₀ fibrils acquired at 294 K for L17, L34, and V36, and at 310 K for M35.²² It can be seen that hydration affects exclusively the M35 spectra. The difference between the corresponding 3-fold- and 2-fold-symmetric spectra is small, with the 2-fold-symmetric spectra being somewhat narrower. Quite a few extraneous factors can cause such global line shape narrowing; quantitative analysis of this feature is not pursued here. Figure S1 is representative of the situation prevailing at all of the experimental temperatures examined.

Figure 4 shows excerpts from the evolution as a function of temperature of the experimental (blue) and simulated (red, in ref 22) ²H spectra of the various probes in the hydrated 3-fold-symmetric polymorph.²² We focus on the experimental (blue) spectra. The line shapes of V36 (e–g), L34 (h–k), and L17 (l–o) represent both dry and hydrated samples, as hydration does not affect these probes. The line shapes of M35 (a–d) were acquired below 260 K, where the majority of the water is frozen.¹² The unfrozen water is tightly-peptide-bound,¹² i.e., largely part of the peptide structure.

Figure 4.

Experimental ²H line shapes from the methyl groups of M35 (a–d), V36 (e–g), L34 (h–k), and L17 (l–o) in the hydrated 3-fold-symmetric Aβ₄₀ fibrils at the temperatures depicted (blue);²² best-fit calculated line shapes from ref 22 (red).

A typical pattern can be discerned: near-rigid-limit spectra at low temperatures (d, g, k, and o), line shapes with a flat top at intermediate temperatures (b, e, i, and m), and line shapes with a rounded top at high temperatures (a, h, and l). This picture is consistent with a dominant major motional mode, with methyl type and methyl location determining its activation energy.

Figure S2a of the Supporting Information depicts the experimental spectra of V36 in the hydrated WT fibrils (red and blue) and the D23N protofibrils (black).²² The typical spectral evolution illustrated in Figure 4 is also exhibited by the D23N fibrils, as well as the WT fibrils although with very small activation energy for local probe motion. We ascribe the latter feature to the relatively large effect of the D23N mutation at the V36 site.²²

Figure S2b shows the ²H spectra of M35 in the three fibril variants.²² As pointed out above, we disregard the differences between the two WT fibrils. Below ~260 K, the WT and D23N mutant spectra exhibit the typical evolution with temperature, with enhanced activation energy for the local motion of the mutant methyl. The WT fibril spectrum changes shape abruptly between 258 and 274 K; the mutant spectrum does so between 238 and 258 K. These interesting features are investigated quantitatively below.

3.2. Quantitative MOMD Analysis

Figure 5a shows the experimental ²H spectra of the M35 methyl moiety in the dry WT fibrils acquired at 238, 258, 274, and 310 K.²² Figure 5b shows the best-fit calculated MOMD spectra. It can be seen that the familiar features described above are well reproduced by MOMD. The temperature dependence of the experimental spectra in the 238–310 K range is quite limited. In this study, we aimed at capturing consistently the important features using few variables. Within the scope of this reasoning, we discuss the average parameters associated with Figure 5b. One has 〈log(R_⊥)〉 = 2.4 and 〈log(R_||)〉 = 4.3, with R_|| and R_⊥ given in s⁻¹. 〈Q〉 = 58 kHz; this yields log(〈Q〉) = 4.8. R_⊥ is substantially smaller than 〈Q〉, affecting the analysis to only a small extent. R_|| is on the order of 〈Q〉; it has a large effect on the analysis but varies with a small activation energy (estimated at 1.2 ± 0.5 kJ/mol).

Figure 5.

Experimental ²H line shapes from the methyl group of M35 in the dry 3-fold-symmetric Aβ₄₀ fibrils (red) and 2-fold-symmetric Aβ₄₀ fibrils (blue) at the temperatures depicted (a). Best-fit calculated MOMD line shapes that correspond to the experimental line shapes shown in (a). The average values of the best-fit MOMD parameters are 〈log(R_⊥)〉 = 2.4, 〈log(R_||)〉 = 4.3, $\langle c_0^2\rangle =2.1$, and $\langle c_2^2\rangle =2.3$. The angle β_MQ is 70° throughout. The effective quadrupole constant used is 〈Q〉 = 58 kHz²² (b).

Both the strength ( $c_0^2$) and the rhombicity ( $c_2^2$) of the potential decrease with increasing temperature. Their average values are $\langle c_0^2\rangle =2.1$ and $\langle c_2^2\rangle =2.3$, respectively. The angle, β_MQ, between Z_M (the principal axis of the R tensor) and Z_Q (the principal axis of the 〈Q〉 tensor) is 70° for all four spectra. Thus, Z_M is pointing along an effective axis rather than the C^γ–S bond that precedes the S–CD₃ bond. Had Z_M been parallel to C^γ–S, β_MQ would have been 99°, as Z_Q is parallel to S–CD₃. Deviations of β_MQ from 99° are implied by environmental constraints. They are indicative of the main ordering axis being an empirical orientation, in accordance with the mesoscopic nature of MOMD.

Figure 6 shows the evolution of the experimental ²H line shape for M35 in the hydrated WT Aβ₄₀ fibrils. The spectra change gradually in the 147–258 and 274–310 K ranges; upon increasing the temperature from 258 to 274 K, they change abruptly. Figure 7 shows the best-fit calculated MOMD spectra. All of the major features are well reproduced; log R_⊥ is 2.2 throughout, which has a very small effect on the analysis. R_|| changes gradually in the entire temperature range investigated, as shown in Figure 8c, where ln(R_||) vs 1000/T K⁻¹ is depicted. By fitting these data to the Arrhenius relation (red line in Figure 8c), an activation energy of 5.9 ± 0. 2 kJ/mol is obtained.

Figure 6.

Experimental ²H line shapes from the methyl group of M35 in the hydrated 3-fold-symmetric Aβ₄₀ fibrils at the temperatures depicted (blue);²² best-fit calculated line shapes from ref 22 (red).

Figure 7.

Best-fit calculated MOMD line shapes that correspond to the experimental line shapes of Figure 6. The best-fit values of $c_0^2,c_2^2$ and log R_|| are given as graphs in Figure 8. The data associated with the temperatures 258 and 274 K, where the abrupt change in the ²H line shape occurs, are depicted. The angle β_MQ is 65° for T = 258 K and below, and 60° for T = 274 K and above. The parameter log R_⊥ is 2.2 throughout. The effective quadrupole constant used is 〈Q〉 = 58 kHz.²²

Figure 8.

Potential coefficient, $c_0^2$, associated with the MOMD spectra of Figure 7, as a function of 1000/T K⁻¹ (a). Potential coefficient, $c_2^2$, associated with the MOMD spectra of Figure 7, as a function of 1000/T K⁻¹ (b). The blue lines connect the experimental points to guide the eye. The parameter ln(R_||), associated with the MOMD spectra of Figure 7, as a function of 1000/T K⁻¹ (c). The red line was obtained by fitting the experimental points to the Arrhenius equation; it yielded an activation energy of 5.9 ± 0.2 kJ/mol.

The potential coefficients $c_0^2$ and $c_2^2$ change gradually in the 147–258 and 274–310 K ranges; they change abruptly upon increasing the temperature from 258 to 274 K (Figure 8a,b). This is precisely the pattern exhibited by the corresponding experimental ²H spectra (Figure 6). Within the temperature ranges exhibiting smooth variations (147–258 and 274–310 K), the strength of the local potential ( $c_0^2$) decreases with increasing temperature (Figure 8a), as expected. The rhombicity of the local potential ( $c_2^2$) increases with increasing temperature (Figure 8b). Similar behavior was observed for globular proteins and interpreted in terms of degrees of freedom that contribute to the rhombicity of the potential being “frozen” at lower temperatures.^19,20 We suggest that interpretation in the present case. For the dry fibrils, $c_2^2$ decreases with increasing temperature (see above), in accordance with fewer degrees of freedom 0being prone to freeze at lower temperatures in these compact structures.

For the hydrated fibrils, the angle β_MQ is 65° in the 147–258 K range and 60° in the 274–310 K range (Figure 7); as shown above, it is 70° for the dry fibrils (Figure 5b). Differences on the order of 5–10° influence the analysis little.

The ²H spectra of M35 in the hydrated D23N fibrils (black in Figure S2b) exhibit a behavior similar to that of the hydrated WT fibrils (red/blue in Figure S2b). For the D23N mutant, the abrupt change occurs between 238 and 258 K, and the activation energy for R_|| below 238 K is larger than the activation energy for R_|| of the WT fibrils. Otherwise, the overall pictures are similar.

The following comment is in order. Here and in previous studies,^19–21 we present unique MOMD-derived pictures of structural dynamics. This is accomplished by analyzing a sizable set of temperature-dependent ²H line shapes. We require that R_|| and R_⊥ increase with increasing temperature (or stay constant when they exceed the time window) and that the potential strength, i.e., $c_0^2$, decreases with increasing temperature. We opt for temperature-independent β_MQ. With these prerequisites fulfilled, ambiguity and uncertainty are largely avoided.

3.3. Effect of Hydration

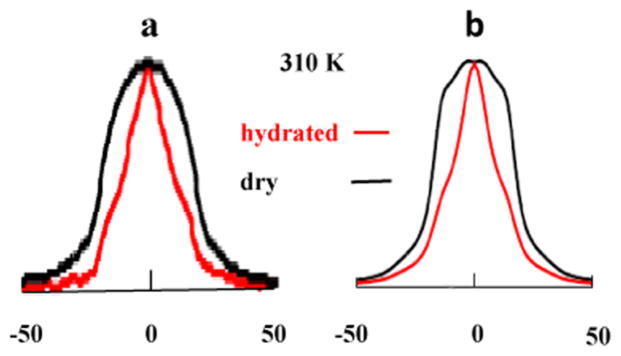
Figure 9a shows the experimental dry (black) and hydrated (red) ²H spectra of M35 in the 3-fold-symmetric fibrils acquired at 310 K. The difference is substantial. Figure 9b shows the best-fit calculated MOMD spectra; the agreement with experiment is good. The best-fit MOMD parameters associated with Figure 9b are shown in Table 1.

Figure 9.

(a) Experimental ²H line shapes from the methyl group of M35 in the dry (black) and hydrated (red) 3-fold-symmetric Aβ₄₀ fibrils at 310 K. (b) Best-fit calculated MOMD line shapes that correspond to the experimental line shapes of (a), with the best-fit parameters given in Table 1.

Table 1.

Best-Fit Values of $c_0^2,c_2^2$, log(R_⊥), log(R_||), and β_MQ Associated with the MOMD Spectra of Figure 9b^a

	$c_0^2$	$c_2^2$	$c_0^2/c_2^2$	$S_0^2$	$S_2^2$	log(R⊥)	log(R||)	βMQ (deg)
hydrated, 274 K	2.3	2.0	1.65	0.336	0.321	2.2	4.5	60
dry, 274 K	2.0	2.2	0.95	0.231	0.409	2.5	4.4	70

^aThe order parameters, $S_0^2$ and $S_2^2$, are calculated from the potential coefficients, $c_0^2$ and $c_2^2$, according to eq 5. Estimated errors (based on visual agreement between experiment and calculation) are ±1° for β_MQ, 10% for $c_0^2$ and $c_2^2$, and 15% for R_⊥ and R_||.

The logarithm of R_⊥ is 2.5 for the dry fibril, affecting the ²H spectra slightly; it is 2.2 for the hydrated fibril, with virtually no effect on the ²H spectra. The logarithm of R_|| is only slightly larger for the hydrated fibril. Thus, the kinetic parameters do not differ much.

On the other hand, the parameters associated with the local structure, $c_0^2,c_2^2,S_0^2,S_2^2$, and β_MQ, differ substantially. We also show in Table 1 the irreducible order parameters, $S_0^2$ and $S_2^2$, calculated from $c_0^2$ and $c_2^2$, according to eq 5. One has $c_0^2/c_2^2=1.65$ and $S_0^2>S_2^2$ for the hydrated fibril and $c_0^2/c_2^2=0.95$ and $S_0^2<S_2^2$ for the dry fibril. The parameter $c_0^2/c_2^2$ indicates that the rhombicity of the potential at the M35 methyl site is larger for the hydrated fibril. The change in the relative magnitude of $S_0^2$ and $S_2^2$ implies a change in the principal axis of the S tensor. It indicates that the symmetry of the potential (also expressed by the change in the sign of (S_xx – S_yy), where S_ii are the components of the Saupe ordering tensor—see section after eq 5) differs for the two fibril forms. A difference of 10° in the angle β_MQ is a large effect.

The temperature dependence of the ²H spectra in the 274–310 range is small (cf. Figure S2b).

3.4. New Insights from Integrated Perspectives

Let us combine information from 3D structure determination,^5–9 the water setup determined in ref 12, and MOMD ²H line shape analysis. The black circles in Figure 1a–d depict M35 methyl groups; all of them reside at inner or outer protofilament interfaces.^5–9 The latter comprise exclusively tightly-peptide-bound water.¹² For the fibrils of Figure 1a,d and those of the E22G mutant (not depicted, as currently no 3D structure is available), it was shown that structural elements residing at protofilament interfaces interact with tightly-peptide-bound water.¹² Direct evidence for such interaction was provided for the M35 methyl moiety of the fibril depicted schematically in Figure 1.¹² MOMD ²H line shape analysis has shown that (a) all of the M35 methyl moieties of Figure 1a–c respond alike to fibril hydration and (b) all of the features of this response can be explained by interaction with tightly-peptide-bound water.

The following insights emerge. (1) The water setup determined in ref 12 is most likely general in nature. (2) The inner interface of the 2-fold-symmetric protofilament (Figure 1b) and the outer interface of the protofibril of the D23N mutant (Figure 1c) comprise tightly-peptide-bound water. (3) Tightly-peptide-bound water plays an important role in the fibril hydration process: it propagates its effect selectively to local sites in the fibril structure.

This study is relevant in the broader context of protein misfolding and aggregation and intermediate structures encountered in the process of Aβ-fibril formation.^26–30

4. CONCLUSIONS

Restricted internal motion of ²H-labeled methyl moieties of L17, L34, M35, and V36 in dry and hydrated 2-fold- and 3-fold-symmetric Aβ₄₀ fibrils and protofibrils of the D23N mutant has been studied with MOMD-based ²H line shape analysis. The level of MOMD utilized describes these motions as axial diffusion around an effective axis in the presence of a rhombic potential, u. We find that R_|| = (0.2–3.3) × 10⁴ s⁻¹, R_⊥ = (2.2–2.5) × 10² s⁻¹, and the activation energies for R_|| are on the order of a few kilojoules per mole. The effective diffusion axis, which is also taken as an effective ordering axis, is tilted at 25–40° from the C–CD₃ or S–CD₃ bonds.

The potential, u, has strength on the order of 2kT and has rhombic symmetry. As expected, u is weaker at higher temperatures. In the hydrated fibrils, the rhombicity of u increases with increasing temperature, as some contributing degrees of freedom are frozen at the lower temperatures.

Our interpretation differs from that of ref 22, which is based on the MSM method. MOMD treats all of the methyl types studied in a similar manner and incorporates the effect of the environment explicitly as an anisotropic potential. The overall model used in ref 22 is specific to each methyl type; the environment is represented partially by activation energies associated with given constituents of the overall models and indirectly by energy differences of exchanging states not complying with the Boltzmann law; linear dependencies on 1/T are imposed on the major parameters determined. These different perspectives yield different pictures.

The MOMD analysis of ²H line shapes provides evidence for the generality of the water setup determined in ref 12. It demonstrates the so far unknown existence of tightly-peptide-bound water at the inner interface of the 2-fold-symmetric protofilament and the outer interface of the protofibril of the D23N mutant. It shows that the impact of fibril hydration is propagated to the fibril structure through interaction with tightly-peptide-bound water.

Prospects include further experimental investigations and application of MOMD to the ²H spectra and the development of MOMD for the ¹⁵N and ¹³C NMR nuclei.