Predicting therapy success for treatment as usual and blended treatment in the domain of depression

Abstract

In this paper, we explore the potential of predicting therapy success for patients in mental health care. Such predictions can eventually improve the process of matching effective therapy types to individuals. In the EU project E-COMPARED, a variety of information is gathered about patients suffering from depression. We use this data, where 276 patients received treatment as usual and 227 received blended treatment, to investigate to what extent we are able to predict therapy success. We utilize different encoding strategies for preprocessing, varying feature selection techniques, and different statistical procedures for this purpose. Significant predictive power is found with average AUC values up to 0.7628 for treatment as usual and 0.7765 for blended treatment. Adding daily assessment data for blended treatment does currently not add predictive accuracy. Cost effectiveness analysis is needed to determine the added potential for real-world applications.

Highlights

• •Exploring possibilities for predicting therapy outcome is important because it can impact and benefit personalized therapy, effectiveness of therapy, and health care cost reduction.
• •The results suggest that significant predictive power is present in the baseline dataset, which leads to reasonable predictive model performances. The results are promising, however, more data and experimentation is needed to investigate the capabilities and accuracy in predictive performance.
• •EMA data has been shown to possess predictive power, however, in the state it was preprocessed coupled with baseline data it does not increase prediction performance.
• •Cost effectiveness analysis is needed to shed light on the actual benefit predictive models can provide in this domain.

1. Introduction

Nowadays, individuals that suffer from mental health problems face a range of different treatment types to choose from such as treatment as usual (TAU) and blended treatment (BT). Making decisions regarding suitable treatment types on an individual level is a challenging problem. In online interventions, an increasing amount of data is collected including socio-demographic aspects, recurring symptomatic questionnaires, Ecological Momentary Assessments (EMA), and outcome related factors. Machine learning techniques can support the decision-making process of therapists and practitioners by extracting valuable information from this wealth of data and providing crucial input regarding therapy success and symptom development. In this context computerized systems can potentially improve the care and accomplishment of practitioners in this field (Garg et al., 2005).

Therefore, we investigate possibilities of predicting therapy success using data from the EU funded project E-COMPARED, in which the effectiveness of TAU and BT are investigated. We define therapy success based on the Patient Health Questionnaire-9 (PHQ-9, (Kroenke et al., 2001)). This is an internationally acknowledged and validated questionnaire that measures the presence and extent of depression. We utilize baseline measures of individuals for TAU and BT and further evaluate if involving EMA data can lead to increased prediction performance in BT. For this purpose, we take advantage of multiple statistical models, preprocessing steps, and feature selection methods. In the case of accurate predictions at intake, more tailored therapy types can potentially be offered, more effective treatment recommendation can be provided, enhanced decision-support tools can be developed, and even health care costs can eventually be reduced.

Related research is scarce due to the fact that the field of predictive modeling in e-mental health is still young. Good examples of relevant work in the context of this paper are Both et al. (2009), where the design and analysis of an ambient intelligent system is described that offers support during therapy of patients that recover from uni-polar depression; and in Duppong Hurley et al. (2015), where changes in therapeutic alliance are investigated to have power to predict therapy outcome in youth with a disruptive-behavior diagnosis.

In the following sections, we introduce the data we utilize, details of the experimental setup and illustrate our results. We finalize the paper by discussing the outcomes, limitations, and future research opportunities.

2. Data

The data utilized for our approach consists of several sub-datasets, each of which represents a certain area of information. For each patient, demographic information is gathered. Additionally, information about current treatment is collected such as current medication usage and psychotic symptoms. Furthermore, validated questionnaires are used to measure psychiatric disorders (M.I.N.I.; Sheehan et al., 1998), depressive symptomatology (QIDS-SR16; Trivedi et al., 2004), severity of depression (PHQ-9 Kroenke et al. (2001)), and generic health status (EQ-5D-5L; Herdman et al., 2011). In addition, information about treatment preferences is available. The TAU and BT have a duration of three months. At the start of the therapy, a baseline measurement is conducted covering all of the measurements described above and follow-up severity of depression (PHQ-9) measurements are repeated at three months, six months, and twelve months.

In BT, additional EMA information is gathered on a daily basis, which is one of the big difference with the usual treatment a patient is given in TAU. Specifically, patients can enter EMA data when reminded by the application, or whenever the patient wants. As displayed in Table 1, the EMA data consists of seven variables such as mood level, worry level, etc, which are measured on an interval scale of [1, 10] (for more information about EMA data and EMA data collection, see Shiffman et al., 2008).

Table 1.

The EMA measures that are present in the dataset.

Abbreviation	EMA question
Mood	How is your mood right now?
Worry	How much do you worry about things at the moment?
Self-esteem	How good do you feel about yourself right now?
Sleep	How did you sleep tonight?
Activities done	To what extent have you carried out enjoyable activities today?
Enjoyed activities	How much have you enjoyed the days activities?
Social contact	How much have you been involved in social interactions today?

There are 780 unique patients suffering from major depressive disorder (DSM-IV) in the dataset for which the intake data is complete. As the data is currently being processed within the project, the number of usable patients declines over time as the data of the follow ups has not been processed yet. Specifically, at three-months 555 patients, at six-months 215 patients, and at twelve-months 116 patients present for the purpose of predicting therapy success.

The total number of raw features collected for each patient is 119, which are mostly categorical in nature. The BT dataset consists of additional EMA data such as the day number, date, time, schedule, and rating related to the different EMA questions. Because of the format of the EMA data, data transformation is required to merge it to the other sub-datasets.

Exploring the sub-datasets for missing data reveals that data regarding current treatment, psychiatric disorders, and depressive symptomatology contain missing values (due to conditional follow-up questions that were not relevant in some situations). Furthermore, there are missing values in the data regarding severity of depression at the three months measurement (five patients), six month measurement (three patients), and twelve month measurement (82 patients). Moreover, missing values are found in the data about treatment preferences, especially about willingness to carry a smart phone.

3. Methods

3.1. Data selection

Because we have two therapy types with different patient for each therapy type, we divide the data in the TAU dataset and the BT dataset. Furthermore, due to data inconsistencies, we need to exclude information. In the TAU dataset, one participant was excluded because the age of the participant is unknown, resulting in 276 patients in this dataset. In the BT dataset, 56 patients were excluded due to merging procedures with the EMA dataset and an insufficient number of observations in EMA (less than seven days). Therefore, we are left with 227 patients in the BT dataset.

3.2. Target feature

Because we seek to have as much data as possible to increase chances of accurate predictions, we choose to compare the three-month follow-up measurement with the baseline measurement. We use this difference in measurement to engineer the target feature that represents therapy success for each patient. The PHQ-9 consists of nine questions which can be scored from zero to three. The total of the scores is used to express the extent of current depressive symptoms. Based on the rationale found in McMillan et al. (2010), we define the therapy to be a success in the following cases:

• 1.PHQ − 9_post < =9 and $\mathrm{\Delta }PHQ-9_{pre\mathrm{\_}post}>50\%$
• 2.PHQ − 9_pre > =5 and PHQ − 9_post < =4.

As displayed in Table 2, this results in 45 successful therapy effects in the TAU dataset and 58 successful therapy effects in the BT data.

Table 2.

The number of successful and unsuccessful therapy effects in the TAU and BT datasets.

Treatment	Nr patients	Unsuccessful	Successful
TAU	276	231	45
BT	227	169	58

3.3. Preprocessing categorical features

A lot of the questionnaire outcomes are categorical. We have a total of 107 categorical features (besides the 12 non-categorical features). These categorical features can be handled in different ways.

One strategy to transform the data is to use dummy encoding, which generates binary variables that indicate the presence or absence of specific categorical values (see e.g. Hardy, 1993). This procedure considers each possible answer and also takes into account the presence of missing values as separate variables. The downside, however, is the increasing amount of features in the datasets. Using the approach sketched above results in 408 dummy features for the TAU dataset and 407 features for the BT dataset. This preprocessing strategy is referred to as the binary encoding condition.

An alternative approach we consider to to transform the categorical values into continuous features. This approach is reasonable because many of the questionnaires include responses with a certain order such as time related questions (e.g., one to six months, etc), extent related questions (e.g. no pain, slight pain, etc.), and confirmation questions (yes, no). However, not all features are compatible. From the 107 categorical variables, we create 45 and 47 continuous features for the TAU and BT dataset respectively and use a binary encoding for the remaining features (resulting in 247 binary features for TAU and 225 for BT) This preprocessing strategy is referred to as the mixed encoding condition.

3.4. Preprocessing the EMA features

To explore if adding EMA data results in increased predictive accuracy, we choose to use the first seven days of EMA data in the analysis. If we are able to predict the success better after a week of therapy this might still be valuable. Possibly, the amount of bad mood scores or mood patterns during the day can help describe the probability of future therapy success. Because the EMA data in its raw form is not compatible with the BT dataset, we transform the answers of each of the seven questions into the sum, mean, slope, standard deviation, minimum, and maximum of the values over the seven days. We separately repeat this process for morning only-, midday only-, evening only measurements, and full day measurements.

We remove features that consist of 80% or more missing data. The missing values in the features that remain after this procedure are imputed with zero. 119 transformed EMA features result from this procedure. Again, this EMA dataset is used as a separate conditional dimension for the BT dataset during experimentation.

3.5. Feature selection

For each feature preprocessing condition, we apply two feature selection procedures. To address the collinearity issue, we use feature similarity (FS) analysis to exclude one of each pair of binary features that have 80% or more resemblance over the different participants. Note that this is done for both the binary preprocessed and mixed preprocessed data, where the in the latter the continuous features are excluded. To address overfitting and increasing generalizability, we apply recursive feature elimination (RFE, see Kuhn, 2012) in addition to FS. RFE sheds insight in which features are mostly responsible for decreasing the prediction error by ordering the features based on their relative importance. We set the RFE method to select a maximum of 50 features. The resulting number of features for each condition after applying the feature selection methods is displayed in Table 3 for the binary encoding and in Table 4 for the mixed encoding conditions.

Table 3.

Number of features of binary encoded dataset, for each feature selection situation.

Feature selection	TAU	BT	BT + EMA
None	420	419	538
FS	119	113	232
FS + RFE	50	50	50

Table 4.

Number of features of mixed encoded dataset, for each feature selection situation.

Feature selection	TAU	BT	BT+EMA
None	292	272	391
FS	83	83	202
FS + RFE	50	50	50

3.6. Model selection

Because predictive techniques can perform differently on data, we choose to use three different types of predictive models during experimentation (using the Caret package (see M.K.C. from Jed Wing et al., 2017) within the R environment (see R Core Team, 2016). First, we select the random forest (RF) model (see e.g. Liaw and Wiener, 2002). The RF model is an ensemble learning method that generates a multitude of decision trees during training and predicts an outcome by taking the outcomes of each decision tree into account. Second, we use the k-nearest neighbors (KNN) model (see e.g. Peterson, 2009). The KNN model is considered to be a simple predictive model that uses the values of k of its closest neighbors to generate the predictive outcome. During training, the k that has the lowest error on the validation set within a cross-validation setting is found. Third, we utilize the general linear model (GLMB) that uses likelihood based boosting (see e.g. Tutz and Binder, 2007). The boosting refers to training a multitude of classifiers that together form predictions for new cases.

3.7. Training and validation strategy

To train the models within each condition, we use 80% of the data as the training set. The remaining independent 20% of the data, the test set, is used to test the performance of the trained models. Within the training set, a 10-fold cross-validation method is used to optimize the parameters of each model. Because there is variation between performances on the test set when using random sampling to divide the training set and test set, we use 20 fixed sample seeds which are constant over the conditions. Therefore, the training and testing procedure is executed 20 times for each condition where the performance on the test set is averaged. To measure the performance of each model, we utilize the Area Under the ROC Curve (AUC) metric. This metric represents the efficiency of a model, specifically true positive ratio versus false positive ratio (see Hanley and McNeil, 1982).

4. Results

We apply all combinations of the different approaches we have described and report the average AUC values, and their 95% confidence intervals (see DeLong et al., 1988) in Table 5. The best results that have a minimum confidence interval value of 0.7 or higher are illustrated in bold.

Table 5.

Resulting AUCs using the different setups including 95% confidence intervals.

Encoding	Feature selection	RF (50)	RF (100)	KNN	GLMB
TAU
Binary	No	0.7282 (0.6802–0.7577)	0.7430 (0.6917–0.7682)	0.5515 (0.4229–0.5217)	0.7027 (0.6475–0.7318)
	FS	0.7401 (0.6897–0.7674)	0.7606(0.7016–0.7769)	0.6257 (0.5686–0.6560)	0.7098 (0.6494–0.7345)
	FS + RFE	0.7289 (0.6689–0.7483)	0.7337 (0.6734–0.7523)	0.6748 (0.6157–0.6984)	0.6856 (0.6381–0.7244)
Mixed	No	0.7616(0.7181–0.7892)	0.7620(0.7160–0.7884)	0.5875 (0.5191–0.6210)	0.6757 (0.6186–0.7121)
	FS	0.7499 (0.6994–0.7728)	0.7628(0.7094–0.7819)	0.6521 (0.5884–0.6754)	0.6871 (0.6350–0.7260)
	FS + RFE	0.7402 (0.6876–0.7650)	0.7531 (0.6959–0.7729)	0.6871 (0.6372–0.7197)	0.6713 (0.6172–0.7100)
BT
Binary	No	0.7151 (0.6484–0.7255)	0.7254 (0.6532–0.7294)	0.6608 (0.5978–0.6841)	0.7344 (0.6758–0.7480)
	FS	0.6968 (0.6422–0.7212)	0.7077 (0.6434–0.7232)	0.6802 (0.6226–0.7046)	0.7404 (0.6836–0.7555)
	FS + RFE	0.6864 (0.6236–0.7054)	0.6968 (0.6239–0.7063)	0.6919 (0.6285–0.7091)	0.7369 (0.6809–0.7543)
Mixed	No	0.7244 (0.6489–0.7271)	0.7145 (0.6435–0.7224)	0.7009 (0.6408–0.7239)	0.7684(0.7051–0.7739)
	FS	0.7115 (0.6409–0.7192)	0.7187 (0.6484–0.7257)	0.6955 (0.6384–0.7198)	0.7765(0.7143–0.7822)
	FS + RFE	0.6899 (0.6202–0.7016)	0.6869 (0.6175–0.6989)	0.6794 (0.6214–0.7033)	0.7496 (0.6888–0.7608)
BT+EMA
Binary	No	0.7126 (0.6463–0.7285)	0.7320 (0.6646–0.7460)	0.6243 (0.5590–0.6503)	0.7383 (0.6793–0.7510)
	FS	0.7229 (0.6709–0.7495)	0.7200 (0.6646–0.7446)	0.6506 (0.5917–0.6737)	0.7543 (0.6963–0.7665)
	FS + RFE	0.6931 (0.6249–0.7063)	0.6962 (0.6246–0.7071)	0.6385 (0.5774–0.6626)	0.7000 (0.6424–0.7208)
Mixed	No	0.7251 (0.6606–0.7421)	0.7196 (0.6538–0.7345)	0.6801 (0.6097–0.6987)	0.7565 (0.6935–0.7632)
	FS	0.7179 (0.6601–0.7404)	0.7124 (0.6547–0.7355)	0.6522 (0.5930–0.6735)	0.7607 (0.6985–0.7679)
	FS + RFE	0.6669 (0.6058–0.6924)	0.6860 (0.6186–0.7040)	0.6399 (0.5803–0.6651)	0.6974 (0.6374–0.7171)

The results indicate that the mixed encoding dataset generally seems to perform a bit better (though not significant). Furthermore, the RF models generate the best results for the TAU dataset and the GLMB models generate the best results for the BT dataset. In general, it is difficult to forecast which predictive model performs best given any problem. Therefore, it can be beneficial experiment with multiple models. Examining the effects of the feature selection methods, the FS (feature similarity) selection procedure results in data with far less features that still are able to produce three out of the six best scores where the other best score results from a condition without any feature selection. The RFE selection procedure coupled with FS does not result in superior results. Finally, adding EMA data to the BT dataset does not result in better predictions.

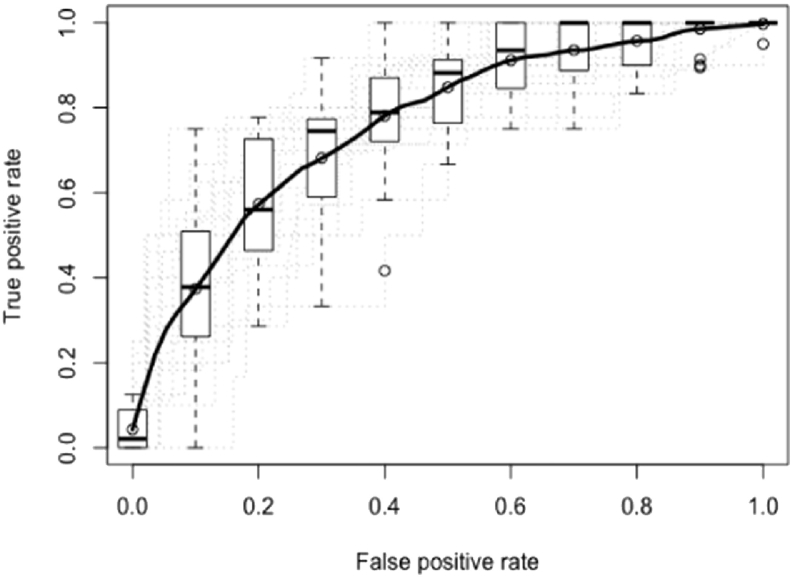
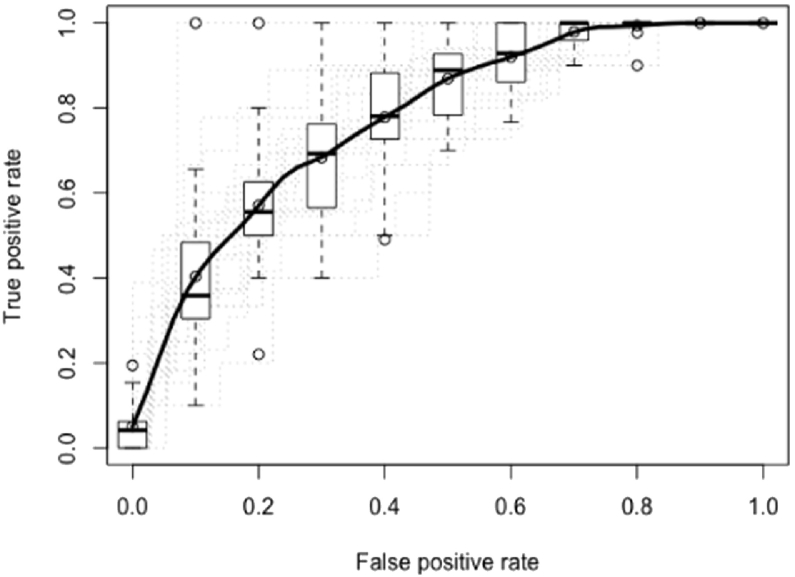
Overall, looking at the confidence intervals, the best predictive model for TAU obtains an average AUC of 0.7620 with 95% confidence intervals of 0.7160–0.7884 (a random forest with 50 trees, mixed encoding and no feature selection) and for BT an average AUC of 0.7765 with 95%confidence intervals of 0.7143–0.7822 (GLMB with FS as features selection and mixed encoding). In Figs. 1 and 2, the ROC curves of these results are displayed. In Tables 6 and 7, the ten features that were most important during training are displayed for the best model of the TAU dataset and of the BT dataset.

Fig. 1.

Average ROC over 20 samples for TAU using a random forest with 50 trees, mixed encoding and no feature selection. The mean AUC is 0.7620 with 95% confidence intervals of 0.7181–0.7892.

Fig. 2.

Average ROC over 20 samples for BT using a GLMB with FS as features selection and mixed encoding. The mean AUC is 0.7765 with 95% confidence intervals of 0.7143–0.7822.

Table 6.

Top 10 features that were found to be important by the predictive model that generated the highest range of AUC values for the TAU dataset, a random forest with 50 trees, mixed encoding and no feature selection. The order of the features are the averaged order over the 20 training iterations.

Imp.	Feature name	Dataset
1	aPHQ_sum	PHQ-9 (eng.)
2	aAge	Demographics
3	atreat17aMPK	Current tr.
4	aQIDS05	QIDS-SR16
5	aPHQ03	PHQ-9
6	aPHQ04	PHQ-9
7	aEQ5D5L4	EQ-5D-5L
8	aPHQ02	PHQ-9
9	aEQ5D5L5	EQ-5D-5L
10	aQIDS14	QIDS-SR16

Table 7.

Top 10 features that were found to be important by the predictive model that generated the highest range of AUC values for the BT dataset, a GLMB with FS as features selection and mixed encoding. The order of the features are the averaged order over the 20 training iterations.

Imp.	Feature name	Dataset
1	ccxPoland	Demographics
2	aQIDS08	QIDS-SR16
3	aQIDS11	QIDS-SR16
4	atreat17a1	Current tr.
5	amini9no	M.I.N.I.
6	atreat4	Current tr.
7	aMarital	Demographics
8	amini7b	M.I.N.I.
9	aQIDS01	QIDS-SR16
10	atreat7	Current tr.

5. Discussion

It is important to explore possibilities for predicting therapy success considering the increasing demand for personalized treatment and the need for the reduction of health care costs. The results show a step in the right direction. We are able to predict TAU and BT therapies with AUC values between 0.71 and 0.78 on an independent test set. The findings are interesting and suggest that the models are potentially able to improve the therapy selection procedure. However, before we consider this to be the case, we need to critically interpret the results, the data, and the experimental setup.

To provide a better impression of how the predictive models actually perform, we interpret the result from our best predictive model for TAU of which the ROC curve is displayed in Fig. 1. To be able to predict individual cases, a criterion value needs to be chosen. Here, we choose a criterion value of 0.09 corresponding to a true positive rate (sensitivity) of 0.8462 and a false positive rate (1 — specificity) of 0.4854. The resulting predictions are displayed in Table 8.1 From the 195 actually successful cases, the model predicts 165 cases correctly, which is very good. However, from the 925 actually not successful cases, the model incorrectly predicts 449 cases to be successful. We strive to develop a model that both has high sensitivity and high specificity, which is not the case here. Therefore, it is important to choose the criterion value that minimizes the corresponding costs related to the four possibilities in the confusion matrix. However, this important step would need a profound separate analysis and therefore is not part of this paper.

Table 8.

The confusion matrix that results from the prediction of the model for TAU using a random forest, no feature selection and mixed encoding with a chosen criterion value of 0.09, which corresponds to a true positive rate of 0.8462 and a false positive rate of 0.4854.

	Actual 0	Actual 1
Predicted 0	476	30
Predicted 1	449	165

One of the limitations is the size of the dataset. Given the complexity of the problem, more data is needed to train the models. Then, better accuracy can be expected and less variations in performance exists when the models are applied on new datasets. Also, the data is fragmented in different ways. For example, country specific patterns are present in the data. As a consequence, the predictive models use these patterns to their benefit, which does not benefit the overall generalizability of the models. A good example, as can be seen in Table 7, is that the model with the best score in BT had “ccxPoland” in the 10 most important variable list. Closer inspection shows that eight out of ten patients from Poland in this dataset had successful therapies. For new cases, specifically in Poland, predictive accuracy would decrease. Therefore, again, considerably more data is needed to filter out signal from noise, to decrease chances of overfitting.

We found that EMA data by itself has some predictive power2 However, adding EMA data to baseline data did not result in increased predictive capabilities. Apparently, the EMA data is quite noisy. By changing encoding strategies, more predictive capability in the EMA data can possibly be leveraged. Another possibility is to use more days of EMA data. The problem with that approach is that predicting success of therapy becomes less interesting when a significant part of the therapy needs to be applied beforehand. We would need significantly more data to determine which features hold predictive performance, and how consistent this would be over time.

For future research, we intend to repeat experimentation with more data. Also, we intend to focus on cost effectiveness analysis, which would offer more elaborate insights in the benefits of predictive modeling in mental health care.

6. Conclusions

Exploring possibilities for predicting therapy outcome is important because it can impact and benefit personalized therapy, effectiveness of therapy, and health care cost reduction.

The results suggest that significant predictive power is present in the baseline dataset. This eventually leads to reasonable predictive model performances. The results are promising, however, more data and experimentation is needed to investigate the capabilities and accuracy in predictive performance of statistical procedures in this context. EMA data has been shown to possess predictive power, however, its consideration (first seven days only) coupled with baseline data does not increase prediction performance.

It is not clear whether the models can provide added value in their current state. A cost effectiveness analysis and specific treatment recommendations based on these types of models can potentially shed light on the actual benefit such analyses can provide.