Quantifying Reversible Surface Binding via Surface-Integrated Fluorescence Correlation Spectroscopy

Abstract

We present a simple and versatile single-molecule-based method for the accurate determination of binding rates to surfaces or surface bound receptors. To quantify the reversible surface attachment of fluorescently labeled molecules, we have modified previous schemes for fluorescence correlation spectroscopy with total internal reflection illumination (TIR-FCS) and camera-based detection. In contrast to most modern applications of TIR-FCS, we completely disregard spatial information in the lateral direction. Instead, we perform correlation analysis on a spatially integrated signal, effectively converting the illuminated surface area into the measurement volume. In addition to providing a high surface selectivity, our new approach resolves association and dissociation rates in equilibrium over a wide range of time scales. We chose the transient hybridization of fluorescently labeled single-stranded DNA to the complementary handles of surface-immobilized DNA origami structures as a reliable and well-characterized test system. We varied the number of base pairs in the duplex, yielding different binding times in the range of hundreds of milliseconds to tens of seconds, allowing us to quantify the respective surface affinities and binding rates.

The binding of proteins to biological surfaces, especially to membranes or membrane proteins, such as receptors, is of key importance for the function and control of many cellular processes. Thus, an accurate determination of surface binding rates and affinities is of great interest for basic research on cells and organisms, but also for biotechnological applications, often targeted toward creating and characterizing new efficient receptor ligands. Consequently, many techniques have been released for the specific task of measuring surface affinities, most prominently label-free ones such as surface plasmon resonance (SPR)^1,2 and quartz crystal microbalance (QCM),^3,4 which probe the binding of molecules to specific surfaces indirectly, through a change in resonance frequency of an electromagnetic or acoustic reference signal upon a mass change of the surface. Other methods commonly used to characterize protein–protein or protein–ligand binding in solution, such as isothermal titration calorimetry (ITC),^5,6 microscale thermophoresis (MST),⁷ or fluorescence correlation spectroscopy (FCS),⁸⁻¹⁰ pose the additional problem of solubilizing the membrane or membrane proteins, which has recently been elegantly solved by the introduction of membrane nanodiscs.¹¹⁻¹³ However, the common key shortcoming of all of these well-established techniques is that they function well for irreversible reactions or for perturbed systems relaxing into equilibrium, but not in quasi-steady state, when the numbers of forward and backward reactions are more or less equilibrated and when most binding sites feature a constant turnover of binders. On the other hand, this situation is physiologically most relevant, as it is frequently found in cellular environments. In other words, direct access to the rates of reversible surface binding in unperturbed, native systems has so far hardly been possible.

In the present study, we aim to overcome this limitation of established methods for analyzing surface binding rates by presenting an elegant new way of combining FCS and surface-selective single-molecule wide-field imaging with camera detection. The high surface selectivity is achieved by a total internal reflection (TIR) scheme for excitation. The idea is to time-correlate the total fluorescence signal detected at a selectively TIR-illuminated surface, collected from all of the fluorescent single molecules that are temporarily attached. Consequently, we refer to our approach as surface-integrated FCS (SI-FCS). Touchdowns and turnovers of molecules at this surface are reflected in intensity fluctuations, which can be resolved if the surface concentration is sufficiently low. These fluctuations have so far been mainly utilized by PAINT (points accumulation for imaging in nanoscale topography) microscopy, surpassing the optical diffraction limit for image acquisition. However, as demonstrated here, the steady-state time-correlation analysis of the fluctuating fluorescence intensity also yields characteristic attachment times, from which surface binding and dissociation rates can be efficiently derived with a high statistical accuracy.

In fact, a very similar concept was already at the basis of early formulations of fluorescence correlation spectroscopy for receptor–ligand binding,¹⁴⁻¹⁶ when Thompson and colleagues recognized that TIRF (total internal reflection fluorescence) microscopy^17,18 is well-suited to analyze signal fluctuations originating from binding events.¹⁴⁻¹⁶ However, before the advent of fast and highly sensitive cameras, wide-field TIRF microscopy with area detectors has not supported data acquisition with sufficiently high signal-to-noise ratios required for FCS. In the following decades, the dynamics of single molecules at surfaces have primarily been analyzed by wide-field imaging and tracking with CCD cameras.¹⁹ Single-particle tracking has been used to quantify residence times in a variety of systems in vitro^20,21 as well as in vivo.²²⁻²⁴ However, tracking of fluorophores relies on sparse and clearly distinguishable binding events, which not only leads to a limitation of accessible concentration ranges but also restricts the number of sampled binding events and, thus, the statistical accuracy and precision.

In contrast, FCS has the potential to access kinetics at regimes where single-particle events cannot be resolved by standard imaging approaches. Thus, the combination of TIR excitation with FCS, termed TIR-FCS, originally introduced by Thompson and co-workers with a wide-field prism illumination,¹⁴ was revisited after shifting to the technically much simpler objective-based illumination.^25,26 TIR-FCS has been applied to measure diffusion in membranes,²⁷⁻³¹ adsorption to C-18 modified glass,³²⁻³⁴ and binding to surface-adsorbed proteins.^35,36 Camera-based FCS, as applied to study diffusion in membranes, significantly improved the multiplexing capabilities compared to confocal FCS, while making it compatible with commonly available TIRF microscopes.^27,30,37 However, the potential originally proposed for TIR-FCS to determine the kinetic rates of transient surface binding with a high statistical accuracy has still not been experimentally confirmed, mainly due to a lack of proper detectors supporting sufficiently sensitive surface integration with a high temporal resolution.

Remarkably, modern camera technology has arrived at a level that allows one to revisit previous TIR-FCS concepts and elevate them to a level that significantly surpasses other established methods to analyze surface affinity, as demonstrated here. We apply FCS analysis to time series of integrated surface areas acquired by standard TIRF microscopes and extract kinetic information encoded in the signal fluctuations caused by reversible surface binding processes in equilibrium. We validate our approach by analyzing the DNA hybridization kinetics of single-stranded DNA (ssDNA) probes to surface-immobilized DNA origami structures exposing complementary handle strands.

Conceptually, SI-FCS extracts the kinetic rates from a fluctuating signal, where the time scales of the fluctuations differentiate surface binding events from diffusion transients. Both the spatial dependence of the TIR excitation in the direction normal to the surface and the residence times of the bound molecules contribute to the discrimination of bound and unbound molecules. In essence, a bound strand stays longer in the detection volume than a freely diffusing strand. As SI-FCS only discriminates between bound and unbound states, binding kinetics can be simply determined from the fluorescence integrated over the sample surface.

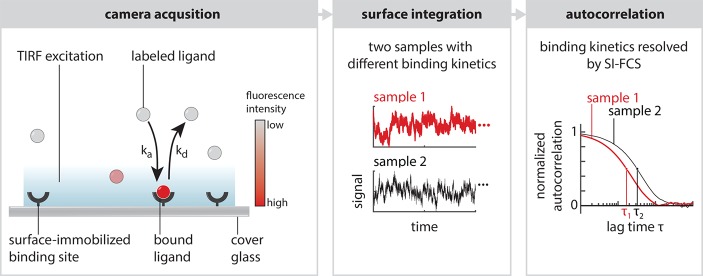
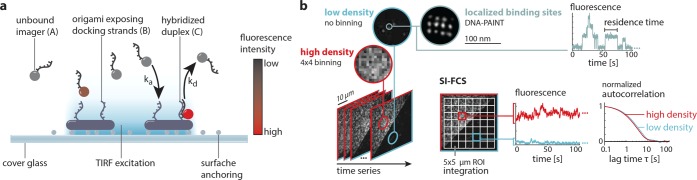
To investigate whether SI-FCS has the desired ability to resolve the rates of reversible surface binding, we studied DNA hybridization kinetics in well-controllable systems. Therefore, we used the DNA origami technique,³⁸ in which a long (typically 7249 nucleotides (nt), M13mp18 phage genome) DNA scaffold can be folded into a manifold of engineered nanostructures. We immobilized sheet-like DNA origami structures exposing 12 single-stranded DNA (ssDNA) docking handles³⁹ on a passivated coverslip surface (Figure 1a and supplementary Methods). Subsequently, we added complementary imager ssDNA labeled with Cy3B, which diffused freely in solution, but occasionally bound reversibly to its complementary strand at the TIR-illuminated surface, thus producing a local burst of fluorescence to be recorded by the camera. This transient DNA hybridization is an ideal model reaction, as the binding dynamics are highly tunable through the DNA duplex length and thus stability. Therefore, we were able to vary the binding kinetics systematically to probe the performance of our SI-FCS approach.

Figure 1.

Application of SI-FCS to quantify DNA hybridization kinetics. (a) Schematic of the transient binding of fluorescently labeled imager ssDNA to the complementary docking strand exposed on a surface-immobilized DNA origami. With TIR excitation, molecules in proximity to the surface, in particular bound molecules, are highlighted. (b) Image series of DNA hybridization events with low (blue) and high (red) surface densities of DNA origami structures. At extremely low densities, individual binding events can be resolved, a super-resolved DNA-PAINT image can be reconstructed, and residence times can be inferred from intensity traces. SI-FCS workflow in low- and high-density regimes (lower right): The signal is integrated over a set of ROIs, yielding an intensity trace for each ROI. From each intensity trace, an autocorrelation curve is calculated and can be fitted by a model function. Depending on the sample, the fit results may be averaged or used to generate a map of binding rates.

When such experiments are performed in a regime of sparse binding events, each hybridization event manifests itself as a bright spot in the camera image. Under the right conditions, these events can be precisely localized and rendered to a super-resolved image (Figure 1b). The localization of transient DNA hybridization events belongs to the variety of localization microscopy approaches and is termed DNA-PAINT.⁴⁰ Moreover, the duration of individual binding events and the time between two consecutive binding events to the same binding site can be used to estimate the association and dissociation rates.^39,40 The determination of residence times with single-particle tracking is quite powerful, but it is restricted to individually discernible events, thereby limiting the range of addressable samples, the concentration of ligand in solution, and the statistical accuracy. Additionally, the localization of binding events requires small pixel sizes and sufficiently high signal-to-noise ratios, which constrains the achievable camera frame rate. To circumvent these limitations toward a more general applicability, we developed a time-correlation-based method, which is independent of the recognition of individual binding events.

Instead of identifying individual particles in every image, we dissect the image into regions of interest (ROIs), integrate the signal over each of these ROIs, and repeat this step for every image, therefore generating an intensity trace for each ROI (Figure 1b). The obtained signal traces are autocorrelated in time and fitted by an appropriate model function, which for the case of simple binding and unbinding is a single exponential G(τ) = G₀ exp(−τ/τ_c). (See the supplementary Theoretical Basis.) G₀ is the amplitude of the autocorrelation function, a constant prefactor. The characteristic decay time of this exponential function is given by

1

Here we introduced the association and dissociation rates k_a and k_d, and the mean concentration of unbound ligand ⟨A⟩. In the special case of hybridization studies, ⟨A⟩ is the concentration of free ssDNA. The functional dependency of τ_c has two major implications: First, in a low concentration regime (⟨A⟩ ≪ k_d/k_a), τ_c equals the inverse dissociation rate, which is commonly termed the surface residence time τ_d. Second, we note that a classical titration of ⟨A⟩ experimentally determines the dependence of τ_c on ⟨A⟩. This dependence can be fitted by eq 1, to simultaneously obtain k_a and k_d. Finally, it is straightforward to calculate the dissociation constant K = k_d/k_a from there. The capability to extract K from SI-FCS measurements is already an attractive feature of the method. The capability to directly measure the dissociation and association rates themselves makes SI-FCS even more powerful. Provided the experimental data can be supported by theoretical predictions of the binding free energy ΔG, it is possible to estimate k_a and k_d from a single measurement in the limiting case of small ligand concentration compared to the dissociation constant ⟨A⟩ ≪ K. (See the supplementary Table S1.)

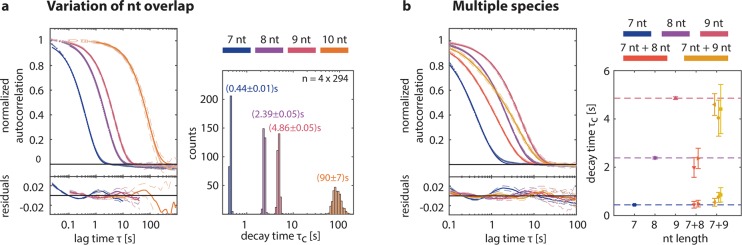
To experimentally explore the kinetics accessible to SI-FCS, we designed four different DNA origami structures, which together with our labeled ssDNA strand form a 7, 8, 9, and 10 nt overlap, respectively. (See the supplementary Methods.) All measurements were taken at a sufficiently low illumination, such that bleaching was negligible. (See the supplementary Figure S1.) Strikingly, the corresponding four experimental autocorrelation curves are clearly distinguishable, but even more importantly, the exponential model describes the curves adequately and unambiguously (Figure 2a). We conclude that the proposed model, which considers only reversible binding and assumes that diffusion dynamics are equilibrated on the relevant time scale, is an appropriate choice. The shifts between the four correlation curves in Figure 2a manifest themselves in significant differences in characteristic decay times τ_c as obtained from the individual fits. We measured decay times τ_c = (0.44 ± 0.01) s for 7 nt, τ_c = (2.39 ± 0.05) s for 8 nt, τ_c = (4.86 ± 0.05) s for 9 nt, and τ_c = (90 ± 7) s for 10 nt (supplementary Table S1). In all cases, the standard deviation was well below 5% of the mean, and individual measurements for the same nt overlap were indistinguishable (supplementary Figure S2). The obtained characteristic decay times reflect the number and type of the base pairing. As expected, the residence time increases with an increasing nt overlap. Moreover, we observed that the relative increase of τ_c from 9 to 10 nt is by far the largest. We attribute this effect to the addition of a stronger binding GC pair from 9 to 10 nt, whereas in the other cases a weaker binding AT pair was added (supplementary Table S1). Having demonstrated the capability of SI-FCS to resolve differences in the number of nucleotide overlaps, we can immediately conclude that single base pair mismatches are also resolvable. According to calculations, the free energy of DNA hybridization decreases to a larger extent by the introduction of a single base pair mismatch than by the removal of a terminal base pair.⁴¹

Figure 2.

Quantification of binding kinetics by SI-FCS. (a) Representative autocorrelation curves and their single-exponential fits for DNA hybridization of 7, 8, 9, and 10 nt. The different hybridization kinetics are clearly distinguishable. The obtained characteristic decay times are highly reproducible and range from 0.5 s to almost 100 s. The histograms correspond to 6 measurements per nt overlap, with 49 ROIs each. (b) Representative autocorrelation curves for mixed samples with two hybridization kinetics exhibit clear shape differences compared to single samples of 7, 8, and 9 nt, respectively. The individual decay times differ by less than a factor of 10. For mixed samples, the decay times from single sample experiments (panel a) are recovered with an error smaller than 20%.

We performed all measurements presented in Figure 2 with 10 nM (for 7–9 nt) or 1 nM (for 10 nt) of labeled ssDNA. The 10 nt sample has the smallest dissociation constant, which is expected to be on the order of 10–100 nM.^40,42 Consequently, the condition ⟨A⟩ ≪ K is met and the dissociation rates are estimated directly by taking the inverse of the reported characteristic decay times τ_c (supplementary Table S1). These estimates of k_d are comparable to previously reported rates.⁴²⁻⁴⁴ Small deviations can likely be attributed to the effect of different sequences and ion concentrations in the buffer, which are known to affect the formation of secondary structures. (For reviews, see refs (45) and (46).) Moreover, we estimated the association rates based on predictions of the binding free energy ΔG (supplementary Table S1).⁴¹ These results are in good agreement with recently reported values.^{40,42−44,47}

To challenge the SI-FCS method even further, we performed measurements on samples with multiple species (Figure 2b). Resolving more than one species is challenging and requires high-quality autocorrelation curves with characteristic decays on separable time scales. We combined 7 nt samples with 8 nt and 9 nt. Thus, the expected values of τ_c differ by less than an order of magnitude, which makes them intrinsically difficult to distinguish. Remarkably, the mixed samples with two kinds of binding sites show autocorrelation curves with a significantly different shape, compared to single-species samples. Consequently, it is justified to apply a biexponential fitting model, with each of the exponents reflecting one kind of binding site. Strikingly, the results from single-species measurements were recovered, although a slight bias (below 20%) was observed. The reliability of the discrimination of two species generally depends on the relative amplitudes and the time separation of the two decays. Moreover, the signal-to-noise ratio and the correlation of the noise itself are of relevance, which makes general predictions regarding the resolvability of two species challenging.

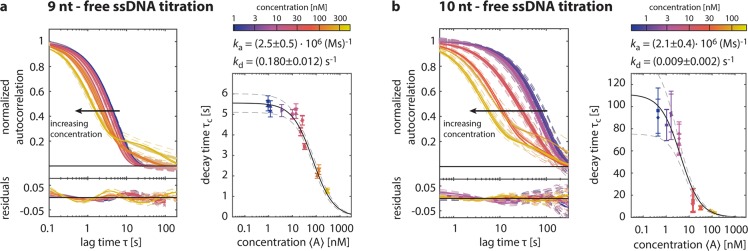
To determine association and dissociation rates without relying on theoretical assumptions, we performed titration experiments, comprising several SI-FCS measurements with identical origami samples but varying concentrations ⟨A⟩ of labeled free ssDNA. Following eq 1, we expected that an increase in the concentration of free strands shifts the autocorrelation curve to shorter times. Indeed, our experiments on 9 and 10 nt showed this effect (Figure 3a,b). For concentrations of free strands higher than 100 nM for 9 nt and 10 nM for 10 nt, respectively, a second component appeared at large lag times in the autocorrelation and was accounted for by a second exponential decay in the fitting model. We speculate that this second component may originate from unspecific binding. Regardless of the nature of this second component, the faster of the two decays was insensitive to changes in the fitting of the slower component. We fitted the dependence of τ_c on the concentration of free ssDNA (Figure 3a,b) and obtained the association and dissociation constants without any further assumptions (Table 1). The obtained dissociation rates are in line with the rates previously determined from measurements with low ligand concentrations (supplementary Table S1). Moreover, we calculated the binding free energy from the titration experiments and reproduced the predicted values (supplementary Table S1) within 10%.

Figure 3.

Determination of association and dissociation rates by SI-FCS. (a) Autocorrelation curves for 9 nt overlap with varying concentrations of complementary ssDNA in solution, ranging from 1 nM to 300 nM. With an increase in concentration, the characteristic decay shifts to shorter times. Autocorrrelation curves for 100 nM and higher were fitted with a biexponential. (See the supplementary Methods.) A fit of the characteristic decay times according to eq 1 yields association and dissociation constants of the binding reaction. The 95% confidence bounds of the fit are indicated (gray dashed lines). (b) as in panel a, but with 10 nt origami and complementary ssDNA concentrations ranging from 300 pM to 100 nM. Autocorrelations for 10 nM and higher were fitted with a biexponential decay model.

Table 1. Hybridization Parameters^a.

sample	kd [s–1]	ka × 10–6 [M–1 s–1]	Kd [nM]	ΔG [kJ/mol]
9 nt	0.180 ± 0.012	2.5 ± 0.5	72 ± 16	40.5 ± 0.6
10 nt	0.009 ± 0.002	2.1 ± 0.4	4.2 ± 1.8	47.5 ± 1.1

^aFor 9 and 10 nt determined by SI-FCS and titration of free ssDNA. Errors are given by the 95% confidence bounds of the fit.

On the basis of eq 1, it is sufficient to perform two independent measurements at significantly different concentrations of ligand to extract k_a and k_d of a specific system. Compared to a full titration series, a measurement at two concentrations saves potentially precious samples and measurement time, but comes at the cost of reduced precision. For pairs of concentrations representing sufficient intervals along the titration curve, the reaction rates for 9 and 10 nt could be recovered within 20% accuracy. (See the supplementary Figure S3.)

The presented results demonstrate that dissociation and association rates of reversible binding reactions are accessible by SI-FCS. The lower limit of accessible characteristic decay times depends only on the time resolution of the camera, the fluorophore’s photon budget, and the diffusion time of ligand, which in our case is considered to be much smaller than the characteristic decay time. Consequently, SI-FCS has the capability to resolve kinetics, which may be potentially too fast for SPR or QCM-D. However, it should be ensured that the time resolution, i.e., the inverse frame rate, is at least 3–10 times shorter than the characteristic decay time (confirmed by simulations, compare supplementary Figure S4, data not shown). On the other hand, in theory, there is no upper limit for the accessible characteristic decay times. For very large residence times, fluorophore photobleaching should be considered, but can typically be handled by identifying an appropriate regime of low irradiance, camera exposure time, and camera acquisition rate. Otherwise, the accessible characteristic decay times are only limited by the stability of the system under investigation. On the basis of a reanalysis of DNA hybridization data and Monte Carlo simulations, we determined that systematic biases stay below 10% of the actual value, provided the total measurement times are at least a factor of 300 longer than the characteristic decay time. (See the supplementary Figure S4.) It should be noted that for samples with sufficiently long τ_c, the required measurement duration can exceed hours, which puts high demands on sample and microscope stability. For example, for a sample that is stable for 1 h, τ_c should not exceed 12 s. If a lower accuracy is sufficient, experiments can also be shorter; e.g., to achieve a bias below 20%, measurements need to be only around 50 times longer than τ_c. (See the supplementary Figure S4.) Nonetheless, in light of potential live cell applications, the maximum accessible values of τ_c are expected to be below 10 s. On the other hand, many in vitro systems are stable over much longer times, thus providing access to slower kinetics by SI-FCS. Note that, irrespectively of the particular value of τ_c, the convergence to the true value is achieved faster than for FCS measurements of 2D diffusion with an equivalent diffusion time τ_D = τ_c.

For long time SI-FCS measurements, an important issue is the axial focus stability, which can be ensured by means of active focus stabilization, a common feature of many commercial TIRF microscopes. In order to avoid potential artifacts, the contribution of the active stabilization system to fluorescence signal fluctuations should be negligible compared to fluctuations originating from transient binding kinetics in the sample. We found that this condition was always satisfied in all our measurements. In fact, the focus stabilization typically operated at small position adjustments in the nanometer range, whereas the method relies on the wide-field detection, where the total detected fluorescence signal is insensitive to nanometer-scale focus adjustments.

SI-FCS does not require specialized equipment but only a regular TIRF microscope, which has become standard equipment in the majority of imaging facilities. Consequently, SI-FCS is easily accessible to a broad variety of researchers. In contrast to other methods, SI-FCS is compatible with other standard light imaging modalities and does not require advanced sample preparation on specialized surfaces. On the contrary, sample preparation approaches that were developed for fluorescence imaging of surface-related processes can be applied without any alterations. Moreover, the compatibility of SI-FCS with regular TIRF or epifluorescence imaging renders it a valuable tool for quality control and sample validation inaccessible to many other methods. For example, for membrane binding kinetics, the integrity of the supported membrane can be validated by a membrane staining.

Conventional confocal FCS measurements rely on an initial calibration measurement to determine the size of the confocal detection volume. In their recent application of TIR-FCS to study lateral diffusion in a supported lipid membrane, Bag and colleagues elegantly varied the software binning during postprocessing of data to circumvent the need for any calibration.³⁰ In our case, SI-FCS was exclusively used to quantify binding dynamics and did not rely on any spatial information. Hence, we did not need any calibration measurement. To demonstrate this, we performed a series of measurements on one sample, altered the axial sample position in between measurements, and thereby the effective projected pixel size. Over a range of more than 3 μm, the determined characteristic decay time was constant within the errors of the measurement. (See the supplementary Figure S5.)

SI-FCS is an equilibrium method, which retrieves information about the nature of the system under investigation from the fluctuations in the detected fluorescence signal. This has two major implications: First, the equilibrium regime in which SI-FCS measurements are performed does not require any perturbations of the system under investigation from the outside. In particular, no pumping is needed to probe a system, nor is a constant flow of liquid above the surface required, which keeps the consumption of valuable ligand to a minimum. Second, SI-FCS requires fluorescent labeling of the ligand, which despite the small size of chemical labels introduces an alteration to the system. On the other hand, the fluorescent label provides specificity, which allows for multiplexing through spectrally separated labels, as well as a dual-color cross-correlation option to potentially investigate cobinding and positive feedbacks.^10,48,49 Moreover, the high specificity through a fluorescent label enables measurements in complex fluids. To take the latter point even further, SI-FCS is compatible with measurements on live cells,^27,28 which, except for single-particle tracking, is intrinsically inaccessible to most other methods that characterize surface binding kinetics. In comparison to single-particle tracking, SI-FCS performs over a wider range of surface densities and still yields accurate results, when the surface concentration of docking sites or fluorescent probes is too high to detect them individually. (See the supplementary Figures S6 and S7.) Moreover, the analysis of the amplitude of the autocorrelation function shows potential to obtain further insights into the surface density of the sample under investigation and will be subject to future studies.

In principle, many systems that are accessible to SPR experiments can also be quantified using SI-FCS. However, SI-FCS has the potential to also measure lateral diffusion in supported lipid bilayers and cell membranes.^{14,27,28,30,31,50} The simultaneous probing of diffusion and binding dynamics by a combination of TIR-FCS and SI-FCS would further broaden the spectrum of possible applications, ranging from membrane binding to membrane-receptor ligand interactions. Furthermore, it is worth noting that SI-FCS is in principle not limited to TIR-illumination and fluorescence detection. Any scheme rendering reversible binding as fluctuating signal separable from diffusion is compatible with surface-integrated correlation spectroscopy. Potential examples include, but are not limited to, FRET to surface-attached acceptors⁵¹ and interferometric scattering.⁵²

To conclude, we quantified the association and dissociation rates of reversible surface binding by camera-based SI-FCS, which is compatible with conventional TIRF microscopes. To demonstrate the versatility of our approach, we studied the reversible hybridization kinetics of DNA as a well-controllable test system. The obtained association and dissociation rates are in agreement with previously reported results, which were obtained using different experimental methods^{40,42−44,47} and thus validate the SI-FCS approach. On the basis of the measured hybridization kinetics, we discussed the range of kinetics accessible to SI-FCS and provided a rule of thumb for the required measurement time. The small sample volumes required for SI-FCS, the potential compatibility with lateral diffusion studies and imaging modalities, and its steady-state operation without the need for external perturbations are the major advantages of the approach. We believe that the application of SI-FCS for the quantification of surface binding can make a major contribution toward understanding important biological systems on the quantitative level.

Glossary

Abbreviations

TIR-FCS

total internal reflection fluorescence correlation spectroscopy

SI-FCS

surface-integrated FCS

PAINT

points accumulation for imaging in nanoscale topography

TIRF

total internal reflection fluorescence

CCD

charge-coupled device

nt

nucleotides.

ssDNA

single-stranded DNA

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.nanolett.8b00875.

• Supplementary methods, theoretical basis, free energy of selected DNA hybridizations, control for photobleaching, reproducibility of SI-FCS measurements, determination of kinetic rates, effect of the measurement time, calibration-free SI-FCS, performance of SI-FCS at different receptor surface densities, custom-built TIRF microscope, DNA-PAINT reconstruction of binding sites on DNA origami structures, measurement of ligand concentration, and effect of ROI size (PDF)

Author Contributions

J.M., P.B., R.J., and P.S. conceived the study. J.M. and P.B. designed, performed, and analyzed the experiments. M.T.S. designed and produced DNA origami samples. J.M., P.B., M.T.S., and E.P.P. performed simulations. J.M., P.B., and P.S. wrote the manuscript. All authors discussed and interpreted results. All authors revised the manuscript and have given approval to the final version of the manuscript. J.M. and P.B. contributed equally to this work.

P.S. acknowledges grant money from the Gottfried Wilhelm Leibniz Prize by the German Research foundation. This work was supported in part by the DFG through the Emmy Noether Program (DFG JU 2957/1-1), the SFB 1032 (Nanoagents for spatiotemporal control of molecular and cellular reactions, Project A11), the ERC through an ERC Starting Grant (MolMap, Grant agreement no. 680241), the Max Planck Society, the Max Planck Foundation, and the Center for Nanoscience (CeNS) to R.J. J.M. is grateful for financial support from the excellence cluster Nanosystems Initiative Munich.

The authors declare no competing financial interest.