Terahertz time-domain spectroscopy for non-invasive assessment of water content in biological samples

Abstract

We apply terahertz time-domain spectroscopy for the quantitative non-invasive assessment of the water content in biological samples, such as Carpinus caroliniana tree leaves and pork muscles. The developed experimental terahertz time-domain spectroscopy system operates both in transmission and reflection modes. The Landau-Looyenga-Lifshitz-based model is used for the calculation of the water concentration within the samples. The results of the water concentration measurements are compared with the results of the gravimetric measurements. The obtained results show that the water content in biological samples can be measured non-invasively, with a high accuracy, utilizing terahertz waves in transmission and reflection modes.

1. Introduction

In recent years, due to unique properties of terahertz (THz) emission, a number of various techniques utilizing THz radiation have been used extensively in a variety of applications. In particular, noticeable frequency resonances (fingerprints or signatures) of many large size molecules are located in the THz frequency range, promising significant impact on identification and security areas [1–3]. Furthermore, it has been demonstrated that the THz bandwidth is able to provide the record capacity for the wireless data transmission [4,5], which is one of the most promising applications of this frequency range. Besides, both pulsed and continuous THz waves are being applied for the non-invasive testing of artworks [6,7] or estimating the quality of multi-layered automotive paints [8].

One of the most significant areas of interest in this field is dedicated to the development of new medical techniques for advanced clinical diagnosis of a range of diseases through examination of biological tissues and organs. In particular, methods for noninvasive glucose level monitoring using THz radiation are being developed [9,10]. Moreover, the possibility to examine teeth caries using THz waves has been shown [11]. Besides, as THz radiation is characterized by the strong water absorption [12], this frequency range can be used as a sensitive and precise non-invasive hydration probe, in particular, to monitor biotissue dehydration [13,14]. The development of a new tool for highly accurate non-invasive assessment the of water content within the biological tissues would help enormously in such areas as cancer diagnosis [15–19], food and other products quality control [8,20] or plants’ stress responses monitoring [21–23].

This study is devoted to the development and testing of the methods for the non-invasive measurement of water concentrations in biological tissues and samples by THz Time-Domain Spectroscopy (THz TDS). Leaves of Carpinus caroliniana tree and samples of pork muscles were tested.

Quantitative assessment of the water content in fresh agricultural products is extremely important due to the steadily worsening ecological situation in the world. Giving that plants and trees are essential for humanity, there is a strong demand for the development of a tool that is able to non-invasively measure and evaluate stress responses of different types of flora, including the response for drought. The water content in a plant’s leaf can correspond to different exogenous and physiological conditions, and, accordingly, is an important indicator of the plant’s health. The investigation of the moisture of pork muscles is a step towards the development of techniques for the diagnostics of human skin and organs pathologies.

The water content in plants can be monitored by destructive methods (gravimetric, pressure chamber [24]). The non-destructive methods used for water content measurement (chlorophyll fluorescence [25], visual estimate), are not very accurate and, therefore, pose limits on the applications. Recently, based on the correlation between water content level and attenuation of transmitted through the sample THz signal, new THz TDS and continuous THz-based methods for the water concentration measurements have been suggested [21–23, 26]. These studies have shown very promising results of the water content monitoring with very high accuracy. However, so far the described approaches operate in the transmission mode, which significantly limits their application, as due to the strong water absorption only thin samples can be probed.

This study demonstrates application of the reflection geometry of the THz TDS system for the water content monitoring. Using the reflection mode for such kind of measurements is a step towards real biomedical applications, as this configuration is significantly less limiting (no need to measure the thickness and roughness of the samples, the thickness of tested samples is unlimited) in comparison to the transmission mode.

Therefore, in order to examine thicker biological objects (pork muscles samples), the reflection geometry was applied. In literature, it was shown that the water content of human and animal skin tissues and organs varies significantly in pathological and healthy zones [18,19,27]. It also should be pointed out, that the THz radiation is non-ionizing [12], therefore, in general, it is more harmless for biological tissues than other types of electromagnetic radiation used for medical diagnostics. A water content sensor operating in the reflection mode would be extremely helpful for distinguishing healthy and injured tissues when the visual assessment is problematic.

2. Methods and materials

2.1 Effective medium theory

The method for retrieving water concentration is based on the effective medium theory and the extended Landau-Looyenga-Lifshitz model [28]. According to this model, a complex water-containing sample can be considered as a compound consisting of several components, including water. It is possible to calculate the volume fractions of each component if the optical properties of the sample and each component are known. Equation (1) shows the relation between the effective permittivity of a water-containing sample and dielectric functions of its components [28]:

$$\sqrt[3]{{\hat{\epsilon }}_{mix}(f)}=a_w\sqrt[3]{{\hat{\epsilon }}_w(f)}+a_1\sqrt[3]{{\hat{\epsilon }}_1(f)}+a_2\sqrt[3]{{\hat{\epsilon }}_2(f)}$$ (1)

where εmix is the permittivity of the sample, ε_w, ε₁, and ε₂ are permittivities of water, the 1st and 2nd components, respectively, a_w, a₁ and a₂ are volume fractions of water, the 1st and 2nd components, respectively.

2.2 Experimental setup

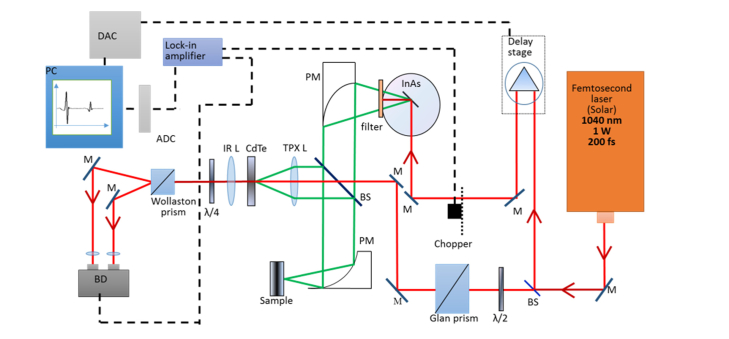
For this study, a series of experiments were performed utilizing the standard commercial spectrometer Mini-Z (Zomega Terahertz Corporation, USA) and the THz TD spectrometer developed in-house, operated, respectively, in transmission and reflection modes. The principal scheme of the THz time-domain reflectometer is presented in Fig. 1.

Fig. 1.

Principal scheme of the THz TDS setup (reflection mode). Filter – set of teflon filters cutting IR frequencies, BS - beam splitter, M – mirror, L – lens, BD – balanced detector, PC – personal computer, PM – parabolic mirror, ADC – analog-to-digital converter, DAC – digital-to-analog converter.

An infrared (1040 nm) beam of 200-fs pulses is divided by a beamsplitter into probe and pump beams. The pump beam is directed through the delay stage and mechanical chopper and focused on the InAs crystal. THz radiation is generated using the Dember effect in magnetic field. As the emitted radiation propagates perpendicularly to the dipoles, the crystal is located in a strong magnetic field (2 T) to redirect THz radiation. A teflon filter is placed on the exit of the magnet to cut off infrared radiation and transmit THz frequencies. Further, the THz beam is collimated using parabolic mirrors, directed through a beamsplitter and focused in a 3 mm diameter spot on the test sample. Radiation, reflected from the sample is focused on the CdTe crystal together with the probe infrared beam using a polymethylpentene (TPX) lens. Before being focused on the CdTe crystal, the probe beam is directed through the Glan prism, which makes it linearly polarized. The half-wave plate in the path of the beam adjusts the direction of polarization. In the case of the THz field absence, the infrared probe beam maintains linear polarization after propagating through the CdTe crystal. After that, the quarter-wave plate makes the probe beam circularly polarized and the Wollaston prism divides the probe beam into two orthogonally polarized beams. Finally, the balance detector calculates the difference between two currents, which is equal to zero in absence of the THz field. In the presence of THz field, the CdTe crystal becomes birefringent and alters the polarization state of the probe beam into elliptical polarization. In this case, the balance detector calculates a non-zero difference between two orthogonal polarizations of the probe beam. This difference corresponds to the strength of the THz field and is plotted on the computer screen versus the delay stage step (time). The described system generates THz radiation in the frequency range of 0.1-0.9 THz with output power up to 30 µW and dynamic range of no less than 40 dB.

Due to the coherence of the probe and pump beams, it is possible to obtain information on the amplitude and phase of the THz field in a single measurement, which enables extracting both real and imaginary parts of optical properties of the sample at the same time.

During the study, a typical measurement of the THz waveform took approximately 7 min. The recorded waveform was later transformed into the spectrum using the window (Lorenz) Fourier Transform in order to compensate the Fabry-Perot effect and increase the signal-to-noise ratio. The window width was chosen appropriately to ensure the echo signal being beyond the window in time domain.

2.3 Samples preparation and configuration

Experiments for the water content assessment were performed both in transmission and reflection geometries. Figure 2 demonstrates the beam interaction with the sample in different modes.

Fig. 2.

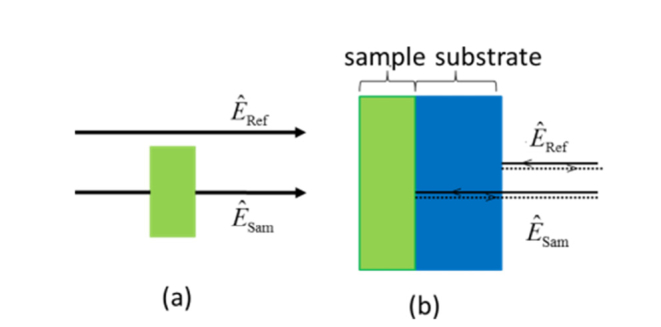
Paths of the reference and sample beams for (a) transmission mode, (b) reflection mode.

In the transmission geometry, the radiation transmitted through the sample was analyzed using the THz signal transmitted through air as the reference [Fig. 2(a)]. Due to the strong water absorption, for the experiments in the transmission mode, thin (hundreds of microns) samples were used: leaves from Carpinus caroliniana tree. Besides, for the reduction of scattering, leaves with small surface roughness were chosen. Leaves were cut along the main vein (the vein was removed, in order to keep the surface of the sample flat) and placed perpendicularly to the THz beam.

For the experiments in the reflection mode, the sample was attached to the silicon window (1 mm thick) in order to ensure the normal incidence, accurately measure the phase of the reflected signal (by monitoring the relative timing of the signal reflected from the sample compared to the reflection from the first surface of the window), enhance the reflection signal intensity, and reduce scattering effects. A special holder was designed and manufactured in order to ensure tight adherence of the sample and the silicon window. In this configuration, the recorded waveform consists of two peaks: the first one is the reflection from the air/silicon interface and the second one is the reflection from the silicon/sample interface.

For the reflection mode, in contrary to the transmission mode, thicker samples (2-4 mm) were chosen for several reasons. First, the opportunity to investigate thick samples in the reflection mode enhances possibility of further clinical applications of the described technique. Besides, in Fig. 2, there is a third interface (sample/air) that produces another reflection signal in the recorded waveform. With thin objects, the last two peaks (from the silicon/sample and sample/air interfaces) would be impossible to resolve and spectral information about the sample would have been lost. Therefore, samples of pork muscles were used for the experiments. The samples of pork muscles were purchased in a local food store and had the following composition (per 100 g): fat – 13.9 g; protein- 27.3 g; water – 62 g. The samples were excised from the animal body 3 days before the experiment and after the purchase were kept at 5° C until the start of the experiment.

2.4 Experimental protocol

According to the Landau-Looyenga-Lifshitz model, the sample was considered as a mixture of several components. In our experiments, we considered two components for each sample: water and the solid component of the sample. Therefore, for calculation of the water concentration of the sample, three sets of optical properties should be measured (one for each component and the sample itself).

The first step in the experimental series was calculation of the water dielectric function in the frequency range of 0.1-0.9 THz. The data obtained experimentally was consistent with the published results [29].

The second step in the experiments was artificial creation of several degrees of dryness of the sample and measurement of the water concentration at each of these stages using THz TDS. During the experiments, the sample was being dried up for several times using a special heater during a certain time. Therefore, a number of different water content levels were obtained within each experiment in order to test the sensitivity of the method based on THz TDS. By the end of each experiment, the sample was dried up as much as it was possible without using any other special equipment. This state of the sample was considered as the solid component of the sample and its optical properties were used in the calculations. In the series of experiments with leaves, the typical temperature of the heating surface was 75°C; typical durations of the heating were 1 min, 3 min, 15 min, 20 min for 1st-4th stages of dryness and 1 hour for the final one. In the series of experiments with samples of pork muscles, the typical temperature was 90°C, and typical durations of the heating were 5 min, 10 min, 25 min, 40 min for 1st-4th stages of dryness and 2 hours for the final one. The photos of the samples at each stage of dryness are presented in Fig. 3. Though only one sample per dryness level was tested within a single experiment, each experiment was repeated approximately 10 times in order to increase statistical significance.

Fig. 3.

Photos of the samples at 5 different stages of dryness: (a) the leaf sample (Carpinus caroliniana) measured in the transmission mode, (b) the sample of pork muscles measured in the reflection mode.

Simultaneously to the THz TDS measurements, the water concentrations were assessed gravimetrically for the reference. The sample was weighted using weight scales (0.005 g precision) at each stage of the experiment. In order to compensate for the sample’s drying independent on our drying procedures, the measurements were performed 2 times at each stage of the experiment (before and after THz measurements). The average value of weight was recorded. In the last stage of the experiment, the weight value of the sample was considered as the weight of the dry component of the sample. The water concentration was calculated using the equation:

$$C_{m,\%}=(\frac{m-m_{\mathit{\text{dry}}}}{m})\times 100\%,$$ (2)

where m is the weight measured at the current measurement stage, m_dry is the weight of the dry component of the sample (weight of the sample at the last stage of the experiment).

For experiments in the transmission mode, the thickness and roughness of the sample were estimated at each degree of dryness. At each stage, several measurements of the thickness were performed using a micrometer (0.5 µm precision). The averaged value was considered as the central value of the thickness deviations. The central value of the roughness was estimated by calculating the standard deviation of the thickness values. Small deviation (about 5 µm) was considered while setting the lower and higher limits for the fitting. Typical constraints for the roughness parameter used in the calculations were 2 – 7 µm.

For the convenient calculation of the water concentrations in the transmission and reflection modes, two programs in Matlab with Graphical User Interface (GUI) were developed. In the programs, the user is asked to upload the waveforms of the dehydrated sample and the investigated sample obtained experimentally. We suggest that in order to control the water status in the leaves from the same plant, it is enough to use the same dehydrated sample as the solid component for testing other samples from the same species.

3. Calculation of water concentration

3.1 Transmission geometry

Generally, the complex transmission coefficient can be presented using the following formula [20]:

$$\hat{T}(\omega )={\hat{t}}_{AS}{\hat{t}}_{SA}{e}^{-\frac{\omega }{c}(\kappa +{\kappa }_{scatt})d}{e}^{i\frac{\omega }{c}(\hat{n}-1)d},$$ (3)

where $\omega$ is the angular frequency, ${\hat{t}}_{AS}$ and ${\hat{t}}_{SA}$are the Fresnel transmission coefficients at the air/sample and sample/air interfaces.

The term $e^{-\frac{\omega }{c}(\kappa +{\kappa }_{scatt})d}$ shows attenuation of the signal transmitted through the medium (Beer–Lambert law), and κ_scatt is the correction coefficient that describes the losses due to scattering [20]:

$${\kappa }_{scatt}=\frac{c}{\omega d}{[(\sqrt{{\epsilon }_{mix}}-1)\frac{4\pi \tau \text{cos}\theta }{\lambda }]}^2,$$ (4)

where τ is the roughness; $e^{i\frac{\omega }{c}(\hat{n}-1)d}$ is the phase shift during the transmission through the medium.

However, the transmission coefficient can be calculated experimentally as a ratio of the sample and reference electric fields:

$$\hat{T}(f)=\frac{{\hat{E}}_{\mathit{\text{sam}}}(f)}{{\hat{E}}_{\mathit{\text{ref}}}(f)},$$ (5)

where f is the frequency in Hz, ${\hat{E}}_{\mathit{\text{sam}}}(f)$and ${\hat{E}}_{\mathit{\text{ref}}}(f)$ are the electric fields of the sample and reference signals, respectively.

The idea of the described technique is the variation of the parameters of the medium until the theoretical transmittance and the experimentally obtained transmittance are equal within a given error. In the method, not only volume fractions of each component of the sample [Eq. (1)] were varied, but also the thickness and roughness of the sample [Eq. (3-4)]. The two latter parameters were being fitted in order to ease the procedure of measuring the water concentration in vivo. Precise measurement of the sample’s thickness and roughness is often problematic and requires special equipment. For the better fitting, the user is asked only to set limits for the thickness and roughness values, so that it is enough to estimate these two parameters in vivo without measuring them precisely.

Therefore, the algorithm of the water content calculation in the transmission geometry is fitting four parameters: the volume fraction of water, the volume fraction of the solid component, the sample’s thickness, and the sample’s roughness. As the values of all of these parameters affect the sample’s optical properties, the refractive index and dielectric constant of the sample are also varied indirectly via sample’s thickness and roughness characteristics and volume fractions of its components.

3.2 Reflection geometry

The time domain of the resulting pulse train detected in the reflection measurements consists of a pulse reflected from the front of the silicon window ‘reference pulse’ and a delayed pulse reflected from the silicon/sample interface ‘sample pulse’. The optical properties of the samples were retrieved from the ratio between the sample and reference electric fields obtained experimentally:

$$\hat{R}(f)=\frac{{\hat{E}}_{\mathit{\text{sam}}}(f)}{{\hat{E}}_{\mathit{\text{ref}}}(f)}.$$ (6)

However, on the other hand, this ratio (or reflection coefficient) could be described analytically:

$$\hat{R}(f)=\frac{t_{ASi}(f){\hat{r}}_{SiSam}{t}_{SiA}(f)}{r_{ASi}(f)}\text{exp}(i\frac{4\pi n_{Si}{d}_{Si}f}{c}),$$ (7)

where f is the frequency, $t_{ASi}(f)$, ${\hat{r}}_{SiSam}$, $t_{SiA}(f)$, $r_{ASi}(f)$, are the Fresnel coefficients:$t_{ASi}(f)$ and $t_{SiA}(f)$ are the transmission coefficients at the air/silicon and silicon-air interfaces, respectively, ${\hat{r}}_{SiSam}$and $r_{ASi}(f)$ are the reflection coefficients at the silicon/sample and air/silicon interfaces, respectively; $d_{Si}$ and $n_{Si}$ are the thickness and the refractive index of silicon.

Assuming that silicon and air have no absorption in the set frequency band, their optical properties are real. However, the sample has both absorption and refraction, therefore, the sample’s optical properties are complex. Thus, three of four Fresnel coefficients are real except for${\hat{r}}_{SiSam}$.

Using the complex correction factor corresponding to the displacement of the sample beam with respect to the reference beam described in Ref [30], the complex refractive index of the sample was presented as:

$$\hat{n}=\frac{\sqrt{n_{Si}^2{(1-{\hat{r}}_{SiSam})}^2+4{\hat{r}}_{SiSam}{\text{sin}}^2\theta }}{1+{\hat{r}}_{SiSam}},$$ (8)

where θ is the angle of incidence.

For retrieving the water concentration, the variation of the compound parameters was being performed until theoretical and experimental values of the reflection coefficient were the same within a certain error. In this algorithm, the angle of incidence was slightly varied (0° to 2°) to account for possible deviation from the normal incidence and ensure better fitting.

Therefore, three parameters were varied in the described algorithm: the volume fraction of water, the volume fraction of the solid component, and the angle of incidence. All of these parameters affect optical properties of the sample, therefore, the refractive index of the sample, its dielectric constant and the complex reflective Fresnel coefficient were also varied indirectly using described three parameters.

It should be mentioned that the water concentration values for both transmission and reflection geometries were calculated for each frequency individually. These values were averaged throughout the frequency range in order to get the final water concentration.

The fitting was performed using the built-in Matlab nonlinear programming solver which finds the minimum of constrained nonlinear multivariable function using 'interior-point' optimization algorithm. The difference between the values of transmission (reflection) coefficients obtained experimentally and calculated analytically is the minimum of the function, which parameters the algorithm is fitting. The minimum of this function was constrained to be less than 0.01.

The error of the measurements was calculated using the following relation [31]:

$$\text{Δ}C=\sqrt{{\displaystyle \sum _{i=1}^N{(\frac{\partial f_i}{\partial A_i}\text{Δ}{A}_i)}^2}}.$$ (9)

Here, ΔC is the absolute error of the THz TDS measurement of the water concentration which was averaged through the used frequency range. A_i stands for those parameters that contained errors which influenced the final result; f_i is a set of functions that relate parameters A_i with the final result of calculations. The error of each of these parameters was calculated using the same principle from corresponding errors of other parameters. Parameters that were considered for the calculation of the error of the THz TDS measurement were: the error of the delay stage step, the consequent time and phase error of the recorded waveforms, the consequent error of the real part of the refractive index, the consequent error of the real part of the dielectric constant, the error of the waveforms amplitude, the consequent error of the imaginary part of the refractive index, and the consequent error of the imaginary part of the dielectric constant.

4. Results and discussion

During the series of experiments, optical properties of different samples in relation to their water concentration were analyzed. The experiments demonstrated that the optical properties of intact samples (at the 1st stage of experiment) are closer to water dispersion, whereas, with drying, optical properties tend to move towards the dispersion of dry tissue (at the final stage of the experiment).

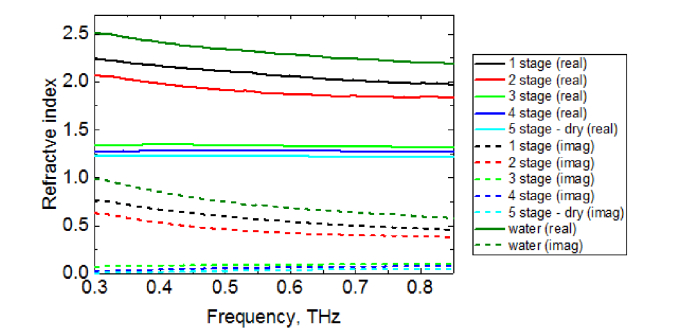
Figure 4 shows typical dispersion of the complex refractive index of the Carpinus caroliniana tree leaf in 5 different stages of dryness obtained in the experiment using the spectrometer in the transmission mode.

Fig. 4.

Dispersion of the complex refractive index of the leaf sample (Carpinus caroliniana) at 5 different stages of dryness in the transmission mode: black, red, green, indigo and blue lines represent the refractive index of the sample at the 1st, 2nd, 3rd, 4th, and 5th stages of dryness, respectively. Dark green lines show the refractive index of water obtained experimentally in the same frequency range. Solid lines show the real part of the refractive index, whereas dashed lines indicate the imaginary one.

Figure 4 demonstrates that at early stages of the experiment, i.e. while the leaf had high moisture level, dispersion of its refractive index was similar to that of water. With increasing of the degree of dryness, the values of the refractive index of the sample decrease and move away from the values of the refractive index of water towards the dispersion of the dry tissue, which, in turn, is quite similar to the refractive index of air (approximately 1). By the 3rd, 4th and final stages of dryness the curves of the refractive index values of the sample were completely flat, which means that dispersion properties of the sample at these stages became relatively negligible.

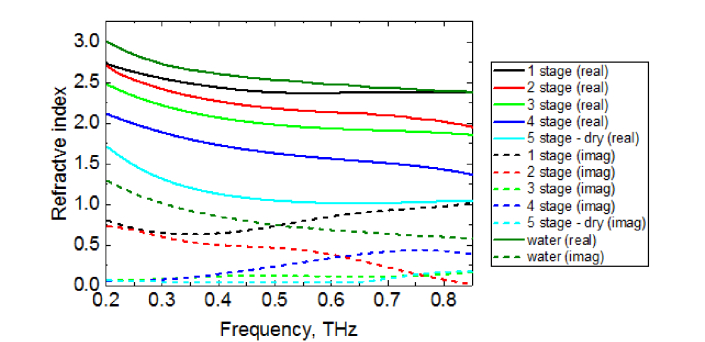
Figure 5 contains typical dispersion of the complex refractive index of the pork muscles sample calculated in experiments in the reflection mode.

Fig. 5.

Dispersion of the complex refractive index of the pork muscles sample at 5 different stages of dryness in the reflection mode: black, red, green, indigo and blue lines represent the refractive index of the sample at the 1st, 2nd, 3rd, 4th, and 5th stages of dryness, respectively. Dark green lines show the refractive index of water obtained experimentally in the same frequency range. Solid lines show the real part of the refractive index, whereas dashed lines indicate the imaginary one.

The real part of the refractive index of the pork muscles sample decreases with the moisture level decreasing. However, the imaginary part of the refractive index for each stage changes its relative position at higher frequencies. Authors assume that this is due to the samples’ surface non-uniformity.

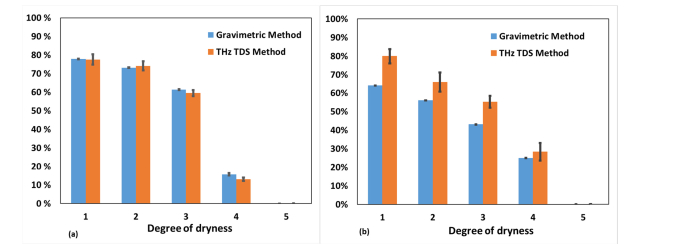
Figure 6 shows the values of the water concentration of different samples in the experiments both in the transmission (a) and the reflection (b) modes at 5 stages of dryness. The results acquired by the THz TDS method were compared to the gravimetric data. The average relative error of gravimetric measurements was 0.01%.

Fig. 6.

Water concentration values retrieved by THz TDS and gravimetric methods at 5 stages of dryness for (a) the leaf sample of Carpinus caroliniana obtained in the transmission mode, (b) the pork muscles sample obtained in the reflection mode.

The values of the water concentration acquired by the THz TD spectrometer in the transmission geometry [Fig. 6 (a)] correlate well with the gravimetric data. Our results are consistent with the data in Ref [22,23]. This proves that a THz TDS system can be used as a precise sensor of hydration in biological samples. The mean absolute error of these measurements is 3%.

The values of the water concentration acquired by the THz TD reflectometer are presented in Fig. 6 (b). The mean absolute error of these measurements is 6%. The values of the water concentration obtained by THz TDS in the reflection mode do not completely coincide with gravimetric measurements. This divergence is due to the fact that the gravimetric method can only allow assessing the average water concentration in the whole volume of a thick (2-4 mm) sample, whereas THz TDS measures the water content in a small spot (3 mm diameter) of the superficial layer of the tissue (few hundreds of microns). Therefore, two measurements should have given slightly different results. The fact that THz TDS results are higher than gravimetric is partially explained by the excess of water on the surface level of the sample due to the pressure of the silicon window. Besides, as the measurement by THz TDS took several minutes while the warmer sample was attached to the colder silicon window, a small amount of condensate could have appeared on the silicon window surface, which was attached to the sample.

5. Summary and conclusions

This study demonstrates the application of transmission and reflection geometries of the THz TDS system for the non-invasive water content monitoring in biological samples. Development of reflection measurements is a step towards real biomedical applications, as this configuration is significantly less restricted by the parameters of the target in comparison to the transmission configuration. The methods were tested for different biological samples: Carpinus caroliniana tree leaves and pork muscles. The obtained results correlate well with gravimetric measurements of water concentrations. The mean error of the data measured with the THz TDS technique is well below the changes in the water content observed in lesions and tumors relative to normal tissues. This approach could provide the valuable pathological insight, as it has the potential to distinguish healthy and injured tissues when the visual assessment is problematic.

Funding

Government of Russian Federation (074-U01); the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement (713606); Academy of Finland (grant 290596); MEPhI Academic Excellence Project (Contract No.: 02.a03.21.0005); National Research Tomsk State University Academic D.I. Mendeleev Fund Program.

Disclosures

The authors declare that there are no conflicts of interest related to this article.