Deep learning-based subdivision approach for large scale macromolecules structure recovery from electron cryo tomograms

Abstract

Motivation

Cellular Electron CryoTomography (CECT) enables 3D visualization of cellular organization at near-native state and in sub-molecular resolution, making it a powerful tool for analyzing structures of macromolecular complexes and their spatial organizations inside single cells. However, high degree of structural complexity together with practical imaging limitations makes the systematic de novo discovery of structures within cells challenging. It would likely require averaging and classifying millions of subtomograms potentially containing hundreds of highly heterogeneous structural classes. Although it is no longer difficult to acquire CECT data containing such amount of subtomograms due to advances in data acquisition automation, existing computational approaches have very limited scalability or discrimination ability, making them incapable of processing such amount of data.

Results

To complement existing approaches, in this article we propose a new approach for subdividing subtomograms into smaller but relatively homogeneous subsets. The structures in these subsets can then be separately recovered using existing computation intensive methods. Our approach is based on supervised structural feature extraction using deep learning, in combination with unsupervised clustering and reference-free classification. Our experiments show that, compared with existing unsupervised rotation invariant feature and pose-normalization based approaches, our new approach achieves significant improvements in both discrimination ability and scalability. More importantly, our new approach is able to discover new structural classes and recover structures that do not exist in training data.

Availability and Implementation

Source code freely available at http://www.cs.cmu.edu/∼mxu1/software.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Cellular processes are governed by macromolecules. Knowledge of the native structures and spatial organizations of macromolecules within a single cell is a prerequisite for our understanding of cellular processes. Cellular Electron CryoTomography (CECT) (Gan and Jensen, 2012; Grünewald et al., 2002; Lučić et al., 2013) enables the 3D visualization of structures at close-to-native state and in sub-molecular resolution within single cells (Asano et al., 2015; Jin et al., 2008; Murata et al., 2010; Rigort et al., 2012). Therefore, if we knew how to systematically mine structures in cryo cellular tomograms, we would gain the desired knowledge on macromolecules’ native structures and organization in their cellular context (Nickell et al., 2006).

However, systematic recovery of macromolecules structures from cryo tomograms is a very difficult task for several reasons. First, the cellular environment is very crowded (Best et al., 2007; Frangakis et al., 2002) with macromolecules that typically adopt different conformations as part of their function. Moreover, one macromolecule interacting with several different macromolecules can dynamically form different complexes at every time point. Therefore, a cellular tomogram has very complex and highly heterogeneous structural content. Second, the sizes of macromolecular complexes are typically smaller than 30 nm, which is only slightly larger than the image resolution (∼4 nm). Finally, there are inherent practical limitations in data acquisition, in the form of low signal to noise ratio (SNR) and missing wedge effects.

Given the above challenges, successful systematic analysis of the macromolecule structures in CECT data relies on processing large amount of structurally highly heterogeneous particles (Asano et al., 2016), possibly at least millions of particles containing hundreds of structural classes. Nowadays, new imaging technologies and advances in automation allow a research lab to obtain hundreds of tomograms within several days (Morado et al., 2016), potentially containing millions of particles represented by 3D subimages (aka subtomograms). However, existing computational approaches have very limited discrimination ability or scalability, making them generally incapable for systematic de novo structural discovery on these amounts of particles.

Early works of analyzing the macromolecular complexes in CECT data focused at locating instances of macromolecular complexes in cells through template search (e.g. Beck et al., 2009; Böhm et al., 2000; Nickell et al., 2006). However, such approaches do not discover new structures. For the reconstruction of novel structures repeating within cryo tomograms (Förster et al., 2005), reference-free subtomogram averaging (Briggs, 2013), classification (e.g. Bartesaghi et al., 2008; Bharat et al., 2015; Chen et al., 2014; Xu et al., 2012; Scheres et al., 2009) and structural pattern mining (Xu et al., 2015) approaches have been developed. These approaches are essentially unsupervised clustering or constrained optimization approaches, and they do not rely on any training data containing subtomograms with structural class labels. However, the scalability of such approaches is very limited, due to computationally intensive steps such as subtomogram alignment or integration over the 6D rigid transformation space. For example, structural pattern mining (Xu et al., 2015) of 10 000 subtomograms containing 22 structural classes would take at least 2 days by running 300 parallel jobs on a computer cluster.

To complement the above approaches, rotation invariant feature (Xu et al., 2009, 2011; Chen et al., 2012), and pose normalization (Xu et al., 2015) methods have been developed and can be used to subdivide highly heterogeneous subtomograms through unsupervised clustering. However, these approaches do not take into account of the missing wedge effect, which introduces anisotropic resolution and is not rotation invariant. In addition, such approaches have limited structural discrimination ability in the presence of high level of noise in the subtomograms.

We aim to overcome the aforementioned challenges and limitations of structural mining in cellular tomograms by complementing with existing approaches. In this article, we propose to use supervised deep learning approach to subdivide a large number of structurally highly heterogeneous subtomograms into structurally more homogeneous smaller subsets with significantly improved accuracy and scalability. After the subdivision, the computationally intensive reference-free structural recovery approaches can be separately applied to selected subsets in a divide and conquer fashion, which would significantly reduce the overall computation cost.

The major component of our new approach is a Convolutional Neural Network (CNN) classifier. Due to its superior scalability and good generalization ability, CNNs have made it computationally feasible to use a large number (e.g. billions) of parameters to approximate the complex mapping inside massive training data. In this article, we propose tailored 3D variants (Section 2.2) of two popular CNN image classification models. These two CNN models have achieved state-of-the-art supervised classification accuracy on popular image classification benchmark datasets (e.g. ImageNet Dataset; Russakovsky et al., 2015). The first model (Section 2.2.1) is characterized by relatively low depth and relatively complex parallel local filter structure (i.e. inception structure (Szegedy et al., 2016b). The second model (Section 2.2.2) is characterized by relatively high depth and very small simple convolution filters. In addition, because the inputs of the models are 3D gray-scale images (i.e. subtomograms) representing the 3D structures of particles contained in the image, it is important for our CNN models to isotropically capture the inherent 3D spatial structure in such 3D images. Therefore, in our models we use single channel 3D filters for convolution and pooling, instead of the 2D filters used in common deep learning based computer vision applications.

The above CNN models are designed for supervised classification. Since the native structures of most macromolecular complexes are unknown (Han et al., 2009; Xu et al., 2011), there is a particular need for discovering macromolecular complex structures that do not exist in the training data. To do this, we combine CNN with unsupervised clustering (Section 2.3). First, we adapt the output layer of a trained CNN classifier to extract structural features that are invariant to both rigid transforms and missing wedge effect. Such structural feature extraction is equivalent to performing a non-linear projection of the testing subtomograms to the structural space spanned by the structures in the training data, an analogy to metric learning (e.g. Xing et al., 2002). Then, we subdivide the projected subtomograms using unsupervised clustering, and recover the structures independently using reference-free classification and averaging (Frazier et al., 2017; Xu et al., 2012).

Our experiments on realistically simulated subtomograms show that the deep structural features extracted by the our CNN models are significantly faster and more robust to imaging noise and missing wedge effect than our previously used rotation invariant feature (Xu et al., 2009, 2011) approach. K-means clustering in the deep structural feature space produced significantly more evenly distributed clusters than our previous approach of k-means clustering of pose normalized subtomograms (Xu et al., 2015). Our proof-of-principle experiments on experimental subtomograms of purified macromolecular complexes also achieved competitive classification performance. Therefore, our experiments validate that our deep learning based approach is in practice a significantly better choice for subdividing millions of subtomograms. More importantly, our experiments (Section 3.3) on simulated data demonstrate that our approach is able to recover new structures that do not exist in the training data.

2 Materials and methods

2.1 Background

In recent years, deep learning has emerged as a powerful tool for many computer vision tasks, such as image classification and object detection. Deep learning has achieved state-of-the-art supervised image classification performance on popular benchmark image datasets such as ImageNet (Russakovsky et al., 2015), which contains more than 14 million images separated into at least 1000 classes. The CNN (LeCun et al., 1998) is one of the most important techniques in deep learning. It is composed of multiple layers, and every layer comprises a number of neurons that perform certain operation, such as convolution and pooling, on the output of previous layer. A typical CNN has alternating convolutional layers and pooling layers, one or more fully connected layers, and lastly a softmax layer. By utilizing multiple stacked processing layers to represent features of data, it allows learning and extracting increasingly abstract image features at increasing scales.

In particular, each convolutional layer consists of a set of learnable filters in the form of neurons with shared weights. Each neuron in this layer is connected to a region of neighboring neurons in the previous layer, called receptive field. Intuitively, it captures the spatial information in the receptive field. For example, the 1D convolution of input x and a filter of size $2m+1$ is defined as $y_i={\sum }_{j=-m}^m{w}_j{x}_{i-j}$, where $x_{i-j}$ is the i–jth input, w_j is the jth weight of the convolutional filter. After the convolution, a nonlinear activation function is applied, such as sigmoid, tanh or a rectified linear unit (ReLU) (Goodfellow et al., 2016). For example, the ReLU activation is defined as $o^{\text{ReLu}}(x)=\max \{0,x\}$. The pooling layer is a form of down sampling used to reduce computation cost and introduce a small amount of rotation and translation invariance. Calculating the local maximum (max pooling) or average (average pooling) values are common forms of such pooling. For example, the 1D max pooling operation is defined as $y_i={\max }_{(i-1)m<j\le im}{x}_j$, where m is the size of the pooling windows. For another example, the 1D average pooling operation is defined as $y_i=\frac{1}{m}{\sum }_{(i-1)m<j\le im}{x}_j$. After stacking several convolutional and pooling layers, one or more fully connected layers are usually added to extract more global features. As the name suggests, each unit in these layers connects to all units from the previous layer, defined as $y_i={\sum }_{j=0}^{n-1}{w}_{ij}{x}_j$ where w_ij is the weight between ith output y_i and jth input x_j, and n is the number of inputs. For multi-class classification tasks, the last output layer is usually a softmax activation layer (Equation 1), calculating a probability of a sample being assigned to each class.

Given training data in form of input-output pairs, the training of a CNN model optimizes weights through back-propagation so that the CNN best fits the training data. The optimization is often performed through variants of gradient descent approaches (Goodfellow et al., 2016) due to their superior scalability and simplicity for implementation.

In 2012, the CNN architecture AlexNet proposed by Krizhevsky et al. (2012), first showed significant performance improvements on the supervised image classification tasks compared with the traditional methods. Since then, CNN has become the dominant approach for large scale supervised 2D image classification tasks, and more advanced architectures have been developed, such as GoogleNet (aka inception network) (Szegedy et al., 2016a), VGG network (VGGNet) (Simonyan and Zisserman, 2014), and ResNet (He et al., 2016).

2.2 CNN-based supervised subtomogram classification

When using CNN for subtomogram classification, the input of the CNN is a 3D subtomogram f, which is a 3D cubic image defined as a function $f:{ℝ}^3\to ℝ$. The output of the CNN is a vector $\mathbf{o}:=(o_1,\dots ,o_L)$, indicating the probability that f is predicted to be each of the L classes defined in the training data. Each class correspond to one macromolecular complex. Given o, the predicted class is $\underset{i}{\text{arg}\hspace{0.17em}\text{max}}\hspace{0.17em}{o}_i$.

In this article, we propose two 3D CNN models based on GoogleNet and VGGNet for supervised subtomogram classification and adapt them for structural feature extraction.

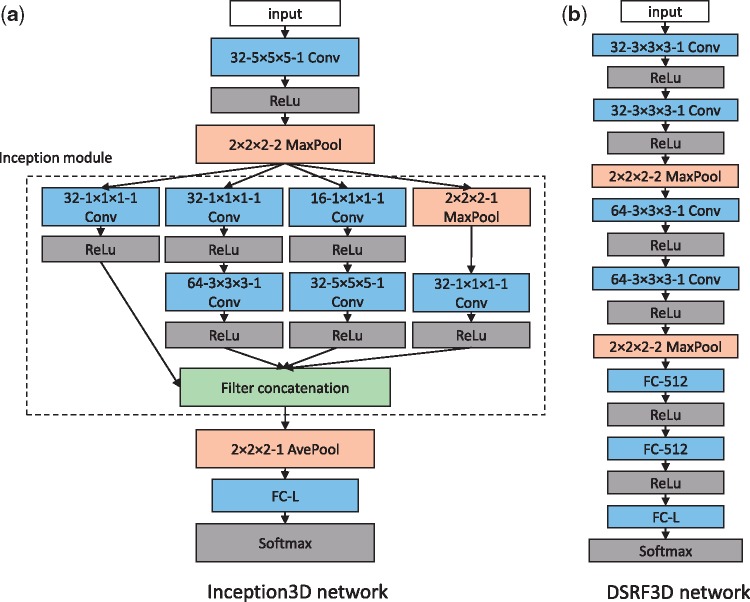
2.2.1. Inception3D network

In this section, we propose a 3D variant of tailored inception network (Szegedy et al., 2016a), denoted as Inception3D. Inception network is a recent successful CNN architecture that has the ability to achieve competitive performance with relatively low computational cost (Szegedy et al., 2016a). The architecture of our model is shown in Figure 1a. It contains one inception module (Szegedy et al., 2016a), where 1 × 1 × 1, 3 × 3 × 3, and 5 × 5 × 5 3D filters are combined with 2 × 2 × 2 3D max pooling layer. The filters are implemented in parallel and concatenated, so that the features extracted at multiple scales using filters of different sizes are simultaneously presented to the following layer. The 1 × 1 × 1 filters before the 3 × 3 × 3 and 5 × 5 × 5 convolutions are designed for dimension reduction. The inception module is followed by a 2 × 2 × 2 average pooling layer, then by a fully connected output layer with the number of units equal to the structure class number. All hidden layers are equipped with the rectified linear (ReLU) activation. The output is a fully connected layer followed by a softmax activation layer.

Fig. 1.

Architectures of our CNN models. These networks both stack multiple layers. Each box represents a layer in the network. The type and configuration of layer are listed in each box. For example, ‘32-5 × 5 × 5-1 Conv’ denotes a 3D convolutional layer with 32 5 × 5 × 5 filters and stride 1. ‘2 × 2 × 2-2 MaxPool’ denotes a 3D max pooling layer implementing max operation over 2 × 2 × 2 regions with stride 2. ‘FC-512’ and ‘FC-L’ denote a fully connected linear layer with 512 and L neurons respectively, where every neuron is connected to every output of the previous layer. L is the number of classes in the training dataset. ‘ReLU’ and ‘Softmax’ denote different types of activation layers

2.2.2. DSRF3D network

In this section, we propose a 3D variant of tailored VGGNet (Simonyan and Zisserman, 2014), which is another CNN architecture that achieved top classification accuracy on popular image benchmark datasets. Our model is denoted as Deep Small Receptive Field (aka DSRF3D). The architecture of our model is shown in Figure 1b. When compared with the Inception3D model, DSRF3D is featured with deeper layers and very small 3D convolution filters of size 3 × 3 × 3. The stacking of multiple small filters has the same effect of one large filter, with the advantages of less parameters to train, and more non-linearity (Simonyan and Zisserman, 2014). The architecture consists of four 3 × 3 × 3 3D convolutional layers and two 2 × 2 × 2 3D max pooling layers, followed by two fully connected layers, then followed by a fully connected output layer with the number of units equal to the structure class number. All hidden layers are equipped with the ReLU activation layers. The output is a fully connected layer with a softmax activation layer.

2.3 Combination of supervised structural feature extraction and unsupervised clustering for structural discovery

2.3.1. Structural feature extraction

For the multi-class classification tasks in Section 2.2, the last fully connected layerst activation functions used in Sections 2.2.1 and 2.2.2 are softmax functions:

$$o_j^{\text{softmax}}(\mathbf{x})=P(j|\mathbf{x})=\frac{e^{f_j(\mathbf{x})}}{{\sum }_{l=1}^L{e}^{f_l(\mathbf{x})}},$$ (1)

where

$$f_j(\mathbf{x})={\mathbf{x}}^{\mathrm{T}}{\mathbf{w}}_j,$$ (2)

x are the inputs of the last fully connected layer, ${\mathbf{w}}_j$ are the weights associated with the jth class, $f_j(\mathbf{x})$ is the output of the last fully connected layer associated with the jth class, and $P(j|\mathbf{x})$ is the probability of the subtomogram is assigned to class j.

Designed for multi-class classification, the softmax activation $o_j^{\text{softmax}}$ re-scales f_j exponentially. Therefore, it encourages output towards binary values, which reduces the extracted structural feature information that are useful for precisely subdividing input subtomograms. Once a CNN is trained for the classification task, we remove the softmax activation layer to obtain the linear activation of the last fully connected layer:

$$o_j^{\text{linear}}(\mathbf{x})=f_j(\mathbf{x})$$ (3)

Using linear activation, we obtain a more continuous representation of the tendency that a subtomogram is predicted to belong to a class. Such continuous outputs produce structural features that are invariant to rigid transformation and missing wedge effect, representing a nonlinear projection of a subtomogram to a low dimension space spanned by structural classes in the training data. In principle, such features can also be extracted from hidden layers, providing richer structural descriptions, as long as they are invariant to rigid transformation of the particle, and invariant to missing wedge effect.

2.3.2. Clustering and structure recovery

The main goal of subdivision is for separating a collection of structurally highly heterogeneous subtomograms into subgroups of subtomograms containing similar structures. Structural recovery (e.g. Xu et al., 2012, 2015) often requires searching in the Cartesian product of the space of class membership and the space of rigid transformations of subtomograms. The subdivision significantly reduces the space of structural class membership. Therefore an accurate subdivision would significantly simplify the complexity of structural recovery of a subgroup of subtomograms. The subdivision is usually performed through clustering. Successful subdividing millions of subtomograms require the clustering to be both accurate and efficient.

We improve the quality of clustering through supervised dimension reduction. Specifically, after projecting the subtomograms to the structural feature space using supervised feature extraction (Section 2.3.1), we over-partition the projected subtomograms using k-means clustering to obtain a finer subdivision of subtomograms. The unsupervised reference free classification (e.g. Bartesaghi et al., 2008; Scheres et al., 2009; Xu et al., 2012) (or structural pattern mining; Xu et al., 2015) is then independently applied to each cluster of subtomograms to recover the representative structures in the cluster.

2.4 Implementation details

The CNN models and training and testing are implemented using Keras (Chollet, 2015) and Tensorflow (Abadi et al., 2016). The Keras_extras library (https://github.com/kuza55/keras-extras) is used for multiple GPU parallelization. A variant of our Tomominer library (Frazier et al., 2017; Xu et al., 2015) is used for reference-free subtomogram classification and other processing. The experiments are performed on a computer equipped with two Nvidia GTX 1080 GPUs, one Intel Core i7-6800K CPU, and 128GB memory.

For the baseline methods, the calculation of rotation invariant features is based on SHTools (Wieczorek et al., 2016). K-means clustering and support vector machine (SVM) based supervised multi-class classification are performed using the Sklearn toolbox (Pedregosa et al., 2011).

3 Results

In this section, we demonstrate two major advantages of our deep learning subdivision approach through empirical study. First, efficient and accurate structural separation of millions of highly heterogeneous particles is key for the systematic detection of the near-native structures and spatial organizations of large macromolecular complexes in cells captured by CECT data. In Section 3.2, we demonstrate that our deep learning based subtomogram subdivision approaches significantly outperform our previously used approaches in terms of scalability and discrimination ability, which would significantly facilitate such structural separation. Second, currently the native structures of most of macromolecular complexes are unknown. Therefore it is necessary for a subtomogram subdivision method to be useful for discovery of unknown structures. In Section 3.3, we demonstrate that, although our deep learning approach is based on supervised training, when combined with unsupervised clustering and reference free subtomogram classification and averaging, our approach can be used to recover structures that do not exist in the training data, therefore our approach can be used to discover new structures in a systematic fashion.

3.1 Datasets generation

3.1.1. Simulated subtomograms from known structures

For a reliable assessment of the approach, we generated subtomograms by simulating the actual tomographic image reconstruction process in a similar way as previous works (Beck et al., 2009; Förster et al., 2008; Nickell et al., 2005; Xu and Alber, 2013), with the proper inclusion of noise, and missing wedge effect, and electron optical factors, such as the contrast transfer function (CTF) and modulation transfer function (MTF). Specifically, macromolecular complexes have an electron optical density proportional to the electrostatic potential. We used the PDB2VOL program from the Situs (Wriggers et al., 1999) package to generate volumes of 40³ voxels with a resolution and voxel spacing of 0.92 nm. The density maps are used to simulate electron micrograph images through a set of tilt-angles. For this article, we set typical tilt-angle ranges of ±60°, ±50° and ±40°. We added noise to electron micrograph images (Förster et al., 2008) to achieve the desired SNR levels, whose range cover the SNRs estimated from experimental data (Section 3.1.2). Next we convoluted the electron micrograph images the CTF and MTF to simulate optical effects (Frank, 2006; Nickell et al., 2005). The acquisition parameters used are typical of those found in experimental tomograms (Zeev-Ben-Mordehai et al., 2016) (Section 3.1.2), with spherical aberration of 2 mm, defocus of -5 μm, and voltage of 300 kV. The MTF is defined as $\sin \mathrm{c}(\pi \omega /2)$ where ω is the fraction of the Nyquist frequency, corresponding to a realistic detector (McMullan et al., 2009). Finally a direct Fourier inversion reconstruction algorithm (implemented in the EMAN2 library; Galaz-Montoya et al., 2015) is used to produce the simulated subtomogram from the tilt series. Figure 3 shows examples of such simulated subtomograms with different SNRs and tilt angle ranges.

Fig. 3.

Left: Isosurface of density map of yeast 20S proteasome (PDB ID: 3DY4). Right: Center slices (in parallel with x–z plane) in the simulated subtomograms with different degree of SNRs and tilt angle ranges

We collected 22 macromolecular complexes from the Protein Databank (PDB) (Berman et al., 2000) (Supplementary Table S1). We constructed a simulated dataset for each pair of SNR and tilt angle range parameters. Inside a dataset, for each complex, we generated 1000 simulated subtomograms that contain randomly rotated and translated particle of that complex. Furthermore, we also simulated 1000 subtomograms that contain no particle. As an outcome, dataset contains 23 000 simulated subtomograms of 23 structural classes.

3.1.2. CryoEM data collection, tomogram reconstruction and preparation of ground truth

We captured tomograms of purified Escherichia coli Ribosome and human 20S Proteasome through similar procedure as (Zeev-Ben-Mordehai et al., 2016). The imaging parameters have been optimized and successfully applied for structure separation of trimeric conformations of natively membrane-anchored full-length herpes simplex virus 1 glycoprotein B (Zeev-Ben-Mordehai et al., 2016). Specifically, Cryo-Electron Microscopy was performed at 300 keV using a TF30 ‘Polara’ electron microscope Field Electron and Ion Company (FEI) equipped with a Quantum postcolumn energy filter (Gatan) operated in zero-loss imaging mode with a 20-eV energy-selecting slit. Images were recorded on a postfilter $\approx$4000 × 4000 K2-summit direct electron detector (Gatan) operated in counting mode with dose fractionation, with a calibrated pixel size of 0.23 nm at the specimen level. Tilt series were collected using SerialEM (Mastronarde, 2005) at defocus ranges of −6 to −5 μm. During data collection, the autofocusing routine was iterated to achieve a very stable defocus through the tilt series with 100 nm accuracy. Tomographic reconstructions were performed using weighted back-projection in IMOD program (Sandberg et al., 2003). The reconstructed tomograms were then four times binned to a voxel spacing of 0.92 nm.

To prepare for ground truth, we performed template-free particle picking similar to (Pei et al., 2016) through convoluting the tomograms with 3D Difference of Gaussian function with scaling factor of $\sigma =$ 7nm and scaling factor ratio K = 1.1 to extract an initial set of 3646 subtomograms of size 40³ voxels. The extracted subtomograms were smoothed by convoluting with a Gaussian kernel of σ = 1 nm. We then aligned the subtomograms against Proteasome and Ribosome templates. These templates were obtained from first generating 4 nm resolution density maps from the PDB structures using PDB2VOL program (Wriggers et al., 1999), then convoluting the density maps with proper CTF according to experimental data (Section 3.1.2). The subtomograms with high alignment scores were selected. Finally, a set of 401 subtomograms were obtained, 201 and 200 were labeled as Proteasome and Ribosome, respectively.

To estimate SNR, for each structural class, we randomly selected 100 pairs of subtomograms that were aligned with the corresponding template, and estimated the SNR given each subtomogram pair according to [Frank and Al-Ali, 1975]. The mean SNRs are 0.06 and 0.08 for Proteasome and Ribosome, respectively.

3.2 Classification performance

3.2.1. On simulated data

To assess the classification performance, for each dataset generated in Section 3.1.1, we randomly separated the subtomograms into two equal sized sets. We used one set for training, and the other set for testing.

The CNN models were trained using stochastic gradient descent (SGD) with Nesterov momentum of 0.9 to minimize the categorical cross-entropy cost function. The initial learning rate was set to 0.01, with a decay factor of 1e-6. A 70% dropout (Srivastava et al., 2014) was implemented in Inception3D network to prevent over-fitting, i.e. a unit in network was retained with probability 70% during the training. SGD training was performed with a batch size of 64 for 20 epochs.

For the baseline method, we used spherical harmonics rotation invariant feature (e.g. Xu et al., 2009, 2011) in combination with SVM with Radial Basis function kernel, denoted as RIF-SVM.

The classification accuracy is summarized in the Table 1. It can be seen that, at realistic SNR and tilt angle range levels, all CNN models achieved significantly higher classification accuracy than the rotation invariant feature based method.

Table 1.

The classification accuracy of simulated datasets of subtomograms at different levels of SNR and tilt angle range

SNR/Tilt angle range	±60°			±50°			±40°
	Inception3D	DSRF3D	RIF-SVM	Inception3D	DSRF3D	RIF-SVM	Inception3D	DSRF3D	RIF-SVM
1000	0.993	0.990	0.992	0.994	0.978	0.983	0.983	0.991	0.967
0.5	0.975	0.972	0.929	0.964	0.967	0.885	0.931	0.951	0.857
0.1	0.851	0.891	0.762	0.807	0.873	0.633	0.809	0.866	0.649
0.05	0.757	0.767	0.592	0.682	0.728	0.455	0.637	0.684	0.468
0.03	0.608	0.658	0.446	0.516	0.604	0.319	0.473	0.556	0.341

We further measured the computation speed. On average, the training time took 0.0034 and 0.0055 s per subtomogram per epoch for Inception3D and DSRF3D networks respectively. Given trained models, the feature extraction and classification take 0.0015 and 0.0017 s per subtomogram for Inception3D and DSRF3D networks respectively. Thus, after training, CNN based structural feature extraction and classification of one million subtomograms would take <1 h on a single affordable desktop computer with two affordable GPUs. In contrast, the unsupervised rotation invariant feature extraction took 0.1 second per subtomogram. With fixed subtomogram size and class number, the training of CNN models scales linearly respect to the number of subtomograms. By contrast, the training of SVM scales quadratically respect to the number of subtomograms.

3.2.2. On experimental data

We randomly split the subtomograms into two equal sized sets and used one set as training and the other set as testing. In the training set, 105 and 95 subtomograms are labeled as Proteasome and Ribosome, respectively. In the testing set, 96 and 105 subtomograms are labeled as Proteasome and Ribosome respectively.

Although the number of samples was significantly smaller than the typical sample size in for deep learning tasks, the Inception3D network still achieved a classification accuracy of 0.905, which is higher than the classification accuracy of 0.890 of the baseline method of rotation invariant feature in combination with SVM. DSRF3D network fail to converge during training due to small sample size.

3.3 Detection of new structures

In this section, we test if our approach in Section 2.3 can be used to facilitate the recovery of structures that do not exist in the training data. The experiments were performed using subtomograms simulated at SNR 0.05 and tilt angle range ±60° (Section 3.1.1).

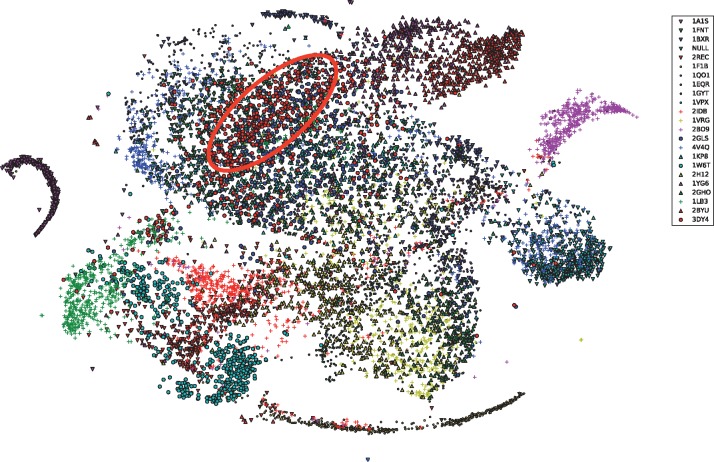
We prepared a training set $S^{\text{train}}$ with all 23 structural classes except Proteasome (PDB ID: 3DY4), and a test set $S^{\text{test}}$ with all 23 structural classes. There are 500 subtomograms in each class in each set. We trained an Inception3D network using $S^{\text{train}}$, then used the trained network to extract the structural features by projecting the subtomograms of $S^{\text{test}}$ into a 22D deep structural feature space ${ℝ}^{22}$ corresponding to the 22 classes in the training data. In such case, each subtomogram in $S^{\text{test}}$ correspond to one point in ${ℝ}^{22}$. For visual inspection, we further embedded the points in ${ℝ}^{22}$ into a 2D space ${ℝ}^2$ using the T-SNE algorithm (Maaten and Hinton, 2008), which is particularly well-suited for embedding high-dimensional data into a space of two or three dimensions for visualization. Figure 2 shows the embedded points. It is evident that samples are generally concentrated in subregions according to their structural classes. Most importantly, although Proteasome subtomograms do not exist in the $S^{\text{train}}$, the Proteasome subtomograms in $S^{\text{test}}$ are still concentrated at certain subregion in ${ℝ}^2$ (Fig. 2), indicating the supervised structural feature extraction can potentially be used to characterize new structures.

Fig. 2.

Subtomograms in the test set projected to the structural feature space of ${ℝ}^{22}$ through structural feature extraction (Section 2.3). The projected subtomograms were further embedded to ${ℝ}^2$ using T-SNE (Maaten and Hinton, 2008) only for visual inspection. The points were shaped and colored according to their true class labels. The region enriched with Proteasome subtomograms (PDB ID: 3DY4) was highlighted using red circle

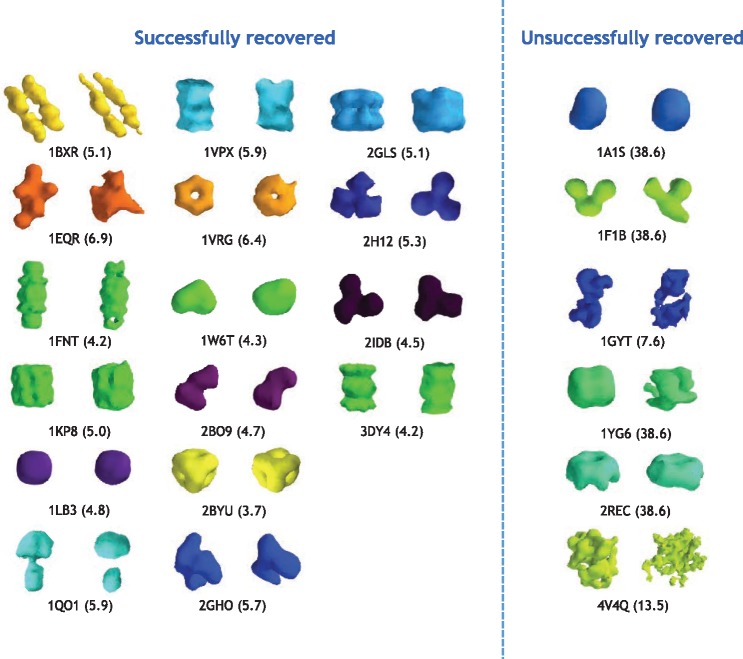
Inspired by the above observations, we systematically examined the possibility of recovering new structures using our approach (Section 2.3) by conducting leave-one-out test to all 22 macromolecular complex structure classes. For each test, we removed subtomograms of a class $C^{\text{true}}$ from training data, then trained an Inception3D model, we then used the trained model to project the subtomograms of $S^{\text{test}}$ into the deep structural feature space ${ℝ}^{22}$ according to Section 2.3. Then we performed k-means clustering in ${ℝ}^{22}$, where k was chosen to be 100, significantly larger than the true number of classes. We then identified the cluster $L^{\text{pred}}$ in which particles of $C^{\text{true}}$ were most enriched. Finally we applied unsupervised reference-free subtomogram classification and averaging (Frazier et al., 2017; Xu et al., 2012) (with three classes, five iterations) to the subtomograms of $L^{\text{pred}}$. Among the classes predicted by unsupervised subtomogram classification, we identified the class $C^{\text{pred}}$ that was mostly enriched with particles of $C^{\text{true}}$. We then calculated the structural discrepancy between the subtomogram average of $C^{\text{pred}}$ and the true structure of $C^{\text{true}}$. Such structural discrepancy is measured using Fourier Shell Correlation (Liao and Frank, 2010) with 0.5 cutoff, representing the maximal size of the structural factors that are discrepant between two structures. When using a structural discrepancy of 7 nm to determine whether the structure recovery is successful, we found 16 out of the 22 leave one out tests correctly recovered structures of $C^{\text{true}}$, even $C^{\text{true}}$ does not exist in $S^{\text{train}}$ (Fig. 4).

Fig. 4.

The isosurfaces of true (left) and predicted (right) structures. The predicted structures were obtained by our approach (Section 2.3). The numbers in parentheses were structural discrepancy between true and predicted structures

We further performed the same test using DSRF3D network, and we were able to get similar results. Specifically, 18 out of 22 structures were successfully recovered (Supplementary Table S2).

We further inspected the cluster size distribution of the result of k-means clustering of subtomograms of $S^{\text{test}}$ projected to the feature space ${ℝ}^{22}$ used for Figure 2. The cluster sizes did not vary too much (Supplementary Fig. S1a). In contrast, when applying our previous pose-normalization method (Xu et al., 2015) to subtomograms in $S^{\text{test}}$, then perform k-means clustering on the pose normalized subtomograms to subdivide the 11 500 subtomograms in the $S^{\text{test}}$ into 100 clusters, we found that most clusters are very small (Supplementary Fig. S1b). Specifically, there were 84 clusters whose size ≤ 10. On the other hand, there were 4 large clusters with size  > 1000, covering 6089 subtomograms, with mixed particles of similar structural sizes. The largest cluster had a size of 2470. The highly uneven cluster size distribution was likely due to the reduced discrimination ability of distance matrics in high-dimensional space (curse of dimensionality) (Aggarwal et al., 2001). Because the true classes in $S^{\text{test}}$ are also equal sized. In addition, when the data samples are uniformly distributed, the k-means algorithm, by definition, tends to produce an even division of data samples. Therefore, compared with our previously used pose-normalization approach, our supervised deep structural feature extraction approach produced subdivisions that are significantly more consistent with the algorithmic property of k-means clustering.

Remark: In our experiments, we used an arbitrary number of 100 clusters for the clustering step. In principle, to efficiently over-partition the data, the cluster number should be chosen to be larger than the number of expected representative structural classes among the collection of subtomograms to be subdivided, and be constrained by the amount of computation affordable. Proper approaches for estimating real cluster number remain to be explored.

4 Discussion

Macromolecular complexes are nano-machines that participate in a wide range of cellular processes. To fully understand these processes, it is necessary to know both native structures and spatial organizations of these complexes inside individual cells. CECT is currently the preferred experimental tool to visualize macromolecular complexes in near native conditions at sub-molecular resolution, when coupled with deep data mining it emerges as a very promising tool for systematic detection of structures and spatial organizations inside single cells. However, due to high level of structural complexity and practical imaging limitations, systematic de novo structural discovery of macromolecules from such tomograms requires the computational analysis of large amount of subtomograms. Existing structural recovery approaches are through reference-free subtomogram averaging (Briggs, 2013), classification (e.g. Xu et al., 2012), or structural pattern mining (Xu et al., 2015), and they have very limited scalability. Therefore, efficient and accurate subdivision of large amount of highly heterogeneous subtomograms is a key step for scaling up such computational intensive structural recovery approaches. On the other hand, our previously used rotation invariant feature (Xu et al., 2009, 2011) and pose normalization (Xu et al., 2015) subdivision approaches have limited discrimination ability and scalability. To complement existing approaches, as a proof-of-principle, in this work we propose to use deep learning based supervised approach to significantly improve both scalability and discrimination ability of subtomogram subdivision. Our preliminary results demonstrated superior performance over our previously used subdivision approaches (Xu et al., 2009, 2011, 2015). An additional advantage of our deep learning approach over our previously used approaches (Xu et al., 2009, 2011, 2015) lies in its potential for handling the molecular crowding: even if a subtomogram contains not only a particle of interest but also neighbor structures due to high molecular crowding (Xu and Alber, 2013), our deep learning based approach by design is likely to be able to automatically focus on the particle of interest and extract structural features only from the particle of interest instead of from the neighbor structures, as shown by many deep learning based image classification tests. Since little is known about the native structures of most macromolecular complexes in cells, it is therefore important for a subtomogram subdivision method to be able to be used for discovering new structures. We demonstrate that, by combining our supervised structural feature extraction with unsupervised clustering and reference-free subtomogram classification and averaging, we are able to detect new structures that do not exist in the training data.

To our knowledge, this work is the first application of deep learning for systematic structural discovery of macromolecular complexes among large amount (millions) of structurally highly heterogeneous particles captured by CECT. It represents an important step towards large scale systematic detection of native structures and spatial organizations of large macromolecular complexes inside single cells. From application perspective, potential uses of our approach are to quickly subdivide the highly heterogeneous particles into subsets, and separately recover the representative structures in each selected subset using computation intensive unsupervised subtomogram classification or pattern mining approaches. Given a recovered structure, one can further verify whether it already exist in training data. The particles of the new structures can be further included into training data to train a new CNN model for more comprehensive disentangling of structural features with enhanced discrimination ability. Besides CECT data analysis, our approach can also be applied to similar analysis tasks arisen in cryo tomograms of cell lysate or purified complexes. Our CNN based classification approach can also be used for template search or particle picking. In addition, our deep learning approach can also be used in analyzing image patches in CECT images, which are small 3D sub-images that are not necessarily cubic.

Our approach is based on supervised learning. Therefore, as a main limiting factor, our method relies on the availability and quality of training data. In practice, the training data can come from diverse sources. They can be from cryo tomograms of purified complexes captured in the same imaging condition as test samples. They can also be from particles in CECT images located through different approaches, such as correlated super-resolution imaging (Chang et al., 2014; Johnson et al., 2015), template search (Beck et al., 2009; Kunz et al., 2015), unsupervised reference-free subtomogram classification (e.g. Xu et al., 2012), or structural pattern mining (Xu et al., 2015). On the other hand, the proper strategies of constructing and processing training data remain to be explored. In addition, the proposed CNN architectures remain to be further optimized for improved performance. Furthermore, the size of the experimental data used in this proof-of-principle study is much smaller than a typical setting required for deep learning. Extensive studies remain to be done through capturing large number of particles of multiple purified macromolecular complexes and performing comprehensive analysis of the accuracy, robustness respect to sample size.