Light-sheet microscopy with digital Fourier analysis measures transport properties over large field-of-view

Abstract

Using light-sheet microscopy combined with digital Fourier methods we probe the dynamics of colloidal samples and DNA molecules. This combination, referred to as selective-plane illumination differential dynamic microscopy (SPIDDM), has the benefit of optical sectioning to study, with minimal photobleaching, thick samples allowing us to measure the diffusivity of colloidal particles at high volume fractions. Further, SPIDDM exploits the inherent spatially-varying thickness of Gaussian light-sheets. Where the excitation sheet is most focused, we capture high spatial frequency dynamics as the signal-to-background is high. In thicker regions, we capture the slower dynamics as diffusion out of the sheet takes longer.

1. Introduction

Measuring transport dynamics allows one to uncover a range of features relevant to material science and biology. Investigations of dynamics within complex fluids or soft materials can reveal viscoelastic properties [1], onsets of (non-)equilibrium phase transitions [2] and spatial or temporal heterogeneities [3]. Within cells, the dynamics of tracers, being single-molecules, particles or small organelles, can reveal active versus passive transport [4], length-scale dependent viscosities [5] and other biophysical properties. Due to the fundamental and practical interest of such properties and the diversity of systems under study, the optical tools for uncovering them are many and under continual development. They include: single-particle tracking [6], light scattering [7], fluorescence correlation spectroscopy (FCS) [8] and many others.

In this work we describe a new tool, selective-plane illumination differential dynamic microscopy (SPIDDM), which synergistically combines recently developed hardware and software. On the hardware side, we use selective-plane illumination microscopy (SPIM) which has emerged over the last several years as having clear advantages over other microscopy methods when it comes to optically sectioning specimens with a minimum of potentially harmful excitation light [9, 10]. Hence, it has been used to study developing organisms [11], functioning neural tissue [12] and single-molecule dynamics within living tissue [13, 14]. It typically operates by employing two orthogonal objectives placed around the sample. One objective, the excitation objective, focuses a thin sheet of light in the sample which coincides with the focal plane of the second objective, the detection objective. In this way, only the plane under observation is illuminated sparing the rest of the sample from needless photodamage or bleaching.

On the software side, we use differential dynamic microscopy (DDM), a recently developed digital Fourier method, to analyze our SPIM-acquired images. DDM was first described by Cerbino and Trappe in 2008 [15] though it bears many similarities to previous imaging and scattering techniques [16, 17]. Unlike many image correlation spectroscopy methods, DDM can be employed in a number of microscopy modalities including transmitted-light and fluorescence methods. It allows one to extract, from a series of time-resolved images, the temporal decay rate of density fluctuations over a range of spatial frequencies which provides the ensemble transport dynamics within the field-of-view. DDM has been shown to work on images where single particles or molecules are clearly resolved [18] as well as on images where lower signal-to-background ratios prohibit single particle localization [19].

We show that not only is DDM compatible with SPIM, it allows more, and often complementary, data to be extracted from SPIM-acquired images than typically done. In many SPIM implementations, the excitation sheet remains tightly focused for only a limited extent. It is within that limited extent, approximately characterized by the Rayleigh range for Gaussian optics: x_R = πw₀²λ⁻¹ where w₀ is the beam waist at the focus and λ is the wavelength, that optical sectioning is best [20]. However, using DDM we extract dynamics from not only the thinnest portion of the light-sheet but also regions on either side where the signal-to-background ratio is much reduced. Moreover, DDM analysis of those regions where the light-sheet thickens provides non-overlapping and complementary information about the dynamics. While DDM analysis of the most optically sectioned portion of acquired images provides details of the higher spatial frequencies, in the thicker light-sheet portions we can extract the slower temporal dynamics as particles spend a longer time within the excitation light before diffusing away. This adds support to the common claim that SPIM illuminates only the portion of the sample under study and therefore minimizes photodamage since now even signal emerging from up- and downstream of the light-sheet’s focus can be made of use.

After describing our implementation of SPIM and the algorithm we use for DDM we show results of SPIDDM using 200-nm diameter fluorescent charged colloidal particles. Such results demonstrate the dynamics that can be extracted with SPIDDM, the accessible time and length scales, and the benefit of using SPIDDM in optically dense and concentrated suspensions where other optical techniques would often fail to extract dynamics. Finally, we highlight how SPIDDM may be advantageous for studying light-sensitive samples, such as biological specimen, by measuring the diffusivity of fluorescent-labeled DNA molecules.

2. Materials and methods

2.1 Light-sheet microscopy

Our SPIM setup was built largely following the OpenSPIM design [21]. Excitation light is provided by a 488-nm 30 mW diode laser (COMPACT-30GC-488, World Star Technologies, Toronto). After optional attenuation by a selection of optical density filters, the excitation light is expanded and passes through an adjustable slit followed by a 50-mm focal length cylindrical lens (ACY254-050, Thorlabs). It is then expanded 2 × before entering the back of a 10 × 0.25 NA excitation objective (PLN 10 × , Olympus). The sample, placed in fluorinated ethylene propylene (FEP) tubing with inner diameter of 0.8 mm and outer diameter of 1.6 mm (EW-06406-60, Cole-Parmer), is positioned within a water bath using a motorized 4D (x, y, z, and θ) stage (USB-4D-Stage, Picard Industries). The water bath is required as we use a 20 × 0.5 NA water-dipping imaging objective (UMPLFLN 20XW, Olympus). Light collected by the imaging objective passes through an emission filter (ET520/40m, Chroma) and is collected by an sCMOS camera (Zyla 4.2, Andor). Micro-Manager is used to acquire images and control the hardware [22].

Our SPIM uses a cylindrical lens and 10 × excitation objective to create a Gaussian light-sheet. Therefore, the light-sheet exhibits variable thickness, w(x), depending on the distance from focus along the direction of propagation, x, which is expected to follow the equation: w(x) = w₀ [1 + (x/x_R)²]^1/2. Our light-sheet does not obey that equation exactly due to, we expect, spherical aberrations due to focusing the excitation light into a water bath using an air objective and, when imaging concentrated samples, scattering of the excitation light. However, by rotating the cylindrical lens 90° we are able to directly measure the sheet thickness and see that at focus the sheet is ~4.5 µm thick (full-width at half-max) and ~38 µm thick 150 µm away in either direction (Fig. 1(e)).

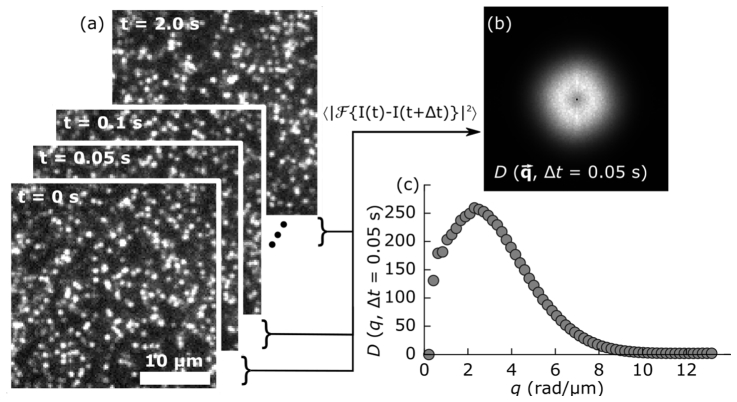
Fig. 1.

(a) The thickness of a Gaussian light-sheet varies along the direction of propagation, x. (b) Therefore, fluorescently-labeled particles may be localized at the light-sheet’s focus but not on either side where the sheet thickens. (c) Cartoon of light-sheet microscope showing the excitation objective (left) and the water-dipping imaging objective (bottom) imaging a sample within a tube placed in a water bath. (d) Image of 200-nm fluorescent beads showing good optical sectioning where the sheet is thinnest (left side) and higher background where the sheet thickens (right side). (e) Image showing the varying thickness of our light-sheet.

2.2 Differential-dynamic microscopy

To extract transport properties of samples imaged with SPIM, we acquire several time-series of images which we then analyze using DDM. The details of the DDM algorithms were presented in the seminal work of Cerbino and Trappe [15] and in follow-up publications [18, 23]. Briefly, the steps in the analysis are as follows. For each sequence of images, we subtract all image pairs separated by a given lag time, Δt: I(t) – I(t + Δt). Each difference is Fourier transformed and squared and then all Fourier power spectrums corresponding to the same lag time are averaged to yield the image structure function D(q, Δt) where q = (q_x, q_y) is the wave-vector. We radially average the image structure function as the dynamics of our samples are isotropic to produce D(q, Δt) where q is the magnitude of the wave-vector. We repeat this process for a range of lag times, typically at least up to Δt = 600 frames (corresponding to 2 s for the typical case of recording at 300 Hz). This process is depicted in Fig. 2.

Fig. 2.

(a) A sequence of captured images is analyzed by subtracting each pair separated by a given lag time, Δt, taking the square of the Fourier transform, and averaging to produce the image structure function, shown in (b). (c) The radially averaged image structure function for Δt = 0.05 s. This procedure is then repeated for a range of lag times.

For each value of q we fit D(q, Δt) to the function:

$$D(q,\Delta t)=A(q)[1-g(q,\Delta t)]+B(q).$$ (1)

The term A(q) depends on the optical transfer function of the microscope as well as the structure of the sample and B(q) is a measure of the noise [15]. Our work here focuses on dynamics by investigating g(q, Δt) but we note that others have fruitfully analyzed A(q) in order to understand the optical properties of the microscope [18,23] or the structure of the sample [32].

Information regarding the dynamics within the sample can be extracted through the analysis of g(q, Δt). For purely diffusive motion, it is expected that g(q, Δt) = exp[–Δt / τ(q)] where τ(q) is the characteristic diffusion time. For active transport, g(q, Δt) = exp[–qvΔt] where v is the characteristic velocity. In this work, we explore only samples exhibiting diffusive motion. Therefore, our analysis focuses on extracting τ(q) from g(q, Δt) and determining the collective diffusion coefficient, D_c, through the relationship τ(q) = (D_cq²)^–1.

For some of our samples, we found that using g(q, Δt) = exp[–Δt / τ(q)] for fitting our data resulted in poor fits at small lag times. Improvements to the fitting function could be realized by using a cumulant fit typically used for polydisperse samples where g(q, Δt) = exp[–Δt / τ(q)] [1 + µ₂Δt² / 2 – µ₃Δt³ / 6] with µ₂ and µ₃ being the second and third order polydispersity indices [19, 24]. Alternatively, we found that a stretched exponential also fit our data well: g(q, Δt) = exp[–(Δt / τ(q))^α(q)] [25, 26]. We chose to fit the data on the colloidal suspensions presented here with the stretched exponential as it more consistently fit our data at all lag times. Therefore, we use four adjustable parameters to fit our data to

$$D(q,\Delta t)=A(q)\text{}[1-\exp {\{-\Delta t/\tau (q)\}}^{\alpha (q)}]+\text{}B(q).$$ (2)

While a stretched exponential has been used to fit diffusing colloidal particles in previous DDM experiments [25], it is general associated with glassy or heterogeneous dynamics where dynamic relaxations occur through multiple mechanisms. We speculate that a simple exponential fails to fit our data well due to polydispersity in our bead solutions and the tendency for these beads to cluster. However, as of present, we have not fully investigated why the stretched exponential function fits best. We note that when using a stretched exponential, we take the mean decay time, τ_m, defined as τ_m = τ α^–1Г(α^–1) where Г is the gamma function [27], when finding the diffusion coefficient. Typically, for data of colloidal suspensions, α varied between 0.8 and 1.0. For the monodisperse DNA data, however, we fit D(q, Δt) to a single, non-stretched exponential.

We are limited to a range of accessible spatial frequencies bounded on the low end by the extent of our analyzed region of interest (ROI). We typically analyze ROIs of 128 × 128 pixels (30 × 30 µm²) which sets q_min = 2π / 30 µm = 0.2 rad/µm. In practice, the low-q limit also depends on the duration of our data set. For 200 nm beads in water we expect, from the Stokes-Einstein equation, a diffusion coefficient of D ~2 µm²/s so density fluctuations corresponding to a frequency of ~0.2 rad/µm are expected to decay on the time scale of (Dq²)^–1 ~12.5 s, necessitating time-series much longer. Determining the high-q limit is the pixel size in the object plane, d: q_max = 2π / 2d where, for all data shown, d = 235 nm and, therefore, q_max ~13 rad/µm. As with the low-q limit, decays of the higher spatial frequency fluctuations must be captured with sufficient temporal resolution. The frame rate, F, sets the limit q_max = (F/D)^1/2. The lowest frame rate used for our samples of 200 nm beads is 300 Hz which sets q_max ~12 rad/µm. However, with the sCMOS camera used we are able to acquire images limited to 128 rows of pixels at frame rates of up to 1578 Hz.

Differential dynamic microscopy has been shown to work with a variety of microscopy modalities including bright-field [28], phase contrast [29, 30], wide-field fluorescence [23, 28], confocal fluorescence [31, 32], polarized [24] and dark-field microscopy methods [33]. Any linear space invariant microscopy method which records a signal proportional to the density of objects under study is suitable. In fact, even linear spatially variant methods such as those with nonuniform illumination patterns can be analyzed with the DDM framework provided either the spatial nonuniformity is much different than the length scales of the investigated dynamics or the spatial nonuniformity is well characterized. The detailed rational for why space variant microscopy techniques can be used was presented in work by Bayles et al. and demonstrated using dark-field microscopy [33]. While our SPIM does produce a spatially inhomogeneous light-sheet due to its Gaussian nature, the variation in the illumination is small over the regions we consider which are typically 30 × 30 µm².

2.3 Sample preparations

To explore the performance of SPIDDM we use various concentrations of nominally 200-nm fluorescent beads (FluoSpheres carboxylate-modified, yellow-green fluorescent (505/515), F8811, Molecular Probes; actual reported size of 180 nm ± 12 nm). The volume fraction, φ, of the stock solution of these beads as provided by the manufacturer is 2 × 10⁻². Less concentrated samples are made by dilution with deionized water. We create more concentrated samples by first centrifuging the stock solution for ~20 minutes at 10,000 rpm followed by decanting a known volume of supernatant. All bead samples are sonicated for >5 minutes before being pipetted into FEP tubing which we then seal with epoxy.

We also image 115 kbp linear DNA which we prepare and fluorescent-label in-house. The double-stranded supercoiled DNA is prepared through the replication of bacterial artificial chromosome in Escherichia coli followed by extraction and purification via the process described in [34, 35]. The DNA is then converted from supercoiled to linear topology using restriction endonuclease Mlul (New England Biolabs). DNA is uniformly labeled using YOYO-I (Invitrogen, Carlsbad, CA) at a dye:basepair ratio of ~1:5. Labeled DNA is imaged in an aqueous buffer of 100 mM K-Pipes (pH 6.8), 1 mM EGTA, 1 mM MgCl2, and 5 µM Paclitaxel. We add 0.02% Tween-20 to inhibit surface interactions and 4% β-mercaptoethanol to reduce photobleaching. The final concentration of DNA in solution is ~25 µg/mL.

3. Results and discussion

3.1 Dependence on light-sheet thickness

At sufficiently low volume fractions (here, φ ≤ 4 × 10⁻³) so that the attenuation and scattering of the light-sheet is minimal we record images with a resolution of 1408 × 128 pixels corresponding to a field-of-view of 330 × 30 µm². With such a long field-of-view (long in x: the direction of propagation of our light-sheet), the light-sheet’s varying thickness is immediately apparent as seen in Fig. 3(a). Single particles are easily identifiable in the center of our image where the light-sheet is most focused and thinnest (~4.5 µm). Looking towards either end of the image, the signal-to-background ratio quickly diminishes and resolving individual particles becomes impossible.

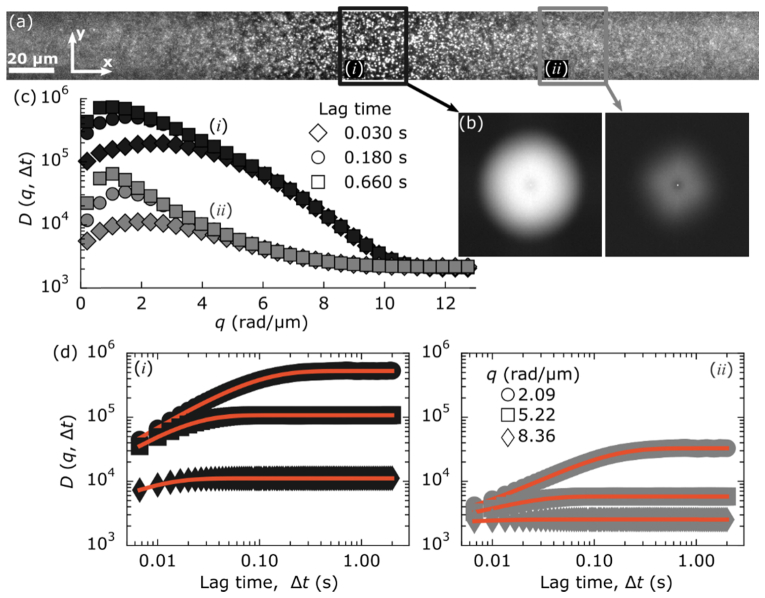
Fig. 3.

Images acquired of 200-nm fluorescent beads, φ = 10⁻³, with 1408 × 128 resolution are broken into eleven ROIs of 128 × 128 pixels and analyzed separately. (a) Full-field of view with two boxes highlighting different ROIs. The black box highlights the ROI (i) where the light-sheet is focused. The gray box highlights an ROI (ii) 90 µm upstream (w.r.t. the propagation of the excitation light-sheet). (b) The image structure functions, D(q,Δt), of the two ROIs are shown (identical intensity scaling). The 2D image structure functions are shown with a lag time of 0.03 seconds. (c) The radial average of D(q,Δt) for both ROIs is plotted as a function of wave-vector for three lag times: 0.03 s (diamonds), 0.18 s (circles) and 0.66 s (squares). (d) For both ROIs, D(q,Δt) is plotted as a function time lag for three separate spatial frequencies: 2.09 rad/µm (circle), 5.22 rad/µm (square) and 8.36 rad/µm (diamond). Red lines are fits to Eq. (2).

To explore how the light-sheet’s varying thickness influences DDM analysis, we crop the images into ROIs of 128 × 128 pixels (30 × 30 µm²). Each ROI is then processed as previously described to yield the image structure function D(q, Δt) and, by fitting D(q, Δt) to Eq. (2), to find the mean characteristic decay time, τ_m, of each wave-vector q.

Across the different ROIs, there is a noticeable difference in the image structure function and its radial average as shown in Fig. 3(b). The amplitude of D(q, Δt) over much of the probed wave-vectors is an order of magnitude or more greater in the thinner, more optically sectioned region than it is 90 µm upstream where the light-sheet is ~5 × thicker (22 µm). Such a result is consistent with the parameter A(q) in the image structure function being related to the power spectrum of the raw image [18]. Regardless of the differences in amplitude across the different ROIs, we find that all D(q, Δt) can be well fit to Eq. (2) for a range of spatial frequencies as seen in Fig. 3(d). Furthermore, from such fits we find the same dependency of the mean decay time, τ_m, on q which yields consistent values for the diffusion coefficient across the different ROIs despite the different light-sheet thicknesses within those ROIs (Fig. 4).

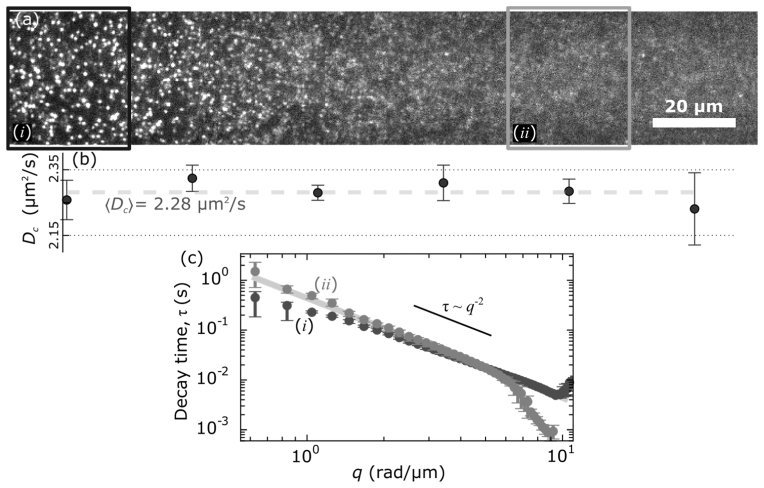
Fig. 4.

(a) Just over half of a full 1408 × 128 field-of-view shown of fluorescent beads with volume fraction φ = 4 × 10⁻⁴. The black box highlights an ROI (i) where the light-sheet is most focused and the gray box (ii) where the light-sheet is thicker (~30 µm versus ~4.5 µm). (b) Five movies of 4000 frames each and of 1408 × 128 resolution were recorded at 300 Hz. For each ROI of 128 × 128 pixels we determined the diffusion coefficient, D_c. We plot the mean D_c as a function of the ROI (corresponding with the image above) with error bars showing the standard deviation across the five movies. Across all ROIs we found D_c = 2.28 µm²/s ± 0.03 µm²/s. The larger uncertainty in D_c for the far right ROI, which is about ± 0.1 µm²/s, is likely due to the higher background. (c) The diffusion coefficients are found by determining where τ_m ∝ q^–2 and calculating the average D_c = τ_m⁻¹q^–2 over that range. The solid gray line is τ_m = (2.28 µm²/s)⁻¹ q^–2. The darker points correspond to ROI i and follow the τ_m ∝ q^–2 scaling from around q ~1.5 rad/µm to q ~10 rad/µm. The gray points correspond to ROI ii and follow τ_m ∝ q^–2 from around q ~0.6 rad/µm to q ~5.5 rad/µm.

While for each ROI we find a range of spatial frequencies where the relation τ_m ∝ q^–2 holds we notice that that range of wave-vectors differs systematically with the light-sheet thickness. Our data may depart from the expected τ_m ∝ q^–2 scaling at low q and can be seen as a plateau in the log-log τ_m versus q plot. At the high-q end, we see either an uptick or downtick in the τ_m versus q plot. We take such signatures of the τ_m versus q plot, noted in previous work with DDM [18, 32], to indicate the spatial or temporal frequencies where our microscope can no longer accurately probe.

Where the light-sheet is thinnest, the τ_m extracted from DDM analysis follows the τ_m ∝ q^–2 trend up to nearly 10 rad/µm. In contrast, analysis of ROIs where the optical sectioning is worse due to the thickening light-sheet we find τ_m ∝ q^–2 begins to fail at lesser q. For instance, using the ROI where the light-sheet thickness is ~30 µm we see that the maximum q is about 6.2 rad/µm (Fig. 4(c)). A complementary trend is observed in the low-q dynamics. Where the light-sheet was thinnest, the transition from τ_m ∝ q^–2 to constant τ (plateau) behavior occurs around 2 rad/µm. Conversely, for the ROIs over the thicker light-sheet regions, we do not observe such a low-q plateau. Rather the τ_m ∝ q^–2 relation holds for q < 1 rad/µm. This relationship between the range of wave-vectors accessible and the thickness of the light-sheet is presented in Fig. 5.

Fig. 5.

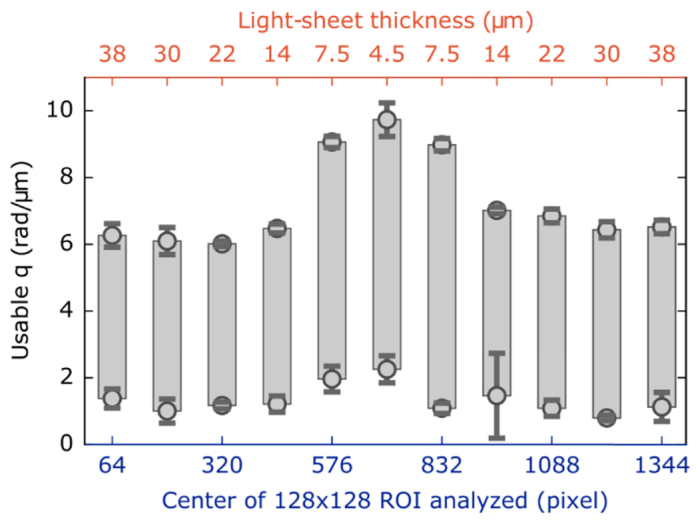
Five movies, each of 4000 images, with 1408 × 128 resolution are taken of fluorescent 200-nm beads of volume fraction φ = 10⁻³ (representative image shown in Fig. 3(a)). Each movie is divided into eleven 128 × 128 ROIs and for each we find the range of wave-vectors, q, where τ_m scales as q^–2. We find that where the light-sheet is thinnest (our central ROI) the expected τ_m ∝ q^–2 scaling holds for larger q-values though it departs from the scaling, on the low-q end, at greater values than in regions where the light-sheet is thicker. Error bars depict the standard deviation of where the τ_m ∝ q^–2 scaling fails on the low and high ends across the five different movies.

In future work, we aim to make a more quantitative connection between the light-sheet thickness and the minimum wave-vector, q_min, for which the τ_m ∝ q^–2 scaling holds. For now we note that, as presented in Fig. 5, for the thinnest light-sheet region q_min is ~2 rad/µm which corresponds to a spatial scale of ~3 µm which is comparable to the light-sheet’s thickness. Previous work has investigated how q_min depends on the degree of optical sectioning [32] and the optical depth of field [23]. We plan on extending similar theoretical analysis to our optical system.

3.2 Dependence on volume fraction

A feature of SPIM is its ability to optically section thick samples. We show that this feature extends to SPIDDM by studying a range of volume fractions from φ = 4 × 10⁻⁴ to 6 × 10⁻² of 200 nm fluorescent beads. As we made no effort to index match the solvent to the particles considerable scattering and attenuation of the excitation sheet is observed at the higher volume fractions. Nonetheless, we are able to extract diffusion coefficients for this range of volume fractions spanning over two orders of magnitude and for volume fractions too high for wide-field fluorescence microscopy to generate DDM-analyzable images.

As described previously, for each volume fraction we analyze 128 × 128 (30 × 30 µm²) ROIs that were cropped from larger fields-of-view. For more dilute suspensions (φ ≤ 4 × 10⁻³) we used a field-of-view of 1408 × 128 to be cropped into eleven regions (as shown in Fig. 3(a)) but for higher volume fractions the attenuation of the illumination sheet limited us to 768 × 128 or 256 × 128 resolution which then produced six or two cropped ROIs, respectively. Yet, even for the reduced fields-of-view at the higher volume fractions we generally observed consistent values for the diffusion coefficient across the cropped ROIs and a similar trend between the range of wave-vectors for which we could extract a meaningful decay time and the sheet thickness as described in the previous section (and as shown in Fig. 5).

The collective diffusion coefficient we find increases with increasing volume fraction (Fig. 6). The data follows the predicted trend of D_c(φ) = D₀ (1 + λφ) [36, 37]. For hard-spheres, it is expected that λ = 1.45 but, with increasingly repulsive interactions between particles, λ will increase. This is consistent with our finding of λ = 10.8 ± 0.8. Previously published results using DDM to measure the diffusion coefficient of colloidal suspensions found λ = 5.6 ± 0.3 for volume fractions from ~10⁻⁶ to ~10⁻² of 440-nm diameter charged particles [36]. The discrepancy between that value of λ and our value is likely due to its sensitivity to particle charge and ionic conditions [37].

Fig. 6.

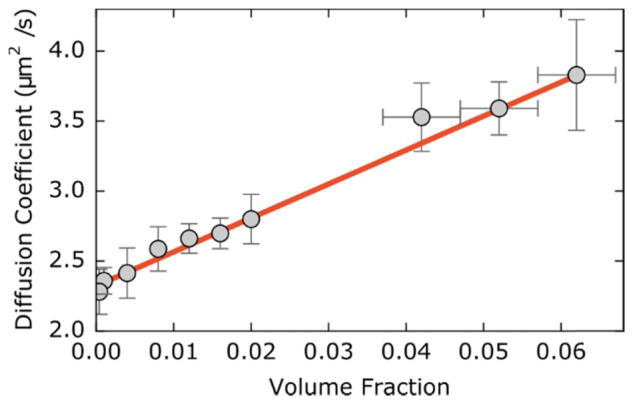
We varied the volume fraction by two orders of magnitude from φ = 4 × 10⁻⁴ to ~6 × 10⁻². We typically recorded five movies at each volume fraction from which we could analyze multiple 128 × 128 ROIs. We include x error bars in the higher volume fractions as some uncertainty in introduced by concentrating the beads from the volume fraction supplied, φ = 2 × 10⁻².

We also use single-particle tracking, using freely available and established software [38], to determine D₀ by finding the slope of the mean squared displacement versus lag time. For the lowest two volume fraction, φ = 4 × 10⁻⁴ and φ = 10⁻³, we analyze, from each movie, a 128 × 128 ROI that corresponds to the most focused region of the light-sheet. From each ROI, we find ~10,000 single-particle trajectories lasting > 20 frames (0.067 s given 300 Hz recordings) and calculate the mean squared displacement as a function of lag time. We determine D₀ = 2.30 µm²/s ± 0.05 µm²/s in agreement with the value of 2.32 µm²/s found from fitting our SPIDDM data to D_c(φ) = D₀ (1 + λφ).

3.3 DNA diffusion

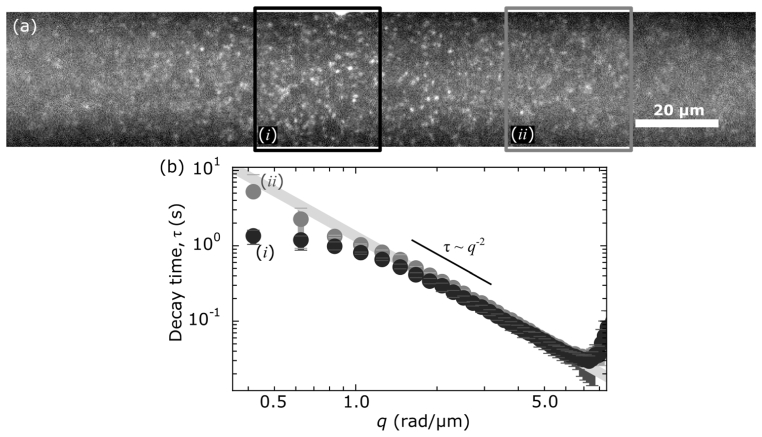
A notable feature of SPIM is the minimal excitation light delivered to samples, making it popular for biological imaging. We show the potential for SPIDDM to measure transport properties of biological molecules by imaging 115-kbp DNA molecules diffusing in physiologically relevant aqueous buffer typically used for in vitro experiments of reconstituted cytoskeleton. We record images at 190 Hz with a resolution of 768 × 128 (180 × 30 µm²) and analyze, as before, ROIs of 128 × 128 (Fig. 7(a)). We find that we are able to measure the diffusion coefficient of the labeled DNA in both regions where single molecules can be localized and in regions where, due to the thickening light-sheet, decreased signal-to-background ratio makes resolving individual molecules difficult or impossible. We also see a similar trend between the range of wave-vectors for which τ ∝ q^–2 and the light-sheet thickness (Fig. 7(b)).

Fig. 7.

Labeled DNA in an aqueous buffer was analyzed with SPIDDM. (a) We recorded several movies of 4000 frames and 768 × 128 pixel resolution at 190 Hz. (b) We observe the same trend as with the colloidal suspension data. Analysis of images from the thinner regions of the light-sheet depart from the expected τ ∝ q^–2 scaling, on the low-q end, at greater q than regions where the light-sheet is thicker. Our data does not follow the τ ∝ q^–2 for as high a wave-vector (typically ~7 rad/ µm) as the data with the colloidal suspension. This is likely due to decreased signal-to-noise as the DNA molecules have fewer dyes molecules than the beads and excitation power had to be minimized to avoid photobleaching. The solid gray line shows τ = D_cq^–2 for D_c = 0.72 µm²/s.

We find an average diffusion coefficient of D_c = 0.72 µm²/s ± 0.08 µm²/s by analyzing, with SPIDDM, five movies with the total field-of-view as seen in Fig. 7(a). We confirm the diffusion coefficient by using single-particle tracking on the 128 × 128 regions of our acquired images where the optical sectioning and signal-to-background ratio permit. For each of the five movies we track ~200 molecules whose trajectories last for at least 20 frames (0.1 s) and found, from the mean squared displacement, D₀ = 0.7 µm²/s ± 0.1 µm²/s. Our measured diffusion coefficients are comparable to previously reported values of the same DNA [35, 39].

With SPIDDM we are able to make efficient use of the excitation light—highly important for biological imaging. If single-particle tracking alone were used to find the diffusion coefficient of the DNA molecules, we could only use the region where the light-sheet is thinnest. In contrast, we are able to extract the diffusive behavior of the DNA with DDM over a larger lateral extent of the field-of-view. Therefore, with SPIDDM, less of the sample needs to be exposed to excitation light in vain.

4. Conclusion

The fact that DDM works well with SPIM is not unexpected given previous applications of DDM to confocal microscopy (ConDDM) [32] and to dark-field microscopy methods (dark-DDM) [33]. Similar to confocal microscopy, SPIM acquires optically sectioned images and the thickness of the optical sectioning will influence DDM analysis. Particles may quickly diffuse out of thin optical sections and the long time (typically corresponding to low wave-vector) dynamics may be missed. Nevertheless, ConDDM has been successfully employed in analyzing dynamics in a range of time scales. Like dark-DDM, a common issue with SPIM is inhomogeneous illumination. Though inhomogeneity in the illumination can be mitigated with multiple methods (e.g., [40, 41]), the most basic SPIM configurations, where the excitation beam is Gaussian, often suffer from stripping artifacts, reduced intensity along the direction of propagation that arise as the illumination sheet passes through adsorbing or scattering samples, and varying light-sheet thickness. We see such inhomogeneous illumination with stripping artifacts and severe attenuation at the higher volume fractions probed. However, we typically analyzed regions of 128 × 128 pixels (30 × 30 µm²) which appear relatively homogenous.

The fact that the light-sheet’s thickness varies along the direction of propagation is taken as a beneficial feature with SPIDDM. This property of Gaussian light-sheets is typically a downside for many SPIM applications and much work has been done on mitigating its effects (e.g., see [42–45]). But we exploit this property by recognizing that the Gaussian light-sheet’s varying thickness allows one to easily examine dynamics over different ranges of spatial frequencies. We extract high spatial frequency dynamics from the thinnest, most focused portion of the light-sheet and capture lower spatial frequency dynamics from the thicker regions of the light-sheet.

This connection between accessible wave-vectors and optical sectioning has been made before though this work is the first to combine SPIM with DDM and demonstrate the influence of varying optical sectioning across a single field-of-view. A thorough theoretical description of the optical properties influencing DDM analysis was presented by Giavazzi et al. [23] with emphasis on imaging in bright-field or other transmitted-light modalities, but connections are made to fluorescence imaging. That work includes a description of how a reduced depth-of-focus will limit one’s ability to extract low-q dynamics with DDM. Experimentally, Lu et al. demonstrated the connection between inaccessible low-q dynamics and increased optical sectioning by comparing data acquired with a point-scanning laser confocal and a spinning disk confocal microscope [32].

An additional benefit of SPIDDM is its ability to analyze thick or concentrated samples. We analyzed colloidal suspensions (up to φ ~6 × 10⁻²) too dense for use with wide-field fluorescence microscopy. With ConDDM it would possible to also study concentrated suspensions as done by Lu et al. They measured dynamics of suspensions up to φ = 0.40 by also index matching the solvent to the colloidal particles. However, a benefit of SPIDDM is that images are acquired at the frame rate of our camera which allows potentially faster dynamics to be captured than is possible with point-scanning methods such as laser-scanning confocal microscopy.

An additional benefit of SPIDDM is its judicious use of excitation light which may make it particularly useful for studying transport properties in light-sensitive biological samples such as DNA. The utility of SPIM with delicate samples has already been well established [46]. Furthermore, studies of cellular dynamics have used SPIM in combination with FCS in order to reduce photobleaching and photodamage [14, 47]. But in many SPIM applications where a Gaussian light-sheet is employed, only the thinnest region of the light-sheet is made of use. However, with SPIDDM, the portions of the sample up- and downstream of that thinnest region need not be illuminated needlessly. Rather, useable information can be extracted about the dynamics despite the reduction in optical sectioning and in signal-to-background ratio.

As with many other SPIM configurations, ours is not optimized for high-resolution imaging. Typically, imaging objectives used in SPIM have an NA < 1.0 as the placement of the excitation and imaging objectives around the sample introduces geometrical constraints. We utilize a 0.5 NA imaging objective. Therefore, SPIDDM, or at least our implementation of it, is not well suited to capturing dynamics that occur on spatial frequencies much greater than ~10 rad/µm (equivalent to spatial scales < ~0.6 µm).

As a final note, we highlight other circumstances where SPIDDM may be unfavorable. As with other ensemble techniques, SPIDDM is not well-suited to samples exhibiting a variety of transport modes. A technique very close to DDM has been used to tease apart both diffusive and active transport occurring simultaneously in samples [48]. Additionally, DDM has been used to measure anisotropic diffusion [29]. However, more complex or heterogeneous dynamics may be difficult to distinguish. We also note that sample preparation for SPIM is distinctly different from other microscopy modalities. This may present challenges for those intending to study samples placed in, for instance, microfluidic devices or in multi-well plates though it is possible to adapt SPIM designs to those formats [49]. Finally, we note that, at least in our case, the DDM algorithm is not real-time. We could speed up analysis time by, for instance, using GPU-enable computation [32] or working to optimize our current code. But, the work presented here was run on the CPU of desktop computers and typically required ~40 minutes to fully analyze a 128 × 128 pixel time-series of 4000 frames where the image structure function was calculated for time lags from one frame to 600 frames. Nonetheless, we think SPIDDM has great potential for efficiently extracting dynamics in light-sensitive samples. It may further extend the reach of SPIM into precise quantitative studies of biological dynamics.

Funding

Student Undergraduate Research Experience (SURE) at the University of San Diego; Air Force Office of Scientific Research Young Investigator Program (FA95550-12-1-0315).