Isotropic resolution diffusion tensor imaging of lumbosacral and sciatic nerves using a phase‐corrected diffusion‐prepared 3D turbo spin echo

Abstract

Purpose

To perform in vivo isotropic‐resolution diffusion tensor imaging (DTI) of lumbosacral and sciatic nerves with a phase‐navigated diffusion‐prepared (DP) 3D turbo spin echo (TSE) acquisition and modified reconstruction incorporating intershot phase‐error correction and to investigate the improvement on image quality and diffusion quantification with the proposed phase correction.

Methods

Phase‐navigated DP 3D TSE included magnitude stabilizers to minimize motion and eddy‐current effects on the signal magnitude. Phase navigation of motion‐induced phase errors was introduced before readout in 3D TSE. DTI of lower back nerves was performed in vivo using 3D TSE and single‐shot echo planar imaging (ss‐EPI) in 13 subjects. Diffusion data were phase‐corrected per k _z plane with respect to T₂‐weighted data. The effects of motion‐induced phase errors on DTI quantification was assessed for 3D TSE and compared with ss‐EPI.

Results

Non–phase‐corrected 3D TSE resulted in artifacts in diffusion‐weighted images and overestimated DTI parameters in the sciatic nerve (mean diffusivity [MD] = 2.06 ± 0.45). Phase correction of 3D TSE DTI data resulted in reductions in all DTI parameters (MD = 1.73 ± 0.26) of statistical significance (P ≤ 0.001) and in closer agreement with ss‐EPI DTI parameters (MD = 1.62 ± 0.21).

Conclusion

DP 3D TSE with phase correction allows distortion‐free isotropic diffusion imaging of lower back nerves with robustness to motion‐induced artifacts and DTI quantification errors. Magn Reson Med 80:609–618, 2018. © 2018 The Authors Magnetic Resonance in Medicine published by Wiley Periodicals, Inc. on behalf of International Society for Magnetic Resonance in Medicine. This is an open access article under the terms of the Creative Commons Attribution NonCommercial License, which permits use, distribution and reproduction in any medium, provided the original work is properly cited and is not used for commercial purposes.

INTRODUCTION

MR imaging of proximal and peripheral nerves, denoted MR neurography (MRN), has been emerging as a more accurate and noninvasive alternative to nerve conduction evaluation in the diagnosis of nerve disorders 1, 2. Moreover, it has been shown that morphological MRN alone can be insufficient in identifying nerve injury and that quantitative MRN can be helpful for a more precise diagnosis 3, 4, 5. Diffusion tensor imaging (DTI) has been leading as a prominent technique to assess disease in human proximal and peripheral nerves 6, 7, 8, 9 due to its capability to provide functional microstructural information of nerve fibers 10, 11 and thus lead to a more accurate diagnosis of nerve lesion compared with conventional T₂‐weighted morphological imaging 12, 13.

In a regime where high resolution is necessary to image small nerves with complex geometries, diffusion‐weighted‐imaging (DWI) methods are in general challenged in their ability to provide sufficient SNR and to circumvent geometric distortions and chemical shift artifacts of the conventionally used 2D single‐shot echo planar imaging (ss‐EPI). While reliable in DWI and DTI of anatomies with less strict resolution requirements, conventional 2D ss‐EPI becomes, in isotropic resolution diffusion imaging of proximal and peripheral nerves, highly susceptible to distortion artifacts resulting from eddy currents and off‐resonance effects 7. Furthermore, in DTI, resolution limitations characteristic of ss‐EPI also impose restrictions on the ability to accurately provide quantitative information of nerves having small diameters. Available alternatives to ss‐EPI for DWI and DTI for reduced geometric distortion and chemical shift artifacts include multishot EPI, readout‐segmented EPI and single‐shot turbo spin echo techniques 14, 15, 16, 17, which have been in part applied in imaging of nerves in the body 18, 19, 20, 21, 22. Specifically, turbo spin echo (TSE) or fast spin echo (FSE) techniques have been shown to yield high resolution diffusion imaging totally free of distortion and chemical shift artifacts in a broad range of body applications 16, 23, 24, 25, 26.

Among TSE methods used for DWI and DTI, diffusion‐prepared (DP) multishot TSE can be combined with a 3D readout to achieve isotropic resolution, which is necessary in diffusion imaging of proximal and peripheral nerves for its feasibility of curved and multiplanar reconstructions and volume reformatting 27, 28. Multishot TSE in DWI and DTI is, however, highly susceptible to intershot phase inconsistencies induced by motion and eddy currents 29, 30, 31, which have been shown to affect both the magnitude and the phase of the diffusion‐weighted TSE signal 32. It has been demonstrated that for DP single‐shot TSE the use of dephasing and rephasing gradients, here referred to as magnitude stabilizers, can minimize effects induced by motion and eddy currents on the signal magnitude, without the need to address effects on the signal phase 16.

In DP multishot TSE, however, motion‐induced phase variations between shots lead to artifacts and diffusion quantification errors, requiring careful considerations on the signal phase. In recent work, DP 3D TSE with magnitude stabilizers has been applied in vivo using velocity compensation 23, 33, 34, effectively reducing motion‐induced phase errors and resulting in reasonable image quality and diffusion quantification. More recent work has also shown, however, that the residual motion‐induced phase in DP 3D TSE not accounted for by magnitude stabilizers can still lead to artifacts and considerable quantification errors, and that these can be eliminated by measuring and correcting the motion‐induced intershot phase variations 30.

The purpose of the present work is to perform in vivo isotropic resolution imaging of lumbosacral and sciatic nerves by developing a phase‐navigated DP 3D TSE acquisition and a modified reconstruction incorporating intershot phase error correction. Using the developed acquisition and reconstruction, the current work intends to investigate the improvement on image quality and on diffusion quantification accuracy resulting from the proposed phase correction.

METHODS

Sequence Development

The proposed phase‐navigated DP 3D TSE sequence (Fig. 1) consists of an adiabatic diffusion preparation followed by a phase‐navigated 3D TSE readout. The adiabatic diffusion preparation has for an RF component a modified four‐segment B₁‐insensitive rotation (BIR‐4) pulse, previously shown to increase robustness against B₀ and transmit B₁ effects when applied for T₂ preparation 35, 36, 37, 38. The modified RF configuration consists of a BIR‐4 pulse with gaps between the three RF components added to fit diffusion‐sensitizing gradients, where the total duration of the BIR‐4 RF pulse without gaps is 10 ms. The frequency sweep of the RF pulse has an amplitude of 3700 Hz. Diffusion‐sensitizing gradients (shown in gray in Fig. 1) use the traditional Stejskal‐Tanner design to minimize the preparation duration TE_prep. A magnitude‐stabilizing gradient (shown in red in Fig. 1) is placed after diffusion sensitization and before the signal tip‐up and is later balanced in the 3D TSE readout 16, 32.

Figure 1.

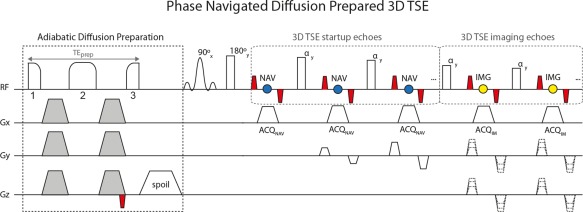
Pulse sequence diagram of phase‐navigated DP 3D TSE. The adiabatic diffusion preparation uses a modified BIR‐4 pulse configuration for minimizing transmit B₁ effects, where 1 indicates excitation, 2 refocusing, and 3 restoration of signal. Diffusion gradients (gray) are placed symmetrically around the refocusing segment of the pulse and a gradient is placed after the restoration segment for spoiling residual transverse magnetization. A magnitude‐stabilizing gradient (red) is placed before signal restoration and later balanced in the 3D TSE readout. In the 3D TSE readout, startup echoes are acquired as navigator echoes (blue) using k_y phase encoding only. Imaging echoes (yellow) are acquired with k_y and k_z phase encoding.

The developed phase‐navigated 3D TSE readout consists of the acquisition of navigator echoes followed by the acquisition of imaging echoes. The acquisition of navigator echoes takes place during the pseudo steady state (PSS) stage of 3D TSE, in which the initial echoes (referred to as startup echoes) are not acquired for imaging purposes to avoid signal oscillations from echo to echo 39, 40, 41. Navigator echoes are only phase‐encoded along the k _y direction. Therefore, the y‐direction resolution of the resulting navigator image depends on the number of startup echoes of the echo train. To increase the y‐direction resolution of the navigator image and hence the capability to capture more complex motion‐induced phase errors, sensitivity encoding (SENSE) can be used. The imaging sequence acquires one full k _z plane in each echo train (also referred to as shot).

Phase Correction and Image Reconstruction

A schematic representation of the implemented phase correction and reconstruction routine is shown in Figure 2. For each shot n, acquired T₂‐weighted (T_2w) navigator k‐space data krefⁿ (kx, ky, 0) and diffusion‐weighted (DW) navigator k‐space data knav^j,n (kx, ky, 0), where j denotes the diffusion acquisition, are first low‐pass filtered using a 2D triangular window, because only the low spatial frequencies of the signal phase are expected to be affected by motion. After 2D reconstruction of low‐resolution T_2w k‐space data $k{\text{ref}}_{\text{lr}}^{\mathrm{n}}$ (kx, ky, 0) and DW navigator k‐space data $k{\text{nav}}_{\text{lr}}^{\mathrm{j},\mathrm{n}}$ (kx, ky, 0), the phase of the low‐resolution DW navigator image‐space data per diffusion acquisition j, ${\text{nav}}_{\text{lr}}^{\mathrm{j},\mathrm{n}}$ (x, y, 0), is compared, per shot n, to the phase of the low‐resolution T_2w navigator image‐space data ${\text{ref}}_{\text{lr}}^{\mathrm{n}}$ (x, y, 0), which are used as a reference. The estimated phase difference map Δϕ^j,n (x, y) is then used on the 2D‐reconstructed imaging hybrid‐space data im^j,n (x, y, kz) to correct for diffusion‐acquisition‐ and shot‐dependent phase by means of complex multiplication. The 1D reconstruction along k _z, equivalently across all shots, results in the final phase‐corrected imaging data im_corr (x, y, z).

Figure 2.

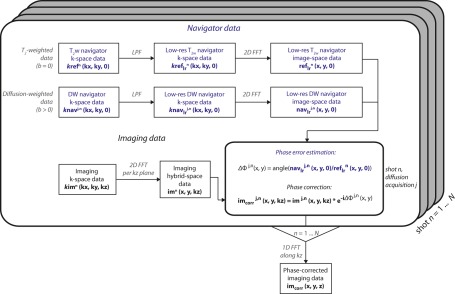
Phase correction and reconstruction in phase‐corrected DP 3D TSE. The phase error map Δϕ j,n (x, y) for each individual diffusion acquisition j and shot n is estimated from the low‐resolution navigator data in image space, where the T₂‐weighted (b = 0) data are used as a reference. Phase correction per shot and per diffusion acquisition of the imaging data with the estimated phase error is done voxel‐wise in the hybrid space (x, y, k_z). Corrected imaging data are then reconstructed along k _z to obtain the final image. LPF, low‐pass filter; FFT, fast Fourier transform.

In Vivo Measurements

Thirteen healthy volunteers (mean age, 29 ± 5 years; 8 males, 5 females) participated in the study. The study was approved by the local institutional review board and conducted in accord with the committee for human research. All subjects gave written informed consent before their participation in the study. All acquisitions were performed on a 3T whole‐body Philips scanner (Philips Ingenia, Best, The Netherlands) with maximum gradient amplitude of 45 mT/m and maximum slew rate of 200 T/m/s, in conjunction with a 16‐channel torso coil and the built‐in‐table 12‐channel posterior coil. The subjects were positioned supine and the coil was centered at the pelvic bone to cover the sacral plexus and the sciatic nerves. Survey scans were acquired in all coronal, sagittal, and axial planes. A coronal T₂‐weighted 3D TSE scan was included to have a visual reference of the nerves in further planning 42. The imaging volumes of all following scans were aligned to the spinal cord and positioned to cover the lumbar 5 (L5) nerve as well as the sciatic nerve after the junction of the L5 and sacral S1, S2, and S3 nerve branches.

DTI with DP 3D TSE was performed coronally in all subjects with the following readout sequence parameters: field of view (FOV) = 400 × 400 × 50 mm³; acquisition voxel = 2.5 × 2.5 × 2.5 mm³; reconstruction voxel = 0.78 × 0.78 × 1.25 mm³; repetition time/echo time (TR/TE) = 1500/35 ms; echo train length = 53; duration of diffusion preparation TE_prep = 32 ms; effective echo time including diffusion preparation 43 TE_eff = 53 ms; fat suppression using spectral adiabatic inversion recovery; number of signal averages = 2 using phase cycling for removal of free induction decay artifacts; parallel imaging using SENSE with reduction factor R = 3 (in the right–left phase encoding direction); b‐values = 0,400 s/mm²; number of diffusion directions = 6; and total scan duration = 11 min 58 s. Phase encoding for navigator echoes was carried out for k _y symmetrically around k _y = 0, with k _{y max} = ± 6 (SENSE factor of 3), and without k _z phase encoding.

DTI with diffusion‐weighted ss‐EPI (DW ss‐EPI) was performed to serve as a reference and to better allow the assessment of motion‐induced effects on DTI data acquired with DP 3D TSE. DW ss‐EPI was performed axially in all subjects and coronally in one subject. Due to severe distortions (see below), coronal DW ss‐EPI data were acquired for qualitative and visualization purposes only. Axial and coronal DW ss‐EPI were planned to cover the same anatomy as coronal DP 3D TSE and axial DW ss‐EPI was matched in FOV in the feet–head direction and in the isotropic voxel size to coronal DP 3D TSE. Axial DW ss‐EPI scans used the following sequence parameters: field of view = 400 × 250 × 250 mm³; acquisition voxel = 2.5 × 2.5 × 2.5 mm³; reconstruction voxel = 0.93 × 0.93 × 2.50 mm³; slice gap = 0 mm; TR/TE = 23832/47 ms; fat suppression using spectral adiabatic inversion recovery; number of signal averages = 3; partial Fourier encoding with factor = 0.74; parallel imaging using SENSE with reduction factor R = 2 (in the right–left phase encoding direction); b‐values = 0,400 s/mm²; number of diffusion directions = 6; and total scan duration = 9 min 8 s.

Coronal DW ss‐EPI scans used the following sequence parameters: field of view = 400 × 400 × 50 mm³; acquisition voxel = 2.5 × 2.5 × 2.5 mm³; reconstruction voxel = 0.93 × 0.93 × 2.50 mm³; slice gap = 0 mm; TR/TE = 3346/58 ms; fat suppression using spectral adiabatic inversion recovery; number of signal averages = 3; partial Fourier encoding with factor = 0.74; parallel imaging using SENSE with reduction factor R = 2 (in the right–left phase encoding direction); b‐values = 0,400 s/mm²; number of diffusion directions = 6; and total scan duration = 1 min 17 s.

DTI scans with DP 3D TSE and axial DW ss‐EPI were additionally carried out three times for five of the 13 subjects with identical sequence parameters for demonstration of repeatability.

An additional 3D two‐echo gradient echo sequence using a bipolar (non–fly‐back) readout was included to generate a B₀ map with the following sequence parameters: field of view = 250 × 400 × 250 mm³; acquisition voxel = 3.2 × 3.2 × 3.2 mm³; reconstruction voxel = 0.78 × 0.78 × 3.20 mm³; TR/TE1/ΔTE = 6.6/1.14/0.8 ms; flip angle = 3 °; six acquired echoes; number of signal averages = 1; and total scan duration = 1 min 4 s. The B₀ map was generated using the vendor's algorithm for performing water‐fat separation of the two‐echo gradient‐echo data 44.

DTI Analysis

Axial b = 400 DW ss‐EPI data were registered to axial b = 0 DW ss‐EPI data using an affine transformation 45, 46 to minimize geometric distortions produced by eddy currents.

Diffusion tensors were estimated from DTI data acquired with DP 3D TSE and with axial DW ss‐EPI using an own nonlinear fitting routine implemented in MATLAB and Statistics Toolbox Release 2016b (The MathWorks, Inc., Natick, MA). DTI parameters were computed from the derived eigenvalues and projections of the primary eigenvectors of DTI DP 3D TSE data on the coronal and sagittal planes were generated for visualization of preferential nerve direction.

For each subject, the sciatic nerve at the level of the greater sciatic foramen was identified on iso‐diffusion‐weighted images (iso‐DWIs) generated from axial DW ss‐EPI data and axially reformatted DP 3D TSE data. Sagittal views were used to locate the left and right sciatic nerves at the height of the base of the femoral head in the feet–head direction. The selected feet–head location relative to the femoral head was then confirmed using coronal views, in which the left–right locations of both nerves were then found. Given the locations noted in feet–head and left–right directions, axial views were finally used to localize both left and right sciatic nerves in all three orthogonal dimensions. https://onlinelibrary.wiley.com/action/downloadSupplement?doi=10.1002%2Fmrm.27072&attachmentId=215920358, which is available online, illustrates the localization procedure described above.

Regions of interest (ROIs) were independently drawn by two MR researchers with 3.5 (B.C.) and 3 (D.W.) years of experience in performing evaluations of quantitative MR neurographic studies. ROIs were drawn on the localized left and right sciatic nerves on axial DW ss‐EPI data and on axially reformatted DP 3D TSE data using 5 mm averages in the feet–head direction using MATLAB and Statistics Toolbox Release 2016b (The MathWorks, Inc., Natick, MA). To minimize quantification errors caused by distortions in DW ss‐EPI, the extraction of DTI metrics was carried out on the sciatic nerve after the junction of the L5, S1, and S2 nerves, where distortions in DW ss‐EPI images were the least severe. Axial, radial, and mean diffusivity (AD, RD, and MD, respectively) maps and fractional anisotropy (FA) maps were masked independently with the ROIs obtained by the two readers and mean values were extracted.

Statistical Analysis

To assess the effect of motion‐induced phase errors and their correction in DP 3D TSE, mean AD, RD, MD, and FA values measured by a single reader (B.C.) were compared across subjects for DP 3D TSE with and without phase correction using a paired t‐test with a significance level of 0.05. To further assess robustness to motion and thus the DTI‐quantification accuracy of phase‐corrected DP 3D TSE, the DTI metrics measured with phase‐corrected DP 3D TSE were compared with those measured with DW ss‐EPI using a paired t‐test with the same properties as specified above.

Interobserver agreement for the extracted DTI metrics was determined by measuring the intraclass correlation coefficients (ICC) for DP 3D TSE with and without phase correction and for DW ss‐EPI. The ICC model was based on a two‐way random comparison of absolute agreement type and the coefficients were computed with a significance level of 0.05. ICCs were first computed per DTI parameter and per method and then averaged for each method.

Repeatability measurements in five subjects were submitted to a similar extraction of mean DTI‐parameter values by a single reader (B.C.). For assessing variance between measurements per DTI metric and per method across scans, root‐mean‐square errors (RMSE) and root‐mean‐square error coefficients of variation (RMSCV) 47 were computed for AD, RD, MD, and FA values measured with DP 3D TSE, phase‐corrected DP 3D TSE and DW ss‐EPI. Interscan agreement of the DTI metrics measured with the three methods was determined by computing ICC values with the model described above.

RESULTS

Effects of Phase Errors on Image Reconstruction and Diffusion Quantification

Estimated phase error maps from DP 3D TSE data shown in the top row of Figure 3 show motion‐induced phase that varies across shots of the 3D TSE readout, highlighting the fundamental importance of phase correction in DP 3D TSE. The corresponding reconstructed DWI shown in the middle row demonstrates the effect of the resulting intershot phase inconsistencies on the signal magnitude when no phase correction is performed, which can take the form of through‐slice ghosting as well as of in‐plane signal loss (dotted arrow and solid arrow, respectively). The reconstructed phase‐corrected image shows the reduction of ghosting and restoration of signal. Derived MD maps in the bottom row display a large overestimation of mean diffusivity values in DP 3D TSE without phase correction and a remarkable restoration of MD values of nerve and muscle to within literature‐reported ranges when phase correction is performed. https://onlinelibrary.wiley.com/action/downloadSupplement?doi=10.1002%2Fmrm.27072&attachmentId=215920358 further illustrates the effects of motion‐induced phase errors on image reconstruction and diffusion quantification in two additional subjects.

Figure 3.

Effects of motion‐induced phase errors in DP 3D TSE on image reconstruction and diffusion quantification. Top: The estimated phase error maps (shown in radians) across four shots of a single diffusion acquisition show motion‐induced phase variations in the frequency and phase encoding directions that are inconsistent across shots. Middle: The reconstruction of the corresponding diffusion data without correction of motion‐induced phase errors results in incorrect signal buildup due to ghosting in the slice encoding direction (dotted arrows) as well as in signal loss in numerous regions, including a large loss of signal in the sciatic nerve (full arrows). The incorporation of phase error correction in the image reconstruction results in the elimination of ghosting artifacts and in the restoration of nerve signal. Bottom: Corresponding MD maps show the overestimation of diffusivity values in nerve and muscle caused by uncorrected motion‐induced phase errors.

DTI and Statistical Analysis

DTI parameters estimated by a single reader from data acquired with DP 3D TSE and with DW ss‐EPI are summarized in Table 1. Diffusion quantification of DP 3D TSE data with and without phase correction resulted in a statistically significant reduction in AD, RD, MD, and FA values in the sciatic nerve after phase correction was performed (P ≤ 0.001 for AD, RD, and MD; P = 0.02 for FA). The estimation of DTI metrics from DW ss‐EPI data compared with phase‐corrected DP 3D TSE data resulted in significantly different AD and MD values (P = 0.03 and P = 0.02, respectively) and in nonsignificant differences in RD and FA values (P = 0.11 and P = 0.27, respectively).

Table 1.

DTI Parameters of the Sciatic Nerve Measured With DP 3D TSE With and Without Phase Correction and DW ss‐EPI^a

	3D TSE
	Uncorra	Phase corrb	ss‐EPIc	Pab	Pbc
AD	3.40 ± 1.04	2.67 ± 0.36	2.47 ± 0.31	0.001b	0.03b
MD	2.06 ± 0.45	1.73 ± 0.26	1.62 ± 0.21	< 0.001b	0.02b
RD	1.39 ± 0.29	1.27 ± 0.27	1.20 ± 0.22	< 0.001b	0.11
FA	0.52 ± 0.11	0.48 ± 0.10	0.45 ± 0.09	0.02b	0.27

^aMean ± SD values within the sciatic nerve measured in 13 healthy subjects in left and right locations. Diffusivity values shown in units of 10⁻⁹ m²/s. P^ab denotes the P value comparing DP 3D TSE with and without phase correction and P^bc denotes the P value comparing phase‐corrected DP 3D TSE and DW ss‐EPI.

^b P < 0.05.

Mean values of the DTI metrics measured by the two readers for DP 3D TSE, phase‐corrected DP 3D TSE, and DW ss‐EPI resulted in average intraclass correlation coefficients (ICC) of 0.98, 0.97, and 0.94, respectively.

Repeatability errors and interscan agreement from data acquired in five subjects over three scans with DP 3D TSE and DW ss‐EPI are summarized in Table 2. Phase error correction of repeated DTI measurements with DP 3D TSE resulted in reduced RMSE in AD, MD, and FA, and in unaltered errors in RD. Similarly, RMSCV decreased for all DTI metrics except for RD, where it increased by one percentage point. RMSE and RMSCV values for DW ss‐EPI were smaller than those for DP 3D TSE. ICC values of all DTI metrics for DP 3D TSE, phase‐corrected DP 3D TSE and DW ss‐EPI were 0.97, 0.98 and 0.99, respectively.

Table 2.

Repeatability Errors and Interscan Agreement for DTI Parameters of the Sciatic Nerve Measured With DP 3D TSE With and Without Phase Correction and DW ss‐EPI

	3D TSE
	Uncorr	Phase corr	ss‐EPI
AD	0.48 [11%]	0.20 [7%]	0.15 [6%]
MD	0.19 [8%]	0.13 [7%]	0.10 [6%]
RD	0.15 [11%]	0.15 [12%]	0.12 [10%]
FA	0.07 [15%]	0.06 [14%]	0.05 [12%]
ICC	0.97	0.98	0.99

RMSE, RMSCV, and intraclass correlation coefficients (ICC) computed for DTI parameters measured in left and right locations in the sciatic nerve in five healthy subjects over three identical scans. RMSE in units of (10⁻⁹ m²/s) for AD, RD, and MD and in (‐) for FA. RMSCV in percentage units for all metrics.

Distortions in Isotropic Resolution Imaging with ss‐EPI

Figure 4 shows distortion problems encountered in nerve imaging with ss‐EPI. The coronal acquisition of the full field of view containing the lower spine and the sciatic nerves with ss‐EPI results in large distortions of the S1 nerves and milder distortions of the sciatic nerves in the phase encoding (left–right) direction compared with 3D TSE, making coronal ss‐EPI an unacceptable acquisition method for this anatomical region. Axial acquisition with ss‐EPI, shown in sagittal reformats for two healthy subjects (bottom rows), considerably reduces distortions but still results in distortions of the nerve course in the anterior–posterior direction compared with 3D TSE in regions with considerable B₀ inhomogeneity.

Figure 4.

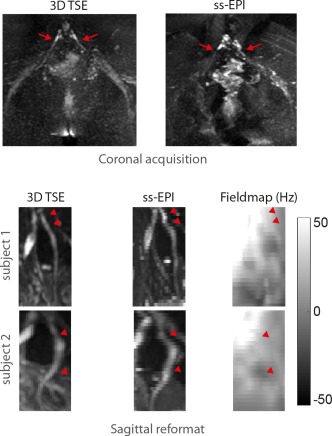
Geometric distortions in ss‐EPI. Top: Coronal ss‐EPI acquisition shows severe geometric distortions of the S1 nerve in the phase encoding (left–right) direction compared with 3D TSE (red arrows). Bottom: The sagittal reformat of axially acquired ss‐EPI shows severe distortions of the L5 nerve in the phase encoding (anterior–posterior) direction compared with sagittally reformatted 3D TSE (red pointers). A B₀ fieldmap shows that distortions in ss‐EPI occur in regions with large B₀ inhomogeneity. Moreover, imperfect slice profiles in the axial ss‐EPI acquisition lead to artificial increase and/or decrease of the nerve signal as compared to the 3D TSE.

Isotropic Resolution DWI and DTI with Phase‐Corrected DP 3D TSE

Figures 5, 6, 7 illustrate DTI results of isotropic resolution imaging of sacral nerves with DP 3D TSE. Iso‐DWIs of the sacral plexus and of the sciatic nerve in coronal, sagittal and axial views in Figure 5 clearly show the roots, ganglia and branches of the L5, S1, and S2 nerves as well as the course of the sciatic nerve. Coronal and sagittal views show the inner structure of the L5 and S1 nerve branches and axial cross sections show the fibular and tibial components of the sciatic nerve near the junction of the lumbosacral nerves. Figure 6 illustrates the advantage of multiview reformatting of isotropic 3D data for diffusion quantification. Sagittal and coronal views of the S1 and sciatic nerves acquired with phase‐corrected DP 3D TSE show DTI parameter maps of the full course of the nerves. Moreover, Figure 7 shows the primary diffusion tensor eigenvector projections on the coronal and sagittal planes for sacral nerves in two healthy subjects. The shown eigenvectors clearly depict the trajectory of the nerves and highlight the internal orientation of small nerve branches.

Figure 5.

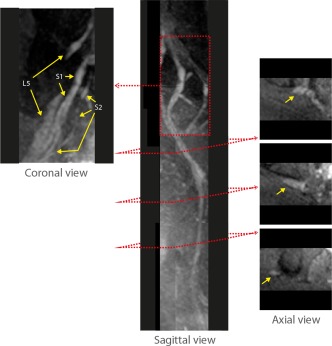
Isotropic resolution multiview DWI of lumbosacral and sciatic nerves with phase‐corrected DP 3D TSE. Coronal, sagittal, and axial views of the iso‐DWI acquired with isotropic resolution phase‐corrected DP 3D TSE show L5, S1, and S2 nerve roots and branches as well as the postjunction sciatic nerve running down in the pelvic region.

Figure 6.

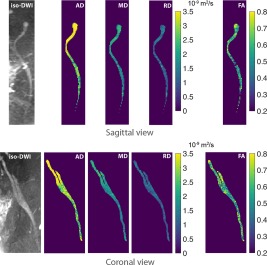
Isotropic resolution DTI of the sciatic nerve with phase‐corrected DP 3D TSE. Sagittal and coronal reformats of iso‐DWI and corresponding DTI maps obtained with phase‐corrected DP 3D TSE illustrate diffusion parameters along the sciatic nerve before and after the junction of the L5 and S1 nerves. High diffusivity values toward the ganglia of the L5 and S1 nerves are believed to be caused by the presence of CSF fluid.

Figure 7.

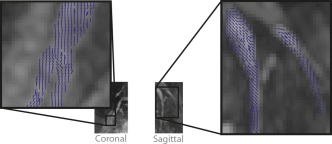
Primary diffusion tensor eigenvector projections of lumbosacral nerves with phase‐corrected DP 3D TSE. Primary diffusion tensor eigenvector projections on coronal and sagittal planes for two healthy subjects superimposed on their corresponding iso‐DWIs generated with phase‐corrected DP 3D TSE depict the course of the L5, S1, and S2 nerves before the junction into the sciatic nerve.

DISCUSSION

The current work presents distortion‐minimized isotropic resolution DTI results of the lower back nerves by proposing a phase‐navigated DP 3D TSE acquisition. In the proposed technique, magnitude modulation induced by motion and eddy currents is minimized with magnitude stabilizers and intershot phase variations induced by motion are measured with navigator echoes before the 3D TSE readout. Because the navigator acquisition uses the existing PSS echoes, its inclusion in the 3D TSE readout does not lead to any change in sequence parameters or to a longer acquisition duration. A phase correction and reconstruction routine is also presented, in which phase measured from navigator data is used to phase‐correct diffusion data during image reconstruction.

DTI can be a highly valuable tool in diagnostic MRN, but DWI of nerves in the body presents a challenging problem for a wide range of acquisition methods 30, 35, 48. ss‐EPI meeting coverage and resolution requirements necessary for imaging of nerves in the body can be particularly vulnerable to geometric distortions and chemical shift artifacts 49, challenging its application in DTI measurements of nerves in the body. Single‐shot TSE techniques circumvent the problems encountered with ss‐EPI 50, 51, 52 but are still limited to 2D and nonisotropic resolution due to SAR restrictions 52, 53, 54, 55, 56. Given the complex geometry of the nervous system in the human body, 3D isotropic imaging is highly desirable for DTI measurements in this anatomy 57, 58. DTI with TSE using a (multishot) 3D readout allows the acquisition of isotropic resolution diffusion images but requires the additional handling of intershot phase errors induced by motion, which interfere with the correct reconstruction of diffusion images when they are inconsistent across shots.

Present results showing the spatial distribution of estimated phase errors corresponding to multiple shots in DW data acquired in vivo with DP 3D TSE demonstrate that phase induced by motion varies from shot to shot. Moreover, the observation of ghosting artifacts and the loss of signal in the associated reconstructed images confirm that motion‐induced phase errors lead to a notable deterioration of image quality when diffusion data are not phase‐corrected. Phase correction of the diffusion data is shown to yield reconstructed images with minimal ghosting and with largely recovered signal. The corruption of DTI eigenvalues by phase errors is emphasized in the presented MD maps derived from DP 3D TSE DTI data reconstructed with and without phase correction. Uncorrected motion‐induced phase errors produce largely overestimated and thus physically meaningless MD values while MD values derived from phase‐corrected data agree with previously reported values 7, 9.

Significant reductions in the mean values of all DTI metrics measured in the sciatic nerves in 13 subjects with phase‐corrected DP 3D TSE compared with non–phase‐corrected DP 3D TSE demonstrate the corruption of the measured, uncorrected diffusion signals by motion, because it is expected that the phase induced by bulk motion during diffusion encoding will lead to the artificial attenuation of diffusion signals and consequently to the overestimation of diffusivity.

Moreover, the reduced standard deviations in all DTI metrics observed in DP 3D TSE measurements with phase correction indicates that the robustness to motion provided by phase correction leads to more consistent diffusion quantification. The closer agreement of mean and standard deviation values observed in phase‐corrected DP 3D TSE DTI metrics to those observed with DW ss‐EPI indicates that motion robustness in the multishot method approaches that in the single‐shot method. Significant differences in AD and MD metrics measured with phase‐corrected DP 3D TSE compared with DW ss‐EPI highlight residual small differences in the quantification performances of the two methods. In the case of phase‐corrected DP 3D TSE, higher values can originate from types of motion that the proposed technique is still insensitive to, such as motion‐induced phase variation in the k_z encoding direction or from microscopic contractions within single imaging voxels that lead to intravoxel dephasing. In the case of DW ss‐EPI, remaining geometric distortions and/or slice profile effects can lead to the incorrect estimation of the DTI metrics in the sciatic nerves. Trends of higher diffusivity metrics measured with DW TSE‐based methods compared with DW ss‐EPI have already been observed 23, 59, 60.

DTI repeatability results further support the above arguments. Reductions in RMSE and RMSCV in all sciatic‐nerve DTI metrics obtained with DP 3D TSE after phase correction show that the proposed phase correction leads to lower variance within and across subjects and across scans. Although of similar order, smaller RMSE and RMSCV values in DW ss‐EPI compared with phase‐corrected DP 3D TSE indicate that the multishot method might still be in part more sensitive to motion than the single‐shot method. We emphasize that the proposed phase‐navigation and phase‐correction technique is meant to increase robustness to motion and is not expected to achieve complete motion insensitivity as DW ss‐EPI.

AD results were most vulnerable to motion effects compared with other DTI metrics. Motion‐induced phase errors can affect different diffusion directions differently. For example, when the motion‐induced phase error induces a signal loss in only one diffusion direction, the affected direction becomes the direction of preferential diffusion, potentially also affecting AD. In contrast, FA values were observed to be least affected by motion. This finding is in agreement with previous reports that have shown that measurements of FA in peripheral nerves vary less significantly than other diffusivity values when different methods are used to estimate the metrics as well as across nerve locations 9.

In vivo results comparing images of lower back nerves acquired with 3D TSE and with ss‐EPI show that severe distortions of the nerves in ss‐EPI data make this acquisition method unsuitable for performing accurate measurements of DTI‐derived parameters in the lumbosacral and sciatic nerves, where B₀ inhomogeneity can be present. DP 3D TSE is shown to provide distortion‐free DWIs and DTI parameter maps in which individual nerves and their internal structure can be visualized and whose course can be clearly and accurately followed. It is further shown that isotropic‐resolution DWIs and DTI parameter maps obtained with phase‐corrected DP 3D TSE can be reformatted in all three orthogonal planes to inspect specific morphological and functional aspects.

The present study has several limitations. First, as any 3D acquisition technique, the proposed 3D TSE technique is associated with significantly longer scan times than the 2D ss‐EPI due to the efficient k‐space traversal of the EPI trajectory and the interleaving capability of 2D acquisitions. Second, regarding SNR efficiency, the proposed DP 3D TSE acquisition has lower SNR efficiency than DW ss‐EPI, which poses a disadvantage for the proposed method. However, as suggested by the obtained results in the current study, DW ss‐EPI is only expected to be suitable for DWI of nerves in the body where isotropic resolutions are not needed and where off‐resonance does not lead to unacceptable geometric distortions and chemical shift artifacts. It is in cases of isotropic resolution requirements, as well as in imaging of anatomies where field inhomogeneity and the presence of fat signal are problematic and unavoidable, that the immunity to off‐resonance of the proposed DP 3D TSE technique can become of superior value despite the compromise in SNR efficiency. A detailed SNR analysis comparing DP 3D TSE and DW ss‐EPI was not performed in this work and would require further investigation.

Third, to be incorporated in the PSS stage preceding each echo‐train readout in 3D TSE, navigator echoes in the proposed method are acquired without phase encoding along the k_z direction. This acquisition effectively results in a 2D navigator image that is the average of the 3D imaging volume along the z direction. Therefore, the proposed technique cannot resolve linear and higher order phase errors along the non–phase‐encoded direction. However, translational motion along the non–phase‐encoded direction, which results in spatially constant phase errors, can still be detected and corrected. The performance of the proposed phase correction technique, hence, depends on the spatial coverage and the severity of motion along the non–phase‐encoded direction. For the application at hand, we have shown significant improvement in image quality and quantitative metrics when the phase correction was used on a slab thickness of 50 mm in the A–P direction in the pelvic area. Because the proposed navigator acquisition is to be obtained for free, without affecting the imaging acquisition, it is undoubtedly beneficial to incorporate the proposed navigation in every multishot DWI TSE sequence.

CONCLUSIONS

We have shown that the proposed phase‐navigated DP 3D TSE acquisition and phase correction can provide DWIs and derived DTI metrics of lumbosacral and sciatic nerves with minimized motion‐induced effects. Namely, the measurement of motion‐induced phase in DP 3D TSE and its subsequent correction is shown to significantly reduce the motion‐induced overestimation of diffusion tensor parameters as well as to remove artifacts from DWIs. The proposed DP 3D TSE method has been shown to provide distortion‐free isotropic resolution DTI of lumbosacral and sciatic nerves.

Supporting information

Fig. S1. Illustrated procedure for localizing the sciatic nerves for DTI analysis. Sagittal, coronal and axial reformats of iso‐diffusion‐weighted images (isoDWIs) from coronal data acquired with DP 3D TSE and from axial data acquired with DW ss‐EPI were created. The femoral head was localized in the sagittal view and the leftright (LR), anterior‐posterior (AP) and feet‐head (FH) positions of its base were marked. The marked position of the femoral‐head base was found and referenced in the coronal view. The sciatic nerve at the marked FH position of the femoral‐head base was localized in the coronal view and its LR and AP positions were marked. The marked FH, LR and AP positions of the sciatic nerve were used to localize the nerve in the axial view. The localization procedure was carried out individually for left and right sciatic nerves for each subject.

Fig. S2. Effect of motion‐induced phase errors in diffusion quantification with DP 3D TSE. Iso‐diffusion‐weighted images (iso‐DWIs) of two healthy subjects obtained with DP 3D TSE show losses of signal in the sciatic nerve and surrounding muscle when the correction of motion‐induced phase errors is not performed. Corresponding mean diffusivity (MD) maps show the overestimation of diffusivity values in nerve and muscle caused by motion‐induced phase errors. Unusually high MD values in some regions result from the incompletely suppressed signal of vessels and CSF fluid.