Abstract
When a lineage originates from hybridization genomic blocks of contiguous ancestry from different ancestors are fragmented through genetic recombination. The resulting blocks are delineated by so called junctions, which accumulate with every generation that passes. Modeling the accumulation of ancestry block junctions can elucidate processes and timeframes of genomic admixture. Previous models have not addressed ancestry block dynamics for chromosomes that consist of a finite number of recombination sites. However, genomic data typically consist of informative markers that are interspersed with fragments for which no ancestry information is available. Hence, repeated recombination events may occur between markers, effectively removing existing junctions. Here, we present an analytical treatment of the dynamics of the mean number of junctions over time, taking into account the number of recombination sites per chromosome, population size, genetic map length, and the frequency of the ancestral species in the founding hybrid swarm. We describe the expected number of junctions using equidistant molecular markers and estimate the number of junctions using random markers. This extended theory of junctions thus reflects properties of empirical data and can serve to study the genomic patterns following admixture.
Keywords: Admixture, hybridization, junctions, population genetics, recombination
Hybridization has long been recognized as a potential driver in the evolution of plants (Grant 1981) and more recently as a process that generates biological diversity in animals (Abbott et al. 2013). Admixture among previously isolated populations may occur naturally, or result from many facets of human induced ecological change in recent historical time (Taylor et al. 2006; Vonlanthen et al. 2012; Bhat et al. 2014). It seems to be conspicuously associated with the colonization of new or perturbed habitats (Nolte et al. 2005; Krehenwinkel and Tautz 2013). In these examples, recent admixture has been suspected to contribute to the ecological success of emerging lineages (Nolte and Tautz 2010). Genetic admixture between differentiated lineages may even lead to hybrid speciation when the joint contribution of both parental species is instrumental in the rise of the new species, for example by creating direct barriers to reproduction with the parental species or by facilitating ecological isolation of the emerging hybrid lineage (Mallet 2007; Nolte and Tautz 2010; Abbott et al. 2013; Schumer et al. 2014). The genomic regions that convey a fitness advantage to a hybrid lineage can be expected to be subject to positive selection. On the other hand, we expect the purging of parental genetic variance that reduces the fitness of an admixed lineage (Buerkle et al. 2000; Barton 2001). Although these studies predicted an initial lag phase during which an emerging hybrid lineage has to go through an evolutionary optimization, empirical studies suggest that hybrid speciation can occur rapidly, possibly within hundreds of generations (Nolte et al. 2005; Buerkle and Rieseberg 2008; Lamichhaney et al. 2017).
Studies considering hybrid speciation are accumulating in recent years, but even well‐studied examples remain contentious (Schumer et al. 2014) and a multitude of evolutionary processes related to hybrids are difficult to generalize (Gompert and Buerkle 2016). On the other hand, hybridization receives great interest from evolutionary biologists and conservationists alike. Hence, there is a need to develop methods that permit extensive comparisons among different study systems to identify shared evolutionary patterns. This includes models that can help to develop neutral evolutionary expectations for hybrid lineages (Stemshorn et al. 2011), which in turn permits to identify candidate genomic loci that may be subject to selection. Conventional molecular clock estimates are too coarse to be applied to any cases of rapid speciation, but lineages of hybrid origin hold the potential to estimate rather short time frames from the ancestry structure of admixed genomes (Ungerer et al. 1998; Buerkle and Rieseberg 2008; Liang and Nielsen 2014; McTavish and Hillis 2014). Newly formed F1 hybrids contain complete chromosomes from either one of the ancestral species that constitute blocks (or tracts) of contiguous genomic ancestry. Genetic recombination leads to an exchange of genetic material between homologous chromosomes, which interrupts blocks of contiguous ancestry. As a consequence, the number of blocks accumulates while their size decreases from generation to generation. Modeling the accumulation of ancestry block junctions can elucidate processes and timeframes of genomic admixture. Since this process begins after the first generation of admixture, it holds the potential to study even the initial evolutionary steps that are of particular interest to study how a hybrid lineage evolves (Nolte and Tautz 2010).
The study of genomic blocks dates back to Fisher, who recognized that genetic material is organized within contiguous haplotype blocks after a hybridization event (Fisher 1949, 1954). He termed the delineations between these blocks junctions, and established that junctions have inheritance properties similar to those of point mutations: over time they are either lost from the population, or they become fixed. Fisher formulated the expected number of junctions given the number of generations passed since the initial hybridization event, for the case of sib‐sib mating (Fisher 1954). Following Fisher, the theory of junctions was quickly extended toward self‐fertilization (Bennett 1953), alternate parent‐offspring mating (Fisher 1959; Gale 1964) and a population of randomly mating individuals (Stam 1980). Apart from the number of junctions per chromosome, the distribution of block sizes has proven to be highly informative as well. Building upon the multilocus clines work of Barton (1983), which describes the block size distribution at equilibrium, Baird developed a robust framework describing the full dynamics of the block size distribution (Baird 1995). Furthermore, using efficient simulation techniques, Baird showed the impact of selection on the distribution of haplotype blocks, and used this framework to infer the onset of hybridization in Helianthus Sunflowers (Ungerer et al. 1998).
Parallel to the development of the theory of junctions, theory has been developed to describe the genomic contribution of past migrants (Gravel 2012; Pool and Nielsen 2009; Liang and Nielsen 2014). Here, the focus is on the breakdown of large ancestry blocks (within this context often referred to as “admixture tracts”) introduced by migrants, either due to a single migratory event (Gravel 2012) or due to ongoing migration (Pool and Nielsen 2009). These studies illustrate that allele frequencies affect the formation of junctions. When only a few, rare blocks (depending on the rate of migration) are introduced into a foreign background the decay of these blocks is asymmetric as it depends on how often they may recombine with blocks that have a shared (here rare) ancestry. This line of research is especially applicable to the study of the history of humans, where migration between for instance European and African populations can be detected from genomic patterns (Hellenthal et al. 2014; Payseur and Rieseberg 2016). Whereas the theory of junctions often focuses on a two‐species mixture (but see (Baird et al. 2003)), the study of admixture tracts allows the application to be broadened to multiple migratory source populations.
The theory of junctions has focused on a starting population inspired by the genome of F1 hybrid individuals that contain equal proportions of the parental genetic material. Although the work of Fisher (Fisher 1949, 1954) and subsequent extensions by Bennett (1953), Stam (1980), Chapman and Thompson (2002, 2003) and MacLeod et al. (2005) allows for deviations of this situation by changes to the initial heterozygosity H 0 at time , typical analysis has focused on the idealized situation of . Such equal proportions are only expected if a hybrid lineage is founded by a sufficiently large population of F1 hybrids. Under natural conditions, however, a hybrid lineage of outcrossing organisms more likely emerges from a heterogeneous hybrid swarm, and the overall ancestry contribution of parental species to the founding hybrid swarm may differ (Edmands et al. 2005; Nolte and Tautz 2010; Stemshorn et al. 2011; Schumer et al. 2016). Deviations from equal founding ancestry proportions and strong stochastic or fitness effects during the first few generations can sway the ancestry of an emerging hybrid lineage in favor of one of the ancestral species. Strong deviations from equality are likely to affect the formation of junctions as they decrease the frequency at which genotypes comprise material from both species. Moreover, the effect of drift is exacerbated when the ancestry contribution is strongly deviating from equal proportions. The impact of deviations from an even ancestry contribution of both ancestral species and the interaction with population size and drift remains understudied so far.
Paramount to applying the theory of junctions, is accurate detection of these junctions. MacLeod et al. 2005 showed that detection success was dependent on two crucial factors: the distribution of markers, and the density of markers (MacLeod et al. 2005). Macleod et al. compared markers that were equidistantly distributed with markers that were randomly distributed over the genome, while keeping the average density constant. Although equidistantly distributed markers did not detect 100% of all junctions, they detected 10–20% more junctions than randomly spaced markers. Furthermore, Macleod et al. found that the required density of markers to detect 90% of all junctions had to be at least 12.5 times the number of junctions. Because the expected number of junctions scales with the number of generations since the onset of hybridization, even for intermediate time‐scales between 500 and 1000 generations, the number of markers required to accurately infer the number of junctions quickly escalates toward extremely high numbers. To circumvent this problem, Buerkle and Rieseberg (2008) used simulations to apply a correction to observed junction densities to infer the true junction density. Our aim is to extend the theory of junctions to better include the effect of a finite number of markers.
Using only a finite number of markers leaves gaps between markers that remain understudied. So far, the theory of junctions has assumed that recombination never occurs twice at the same location (e.g., there is an infinite number of recombination sites along the chromosome) (Fisher 1954; Stam 1980; Chapman and Thompson 2003) and, accordingly, that all recombination events are detected. However, recent work has shown that such a distribution of the recombination rate might be the exception, rather than the rule, and that the recombination landscape is often organized into “warm” and “cold” areas, including hot spots (Gerton et al. 2000; Myers et al. 2005; Mackiewicz et al. 2013; Singhal et al. 2015; Arbeithuber et al. 2015; Smagulova et al. 2011). Repeated crossovers in the same area can impact the formation of new junctions, and can cause existing junctions to disappear. The same effect may manifest in genomic data even in the absence of recombination hotspots. Across the genome, ancestry informative markers are typically interspersed with fragments for which no ancestry information is available. As a result, recombination may occur repeatedly between markers. Hence, inclusion of recurrent recombination into the theory of junctions could add to our understanding of recombination hot spots and accommodates effects of incomplete information in studies using molecular markers.
This warrants methods that can be applied broadly in empirical studies on the consequences of admixture. Here, we present an extension to the theory of junctions including a finite number of recombination sites, and for hybrid swarms with an arbitrary contribution of either parental species. We first extend the theory of junctions toward a finite number of recombination sites in infinite populations, and then extend this framework toward finite populations. Then, using a novel approach, we derive a generalized theory of junctions, which only depends on the number of junctions obtained at equilibrium (e.g., at ). Lastly, using individual‐based simulations, we demonstrate the validity of our framework, and explore the implications of marker distributions on junction detection.
Analytical Model
Our aim is to derive the expected number of junctions per chromosome, in an isolated hybrid lineage depending on the time since the onset of hybridization. A scenario in which a single mating event and the resulting F1 hybrids are the sole founders of a hybrid lineage seems to be too constrained to represent the breadth of results from empirical studies. Conversely, we assume that a hybrid lineage emerges from a hybrid swarm. Individuals representing parental species or backcrossed individuals may become part of the hybrid swarm and bias the overall ancestry proportions of the founding population. As such, the hybrid swarm approach allows us to study situations in which there are deviations from a 50–50 distribution of ancestral genomic material at the onset of a hybrid lineage. Note that the special case of a founding population of only F1 individuals constitutes a special case of the more permissive scenario studied here. We assume full knowledge of ancestry along the genome. For simplicity, we ignore selection and drift and study the dynamics of junctions in neutrality. We assume that a Poisson number mean C crossover events occurs per chromosome per meiosis, which corresponds to the assumption that chromosomes are C Morgan long. The recombination rate is assumed to be uniform across the chromosome. Each individual is diploid. Orthologous chromosome pairs are interchangeable and paralogous chromosome pairs are inherited independently, which allows us to track junctions within only one chromosome pair, rather than all pairs simultaneously. Furthermore, we assume that populations are in Hardy–Weinberg equilibrium.
AN INFINITE NUMBER OF RECOMBINATION SITES
We first assume infinite population size and an infinite number of recombination sites along the chromosome. We denote the frequency of genomic material of parental species P by p, and the frequency of genomic material of the other parental species Q by q, where . The initial average heterogenicity across the genome is then defined by: , where is the heterogenicity at time t. Heterogenicity here refers to the mean proportion of the genome heterozygous by source, for example stemming from different parental species (sensu (Fisher 1954, 1959; Stam 1980)). If we would substitute all genomic content from species P by allele A, and all genomic content from species Q by allele a, it follows that the mean heterogenicity is equivalent to the mean heterozygosity across the genome. In our following derivations it turns out that we can use known expressions for the change in mean heterozygosity, which makes it important to realize that here, the mean heterozygosity is equivalent to the mean heterogenicity.
During crossover, a junction is only formed if crossover takes place at a site that is heterozygous for the parental genomic content. Thus, in an infinite population with an infinite number of recombination sites along the chromosome, the average number of junctions per chromosome, after t generations, is given by (Chapman and Thompson 2002; MacLeod et al. 2005; Buerkle and Rieseberg 2008)
| (1) |
where is the proportion of the heterozygous genomic material (following (Fisher 1954; MacLeod et al. 2005; Buerkle and Rieseberg 2008)) in an infinite population, where the proportion of heterozyous genomic material does not change over time. In a finite population, the average heterozygosity changes over time (Crow and Kimura 1970) as
| (2) |
Assuming a constant population size over time, for all t, and substituting in equation (1) by equation (2), we obtain an expression for the average number of junctions at time t, in a finite population (Chapman and Thompson 2002)
| (3) |
In the limit of we recover equation (1). For , we have (MacLeod et al. 2005)
| (4) |
Thus, for finite N the expected number of blocks in the descendant hybrid lineage converges to a finite number determined by the population size, the size of the chromosome in Morgan, and the initial heterozygosity (which in turn depends on the frequency of the ancestral species in the hybrid swarm).
A FINITE NUMBER OF RECOMBINATION SPOTS
In the previous section, we have assumed that recombination never occurs twice at the same spot. In reality, a chromosome can not be indefinitely divided into smaller parts. Furthermore, the presence of recombination hot spots (Gerton et al. 2000; Myers et al. 2005; Smagulova et al. 2011; Mackiewicz et al. 2013; Arbeithuber et al. 2015; Singhal et al. 2015) indicates that recombination in fact often does occur multiple times at the same site. We therefore proceed to study the change in number of junctions in a chromosome consisting of different genomic segments, where each segment represents a minimal genomic element that cannot be broken down further due to recombination. The most general interpretation would be a genomic area delineated by two genetic markers. Considering a chromosome of genomic segments, there are R possible junction sites (we do not distinguish the process of junction formation at different recombination positions, we validate this assumption using individual‐based simulations, see the section“Individual Based Simulations”). We assume that the genomic segments are of equal size, and as a result, the R junction sites are uniformly spaced across the chromosome (in Section “A finite number of markers” we relax this assumption). Given that at time t, there are junctions, the probability that a recombination event takes place at an existing junction is then given by
We focus on the dynamics of one of the two produced chromosomes. Because the choice of chromosome is random, averaging across a large number of recombinations ensures that we cover all possible outcomes. During recombination, we can then distinguish four possible events, taking into account the location of recombination on both chromosomes (Fig. 1):
-
(A)
With probability α2, recombination takes place on an existing junction on both chromosomes. In this case, there are two possible outcomes, depending on the transitions that the two junctions represent. Either there is no change in the number of junctions (when the transitions of the two junctions are identical), or a decrease in the number of junctions (when the transitions of the two junctions are of opposing type). The probability of either event happening is , yielding an average change in the number of junctions when crossover takes place on an existing junction on both chromosomes of .
-
(B)
With probability , recombination takes place on an existing junction on one chromosome, and within a block on the other chromosome. There are two possibilities: either the block on the other chromosome is of the same type as the genomic material before the existing junction, or it is of the other type. If it is of the same type, the existing junction disappears, and the number of junctions decreases by one. If it is of the other type, the existing junction remains and the number of junctions does not change. The probability of either event happening is , and hence we expect the number of junctions on average to change by .
-
(C)
With probability , recombination takes place on within a block on one chromosome, and on an existing junction on the other chromosome. The outcome is exactly the opposite of case (B). If the genetic material after the junction on the second chromosome is of the same type as the block on the first chromosome, no new junction is formed and the number of junctions stays the same. If the genetic material after the junction on the second chromosome is of a different type than that of the block on the first chromosome, a new junction is formed and the number of junctions increases by one. The probability of either event happening is , and hence we expect the number of junctions on average to change by .
-
(D)With probability , recombination takes place within a block on both chromosomes. In this case, matters proceed as described for the continuous chromosome: with probability H 0 we observe an increase in the number of junctions. However, since we are dealing with a finite number of recombination positions along the chromosome, the frequency of recombination sites of a genomic type is no longer directly related to H 0. If there would be no blocks, that is if the genomic material would be distributed in an uncorrelated way, potential recombination sites are of type P, that is, they are within a block of type P. Similarly, potential recombination sites are within a block of type Q. As new junctions are formed, the number of potential recombination sites that are still within a block decreases. With the formation of a new block, on average both a recombination site within a block of type P and a recombination site within a block of type Q are lost, such that on average, after the formation of a new junction, the number of recombination sites of type P decreases by . Thus the number of recombination sites within a block of type P is . Similarly, the number of recombination sites within a block of type Q is . The probability of selecting a recombination site within a block of type P is then given by the number of recombination sites of type P divided by the total number of recombination sites. Let us denote the probability of selecting a recombination site of type P by , which is then given by:
Concluding, for scenario D, we observe that the number of junctions increases on average by (where ).(5)
Figure 1.

Change in number of junctions depending on the genomic match between blocks. Full chromosomes are shown here, but the same rationale applies to subsets of a chromosome. Top rows within each panel indicate the two parental chromosomes, bottom row indicates one of two possible resulting chromosomes aftermeiosis, where recombination takes place at the dashed gray line. Genomic material of type P is indicated in black, genomic material of type Q is indicated in white. (A) With probability α2 recombination takes place on an existing junction on both chromosomes, (B) with probability recombination takes place on an existing junction on one chromosome, and within a block on the other chromosome, (C) with probability recombination takes place on within a block on one chromosome, and on an existing junction on the other chromosome, (D) with probability recombination takes place within a block on both chromosomes.
Combining the scenarios (A)–(D), and noticing that , we can formulate the total expected change in number of junctions
| (6) |
The solution of recursion equation (6) is given by
| (7) |
which is reminiscent of equation (3). The exponentially decaying term leads to convergence at , where we obtain
| (8) |
Note that the number of junctions obtained at does not depend on the size of the chromosome in Morgans C, but the speed of convergence does. A Taylor expansion of equation (7) at shows that initially, the number of blocks increases linearly
Once the number of junctions has reached the limit , new junctions will still be formed. Nevertheless, the average number of junctions does not increase further, because the population has reached the maximum packing density of junctions. Another approach to understanding the link between genome size and the maximum packing density of junctions is the following: As , all alleles are in linkage equilibrium, and we can consider the probability of observing either allele P or Q as independent along the chromosome. Then, assuming that each allele has a probability p of being P, the sequence consists of independent Bernouilli trials, and the number of consecutive P sites (and Q sites) is given by a Negative Binomial distribution parameterized with (the number of successes before 1 failure) and p. The full haplotype sequence then consists of alternating sequences of NB(1,p) sites of type P and NB(1,q) sites of type Q. The mean length of junctions intervals is then given by:
Then, the average number of junctions packed in a chromosome of length, is given by , which is identical to our previous result in equation (8). Hence, whereas initially accumulation of junctions is hampered by repeated recombination in the same site, at equilibrium it is the maximum packing density of junctions, rather than the dynamic equilibrium between formation and removal of junctions, that determines the maximum number of junctions across the population.
A FINITE NUMBER OF RECOMBINATION SPOTS IN A FINITE POPULATION
Arguably the most realistic scenario involves a finite number of recombination sites, within a finite population. For a finite chromosome in a finite population, accumulation of junctions is limited by two processes: decay of the heterozygous proportion of the genome due to drift in a finite population, and the probability of junction removal due to recombination occurring at a previous recombination site. We have described limitation of junction accumulation due to repeated recombination at the same site as a recurrence equation (cf. eq. 6). We can similarly express the limitation of junction accumulation due to the decrease in the proportion of the genome heterozygous due to finite population size (eq. 3) as
| (9) |
In equation (6) the accumulation of junctions over time is slowed down by the term , representing the slowdown of junction accumulation due to repeated recombination at the samesite. For a finite population we observe a similar pattern, where the accumulation of junctions is slowed down by the term , which represents the decay of the portion of genome heterozygous. Assuming that these two effects are independent, and only focusing on mean junction dynamics (ignoring drift in p) (we will show with individual‐based simulations that these assumptions are good approximations), the combined effect of a finite population and of a finite number of recombination sites, is then given by
| (10) |
The solution to equation (10) is given by
| (11) |
the exponentially decaying term leads to a convergence at , where we obtain
| (12) |
For , equation (12) simplifies to equation (4), and for equation (12) simplifies to equation (8).
Generalized Junction Dynamics
The general pattern of the accumulation of junctions over time is highly similar across the different scenarios we have studied here: after an initial period of a strong increase in the number of junctions, the increase in the number of junctions slows down and eventually approaches a maximum. Furthermore, comparing equations (3), (7), and (11) we observe that there are some generalities. Generally speaking, we can express the number of junctions at time t as a function of the maximum number obtained at . We find (a full derivation can be found in the Appendix)
| (13) |
Where K is the maximum number of blocks obtained at . the derivation is graphically summarized in Figure 2: although for different values of N and R, junction accumulation curves differ strongly (Fig. 2A), we find that after normalizing the curves by the number of junctions obtained at (Fig. 2B), the curves partially collapse on each other. After rescaling the time axis by the initial slope of each curve, all curves collapse on each other (Fig. 2C), and are described by equation (13). In the most general case, K is then given by equation (12).
Figure 2.
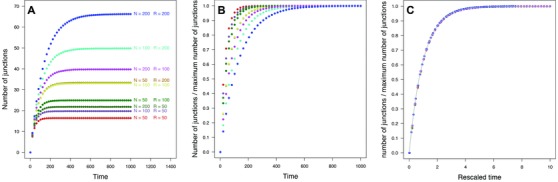
Graphical example of the construction of universal junction dynamics using results from individual based simulations. (A) Mean number of junctions for , and , number of replicates = 10,000. (B) The mean number of junctions for the same parameter combinations, after rescaling the number of blocks relative to the maximum number of junctions K. (C) The rescaled number of junctions versus rescaled time, by rescaling time according to β in equation (A6). After rescaling both the number of junctions according to K, and time according to β, all curves for different values of N and R reduce to a single, universal, curve, which follows equation (13).
The Limit of Accuracy
Given knowledge of the number of junctions and the population size, one can use information about the number of junctions to infer the onset of hybridization, which is given by (cf. eq. 11)
| (14) |
In contrast to using a molecular clock, information about the number of junctions provides information on a relatively short timescale. However, because the number of junctions plateaus over time, there is a limit in the accuracy of this method. The maximum accurate time τMAT for which one can still infer the onset of hybridization using equation (14), is given by (the full derivation can be found in the Supplementary Material):
| (15) |
where K is given by equation (12). Figure 3 shows that τMAT scales roughly exponential with both population size and chromosome size.
Figure 3.
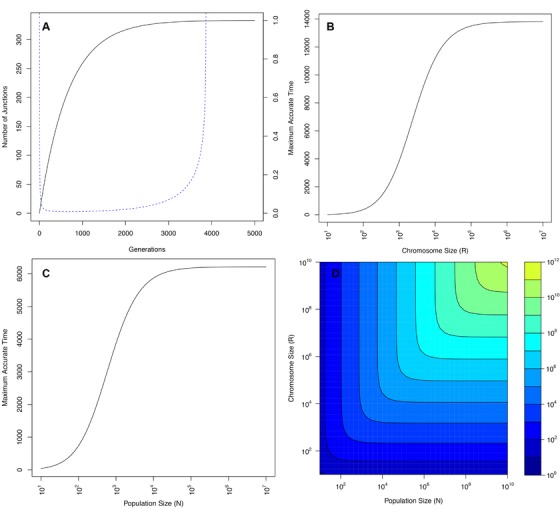
(A) Number of junctions over time for (black line), and the associated relative error (eq. 4 in the Supplementary Material) (dashed blue line). Y‐axis at the left hand side corresponds to the number of junctions, y‐axis on the right hand side corresponds to the associated relative error. As the number of junctions approaches K, the relative error approaches infinity. (B) Maximum accurate time (eq. 15) for , for an increasing number of markers. As the number of markers increases toward high numbers (107), the maximum accurate time approaches 14,000. (C) Maximum accurate time (eq. 15) for , for increasing population size. As population size increases toward large values, the maximum accurate time plateaus around 6000 generations. (D) Maximum Accurate Time (τMAT) for N and R, please note the logarithmic scale. Results show that the accurate range increases exponentially with increasing N and R. Results show that the accurate range increases exponentially with increasing N and R. For all four plots, .
Individual‐based Simulations
To verify our analytical framework, and test the impact of marker distributions, we test our findings using an individual‐based model. We use a Wright–Fisher process, extended with recombination, assuming a constant population size N, diploid individuals, and a uniform recombination rate across the genome. During initialization of the model, N individuals are generated, where each individual can have either two parents of type P (with probability p 2), two parents of type Q (with probability q 2) or one parent of type P and one parent of type Q (with probability ). In every consecutive time step, N new individuals are produced, where each individual is the product of a reproduction event between two individuals from the previous generation. Parental individuals are drawn with replacement, such that one individual could reproduce multiple times, but will on average reproduce one time. We assume that in a mating event, both parents produce a large number of haploid gametes from which two gametes (one from each parent) are chosen to form the new offspring. During production of the gametes, the number of recombination sites is drawn from a Poisson distribution with a mean of C.
AN INFINITE NUMBER OF RECOMBINATION SITES
To model an infinite number of recombination sites, we represent each chromosome as a continuous line of arbitrary length, that can be subdivided into an infinite number of smaller lines. We only keep track of junctions delineating the end of a block (following Baird (1995); Ungerer et al. (1998)). For each junction, we record the position along the chromosome and whether the transition is from genetic material of type or . We observe that over time, the number of junctions reaches a maximum value, but only if the population is finite (Fig. 4), in line with our mathematical predictions. In the first few generations the accumulation of junctions follows that of an infinite population (dashed line in left panel in Fig. 4), but rapidly simulation results start deviating from the infinite population dynamics. When one of the two ancestral species is overrepresented in the initial hybrid swarm (e.g., ), the maximum number of junctions is lower (as expected, following eq. (4), and is reached within a shorter timespan.
Figure 4.
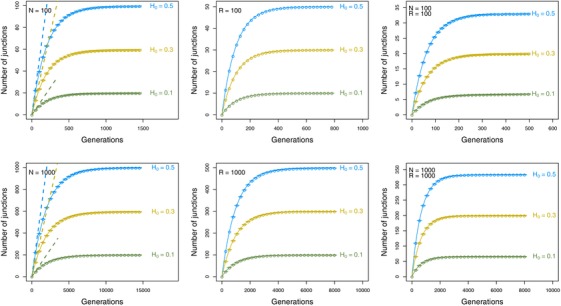
Number of junctions over time for individual‐based simulations, and analytical predictions. Left column: Results assuming a chromosome with an infinite number of junction sites, , and a population size (N) of 100 or 1000 individuals (circles), the analytical prediction for an infinite population size (dashed line), or the analytical prediction for a finite population size (eq. (3)), solid line. Middle column: Results assuming a chromosome with a finite number (R) of junction sites, where R is 100 or 1000, and a population size of 100,000 (circles), or the analytical prediction according to equation (7) (solid line). Right column: Results for a chromosome with a finite number of junction sites of length R of 100 or 1000, and a finite population of size N is 100 or 1000 (circles), or the analytical prediction according to equation (11). Error bars indicate the standard error of the mean across 1000 replicates. Shown are results for different initial frequencies of heterozysity H 0. For all results shown, .
A FINITE NUMBER OF RECOMBINATION SITES
To represent a chromosome consisting of a finite number of genomic elements, we model the chromosome as a bitstring, where a 0 indicates a chromosomal segment of type P, and a 1 indicates a chromosomal segment of type Q. To approximate an infinite population we use a population size of 100,000 (simulation results using a population size of 100,000 are very close to our predictions assuming an infinite population size). The mean number of junctions in the stochastic simulations closely follow our analytical estimates (Fig. 4, middle column), for all chromosome lengths considered here. Again we observe that for strongly skewed ancestral proportions (), the maximum number of junctions is lower (as expected following eq. 8), and the maximum is reached within a shorter timeframe. When we simulate using a finite population size and a finite number of genomic elements (Fig. 4, right column), we observe similar patterns, where the number of junctions approaches a maximum value, albeit that this maximum value is lower than for an infinite population. Furthermore we observe that mean results of simulations are highly similar to our analytical expectations following equation (11). We have shown here only results for , which ensures that limitation in the accumulation of junctions is the result of both the effect of a finite chromosome size, and of a finite population size (see equation (A14) in the Appendix). For , our results reduce to the infinite chromosome case.
THE DISTRIBUTION OF JUNCTIONS IN THE POPULATION
So far, we have focused on the mean number of junctions within the population. Apart from the mean, the distribution of junctions within the population has some interesting properties as well. Most interestingly, the number of chromosomes with an even and with an odd number of junctions is not distributed equally. We find that for increasing deviations from , the frequency distribution of junctions starts to resemble more and more a ”stegosaurus” pattern, where the high peaks are associated with chromosomes with an even number of junctions, and the low peaks (the back of the stegosaurus) are associated with chromosomes with an odd number of junctions (See Fig. 5A). Furthermore, we find that the degree of “stegosaurusness,” for example the relative frequency of chromosomes with an even number of junctions, is directly proportional to p (Fig. 5B). The number of even and uneven junctions could therefore potentially be used as an independent estimator of p. However, empirically estimating the exact number of junctions per chromosome is hard, and errors in estimating the number of junctions smoothens out the distribution, making the relative frequency of even chromosomes an unreliable predictor of p. Furthermore, due to this smoothing, for empirical applications it seems better to focus on the mean of the distribution (as described in the previous and next section), rather than focus on the peculiarities of this distribution. Lastly, although the disparity between chromosomes containing even and uneven numbers of junctions could introduce errors when estimating the mean number of junctions at t, we do not find such errors (See Fig. 5C), most likely because we focus here on the mean, rather than variation round the mean. This shows that although from a mathematical viewpoint interesting patterns appear, for practical purposes it is possible to ignore these.
Figure 5.
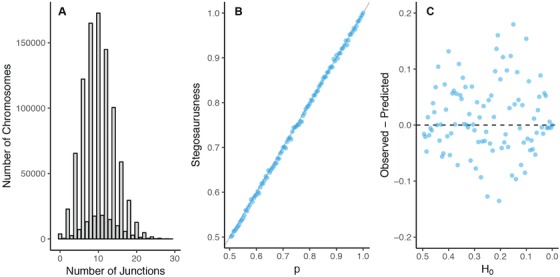
(A) Example distribution of number of chromosomes with n junctions. Results are shown for , , , at . Results show the “stegosaurus” pattern, where chromosomes with an even number of junctions are more frequent than chromosomes with an odd number of junctions. (B) Linear relationship between the degree of “stegosaurusness” and the frequency of the most common ancestor in the hybrid swarm, p. Results are shown for , , at . (C) Inaccuracy in the estimate of the maximum number of blocks K, depending on the initial heterozygosity . Although the degree of stegosaurusness increases with decreasing H 0, error in the estimate of K, and overall estimate in the accumulation of junctions, does not increase. Points are the mean of 10 replicates.
A FINITE NUMBER OF MARKERS
A finite number of recombination sites can also be interpreted as a number of markers uniformly spaced across the genome. In reality, however, markers are seldom placed uniformly spaced across the genome. In this section, we numerically explore the impact of having randomly spaced markers along the genome. We simulated markers by simulating a chromosome consisting of an infinite number of recombination sites (as described above), and then superimposing a fixed (random) marker distribution. For each marker position, we assessed the ancestral state by checking the transition direction at the junctions surrounding the marker position.
We performed individual‐based simulations for , and 1000, , and explored marker numbers , and 5000. Per parameter combination we simulated 100 random marker distributions, and per marker distribution, 100 replicate simulations. We find (Fig. 6A and D, dots) that the number of detected junctions is lower than expected using K based on evenly spaced markers (eq. 12) (Fig. 6, A, D, dashed line). Because K is the number of junctions obtained in the limit , we can substitute the maximum number of junctions obtained at the end of the simulations (e.g., a numerical estimate for K), and plot the expected number of junctions over time following the generalized framework (eq. 13) (Fig. 6A and D, dashed lines). We find that the simulation data follows the expected number of junctions reasonably well. Nevertheless, it appears that in the initial generations, the detected number of junctions is lower than that expected under this adjusted framework (Fig. 6B and E). Indeed, we find (Fig. 6B and E) that the detected number of junctions divided by the number of junctions expected using the value of K estimated from the simulations, tends to one as t tends to large values (as expected), but is lower in the initial stages of hybridization, and can be as low as 0.8. Nevertheless, we find that the observed values of K (e.g., the number of junctions at the end of the simulation), and those expected for the respective R values, correlate strongly (Fig. 6, right panel). For we find a slope of 0.97 (), for we find a slope of 0.88 (, figure not shown) and for we find a slope of 0.84 (). Hence, we find that the difference between the expected and observed value of K increases with increasing N. This seems to suggest an interaction between population size and the number of randomly distributed markers that we cannot account for. If the effect of randomly distributed markers follows generalized underlying dynamics, we expect to be able to rescale obtained junction accumulation curves in a similar fashion as shown in Figure 2 and in Section “Generalized Junction Dynamics,” for example by first rescaling the number of junctions by the obtained maximum, and then rescaling time by the initial slope. We find that after rescaling, the curves do not line up (results in the Supplementary Material), suggesting that there are effects affecting the number of detected junctions other than a fixed penalty of junction detection. Nevertheless, as R increases, the approximation of an even marker distribution becomes increasingly accurate, which is demonstrated by the close fit of , , as shown in Figure 6. This might also reflect the decaying impact of a finite number of markers, which suggests that the impact of a finite number of markers is less important if (derivation in the Appendix).
Figure 6.

Shown are results for two different population sizes: (A–C) and (D–F). (A and C) The number of junctions over time (, ). The black line indicates the true number of junctions, assuming an infinite number of recombination sites. The dashed lines indicate the expected number of junctions for a chromosome consisting of a finite number of recombination sites, where , and 5000, respectively. Dots indicate the mean number of junctions from simulations using randomly spaced markers across the chromosome. The solid line indicates the expected number of junctions, using the generalized framework with K equal to the maximum mean number of junctions from simulations using random markers. (B and E) Correlation between the observed value of K, and the expected value for K, with , and 5000, and (B), and (E). R 2 values are for both population sizes above 0.99. Slopes are 0.97, and 0.84 for and , respectively. (C and F) The ratio between the mean number of junctions with , and 5000 in simulations using randomly spaced markers, and the expected number of junctions using the universal framework with K equal to the maximum mean number of junctions from simulations using random markers.
Discussion
Although the theory of junctions dates back to Fisher (1949) and has been developed toward modern analysis of hybrid zones (Barton 1983; Baird 1995) empirical studies on the evolution of junctions in admixed lineages are still scarce. This may be partly owed to the fact that genomic data and relevant study systems are only starting to become available. Moreover, existing methods were challenging to use. Whereas previous work on the theory of junctions assumes a chromosome that consists of an infinite number of recombination sites, we take into account a finite number of recombination sites, and a nonzero probability of recurrent recombination events (eq. 7). This accommodates study systems where the recombination landscape is not homogenous and where the number of markers that are informative of ancestry is limited. We developed a novel framework that describes the accumulation of junctions over time as a generalized function only dependent on the number of junctions obtained at (eq. 13). Furthermore, we have derived general expressions that provide the upper limit for inferring the age of hybridization, given the number of molecular markers used (R) and the population size (N). Lastly, we have used this general framework to study the effect of randomly distributed markers as compared to evenly distributed markers.
Our framework can serve as a neutral model of the accumulation of ancestry junctions in studies that seek to analyze the early stages of hybrid speciation and recent admixture, which are particularly informative of evolutionary processes (Nolte and Tautz 2010; Gompert and Buerkle 2016). The junction framework that we have presented provides a neutral expectation but it considers only certain effects of drift. Drift causes allele frequencies to change over time. Initially these changes are coupled among linked markers, but they become more and more independent through consecutive rounds of recombination. As a result, within genome variation in allele frequencies increases over time (Stemshorn et al. 2011) that might impact junction formation. For simplicity, we have not taken into account the effect of inter and intrachromosomal variation in allele frequencies on junction formation, and have only modeled the effects of population size on drift, as described by Crow and Kimura (Crow and Kimura 1970). However, effects of recombination on drift were explicitly modeled in the individual‐based simulations. It is reassuring that the mean dynamics of the simulations agree well with our mathematical model (Fig. 6). Nevertheless, we acknowledge that for a complete and full description of neutral junction dynamics, the effect of within genome variation in allele frequencies on junction formation should be taken into account.
Here, we summarize properties of our method and we discuss processes that may cause deviations from the model that may be relevant to interpret results. Our extension of the theory of junctions accurately describes the expected number of detected junctions, provided that the markers are regularly spaced across the chromosome. Unfortunately, regular marker spacing can be difficult to obtain in reality. We have therefore simulated the effect of randomly spaced markers, while keeping the overall marker density across the chromosome fixed. We found that the amount of junctions that remained undetected varied over time, and that applying a fixed ratio to correct the expected number of junctions did not resolve this issue. In the absence of an explicit description of the number of detected junctions over time, we have shown how to obtain a numerical approximation by using simulations to estimate the value of K within our generalized framework. Although this approximation still tends to overestimate the number of junctions at intermediate timescales, estimates are much closer than predictions from the evenly spaced markers model. The overestimation of the approximation seems to be the result of an interaction between the number of markers, the number of junctions and the population size. This is in line with previous findings by MacLeod et al. (2005), who found that the ratio between markers and junctions (e.g., ) was the main factor driving the detection probability. We would like to note, that the mismatch between our predictions and the observed number of junctions due to the difference between evenly and randomly spaced markers reduces significantly as the number of markers (R) increases (see Fig. 6). Note also, that although it has become increasingly feasible to analyze large numbers of markers, alleles in empirical data are often not fully ancestry informative. The ancestry of genomic blocks can still be determined with a degree of uncertainty (see for instance Corbett‐Detig and Nielsen (2017)), but problems arising from ancestry uncertainty are outside the scope of the current work.
Processes that cause deviations from the neutral model fall into two general categories: either processes acting upon the underlying genomic content, or processes that affect population dynamics. When a genomic region from only one parent is under selection this reduces heterozygosity and therefore recombination events in this region, as individuals recombined in this region are selected against (Kimura 1956; Lewontin and Hull 1967). Hence, selection can slow down the formation of new junctions. Future work could focus on the minimal level of selection to offset neutral junction dynamics, or whether deviations from neutral junction dynamics can be used to identify genomic areas that are under selection. However, caution should be taken as the signal of selection may be lost due to overshadowing effects of drift due to limited population size, or changes in population demography (see also below).
Chromosomes share the same evolutionary history but constitute separate genetic elements. Hence, it would be conceivable that a comparison of the number of junctions could reveal interesting differences at the level of chromosomes. Under neutral dynamics, the number of junctions per chromosome is expected to be approximately Poisson distributed. Although we have a firm understanding of the expected mean of this distribution, an understanding of the expected variation around the mean has so far only been accessible through simulation (Chapman and Thompson 2002, 2003). Using our simulations, we have also explored how variation in the number of junctions changes over time (see Supplementary Material). It appears that the variation does not follow straightforward dynamics, especially if the population is finite in size. Furthermore, the variation appears unrelated to the mean, suggesting that a Poisson approximation is invalid (see also (Chapman and Thompson 2002, 2003)). We observe that variation increases initially until a tipping point is reached, where the increase in variation due to the creation of new junctions is offset by the reduction in variation due to fixation as a result of finite population size. After this point, variation decreases until all junctions are fixed in the population. The exact mathematical description of the expected variance of the number of junctions among chromosomes currently lies outside our grasp.
A non‐uniform recombination rate across the physical chromosome could also cause deviations from neutral junction dynamics. Empirical work has shown that recombination rates are often not equal across the chromosome, but may be increased towards the peripheral ends of the chromosome (Lukaszewski and Curtis 1993; Pan et al. 2012; Roesti et al. 2012)). As long as the number of recombination sites is infinite in the chromosome, the exact shape of the recombination landscape has no effect on junction dynamics. For a chromosome with a finite number of recombination sites, however, junction dynamics change (see the Supplementary Material for a demonstration of increased recombination toward the peripheral ends). If some sites have an increased probability of recombination compared to others, recombination is more likely to occur at a site that has already experienced a recombination event before. As a result, the formation of new junctions is slower than expected under uniform recombination. Interestingly, the maximum number of junctions that can be reached remains unaffected.
Population level processes are also expected to affect junction dynamics. Firstly, deviations from having a constant‐population size over time are expected to cause deviations from our universal junction framework. A natural extension of this study would be to include either exponentially or logistically growing populations to mimic real‐life dynamics more closely. In exponentially growing populations, the average heterozygosity does not change (Crow and Kimura 1970), which results in dynamics that resemble an infinite population. Similarly, for logistically growing populations, during the initial growth phase, junction dynamics are expected to closely resemble junction dynamics in an infinite population. We do have to take into account drift effects even though a population (hybrid lineage) is growing exponentially when this involves a wave front invasion of an open habitat or space (Hallatschek et al. 2007). This could be particularly relevant to cases of hybrid speciation that involve the segregation of a hybrid lineage into a habitat that is not available to the parental species (Mallet 2007; Nolte and Tautz 2010). How drift and the rate of growth interact and influence junction dynamics remains the subject of future study. Population subdivision, founder effects, a bottleneck or a permanent decrease in population size could speed up fixation of junctions in the population through drift. Accordingly, the average heterozygosity decreases faster than expected, and the accumulation of new junctions is slowed down. Furthermore, the maximum number of junctions decreases as well (following eq. 12) although previously accumulated “excess” junctions might not be lost after a population change. Thus, depending on the speed and timing of the decrease, individuals in the final population potentially display a larger number of junctions than expected from the current population size, retaining junctions fixed in the population before the population decreased in size.
An important population level process that affects junction dynamics is given by secondary introgression of genetic material from parental populations after the hybrid lineage has emerged. This can be expected to occur in young systems studied in the context of hybrid speciation (Stemshorn et al. 2011; Trier et al. 2014) and introduces parental genomic blocks into the population that have not yet recombined. It leads to an apparent reduction of the number of junctions (Pool and Nielsen 2009) effectively turning back time in an analysis of junctions if not taken into account. Secondary introgression introduces haplotype blocks that are disproportionally large, compared to the standing haplotype block size distribution and these blocks are expected to be randomly distributed across the genome as opposed to larger blocks that were fixed through selection (Baird 1995; Ungerer et al. 1998). The haplotype block size distribution therefore provides information that can help to assess whether secondary introgression leaves a strong footprint in an admixed lineage (Barton 1983; Baird 1995; Ungerer et al. 1998; Pool and Nielsen 2009).
We expect that there are more processes that can affect the accumulation of junctions, including, but not limited to, sib mating, interference between recombination events, chromosomal inversion polymorphisms, mutation, meiotic drive, segregation distortion, and heterochiasmy. All processes mentioned above cause a slowdown in the accumulation of junctions. In contrast, the formation of new junctions could speed up under balancing selection, when the combination of alleles from both parents provides a selective advantage. The resulting overdominance favors a heterozygous genotype (Maruyama and Nei 1981), in turn favoring the formation of new junctions. Likewise, positive epistasis among linked loci could favor a combination of alleles of different parents. As a result, recombination between these loci would be selected for, speeding up junction formation. With the exception of overdominance or positive epistasis, this suggests that the additions to the theory of junctions that we have presented here provides an upper speed limit to junction dynamics. Thus, estimates of the onset of hybridization using our framework reflect the youngest age of the hybrids in question. Our framework will help to identify patterns of admixed genome evolution and provide insights in the early evolutionary history of hybrid lineages.
CODE AVAILABILITY
Code used for the individual‐based simulations, and code to evaluate relevant equations has been made available in the cran‐R package “junctions” (https://CRAN.R-project.org/package=junctions), and has been included in the Supplementary Information as stand‐alone R code.
Associate Editor: R. Azevedo
Handling Editor: M. Servedio
Supporting information
Deriving the Maximum Accurate Time.
Figure 1. Maximum Accurate Time results.
Figure 2. Individual based simulation results for an increased recombination rate to the peripheral ends of the chromosome.
Figure 3. Rescaling junction accumulation for random markers, analogous to figure 2 in the main text.
Figure 4. Individual based simulation results showing the variation in number of blocks within the population.
AUTHOR CONTRIBUTIONS
T.J., A.W.N. and A.T. designed the project, T.J. and A.T. developed the mathematical framework, T.J. performed the numerical analysis and individual‐based simulations. T.J. wrote the first version of the manuscript upon which A.W.N. and A.T. improved.
ACKNOWLEDGMENTS
We thank S.J.E. Baird for helpful comments and for directing us toward the maximum packing density of junctions and the disparity between chromosomes with even and odd numbers of junctions. Furthermore, we thank N.H. Barton, L. Odenthal‐Hesse and Y. Pichugin for helpful comments and discussion. We acknowledge support through the Max Planck Society. A.W.N. was supported through funding from the ERC starting grant EVOLMAPPING. T.J. is grateful for use of the computational cluster ADA of the Max Planck Institute for Evolutionary Biology, Plön. The authors declare that there is no conflict of interest regarding the publication of this article.
DATA ARCHIVING
Data files archival location is https://doi.org/10.5061/dryad.c0t6s.
DERIVING THE UNIFYING FRAMEWORK
Generally, we can infer that the maximum number of junctions is dependent on p, N, R, and C, as do the time dynamics required to reach this maximum. Hence, we can describe the number of junctions relative to the number of junctions at , which we define here as K. During meiosis, the average number of junctions in the most ideal case can increase with γ junctions. There might be limitations, dependent on p, N, R or the number of already existing junctions. As such, we make the ansatz
| (A1) |
where γ is the maximum growth rate and λ encompasses all factors limiting the formation of new junctions. This includes, but is not limited to, factors induced by a finite population size N and by a finite number of recombination spots R. Defining , we can rescale time in equation (A1) such that
| (A2) |
Measuring the number of junctions in terms of their asymptotic values, , we obtain
| (A3) |
The solution of equation (A3) is of the form
| (A4) |
(Please note that we refer to the number of junctions in continuous time as and the number of junctions in discrete time as ). We can find the scaling of time by solving
| (A5) |
By definition is zero, which allows us to calculate β
| (A6) |
Returning to discrete time, we can formulate the universal dynamics as
| (A7) |
For , this converges to K, and for this is equal to zero. Equation (A7) provides us with a general scalable equation where all junction dynamics are described in terms of K and J(1).
To implement the unifying equation (A7), we only need to know K and J(1). Since , we obtain from equation (10) . Thus, regardless whether the chromosome contains a finite or infinite number of recombination sites, and regardless of whether the population is finite or infinite, we find that the initial change is always , and that . This also makes intuitive sense: in the first generation, none of the factors that limit recombination as a result of finite population size, or finite chromosome size come into play yet. When the population is finite, the formation of new blocks is limited by recombination taking place at a recombination spot where in a previous generation recombination has already taken place. However, in the first generation, all chromosomes are nonrecombined, and finite population effects have no effect yet. When the number of recombination sites is finite, the formation of new blocks is limited by the maximum packing density of junctions. However, in the first generation, no junctions are apparent yet, and this effect is negligible. Concluding, we can formulate our general haplotype framework as (eq. 13 in the main text):
| (A8) |
Importance of finite chromosome length
Our universal framework introduces the possibility to take into account a finite number of recombination sites. Previous work has inferred junction dynamics for chromosomes with an infinite number of recombination sites. An important question to be answered is for which values of R our universal framework approaches previous results.
For small , we can approximate our unifying framework (eq. A8 in the Appendix, and eq. 13 in the maintext) by
| (A9) |
Where the last term describes the limitation in the number of junctions dependent on K. For , we recover . Substituting the upper limit for finite R, in equation (A9), we obtain
| (A10) |
We expect that the impact of R is negligible compared to the linear term in t if the second term of equation (A10) is much smaller than the first term. This implies that
| (A11) |
which for is approximately ; the approximation of an infinite R is good as long as the time in generations is much shorter than twice the length of the chromosome (in genetic elements), divided by the size in Morgan.
When both R and N are finite, we can substitute the appropriate K (eq. 12) into equation (A9), and obtain
| (A12) |
Comparing this with the approximation for a finite population (but an infinite number of recombination spots), where , we see that
| (A13) |
Differences induced by a finite R (e.g., differences between equations (A12) and (A13)) are then due to the term in equation (A12), and the impact of finite R thus decreases rapidly with increasing R. Furthermore, the impact of R on the number of junctions, compared to the impact of N, is negligible if:
| (A14) |
LITERATURE CITED
- Abbott, R. , Albach D., Ansell S., Arntzen J. W., Baird S. J. E., Bierne N., Boughman J., Brelsford A., Buerkle C. A., Buggs R., et al. 2013. Hybridization and speciation. J. Evol. Biol. 26:229–246. [DOI] [PubMed] [Google Scholar]
- Arbeithuber, B. , Betancourt A. J., Ebner T., and Tiemann‐Boege I.. 2015. Crossovers are associated with mutation and biased gene conversion at recombination hotspots. Proc. Natl. Acad. Sci. 112:2109–2114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baird, S . 1995. A simulation study of multilocus clines. Evolution 49:1038–1045. [DOI] [PubMed] [Google Scholar]
- Baird, S. , Barton N., and Etheridge A.. 2003. The distribution of surviving blocks of an ancestral genome. Theoret. Popul. Biol. 64:451–471. [DOI] [PubMed] [Google Scholar]
- Barton, N . 2001. The role of hybridization in evolution. Mol. Ecol. 10:551–568. [DOI] [PubMed] [Google Scholar]
- Barton, N. H . 1983. Multilocus clines. Evolution 37:454–471. [DOI] [PubMed] [Google Scholar]
- Bennett, J . 1953. Junctions in inbreeding. Genetica 26:392–406. [DOI] [PubMed] [Google Scholar]
- Bhat, S. , Amundsen P.‐A., Knudsen R., Gjelland K. Ø., Fevolden S.‐E., Bernatchez L., and Præbel K.. 2014. Speciation reversal in European whitefish (Coregonus lavaretus (l.)) caused by competitor invasion. PLoS ONE 9:e91208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buerkle, C. A. , Morris R. J., Asmussen M. A., and Rieseberg L. H.. 2000. The likelihood of homoploid hybrid speciation. Heredity 84:441–451. [DOI] [PubMed] [Google Scholar]
- Buerkle, C. A. , and Rieseberg L. H.. 2008. The rate of genome stabilization in homoploid hybrid species. Evolution 62:266–275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chapman, N. , and Thompson E.. 2003. A model for the length of tracts of identity by descent in finite random mating populations. Theoret. Popul. Biol. 64:141–150. [DOI] [PubMed] [Google Scholar]
- Chapman, N. H. , and Thompson E. A.. 2002. The effect of population history on the lengths of ancestral chromosome segments. Genetics 162:449–458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Corbett‐Detig, R. , and Nielsen R.. 2017. A hidden markov model approach for simultaneously estimating local ancestry and admixture time using next generation sequence data in samples of arbitrary ploidy. PLoS Genet. 13:e1006529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crow, J. F. , and Kimura M.. 1970. An introduction to population genetics theory. Harper and Row, New York. [Google Scholar]
- Edmands, S. , Feaman H., Harrison J., and Timmerman C.. 2005. Genetic consequences of many generations of hybridization between divergent copepod populations. J. Heredity 96:114–123. [DOI] [PubMed] [Google Scholar]
- Fisher, R. A. 1949. The theory of inbreeding. Oliver and Boyd. [Google Scholar]
- Fisher, R. A 1954. A fuller theory of “junctions” in inbreeding. Heredity 8:187–197. [Google Scholar]
- Fisher, R. A 1959. An algebraically exact examination of junction formation and transmission in parent‐offspring inbreeding. Heredity 13:179–186. [Google Scholar]
- Gale, J . 1964. Some applications of the theory of junctions. Biometrics 20:85–117. [Google Scholar]
- Gerton, J. L. , DeRisi J., Shroff R., Lichten M., Brown P. O., and Petes T. D.. 2000. Global mapping of meiotic recombination hotspots and coldspots in the yeast Saccharomyces cerevisiae . Proc Natl. Acad. Sci. 97:11383–11390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gompert, Z. , and Buerkle C. A.. 2016. What, if anything, are hybrids: enduring truths and challenges associated with population structure and gene flow. Evol. Appl. 9:909–923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grant, V. 1981. Plant speciation. Columbia Univ. Press, Columbia. [Google Scholar]
- Gravel, S . 2012. Population genetics models of local ancestry. Genetics 191:607–619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hallatschek, O. , Hersen P., Ramanathan S., and Nelson D. R.. 2007. Genetic drift at expanding frontiers promotes gene segregation. Proc. Natl. Acad. Sci. 104:19926–19930. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hellenthal, G. , Busby G. B., Band G., Wilson J. F., Capelli C., Falush D., and Myers S.. 2014. A genetic atlas of human admixture history. Science 343:747–751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kimura, M . 1956. A model of a genetic system which leads to closer linkage by natural selection. Evolution 10:278–287. [Google Scholar]
- Krehenwinkel, H. , and Tautz D.. 2013. Northern range expansion of european populations of the wasp spider Argiope bruennichi is associated with global warming–correlated genetic admixture and population‐specific temperature adaptations. Mol. Ecol. 22:2232–2248. [DOI] [PubMed] [Google Scholar]
- Lamichhaney, S. , Han F., Webster M. T., Andersson L., Grant B. R., and Grant P. R.. 2017. Rapid hybrid speciation in Darwin's finches. Science P. eaao4593. [DOI] [PubMed]
- Lewontin, R. , and Hull P.. 1967. The interaction of selection and linkage iii synergistic effect of blocks of genes. Der Züchter 37:93–98. [Google Scholar]
- Liang, M. , and Nielsen R.. 2014. The lengths of admixture tracts. Genetics 197:953–967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lukaszewski, A. , and Curtis C.. 1993. Physical distribution of recombination in b‐genome chromosomes of tetraploid wheat. Theoret. Appl. Genet. 86:121–127. [DOI] [PubMed] [Google Scholar]
- Mackiewicz, D. , de Oliveira P. M. C., de Oliveira S. M., and Cebrat S.. 2013. Distribution of recombination hotspots in the human genome–a comparison of computer simulations with real data. PloS ONE 8:e65272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacLeod, A. , Haley C., Woolliams J., and Stam P.. 2005. Marker densities and the mapping of ancestral junctions. Genet. Res. 85:69–79. [DOI] [PubMed] [Google Scholar]
- Mallet, J . 2007. Hybrid speciation. Nature 446:279–283. [DOI] [PubMed] [Google Scholar]
- Maruyama, T. , and Nei M.. 1981. Genetic variability maintained by mutation and overdominant selection in finite populations. Genetics 98:441–459. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McTavish, E. J. , and Hillis D. M.. 2014. A genomic approach for distinguishing between recent and ancient admixture as applied to cattle. J. Heredity 105:445–456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Myers, S. , Bottolo L., Freeman C., McVean G., and Donnelly P.. 2005. A fine‐scale map of recombination rates and hotspots across the human genome. Science 310:321–324. [DOI] [PubMed] [Google Scholar]
- Nolte, A. W. , Freyhof J., Stemshorn K. C., and Tautz D.. 2005. An invasive lineage of sculpins, cottus sp. (pisces, teleostei) in the rhine with new habitat adaptations has originated from hybridization between old phylogeographic groups. Proc. R. Soc. B 272:2379–2387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nolte, A. W. , and Tautz D.. 2010. Understanding the onset of hybrid speciation. Trends Genet. 26:54–58. [DOI] [PubMed] [Google Scholar]
- Pan, Q. , Ali F., Yang X., Li J., and Yan J.. 2012. Exploring the genetic characteristics of two recombinant inbred line populations via high‐density snp markers in maize. PLoS ONE 7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Payseur, B. A. , and Rieseberg L. H.. 2016. A genomic perspective on hybridization and speciation. Mol. Ecol. 25:2337–2360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pool, J. E. , and Nielsen R.. 2009. Inference of historical changes in migration rate from the lengths of migrant tracts. Genetics 181:711–719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roesti, M. , Hendry A. P., Salzburger W., and Berner D.. 2012. Genome divergence during evolutionary diversification as revealed in replicate lake–stream stickleback population pairs. Mol. Ecol. 21:2852–2862. [DOI] [PubMed] [Google Scholar]
- Schumer, M. , Cui R., Powell D. L., Rosenthal G. G., and Andolfatto P.. 2016. Ancient hybridization and genomic stabilization in a swordtail fish. Mol. Ecol. 25:2661–2679. [DOI] [PubMed] [Google Scholar]
- Schumer, M. , Rosenthal G. G., and Andolfatto P.. 2014. How common is homoploid hybrid speciation? Evolution 68:1553–1560. [DOI] [PubMed] [Google Scholar]
- Singhal, S. , Leffler E. M., Sannareddy K., Turner I., Venn O., Hooper D. M., Strand A. I., Li Q., Raney B., Balakrishnan C. N., et al. 2015. Stable recombination hotspots in birds. Science 350:928–932. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smagulova, F. , Gregoretti I. V., Brick K., Khil P., Camerini‐Otero R. D., and Petukhova G. V.. 2011. Genome‐wide analysis reveals novel molecular features of mouse recombination hotspots. Nature 472:375–378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stam, P . 1980. The distribution of the fraction of the genome identical by descent in finite random mating populations. Genet. Res. 35:131–155. [Google Scholar]
- Stemshorn, K. C. , Reed F. A., Nolte A. W., and Tautz D.. 2011. Rapid formation of distinct hybrid lineages after secondary contact of two fish species (cottus sp.). Mol. Ecol. 20:1475–1491. [DOI] [PubMed] [Google Scholar]
- Taylor, E. , Boughman J., Groenenboom M., Sniatynski M., Schluter D., and Gow J.. 2006. Speciation in reverse: morphological and genetic evidence of the collapse of a three‐spined stickleback (Gasterosteus aculeatus) species pair. Mol. Ecol. 15:343–355. [DOI] [PubMed] [Google Scholar]
- Trier, C. N. , Hermansen J. S., Sætre G.‐P., and Bailey R. I.. 2014. Evidence for mito‐nuclear and sex‐linked reproductive barriers between the hybrid italian sparrow and its parent species. PLoS Genet. 10:e1004075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ungerer, M. C. , Baird S. J., Pan J., and Rieseberg L. H.. 1998. Rapid hybrid speciation in wild sunflowers. Proc. Natl. Acad. Sci. 95:11757–11762. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vonlanthen, P. , Bittner D., Hudson A. G., Young K. A., Müller R., Lundsgaard‐Hansen B., Roy D., Piazza S. Di, Largiadèr C. R., and Seehausen O.. 2012. Eutrophication causes speciation reversal in whitefish adaptive radiations. Nature 482:357–362. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Deriving the Maximum Accurate Time.
Figure 1. Maximum Accurate Time results.
Figure 2. Individual based simulation results for an increased recombination rate to the peripheral ends of the chromosome.
Figure 3. Rescaling junction accumulation for random markers, analogous to figure 2 in the main text.
Figure 4. Individual based simulation results showing the variation in number of blocks within the population.


